Effects of Printing Paths on Compressive Strength of 3D-Printed Continuous Fiber-Reinforced Composite Lattice Unit Cell
Abstract
1. Introduction
2. Compression Test
2.1. Specimen Preparation
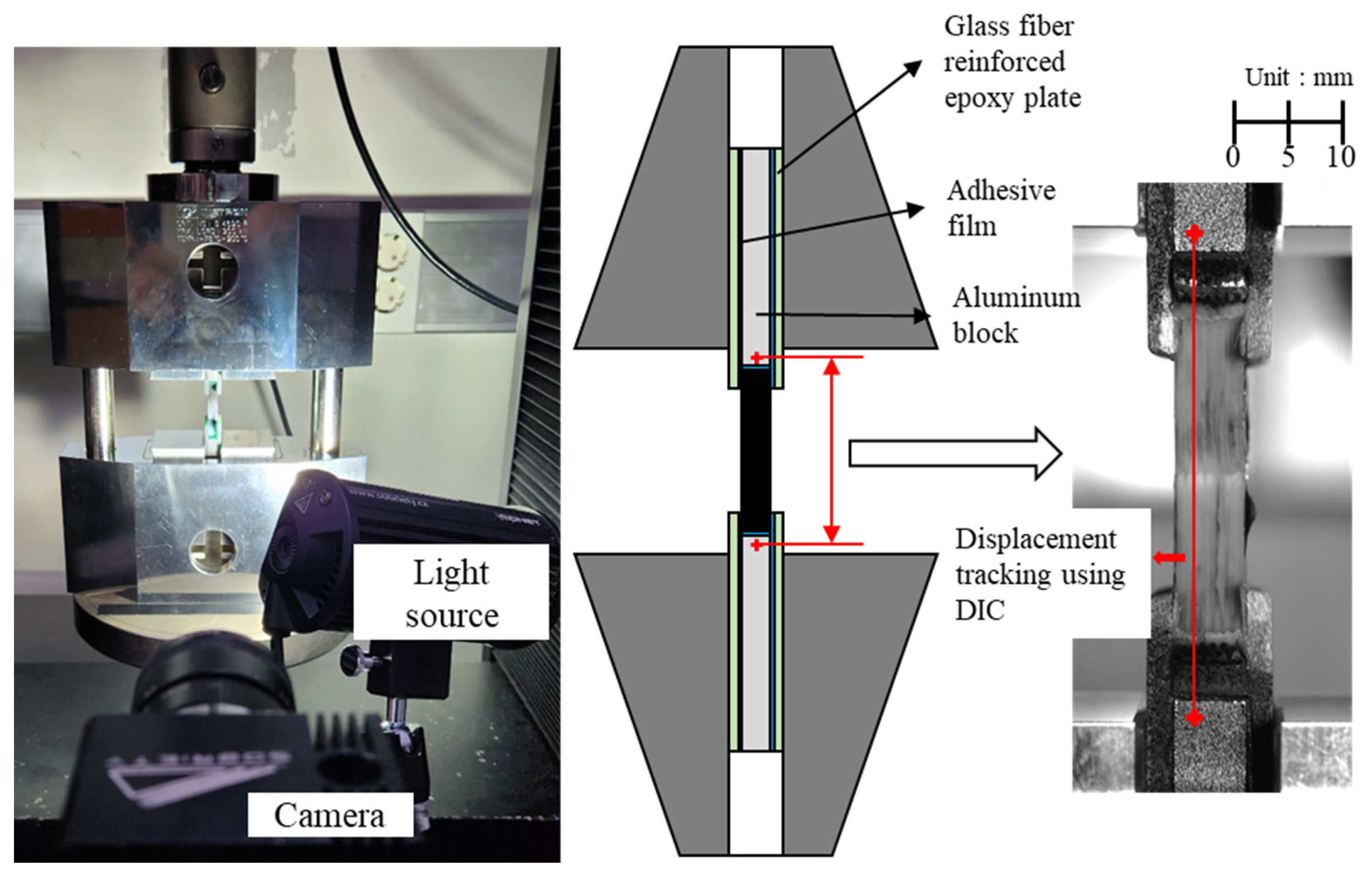
2.2. Compression Test Procedure
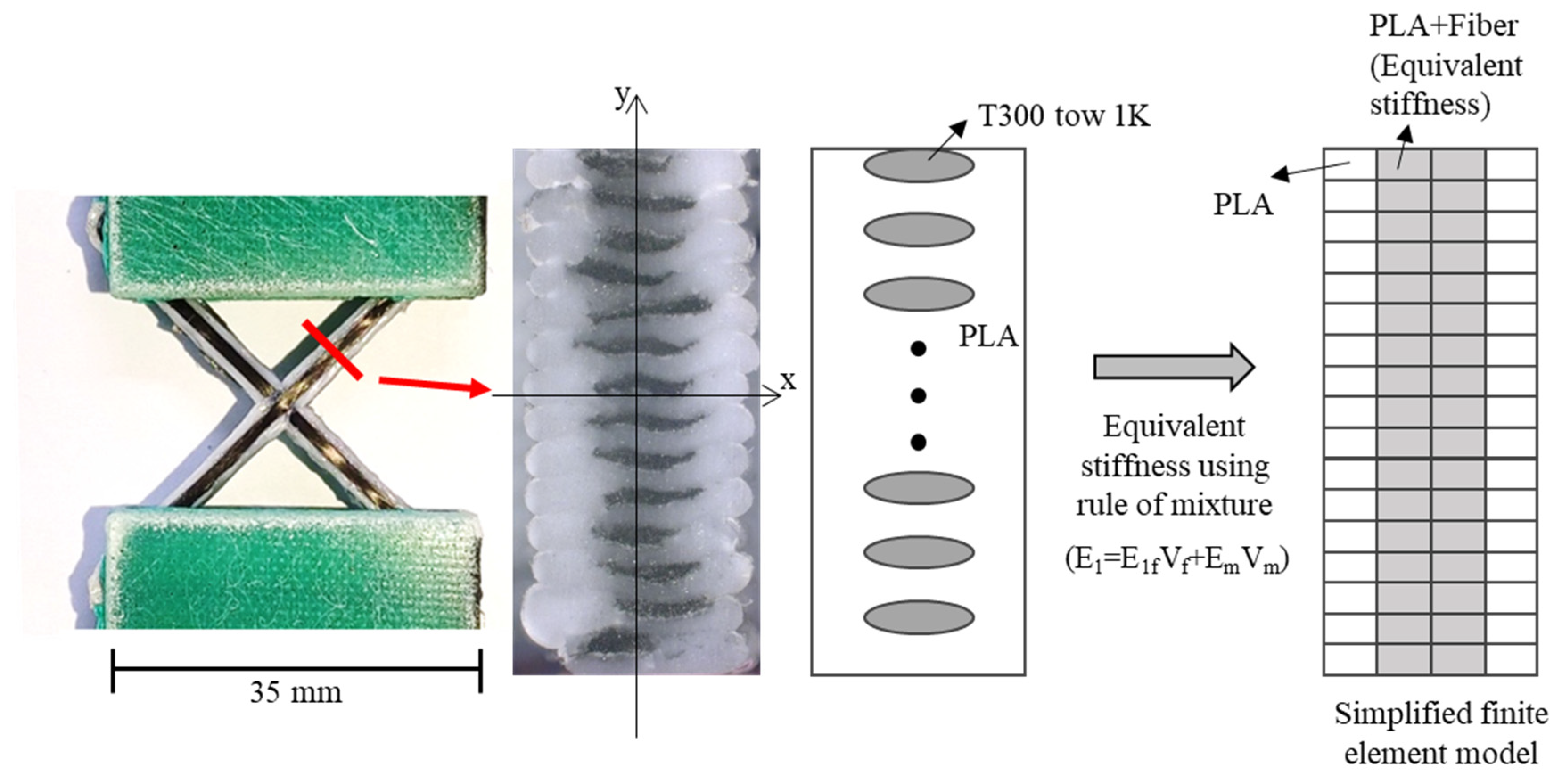
3. Finite Element Analysis
4. Results and Discussion
4.1. Test Results
4.2. Design Criterion Using Knockdown Factor
4.3. Bifurcation Buckling Analysis for Path B
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, T.; Chen, Y.; Hu, X.; Li, Y.; Wang, L. Exploiting negative Poisson’s ratio to design 3D-printed composites with enhanced mechanical properties. Mater. Des. 2018, 142, 247–258. [Google Scholar] [CrossRef]
- Zhou, J.; Liu, H.; Dear, J.P.; Falzon, B.G.; Kazancı, Z. Comparison of different quasi-static loading conditions of additively manufactured composite hexagonal and auxetic cellular structures. Int. J. Mech. Sci. 2023, 244, 108054. [Google Scholar] [CrossRef]
- Teng, X.C.; Ren, X.; Zhang, Y.; Jiang, W.; Pan, Y.; Zhang, X.G.; Zhang, X.Y.; Xie, Y.M. A simple 3D re-entrant auxetic metamaterial with enhanced energy absorption. Int. J. Mech. Sci. 2022, 229, 107524. [Google Scholar] [CrossRef]
- He, P.; Wang, S.; Zhang, M.; Sang, L.; Tong, L.; Hou, W. Compression performance of 3D-printed thermoplastic auxetic structures. Thin Walled Struct. 2024, 197, 111558. [Google Scholar] [CrossRef]
- Zhang, H.; Zhou, H.; Zhou, Z.; Zeng, H.; Zhang, X.; Yang, J.; Lei, H.; Han, F. Energy absorption diagram characteristic of metallic self-supporting 3D lattices fabricated by additive manufacturing and design method of energy absorption structure. Int. J. Solids Struct. 2021, 226, 111082. [Google Scholar] [CrossRef]
- Günaydın, K.; Rea, C.; Kazancı, Z. Energy absorption enhancement of additively manufactured hexagonal and re-entrant (auxetic) lattice structures by using multi-material reinforcements. Addit. Manuf. 2022, 59, 103076. [Google Scholar] [CrossRef]
- Zhang, X.G.; Ren, X.; Jiang, W.; Zhang, X.Y.; Luo, C.; Zhang, Y.; Xie, Y.M. A novel auxetic chiral lattice composite: Experimental and numerical study. Compos. Struct. 2022, 282, 115043. [Google Scholar] [CrossRef]
- Cheng, P.; Peng, Y.; Li, S.; Rao, Y.; Le Duigou, A.; Wang, K.; Ahzi, S. 3D printed continuous fiber reinforced composite lightweight structures: A review and outlook. Compos. Part B Eng. 2023, 250, 110450. [Google Scholar] [CrossRef]
- Ichihara, N.; Ohno, S.; Ueda, M.; Deshpande, V.S. High axial compressive strength in 3D-printed continuous carbon fiber reinforced thermoplastics by controlling printing forces. Compos. Part B Eng. 2025, 250, 112052. [Google Scholar] [CrossRef]
- Pascual-González, C.; Martín, P.S.; Lizarralde, I.; Fernández, A.; León, A.; Lopes, C.S.; Fernández-Blázquez, J.P. Post-processing effects on microstructure, interlaminar and thermal properties of 3D printed continuous carbon fibre composites. Compos. Part B Eng. 2021, 210, 108652. [Google Scholar] [CrossRef]
- Touchard, F.; Chocinski-Arnault, L.; Fournier, T.; Magro, C.; Lafitte, A.; Caradec, A. Interfacial adhesion quality in 3D printed continuous CF/PA6 composites at filament/matrix and interlaminar scales. Compos. Part B Eng. 2021, 218, 108891. [Google Scholar] [CrossRef]
- Zhu, W.; Fu, L.; Tian, X.; Zhi, Q.; Hou, Z.; Zhang, Z.; Wang, N.; Liu, T.; Sun, H.; Matsuzaki, R.; et al. Three-dimensional printing of high-performance continuous fiber-reinforced thermoplastic composites: Causes and elimination of process-induced defects. Compos. Part B Eng. 2025, 292, 112080. [Google Scholar] [CrossRef]
- Yavas, D.; Zhang, Z.; Liu, Q.; Wu, D. Interlaminar shear behavior of continuous and short carbon fiber reinforced polymer composites fabricated by additive manufacturing. Compos. Part B Eng. 2021, 204, 108460. [Google Scholar] [CrossRef]
- Caminero, M.A.; Chacón, J.M.; García-Moreno, I.; Reverte, J.M. Interlaminar bonding performance of 3D printed continuous fibre reinforced thermoplastic composites using fused deposition modelling. Polym. Test. 2018, 68, 415–423. [Google Scholar] [CrossRef]
- Tóth, C.; Virág, Á.D.; Vas, L.M.; Kovács, N.K. Prediction and analysis of flexural stiffness for 3D-printed continuous fiber–reinforced composites with different matrix fill ratios and layer orders. Polym. Test. 2024, 135, 108459. [Google Scholar] [CrossRef]
- Liu, L.; Deng, Q.; Wang, R.; Hu, X.; Su, M.; An, M.; Wang, Y.; He, H.; Miao, Y. Dynamic enhancement induced by interface for additively manufactured continuous carbon fiber reinforced composites. Polym. Test. 2024, 132, 108382. [Google Scholar] [CrossRef]
- Wang, K.; Chen, Y.; Long, H.; Baghani, M.; Rao, Y.; Peng, Y. Hygrothermal aging effects on the mechanical properties of 3D printed composites with different stacking sequence of continuous glass fiber layers. Polym. Test. 2021, 100, 107242. [Google Scholar] [CrossRef]
- Wang, G.; Wang, F.; Guan, S.; Fu, R.; Wang, H.; Lei, Y. A new path planning strategy driven by geometric features and tensile properties for 3D printing of continuous fiber reinforced thermoplastic composites. Compos. Part B Eng. 2025, 288, 111885. [Google Scholar] [CrossRef]
- Ichihara, N.; Ueda, M. 3D-printed high-toughness composite structures by anisotropic topology optimization. Compos. Part B Eng. 2023, 253, 110572. [Google Scholar] [CrossRef]
- Fedulov, B.; Fedorenko, A.; Khaziev, A.; Antonov, F. Optimization of parts manufactured using continuous fiber three-dimensional printing technology. Compos. Part B Eng. 2021, 227, 109406. [Google Scholar] [CrossRef]
- Li, N.; Link, G.; Wang, T.; Ramopoulos, V.; Neumaier, D.; Hofele, J.; Walter, M.; Jelonnek, J. Path-designed 3D printing for topological optimized continuous carbon fibre reinforced composite structures. Compos. Part B Eng. 2020, 182, 107612. [Google Scholar] [CrossRef]
- Hao, W.; Liu, Y.; Zhou, H.; Chen, H.; Fang, D. Preparation and characterization of 3D printed continuous carbon fiber reinforced thermosetting composites. Polym. Test. 2018, 65, 29–34. [Google Scholar] [CrossRef]
- Wang, B.; Ming, Y.; Zhou, J.; Xiao, H.; Wang, F.; Duan, Y.; Kazancı, Z. Fabrication of triangular corrugated structure using 3D printed continuous carbon fiber-reinforced thermosetting epoxy composites. Polym. Test. 2022, 106, 107469. [Google Scholar] [CrossRef]
- Huang, Y.; Tian, X.; Li, W.; He, S.; Zhao, P.; Hu, H.; Jia, Q.; Luo, M. 3D printing of topologically optimized wing spar with continuous carbon fiber reinforced composites. Compos. Part B Eng. 2024, 272, 111166. [Google Scholar] [CrossRef]
- Azarov, A.V.; Antonov, F.K.; Golubev, M.V.; Khaziev, A.R.; Ushanov, S.A. Composite 3D printing for the small size unmanned aerial vehicle structure. Compos. Part B Eng. 2019, 169, 157–163. [Google Scholar] [CrossRef]
- Vasiliev, V.; Barynin, V.; Rasin, A. Anisogrid lattice structures–survey of development and application. Compos. Struct. 2001, 54, 361–370. [Google Scholar] [CrossRef]
- Vasiliev, V.V.; Barynin, V.A.; Razin, A.F. Anisogrid composite lattice structures–Development and aerospace application. Compos. Struct. 2012, 949, 1117–1127. [Google Scholar] [CrossRef]
- Giusto, G.; Totaro, G.; Spena, P.; De Nicola, F.; Di Caprio, F.; Zallo, A.; Grilli, A.; Mancini, V.; Kiryenko, S.; Das, S. Composite grid structure technology for space applications. Mater. Today Proc. 2021, 34, 332–340. [Google Scholar] [CrossRef]
- Lee, Y.-G.; Choi, J.-H.; Lee, M.-J.; Kim, S.-M. Compressive strength stabilizing manufacturing method of anisogrid composite structure ribs without an outer skin. Compos. Part B Eng. 2020, 203, 108452. [Google Scholar] [CrossRef]
- Smeets, B.J.R.; Fagan, E.M.; Matthews, K.; Telford, R.; Murray, B.R.; Pavlov, L.; Weafer, B.; Meier, P.; Goggins, J. Structural testing of a shear web attachment point on a composite lattice cylinder for aerospace applications. Compos. Part B Eng. 2021, 212, 108691. [Google Scholar] [CrossRef]
- Hunt, C.J.; Morabito, F.; Grace, C.; Zhao, Y.; Woods, B.K. A review of composite lattice structures. Compos. Struct. 2022, 284, 115120. [Google Scholar] [CrossRef]
- Zeng, C.; Liu, L.; Bian, W.; Leng, J.; Liu, Y. Compression behavior and energy absorption of 3D printed continuous fiber reinforced composite honeycomb structures with shape memory effects. Addit. Manuf. 2021, 38, 101842. [Google Scholar] [CrossRef]
- Dong, K.; Wang, Y.; Wang, Z.; Qiu, W.; Zheng, P.; Xiong, Y. Reusability and energy absorption behavior of 4D printed continuous fiber-reinforced auxetic composite structures. Compos. Part A Appl. Sci. Manuf. 2023, 169, 107529. [Google Scholar] [CrossRef]
- Sugiyama, K.; Matsuzaki, R.; Ueda, M.; Todoroki, A.; Hirano, Y. 3D printing of composite sandwich structures using continuous carbon fiber and fiber tension. Compos. Part A Appl. Sci. Manuf. 2018, 113, 114–121. [Google Scholar] [CrossRef]
- Cheng, P.; Wang, K.; Peng, Y.; Ahzi, S. Effects of cellular crossing paths on mechanical properties of 3D printed continuous fiber reinforced biocomposite honeycomb structures. Compos. Part A Appl. Sci. Manuf. 2024, 178, 107972. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, G.; Ren, H.; Liu, G.; Xiong, Y. Fabrication strategy for joints in 3D printed continuous fiber reinforced composite lattice structures. Compos. Commun. 2022, 30, 101080. [Google Scholar] [CrossRef]
- Wang, K.; Wang, D.; Liu, Y.; Gao, H.; Yang, C.; Peng, Y. Path Planning and Bending Behaviors of 3D Printed Continuous Carbon Fiber Reinforced Polymer Honeycomb Structures. Polymers 2023, 15, 4485. [Google Scholar] [CrossRef]
- Ren, H.; Zhang, G.; Wang, Y.; Wang, D.; Xiong, Y. Buckling performance-aware path planning for 3D printing of curved grid-stiffened fiber-reinforced polymer composite structures. J. Manuf. Process. 2024, 116, 192–201. [Google Scholar] [CrossRef]
- Ma, W.; Dong, Q.; Zhao, H.; Li, X.; Xiong, L.; Hu, N. Mechanics-guided manufacturing optimization framework to enhance the strength of architected lattice made from recycled plastic wastes. Addit. Manuf. 2024, 81, 103997. [Google Scholar] [CrossRef]
- Jeon, M.-H.; Cho, H.-J.; Lee, M.-Y.; Kim, Y.-J.; Kim, I.-G. Compressive strength prediction of composite lattice structure using compression test results of subelement specimens. Mech. Adv. Mater. Struc. 2023, 31, 3333–3347. [Google Scholar] [CrossRef]
- Jeon, M.-H.; Kim, I.-G.; Woo, K. Progressive failure analysis of anisogrid cylindrical composite lattice structure with manufacturing defects. Compos. Struct. 2023, 321, 117237. [Google Scholar] [CrossRef]
- Lopatin, A.; Morozov, E.; Shatov, A. Axial deformability of the composite lattice cylindrical shell under compressive loading: Application to a load-carrying spacecraft tubular body. Compos. Struct. 2016, 146, 201–206. [Google Scholar] [CrossRef]
- Morozov, E.; Lopatin, A.; Nesterov, V. Finite-element modelling and buckling analysis of anisogrid composite lattice cylindrical shells. Compos. Struct. 2011, 93, 308–323. [Google Scholar] [CrossRef]
- Totaro, G.; De Nicola, F.; Caramuta, P. Local buckling modelling of anisogrid lattice structures with hexagonal cells: An experimental verification. Compos. Struct. 2013, 106, 734–741. [Google Scholar] [CrossRef]
- ASTM D3410; Standard Test Method for Compressive Properties of Polymer Matrix Composite Materials with Unsupported Gage Section by Shear Loading. ASTM: West Conshohocken, PA, USA, 2021. Available online: www.astm.org/d3410_d3410m-16e01.html (accessed on 1 January 2024).
- Toray T300 Technical Data Sheet. 2018. Available online: www.cf-composites.toray/resources/data_sheets/ (accessed on 1 January 2024).















| Strength (N/mm2) | Failure Mode | ||
|---|---|---|---|
| ϕ = 45° | Path A | 7.7 | In-plane buckling |
| Path B | 8.2 | In-plane buckling | |
| Path C | 8.5 | In-plane buckling | |
| ϕ = 60° | Path A | 17.5 | Interlaminar fracture |
| Path B | 19.3 | In-plane buckling | |
| Path C | 15.3 | Interlaminar fracture | |
| ϕ = 75° | Path A | 31.8 | Interlaminar fracture |
| Path B | 46.1 | In-plane buckling | |
| Path C | 26.6 | Interlaminar fracture |
| = 45° | = 60° | = 75° | |
|---|---|---|---|
| Inner surface | 9.0% | 5.4% | 1.8% |
| Outer surface | 12.4% | 7.1% | 0.2% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeon, M.-H.; Shin, G.S.; Hwang, J.Y.; Ho-Nguyen-Tan, T.; Kim, M.; Yoon, S.H. Effects of Printing Paths on Compressive Strength of 3D-Printed Continuous Fiber-Reinforced Composite Lattice Unit Cell. Polymers 2025, 17, 850. https://doi.org/10.3390/polym17070850
Jeon M-H, Shin GS, Hwang JY, Ho-Nguyen-Tan T, Kim M, Yoon SH. Effects of Printing Paths on Compressive Strength of 3D-Printed Continuous Fiber-Reinforced Composite Lattice Unit Cell. Polymers. 2025; 17(7):850. https://doi.org/10.3390/polym17070850
Chicago/Turabian StyleJeon, Min-Hyeok, Geun Sik Shin, Jun Yeon Hwang, Thuan Ho-Nguyen-Tan, Minkook Kim, and Soon Ho Yoon. 2025. "Effects of Printing Paths on Compressive Strength of 3D-Printed Continuous Fiber-Reinforced Composite Lattice Unit Cell" Polymers 17, no. 7: 850. https://doi.org/10.3390/polym17070850
APA StyleJeon, M.-H., Shin, G. S., Hwang, J. Y., Ho-Nguyen-Tan, T., Kim, M., & Yoon, S. H. (2025). Effects of Printing Paths on Compressive Strength of 3D-Printed Continuous Fiber-Reinforced Composite Lattice Unit Cell. Polymers, 17(7), 850. https://doi.org/10.3390/polym17070850






