Exploring the Feasibility of Deep Learning for Predicting Lignin GC-MS Analysis Results Using TGA and FT-IR
Abstract
1. Introduction
- Decoder-Based Generative Models: A deep learning model incorporating the distinct features of TGA, FT-IR, and GC-MS data to generate synthetic datasets.
- Predictive Modeling in Limited Data Scenarios: Synthetic data augmentation to enable training under data-scarce conditions.
- GC-MS Predictability Using TGA and FT-IR Data: Development and evaluation of a GC-MS prediction model based on TGA and FT-IR inputs.
2. Proposed Method
2.1. Dataset Overview
2.1.1. Tga Data Preprocessing and Generation
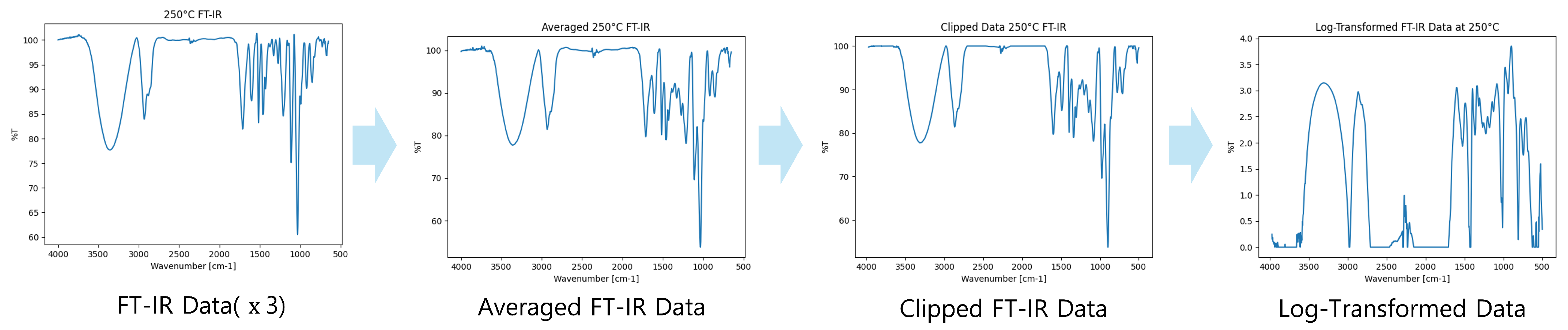
2.1.2. FT-IR Data Preprocessing and Generation
2.1.3. GC-MS Data Preprocessing and Generation
2.2. Proposed GC-MS Prediction Model
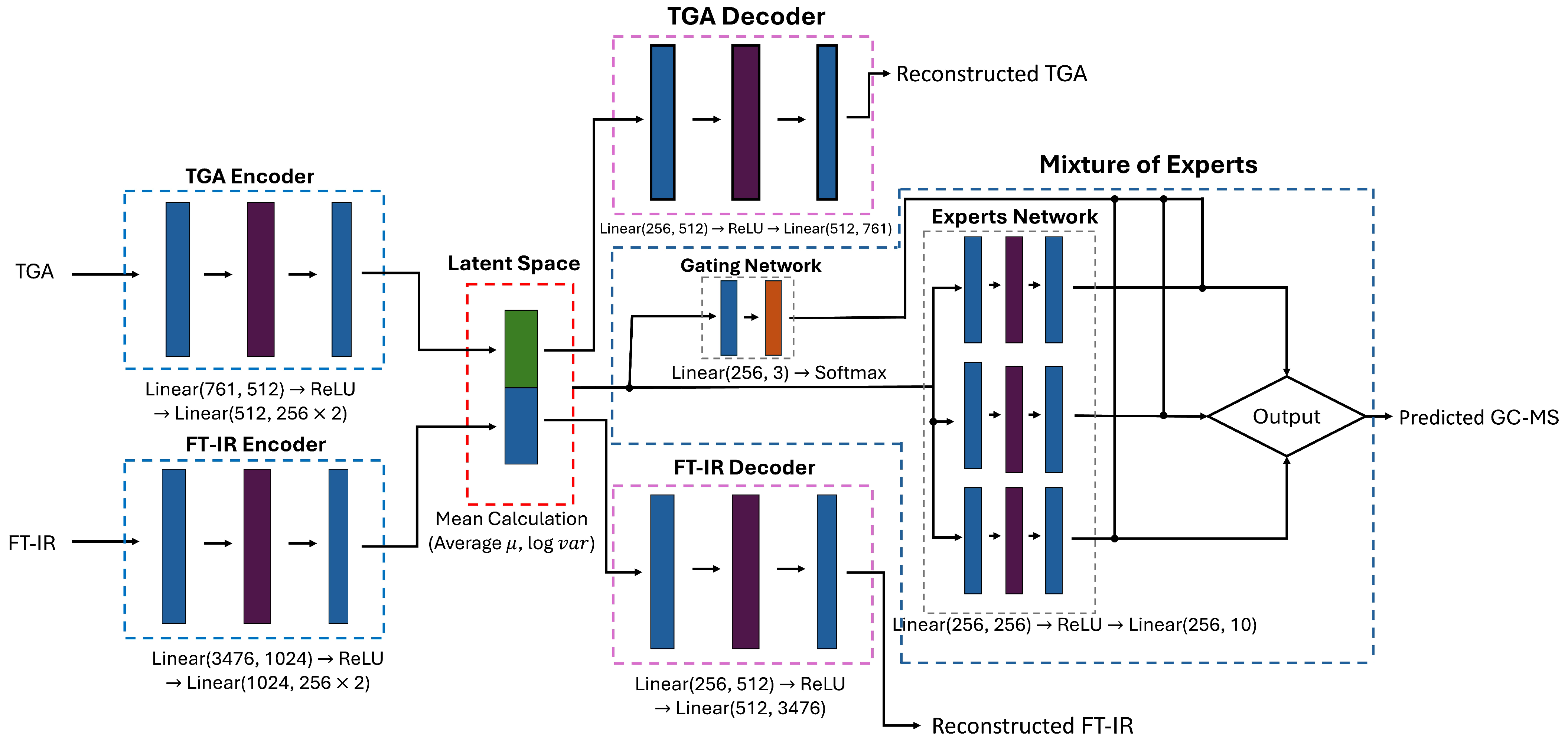
2.2.1. Model Architecture
2.2.2. Loss Function
3. Experimental Result
3.1. Evaluate Each Data Generation Model
3.1.1. TGA Data Generation Model
3.1.2. FT-IR Data Generation Model
3.1.3. GC-MS Data Generation Model
3.2. Evaluate GC-MS Prediction Model
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Groups | Derivative | Chemical Formula |
|---|---|---|
| Syringyl | Phenol, 2,6-dimethoxy- | C8H10O3 |
| 4-methylsyringol; 3,5-Dimethoxy-4-hydroxytoluene | C9H12O3 | |
| 4-Ethylsyringol; 4-Ethyl-2,6-dimethoxyphenol | C10H14O3 | |
| 4-Propylsyringol; 2,6-Dimethoxy-4-propylphenol | C11H16O3 | |
| Syringaldehyde; Benzaldehyde, 4-hydroxy-3,5-dimethoxy- | C9H10O4 | |
| (E)-4-Propenylsyringol (E)-2,6-Dimethoxy-4-(prop-1-en-1-yl) phenol | C11H14O3 | |
| 4-Acetylsyringol; Acetosyringon; Ethanone, 1-(4-hydroxy-3,5-dimethoxyphenyl)- | C10H12O4 | |
| Syringylacetone | C11H14O4 | |
| Syringyl alcohol; 3,5-Dimethoxy-4-hydroxybenzeneethanol | C10H14O4 | |
| Butylsyringone | C12H16O4 | |
| Acetyl syringic acid, ethyl ester | C13H16O6 | |
| Propiosyringone; 1-Propanone, 1-(4-hydroxy-3,5-dimethoxyphenyl)- | C11H14O4 | |
| Dihydrosyringenin; 3-Syringylpropanol | C11H16O4 | |
| Guaiacyl | Guaiacol; Phenol, 2-methoxy- | C7H8O2 |
| 5-Methylguaiacol; m-Creosol; 2-Methoxy-5-methylphenol | C8H10O2 | |
| 4-Ethylguaiacol; Phenol, 4-ethyl-2-methoxy- | C9H12O2 | |
| 4-Propylguaiacol; Phenol, 2-methoxy-4-propyl- | C10H14O2 | |
| Benzaldehyde, 3-hydroxy-4-methoxy- | C8H8O3 | |
| Allylguaiacol; Eugenol | C10H12O2 | |
| Guaiacylacetone; 2-Propanone, 1-(4-hydroxy-3-methoxyphenyl)- | C10H12O3 | |
| 4-(2-Hydroxyethyl)guaiacol; Homovanillyl alcohol | C9H12O3 | |
| 3-(4-guaiacyl)propanol; Benzenepropanol, 4-hydroxy-3-methoxy- | C10H14O3 | |
| Poly aromatics | Naphthalene | C10H8 |
| 7-Methoxy-1-naphthol | C11H10O2 | |
| 2-Naphthalenol, 3-methoxy- | C11H10O2 | |
| 1,6-Dimethoxynaphthalene | C12H12O2 | |
| Naphthalene, 2,3-dimethoxy- | C12H12O2 | |
| 1,6-Dimethoxynaphthalene | C12H12O2 | |
| Retene | C18H18 | |
| 2-Isopropyl-10-methylphenanthrene | C18H18 | |
| Methyl dehydroabietate | C21H30O2 | |
| 8-Isopropyl-1,3-dimethylphenanthrene | C19H20 | |
| Other aromatics | Phenol | C6H6O |
| p-Cresol | C7H8O | |
| o-Cresol; Phenol, 2-methyl- | C7H8O | |
| Creosol | C8H10O2 | |
| Catechol | C6H6O2 | |
| 1-Propanone, 1-(5-methyl-2-thienyl)- | C8H10OS | |
| 2-Acetyl-4-methylphenol; o-Acetyl-p-cresol | C9H10O2 | |
| 3-methoxycatechol; 1,2-Benzenediol, 3-methoxy- | C7H8O3 | |
| Hydroquinone | C6H6O2 | |
| 4-Methylcatechol; 1,2-Benzenediol, 4-methyl- | C7H8O2 | |
| 3-Methylcatechol; 1,2-Benzenediol, 3-methyl- | C7H8O2 | |
| Phenol, 4-methoxy-3-methyl- | C8H10O2 | |
| 2,3-Dimethoxyphenol | C8H10O3 | |
| Phenol, 3,4-dimethoxy- | C8H10O3 | |
| 5-Methoxy-m-cresol; 3-Methoxy-5-methylphenol | C8H10O2 | |
| 2,6-Dimethoxyhydroquinone | C8H10O4 | |
| 1,4-Benzenedicarboxaldehyde, 2-methyl- 2-Methylterephthalaldehyde | C9H8O2 | |
| Ethanone, 1-(2-hydroxy-5-methylphenyl)- | C9H10O2 | |
| Ethanone, 1-(2-hydroxy-6-methoxyphenyl)- | C9H10O3 | |
| 1,2,3-Trimethoxybenzene | C9H12O3 | |
| 4-Ethylcatechol | C8H10O2 | |
| 1,4-Benzenediol, 2,3,5-trimethyl- Trimethylhydroquinone | C9H12O2 | |
| Ethanone, 1-(2,3,4-trihydroxyphenyl)- | C8H8O4 | |
| Vanillin | C8H8O3 | |
| 3-Ethoxy-4-methoxyphenol | C9H12O3 | |
| Phenol, 2-methoxy-4-(2-propenyl)-, acetate; Aceto eugenol | C12H14O3 | |
| 3-Acetylphenol; Ethanone, 1-(3-hydroxyphenyl)- | C8H8O2 | |
| 2-methoxy-5-acetylphenol; Ethanone, 1-(3-hydroxy-4-methoxyphenyl)- | C9H10O3 | |
| Apocynin | C9H10O3 | |
| Benzene, 1,2,3-trimethoxy-5-methyl- | C10H14O3 | |
| 2-Propanone, 1-(4-hydroxy-3-methoxyphenyl)- | C10H12O3 | |
| 3-Hydroxy-4-methoxybenzoic acid | C8H8O4 | |
| Flopropione | C9H10O4 | |
| 3,4-Dimethoxyphenylacetone | C11H14O3 | |
| 1-Propanone, 1-(4-hydroxy-3-methoxyphenyl)- | C10H12O3 | |
| Butyrovanillone | C11H14O3 | |
| Homovanillic acid | C9H10O4 | |
| Benzenepropanol, 4-hydroxy-3-methoxy- | C10H14O3 | |
| Phenol, 2-methoxy-4-methyl-6-[propenyl]- | C11H14O2 | |
| 2,3-Dimethoxy-5-aminocinnamonitrile | C11H12N2O2 | |
| 5-(3-Hydroxypropyl)-2,3-dimethoxyphenol | C11H16O4 | |
| Asarone | C12H16O3 | |
| Benzene, 1,2,3-trimethoxy-5-(2-propenyl)- | C12H16O3 | |
| 3,4-Divanillyltetrahydrofuran | C20H24O5 | |
| 1-(2,4-Dihydroxyphenyl)-2-(3,4-dimethoxyphenyl)ethan one | C16H16O5 | |
| 1-(2,4-Dihydroxyphenyl)-2-(3,5- | C17H18O5 | |
| Dehydroabietate | C20H28O2 | |
| 3,4-Dimethoxyphenol, 2- methylpropionate | - | |
| Alkanes (Paraffins) | Propane, 1,1-diethoxy- | C7H16O2 |
| 1,3,5-Trioxane | C3H6O3 | |
| Propanal ethyl isopentyl acetal 1-(1-Ethoxypropoxy)-3-methylbutane | C10H22O2 | |
| Cyclic | Oxazolidin-2-one | C3H5NO2 |
| Butyrolactone | C4H6O2 | |
| 2-Cyclopenten-1-one, 3-methyl- | C6H8O | |
| 1,2-Cyclopentanedione, 3-methyl- | C6H8O2 | |
| 2-Cyclopenten-1-one, 2-hydroxy-3-methyl- | C6H8O2 | |
| 2-Cyclopenten-1-one, 2,3-dimethyl- | C7H10O | |
| Fatty Acids | Propanoic acid | C3H6O2 |
| Butanoic acid, 4-hydroxy- | C4H8O3 | |
| Methyltartronic acid | C4H6O5 | |
| Lactic acid; Propanoic acid, 2-hydroxy-, ethyl ester | C5H10O3 | |
| Pentanoic acid, 4-oxo- | C5H8O3 | |
| Pentanoic acid, 4-oxo-, ethyl ester | C7H12O3 | |
| Butanoic acid, anhydride | C8H14O3 | |
| Butanoic acid, 2-methylpropyl ester | C8H16O2 | |
| Propanoic acid, 2-methyl-, anhydride | C8H14O3 | |
| Pentanoic acid, 4-oxo-, 2-methylpropyl ester | C9H16O3 | |
| Dodecanoic acid, methyl ester Pentanoic acid, 2-methyl-4-oxo- | C13H26O2 | |
| Alcohols | 1,3-Propanediol | C3H8O2 |
| Ethanol, 2,2’-oxybis- | C4H10O3 | |
| 1,2-Propanediol, 3-methoxy- | C4H10O3 | |
| 1-Propanol, 2-(2-hydroxypropoxy)- | C6H14O3 | |
| Glycerol-derived | 3-Ethoxy-1,2-propanediol; Glycerol 1-ethyl ether | C5H12O3 |
| Glycerol triethyl ether | C9H20O3 | |
| 1,3-Dioxolane-4-methanol, 2-ethyl- | C6H12O3 | |
| Glycerin | C3H8O3 | |
| 1,2,3-Propanetriol, 1-acetate | C5H10O4 | |
| Glycerol 1,2-diacetate | C7H12O5 | |
| Alpha-monopropionin | C6H12O4 | |
| Hydroxyacetone; 2-Propanone, 1-hydroxy- | C3H6O2 | |
| Ethylene glycol Formate Isobutyrate | C7H12O4 | |
| 2,3-dihydroxypropyl isobutyrate | C7H14O4 |
References
- Beaucamp, A.; Muddasar, M.; Amiinu, I.S.; Leite, M.M.; Culebras, M.; Latha, K.; Gutiérrez, M.C.; Rodriguez-Padron, D.; del Monte, F.; Kennedy, T.; et al. Lignin for energy applications—State of the art, life cycle, technoeconomic analysis and future trends. Green Chem. 2022, 24, 8193–8226. [Google Scholar] [CrossRef]
- Yu, O.; Kim, K.H. Lignin to materials: A focused review on recent novel lignin applications. Appl. Sci. 2020, 10, 4626. [Google Scholar] [CrossRef]
- Huang, Z.; Zhang, Y.; Zhang, C.; Yuan, F.; Gao, H.; Li, Q. Lignin-based composite film and its application for agricultural mulching. Polymers 2024, 16, 2488. [Google Scholar] [CrossRef]
- Mun, J.S.; Mun, S.P. Structural and thermal characterization of milled wood lignin from bamboo (Phyllostachys pubescens) grown in Korea. Molecules 2024, 29, 183. [Google Scholar] [CrossRef]
- Ragauskas, A.J.; Beckham, G.T.; Biddy, M.J.; Chandra, R.; Chen, F.; Davis, M.F.; Davison, B.H.; Dixon, R.A.; Gilna, P.; Keller, M.; et al. Lignin Valorization: Improving Lignin Processing in the Biorefinery. Science 2014, 344, 1246843. [Google Scholar] [CrossRef]
- Elliott, D.C.; Biller, P.; Ross, A.B.; Schmidt, A.J.; Jones, S.B. Hydrothermal liquefaction of biomass: Developments from batch to continuous process. Bioresour. Technol. 2015, 178, 147–156. [Google Scholar] [CrossRef]
- Zakzeski, J.; Bruijnincx, P.C.A.; Jongerius, A.L.; Weckhuysen, B.M. The Catalytic Valorization of Lignin for the Production of Renewable Chemicals. Chem. Rev. 2010, 110, 3552–3599. [Google Scholar] [CrossRef]
- Wang, Y.-Y.; Meng, X.; Pu, Y.; Ragauskas, A.J. Recent Advances in the Application of Functionalized Lignin in Value-Added Polymeric Materials. Polymers 2020, 12, 2277. [Google Scholar] [CrossRef]
- Blindheim, F.H.; Ruwoldt, J. The effect of sample preparation techniques on lignin Fourier transform infrared spectroscopy. Polymers 2023, 15, 2901. [Google Scholar] [CrossRef]
- Sebio-Puñal, T.; Naya, S.; López-Beceiro, J.; Tarrío-Saavedra, J.; Artiaga, R. Thermogravimetric analysis of wood, holocellulose, and lignin from five wood species. J. Therm. Anal. Calorim. 2012, 109, 1163–1167. [Google Scholar] [CrossRef]
- Takada, D.; Ehara, K.; Saka, S. Gas chromatographic and mass spectrometric (GC-MS) analysis of lignin-derived products from Cryptomeria japonica treated in supercritical water. J. Wood Sci. 2004, 50, 253–259. [Google Scholar] [CrossRef]
- Ehara, K.; Takada, D.; Saka, S. GC-MS and IR spectroscopic analyses of the lignin-derived products from softwood and hardwood treated in supercritical water. J. Wood Sci. 2005, 51, 256–261. [Google Scholar] [CrossRef]
- Guillén, M.D.; Ibargoitia, M.L. GC/MS analysis of lignin monomers, dimers and trimers in liquid smoke flavourings. J. Sci. Food Agric. 1999, 79, 1889–1903. [Google Scholar] [CrossRef]
- Washington State University. Analytical Chemistry Service Center–Equipment Rates. Available online: https://bsyse.wsu.edu/acsc/rates/ (accessed on 1 February 2025).
- Wen, Y.; Liu, X.; He, F.; Shi, Y.; Chen, F.; Li, W.; Song, Y.; Li, L.; Jiang, H.; Zhou, L.; et al. Machine Learning Prediction of Stalk Lignin Content Using Fourier Transform Infrared Spectroscopy in Large Scale Maize Germplasm. Int. J. Biol. Macromol. 2024, 280, 136140. [Google Scholar] [CrossRef]
- Ge, H.; Liu, Y.; Zhu, B.; Xu, Y.; Zhou, R.; Xu, H.; Li, B. Machine Learning Prediction of Delignification and Lignin Structure Regulation of Deep Eutectic Solvents Pretreatment Processes. Ind. Crops Prod. 2023, 203, 117138. [Google Scholar] [CrossRef]
- Diment, D.; Löfgren, J.; Alopaeus, M.; Stosiek, M.; Cho, M.; Xu, C.; Hummel, M.; Rigo, D.; Rinke, P.; Balakshin, M. Enhancing Lignin-Carbohydrate Complexes Production and Properties with Machine Learning. ChemSusChem 2024, e202401711. [Google Scholar] [CrossRef] [PubMed]
- Löfgren, J.; Tarasov, D.; Koitto, T.; Rinke, P.; Balakshin, M.; Todorovic, M. Machine Learning Optimization of Lignin Properties in Green Biorefineries. ACS Sustain. Chem. Eng. 2022, 10, 9469–9479. [Google Scholar] [CrossRef]
- Shorten, C.; Khoshgoftaar, T.M. A survey on image data augmentation for deep learning. J. Big Data 2019, 6, 60. [Google Scholar] [CrossRef]
- Luo, W.; Yang, M.; Zheng, W. Weakly-supervised semantic segmentation with saliency and incremental supervision updating. Pattern Recognit. 2021, 115, 107858. [Google Scholar] [CrossRef]
- Lemley, J.; Bazrafkan, S.; Corcoran, P. Smart augmentation: Learning an optimal data augmentation strategy. IEEE Access 2017, 5, 5858–5869. [Google Scholar] [CrossRef]
- Montesinos López, O.A.; Montesinos López, A.; Crossa, J. (Eds.) Overfitting, model tuning, and evaluation of prediction performance. In Multivariate Statistical Machine Learning Methods for Genomic Prediction; Springer International Publishing: Berlin/Heidelberg, Germany, 2022; pp. 109–139. [Google Scholar] [CrossRef]
- Lin, M.; Chen, Q.; Yan, S. Network in Network. arXiv 2014, arXiv:1312.4400. [Google Scholar] [CrossRef]
- Suzuki, M.; Nakayama, K.; Matsuo, Y. Improving Bi-directional Generation between Different Modalities with Variational Autoencoders. arXiv 2018, arXiv:1801.08702. [Google Scholar] [CrossRef]
- Jacobs, R.A.; Jordan, M.I.; Nowlan, S.J.; Hinton, G.E. Adaptive Mixtures of Local Experts. Neural Comput. 1991, 3, 79–87. [Google Scholar] [CrossRef]
- Kingma, D.P.; Welling, M. Auto-Encoding Variational Bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On Information and Sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Aboussalah, A.M.; Kwon, M.J.; Patel, R.G.; Chi, C.; Lee, C.G. Don’t overfit the history—Recursive time series data augmentation. arXiv 2023, arXiv:2207.02891. [Google Scholar] [CrossRef]
- Lim, S.S.; Kang, B.O.; Kwon, O.W. Improving transformer-based speech recognition performance using data augmentation by local frame rate changes. J. Acoust Soc. Korea 2022, 41, 122–129. [Google Scholar] [CrossRef]
- Tian, L.; Wang, Z.; Liu, W.; Cheng, Y.; Alsaadi, F.E.; Liu, X. A new GAN-based approach to data augmentation and image segmentation for crack detection in thermal imaging tests. Cogn. Comput. 2021, 13, 1263–1273. [Google Scholar] [CrossRef]
- Dunphy, K.; Fekri, M.N.; Grolinger, K.; Sadhu, A. Data augmentation for deep-learning-based multiclass structural damage detection using limited information. Sensors 2022, 22, 6193. [Google Scholar] [CrossRef]
- Oh, C.; Han, S.; Jeong, J. Time-series data augmentation based on interpolation. Procedia Comput. Sci. 2020, 175, 64–71. [Google Scholar] [CrossRef]
- Botchkarev, A. Performance metrics (error measures) in machine learning regression, forecasting and prognostics: Properties and typology. arXiv 2018, arXiv:1809.03006. [Google Scholar] [CrossRef]
- Willmott, C.J.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- Draper, N.R.; Smith, H. Applied Regression Analysis, 3rd ed.; Wiley-Interscience: New York, NY, USA, 1998; ISBN 978-0-471-17082-2. [Google Scholar] [CrossRef]
- Asuero, A.G.; Sayago, A.; González, A.G. The Correlation Coefficient: An Overview. Crit. Rev. Anal. Chem. 2006, 36, 41–59. [Google Scholar] [CrossRef]
- Villani, C. Topics in Optimal Transportation; American Mathematical Society: Providence, RI, USA, 2003. [Google Scholar] [CrossRef]


| Configuration | Output Shape | |
|---|---|---|
| Feature Extractor (CNN) | ||
| Conv1D(1, 16, kernel=3, stride=1, padding=1) | → ReLU | (batch, 16, input_size) |
| Conv1D(16, 32, kernel=3, stride=1, padding=1) | → ReLU | (batch, 32, input_size) |
| Flatten | (batch, 32 × input_size) | |
| Fully Connected Layers | ||
| Linear (32 × input_size, 1024) | → ReLU | (batch, 1024) |
| Linear (1024, output_size) | (batch, 761) | |
| Configuration | Output Shape | |
|---|---|---|
| Feature Extractor (CNN) | ||
| Conv1D (1, 16, kernel=3, stride=1, padding=1) | → ReLU | (batch, 16, input_size) |
| Conv1D (16, 32, kernel=3, stride=1, padding=1) | → ReLU | (batch, 32, input_size) |
| Conv1D (32, 64, kernel=3, stride=1, padding=1) | → ReLU | (batch, 64, input_size) |
| Flatten | (batch, 64 × input_size) | |
| Fully Connected Layers | ||
| Linear (64 × 1, 1024) | → ReLU | (batch, 1024) |
| Dropout (0.3) | (batch, 1024) | |
| Linear (1024, 3476) | (batch, 3476) | |
| Configuration | Output Shape | |
|---|---|---|
| Feature Extractor (CNN) | ||
| Conv1D (1, 64, kernel=3, padding=1) | → ReLU | (batch, 64, input_size) |
| Conv1D (64, 64, kernel=3, padding=1) | → ReLU | (batch, 64, input_size) |
| Conv1D (64, 64, kernel=3, padding=1) | → ReLU | (batch, 64, input_size) |
| Global Average Pooling | (batch, 64) | |
| Fully Connected Layers | ||
| Linear (64, 128) | → ReLU | (batch, 128) |
| Linear (128, 10) | → Softmax | (batch, 10) |
| Temperature | Wasserstein Distance |
|---|---|
| 250 °C | |
| 300 °C | |
| 350 °C | |
| 400 °C |
| Temperature | MAE | Correlation | |
|---|---|---|---|
| 260 °C | 0.99846 | 0.99927 | |
| 280 °C | 0.99677 | 0.99856 | |
| 315 °C | 0.99936 | 0.99974 | |
| 345 °C | 0.99695 | 0.99895 | |
| 365 °C | 0.99775 | 0.99930 | |
| 390 °C | 0.99985 | 0.99994 |
| Temperature | MAE | Correlation | |
|---|---|---|---|
| 260 °C | 0.99982 | 0.99991 | |
| 280 °C | 0.99969 | 0.99986 | |
| 315 °C | 0.99942 | 0.99973 | |
| 345 °C | 0.99918 | 0.99961 | |
| 365 °C | 0.99936 | 0.99968 | |
| 390 °C | 0.99974 | 0.99987 |
| Temperature | MAE | Correlation | |
|---|---|---|---|
| 260 °C | 0.98418 | 0.99341 | |
| 280 °C | 0.64181 | 0.82605 | |
| 315 °C | 0.98445 | 0.99749 | |
| 345 °C | 0.98645 | 0.99837 | |
| 365 °C | 0.96308 | 0.98587 | |
| 390 °C | 0.9756 | 0.99835 |
| Temperature | Syringyl | Guaiacyl | Poly Aromatics (C10–C21) | Other Aromatics (C6–C20) | Alkanes | Cyclic | Fatty Acids | Alcohol | Glycerol- Derived | Other |
|---|---|---|---|---|---|---|---|---|---|---|
| 260 °C | 0.21477 | 0.17646 | 0.05685 | 0.29564 | 0.01579 | 0.04039 | 0.05028 | 0.01391 | 0.07410 | 0.15986 |
| 280 °C | 0.05852 | 0.10754 | 0.02521 | 0.33085 | 0.00343 | 0.07756 | 0.00424 | 0.02082 | 0.19208 | 0.09062 |
| 315 °C | 0.16934 | 0.09127 | 0.04828 | 0.28594 | 0.00831 | 0.02845 | 0.00364 | 0.01301 | 0.16618 | 0.07224 |
| 345 °C | 0.07758 | 0.06217 | 0.05289 | 0.30754 | 0.01026 | 0.03029 | 0.07295 | 0.01783 | 0.11612 | 0.07224 |
| 365 °C | 0.15026 | 0.14106 | 0.01434 | 0.32278 | 0.00312 | 0.00299 | 0.08885 | 0.05081 | 0.23030 | 0.02578 |
| 390 °C | 0.14120 | 0.12963 | 0.00629 | 0.26187 | 0.08833 | 0.02704 | 0.01767 | 0.01606 | 0.10773 | 0.09065 |
| Temperature | MAE | Correlation | |
|---|---|---|---|
| 260 °C | 0.6916 | 0.89697 | |
| 280 °C | 0.34032 | 0.69668 | |
| 315 °C | 0.39581 | 0.76097 | |
| 345 °C | −0.31819 | 0.40104 | |
| 365 °C | 0.76062 | 0.92887 | |
| 390 °C | 0.51835 | 0.72818 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, M.; Um, B.H.; Park, S.-H.; Kim, D.-Y. Exploring the Feasibility of Deep Learning for Predicting Lignin GC-MS Analysis Results Using TGA and FT-IR. Polymers 2025, 17, 806. https://doi.org/10.3390/polym17060806
Park M, Um BH, Park S-H, Kim D-Y. Exploring the Feasibility of Deep Learning for Predicting Lignin GC-MS Analysis Results Using TGA and FT-IR. Polymers. 2025; 17(6):806. https://doi.org/10.3390/polym17060806
Chicago/Turabian StylePark, Mingyu, Byung Hwan Um, Seung-Hyun Park, and Dae-Yeol Kim. 2025. "Exploring the Feasibility of Deep Learning for Predicting Lignin GC-MS Analysis Results Using TGA and FT-IR" Polymers 17, no. 6: 806. https://doi.org/10.3390/polym17060806
APA StylePark, M., Um, B. H., Park, S.-H., & Kim, D.-Y. (2025). Exploring the Feasibility of Deep Learning for Predicting Lignin GC-MS Analysis Results Using TGA and FT-IR. Polymers, 17(6), 806. https://doi.org/10.3390/polym17060806







