Generation of Liquid Crystal Elastomer Fibers via a Wet Spinning Technology with Two-Stage Crosslinking
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Preparation of LCE-Spinning Solution
2.3. Characterization of Crosslinking Kinetics
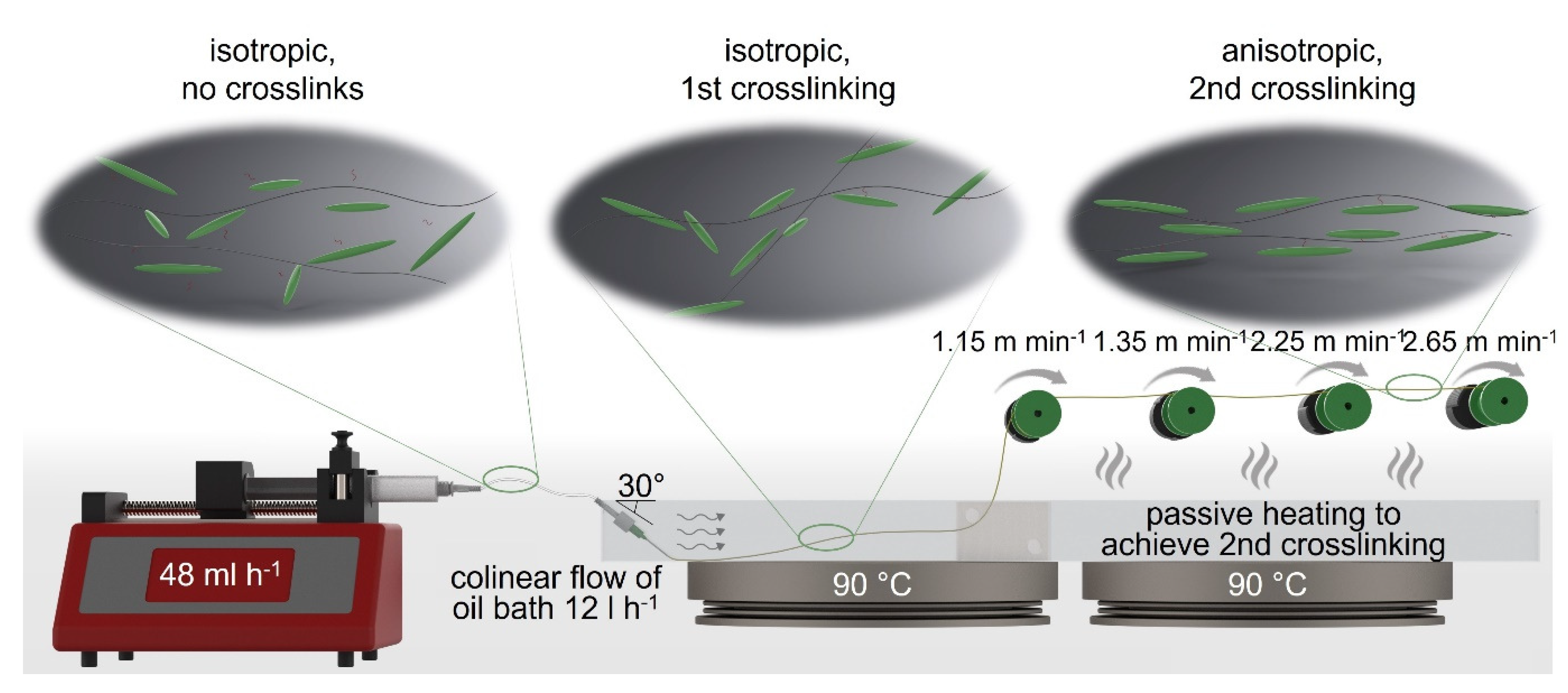
2.4. LCE-Fiber Spinning
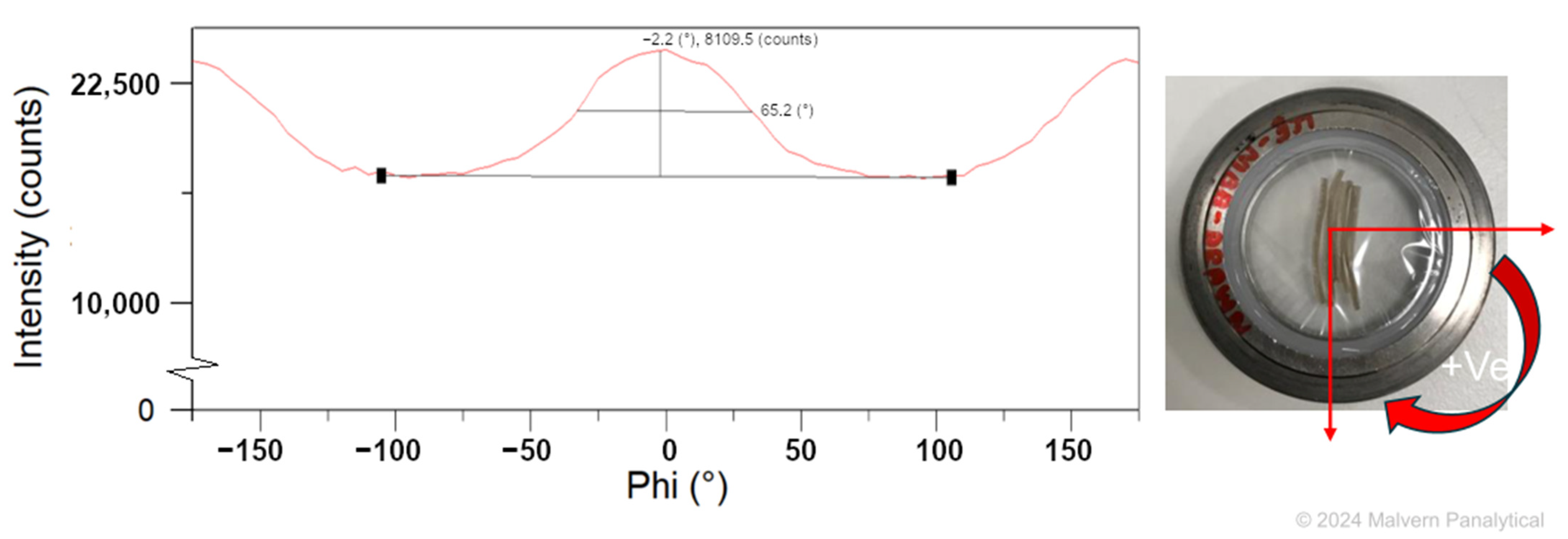
2.5. Mesogen Orientation
2.6. Determination of Nematic–Isotropic Transition Temperature
2.7. Characterization of Mechanical Properties
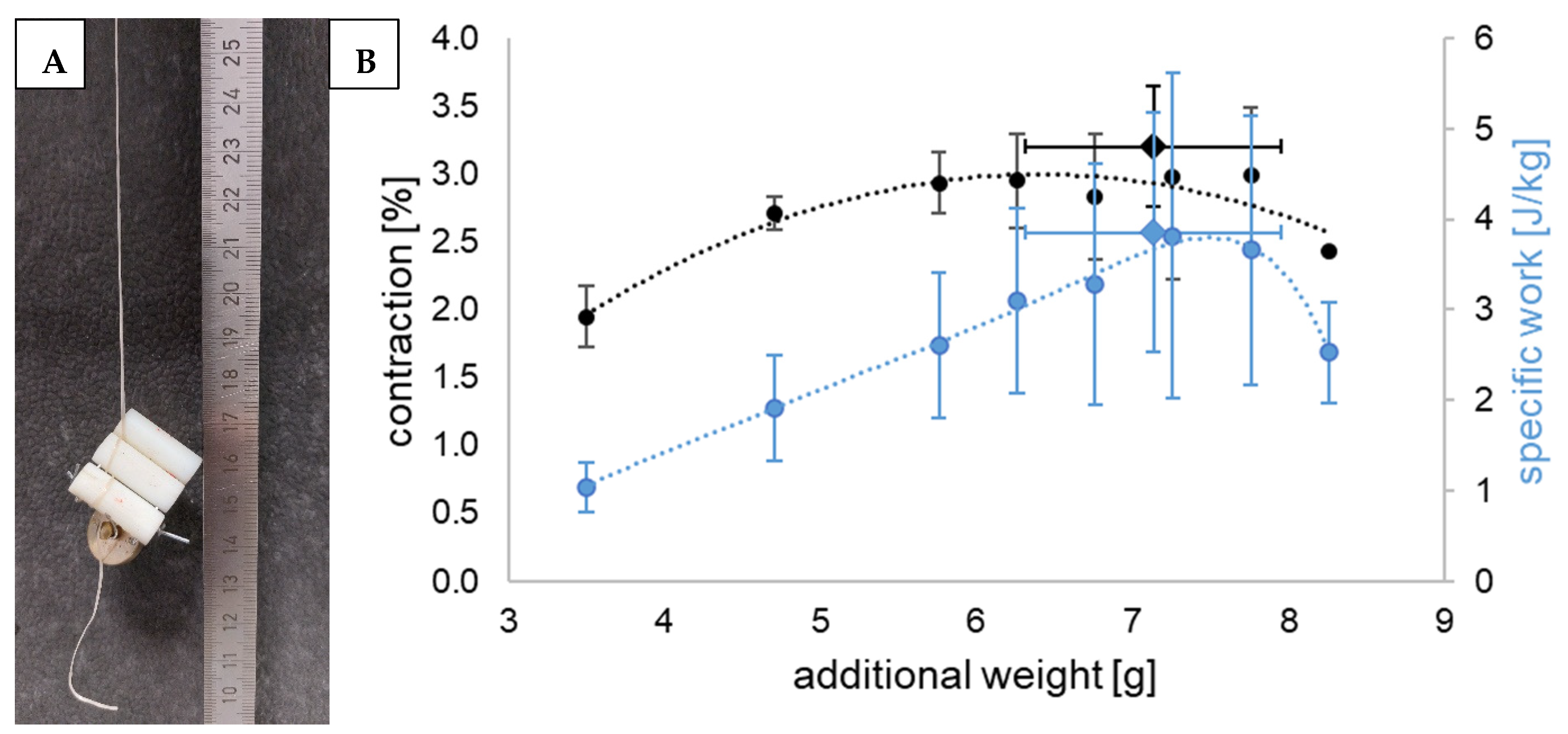
2.8. Characterization of Contractile Capacity and Specific Work
3. Results
3.1. Crosslinking Kinetics
3.2. LCE-Fiber Spinning
3.3. Nematic–Isotropic Transition (TNI) of LCEF
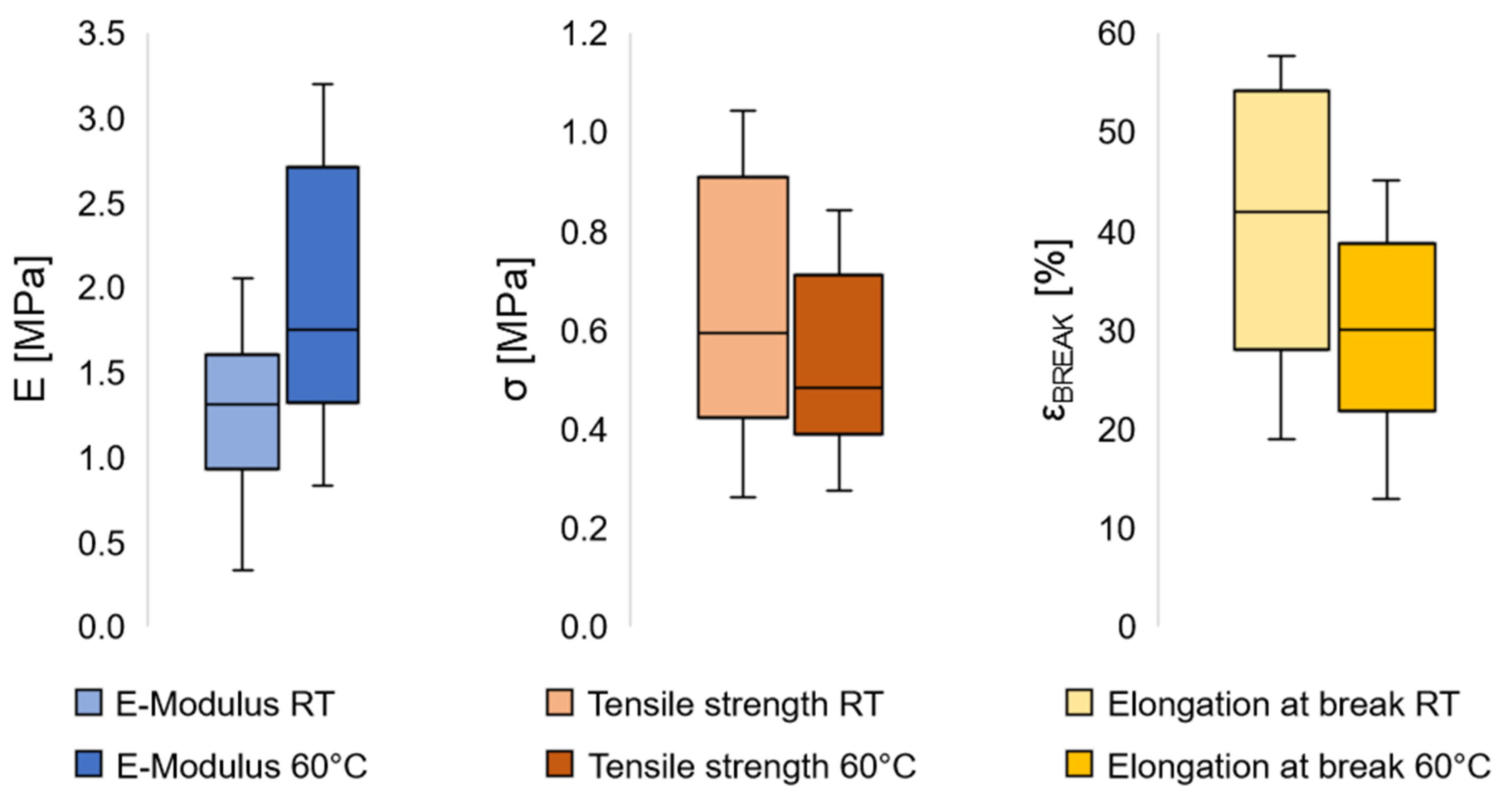
3.4. Mechanical Properties
3.5. Contractile Capacity and Specific Work
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kularatne, R.S.; Kim, H.; Boothby, J.M.; Ware, T.H. Liquid crystal elastomer actuators: Synthesis, alignment, and applications. J. Polym. Sci. Part B Polym. Phys. 2017, 55, 395–411. [Google Scholar] [CrossRef]
- Behl, M.; Zotzmann, J.; Lendlein, A. Shape-Memory Polymers and Shape-Changing Polymers. Shape-Mem. Polym. 2009, 226, 1–40. [Google Scholar]
- Petsch, S.; Rix, R.; Khatri, B.; Schuhladen, S.; Müller, P.; Zentel, R.; Zappe, H. Smart artificial muscle actuators: Liquid crystal elastomers with integrated temperature feedback. Sens. Actuators A Phys. 2015, 231, 44–51. [Google Scholar] [CrossRef]
- White, T.J.; Broer, D.J. Programmable and adaptive mechanics with liquid crystal polymer networks and elastomers. Nat. Mater. 2015, 14, 1087–1098. [Google Scholar] [CrossRef]
- Lehmann, W.; Skupin, H.; Tolksdorf, C.; Gebhard, E.; Zentel, R.; Krüger, P.; Lösche, M.; Kremer, F. Giant lateral electrostriction in ferroelectric liquid-crystalline elastomers. Nature 2001, 410, 447–450. [Google Scholar] [CrossRef]
- Guin, T.; Settle, M.J.; Kowalski, B.A.; Auguste, A.D.; Beblo, R.V.; Reich, G.W.; White, T.J. Layered liquid crystal elastomer actuators. Nat. Commun. 2018, 9, 2531. [Google Scholar] [CrossRef]
- Selinger, J.V.; Jeon, H.G.; Ratna, B.R. Isotropic-nematic transition in liquid-crystalline elastomers. Phys. Rev. Lett. 2002, 89, 225701. [Google Scholar] [CrossRef]
- Boothby, J.M.; van Volkenburg, T.; Le, N.Q.; Ohiri, K.; Hagedon, M.; Xia, Z. Effects of network structure on the mechanical and thermal responses of liquid crystal elastomers. Multifunct. Mater. 2020, 3, 15002. [Google Scholar] [CrossRef]
- Zhou, X.; Chen, G.; Jin, B.; Feng, H.; Chen, Z.; Fang, M.; Yang, B.; Xiao, R.; Xie, T.; Zheng, N. Multimodal Autonomous Locomotion of Liquid Crystal Elastomer Soft Robot. Adv. Sci. 2024, 11, e2402358. [Google Scholar] [CrossRef]
- Chen, H.; Yao, X.; Qin, H.; Cong, H.-P.; Yu, S.-H. A Photoactivated Self-Adaptive Liquid Crystal Elastomer Oscillator From Orientation and Polymerization Guided by Nanowire Assembly. Adv. Funct. Mater. 2025, 35, 2412728. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, G.; Zhang, K.; Jin, B.; Zhao, Q.; Xie, T. Repeatedly Programmable Liquid Crystal Dielectric Elastomer with Multimodal Actuation. Adv. Mater. 2024, 36, e2313078. [Google Scholar] [CrossRef] [PubMed]
- Saeed, M.H.; Choi, M.-Y.; Kim, K.; Lee, J.-H.; Kim, K.; Kim, D.; Kim, S.-U.; Kim, H.; Ahn, S.-K.; Lan, R.; et al. Electrostatically Powered Multimode Liquid Crystalline Elastomer Actuators. ACS Appl. Mater. Interfaces 2023, 15, 56285–56292. [Google Scholar] [CrossRef] [PubMed]
- De Gennes, P.G. Reflexions sur un type de polymeres nematiques. C. R. Acad. Sci. Ser. B 1975, 281, 101–103. [Google Scholar]
- Küpfer, J.; Finkelmann, H. Nematic liquid single crystal elastomers. Die Makromol. Chem. Rapid Commun. 1991, 12, 717–726. [Google Scholar] [CrossRef]
- Naciri, J.; Srinivasan, A.; Jeon, H.; Nikolov, N.; Keller, P.; Ratna, B.R. Nematic Elastomer Fiber Actuator. Macromolecules 2003, 36, 8499–8505. [Google Scholar] [CrossRef]
- Krause, S.; Dersch, R.; Wendorff, J.H.; Finkelmann, H. Photocrosslinkable Liquid Crystal Main-Chain Polymers: Thin Films and Electrospinning. Macromol. Rapid Commun. 2007, 28, 2062–2068. [Google Scholar] [CrossRef]
- Ohm, C.; Kapernaum, N.; Nonnenmacher, D.; Giesselmann, F.; Serra, C.; Zentel, R. Microfluidic synthesis of highly shape-anisotropic particles from liquid crystalline elastomers with defined director field configurations. J. Am. Chem. Soc. 2011, 133, 5305–5311. [Google Scholar] [CrossRef]
- Zhao, L.; Tian, H.; Liu, H.; Zhang, W.; Zhao, F.; Song, X.; Shao, J. Bio-Inspired Soft-Rigid Hybrid Smart Artificial Muscle Based on Liquid Crystal Elastomer and Helical Metal Wire. Small 2023, 19, e2206342. [Google Scholar] [CrossRef]
- Yu, Y.; Li, L.; Liu, E.; Han, X.; Wang, J.; Xie, Y.-X.; Lu, C. Light-driven core-shell fiber actuator based on carbon nanotubes/liquid crystal elastomer for artificial muscle and phototropic locomotion. Carbon 2022, 187, 97–107. [Google Scholar] [CrossRef]
- Liu, H.; Tian, H.; Li, X.; Chen, X.; Zhang, K.; Shi, H.; Wang, C.; Shao, J. Shape-programmable, deformation-locking, and self-sensing artificial muscle based on liquid crystal elastomer and low-melting point alloy. Sci. Adv. 2022, 8, eabn5722. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, J.; Liao, W.; Yang, Z. Liquid Crystal Elastomer Twist Fibers toward Rotating Microengines. Adv. Mater. 2022, 34, e2107840. [Google Scholar] [CrossRef] [PubMed]
- Hu, Z.; Li, Y.; Zhao, T.; Lv, J.-A. Self-winding liquid crystal elastomer fiber actuators with high degree of freedom and tunable actuation. Appl. Mater. Today 2022, 27, 101449. [Google Scholar] [CrossRef]
- Wang, Y.; Liao, W.; Sun, J.; Nandi, R.; Yang, Z. Bioinspired Construction of Artificial Cardiac Muscles Based on Liquid Crystal Elastomer Fibers. Adv. Mater. Technol. 2022, 7, 2100934. [Google Scholar] [CrossRef]
- Wu, D.; Zhang, Y.; Yang, H.; Wei, A.; Zhang, Y.; Mensah, A.; Yin, R.; Lv, P.; Feng, Q.; Wei, Q. Scalable functionalized liquid crystal elastomer fiber soft actuators with multi-stimulus responses and photoelectric conversion. Mater. Horiz. 2023, 10, 2587–2598. [Google Scholar] [CrossRef]
- Hou, W.; Wang, J.; Lv, J.-A. Bioinspired Liquid Crystalline Spinning Enables Scalable Fabrication of High-Performing Fibrous Artificial Muscles. Adv. Mater. 2023, 35, e2211800. [Google Scholar] [CrossRef]
- Li, C.; Liu, Y.; Huang, X.; Jiang, H. Direct Sun-Driven Artificial Heliotropism for Solar Energy Harvesting Based on a Photo-Thermomechanical Liquid-Crystal Elastomer Nanocomposite. Adv. Funct. Mater. 2012, 22, 5166–5174. [Google Scholar] [CrossRef]
- Li, C.; Liu, Y.; Lo, C.-w.; Jiang, H. Reversible white-light actuation of carbon nanotube incorporated liquid crystalline elastomer nanocomposites. Soft Matter 2011, 7, 7511. [Google Scholar] [CrossRef]
- Tanaka, T.; Fujita, M.; Takeuchi, A.; Suzuki, Y.; Uesugi, K.; Ito, K.; Fujisawa, T.; Doi, Y.; Iwata, T. Formation of Highly Ordered Structure in Poly[(R)-3-hydroxybutyrate-co-(R)-3-hydroxyvalerate] High-Strength Fibers. Macromolecules 2006, 39, 2940–2946. [Google Scholar] [CrossRef]
- Ohm, C.; Brehmer, M.; Zentel, R. Liquid crystalline elastomers as actuators and sensors. Adv. Mater. 2010, 22, 3366–3387. [Google Scholar] [CrossRef]
- Warner, M.; Terentjev, E. Liquid Crystal Elastomers; International Series of Monographs on Physics 120; Clarendon Press: Oxford, UK, 2009. [Google Scholar]
- Niu, H.; Wang, Y.; Wang, J.; Yang, W.; Dong, Y.; Bi, M.; Zhang, J.; Xu, J.; Bi, S.; Wang, B.; et al. Reducing the actuation threshold by incorporating a nonliquid crystal chain into a liquid crystal elastomer. RSC Adv. 2018, 8, 4857–4866. [Google Scholar] [CrossRef]
- Qin, B.; Yang, W.; Xu, J.; Wang, X.; Li, X.; Li, C.; Gao, Y.; Wang, Q.-E. Photo-Actuation of Liquid Crystalline Elastomer Materials Doped with Visible Absorber Dyes under Quasi-Daylight. Polymers 2019, 12, 54. [Google Scholar] [CrossRef] [PubMed]
- Torras, N.; Zinoviev, K.E.; Camargo, C.J.; Campo, E.M.; Campanella, H.; Esteve, J.; Marshall, J.E.; Terentjev, E.M.; Omastová, M.; Krupa, I.; et al. Tactile device based on opto-mechanical actuation of liquid crystal elastomers. Sens. Actuators A Phys. 2014, 208, 104–112. [Google Scholar] [CrossRef]
- Xu, J.; Chen, S.; Yang, W.; Qin, B.; Wang, X.; Wang, Y.; Cao, M.; Gao, Y.; Li, C.; Dong, Y. Photo actuation of liquid crystalline elastomer nanocomposites incorporated with gold nanoparticles based on surface plasmon resonance. Soft Matter. 2019, 15, 6116–6126. [Google Scholar] [CrossRef]
- Madden, J.D.W.; Vandesteeg, N.A.; Anquetil, P.A.; Madden, P.G.A.; Takshi, A.; Pytel, R.Z.; Lafontaine, S.R.; Wieringa, P.A.; Hunter, I.W. Artificial Muscle Technology: Physical Principles and Naval Prospects. IEEE J. Ocean. Eng. 2004, 29, 706–728. [Google Scholar] [CrossRef]
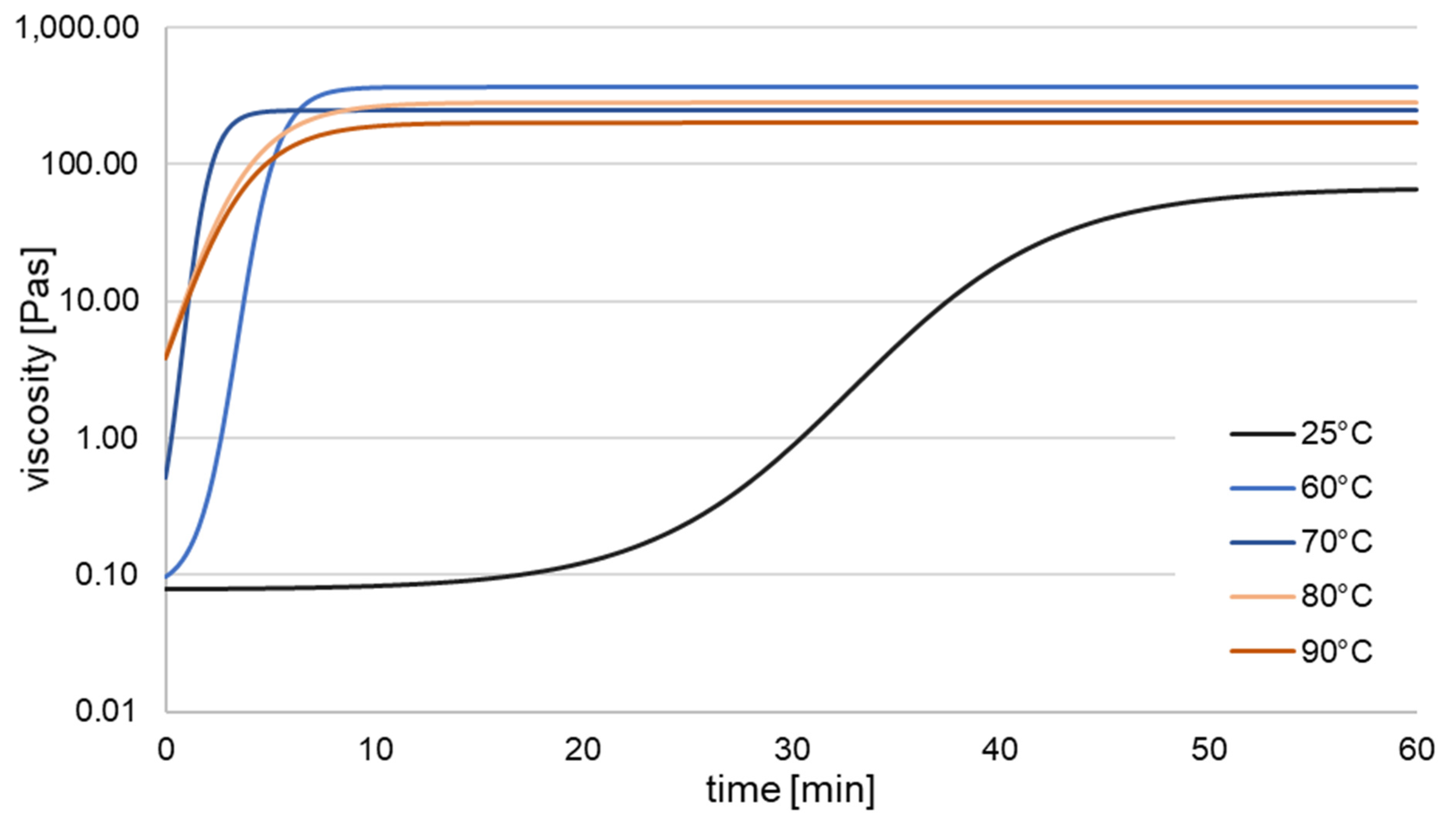


| Crosslinking Temperature | ηmax | (Theoretical) Set-on Crosslinking | Slope | Fitting Parameters | |||
|---|---|---|---|---|---|---|---|
| a | b | c | d | ||||
| 25 °C | (66.83 Pa s) * | 23.32 min | 0.15 Pa s min−1 | 2.94 | −1.11 | 838.12 | 0.09 |
| 60 °C | 369.35 Pa s | 1.33 min | 0.95 Pa s min−1 | 3.68 | −1.11 | 36.43 | 0.45 |
| 70 °C | 246.86 Pa s | −0.67 min | 1.28 Pa s min−1 | 3.50 | −1.11 | 3.27 | 0.63 |
| 80 °C | 282.34 Pa s | −4.34 min | 0.43 Pa s min−1 | 3.56 | −1.11 | 1.07 | 0.21 |
| 90 °C | 203.76 Pa s | −4.34 min | 0.42 Pa s min−1 | 3.42 | −1.11 | 1.02 | 0.21 |
| Additional Weights | Contraction | Mass Specific Work | |
|---|---|---|---|
| 3.50 g | 1.95 ± 0.22% | 1.036 ± 0.281 J kg−1 | |
| 4.71 g | 2.72 ± 0.12% | 1.919 ± 0.588 J kg−1 | |
| 5.76 g | 2.94 ± 0.22% | 2.607 ± 0.803 J kg−1 | |
| 6.26 g | 2.95 ± 0.35% | 3.101 ± 1.023 J kg−1 | |
| 6.76 g | 2.83 ± 0.46% | 3.279 ± 1.338 J kg−1 | |
| 7.26 g | 2.98 ± 0.76% | 3.821 ± 1.793 J kg−1 | |
| 7.76 g | 2.99 ± 0.50% | 3.662 ± 1.488 J kg−1 | |
| 8.26 g | 2.43 ± 0.00% * | 2.528 ± 0.555 J kg−1 * | |
| Max. values | 7.14 ± 0.82 g | 3.21 ± 0.44% | 3.857 ± 1.318 J kg−1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Benecke, L.; Schwingshackl, S.A.; Schyra, P.; Cherif, C.; Aibibu, D. Generation of Liquid Crystal Elastomer Fibers via a Wet Spinning Technology with Two-Stage Crosslinking. Polymers 2025, 17, 494. https://doi.org/10.3390/polym17040494
Benecke L, Schwingshackl SA, Schyra P, Cherif C, Aibibu D. Generation of Liquid Crystal Elastomer Fibers via a Wet Spinning Technology with Two-Stage Crosslinking. Polymers. 2025; 17(4):494. https://doi.org/10.3390/polym17040494
Chicago/Turabian StyleBenecke, Lukas, Sina Anna Schwingshackl, Peter Schyra, Chokri Cherif, and Dilbar Aibibu. 2025. "Generation of Liquid Crystal Elastomer Fibers via a Wet Spinning Technology with Two-Stage Crosslinking" Polymers 17, no. 4: 494. https://doi.org/10.3390/polym17040494
APA StyleBenecke, L., Schwingshackl, S. A., Schyra, P., Cherif, C., & Aibibu, D. (2025). Generation of Liquid Crystal Elastomer Fibers via a Wet Spinning Technology with Two-Stage Crosslinking. Polymers, 17(4), 494. https://doi.org/10.3390/polym17040494







