Steel Plates Versus Hybrid CFRP/Steel Stirrups for Strengthening of Shear-Deficient Concrete Wide Beams Supporting Columns
Abstract
1. Introduction
2. Experimental Campaign
2.1. Test Specimens
2.2. Properties of Materials
2.3. Properties of Materials
2.3.1. Shear Strengthening Using Steel Plate (BS-S1)
2.3.2. Shear Strengthening Using CFRP Sheet with U-Stirrups (BS-S2)
2.4. Testing Configuration and Instrumentation
3. Test Results and Discussion
3.1. Failure Modes
3.1.1. Control Specimen BS-CON
3.1.2. Control Specimen BS-ACI
3.1.3. Strengthened Specimen BS-S1
3.1.4. Strengthened Specimen BS-S2
3.2. Load Versus Displacement and Strain Response
3.2.1. Control Specimen BS-CON
3.2.2. Control Specimen BS-ACI
3.2.3. Strengthened Specimen BS-S1
3.2.4. Strengthened Specimen BS-S2
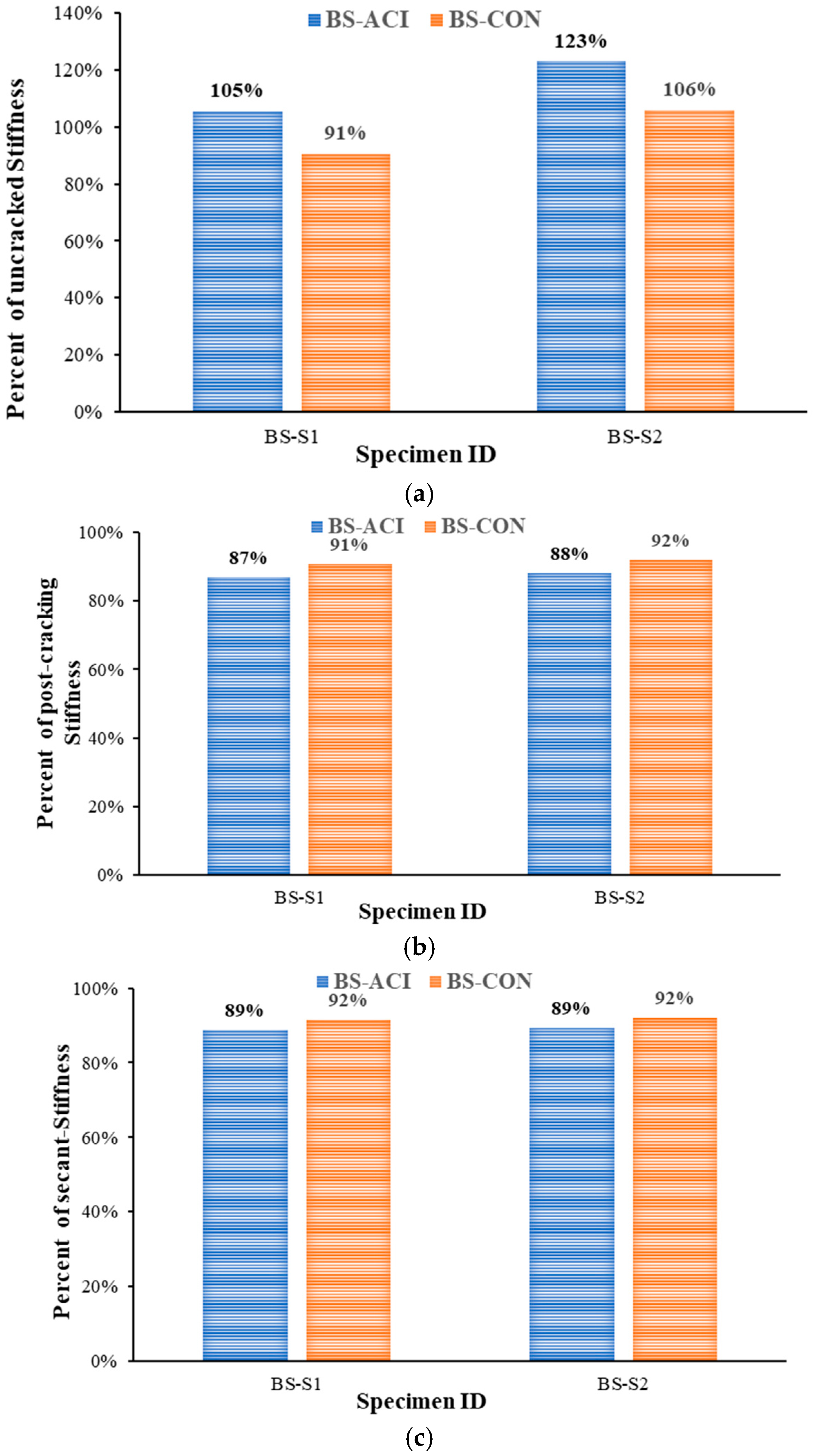
3.3. Comparison of Test Results
4. Analytical Prediction of Shear Capacities
4.1. Control Specimens
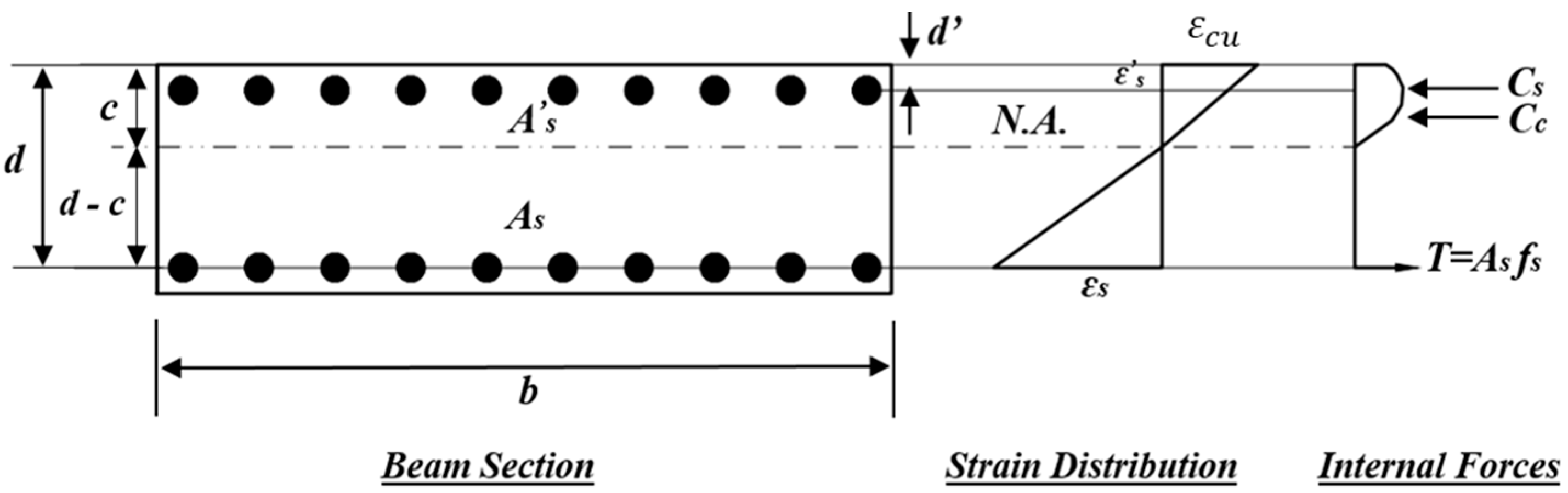
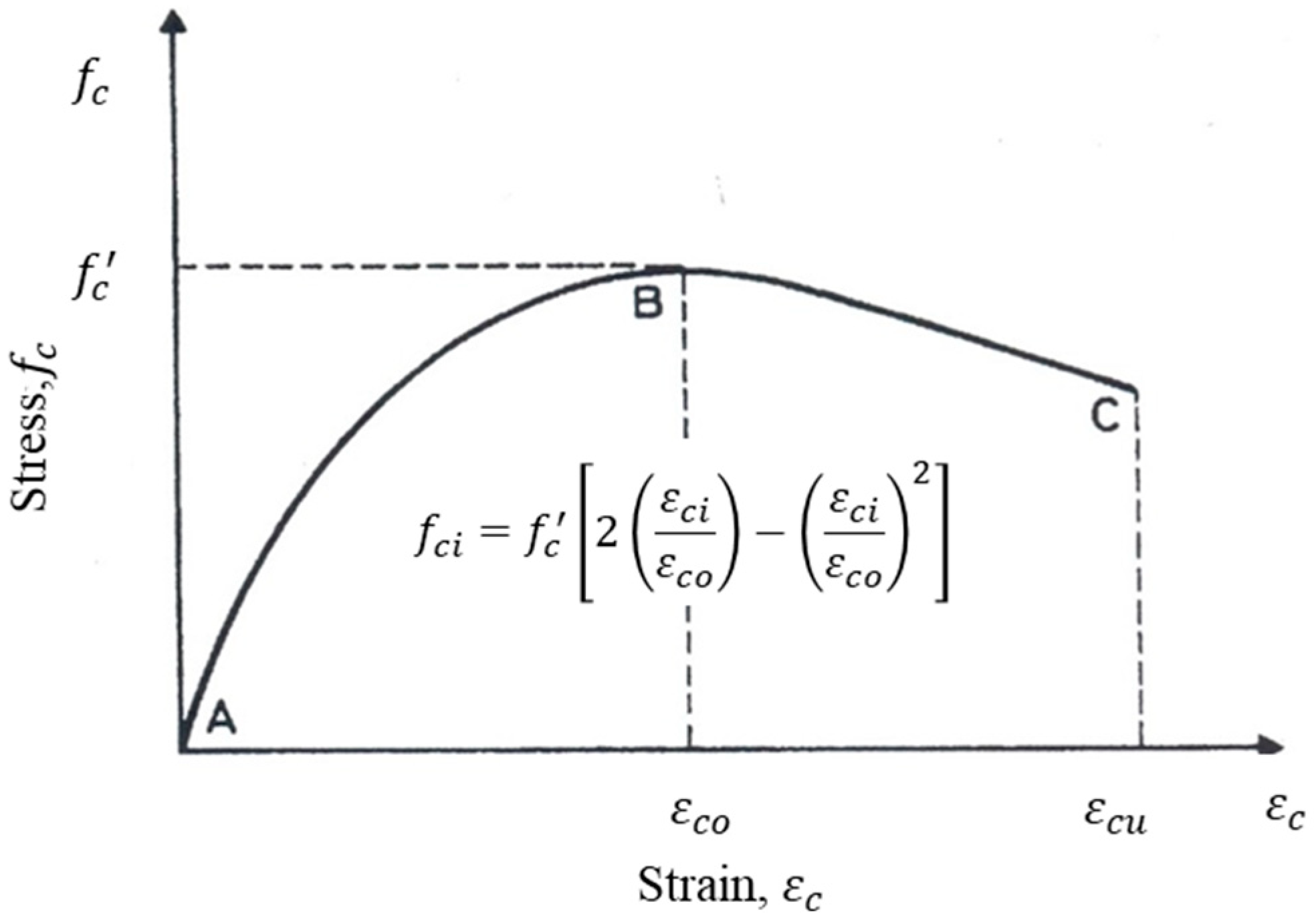
4.1.1. Calculation of Flexural Capacity
4.1.2. Calculation of Shear Capacity
4.2. Strengthened Specimens
4.2.1. Estimation of Shear Capacity for BS-S1
4.2.2. Estimation of Shear Capacity for BS-S2
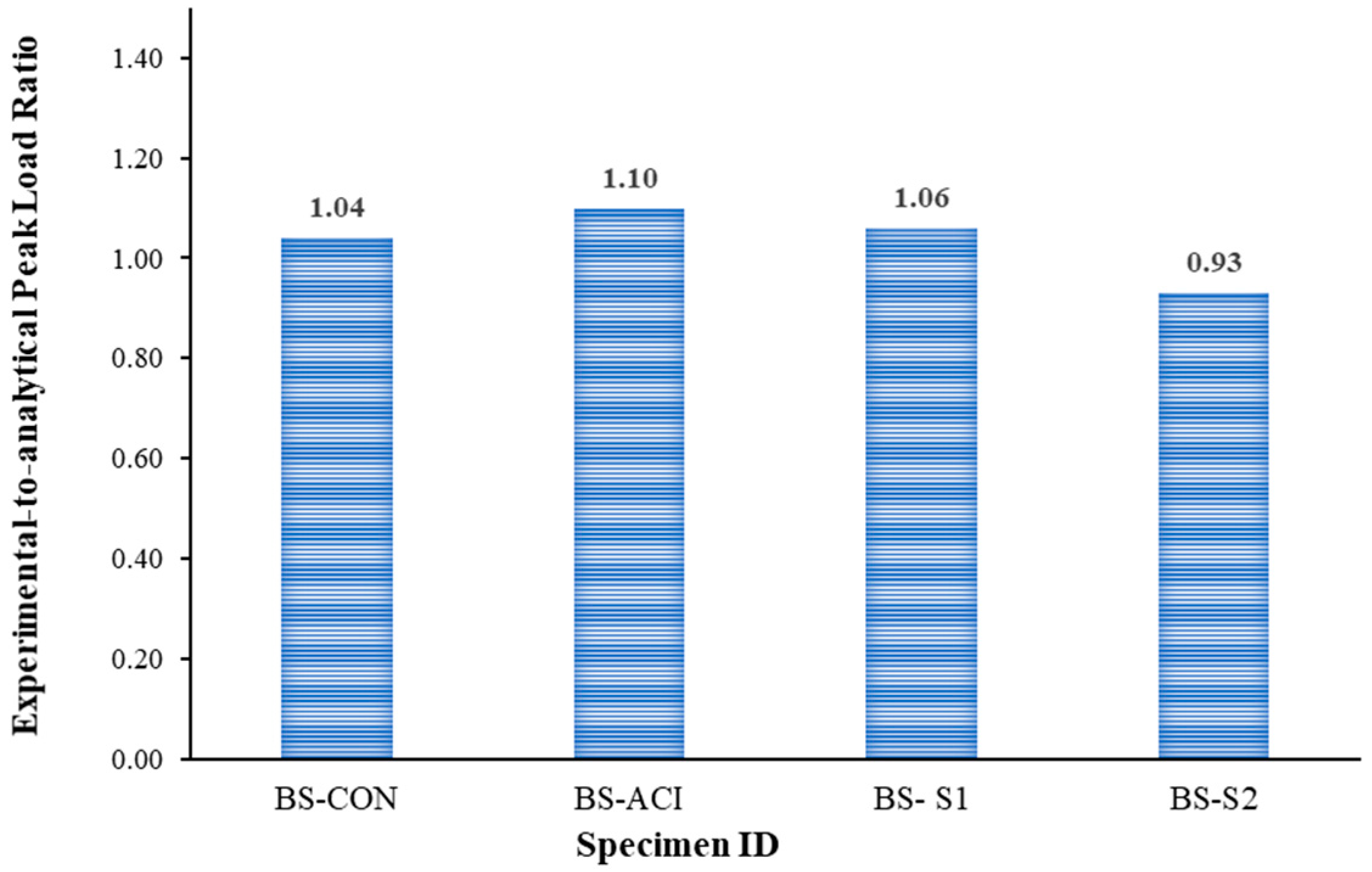
4.3. Peak Load Comparison of Tested Specimens
5. Conclusions
- Shear reinforcement in RC wide beams, provided in accordance with the design codes (e.g., ACI 318-19), changes the mode of failure from shear to flexure, thereby making it ductile.
- For avoiding brittle failure in RC wide beams supporting columns, their shear strength must exceed flexural capacity, by designing as per the current code requirements.
- The failure mode observed in the strengthened specimen BS-S1 indicates that the presence of the external steel plates technique had an insignificant influence on the shear resistance of wide beams compared to the control specimen BS-CON, which is deficient in shear. Therefore, it is suggested to add internal stirrups along with external plates.
- The shear strengthening of CFRP U-wraps combined with steel U-stirrups in the strengthened specimen BS-S2 improved the shear resistance of wide beams by 82% compared to the control specimen. Moreover, this strengthening scheme showed an increase in uncrack stiffness by 6% in comparison with the control specimens BS-CON.
- The strengthening schemes applied to specimens BS-S1 and BS-S2 led to increases in dissipated energy of approximately 59% and 184%, respectively, in comparison with the control specimen (BS-CON).
- It is recommended to review and incorporate international design codes that address the specific challenges of wide beams supporting columns to ensure adherence to best practices in structural safety. Also, it is recommended to conduct a finite element analysis to model the shear response of RC wide beams having columns and compare the results with the experimental findings obtained in this investigation.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sherwood, E.G.; Lubell, A.S.; Bentz, E.C.; Collins, M.P. One-Way Shear Strength of Thick Slabs and Wide Beams. ACI Struct. J. 2006, 103, 794–802. [Google Scholar] [CrossRef] [PubMed]
- Haido, J.H.; Musa, I.H. Cracking Strength of Steel Fiber Reinforced Concrete Shallow Beams under Impact Actions. Int. J. Sci. Eng. Res. 2013, 4, 1–9. [Google Scholar]
- Abbas, R.F.; Sultan, W.H.; Fahad, J.J. Strengthening of Reinforced Concrete Wide Beams Using Steel Plates Within Shear Zone. IJCIET 2018, 9, 89–900. [Google Scholar]
- Conforti, A.; Minelli, F.; Plizzari, G.A. Wide-Shallow Beams with and without Steel Fibres: A Peculiar Behaviour in Shear and Flexure. Compos. Part B Eng. 2013, 51, 282–290. [Google Scholar] [CrossRef]
- ACI Committee 318. Building Code Requirements for Structural Concrete and Commentary; American Concrete Institute (ACI): Detroit, MI, USA, 2019. [Google Scholar]
- SBC Committee 304. The Saudi Building Code for Concrete Structures SBC 304; Saudi Building Code (SBC) National Committee: Saudi, Arabia, 2018.
- Lotfy, E.M.; Mohamadien, H.A.; Hassan, H.M. Effect of Web Reinforcement on Shear Strength of Shallow Wide Beams. Int. J. Eng. Tech. Res. 2014, 2, 98–107. [Google Scholar]
- Said, M.; Elrakib, T.M. Enhancement of Shear Strength and Ductility for Reinforced Concrete Wide Beams Due to Web Reinforcement. HBRC J. 2013, 9, 235–242. [Google Scholar] [CrossRef]
- Hanafy, M.M.; Mohamed, H.M.; Yehia, N.A.B. On the Contribution of Shear Reinforcement in Shear Strength of Shallow Wide Beams. Life Sci. J. 2012, 09, 484–498. [Google Scholar]
- Soliman, A.A.; Mansour, D.M.; Khalil, A.H.; Ebid, A. The Impact of Shear Reinforcement Amount and Arrangement on the Shear Capacity of Shallow RC Beams: An Experimental Study. Civ. Eng. J. 2023, 9, 3147–3160. [Google Scholar] [CrossRef]
- Lubell, A.S.; Bentz, E.C.; Collins, M.P. Shear Reinforcement Spacing in Wide Members. ACI Struct. J. 2009, 106, 205–214. [Google Scholar] [CrossRef]
- Shuraim, A.B. Transverse Stirrup Configurations in RC Wide Shallow Beams Supported on Narrow Columns. J. Struct. Eng. 2012, 138, 416–424. [Google Scholar] [CrossRef]
- Barnes, R.A.; Baglin, P.S.; Mays, G.C.; Subedi, N.K. External Steel Plate Systems for the Shear Strengthening of Reinforced Concrete Beams. Eng. Struct. 2001, 23, 1162–1176. [Google Scholar] [CrossRef]
- Abadel, A.A. Experimental Investigation for Shear Strengthening of Reinforced Self-Compacting Concrete Beams Using Different Strengthening Schemes. J. Mater. Res. Technol. 2021, 15, 1815–1829. [Google Scholar] [CrossRef]
- Elsanadedy, H.M.; Al-Salloum, Y.A.; Almusallam, T.H.; Alshenawy, A.O.; Abbas, H. Experimental and Numerical Study on FRP-Upgraded RC Beams with Large Rectangular Web Openings in Shear Zones. Constr. Build. Mater. 2019, 194, 322–343. [Google Scholar] [CrossRef]
- Albidah, A.; Abadel, A.; Abbas, H.; Almusallam, T.; Al-Salloum, Y. Experimental and Analytical Study of Strengthening Schemes for Shear Deficient RC Deep Beams. Constr. Build. Mater. 2019, 216, 673–686. [Google Scholar] [CrossRef]
- Al-Salloum, Y.A.; Siddiqui, N.A.; Elsanadedy, H.M.; Abadel, A.A.; Aqel, M.A. Textile-Reinforced Mortar versus FRP as Strengthening Material for Seismically Deficient RC Beam-Column Joints. J. Compos. Constr. 2011, 15, 920–933. [Google Scholar] [CrossRef]
- Liao, J.; Zeng, J.J.; Jiang, C.; Li, J.X.; Yuan, J.S. Stress-strain behavior and design-oriented model for FRP spiral strip-confined concrete. Compos. Struct. 2022, 293, 115747. [Google Scholar] [CrossRef]
- Ye, Y.Y.; Zhuge, Y.; Smith, S.T.; Zeng, J.J.; Bai, Y.L. Behavior of GFRP-RC columns under axial compression: Assessment of existing models and a new axial load-strain model. J. Build. Eng. 2022, 47, 103782. [Google Scholar] [CrossRef]
- Abass, A.L.; Hassan, Y.R. Shear Behavior of Reinforced Concrete Wide Beams Strengthened with CFRP Sheet without Stirrups. Diyala J. Eng. Sci. 2019, 12, 80–98. [Google Scholar] [CrossRef]
- Kim, M.S.; Kang, J.; Lee, Y.H. Shear Strength of Concrete Wide Beams Shear Reinforced with GFRP Plates. Polym. Polym. Compos. 2018, 26, 111–118. [Google Scholar] [CrossRef]
- Mohamed, Y.T.; Taher, S.E.-D.; Nagy, A.; Mahfouz, S.Y. Shear Behavior of Shallow-Wide Beams Strengthened by External SHCC Jacket. HBRC J. 2020, 16, 351–363. [Google Scholar] [CrossRef]
- Moubarak, A.M.R.; Elwardany, H.; Abu El-hassan, K.; El-Din Taher, S. Shear Strengthening of Wide-Shallow Beams by Inserted Fasteners. Eng. Struct. 2022, 268, 114554. [Google Scholar] [CrossRef]
- ASTM C39/C39M; Standard Test Method for Compressive Strength of Cylindrical. ASTM International: West Conshohocken, PA, USA, 2018.
- ASTM E8/E8M; Standard Test Methods for Tension Testing of Metallic Materials. ASTM International: West Conshohocken, PA, USA, 2016.
- ASTM A370–17; Standard Test Methods and Definitions for Mechanical Testing of Steel Products. ASTM International: West Conshohocken, PA, USA, 2017.
- Sika Thixotropic Epoxy Resin Adhesive. Available online: https://lbn.sika.com/dms/getdocument.get/3768ebb4-85cc-3ed5-b870-764a2dc4854e/Sikadur%20%20-31CF.pdf (accessed on 23 October 2025).
- Sika Anchoring Adhesive for Medium to High Loads. Available online: https://ind.sika.com/dam/dms/in01/h/sika_anchorfix_-2tropical.pdf (accessed on 23 October 2025).
- ACI Committee 440. Guide for the Design and Construction of Externally Bonded FRP Systems for Strengthening Concrete Structures; American Concrete Institute: Farmington Hills, MI, USA, 2017; ISBN 978-1-945487-59-0. [Google Scholar]
- Lin, C.-H.; Lin, S.-P.; Tseng, C.-H. High-Workability Concrete Columns Under Concentric Compression. Struct. J. 2004, 101, 85–93. [Google Scholar] [CrossRef]
- Mohamed, H.A. Improvement in the Ductility of Over-Reinforced NSC and HSC Beams by Confining the Compression Zone. Structures 2018, 16, 129–136. [Google Scholar] [CrossRef]
- Hognestad, E. Study of Combined Bending and Axial Load in Reinforced Concrete Members. University of Illinois. Engineering Experiment Station. Bulletin; no. 399. 1951. Available online: https://www.ideals.illinois.edu/items/4902 (accessed on 23 October 2025).
- Canadian Standards Association (CSA). Design of Concrete Structures, 6th ed.; CSA A23.3-14; CSA Group: Mississauga, ON, Canada, 2015. [Google Scholar]
- European Committee for Standardization. Eurocode 2: Design of Concrete Structures—Part 1-1: General Rules and Rules for Buildings; European Committee for Standardization: Brussels, Belgium, 2004. [Google Scholar]
- Standards Australia. AS 3600 Concrete Structures, 4th ed.; Standards Australia: Sydney, Australia, 2009; ISBN 978-0-7337-9347-9. [Google Scholar]
- Japan Society of Civil Engineers (JSCE). Standard Specifications for Concrete Structures; Japan Society of Civil Engineers (JSCE): Tokyo, Japan, 2007. [Google Scholar]
- Kim, J.-K.; Park, Y.-D. Prediction of Shear Strength of Reinforced Concrete Beams without Web Reinforcement. Mater. J. 1996, 93, 213–222. [Google Scholar] [CrossRef]
- Rebeiz, K.S. Shear Strength Prediction for Concrete Members. J. Struct. Eng. 1999, 125, 301–308. [Google Scholar] [CrossRef]
- Bentz, E.C. Empirical Modeling of Reinforced Concrete Shear Strength Size Effect for Members without Stirrups. ACI Struct. J. 2005, 102, 232–241. [Google Scholar] [CrossRef] [PubMed]
- Cladera, A.; Marí, A.R. Shear Design Procedure for Reinforced Normal and High-Strength Concrete Beams Using Artificial Neural Networks. Part I: Beams without Stirrups. Eng. Struct. 2004, 26, 917–926. [Google Scholar] [CrossRef]
- Alluqmani, A.E. Development of Prediction and Design Models for Wide Concrete Beams with Various Load and Support Widths. Ph.D. Thesis, The University of Strathclyde, Glasgow, UK, 2014. [Google Scholar]
- ECP 203. Egyptian Code of Practice for Design and Construction of Reinforced Concrete Structures; Research Centre for Houses Building and Physical Planning Cairo: Giza, Egypt, 2018. [Google Scholar]
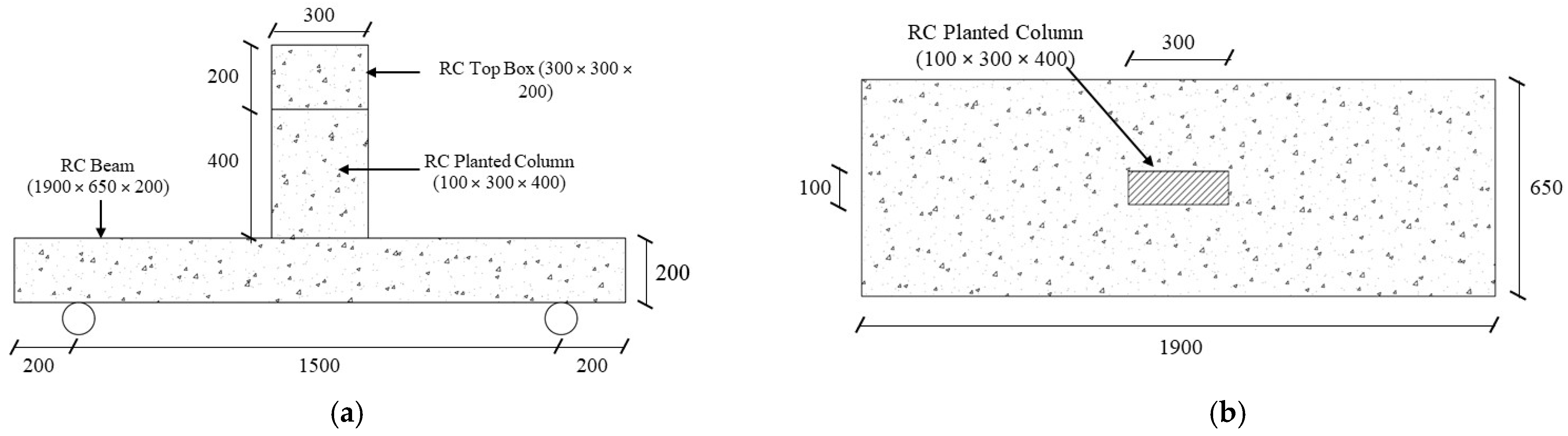
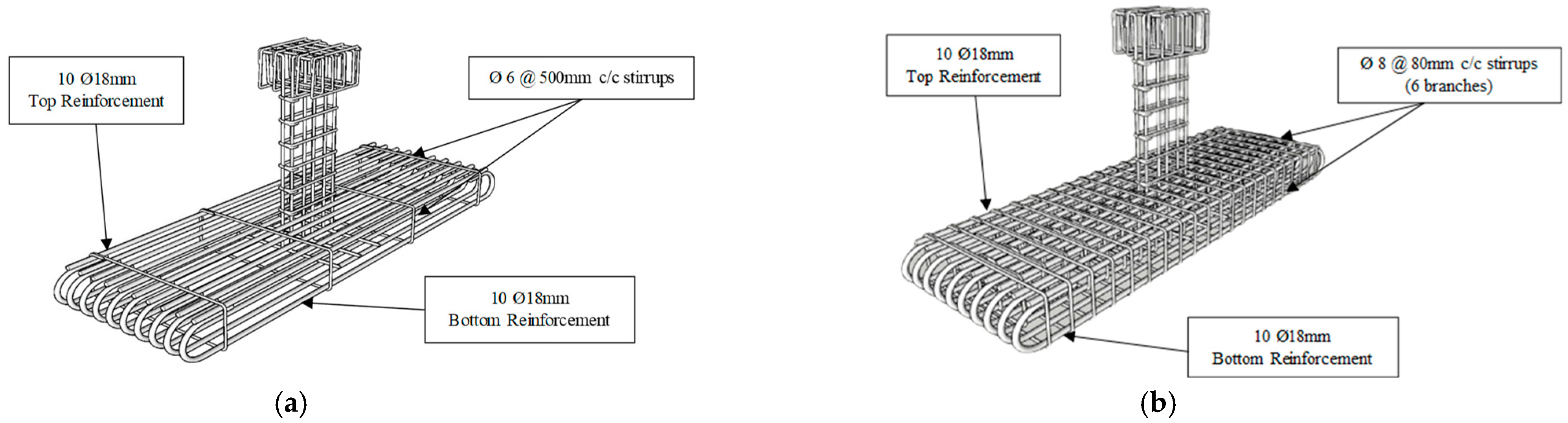

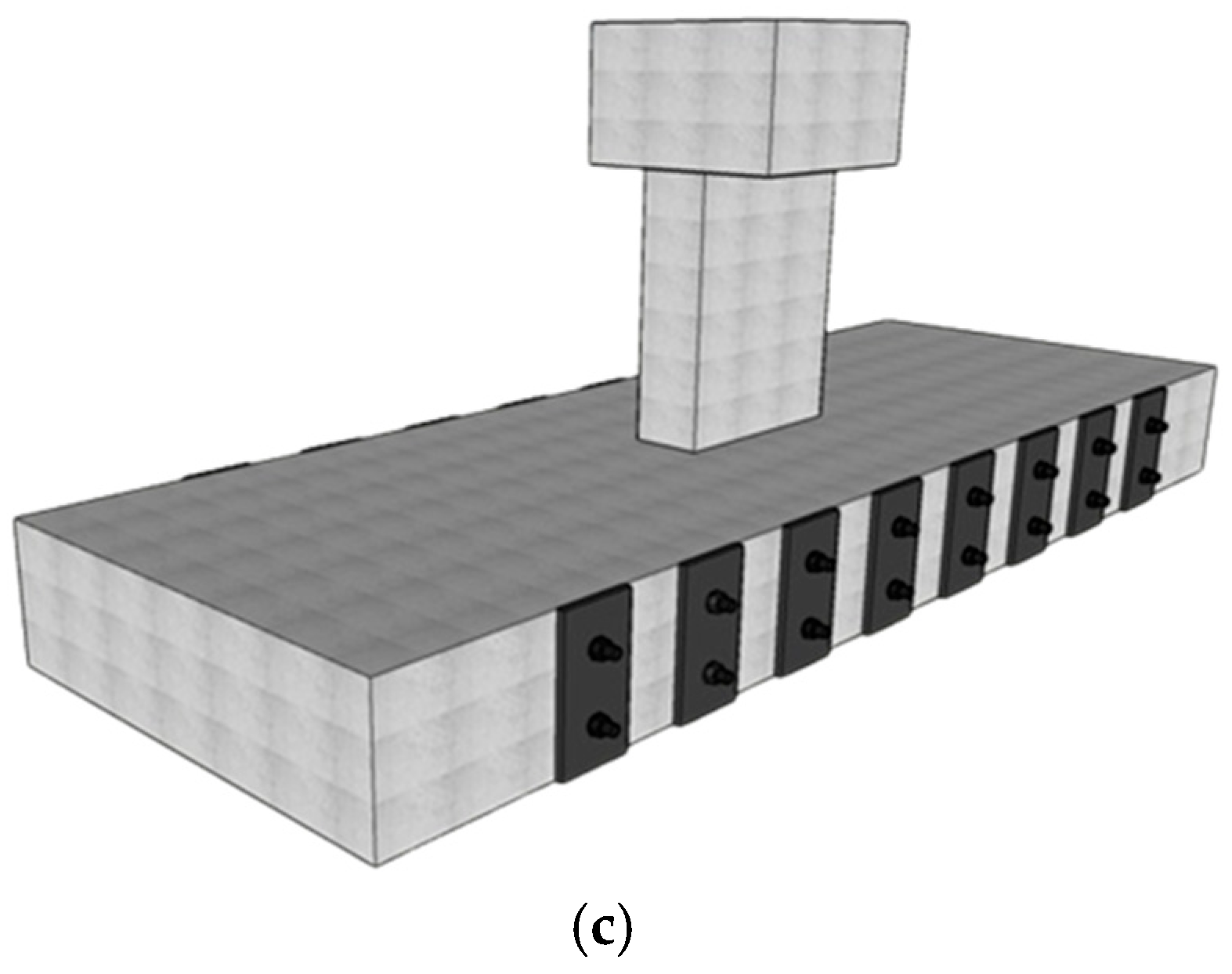
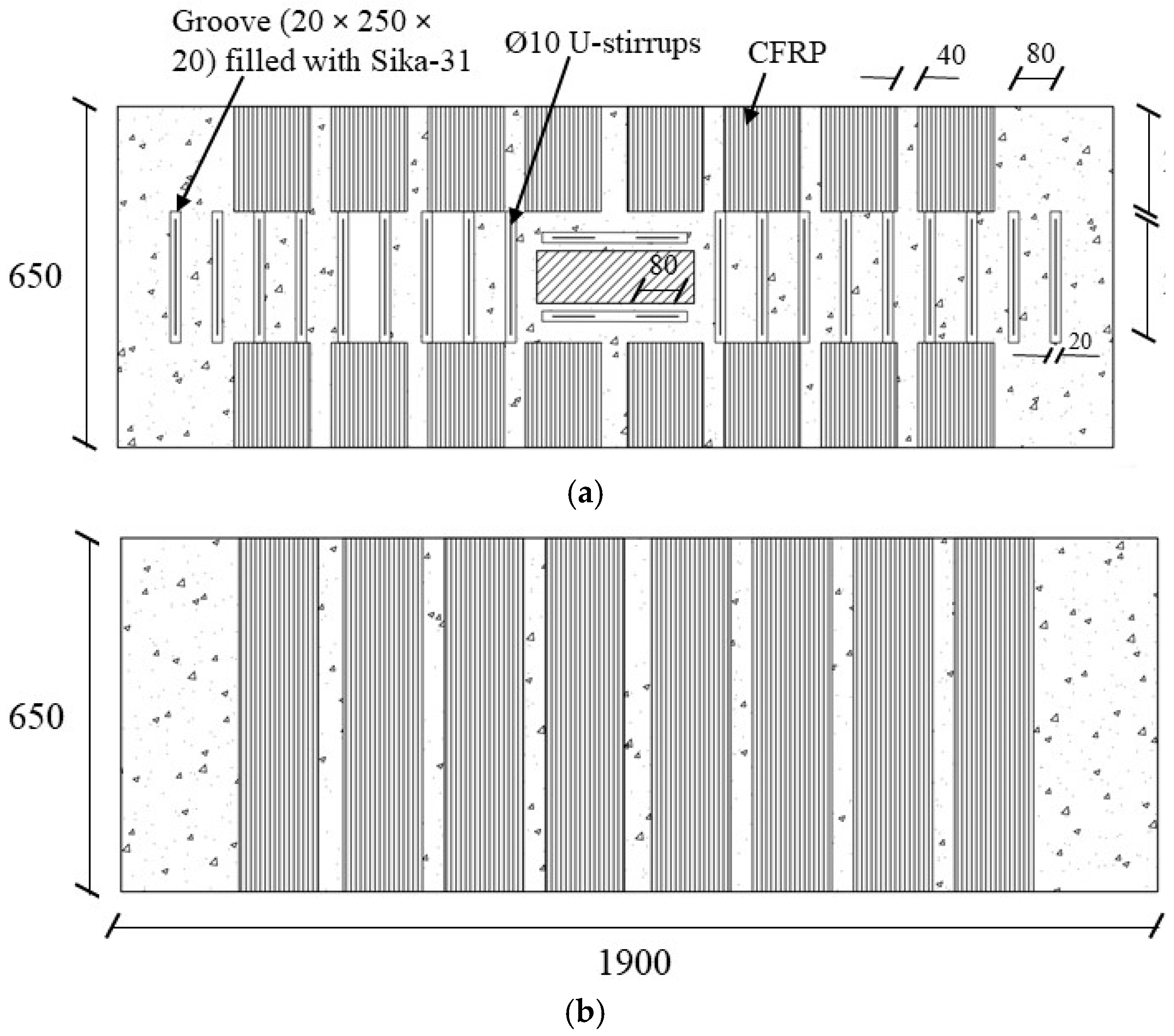
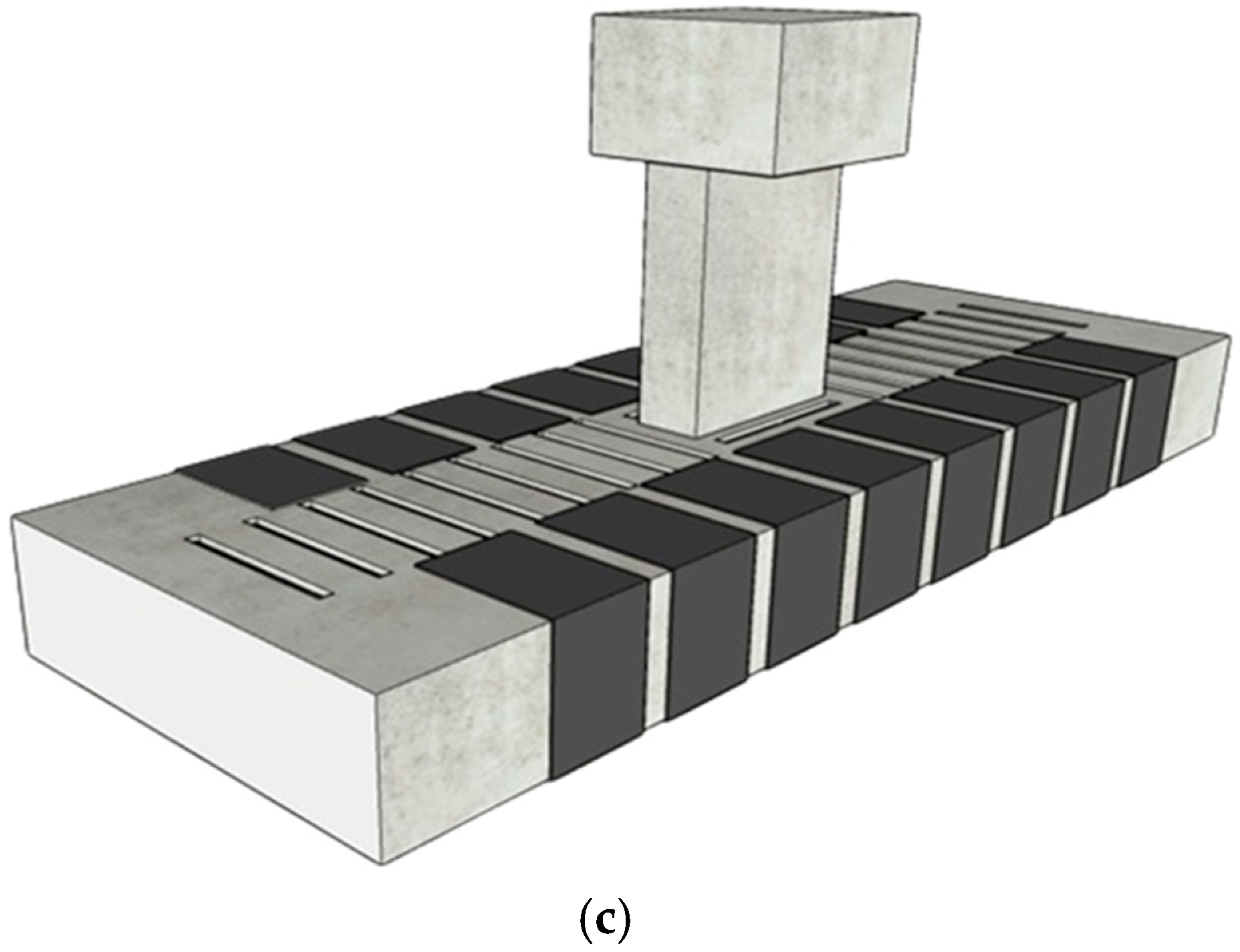
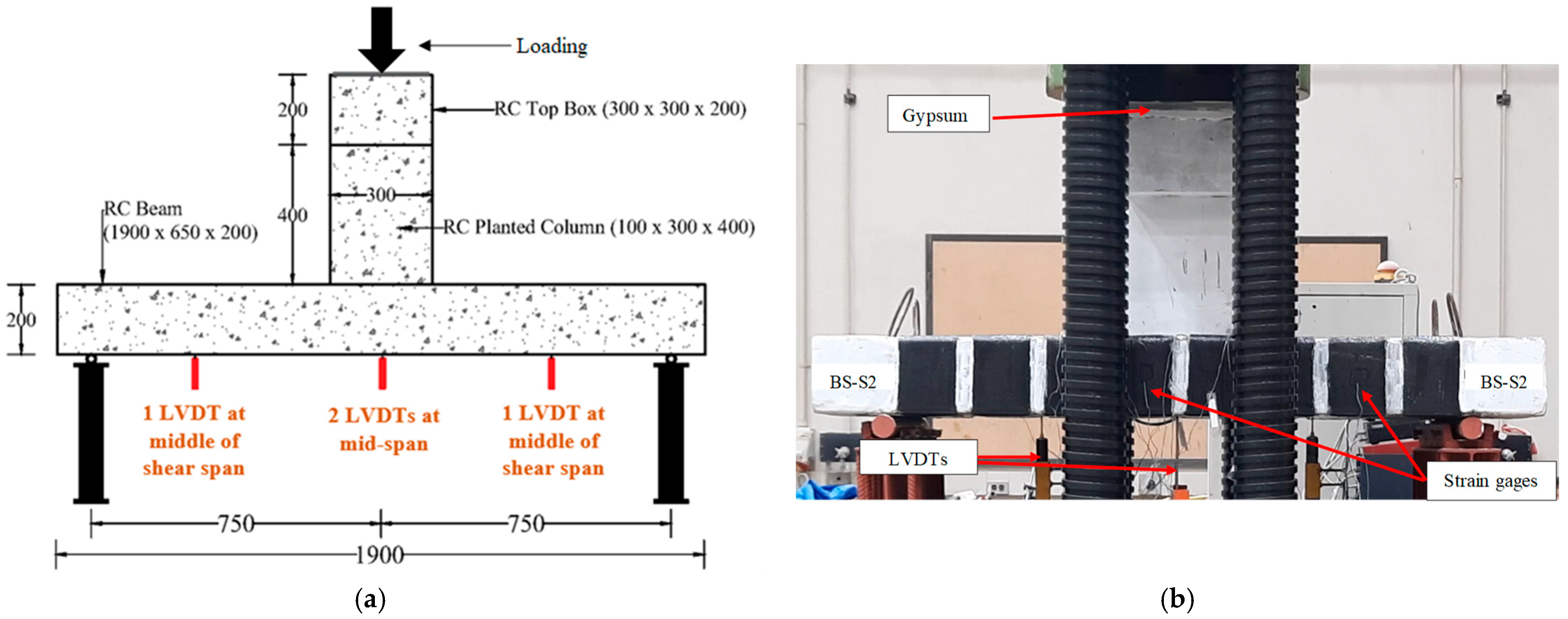






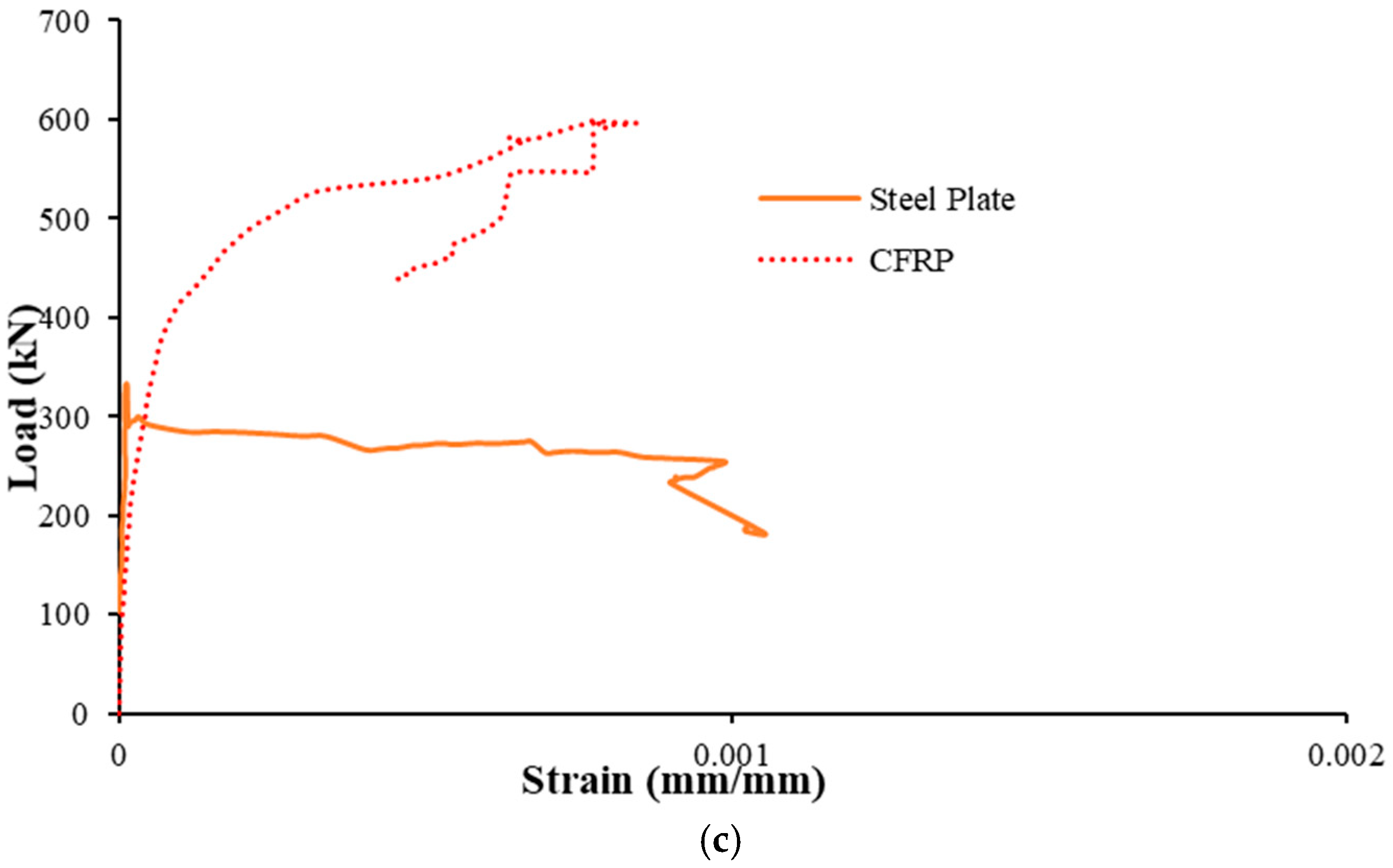
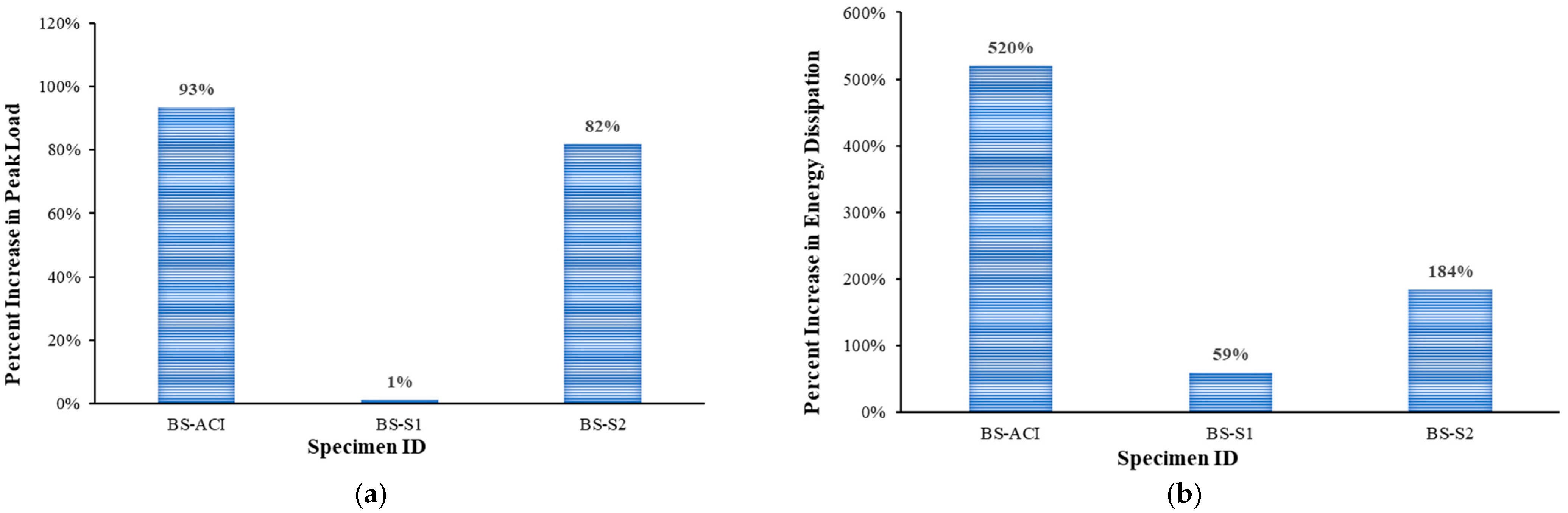

| Specimen ID | Shear Stirrups | Specimen Type | Shear Strengthening | No. of Beams |
|---|---|---|---|---|
| BS-CON | 2L-Ø6@500 | Control specimen | None | 1 |
| BS-ACI | 6L-Ø8@80 | Control specimen | None | 1 |
| BS-S1 | 2L-Ø6@500 | Strengthened specimen | Scheme 1—Externally bonded steel plates | 1 |
| BS-S2 | 2L-Ø6@500 | Strengthened specimen | Scheme 2—Externally bonded CFRP U-wraps combined with planted steel U-stirrups | 1 |
| Total No. of specimens | 4 | |||
| Concrete | ||
| 28-day compressive strength | 39 MPa | |
| Compressive strength on testing day | 40 MPa | |
| Steel reinforcement | ||
| Rebar diameter (mm) | Tensile strength (MPa) | |
| Yield | Ultimate | |
| Ø 6 | 440 | 505 |
| Ø 8 | 635 | 667 |
| Ø 10 | 547 | 572 |
| Ø 18 | 526 | 654 |
| CFRP Sheet | ||
| Elastic modulus | 71.46 GPa | |
| Rupture strain | 0.01 mm/mm | |
| Ultimate tensile strength | 710 MPa | |
| Thickness per layer | 1.3 mm | |
| Steel plate | ||
| Thickness | 10 mm | |
| Elastic modulus | 200 GPa | |
| Yield tensile strength | 249 MPa | |
| Ultimate tensile strength | 335 MPa | |
| Fast Curing Anchoring Adhesive (Sika AnchorFix®-2) | ||
| Compressive strength | 70 MPa | |
| Tensile strength | 29 MPa | |
| Elastic modulus | 3800 MPa | |
| Epoxy-based mortar (Sikadur-31) | ||
| Compressive strength | 40–45 MPa | |
| Tensile strength | 15–20 MPa | |
| Young’s modulus | 4.3 GPa | |
| Specimen ID | Pcr (kN) | Py (kN) | Pu (kN) | Δcr (mm) | Δy (mm) | Δpu (mm) | Δu (mm) | Failure Pattern |
|---|---|---|---|---|---|---|---|---|
| BS-CON | 45 | - | 330 | 0.38 | - | 4.76 | 9.7 | Shear |
| BS-ACI | 74 | 518 | 638 | 0.74 | 7.25 | 11.40 | 68.0 | Flexure |
| BS-S1 | 51 | - | 334 | 0.47 | - | 5.26 | 10.8 | Shear |
| BS-S2 | 63 | 524 | 601 | 0.5 | 8.20 | 11.52 | 16.0 | Flexure-shear |
| Specimen ID | (kN/mm) | (kN/mm) | (kN/mm) | Euf (kN/mm) | Eus (kN/mm) | |||
|---|---|---|---|---|---|---|---|---|
| BS-CON | 119.53 | 65.02 | 69.37 | 6102 | 2209 | 1 | 2 | 6.8 |
| BS-ACI | 102.78 | 67.99 | 71.45 | 37811 | 37313 | 1.6 | 9 | 9.6 |
| BS-S1 | 108.30 | 59.10 | 63.50 | 9725 | 2466 | 1 | 2 | 9.5 |
| BS-S2 | 126.44 | 59.84 | 63.90 | 17313 | 6996 | 1.4 | 2 | 6.5 |
| Specimen ID | εs,pu | εsu | εsp,u | εs,CFRPu |
|---|---|---|---|---|
| BS-CON | 0.001884 | 0.00189 | - | - |
| BS-ACI | 0.00592 | 0.00615 | - | - |
| BS-S1 | 0.001925 | 0.001925 | 0.001 | - |
| BS-S2 | 0.004179 | 0.006627 | - | 0.000842 |
| Reference | Shear Capacity of Concrete, Vc (Units: N, mm) | Vc (kN) | Vc,exp/Vc |
|---|---|---|---|
| ACI 318 [5] | are the width and effective depth of the beam | 120 | 1.38 |
| ACI 318 [5] | = concrete’s compressive strength = factored bending moment and shear force = main rebar ratio | 120 | 1.38 |
| CSA A23.3-14 [33] | = factor for concrete unit weight = 1.0 for normal weight concrete where = factored moment and shear force, where = Effective shear depth, defined as the greater of 0.9 d or 0.72 h where h is the total depth of the beam. = modulus of elasticity of steel; = Cross-sectional area of the tensile reinforcement. = maximum size of coarse aggregate. not exceeding 64 MPa | 105 | 1.57 |
| Eurocode 2 [34] | Characteristic compressive cylinder strength of concrete | 175 | 0.94 |
| AS 3600 [35] | for members subjected to axial compression; N = compressive axial force; | 172 | 0.96 |
| JSCE Guidelines [36] | 158 | 1.04 | |
| Kim and Park [37] | 171 | 0.96 | |
| Rebeiz [38] | 175 | 0.94 | |
| Bentz [39] | 121 | 1.36 | |
| Cladera and Mari [40] | 171 | 0.96 |
| Specimen ID | Pu,exp (kN) | Pu (kN) | Pu,exp/Pu |
|---|---|---|---|
| BS-CON | 330 | 316 | 1.04 |
| BS-ACI | 638 | 582 | 1.10 |
| BS-S1 | 334 | 316 | 1.06 |
| BS-S2 | 601 | 643 | 0.93 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Hamed, O.; Abadel, A.; Almusallam, T.; Elsanadedy, H.; Abbas, H.; Al-Salloum, Y. Steel Plates Versus Hybrid CFRP/Steel Stirrups for Strengthening of Shear-Deficient Concrete Wide Beams Supporting Columns. Polymers 2025, 17, 2857. https://doi.org/10.3390/polym17212857
Al-Hamed O, Abadel A, Almusallam T, Elsanadedy H, Abbas H, Al-Salloum Y. Steel Plates Versus Hybrid CFRP/Steel Stirrups for Strengthening of Shear-Deficient Concrete Wide Beams Supporting Columns. Polymers. 2025; 17(21):2857. https://doi.org/10.3390/polym17212857
Chicago/Turabian StyleAl-Hamed, Omar, Aref Abadel, Tarek Almusallam, Hussein Elsanadedy, Husain Abbas, and Yousef Al-Salloum. 2025. "Steel Plates Versus Hybrid CFRP/Steel Stirrups for Strengthening of Shear-Deficient Concrete Wide Beams Supporting Columns" Polymers 17, no. 21: 2857. https://doi.org/10.3390/polym17212857
APA StyleAl-Hamed, O., Abadel, A., Almusallam, T., Elsanadedy, H., Abbas, H., & Al-Salloum, Y. (2025). Steel Plates Versus Hybrid CFRP/Steel Stirrups for Strengthening of Shear-Deficient Concrete Wide Beams Supporting Columns. Polymers, 17(21), 2857. https://doi.org/10.3390/polym17212857






