High Interfacial Adsorption of Light Gases on Nano-Thin Molten Polyethylene Films
Abstract
1. Introduction
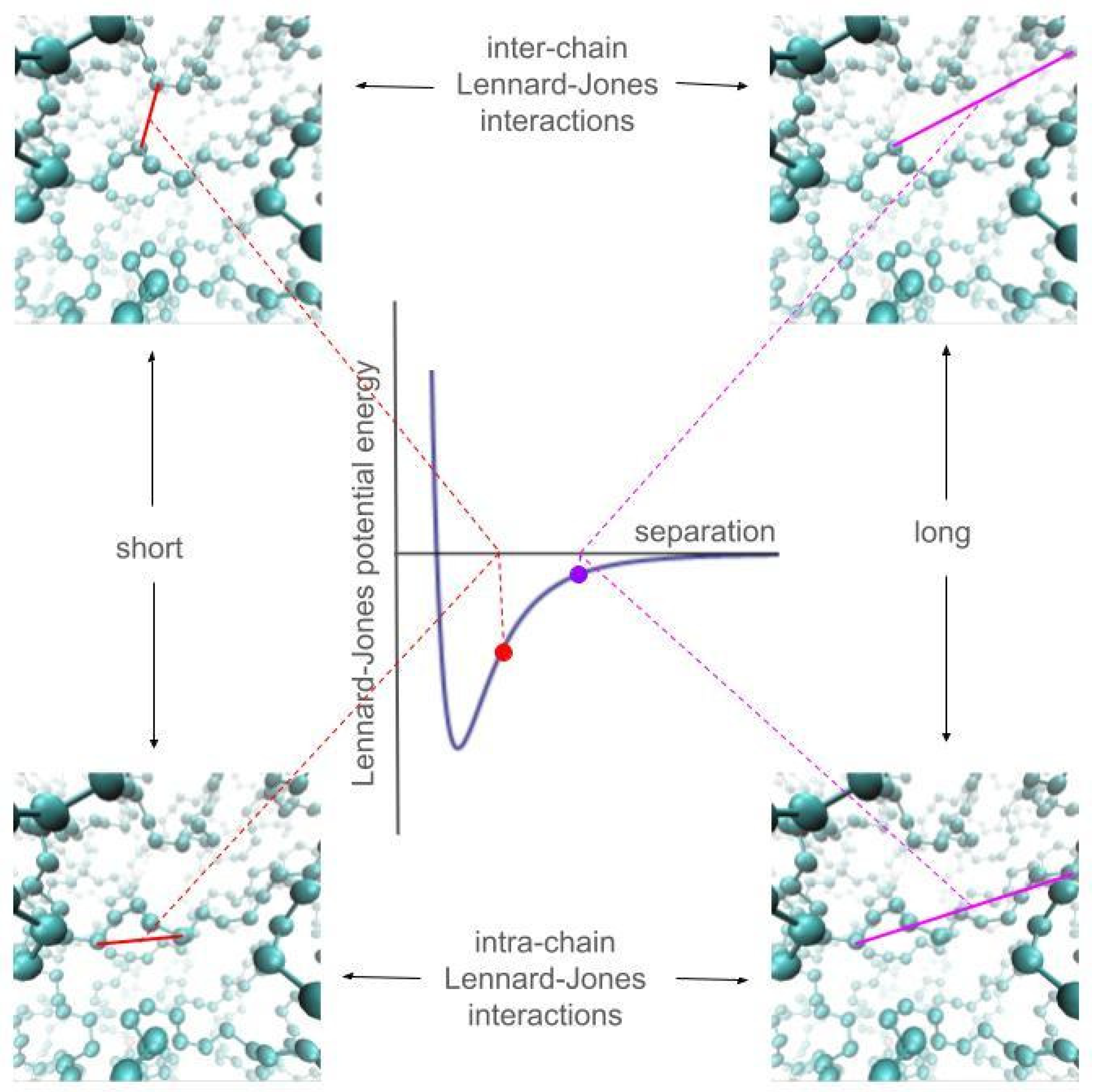
2. Methodology
3. Results and Discussion
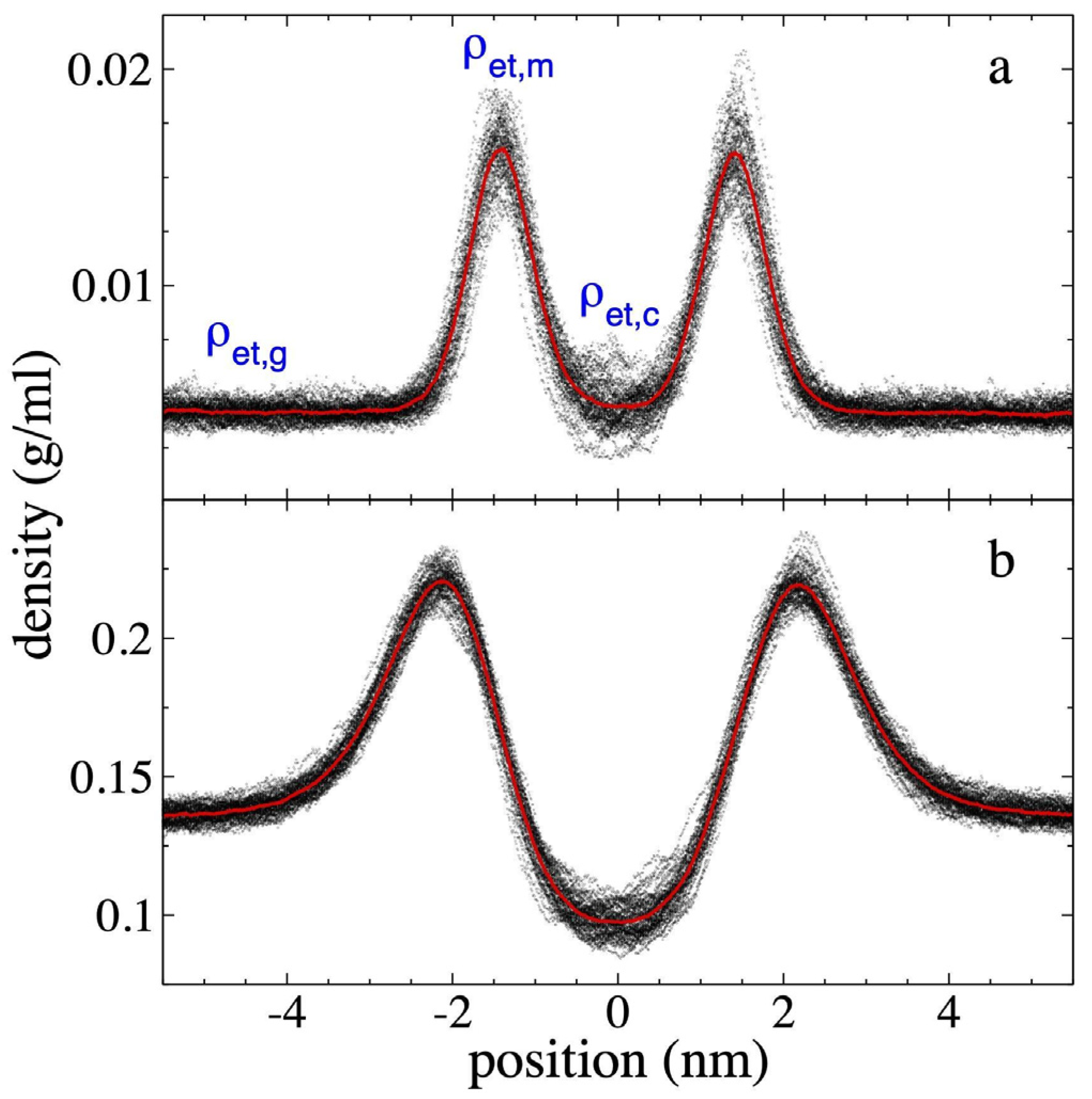
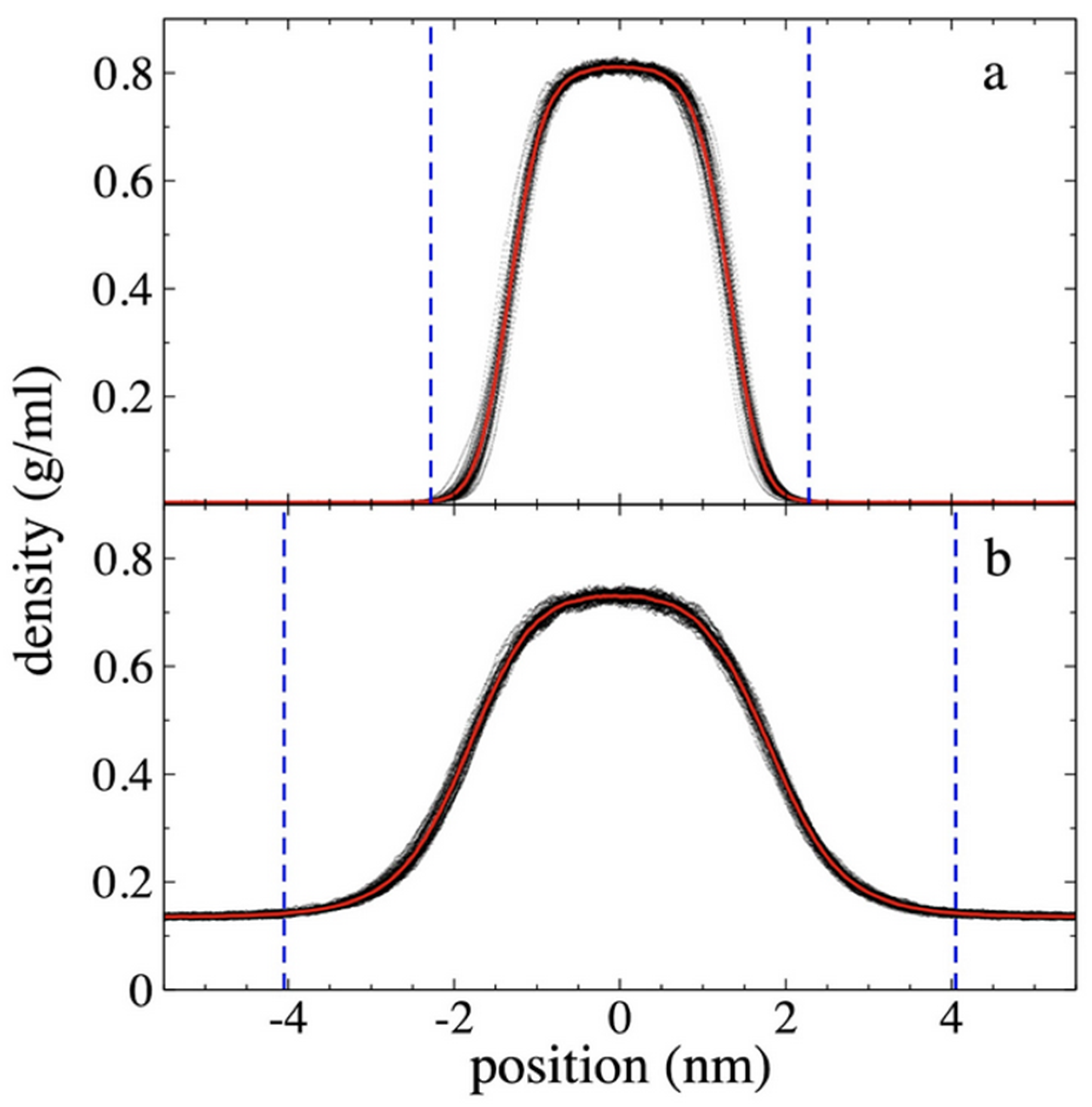
3.1. Density Profiles
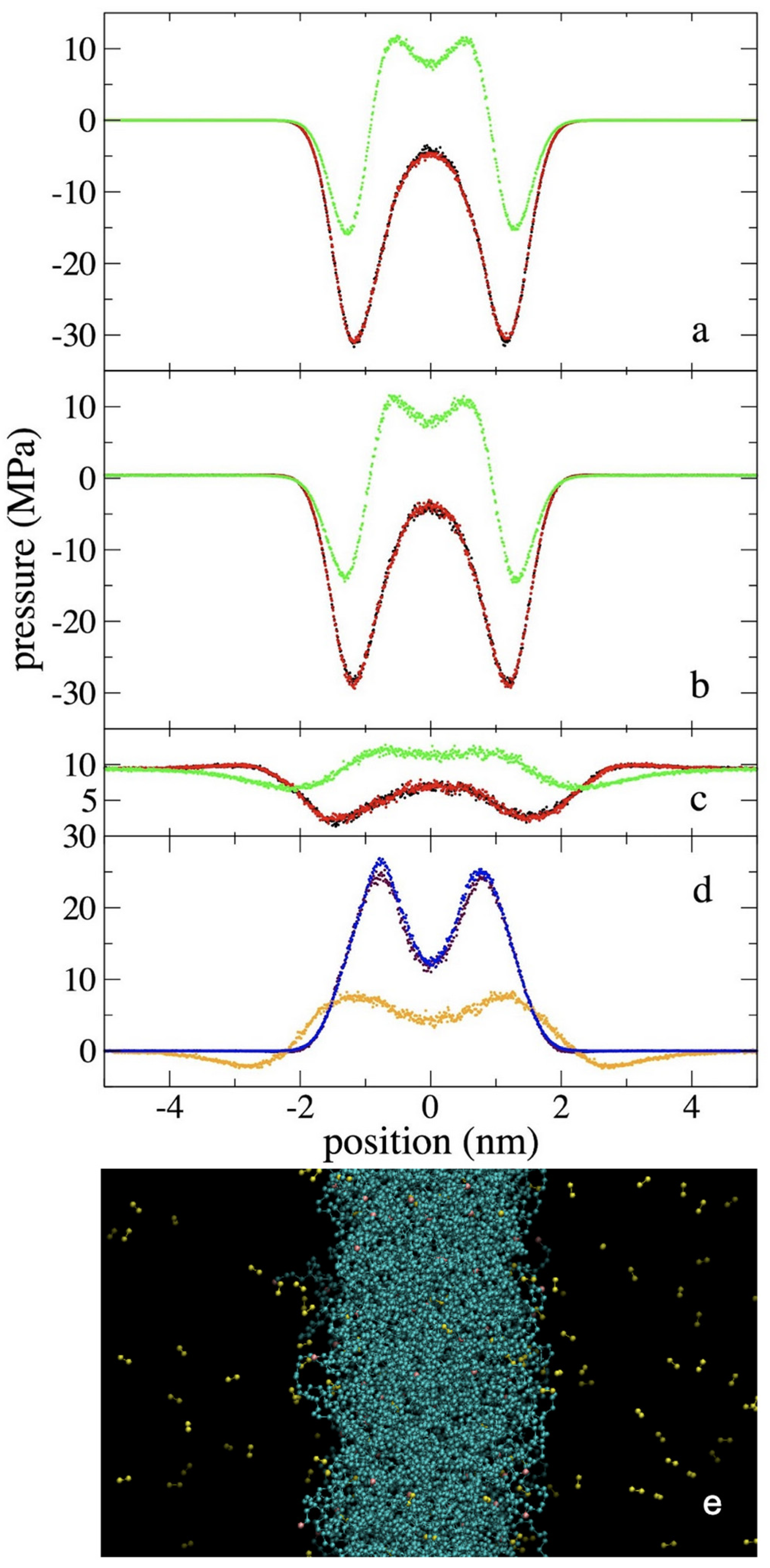
3.2. Pressure Profiles
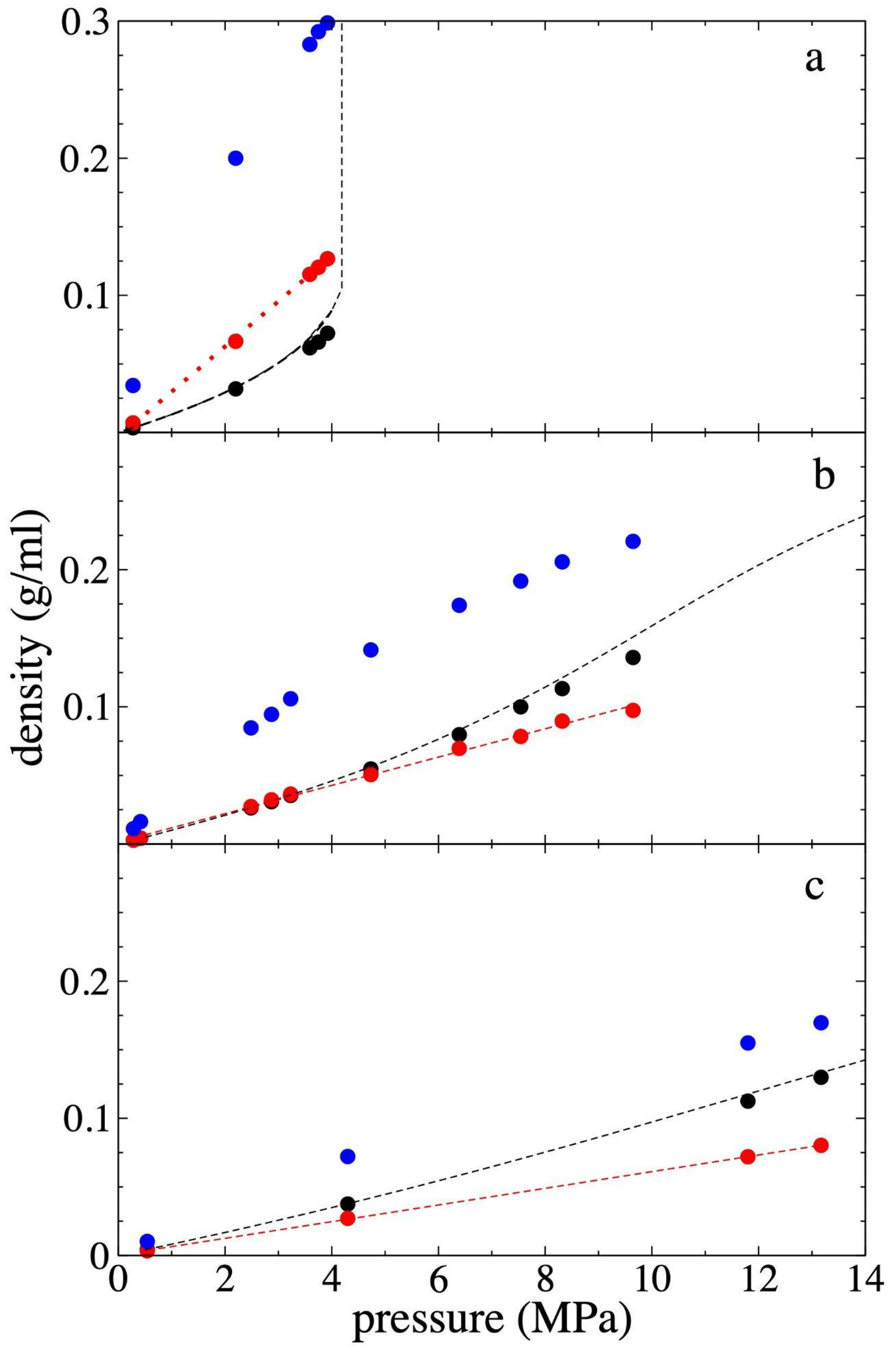
3.3. Pressure–Density of Supercritical Gas Ethane
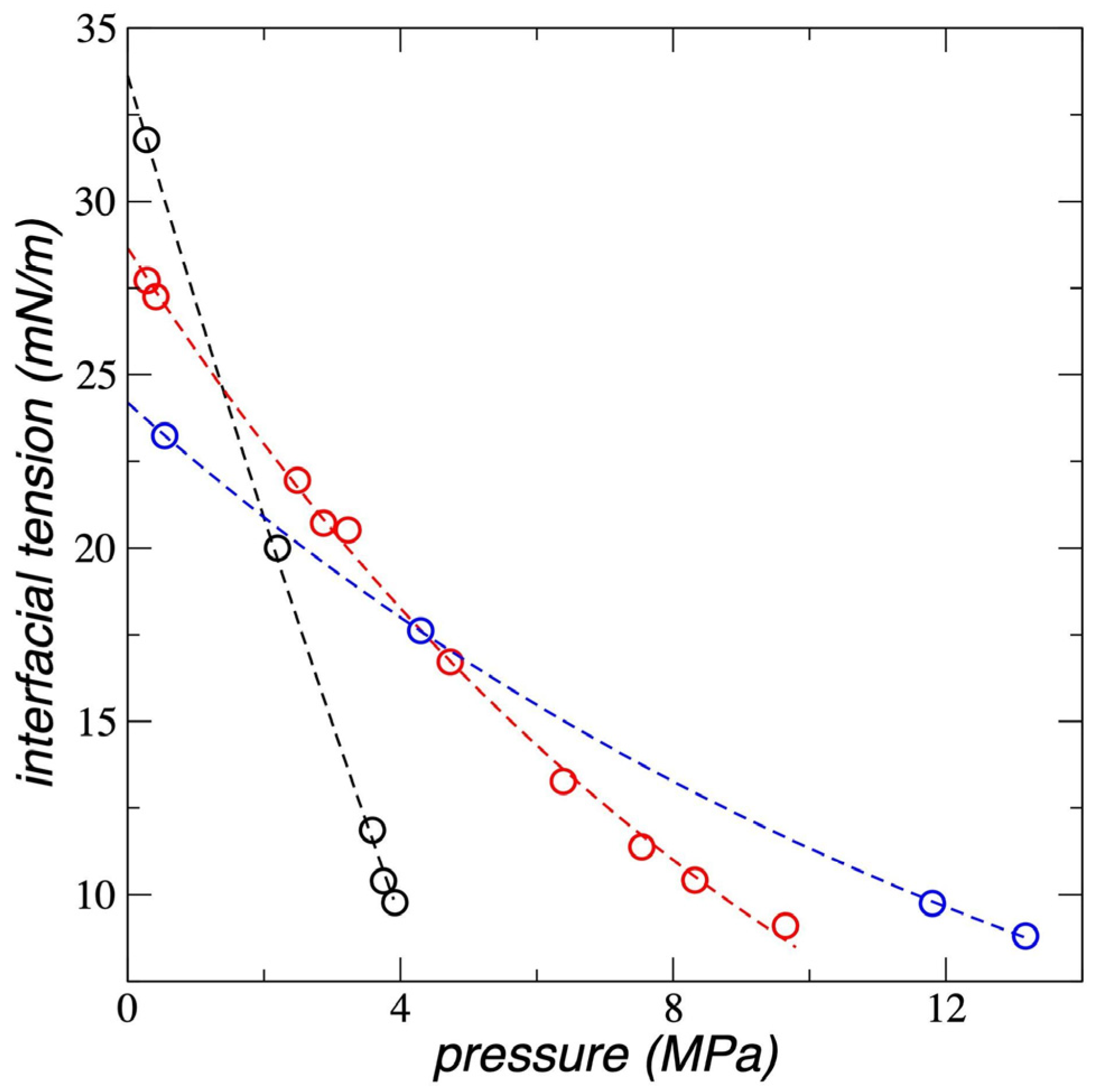
3.4. Interfacial Tension
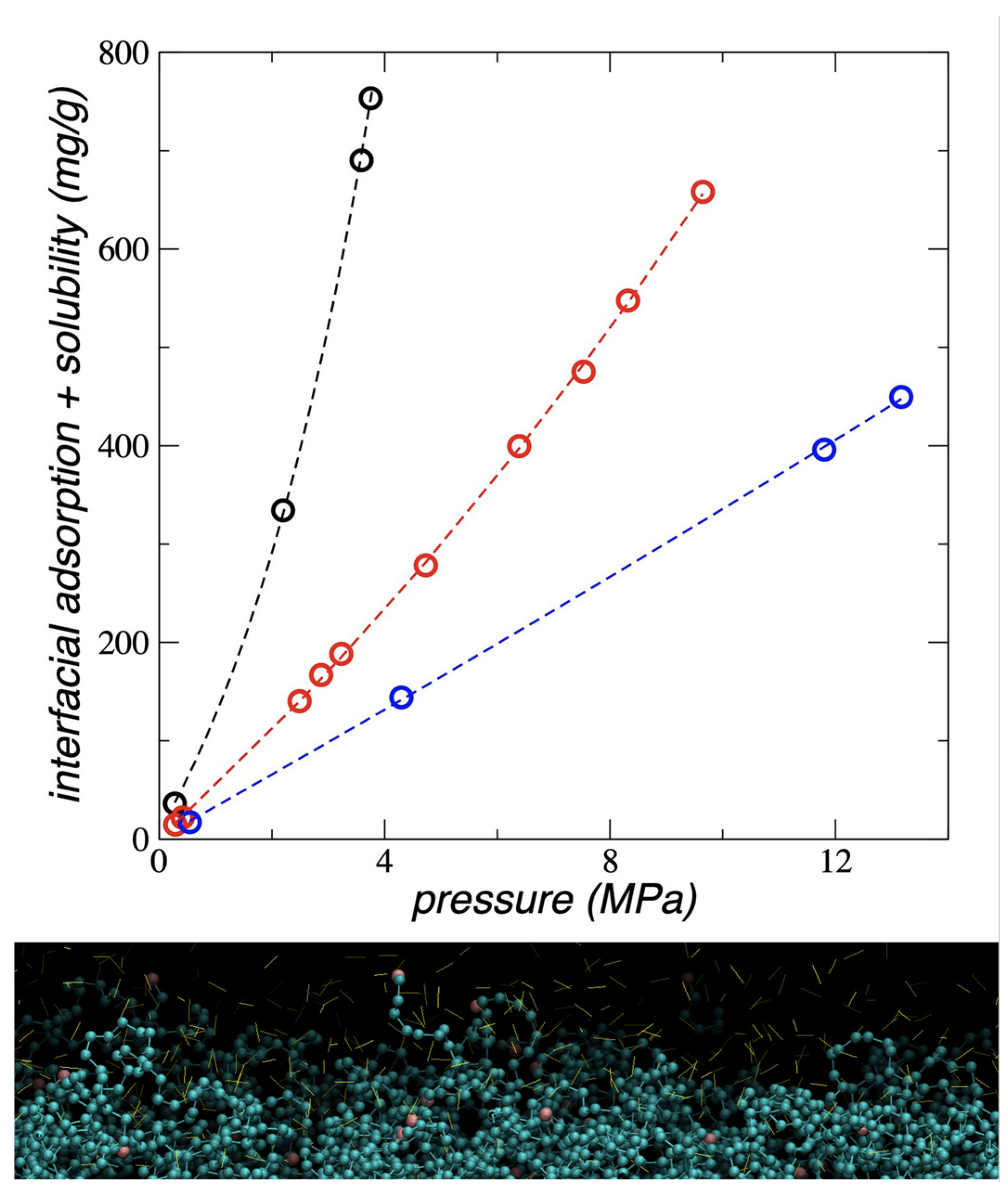
3.5. Interfacial and Soluble Load
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, R.; Peng, X.; Ge, B.; Deng, C.; Liu, B.; Sun, C.; Chen, G. Novel Ethane Recovery Process from Natural Gas Using ZIF-8/Water–Glycol Slurry: Techno-Economic and Energy Consumption Evaluation. Sep. Purif. Technol. 2024, 343, 127117. [Google Scholar] [CrossRef]
- Cho, K.H.; Yoon, J.W.; Lee, J.H.; Kim, J.C.; Jo, D.; Park, J.; Lee, S.-K.; Kwak, S.K.; Lee, U.-H. Design of Pore Properties of an Al-Based Metal–Organic Framework for the Separation of an Ethane/Ethylene Gas Mixture via Ethane-Selective Adsorption. ACS Appl. Mater. Interfaces 2023, 15, 30975–30984. [Google Scholar] [CrossRef]
- Liao, P.-Q.; Zhang, W.-X.; Zhang, J.-P.; Chen, X.-M. Efficient Purification of Ethene by an Ethane-Trapping Metal-Organic Framework. Nat. Commun. 2015, 6, 8697. [Google Scholar] [CrossRef]
- Fan, J.; Liu, Y.; Xing, Z.-W.; Li, Y.-X.; Sun, L.-B. Efficient Ethylene/Ethane Separation Using Commercial Zeolites: Structure-Performance Relationships and Mechanistic Insights. Sep. Purif. Technol. 2025, 379, 134879. [Google Scholar] [CrossRef]
- Seabra, R.; Martins, V.F.D.; Ribeiro, A.M.; Rodrigues, A.E.; Ferreira, A.P. Ethylene/Ethane Separation by Gas-Phase SMB in Binderfree Zeolite 13X Monoliths. Chem. Eng. Sci. 2021, 229, 116006. [Google Scholar] [CrossRef]
- Yang, Y.; Burke, N.; Ali, S.; Huang, S.; Lim, S.; Zhu, Y. Experimental Studies of Hydrocarbon Separation on Zeolites, Activated Carbons and MOFs for Applications in Natural Gas Processing. RSC Adv. 2017, 7, 12629–12638. [Google Scholar] [CrossRef]
- Stephens, E.R.; Hanst, P.L.; Doerr, R.C.; Scott, W.E. Reactions of Nitrogen Dioxide and Organic Compounds in Air. Ind. Eng. Chem. 1956, 48, 1498–1504. [Google Scholar] [CrossRef]
- Ghoshal, A.K.; Manjare, S.D. Selection of Appropriate Adsorption Technique for Recovery of VOCs: An Analysis. J. Loss Prev. Process Ind. 2002, 15, 413–421. [Google Scholar] [CrossRef]
- Xiang, H.; Zhang, H.; Liu, P.; Yan, Y. Adsorption Dynamics of Ethane from Air in Structured Fixed Beds with Different Microfibrous Composites. Chin. J. Chem. Eng. 2023, 53, 14–24. [Google Scholar] [CrossRef]
- Nareswari, C.; Zulfiani, U.; Junaidi, A.; Gunawan, T.; Widiastuti, N. Adsorption of CO2 and H2 on the Polymer-Based Membrane from High-Density Polyethylene (HDPE) Plastic. S. Afr. J. Chem. Eng. 2024, 49, 105–113. [Google Scholar] [CrossRef]
- Yang, Y.; Narayanan Nair, A.K.; Sun, S. Adsorption and Diffusion of Methane and Carbon Dioxide in Amorphous Regions of Cross-Linked Polyethylene: A Molecular Simulation Study. Ind. Eng. Chem. Res. 2019, 58, 8426–8436. [Google Scholar] [CrossRef]
- Li, N.N.; Long, R.B. Permeation through Plastic Films. AIChE J. 1969, 15, 73–80. [Google Scholar] [CrossRef]
- Fries, E.; Zarfl, C. Sorption of Polycyclic Aromatic Hydrocarbons (PAHs) to Low and High Density Polyethylene (PE). Environ. Sci. Pollut. Res. 2011, 19, 1296–1304. [Google Scholar] [CrossRef]
- Rios, L.M.; Jones, P.R.; Moore, C.; Narayan, U.V. Quantitation of Persistent Organic Pollutants Adsorbed on Plastic Debris from the Northern Pacific Gyre’s “Eastern Garbage Patch”. J. Environ. Monit. 2010, 12, 2226–2236. [Google Scholar] [CrossRef]
- Wang, T.; Yu, C.; Chu, Q.; Wang, F.; Lan, T.; Wang, J. Adsorption Behavior and Mechanism of Five Pesticides on Microplastics from Agricultural Polyethylene Films. Chemosphere 2020, 244, 125491. [Google Scholar] [CrossRef]
- Norton, M.G. Polyethylene—The Material of Chance. In Ten Materials That Shaped Our World; Norton, M.G., Ed.; Springer Nature: Cham, Switzerland, 2025; pp. 151–166. [Google Scholar]
- Sand, A.; Vyas, A.; Tuteja, J. Polyethylene–Its Properties and Application in Industry and in Households. In Polyethylene–New Developments and Applications; Sand, A., Tuteja, J., Eds.; IntechOpen: Rijeka, Croatia, 2024; pp. 1–6. [Google Scholar]
- Wang, Y.; Feng, G.; Lin, N.; Lan, H.; Li, Q.; Yao, D.; Tang, J. A Review of Degradation and Life Prediction of Polyethylene. Appl. Sci. 2023, 13, 3045. [Google Scholar] [CrossRef]
- Heuer, T.; Peuschel, G.-P.; Rätzsch, M.; Wohlfarth, C. Untersuchungen Zur Löslichkeit von Ethen, Propan, Propen Und But-1-En in Schmelzen von Oligomeren Des Polyethylens Bzw. (Ethen-Vinylacetat)-Copolymeren Bei Temperaturen Bis 473,15 k Und Drücken Bis 30 MPA.; Teil, I. Apparaturen Und Ergebnisse. Acta Polym. 1989, 40, 272–278. [Google Scholar] [CrossRef]
- Haslam, A.J.; von Solms, N.; Adjiman, C.S.; Galindo, A.; Jackson, G.; Paricaud, P.; Michelsen, M.L.; Kontogeorgis, G.M. Predicting Enhanced Absorption of Light Gases in Polyethylene Using Simplified PC-SAFT and SAFT-VR. Fluid Phase Equilibria 2006, 243, 74–91. [Google Scholar] [CrossRef]
- Surana, R.K.; Danner, R.P.; de Haan, A.; Beckers, N. New Technique to Measure High-Pressure and High-Temperature Polymer-Solvent Vapor-Liquid Equilibrium. Fluid Phase Equilibria 1997, 139, 361–370. [Google Scholar] [CrossRef]
- von Solms, N.; Michelsen, M.L.; Kontogeorgis, G.M. Prediction and Correlation of High-Pressure Gas Solubility in Polymers with Simplified PC-SAFT. Ind. Eng. Chem. Res. 2005, 44, 3330–3335. [Google Scholar] [CrossRef]
- Chmelař, J.; Smolná, K.; Haškovcová, K.; Podivinská, M.; Maršálek, J.; Kosek, J. Equilibrium Sorption of Ethylene in Polyethylene: Experimental Study and PC-SAFT Simulations. Polymer 2015, 59, 270–277. [Google Scholar] [CrossRef]
- Long, R.B. Liquid Permeation through Plastic Films. Ind. Eng. Chem. Fundam. 1965, 4, 445–451. [Google Scholar] [CrossRef]
- González-Mijangos, J.A.; Lima, E.; Guerra-González, R.; Ramírez-Zavaleta, F.I.; Rivera, J.L. Critical Thickness of Free-Standing Nanothin Films Made of Melted Polyethylene Chains via Molecular Dynamics. Polymers 2021, 13, 3515. [Google Scholar] [CrossRef]
- Ramírez-Zavaleta, F.I.; Torres-Dominguez, V.M.; Viramontes-Gamboa, G.; Rivera, J.L. Interfacial Forces in Free-Standing Layers of Melted Polyethylene, from Critical to Nanoscopic Thicknesses. Polymers 2022, 14, 3865. [Google Scholar] [CrossRef]
- Rivera, J.L.; Douglas, J.F. Reducing Uncertainty in Simulation Estimates of the Surface Tension through a Two-Scale Finite-Size Analysis: Thicker Is Better. RSC Adv. 2019, 9, 35803–35812. [Google Scholar] [CrossRef]
- Rivera, J.L.; Douglas, J.F. Influence of Film Thickness on the Stability of Free-Standing Lennard-Jones Fluid Films. J. Chem. Phys. 2019, 150, 144705. [Google Scholar] [CrossRef] [PubMed]
- Li, R.; Wang, Z.; Sun, W.; Zhang, H.; Zeng, Y.; Zhao, X.; Hu, W.; Deng, H.; Loh, K.P.; Fu, Q. Scalable Production of Critically Thin Polyethylene Films via Multistep Stretching. Nat. Chem. Eng. 2024, 1, 702–709. [Google Scholar] [CrossRef]
- Lew, J.H.; Hue, K.Y.; Matar, O.K.; Müller, E.A.; Luckham, P.F.; Santos, A.S.; Myo Thant, M.M. Atomic Force Microscopy and Molecular Dynamic Simulation of Adsorption of Polyacrylamide with Different Chemistries onto Calcium Carbonate. Polymers 2024, 16, 494. [Google Scholar] [CrossRef]
- Huang, H.; Liu, B.; Zheng, D.; Xin, F.; Shi, X. Transport Property of Hydrogen Sulfide in Amorphous Polyethylene Using Grand Canonical Monte Carlo and Molecular Dynamics Simulations. Fuel 2024, 360, 130532. [Google Scholar] [CrossRef]
- López-Chávez, E.; Peña-Castañeda, Y.A.; Garcia-Quiroz, A.; Góngora, J.A.I.D.; de Landa Castillo-Alvarado, F. Thermophysical Properties of Graphene Reinforced with Polymethyl Methacrylate Nanoparticles for Technological Applications: A Molecular Model. J. Mol. Model. 2025, 31, 52. [Google Scholar] [CrossRef]
- Thompson, A.P.; Aktulga, H.M.; Berger, R.; Bolintineanu, D.S.; Brown, W.M.; Crozier, P.S.; in ’t Veld, P.J.; Kohlmeyer, A.; Moore, S.G.; Nguyen, T.D.; et al. LAMMPS–a Flexible Simulation Tool for Particle-Based Materials Modeling at the Atomic, Meso, and Continuum Scales. Comput. Phys. Commun. 2022, 271, 108171. [Google Scholar] [CrossRef]
- Nosé, S. A Unified Formulation of the Constant Temperature Molecular Dynamics Methods. J. Chem. Phys. 1984, 81, 511–519. [Google Scholar] [CrossRef]
- Martin, M.G.; Siepmann, J.I. Transferable Potentials for Phase Equilibria. 1. United-Atom Description of n-Alkanes. J. Phys. Chem. B 1998, 102, 2569–2577. [Google Scholar] [CrossRef]
- Wagner, R.J.; Silberstein, M.N. A Foundational Framework for the Mesoscale Modeling of Dynamic Elastomers and Gels. J. Mech. Phys. Solids 2025, 194, 105914. [Google Scholar] [CrossRef]
- Zerze, H.; Gupta, A.; Baksi, A.; Chakraborty, D.; Vekilov, P.G.; Rimer, J.D.; Zerze, G.H. A Coarse-Graining Approach to Model Molecular Liquids for Mesoscale Problems. AIChE J. 2025, 71, e18700. [Google Scholar] [CrossRef]
- Shi, K.; Smith, E.R.; Santiso, E.E.; Gubbins, K.E. A Perspective on the Microscopic Pressure (Stress) Tensor: History, Current Understanding, and Future Challenges. J. Chem. Phys. 2023, 158, 040901. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Madura, J.D.; Swenson, C.J. Optimized Intermolecular Potential Functions for Liquid Hydrocarbons. J. Am. Chem. Soc. 1984, 106, 6638–6646. [Google Scholar] [CrossRef]
- Trokhymchuk, A.; Alejandre, J. Computer Simulations of Liquid/Vapor Interface in Lennard-Jones Fluids: Some Questions and Answers. J. Chem. Phys. 1999, 111, 8510–8523. [Google Scholar] [CrossRef]
- Rivera, J.L.; Molina-Rodríguez, L.; Ramos-Estrada, M.; Navarro-Santos, P.; Lima, E. Interfacial Properties of the Ionic Liquid [Bmim][Triflate] over a Wide Range of Temperatures. RSC Adv. 2018, 8, 10115–10123. [Google Scholar] [CrossRef]
- Arroyo-Valdez, J.A.; Viramontes-Gamboa, G.; Guerra-Gonzalez, R.; Ramos-Estrada, M.; Lima, E.; Rivera, J.L. Cation Folding and the Thermal Stability Limit of the Ionic Liquid [BMIM+][BF4−] under Total Vacuum. RSC Adv. 2021, 11, 12951–12960. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Larson, R.G. A Metastable Nematic Precursor Accelerates Polyethylene Oligomer Crystallization as Determined by Atomistic Simulations and Self-Consistent Field Theory. J. Chem. Phys. 2019, 150, 244903. [Google Scholar] [CrossRef]
- Ramos, J.; Vega, J.F.; Martínez-Salazar, J. Molecular Dynamics Simulations for the Description of Experimental Molecular Conformation, Melt Dynamics, and Phase Transitions in Polyethylene. Macromolecules 2015, 48, 5016–5027. [Google Scholar] [CrossRef]
- Eggimann, B.L.; Siepmann, J.I.; Fried, L.E. Application of the TraPPE Force Field to Predicting Isothermal Pressure–Volume Curves at High Pressures and High Temperatures. Int. J. Thermophys. 2007, 28, 796–804. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual Molecular Dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Harasima, A. Molecular Theory of Surface Tension. In Advances in Chemical Physics; Prigogine, I., Debye, P., Eds.; Springer: Dordrecht, The Netherlands, 1957; pp. 203–237. [Google Scholar]
- Mejía, A.; Cartes, M.; Chaparro, G.; Feria, E.; Blas, F.J.; Míguez, J.M.; Algaba, J.; Müller, E.A. Phase Equilibria and Interfacial Properties of Selected Methane + N-Alkane Binary Mixtures. J. Mol. Liq. 2021, 341, 116918. [Google Scholar] [CrossRef]
- Nourozieh, H.; Kariznovi, M.; Abedi, J. Vapor–Liquid Equilibrium Measurement and Thermodynamic Modeling of Binary Systems (Methane + n-Tetradecane). Fluid Phase Equilibria 2012, 318, 96–101. [Google Scholar] [CrossRef]
- Lopez, J.; Trejos Montoya, V.; Cardona, C.A. Objective Functions Analysis in the Minimization of Binary VLE Data for Asymmetric Mixtures at High Pressures. Fluid Phase Equilibria 2006, 248, 147–157. [Google Scholar] [CrossRef]
- Morrow, B.H.; Harrison, J.A. Interfacial Properties of Linear Alkane/Nitrogen Binary Mixtures: Molecular Dynamics Vapor–Liquid Equilibrium Simulations. J. Phys. Chem. B 2022, 126, 4379–4388. [Google Scholar] [CrossRef]
- Garrido, J.M.; Cartes, M.; Mejía, A. Coarse-Grained Theoretical Modeling and Molecular Simulations of Nitrogen + n-Alkanes: (N-Pentane, n-Hexane, n-Heptane, n-Octane). J. Supercrit. Fluids 2017, 129, 83–90. [Google Scholar] [CrossRef]
- Qiu, Y.; Molinero, V. Strength of Alkane–Fluid Attraction Determines the Interfacial Orientation of Liquid Alkanes and Their Crystallization through Heterogeneous or Homogeneous Mechanisms. Crystals 2017, 7, 86. [Google Scholar] [CrossRef]
- Clint, J.H. Adsorption at Liquid Interfaces. In Surfactant Aggregation; Clint, J.H., Ed.; Springer: Dordrecht, The Netherlands, 1992; pp. 13–32. [Google Scholar]
- Grange, R.A. Estimating the Hardenability of Carbon Steels. Metall. Trans. 1973, 4, 2231–2244. [Google Scholar] [CrossRef]
- Rabinowitz, J.D.; Wensley, M.; Lloyd, P.; Myers, D.; Shen, W.; Lu, A.; Hodges, C.; Hale, R.; Mufson, D.; Zaffaroni, A. Fast Onset Medications through Thermally Generated Aerosols. J. Pharmacol. Exp. Ther. 2004, 309, 769–775. [Google Scholar] [CrossRef]
- Myers, D.J.; Timmons, R.D.; Lu, A.T.; Hale, R.L.; Solas, D.W.; Soni, P.; Rabinowitz, J.D. The Effect of Film Thickness on Thermal Aerosol Generation. Pharm. Res. 2007, 24, 336–342. [Google Scholar] [CrossRef]
- Wu, C. Critical Thicknesses of Free-Standing Thin Films of Molten Polymers: A Multiscale Simulation Study. J. Phys. Chem. B 2022, 126, 6500–6510. [Google Scholar] [CrossRef]
- Bücker, D.; Wagner, W. A Reference Equation of State for the Thermodynamic Properties of Ethane for Temperatures from the Melting Line to 675 K and Pressures up to 900 MPa. J. Phys. Chem. Ref. Data 2006, 35, 205–266. [Google Scholar] [CrossRef]
- Wang, Y.; Rafailovich, M.; Sokolov, J.; Gersappe, D.; Araki, T.; Zou, Y.; Kilcoyne, A.D.L.; Ade, H.; Marom, G.; Lustiger, A. Substrate Effect on the Melting Temperature of Thin Polyethylene Films. Phys. Rev. Lett. 2006, 96, 028303. [Google Scholar] [CrossRef] [PubMed]
- Rice, O.K. The Effect of Pressure on Surface Tension. J. Chem. Phys. 1947, 15, 333–335. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guerra-González, R.; Lemus-Solorio, M.A.; Lemus-Solorio, A.; Rivera, J.L. High Interfacial Adsorption of Light Gases on Nano-Thin Molten Polyethylene Films. Polymers 2025, 17, 2751. https://doi.org/10.3390/polym17202751
Guerra-González R, Lemus-Solorio MA, Lemus-Solorio A, Rivera JL. High Interfacial Adsorption of Light Gases on Nano-Thin Molten Polyethylene Films. Polymers. 2025; 17(20):2751. https://doi.org/10.3390/polym17202751
Chicago/Turabian StyleGuerra-González, Roberto, Martha A. Lemus-Solorio, Alfonso Lemus-Solorio, and José L. Rivera. 2025. "High Interfacial Adsorption of Light Gases on Nano-Thin Molten Polyethylene Films" Polymers 17, no. 20: 2751. https://doi.org/10.3390/polym17202751
APA StyleGuerra-González, R., Lemus-Solorio, M. A., Lemus-Solorio, A., & Rivera, J. L. (2025). High Interfacial Adsorption of Light Gases on Nano-Thin Molten Polyethylene Films. Polymers, 17(20), 2751. https://doi.org/10.3390/polym17202751







