Coarse-Grained Molecular Dynamics Study of the Melting Dynamics in Long Alkanes
Abstract
1. Introduction
2. Simulation Methodology
2.1. Force Field and Equilibration
2.2. Simulation Procedure
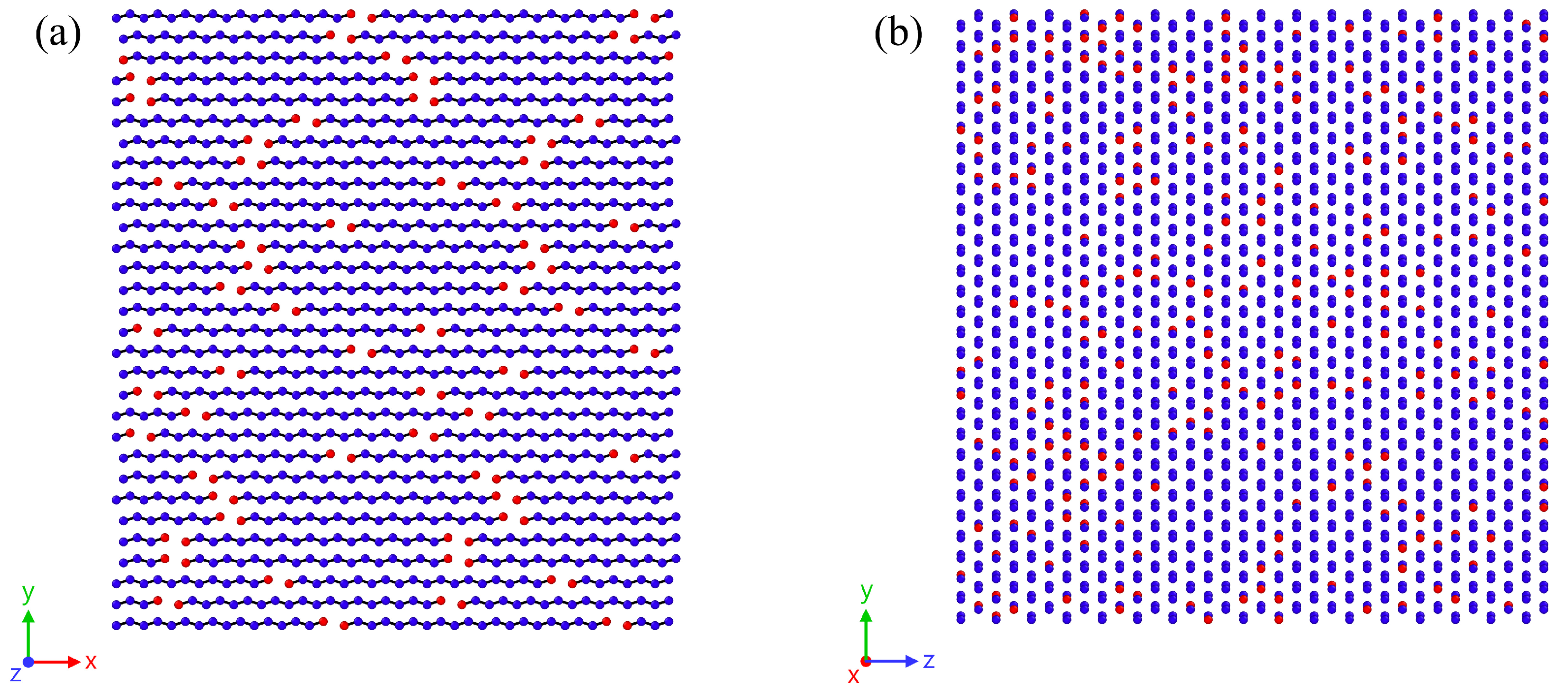
2.3. Evaluation of the Microscopic Structure
3. Results
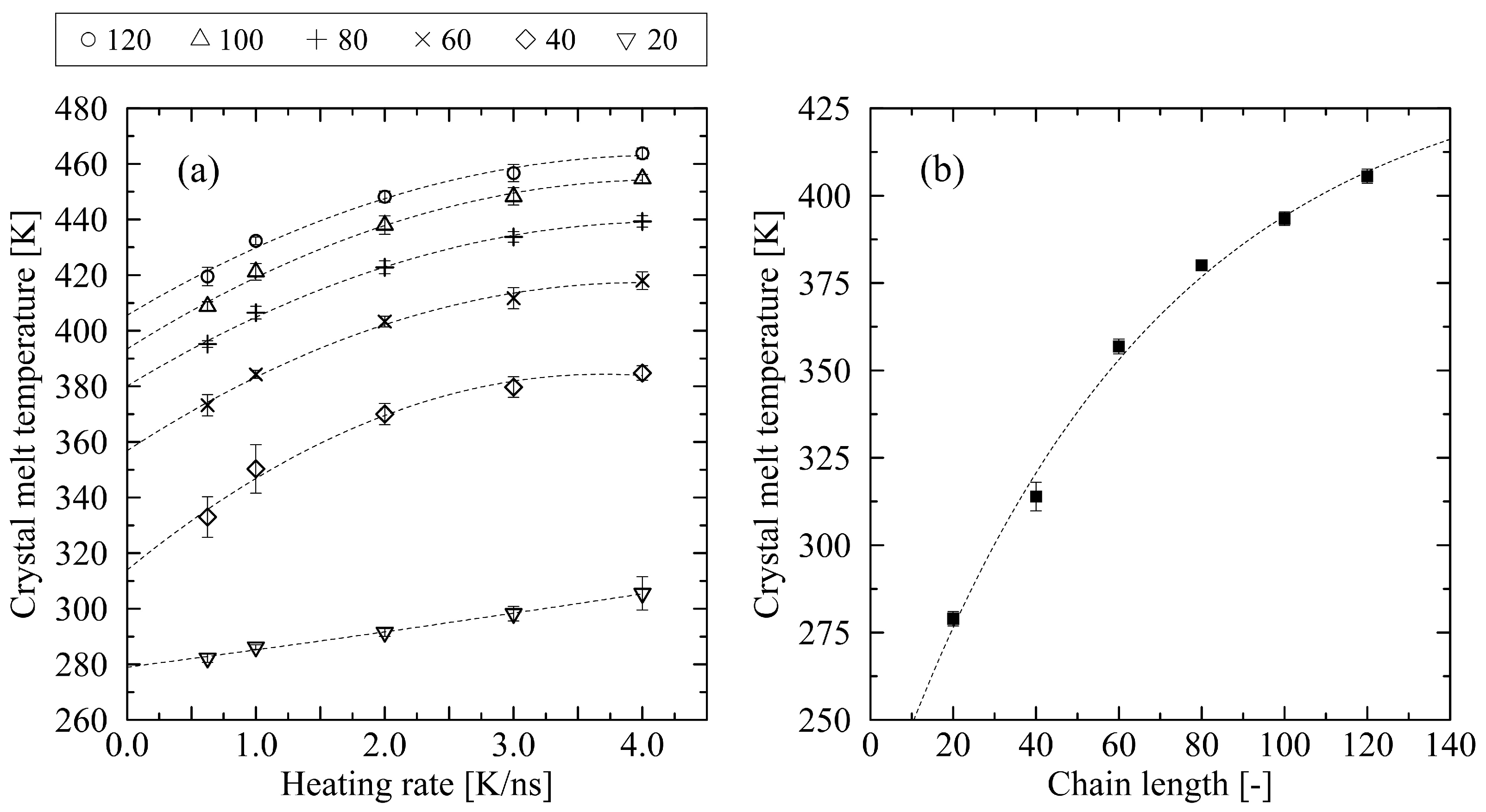
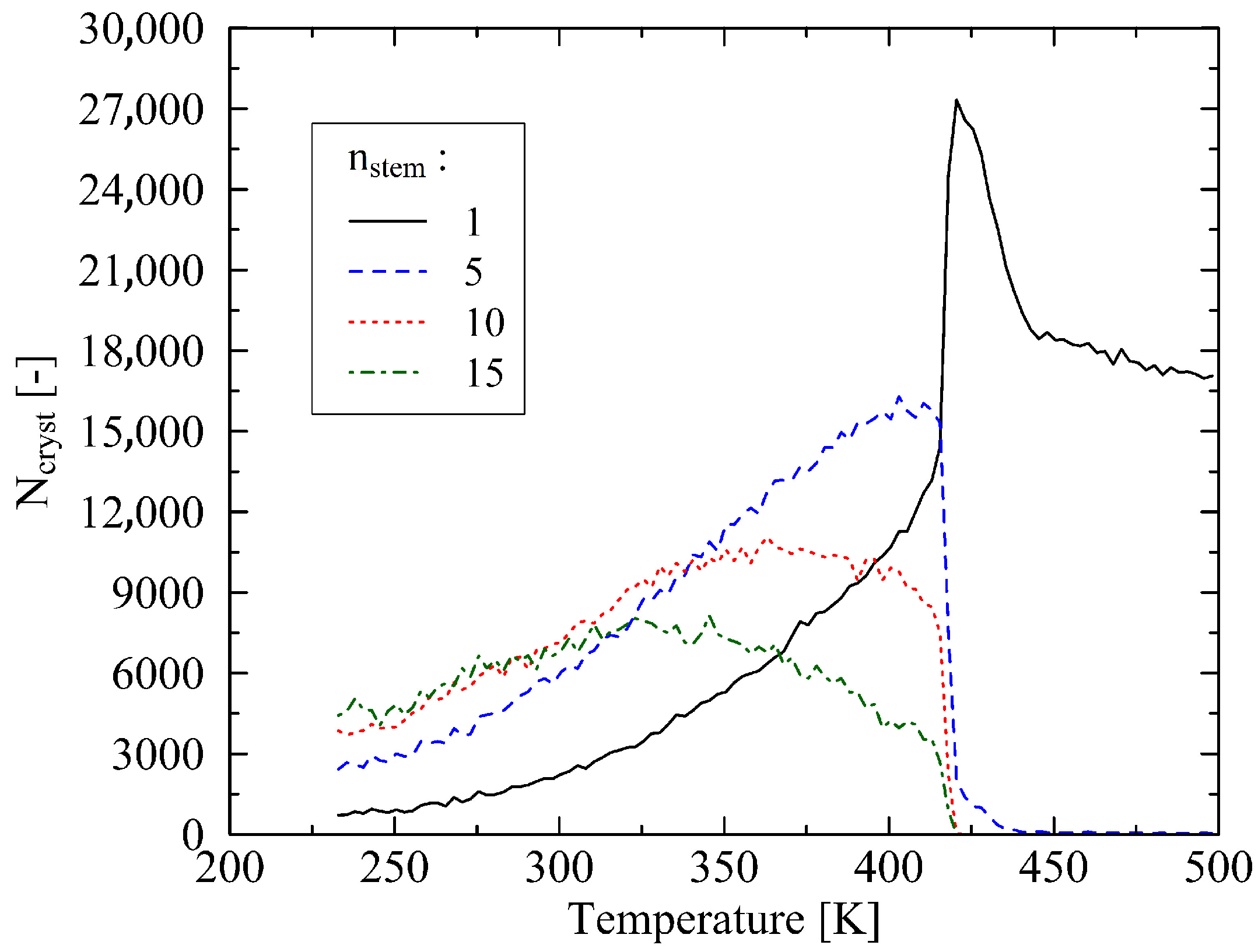
3.1. Determination of the Crystal Melt Temperature
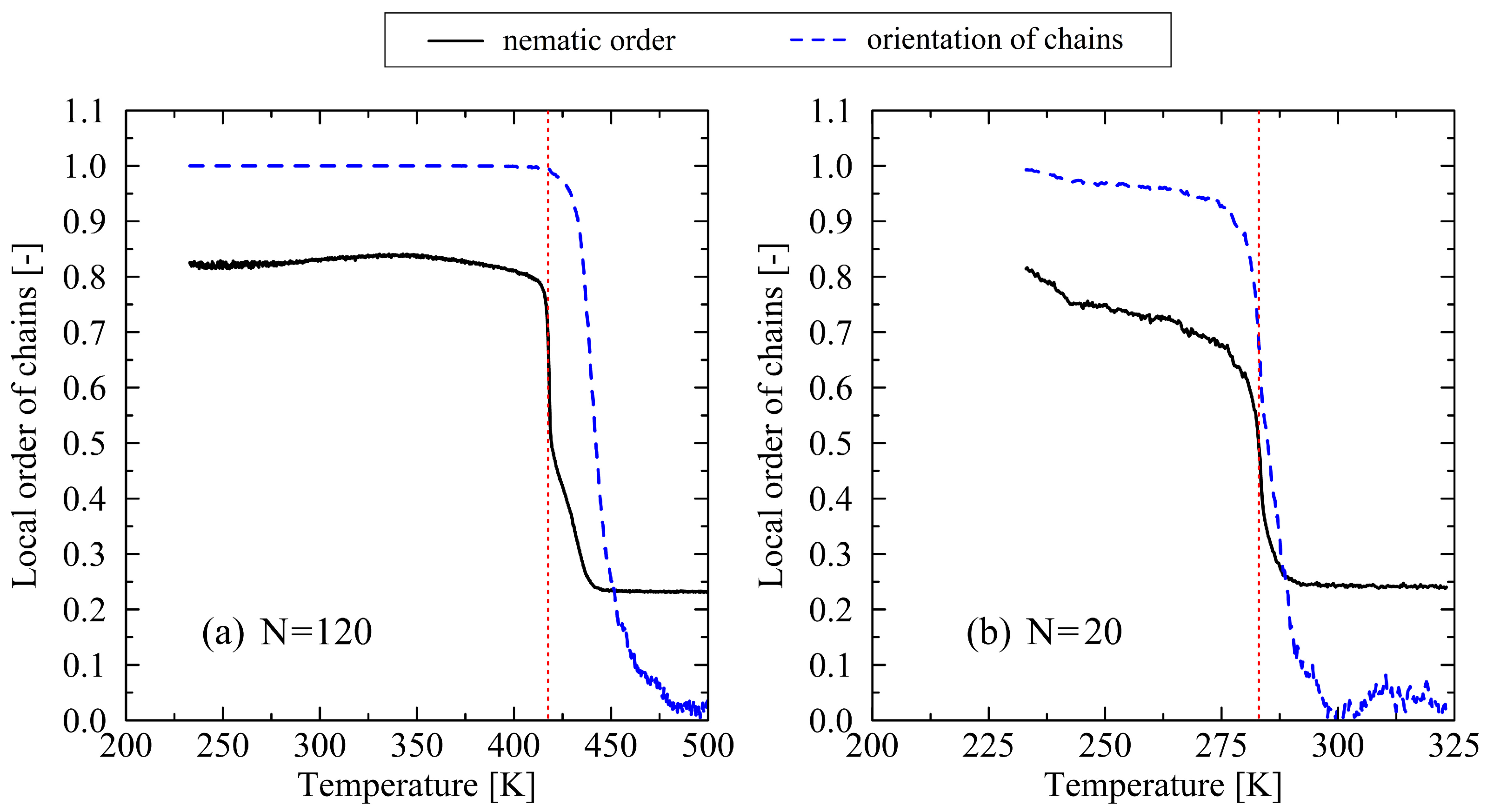
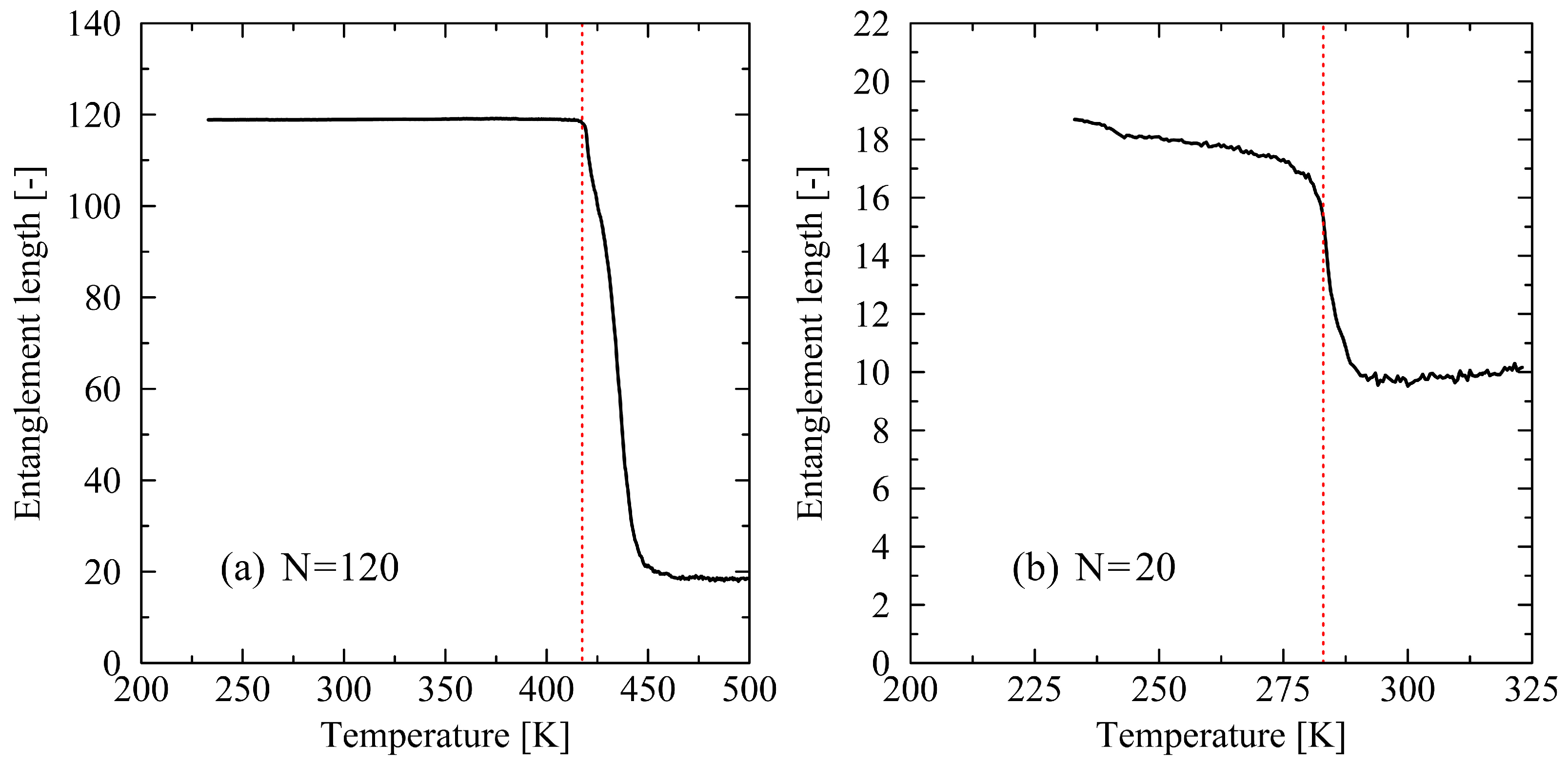
3.2. Analysis of the Melting Dynamics
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rao, Z.; Wang, S.; Wu, M.; Zhang, Y.; Li, F. Molecular dynamics simulations of melting behavior of alkane as phase change materials slurry. Energy Convers. Manag. 2012, 64, 152–156. [Google Scholar] [CrossRef]
- Ogden, S.; Klintberg, L.; Thornell, G.; Hjort, K.; Bodén, R. Review on miniaturized paraffin phase change actuators, valves, and pumps. Microfluid. Nanofluid. 2014, 17, 53–71. [Google Scholar] [CrossRef]
- Cafolla, C.; Voïtchovsky, K. Impact of water on the lubricating properties of hexadecane at the nanoscale. Nanoscale 2020, 12, 14504–14513. [Google Scholar] [CrossRef] [PubMed]
- Müller, A. An X-ray investigation of normal paraffins near their melting points. Proc. R. Soc. A 1932, 138, 514–530. [Google Scholar]
- Strobl, G.; Ewen, B.; Fischer, E.; Piesczek, W. Defect structure and molecular motion in the four modifications of n -tritriacontane. I. Study of defect structure in the lamellar interfaces using small angle X-ray scattering. J. Chem. Phys. 1974, 61, 5257–5264. [Google Scholar] [CrossRef]
- Sirota, E.B.; King, H.E., Jr.; Singer, D.M.; Shao, H.H. Rotator phases of the normal alkanes: An X-ray scattering study. J. Chem. Phys. 1993, 98, 5809–5824. [Google Scholar] [CrossRef]
- Yamashita, M.; Hirao, A.; Kato, M. The effect of pressure on the phase transition behavior of tridecane, pentadecane, and heptadecane: A Fourier transform infrared spectroscopy study. J. Chem. Phys. 2011, 134, 144503. [Google Scholar] [CrossRef]
- Arteca, G.A. Dynamic Molecular Shape Analysis of Configurational Transitions Associated with Melting and Premelting of n-Alkane Chains. J. Phys. Chem. B 1997, 101, 4097–4104. [Google Scholar] [CrossRef]
- Wentzel, N.; Milner, S.T. Crystal and rotator phases of n-alkanes: A molecular dynamics study. J. Chem. Phys. 2010, 132, 044901. [Google Scholar] [CrossRef]
- Marbeuf, A.; Brown, R. Molecular dynamics in n-alkanes: Premelting phenomena and rotator phases. J. Chem. Phys. 2006, 124, 054901. [Google Scholar] [CrossRef]
- Jarrett, W.L.; Mathias, L.J.; Alamo, R.G.; Mandelkern, L.; Dorset, D.L. Thermally-Induced Molecular Motion and Premelting in Hexacontane. Macromolecules 1992, 25, 3468–3472. [Google Scholar] [CrossRef]
- Ewen, B.; Fischer, E.W.; Piesczek, W.; Strobl, G. Defect structure and molecular motion in the four modifications of n -tritriacontane. II. Study of molecular motion using infrared spectroscopy and wide-line nuclear magnetic resonance measurements. J. Chem. Phys. 1974, 61, 5265–5272. [Google Scholar] [CrossRef]
- Yamakawa, H.; Matsukawa, S.; Kurosu, H.; Kuroki, S.; Ando, I. Diffusional behavior of n alkanes in the rotator phase as studied by pulse field-gradient spin-echo H1 NMR method. J. Chem. Phys. 1999, 111, 7110–7115. [Google Scholar] [CrossRef]
- Rajabalee, F.; Negrier, P.; Mondieig, D.; Cuevas-Diarte, M.A. Ordered Phases in n-Heptacosane (C27H56). Structure Determination of the Mdci Phase. Chem. Mater. 2002, 14, 4081–4087. [Google Scholar] [CrossRef][Green Version]
- Maroncelli, M.; Qi, S.P.; Strauss, H.L.; Snyder, R.G. Nonplanar conformers and the phase behavior of solid n-alkanes. J. Am. Chem. Soc. 1982, 104, 6237–6247. [Google Scholar] [CrossRef]
- Wang, S.; Tozaki, K.I.; Hayashi, H.; Hosaka, S.; Inaba, H. Observation of multiple phase transitions in n-C22H46 using a high resolution and super-sensitive DSC. Thermochim. Acta 2003, 408, 31–38. [Google Scholar] [CrossRef]
- Kotula, A.P.; Walker, A.R.H.; Migler, K.B. Raman analysis of bond conformations in the rotator state and premelting of normal alkanes. Soft Matter 2016, 12, 5002–5010. [Google Scholar] [CrossRef]
- Pocheć, M.; Orzechowski, K.; Rutkowski, K. Indicators of premelting in 1-decanol and 1-nonanol studied by FTIR spectroscopy. Surf. Interfaces 2022, 28, 101676. [Google Scholar] [CrossRef]
- Allen, M.; Tildesley, D. Computer Simulation of Liquids, 2nd ed.; Oxford University Press: Oxford, UK, 2017. [Google Scholar]
- Burrows, S.A.; Lin, E.E.; Cholakova, D.; Richardson, S.; Smoukov, S.K. Structure of the Hexadecane Rotator Phase: Combination of X-ray Spectra and Molecular Dynamics Simulation. J. Phys. Chem. B 2023, 127, 7772–7784. [Google Scholar] [CrossRef]
- Esselink, K.; Hilbers, P.A.J.; van Beest, B.W.H. Molecular dynamics study of nucleation and melting of n-alkanes. J. Chem. Phys. 1994, 101, 9033–9041. [Google Scholar] [CrossRef]
- Waheed, N.; Lavine, M.S.; Rutledge, G.C. Molecular simulation of crystal growth in n-eicosane. J. Chem. Phys. 2002, 116, 2301–2309. [Google Scholar] [CrossRef]
- Hall, K.W.; Percec, S.; Klein, M.L. Polymer nucleation under high-driving force, long-chain conditions: Heat release and the separation of time scales. J. Chem. Phys. 2019, 150, 114901. [Google Scholar] [CrossRef] [PubMed]
- Grommes, D.; Reith, D. Determination of Relevant Mechanical Properties for the Production Process of Polyethylene by Using Mesoscale Molecular Simulation Techniques. Soft Mater. 2020, 18, 242–261. [Google Scholar] [CrossRef]
- Grommes, D.; Schenk, M.R.; Bruch, O.; Reith, D. Investigation of crystallization and relaxation effects in coarse-grained polyethylene systems after uniaxial stretching. Polymers 2021, 13, 4466. [Google Scholar] [CrossRef]
- Grommes, D.; Schenk, M.R.; Bruch, O.; Reith, D. Initial Crystallization Effects in Coarse-Grained Polyethylene Systems After Uni- and Biaxial Stretching in Blow-Molding Cooling Scenarios. Polymers 2022, 14, 5144. [Google Scholar] [CrossRef]
- Eichenberger, A.P. Molecular Dynamics Simulation of Alkanes and Proteins: Methodology, Prediction of Properties and Comparison to Experimental Data. Ph.D. Thesis, Eidgenössische Technische Hochschule Zürich, Zürich, Switzerland, 2013. [Google Scholar]
- Halverson, J.D.; Brandes, T.; Lenz, O.; Arnold, A.; Bevc, S.; Starchenko, V.; Kremer, K.; Stuehn, T.; Reith, D. ESPResSo++: A Modern Multiscale Simulation Package for Soft Matter Systems. Comput. Phys. Commun. 2013, 184, 1129–1149. [Google Scholar] [CrossRef]
- Guzman, H.V.; Tretyakov, N.; Kobayashi, H.; Fogarty, A.C.; Kreis, K.; Krajniak, J.; Junghans, C.; Kremer, K.; Stuehn, T. ESPResSo++ 2.0: Advanced Methods for Multiscale Molecular Simulation. Comput. Phys. Commun. 2019, 238, 66–76. [Google Scholar] [CrossRef]
- Lavine, M.S.; Waheed, N.; Rutledge, G.C. Molecular dynamics simulation of orientation and crystallization of polyethylene during uniaxial extension. Polymer 2003, 44, 1771–1779. [Google Scholar] [CrossRef]
- Ko, M.J.; Waheed, N.; Lavine, M.S.; Rutledge, G.C. Characterization of polyethylene crystallization from an oriented melt by molecular dynamics simulation. J. Chem. Phys. 2004, 121, 2823–2832. [Google Scholar] [CrossRef]
- Sliozberg, Y.R.; Yeh, I.C.; Kroeger, M.; Masser, K.A.; Lenhart, J.L.; Andzelm, J.W. Ordering and Crystallization of Entangled Polyethylene Melt under Uniaxial Tension: A Molecular Dynamics Study. Macromolecules 2018, 51, 9635–9648. [Google Scholar] [CrossRef]
- Moyassari, A.; Gkourmpis, T.; Hedenqvist, M.S.; Gedde, U.W. Molecular Dynamics Simulation of Linear Polyethylene Blends: Effect of Molar Mass Bimodality on Topological Characteristics and Mechanical Behavior. Polymer 2019, 161, 139–150. [Google Scholar] [CrossRef]
- Ramasubramani, V.; Dice, B.D.; Harper, E.S.; Spellings, M.P.; Anderson, J.A.; Glotzer, S.C. freud: A Software Suite for High Throughput Analysis of Particle Simulation Data. Comput. Phys. Commun. 2020, 254, 107275. [Google Scholar] [CrossRef]
- Everaers, R.; Sukumaran, S.K.; Grest, G.S.; Svaneborg, C.; Sivasubramanian, A.; Kremer, K. Rheology and Microscopic Topology of Entangled Polymeric Liquids. Science 2004, 303, 823–826. [Google Scholar] [CrossRef] [PubMed]
- Edwards, S.F. The statistical mechanics of polymerized material. Proc. Phys. Soc. 1967, 92, 9–16. [Google Scholar] [CrossRef]
- Edwards, S.F. The theory of rubber elasticity. Br. Polym. J. 1977, 9, 140–143. [Google Scholar] [CrossRef]
- de Gennes, P.G. Reptation of a polymer chain in the presence of fixed obstacles. J. Chem. Phys. 1971, 55, 572–579. [Google Scholar] [CrossRef]
- Ungar, G.; Stejny, J.; Keller, A.; Bidd, I.; Whiting, M.C. The Crystallization of Ultralong Normal Paraffins: The Onset of Chain Folding. Science 1985, 229, 386–389. [Google Scholar] [CrossRef]
- Fatou, J.G.; Mandelkern, L. The Effect of Molecular Weight on the Melting Temperature and Fusion of Polyethylene. J. Phys. Chem. 1965, 69, 417–428. [Google Scholar] [CrossRef]
- Stack, G.M.; Mandelkern, L.; Voigt-Martin, I.G. Crystallization, melting, and morphology of low molecular weight polyethylene fractions. Macromolecules 1984, 17, 321–331. [Google Scholar] [CrossRef]
- Stack, G.M.; Mandelkern, L.; Kroehnke, C.; Wegner, G. Melting and crystallization kinetics of a high molecular weight n-alkane: C192H386. Macromolecules 1989, 22, 4351–4361. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grommes, D.; Bruch, O.; Imhof, W.; Reith, D. Coarse-Grained Molecular Dynamics Study of the Melting Dynamics in Long Alkanes. Polymers 2025, 17, 2500. https://doi.org/10.3390/polym17182500
Grommes D, Bruch O, Imhof W, Reith D. Coarse-Grained Molecular Dynamics Study of the Melting Dynamics in Long Alkanes. Polymers. 2025; 17(18):2500. https://doi.org/10.3390/polym17182500
Chicago/Turabian StyleGrommes, Dirk, Olaf Bruch, Wolfgang Imhof, and Dirk Reith. 2025. "Coarse-Grained Molecular Dynamics Study of the Melting Dynamics in Long Alkanes" Polymers 17, no. 18: 2500. https://doi.org/10.3390/polym17182500
APA StyleGrommes, D., Bruch, O., Imhof, W., & Reith, D. (2025). Coarse-Grained Molecular Dynamics Study of the Melting Dynamics in Long Alkanes. Polymers, 17(18), 2500. https://doi.org/10.3390/polym17182500





