Design and Interlaminar Stress Analysis of Composite Fan Blade Shank
Abstract
1. Introduction
2. Relevant Concepts and Definitions
2.1. Classical Laminate Theory
2.1.1. Strain–Displacement Relationship of Laminated Plates
2.1.2. Stress–Strain Relationship of Laminated Plates
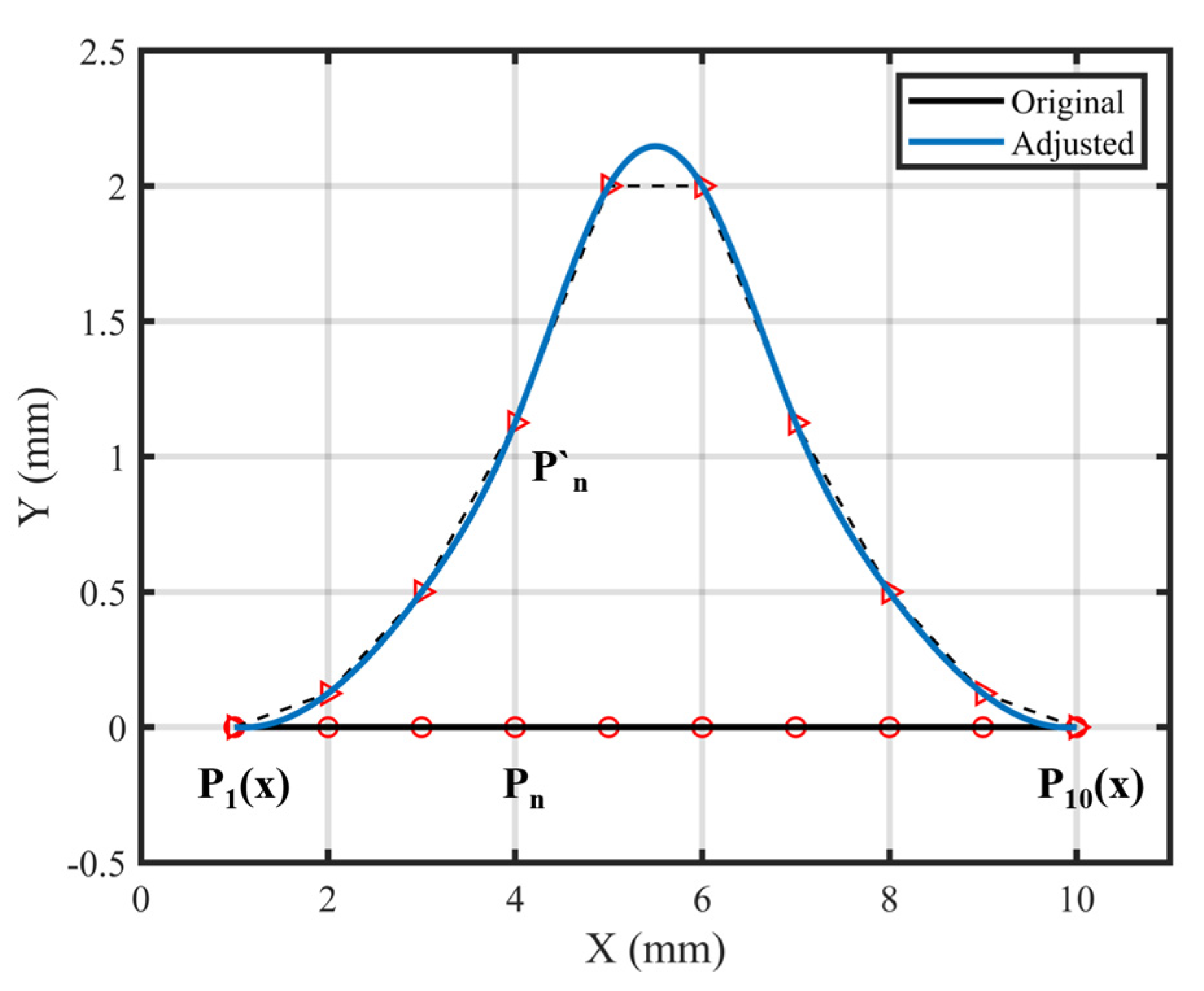
2.2. Bézier Curves
3. Materials and Methods
3.1. Materials
3.2. Bézier Curves and Shank Design
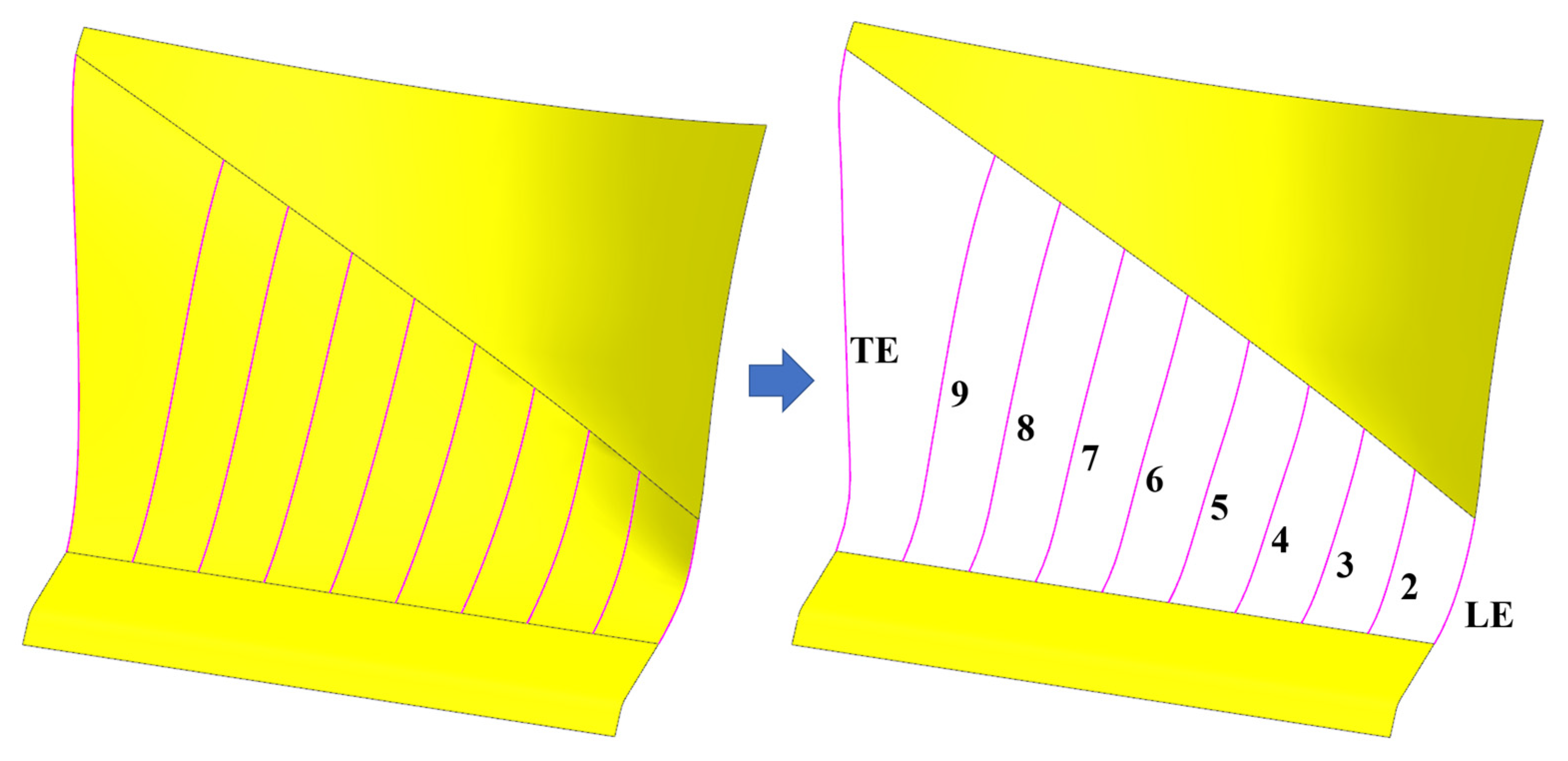
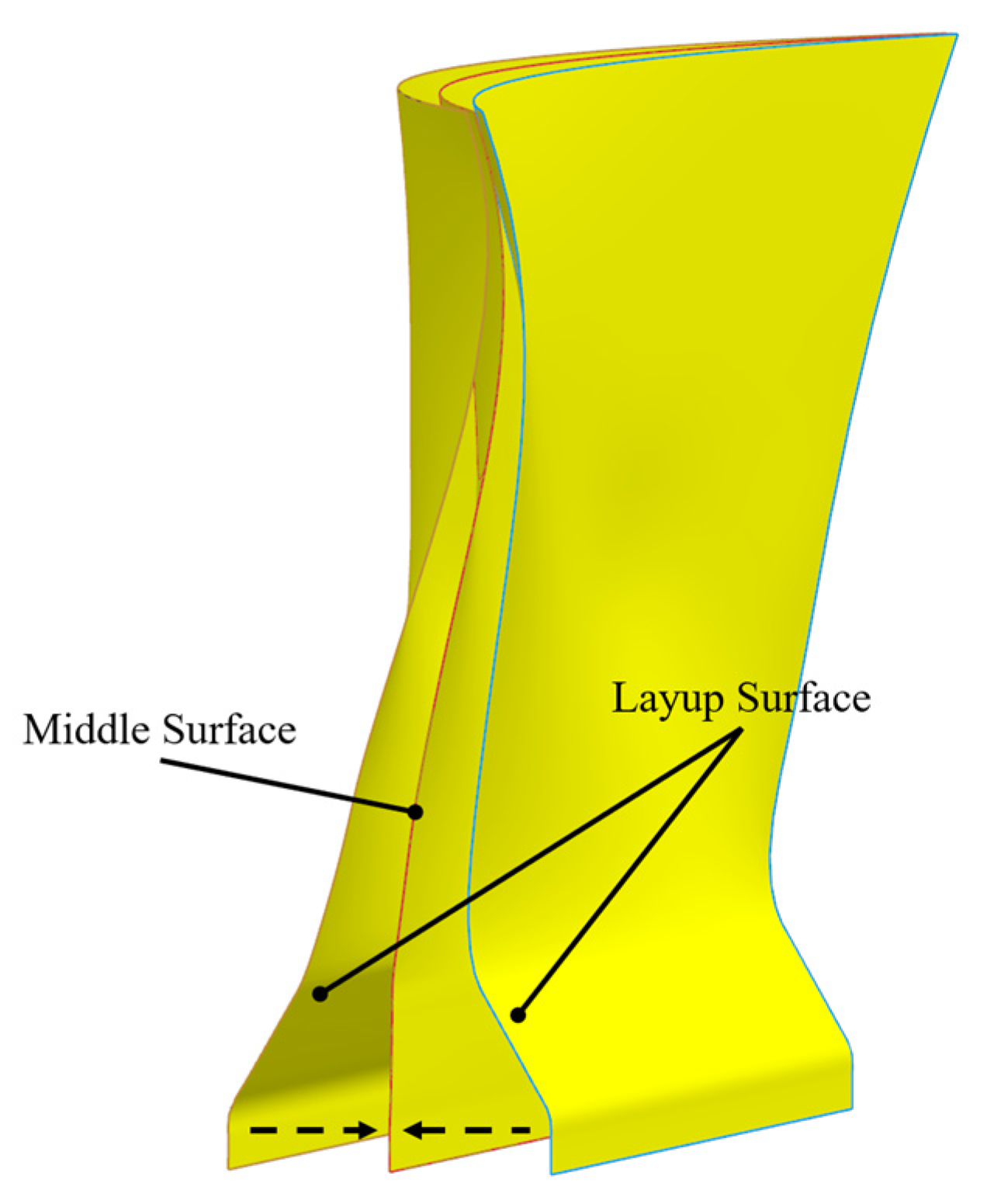
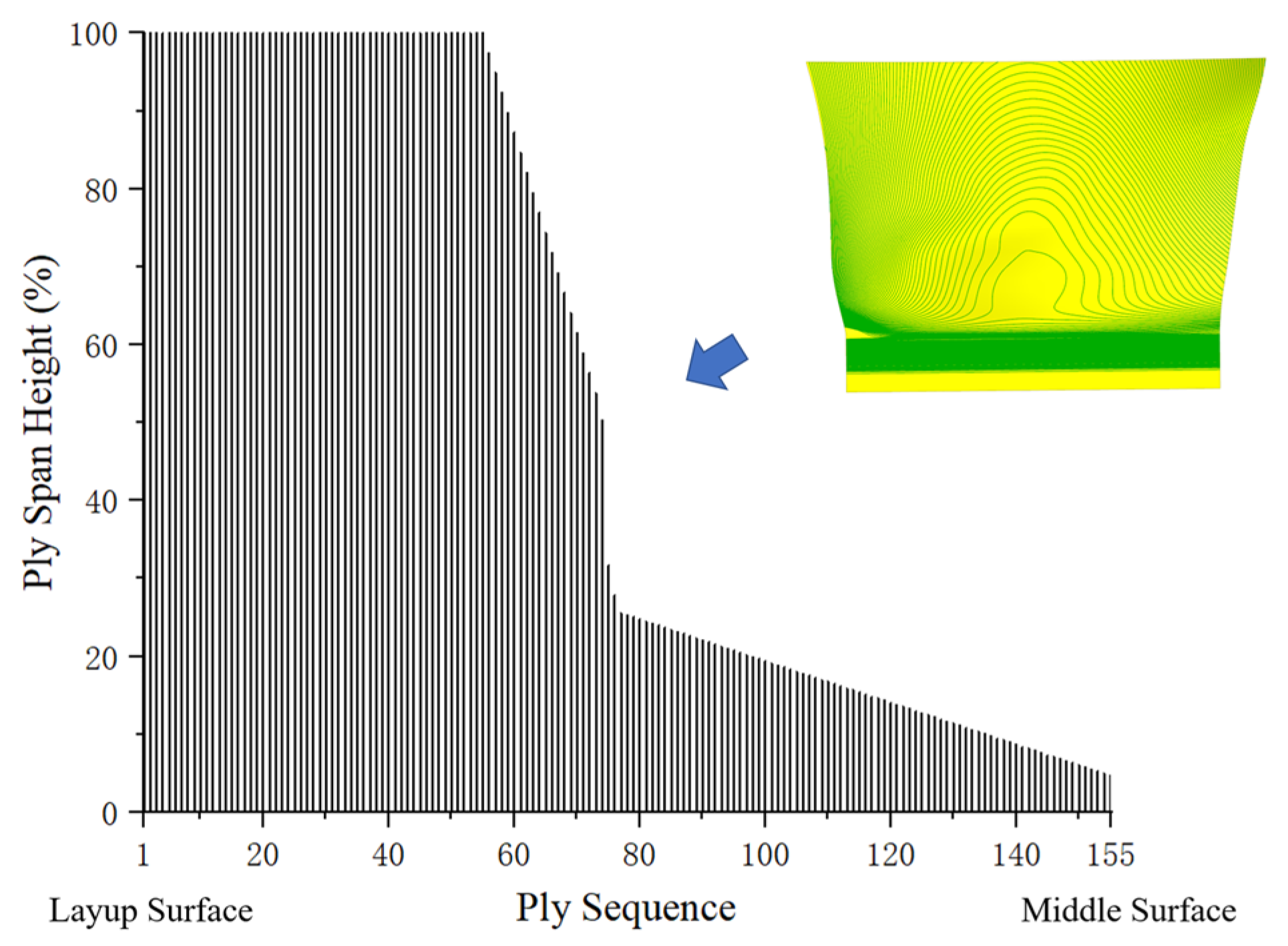
3.3. Ply/Shuffle Design
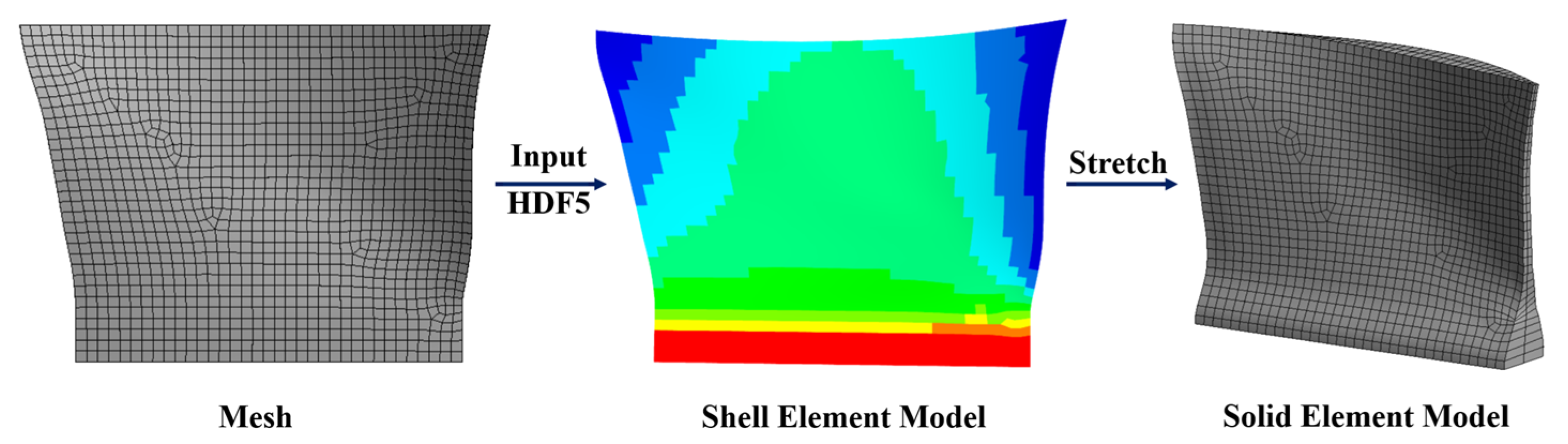
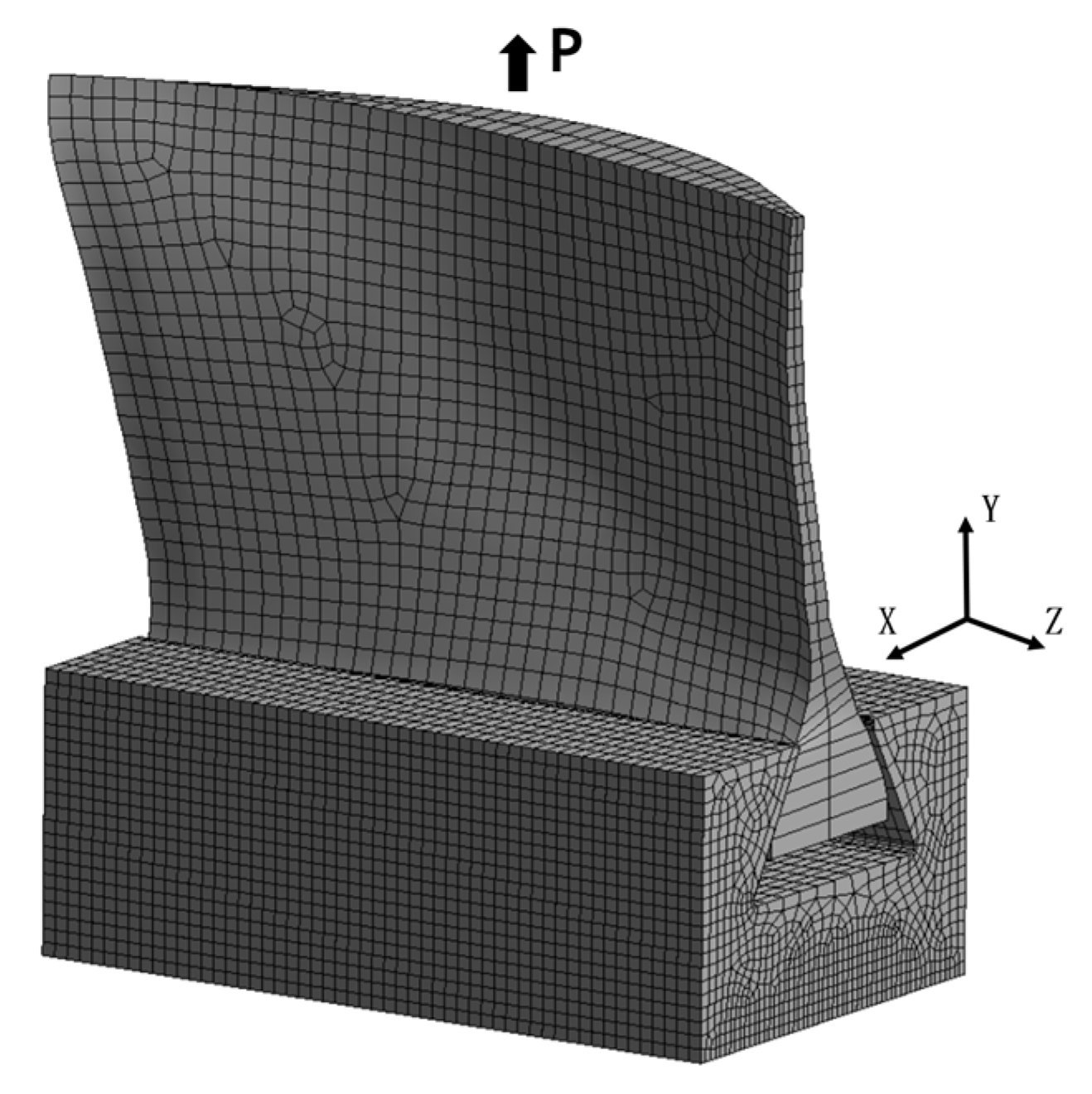
3.4. Shank Structural Analysis
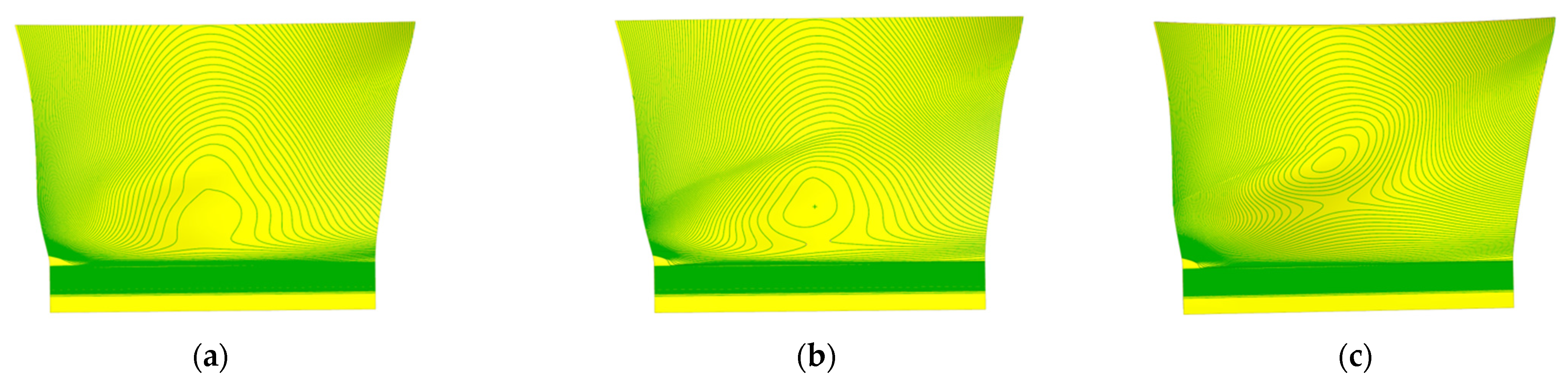
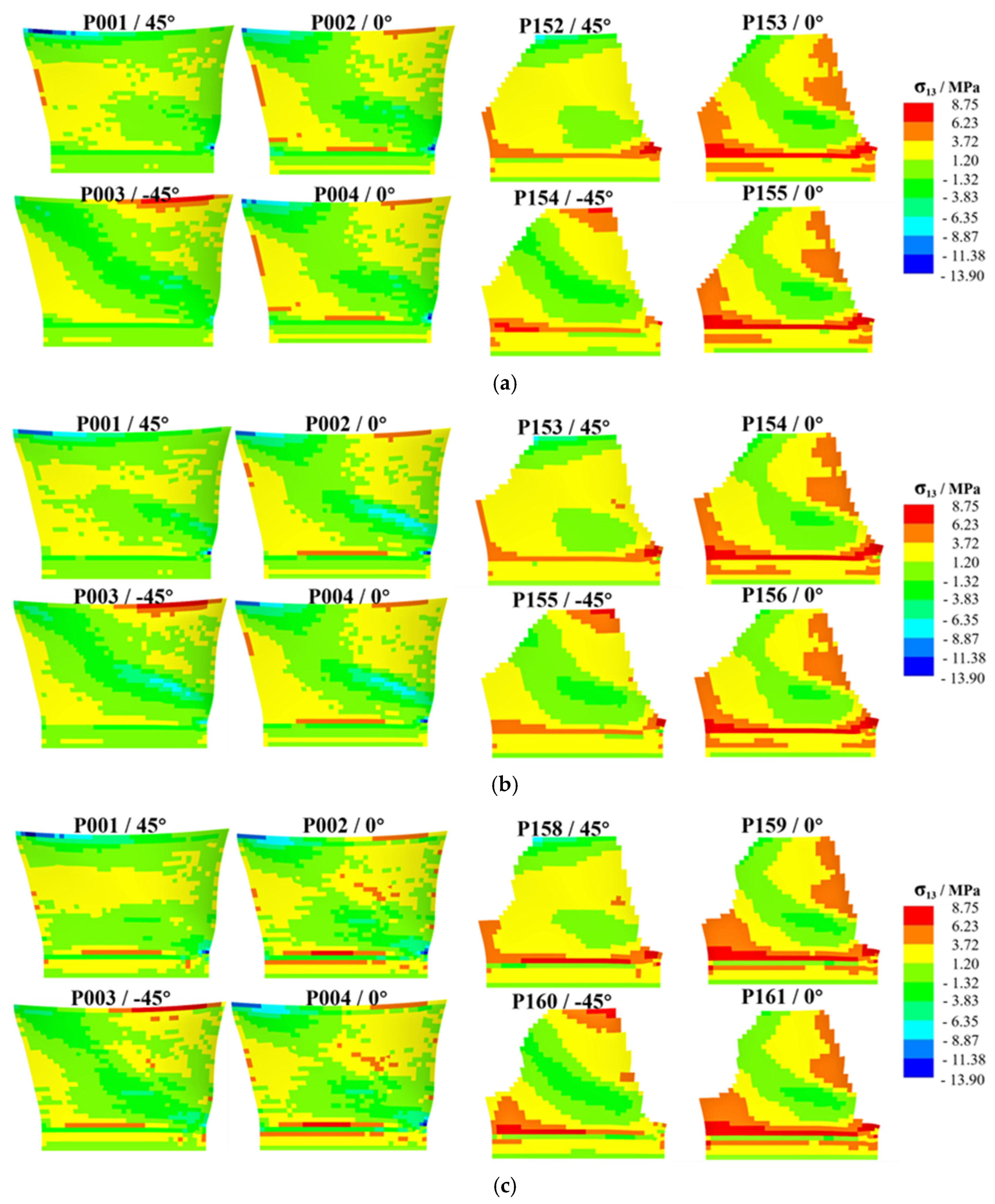
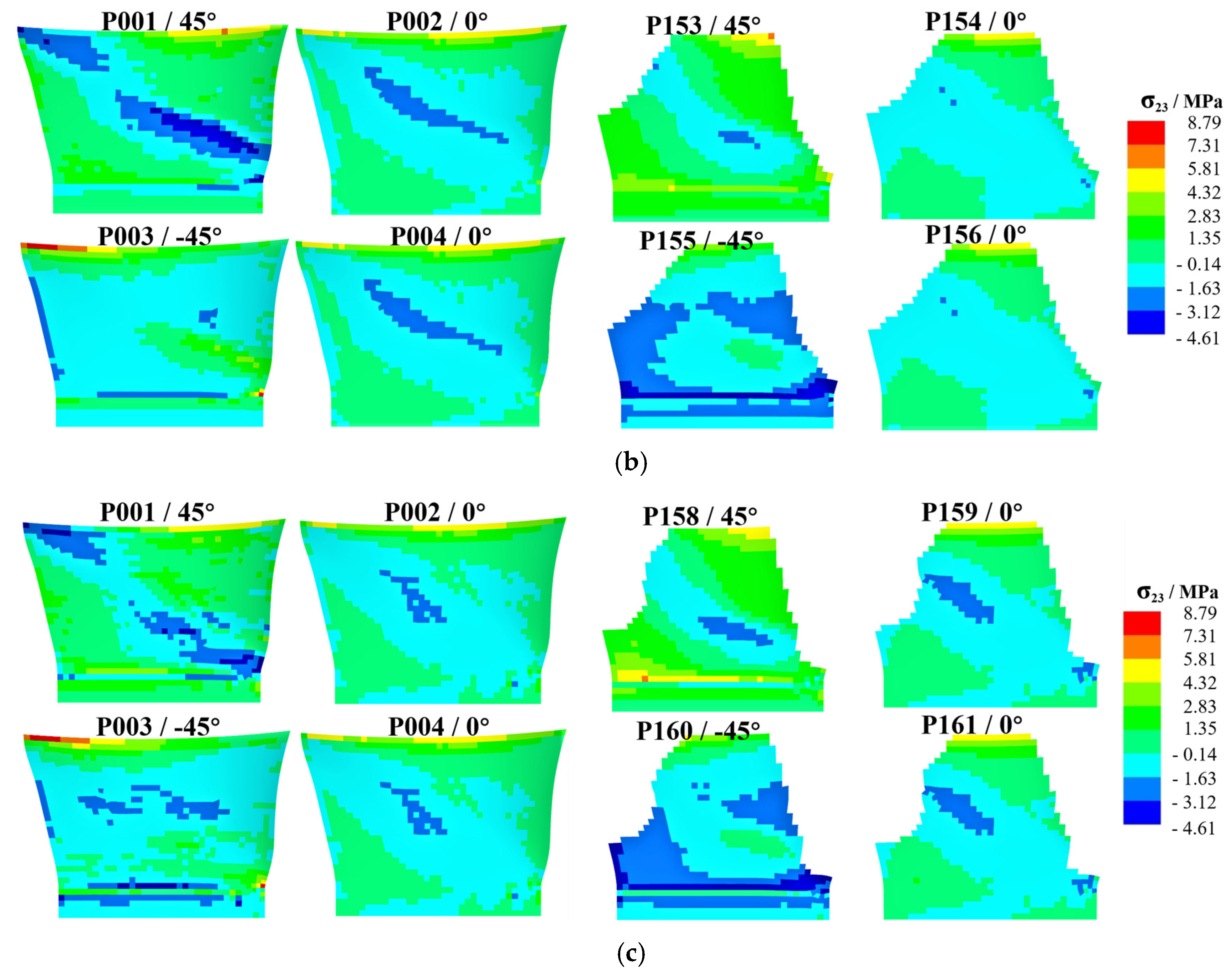
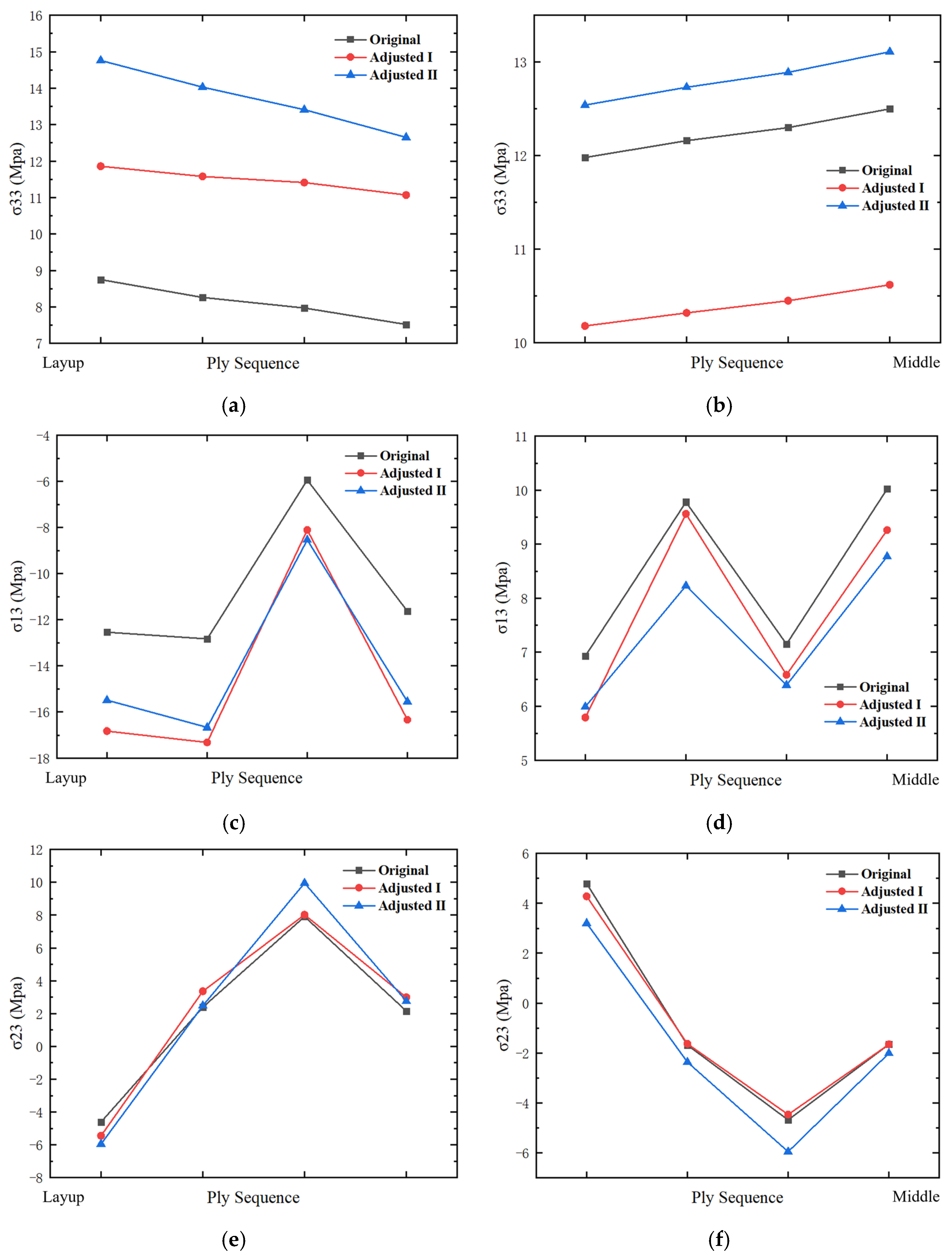
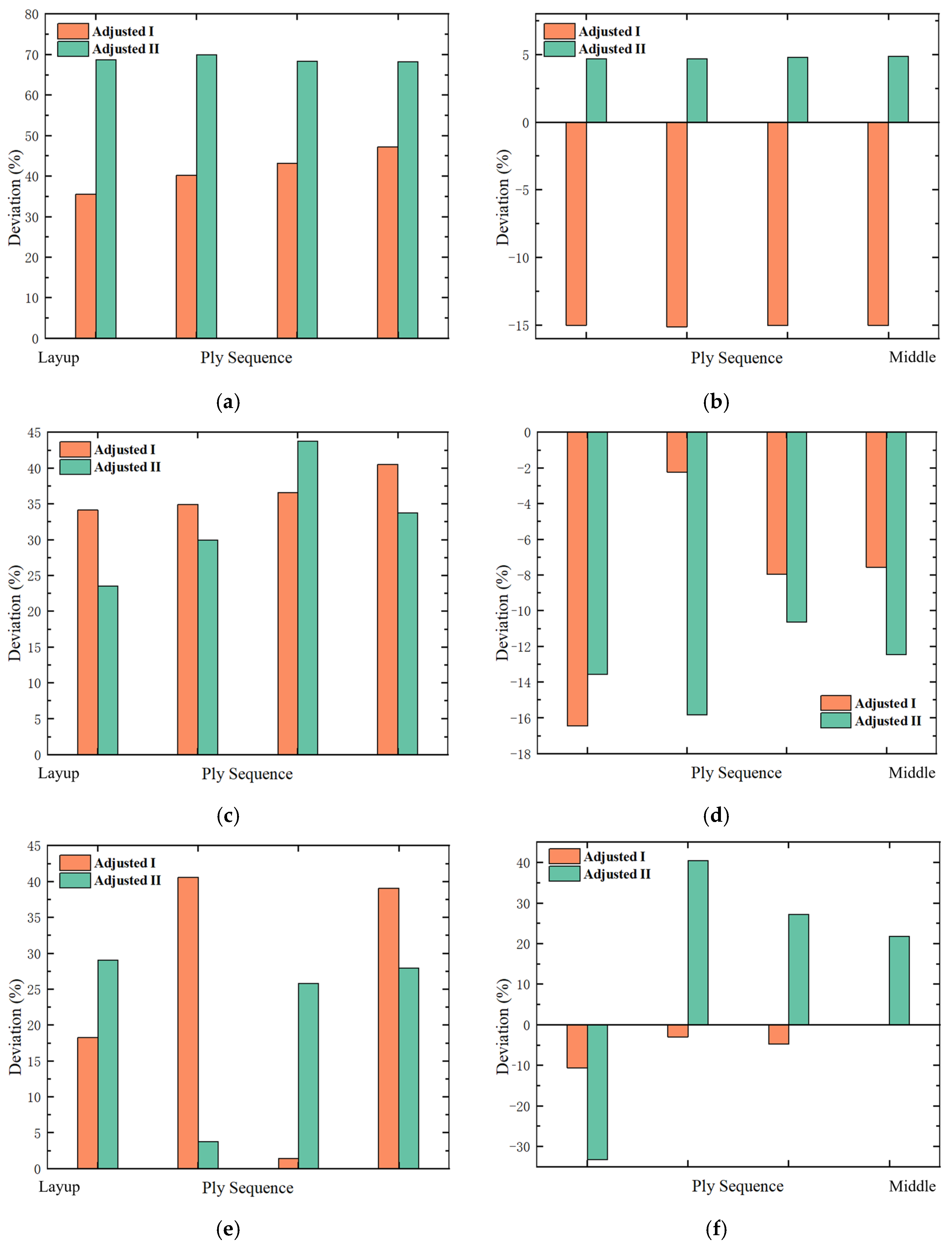
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Aviation Outlook: Composites in Commercial Aircraft Jet Engines. Available online: https://www.compositesworld.com/articles/aviation-outlook-composites-in-commercial-aircraft-jet-engines (accessed on 9 September 2008).
- Upadhyay, R.; Sinha, S. 3.6 GE-90 and derivative fan blade manufacturing design. In Comprehensive Composite Materials II, 2nd ed.; Peter, B., Carl, Z., Eds.; Elsevier: Amsterdam, The Netherlands, 2018; Volume 3, pp. 65–82. ISBN 9780081005347. [Google Scholar]
- Jeon, T.H.; Jeon, M. Design and manufacturing of a thermoplastic composite fan blade: Process-induced deformation simulation with fiber-draping analysis and its experimental validation. Compos. Part B Eng. 2024, 283, 111599. [Google Scholar] [CrossRef]
- Liu, Q.; Zhao, L.; Huang, F. Present conditions and development of composite fan blades of high bypass ratio commercial jet engines. Aeronaut. Manuf. Technol. 2014, 15, 58–62. [Google Scholar] [CrossRef]
- Song, C. Research on Design and Manufacture for Composite Blade in Aircraft Turbine. Ph.D. Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2014. [Google Scholar]
- Hetal, N.; Akash, B. A review on approaches for handling Bezier curves in CAD for manufacturing. Procedia Eng. 2014, 97, 1155–1166. [Google Scholar] [CrossRef]
- Ferguson, D. An introduction to NURBS; Morgan Kaufmann: San Francisco, CA, USA, 2001; ISBN 9781558606692. [Google Scholar]
- Li, Z.; Zheng, X. Review of design optimization methods for turbomachinery aerodynamics. Prog. Aerosp. Sci. 2017, 93, 1–23. [Google Scholar] [CrossRef]
- Zhang, B.; Kawashita, L.F.; Jones, M.I.; Lander, J.K.; Hallett, S.R. An experimental and numerical investigation into damage mechanisms in tapered laminates under tensile loading. Compos. Part A 2020, 133, 105862. [Google Scholar] [CrossRef]
- Zhang, T.; Huang, A.H.; Li, X.Q. Effect of ply-drops with gaps in tapered laminate. Compos. Commun. 2020, 18, 26–31. [Google Scholar] [CrossRef]
- Hallett, S.R.; Lander, J.K.; Jones, M.I.; Kawashita, L.F.; Wisnom, M.R. Testing and Modelling of a Severely Tapered Composite Specimen. In Proceedings of the 5th International Conference on Composites Testing and Model Simulation (CompTest), Lausanne, Switzerland, 14 February 2011. [Google Scholar]
- Gan, K.W.; Allegri, G.; Hallett, S.R. A simplified layered beam approach for predicting ply drop delamination in thick composite laminates. Mater. Des. 2016, 108, 570–580. [Google Scholar] [CrossRef]
- Hosseinpour, D.S.; Parnas, L.; Coker, D.; Bozkurt, M.O.; Ozen, E.B. In-situ observation and numerical study of dynamic delamination in tapered composite laminates. Compos. Struct. 2023, 312, 116841. [Google Scholar] [CrossRef]
- Zhang, Y.K.; Chen, Y.; Tang, X. Test Method for Static Strength of Laminated Composite Fan Blade Dovetail in Element Level. J. Propuls. Technol. 2022, 43, 342–351. [Google Scholar] [CrossRef]
- Shen, Z.; Huang, Z.Y.; Wang, J.; Zheng, L.Q.; Qian, H.J. Investigation of fretting fatigue performance for IN718 dovetail joint in very high cycle regime. Int. J. Fatigue 2025, 195, 108874. [Google Scholar] [CrossRef]
- Noh, H.K.; Go, M.S.; Lim, J.H.; Choi, Y.H.; Kim, J.G. Numerical modeling and experimental validation of lamina fracture and progressive delamination in composite dovetail specimens under tensile loading. Compos. Struct. 2023, 325, 117578. [Google Scholar] [CrossRef]
- Kogo, Y.; Hatta, H.; Toyoda, M.; Sugibayashi, T. Application of three-dimensionally reinforced carbon–carbon composites to dovetail joint structures. Compos. Sci. Technol. 2002, 62, 2143–2152. [Google Scholar] [CrossRef]
- Qin, Y.; Xiong, C.; Zhu, X.J.; Yin, J.H.; Zhang, Y. Strength analysis of carbon-fiber dovetail tenon connections under quasi-static tension. Structures 2024, 67, 106925. [Google Scholar] [CrossRef]
- Gao, P.; Dong, B. Photoelastic optimization design of turbine blade root structure in engine. Aeroengine 1995, 1, 19–23. [Google Scholar]
- Wang, R.; Mo, R.; Yin, Y.; Dang, S. Research on parametric design method of turbine gas-cooled moving blade root segment. Aerosp. Comput. Technol. 2008, 38, 1–4, 21. [Google Scholar] [CrossRef]
- Zhu, Q.; Ning, T.; Xi, P. Root extending section of turbine blade modeling method based on guide curves. J. Beijing Univ. Aeronaut. Astronaut. 2012, 38, 1085–1089. [Google Scholar] [CrossRef]
- Ren, Y.; Zhang, C.; Gao, J.; Li, Y. Shape design and optimization for shank of aeroengine fan blade. J. Aerosp. Power 2017, 32, 2824–2834. [Google Scholar] [CrossRef]
- Chahine, C. Multidisciplinary Design Optimisation of Aero-Engine Fan Blades. Ph.D. Thesis, University of Oxford, Oxford, UK, 2018. [Google Scholar]
- Gibson, R.F. Principles of Composite Material Mechanics, 4th ed.; CRC Press: Boca Raton, FL, USA, 2016; pp. 57–94. [Google Scholar]
- Zhu, Q.; Chen, Y.; Xiao, J. Research on lay-up design method of composite fan blades. Aeroengine 2018, 44, 49–54. [Google Scholar] [CrossRef]
- Xiao, J.; Chen, Y.; Zhu, Q.; Lee, J.; Ma, T. A general ply design for aero engine composite fan blade. In Proceedings of the ASME Turbo Expo 2017: Turbomachinery Technical Conference and Exposition, Charlotte, NC, USA, 26–30 June 2017. [Google Scholar] [CrossRef]
- Kang, Y.; Chen, Y. Laminate design of composite fan blade dovetail. Synth. Fibers 2020, 49, 44–51. [Google Scholar] [CrossRef]
- Zhu, Q.; Chen, Y. Modal simulation analysis of a composite wide-chord fan blade. Aeroengine 2019, 45, 28–32. [Google Scholar] [CrossRef]
- Kang, Y.; Chen, Y. Inter-laminar stress analysis of laminated composite fan blade dovetail. J. Aerosp. Power 2020, 35, 388–396. [Google Scholar] [CrossRef]
- Zhao, L.; Gong, Y.; Zhang, J. A survey on delamination growth behavior in fiber reinforced composite laminates. Acta Aeronaut. Astronaut. Sin. 2019, 40, 522509. [Google Scholar] [CrossRef]






| Properties | Value |
|---|---|
| Density/(Kg/m3) | 1490 |
| Young’s Modulus in x Direction/GPa | 121 |
| Young’s Modulus in y&z Direction/GPa | 8.6 |
| Shear Modulus in xy&xz Direction/GPa | 4.7 |
| Shear Modulus in yz Direction/GPa | 3.1 |
| Tensile Stress Limit in x Direction/MPa | 2231 |
| Tensile Stress Limit in y&z Direction/MPa | 29 |
| Compressive Stress Limit in x Direction/MPa | −1082 |
| Compressive Stress Limit in y&z Direction/MPa | −100 |
| Shear Stress Limit in xy&xz Direction/MPa | 60 |
| Shear Stress Limit in yz Direction/MPa | 32 |
| Properties | Value |
|---|---|
| Density/(Kg/m3) | 1160 |
| Young’s Modulus/MPa | 3780 |
| Shear Modulus/MPa | 1400 |
| Poisson’s Ratio | 0.35 |
| Part | Element Sizes/mm | Nodes Number | Solid Number |
|---|---|---|---|
| Shank (Origin/I/II) | 6 | 3960 | 2494 |
| Disk | 4 | 168,558 | 38,826 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Zhang, Y.; Wang, Z.; Jin, L.; Tang, X.; Li, X.; Chen, Y. Design and Interlaminar Stress Analysis of Composite Fan Blade Shank. Polymers 2025, 17, 2445. https://doi.org/10.3390/polym17182445
Wu Y, Zhang Y, Wang Z, Jin L, Tang X, Li X, Chen Y. Design and Interlaminar Stress Analysis of Composite Fan Blade Shank. Polymers. 2025; 17(18):2445. https://doi.org/10.3390/polym17182445
Chicago/Turabian StyleWu, Yongjun, Yukun Zhang, Zijian Wang, Lu Jin, Xu Tang, Xuyang Li, and Yong Chen. 2025. "Design and Interlaminar Stress Analysis of Composite Fan Blade Shank" Polymers 17, no. 18: 2445. https://doi.org/10.3390/polym17182445
APA StyleWu, Y., Zhang, Y., Wang, Z., Jin, L., Tang, X., Li, X., & Chen, Y. (2025). Design and Interlaminar Stress Analysis of Composite Fan Blade Shank. Polymers, 17(18), 2445. https://doi.org/10.3390/polym17182445






