Polymeric and Polymer-Functionalized Drug Delivery Vectors: From Molecular Architecture and Elasticity to Cellular Uptake
Abstract
1. Introduction
2. Structural and Elastic Characterization
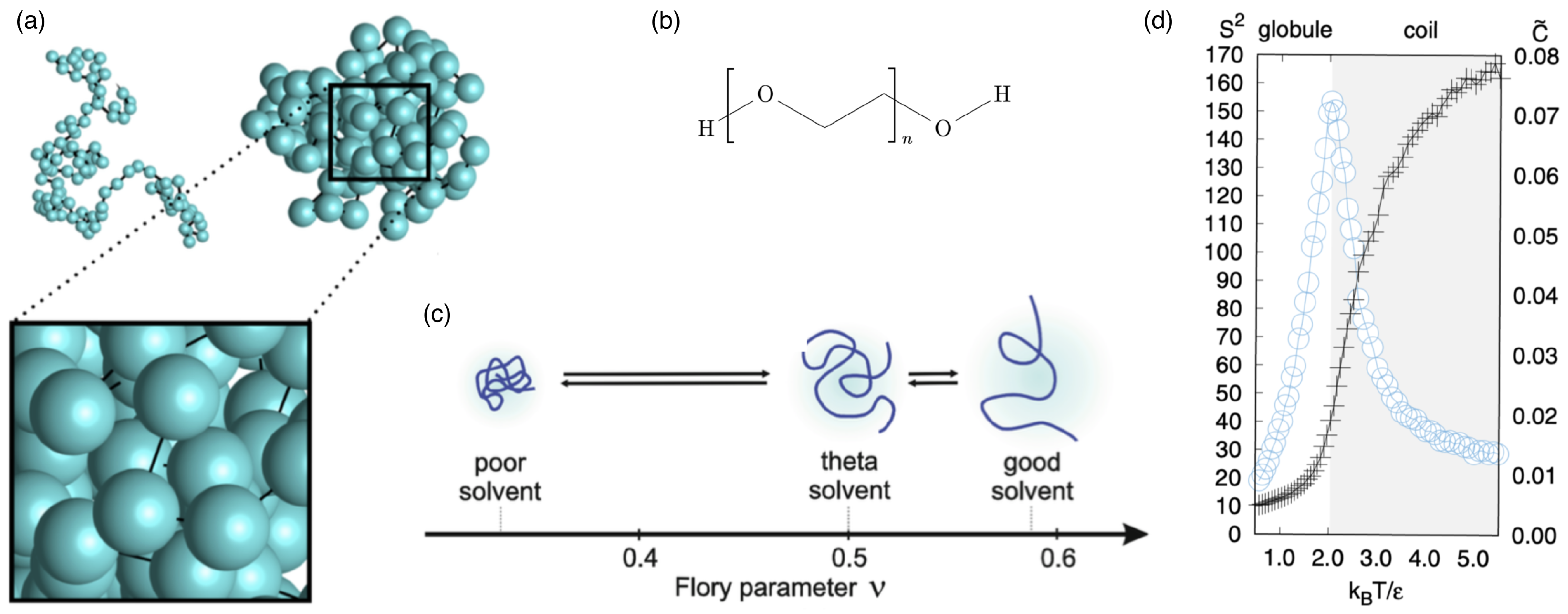
2.1. Linear Polymers
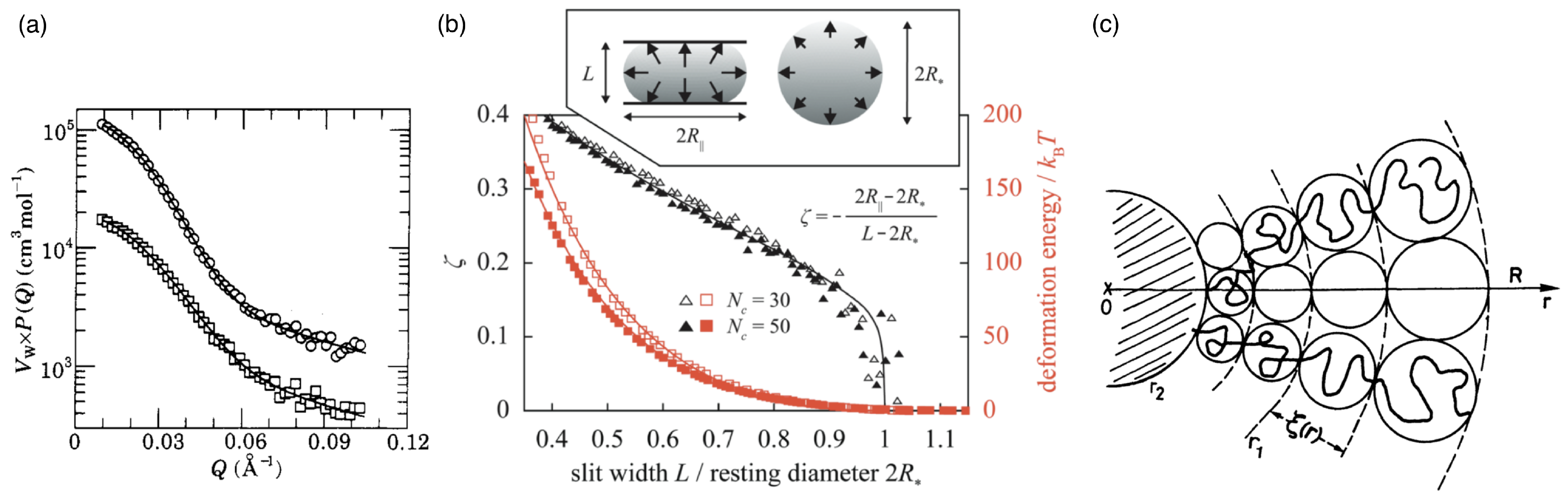
2.2. Star Polymers
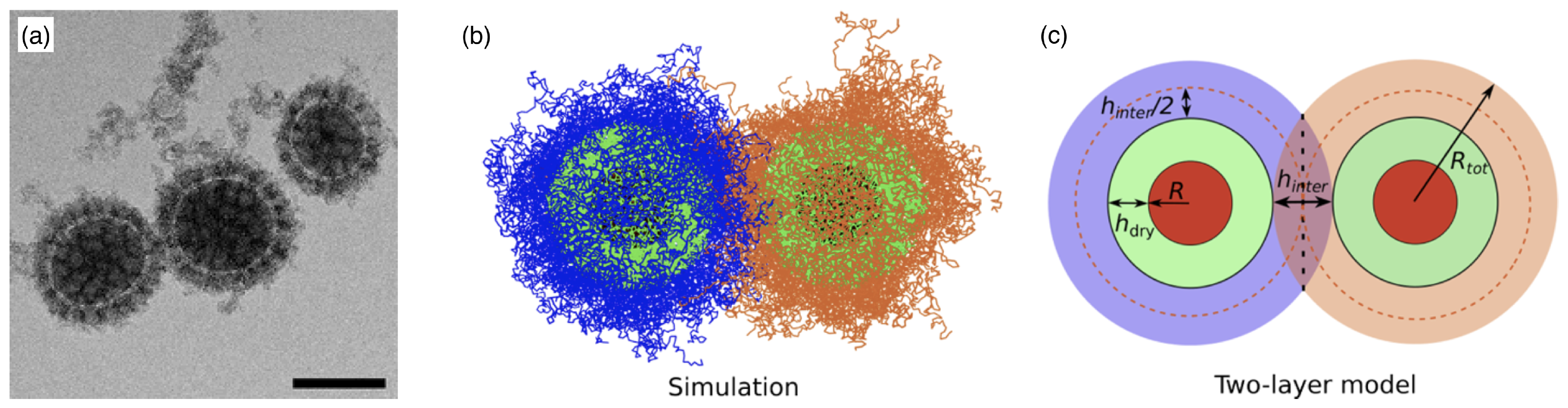
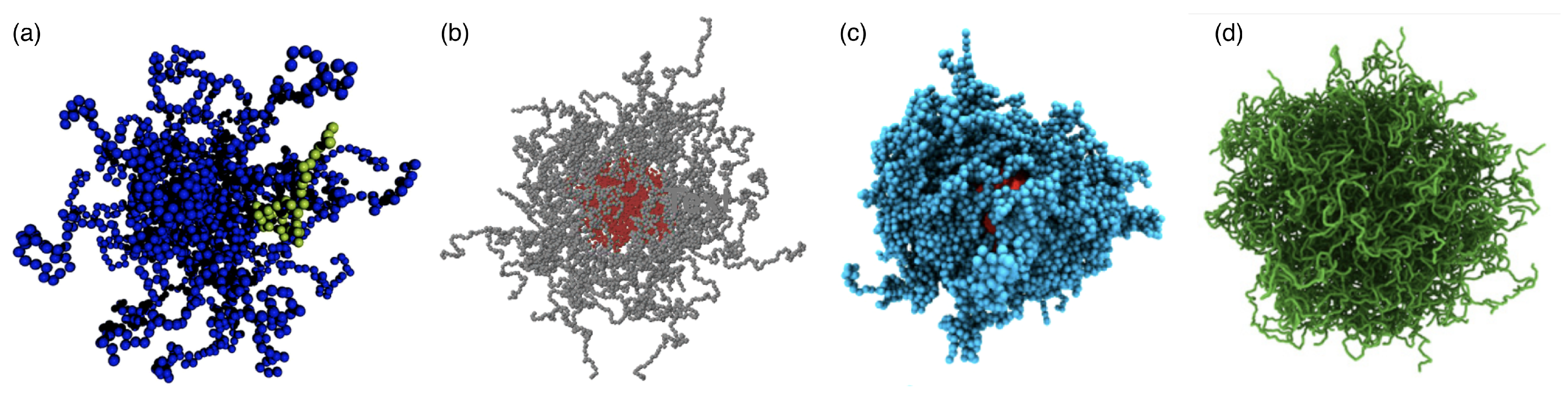
2.3. Polymer-Grafted Nanoparticles
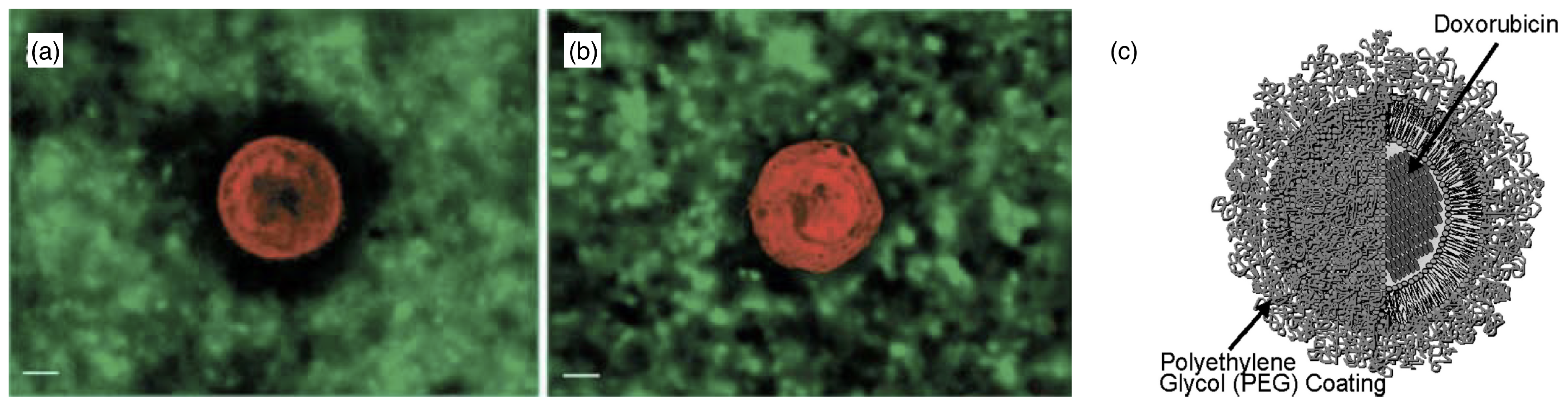
2.4. Polymersomes and Stealth Liposomes
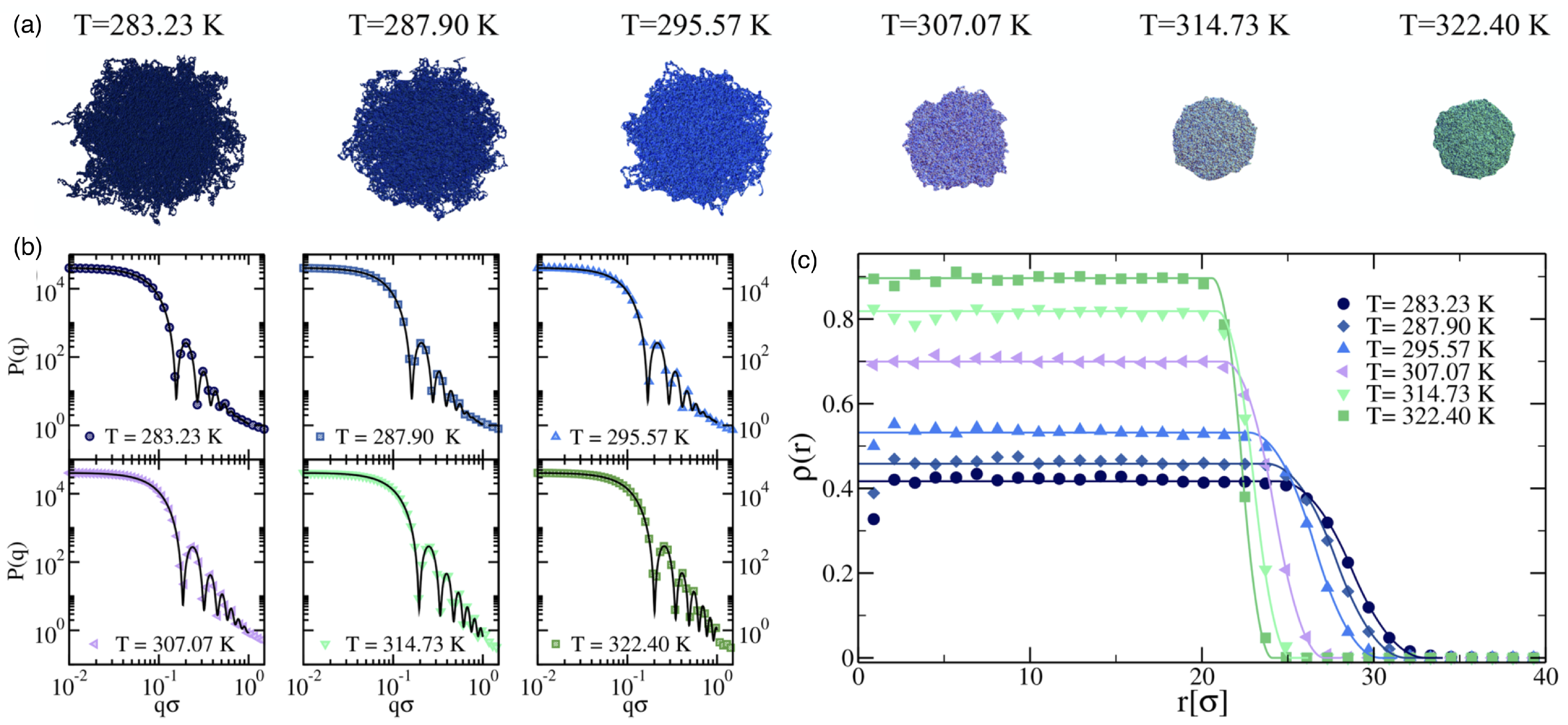
2.5. Nano- and Microgels
2.6. Biomolecular Condensates
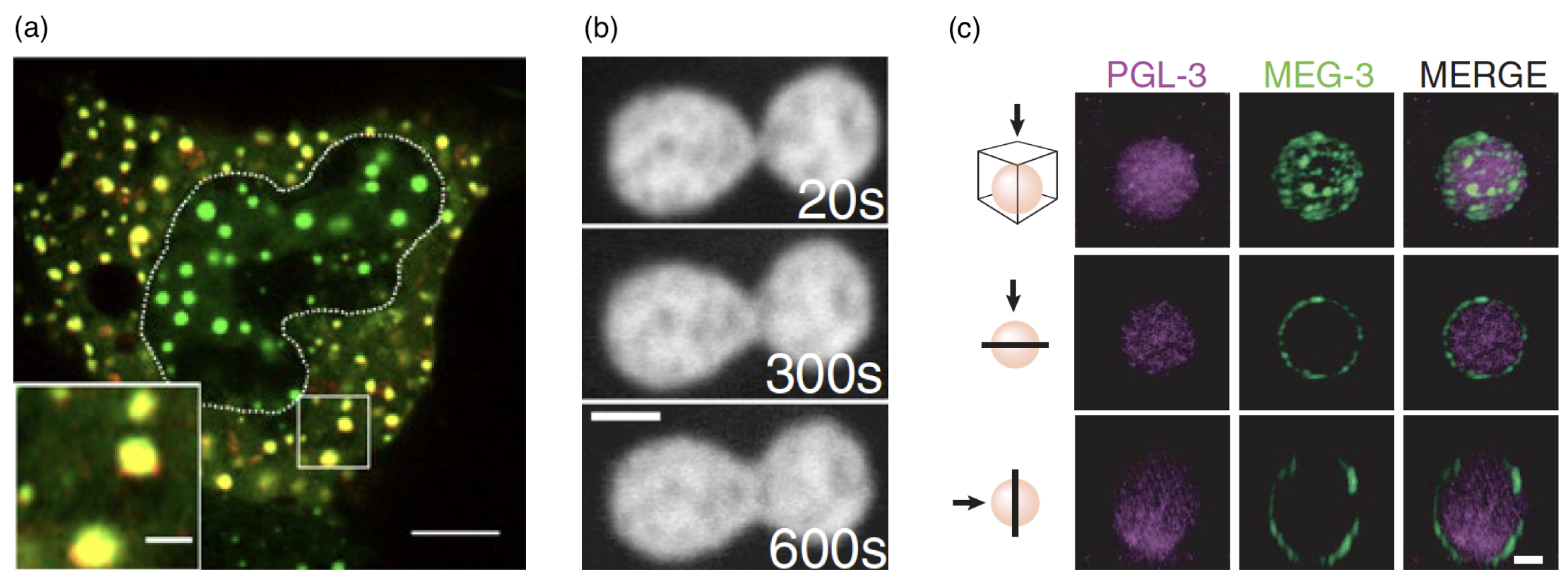
3. Circulation Times
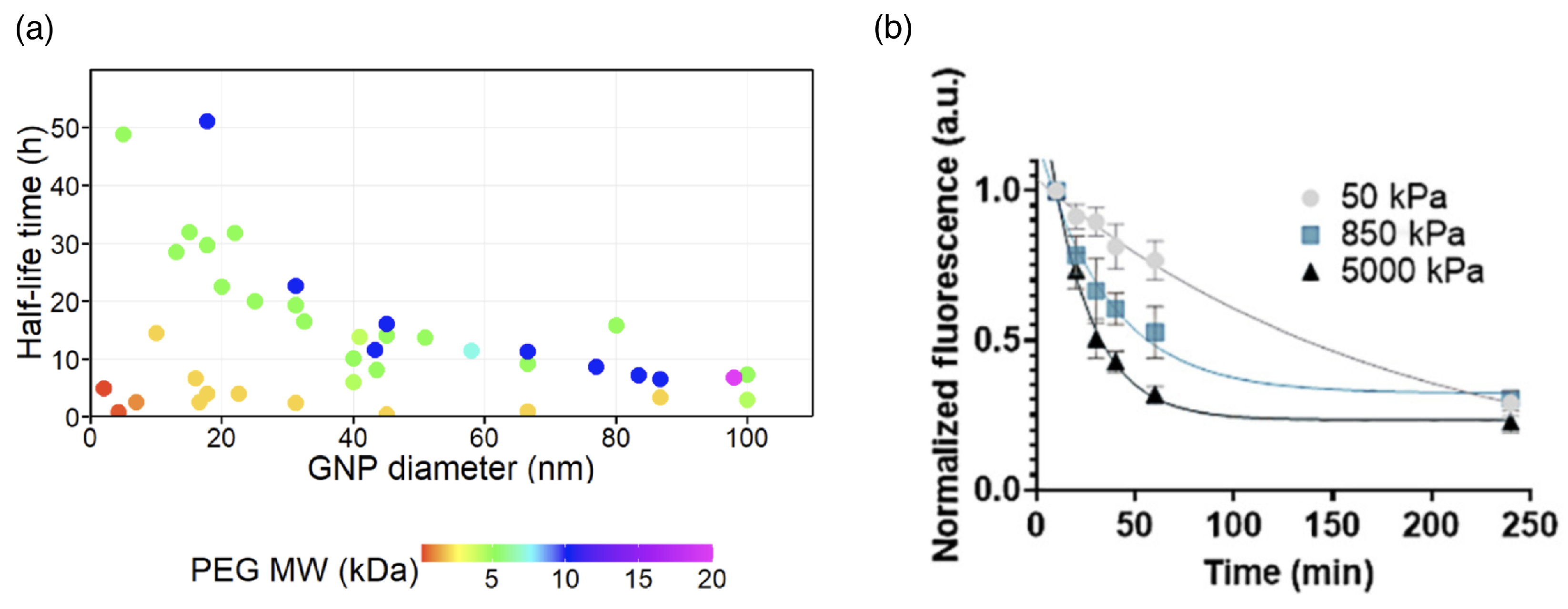
| Particle | Surface Properties | Hydrodyn. Diam. | Half-Life Time | References |
|---|---|---|---|---|
| lipid nanoparticles | bare | [217] | ||
| lipid nanoparticles | HEP | [217] | ||
| lipid nanoparticles | PEG | [217] | ||
| lipid nanoparticles | PEG/HEP | [217] | ||
| liposomes, first dose | bare | [219] | ||
| liposomes, second dose | bare | [219] | ||
| liposomes, first dose | PEG | [219] | ||
| liposomes, second dose | PEG | [219] | ||
| liposomes, first dose | HPMA | [219] | ||
| liposomes, second dose | HPMA | [219] | ||
| gold nanoparticles, diameter | PEG | [81] | ||
| gold nanoparticles, diameter | PEG | [81] | ||
| gold nanoparticles, diameter | PEG | [81] |
4. Cellular Uptake Mechanisms
4.1. Characterizing Cellular Uptake
4.2. Lipid-Bilayer Translocation
4.3. Passive Endocytosis
4.4. Active Cellular Uptake Processes
5. Polymers In Vivo Relevant to Drug Delivery
6. Summary
7. Outlook
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AFM | Atomic force microscopy |
| BIS | N,N′-methylenebis(acrylamide) |
| DMA | Dopamine methacrylamide |
| DNA | Deoxyribonucleic acid |
| DOPE | 1,2-Dioleoyl-sn-glycero-3-phosphoethanolamine |
| FOCTS | Trichloro(1H,1H,2H,2H-perfluorooctyl)silane |
| GNP | Gold nanoparticles |
| GUV | Giant unilamellar vesicle |
| HEP | Heparin |
| HPMA | N-(2-Hydroxypropyl)methacrylamide (HPMA) |
| LCST | Lower critical solution temperature |
| LLPS | Liquid–liquid phase separation |
| MPS | Mononuclear phagocyte system |
| ODS | N-octadecyltrimethoxysilane |
| PAcM | Poly(N-acryloyl morpholine) |
| PDMA | Poly(N,N-dimethylacrylamide) |
| PEG | Polyethylene glycol |
| PEO | Polyethylene oxide |
| PG | Polypropylene glycol |
| PGN | Polymer-grafted (hairy) (nano-)particles |
| PNIPAM | Poly(N-isopropylacrylamide) |
| PNIPMAM | Poly(N-isopropylmethacrylamide) |
| POPC | 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine |
| POPG | 1-Palmitoyl-2-oleoyl-sn-glycero-3-phosphoglycerol |
| PVP | Poly(vinylpyrrolidone) |
| RES | Reticuloendothelial system |
| RNA | Ribonucleic acid |
| SCL | Self-crosslinked |
| UCST | Upper critical solution temperature |
| ULC | Ultra-low crosslinked |
| VPTT | Volume phase transition temperature |
| WCA | Weeks–Chandler–Andersen |
References
- Nifontova, G.; Tsoi, T.; Karaulov, A.; Nabiev, I.; Sukhanova, A. Structure–function relationships in polymeric multilayer capsules designed for cancer drug delivery. Biomater. Sci. 2022, 10, 5092–5115. [Google Scholar] [CrossRef] [PubMed]
- Pérez-Ferreiro, M.; Abelairas, A.M.; Criado, A.; Gómez, I.J.; Mosquera, J. Dendrimers: Exploring Their Wide Structural Variety and Applications. Polymers 2023, 15, 4369. [Google Scholar] [CrossRef]
- Chauhan, A.S. Dendrimers for Drug Delivery. Molecules 2018, 23, 938. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Zhang, L.; Wang, J.; Feng, Q.; Liu, D.; Yin, Q.; Xu, D.; Wei, Y.; Ding, B.; Shi, X.; et al. Tunable Rigidity of (Polymeric Core)–(Lipid Shell) Nanoparticles for Regulated Cellular Uptake. Adv. Mater. 2015, 27, 1402–1407. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Zhou, X.; Mao, Z.; Yu, D.; Wang, B.; Gao, C. Uptake of hydrogel particles with different stiffness and its influence on HepG2 cell functions. Soft Matter 2012, 8, 9235. [Google Scholar] [CrossRef]
- Banquy, X.; Suarez, F.; Argaw, A.; Rabanel, J.M.; Grutter, P.; Bouchard, J.F.; Hildgen, P.; Giasson, S. Effect of mechanical properties of hydrogel nanoparticles on macrophage cell uptake. Soft Matter 2009, 5, 3984. [Google Scholar] [CrossRef]
- Beningo, K.A.; Wang, Y.L. Fc-receptor-mediated phagocytosis is regulated by mechanical properties of the target. J. Cell Sci. 2002, 115, 849–856. [Google Scholar] [CrossRef]
- Mayer, C.; Likos, C.N. A Coarse-Grained Description of Star-Linear Polymer Mixtures. Macromolecules 2007, 40, 1196–1206. [Google Scholar] [CrossRef]
- Bedrov, D.; Ayyagari, C.; Smith, G.D. Multiscale Modeling of Poly(ethylene oxide)-Poly(propylene oxide)-Poly(ethylene oxide) Triblock Copolymer Micelles in Aqueous Solution. J. Chem. Theory Comput. 2006, 2, 598–606. [Google Scholar] [CrossRef]
- Midya, J.; Rubinstein, M.; Kumar, S.K.; Nikoubashman, A. Structure of Polymer-Grafted Nanoparticle Melts. ACS Nano 2020, 14, 15505–15516. [Google Scholar] [CrossRef]
- Nikolov, S.V.; Fernandez-Nieves, A.; Alexeev, A. Behavior and mechanics of dense microgel suspensions. Proc. Natl. Acad. Sci. USA 2020, 117, 27096–27103. [Google Scholar] [CrossRef]
- Zhang, Y.; Fu, L.; Li, S.; Yan, J.; Sun, M.; Giraldo, J.P.; Matyjaszewski, K.; Tilton, R.D.; Lowry, G.V. Star Polymer Size, Charge Content, and Hydrophobicity Affect their Leaf Uptake and Translocation in Plants. Environ. Sci. Technol. 2021, 55, 10758–10768. [Google Scholar] [CrossRef]
- Chen, Y.; Lord, M.S.; Piloni, A.; Stenzel, M.H. Correlation between Molecular Weight and Branch Structure of Glycopolymers Stars and Their Binding to Lectins. Macromolecules 2015, 48, 346–357. [Google Scholar] [CrossRef]
- Georgiou, T.K.; Vamvakaki, M.; Patrickios, C.S.; Yamasaki, E.N.; Phylactou, L.A. Nanoscopic Cationic Methacrylate Star Homopolymers: Synthesis by Group Transfer Polymerization, Characterization and Evaluation as Transfection Reagents. Biomacromolecules 2004, 5, 2221–2229. [Google Scholar] [CrossRef] [PubMed]
- Hedden, R.C.; Bauer, B.J. Structure and Dimensions of PAMAM/PEG Dendrimer-Star Polymers. Macromolecules 2003, 36, 1829–1835. [Google Scholar] [CrossRef]
- Bagheri, M.; Bresseleers, J.; Varela-Moreira, A.; Sandre, O.; Meeuwissen, S.A.; Schiffelers, R.M.; Metselaar, J.M.; Van Nostrum, C.F.; Van Hest, J.C.M.; Hennink, W.E. Effect of Formulation and Processing Parameters on the Size of mPEG-b-p(HPMA-Bz) Polymeric Micelles. Langmuir 2018, 34, 15495–15506. [Google Scholar] [CrossRef]
- Zinn, T.; Willner, L.; Lund, R.; Pipich, V.; Richter, D. Equilibrium exchange kinetics in n-alkyl–PEO polymeric micelles: Single exponential relaxation and chain length dependence. Soft Matter 2012, 8, 623–626. [Google Scholar] [CrossRef]
- Forman-Kay, J.D.; Ditlev, J.A.; Nosella, M.L.; Lee, H.O. What are the distinguishing features and size requirements of biomolecular condensates and their implications for RNA-containing condensates? RNA 2022, 28, 36–47. [Google Scholar] [CrossRef]
- Cochard, A.; Garcia-Jove Navarro, M.; Piroska, L.; Kashida, S.; Kress, M.; Weil, D.; Gueroui, Z. RNA at the surface of phase-separated condensates impacts their size and number. Biophys. J. 2022, 121, 1675–1690. [Google Scholar] [CrossRef]
- Folkmann, A.W.; Putnam, A.; Lee, C.F.; Seydoux, G. Regulation of biomolecular condensates by interfacial protein clusters. Science 2021, 373, 1218–1224. [Google Scholar] [CrossRef]
- Bonham, J.A.; Faers, M.A.; Van Duijneveldt, J.S. Non-aqueous microgel particles: Synthesis, properties and applications. Soft Matter 2014, 10, 9384–9398. [Google Scholar] [CrossRef]
- Fox, T.L.; Tang, S.; Horton, J.M.; Holdaway, H.A.; Zhao, B.; Zhu, L.; Stewart, P.L. In Situ Characterization of Binary Mixed Polymer Brush-Grafted Silica Nanoparticles in Aqueous and Organic Solvents by Cryo-Electron Tomography. Langmuir 2015, 31, 8680–8688. [Google Scholar] [CrossRef]
- He, C.; Hu, Y.; Yin, L.; Tang, C.; Yin, C. Effects of particle size and surface charge on cellular uptake and biodistribution of polymeric nanoparticles. Biomaterials 2010, 31, 3657–3666. [Google Scholar] [CrossRef]
- Lv, S.; Liu, L.; Yang, W. Preparation of Soft Hydrogel Nanoparticles with PNIPAm Hair and Characterization of Their Temperature-Induced Aggregation. Langmuir 2010, 26, 2076–2082. [Google Scholar] [CrossRef]
- Cui, F.; Qian, F.; Yin, C. Preparation and characterization of mucoadhesive polymer-coated nanoparticles. Int. J. Pharm. 2006, 316, 154–161. [Google Scholar] [CrossRef]
- Rideau, E.; Dimova, R.; Schwille, P.; Wurm, F.R.; Landfester, K. Liposomes and polymersomes: A comparative review towards cell mimicking. Chem. Soc. Rev. 2018, 47, 8572–8610. [Google Scholar] [CrossRef] [PubMed]
- Büber, E.; Schröder, T.; Scheckenbach, M.; Dass, M.; Franquelim, H.G.; Tinnefeld, P. DNA Origami Curvature Sensors for Nanoparticle and Vesicle Size Determination with Single-Molecule FRET Readout. ACS Nano 2023, 17, 3088–3097. [Google Scholar] [CrossRef] [PubMed]
- Veneziano, R.; Moyer, T.J.; Stone, M.B.; Wamhoff, E.C.; Read, B.J.; Mukherjee, S.; Shepherd, T.R.; Das, J.; Schief, W.R.; Irvine, D.J.; et al. Role of nanoscale antigen organization on B-cell activation probed using DNA origami. Nat. Nanotechnol. 2020, 15, 716–723. [Google Scholar] [CrossRef] [PubMed]
- Bastings, M.M.C.; Anastassacos, F.M.; Ponnuswamy, N.; Leifer, F.G.; Cuneo, G.; Lin, C.; Ingber, D.E.; Ryu, J.H.; Shih, W.M. Modulation of the Cellular Uptake of DNA Origami through Control over Mass and Shape. Nano Lett. 2018, 18, 3557–3564. [Google Scholar] [CrossRef]
- Li, Z.; Wei, B.; Nangreave, J.; Lin, C.; Liu, Y.; Mi, Y.; Yan, H. A Replicable Tetrahedral Nanostructure Self-Assembled from a Single DNA Strand. J. Am. Chem. Soc. 2009, 131, 13093–13098. [Google Scholar] [CrossRef]
- Sivadasan, D.; Sultan, M.H.; Madkhali, O.A.; Alsabei, S.H.; Alessa, A.A. Stealth Liposomes (PEGylated) Containing an Anticancer Drug Camptothecin: In Vitro Characterization and In Vivo Pharmacokinetic and Tissue Distribution Study. Molecules 2022, 27, 1086. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, S.; Zeiser, M.; Hellweg, T.; Duschl, C.; Fery, A.; Möhwald, H. Adhesion and Mechanical Properties of PNIPAM Microgel Films and Their Potential Use as Switchable Cell Culture Substrates. Adv. Funct. Mater. 2010, 20, 3235–3243. [Google Scholar] [CrossRef]
- Strobl, G. The Physics of Polymers: Concepts for Understanding Their Structures and Behaviour, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- de Gennes, P.G. Scaling Concepts in Polymer Physics, 1st ed.; Cornell University Press: New York, NY, USA, 1979. [Google Scholar]
- Sherck, N.; Webber, T.; Brown, D.R.; Keller, T.; Barry, M.; DeStefano, A.; Jiao, S.; Segalman, R.A.; Fredrickson, G.H.; Shell, M.S.; et al. End-to-End Distance Probability Distributions of Dilute Poly(ethylene oxide) in Aqueous Solution. J. Am. Chem. Soc. 2020, 142, 19631–19641. [Google Scholar] [CrossRef]
- Lee, H.; Venable, R.M.; MacKerell, A.D.; Pastor, R.W. Molecular Dynamics Studies of Polyethylene Oxide and Polyethylene Glycol: Hydrodynamic Radius and Shape Anisotropy. Biophys. J. 2008, 95, 1590–1599. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, Z.; Gooding, E.A.; Pimenov, K.V.; Wang, L.; Asher, S.A. UV Resonance Raman Determination of Molecular Mechanism of Poly(N -isopropylacrylamide) Volume Phase Transition. J. Phys. Chem. B 2009, 113, 4248–4256. [Google Scholar] [CrossRef]
- Kubota, K.; Fujishige, S.; Ando, I. Solution Properties of Poly(N-isopropylacrylamide) in Water. Polym. J. 1990, 22, 15–20. [Google Scholar] [CrossRef]
- Chen, H.; Meisburger, S.P.; Pabit, S.A.; Sutton, J.L.; Webb, W.W.; Pollack, L. Ionic strength-dependent persistence lengths of single-stranded RNA and DNA. Proc. Natl. Acad. Sci. USA 2012, 109, 799–804. [Google Scholar] [CrossRef] [PubMed]
- Murphy, M.; Rasnik, I.; Cheng, W.; Lohman, T.M.; Ha, T. Probing Single-Stranded DNA Conformational Flexibility Using Fluorescence Spectroscopy. Biophys. J. 2004, 86, 2530–2537. [Google Scholar] [CrossRef]
- Li, J.; Dao, M.; Lim, C.; Suresh, S. Spectrin-Level Modeling of the Cytoskeleton and Optical Tweezers Stretching of the Erythrocyte. Biophys. J. 2005, 88, 3707–3719. [Google Scholar] [CrossRef]
- Garcia, H.G.; Grayson, P.; Han, L.; Inamdar, M.; Kondev, J.; Nelson, P.C.; Phillips, R.; Widom, J.; Wiggins, P.A. Biological consequences of tightly bent DNA: The other life of a macromolecular celebrity. Biopolymers 2007, 85, 115–130. [Google Scholar] [CrossRef]
- Abels, J.; Moreno-Herrero, F.; Van Der Heijden, T.; Dekker, C.; Dekker, N. Single-Molecule Measurements of the Persistence Length of Double-Stranded RNA. Biophys. J. 2005, 88, 2737–2744. [Google Scholar] [CrossRef] [PubMed]
- Ghavanloo, E. Persistence length of collagen molecules based on nonlocal viscoelastic model. J. Biol. Phys. 2017, 43, 525–534. [Google Scholar] [CrossRef] [PubMed]
- Rölleke, U.; Kumari, P.; Meyer, R.; Köster, S. The unique biomechanics of intermediate filaments—From single filaments to cells and tissues. Curr. Opin. Cell Biol. 2023, 85, 102263. [Google Scholar] [CrossRef]
- Gittes, F.; Mickey, B.; Nettleton, J.; Howard, J. Flexural rigidity of microtubules and actin filaments measured from thermal fluctuations in shape. J. Cell Biol. 1993, 120, 923–934. [Google Scholar] [CrossRef]
- Pampaloni, F.; Lattanzi, G.; Jonáš, A.; Surrey, T.; Frey, E.; Florin, E.L. Thermal fluctuations of grafted microtubules provide evidence of a length-dependent persistence length. Proc. Natl. Acad. Sci. USA 2006, 103, 10248–10253. [Google Scholar] [CrossRef]
- Porello, I.; Bono, N.; Candiani, G.; Cellesi, F. Advancing nucleic acid delivery through cationic polymer design: Non-cationic building blocks from the toolbox. Polym. Chem. 2024, 15, 2800–2826. [Google Scholar] [CrossRef]
- Farshbaf, M.; Davaran, S.; Zarebkohan, A.; Annabi, N.; Akbarzadeh, A.; Salehi, R. Significant role of cationic polymers in drug delivery systems. Artif. Cells Nanomed. Biotechnol. 2017, 46, 1872–1891. [Google Scholar] [CrossRef]
- Seror, J.; Zhu, L.; Goldberg, R.; Day, A.J.; Klein, J. Supramolecular synergy in the boundary lubrication of synovial joints. Nat. Commun. 2015, 6, 6497. [Google Scholar] [CrossRef]
- Kim, J.U.; Matsen, M.W. Repulsion Exerted on a Spherical Particle by a Polymer Brush. Macromolecules 2008, 41, 246–252. [Google Scholar] [CrossRef]
- Ruckenstein, E.; Li, B. Steric interactions between two grafted polymer brushes. J. Chem. Phys. 1997, 107, 932–942. [Google Scholar] [CrossRef]
- Dietz, L.; Oberländer, J.; Mateos-Maroto, A.; Schunke, J.; Fichter, M.; Krämer-Albers, E.; Landfester, K.; Mailänder, V. Uptake of extracellular vesicles into immune cells is enhanced by the protein corona. J. Extracell. Vesicles 2023, 12, e12399. [Google Scholar] [CrossRef]
- Zou, Y.; Ito, S.; Yoshino, F.; Suzuki, Y.; Zhao, L.; Komatsu, N. Polyglycerol Grafting Shields Nanoparticles from Protein Corona Formation to Avoid Macrophage Uptake. ACS Nano 2020, 14, 7216–7226. [Google Scholar] [CrossRef]
- Wang, Y.; Ukwattage, V.; Xiong, Y.; Such, G.K. Advancing endosomal escape of polymeric nanoparticles: Towards improved intracellular delivery. Mater. Horiz. 2025, 12, 3622–3632. [Google Scholar] [CrossRef]
- Vermeulen, L.M.; De Smedt, S.C.; Remaut, K.; Braeckmans, K. The proton sponge hypothesis: Fable or fact? Eur. J. Pharm. Biopharm. 2018, 129, 184–190. [Google Scholar] [CrossRef]
- Hong, S.; Leroueil, P.R.; Janus, E.K.; Peters, J.L.; Kober, M.M.; Islam, M.T.; Orr, B.G.; Baker, J.R.; Banaszak Holl, M.M. Interaction of Polycationic Polymers with Supported Lipid Bilayers and Cells: Nanoscale Hole Formation and Enhanced Membrane Permeability. Bioconjugate Chem. 2006, 17, 728–734. [Google Scholar] [CrossRef] [PubMed]
- Casper, J.; Schenk, S.H.; Parhizkar, E.; Detampel, P.; Dehshahri, A.; Huwyler, J. Polyethylenimine (PEI) in gene therapy: Current status and clinical applications. J. Control. Release 2023, 362, 667–691. [Google Scholar] [CrossRef]
- Fischer, D.; Li, Y.; Ahlemeyer, B.; Krieglstein, J.; Kissel, T. In vitro cytotoxicity testing of polycations: Influence of polymer structure on cell viability and hemolysis. Biomaterials 2003, 24, 1121–1131. [Google Scholar] [CrossRef]
- Kostyurina, E.; Allgaier, J.; Kruteva, M.; Frielinghaus, H.; Csiszár, A.; Förster, S.; Biehl, R. Passive Macromolecular Translocation Mechanism through Lipid Membranes. J. Am. Chem. Soc. 2022, 144, 15348–15354. [Google Scholar] [CrossRef] [PubMed]
- Schneider, G.; Allgaier, J.; Fleury, J.B. Translocation of Synthetic Polymers by Lipid Membranes. WO 2018065583 A1, 12 April 2018. [Google Scholar]
- Werner, M.; Sommer, J.U. Translocation and Induced Permeability of Random Amphiphilic Copolymers Interacting with Lipid Bilayer Membranes. Biomacromolecules 2015, 16, 125–135. [Google Scholar] [CrossRef] [PubMed]
- Werner, M.; Sommer, J.U.; Baulin, V.A. Homo-polymers with balanced hydrophobicity translocate through lipid bilayers and enhance local solvent permeability. Soft Matter 2012, 8, 11714. [Google Scholar] [CrossRef]
- Sommer, J.U.; Werner, M.; Baulin, V.A. Critical adsorption controls translocation of polymer chains through lipid bilayers and permeation of solvent. EPL 2012, 98, 18003. [Google Scholar] [CrossRef]
- Cho, H.Y.; Gao, H.; Srinivasan, A.; Hong, J.; Bencherif, S.A.; Siegwart, D.J.; Paik, H.j.; Hollinger, J.O.; Matyjaszewski, K. Rapid Cellular Internalization of Multifunctional Star Polymers Prepared by Atom Transfer Radical Polymerization. Biomacromolecules 2010, 11, 2199–2203. [Google Scholar] [CrossRef]
- Somers, K.; Wen, V.W.; Middlemiss, S.M.C.; Osborne, B.; Forgham, H.; Jung, M.; Karsa, M.; Clifton, M.; Bongers, A.; Gao, J.; et al. A novel small molecule that kills a subset of MLL-rearranged leukemia cells by inducing mitochondrial dysfunction. Oncogene 2019, 38, 3824–3842. [Google Scholar] [CrossRef]
- Durmaz, Y.Y.; Lin, Y.; ElSayed, M.E.H. Development of Degradable, pH-Sensitive Star Vectors for Enhancing the Cytoplasmic Delivery of Nucleic Acids. Adv. Funct. Mater. 2013, 23, 3885–3895. [Google Scholar] [CrossRef]
- Bayat, N.; McOrist, N.; Ariotti, N.; Lai, M.; Sia, K.C.; Li, Y.; Grace, J.L.; Quinn, J.F.; Whittaker, M.R.; Kavallaris, M.; et al. Thiol-Reactive Star Polymers Functionalized with Short Ethoxy-Containing Moieties Exhibit Enhanced Uptake in Acute Lymphoblastic Leukemia Cells. Int. J. Nanomed. 2019, 14, 9795–9808. [Google Scholar] [CrossRef] [PubMed]
- Latorre, R.; Ramírez-Garcia, P.D.; Hegron, A.; Grace, J.L.; Retamal, J.S.; Shenoy, P.; Tran, M.; Aurelio, L.; Flynn, B.; Poole, D.P.; et al. Sustained endosomal release of a neurokinin-1 receptor antagonist from nanostars provides long-lasting relief of chronic pain. Biomaterials 2022, 285, 121536. [Google Scholar] [CrossRef]
- Wang, H.; Chen, W.; Xie, H.; Wei, X.; Yin, S.; Zhou, L.; Xu, X.; Zheng, S. Biocompatible, chimeric peptide-condensed supramolecular nanoparticles for tumor cell-specific siRNA delivery and gene silencing. Chem. Commun. 2014, 50, 7806–7809. [Google Scholar] [CrossRef]
- Wang, J.; Sun, J.; Chen, Q.; Gao, Y.; Li, L.; Li, H.; Leng, D.; Wang, Y.; Sun, Y.; Jing, Y.; et al. Star-shape copolymer of lysine-linked di-tocopherol polyethylene glycol 2000 succinate for doxorubicin delivery with reversal of multidrug resistance. Biomaterials 2012, 33, 6877–6888. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.; He, J.; Zhang, M.; Ni, P. Precise modular synthesis and a structure–property study of acid-cleavable star-block copolymers for pH-triggered drug delivery. Polym. Chem. 2015, 6, 1553–1566. [Google Scholar] [CrossRef]
- Qiu, F.; Tu, C.; Wang, R.; Zhu, L.; Chen, Y.; Tong, G.; Zhu, B.; He, L.; Yan, D.; Zhu, X. Emission enhancement of conjugated polymers through self-assembly of unimolecular micelles to multi-micelle aggregates. Chem. Commun. 2011, 47, 9678. [Google Scholar] [CrossRef]
- Hong, H.; Mai, Y.; Zhou, Y.; Yan, D.; Cui, J. Self-Assembly of Large Multimolecular Micelles from Hyperbranched Star Copolymers. Macromol. Rapid Commun. 2007, 28, 591–596. [Google Scholar] [CrossRef]
- Mai, Y.; Zhou, Y.; Yan, D. Synthesis and Size-Controllable Self-Assembly of a Novel Amphiphilic Hyperbranched Multiarm Copolyether. Macromolecules 2005, 38, 8679–8686. [Google Scholar] [CrossRef]
- Dutta, S.; Parida, S.; Maiti, C.; Banerjee, R.; Mandal, M.; Dhara, D. Polymer grafted magnetic nanoparticles for delivery of anticancer drug at lower pH and elevated temperature. J. Colloid Interface Sci. 2016, 467, 70–80. [Google Scholar] [CrossRef]
- Paris, J.L.; Cabañas, M.V.; Manzano, M.; Vallet-Regí, M. Polymer-Grafted Mesoporous Silica Nanoparticles as Ultrasound-Responsive Drug Carriers. ACS Nano 2015, 9, 11023–11033. [Google Scholar] [CrossRef]
- Kirchhausen, T.; Owen, D.; Harrison, S.C. Molecular Structure, Function, and Dynamics of Clathrin-Mediated Membrane Traffic. Cold Spring Harb. Perspect. Biol. 2014, 6, a016725. [Google Scholar] [CrossRef] [PubMed]
- Champion, J.A.; Walker, A.; Mitragotri, S. Role of Particle Size in Phagocytosis of Polymeric Microspheres. Pharm. Res. 2008, 25, 1815–1821. [Google Scholar] [CrossRef] [PubMed]
- Tabata, Y.; Ikada, Y. Effect of the size and surface charge of polymer microspheres on their phagocytosis by macrophage. Biomaterials 1988, 9, 356–362. [Google Scholar] [CrossRef]
- Perrault, S.D.; Walkey, C.; Jennings, T.; Fischer, H.C.; Chan, W.C.W. Mediating Tumor Targeting Efficiency of Nanoparticles Through Design. Nano Lett. 2009, 9, 1909–1915. [Google Scholar] [CrossRef] [PubMed]
- Nevozhay, D.; Rauch, R.; Wang, Z.; Sokolov, K.V. Optimal size and PEG coating of gold nanoparticles for prolonged blood circulation: A statistical analysis of published data. Nanoscale Adv. 2025, 7, 722–727. [Google Scholar] [CrossRef]
- Discher, D.E.; Eisenberg, A. Polymer Vesicles. Science 2002, 297, 967–973. [Google Scholar] [CrossRef]
- Klermund, L.; Poschenrieder, S.T.; Castiglione, K. Biocatalysis in Polymersomes: Improving Multienzyme Cascades with Incompatible Reaction Steps by Compartmentalization. ACS Catal. 2017, 7, 3900–3904. [Google Scholar] [CrossRef]
- Otrin, L.; Marušič, N.; Bednarz, C.; Vidaković-Koch, T.; Lieberwirth, I.; Landfester, K.; Sundmacher, K. Toward Artificial Mitochondrion: Mimicking Oxidative Phosphorylation in Polymer and Hybrid Membranes. Nano Lett. 2017, 17, 6816–6821. [Google Scholar] [CrossRef] [PubMed]
- Wen, P.; Dirisala, A.; Guo, H.; Liu, X.; Kobayashi, S.; Kinoh, H.; Anada, T.; Tanaka, M.; Kataoka, K.; Li, J. Engineering durable antioxidative nanoreactors as synthetic organelles for autoregulatory cellular protection against oxidative stress. J. Control. Release 2025, 382, 113683. [Google Scholar] [CrossRef]
- Lomas, H.; Canton, I.; MacNeil, S.; Du, J.; Armes, S.; Ryan, A.; Lewis, A.; Battaglia, G. Biomimetic pH Sensitive Polymersomes for Efficient DNA Encapsulation and Delivery. Adv. Mater. 2007, 19, 4238–4243. [Google Scholar] [CrossRef]
- Ahmed, F.; Pakunlu, R.I.; Brannan, A.; Bates, F.; Minko, T.; Discher, D.E. Biodegradable polymersomes loaded with both paclitaxel and doxorubicin permeate and shrink tumors, inducing apoptosis in proportion to accumulated drug. J. Control. Release 2006, 116, 150–158. [Google Scholar] [CrossRef]
- Barbieri, V.; González Colsa, J.; Matias, D.; Duro Castano, A.; Thapa, A.; Ruiz-Pérez, L.; Albella, P.; Volpe, G.; Battaglia, G. Thermoplasmonic Polymersome Membranes by In Situ Synthesis. ACS Nano 2025, 19, 15331–15344. [Google Scholar] [CrossRef] [PubMed]
- Bleher, S.; Buck, J.; Muhl, C.; Sieber, S.; Barnert, S.; Witzigmann, D.; Huwyler, J.; Barz, M.; Süss, R. Poly(Sarcosine) Surface Modification Imparts Stealth-Like Properties to Liposomes. Small 2019, 15, 1904716. [Google Scholar] [CrossRef] [PubMed]
- Senior, J.; Delgado, C.; Fisher, D.; Tilcock, C.; Gregoriadis, G. Influence of surface hydrophilicity of liposomes on their interaction with plasma protein and clearance from the circulation: Studies with poly(ethylene glycol)-coated vesicles. Biochim. Biophys. Acta, Biomembr. 1991, 1062, 77–82. [Google Scholar] [CrossRef]
- Woodle, M.C.; Newman, M.S.; Cohen, J.A. Sterically Stabilized Liposomes: Physical and Biological Properties. J. Drug Target. 1994, 2, 397–403. [Google Scholar] [CrossRef]
- Sivakumaran, D.; Maitland, D.; Hoare, T. Injectable Microgel-Hydrogel Composites for Prolonged Small-Molecule Drug Delivery. Biomacromolecules 2011, 12, 4112–4120. [Google Scholar] [CrossRef]
- Jiang, Y.; Chen, J.; Deng, C.; Suuronen, E.J.; Zhong, Z. Click hydrogels, microgels and nanogels: Emerging platforms for drug delivery and tissue engineering. Biomaterials 2014, 35, 4969–4985. [Google Scholar] [CrossRef]
- Dave, R.; Randhawa, G.; Kim, D.; Simpson, M.; Hoare, T. Microgels and Nanogels for the Delivery of Poorly Water-Soluble Drugs. Mol. Pharm. 2022, 19, 1704–1721. [Google Scholar] [CrossRef]
- Vinogradov, S. Colloidal Microgels in Drug Delivery Applications. Curr. Pharm. Des. 2006, 12, 4703–4712. [Google Scholar] [CrossRef] [PubMed]
- Bysell, H.; Månsson, R.; Hansson, P.; Malmsten, M. Microgels and microcapsules in peptide and protein drug delivery. Adv. Drug Deliv. Rev. 2011, 63, 1172–1185. [Google Scholar] [CrossRef]
- Saunders, B.R.; Laajam, N.; Daly, E.; Teow, S.; Hu, X.; Stepto, R. Microgels: From responsive polymer colloids to biomaterials. Adv. Colloid Interface Sci. 2009, 147–148, 251–262. [Google Scholar] [CrossRef]
- Guo, P.; Liu, D.; Subramanyam, K.; Wang, B.; Yang, J.; Huang, J.; Auguste, D.T.; Moses, M.A. Nanoparticle elasticity directs tumor uptake. Nat. Commun. 2018, 9, 130. [Google Scholar] [CrossRef] [PubMed]
- Lee, E.; Dang, L.N.; Choi, J.; Kim, H.; Bastatas, L.; Park, S. Elasticity-Driven Nanomechanical Interaction to Improve the Targeting Ability of Lipid Nanoparticles in the Malignant Tumor Microenvironment. Adv. Sci. 2025, 12, 2502073. [Google Scholar] [CrossRef] [PubMed]
- Vanthienen, T.; Demeester, J.; Desmedt, S. Screening poly(ethyleneglycol) micro- and nanogels for drug delivery purposes. Int. J. Pharm. 2008, 351, 174–185. [Google Scholar] [CrossRef]
- Wang, J.; Liu, Y.; Chen, R.; Zhang, Z.; Chen, G.; Chen, H. Ultralow Self-Cross-Linked Poly(N-isopropylacrylamide) Microgels Prepared by Solvent Exchange. Langmuir 2019, 35, 13991–13998. [Google Scholar] [CrossRef]
- Scotti, A.; Brugnoni, M.; Lopez, C.G.; Bochenek, S.; Crassous, J.J.; Richtering, W. Flow properties reveal the particle-to-polymer transition of ultra-low crosslinked microgels. Soft Matter 2020, 16, 668–678. [Google Scholar] [CrossRef]
- Bachman, H.; Brown, A.C.; Clarke, K.C.; Dhada, K.S.; Douglas, A.; Hansen, C.E.; Herman, E.; Hyat, J.S.; Kodlekere, P.; Meng, Z.; et al. Ultrasoft, highly deformable microgels. Soft Matter 2015, 11, 2018–2028. [Google Scholar] [CrossRef]
- Douglas, A.M.; Fragkopoulos, A.A.; Gaines, M.K.; Lyon, L.A.; Fernandez-Nieves, A.; Barker, T.H. Dynamic assembly of ultrasoft colloidal networks enables cell invasion within restrictive fibrillar polymers. Proc. Natl. Acad. Sci. USA 2017, 114, 885–890. [Google Scholar] [CrossRef]
- Brown, A.C.; Stabenfeldt, S.E.; Ahn, B.; Hannan, R.T.; Dhada, K.S.; Herman, E.S.; Stefanelli, V.; Guzzetta, N.; Alexeev, A.; Lam, W.A.; et al. Ultrasoft microgels displaying emergent platelet-like behaviours. Nat. Mater. 2014, 13, 1108–1114. [Google Scholar] [CrossRef]
- Hirai, Y.; Kawaguchi, Y.; Kasahara, C.; Hirose, H.; Futaki, S. Liquid Droplet-Mediated Formulation of Lipid Nanoparticles Encapsulating Immunoglobulin G for Cytosolic Delivery. Mol. Pharm. 2024, 21, 1653–1661. [Google Scholar] [CrossRef] [PubMed]
- Chen, K.; Liu, Y.; Duan, G.; Shi, M.; Yang, C.; Xing, R.; Yan, X. Biomolecular Condensates Based on Amino Acid for Enhancing Oral Bioavailability and Therapeutic Efficacy of Hydrophobic Drugs. ACS Appl. Mater. Interfaces 2024, 16, 58370–58378. [Google Scholar] [CrossRef] [PubMed]
- Pyo, A.G.T.; Zhang, Y.; Wingreen, N.S. Proximity to criticality predicts surface properties of biomolecular condensates. Proc. Natl. Acad. Sci. USA 2023, 120, e2220014120. [Google Scholar] [CrossRef] [PubMed]
- Ukmar-Godec, T.; Wegmann, S.; Zweckstetter, M. Biomolecular condensation of the microtubule-associated protein tau. Semin. Cell Dev. Biol. 2020, 99, 202–214. [Google Scholar] [CrossRef]
- Chowdhury, P.; Saha, B.; Bauri, K.; Sumerlin, B.S.; De, P. Hydrogen Bonding-Driven Self-Coacervation of Nonionic Homopolymers for Stimuli-Triggered Therapeutic Release. J. Am. Chem. Soc. 2024, 146, 21664–21676. [Google Scholar] [CrossRef]
- Shebanova, A.; Perrin, Q.M.; Zhu, K.; Gudlur, S.; Chen, Z.; Sun, Y.; Huang, C.; Lim, Z.W.; Mondarte, E.A.; Sun, R.; et al. Cellular Uptake of Phase-Separating Peptide Coacervates. Adv. Sci. 2024, 11, 2402652. [Google Scholar] [CrossRef]
- Lu, T.; Hu, X.; Van Haren, M.H.I.; Spruijt, E.; Huck, W.T.S. Structure-Property Relationships Governing Membrane-Penetrating Behaviour of Complex Coacervates. Small 2023, 19, 2303138. [Google Scholar] [CrossRef]
- Sun, Y.; Lau, S.Y.; Lim, Z.W.; Chang, S.C.; Ghadessy, F.; Partridge, A.; Miserez, A. Phase-separating peptides for direct cytosolic delivery and redox-activated release of macromolecular therapeutics. Nat. Chem. 2022, 14, 274–283. [Google Scholar] [CrossRef]
- Panja, P.; Jana, N.R. Lipid-Raft-Mediated Direct Cytosolic Delivery of Polymer-Coated Soft Nanoparticles. J. Phys. Chem. B 2020, 124, 5323–5333. [Google Scholar] [CrossRef]
- Son, J.; Jung, Y. Lipid coated protein condensates as stable protocells with selective uptake abilities for biomolecules. Chem. Sci. 2022, 13, 11841–11848. [Google Scholar] [CrossRef]
- Theodorou, D.N.; Suter, U.W. Shape of unperturbed linear polymers: Polypropylene. Macromolecules 1985, 18, 1206–1214. [Google Scholar] [CrossRef]
- Le Guillou, J.C.; Zinn-Justin, J. Critical Exponents for the n -Vector Model in Three Dimensions from Field Theory. Phys. Rev. Lett. 1977, 39, 95–98. [Google Scholar] [CrossRef]
- Wei, Q.; Melko, R.G.; Chen, J.Z.Y. Identifying polymer states by machine learning. Phys. Rev. E 2017, 95, 032504. [Google Scholar] [CrossRef] [PubMed]
- Schnabel, S.; Seaton, D.T.; Landau, D.P.; Bachmann, M. Microcanonical entropy inflection points: Key to systematic understanding of transitions in finite systems. Phys. Rev. E 2011, 84, 011127. [Google Scholar] [CrossRef] [PubMed]
- Wöll, D. Fluorescence Correlation Spectroscopy Studies of Polymer Systems. In Fluorescence Studies of Polymer Containing Systems; Springer Series on Fluorescence; Springer International Publishing: Cham, Switzerland, 2016; Volume 16, pp. 256–297. [Google Scholar]
- Doukas, A.K.; Likos, C.N.; Ziherl, P. Structure formation in soft nanocolloids: Liquid-drop model. Soft Matter 2018, 14, 3063–3072. [Google Scholar] [CrossRef]
- Rajamani, S.; Truskett, T.M.; Garde, S. Hydrophobic hydration from small to large lengthscales: Understanding and manipulating the crossover. Proc. Natl. Acad. Sci. USA 2005, 102, 9475–9480. [Google Scholar] [CrossRef]
- Willner, L.; Jucknischke, O.; Richter, D.; Farago, B.; Fetters, L.J.; Huang, J.S. Ordering Phenomena of Star Polymers in Solution by SANS. Europhys. Lett. 1992, 19, 297–303. [Google Scholar] [CrossRef]
- Daoud, M.; Cotton, J. Star shaped polymers: A model for the conformation and its concentration dependence. J. Phys. France 1982, 43, 531–538. [Google Scholar] [CrossRef]
- Cohen, M.; Klein, E.; Geiger, B.; Addadi, L. Organization and Adhesive Properties of the Hyaluronan Pericellular Coat of Chondrocytes and Epithelial Cells. Biophys. J. 2003, 85, 1996–2005. [Google Scholar] [CrossRef]
- Allen, T.M.; Martin, F.J. Advantages of liposomal delivery systems for anthracyclines. Semin. Oncol. 2004, 31, 5–15. [Google Scholar] [CrossRef]
- Bickel, T.; Marques, C.; Jeppesen, C. Grafted polymers are miniaturized pressure tools. Comptes Rendus l’Académie Sci.—Ser. IV—Phys. 2000, 1, 661–664. [Google Scholar] [CrossRef][Green Version]
- Werner, M.; Sommer, J.U. Polymer-decorated tethered membranes under good- and poor-solvent conditions. Eur. Phys. J. E 2010, 31, 383–392. [Google Scholar] [CrossRef]
- Evans, A.R.; Turner, M.S.; Sens, P. Interactions between proteins bound to biomembranes. Phys. Rev. E 2003, 67, 041907. [Google Scholar] [CrossRef] [PubMed]
- Bickel, T.; Jeppesen, C.; Marques, C. Local entropic effects of polymers grafted to soft interfaces. Eur. Phys. J. E 2001, 4, 33–43. [Google Scholar] [CrossRef]
- Bickel, T.; Marques, C.; Jeppesen, C. Pressure patches for membranes: The induced pinch of a grafted polymer. Phys. Rev. E 2000, 62, 1124–1127. [Google Scholar] [CrossRef]
- Auth, T.; Gompper, G. Fluctuation spectrum of membranes with anchored linear and star polymers. Phys. Rev. E 2005, 72, 031904. [Google Scholar] [CrossRef]
- Auth, T.; Gompper, G. Self-avoiding linear and star polymers anchored to membranes. Phys. Rev. E 2003, 68, 051801. [Google Scholar] [CrossRef]
- Bickel, T.; Marques, C. Scale-dependent rigidity of polymer-ornamented membranes. Eur. Phys. J. E 2002, 9, 349–352. [Google Scholar] [CrossRef]
- Hiergeist, C.; Lipowsky, R. Elastic Properties of Polymer-Decorated Membranes. J. Phys. II France 1996, 6, 1465–1481. [Google Scholar] [CrossRef]
- Discher, D.E.; Ahmed, F. Polymersomes. Annu. Rev. Biomed. Eng. 2006, 8, 323–341. [Google Scholar] [CrossRef]
- Kostina, N.Y.; Rahimi, K.; Xiao, Q.; Haraszti, T.; Dedisch, S.; Spatz, J.P.; Schwaneberg, U.; Klein, M.L.; Percec, V.; Möller, M.; et al. Membrane-Mimetic Dendrimersomes Engulf Living Bacteria via Endocytosis. Nano Lett. 2019, 19, 5732–5738. [Google Scholar] [CrossRef]
- Helfrich, W. Elastic Properties of Lipid Bilayers: Theory and Possible Experiments. Z. Naturforsch. C 1973, 28, 693–703. [Google Scholar] [CrossRef] [PubMed]
- Gnan, N.; Rovigatti, L.; Bergman, M.; Zaccarelli, E. In Silico Synthesis of Microgel Particles. Macromolecules 2017, 50, 8777–8786. [Google Scholar] [CrossRef]
- Strauch, C.; Schneider, S. Monte Carlo simulation of the ionization and uptake behavior of cationic oligomers into pH-responsive polyelectrolyte microgels of opposite charge—A model for oligopeptide uptake and release. Soft Matter 2024, 20, 1263–1274. [Google Scholar] [CrossRef]
- Wilms, D.; Adler, Y.; Schröer, F.; Bunnemann, L.; Schmidt, S. Elastic modulus distribution in poly(N -isopopylacrylamide) and oligo(ethylene glycol methacrylate)-based microgels studied by AFM. Soft Matter 2021, 17, 5711–5717. [Google Scholar] [CrossRef]
- Ninarello, A.; Crassous, J.J.; Paloli, D.; Camerin, F.; Gnan, N.; Rovigatti, L.; Schurtenberger, P.; Zaccarelli, E. Modeling Microgels with a Controlled Structure across the Volume Phase Transition. Macromolecules 2019, 52, 7584–7592. [Google Scholar] [CrossRef]
- Boon, N.; Schurtenberger, P. Swelling of micro-hydrogels with a crosslinker gradient. Phys. Chem. Chem. Phys. 2017, 19, 23740–23746. [Google Scholar] [CrossRef] [PubMed]
- Stieger, M.; Richtering, W.; Pedersen, J.S.; Lindner, P. Small-angle neutron scattering study of structural changes in temperature sensitive microgel colloids. J. Chem. Phys. 2004, 120, 6197–6206. [Google Scholar] [CrossRef]
- Raßmann, N.; Trippmacher, S.; Specht, A.; Theis, K.; Rößler, T.; Wohlrab, S.; Kellnberger, R.; Salehi, S.; Bargel, H.; Helfricht, N.; et al. Determining the Elastic Modulus of Microgel Particles by Nanoindentation. ACS Appl. Nano Mater. 2025, 8, 5383–5398. [Google Scholar] [CrossRef]
- Schulte, M.F.; Izak-Nau, E.; Braun, S.; Pich, A.; Richtering, W.; Göstl, R. Microgels react to force: Mechanical properties, syntheses, and force-activated functions. Chem. Soc. Rev. 2022, 51, 2939–2956. [Google Scholar] [CrossRef]
- Kozlovskaya, V.; Dolmat, M.; Kharlampieva, E. Polymeric Particulates of Controlled Rigidity for Biomedical Applications. ACS Appl. Polym. Mater. 2021, 3, 2274–2289. [Google Scholar] [CrossRef]
- Scheffold, F.; Díaz-Leyva, P.; Reufer, M.; Ben Braham, N.; Lynch, I.; Harden, J.L. Brushlike Interactions between Thermoresponsive Microgel Particles. Phys. Rev. Lett. 2010, 104. [Google Scholar] [CrossRef]
- Scotti, A.; Schulte, M.F.; Lopez, C.G.; Crassous, J.J.; Bochenek, S.; Richtering, W. How Softness Matters in Soft Nanogels and Nanogel Assemblies. Chem. Rev. 2022, 122, 11675–11700. [Google Scholar] [CrossRef] [PubMed]
- Hazra, N.; Ninarello, A.; Scotti, A.; Houston, J.E.; Mota-Santiago, P.; Zaccarelli, E.; Crassous, J.J. Structure of Responsive Microgels down to Ultralow Cross-Linkings. Macromolecules 2024, 57, 339–355. [Google Scholar] [CrossRef]
- Scotti, A.; Bochenek, S.; Brugnoni, M.; Fernandez-Rodriguez, M.A.; Schulte, M.F.; Houston, J.E.; Gelissen, A.P.H.; Potemkin, I.I.; Isa, L.; Richtering, W. Exploring the colloid-to-polymer transition for ultra-low crosslinked microgels from three to two dimensions. Nat. Commun. 2019, 10, 1–8. [Google Scholar] [CrossRef]
- Kot, M.; Nagahashi, H.; Szymczak, P. Elastic moduli of simple mass spring models. Vis. Comput. 2015, 31, 1339–1350. [Google Scholar] [CrossRef]
- Lakes, R. Deformation mechanisms in negative Poisson’s ratio materials: Structural aspects. J. Mater. Sci. 1991, 26, 2287–2292. [Google Scholar] [CrossRef]
- Rovigatti, L.; Gnan, N.; Ninarello, A.; Zaccarelli, E. Connecting Elasticity and Effective Interactions of Neutral Microgels: The Validity of the Hertzian Model. Macromolecules 2019, 52, 4895–4906. [Google Scholar] [CrossRef]
- Hazra, N.; Rudov, A.A.; Midya, J.; Babenyshev, A.; Bochenek, S.; Frenken, M.; Richtering, W.; Gompper, G.; Auth, T.; Potemkin, I.I.; et al. Capillary-driven self-assembly of soft ellipsoidal microgels at the air–water interface. Proc. Natl. Acad. Sci. USA 2024, 121, e2403690121. [Google Scholar] [CrossRef]
- Liu, X.; Auth, T.; Hazra, N.; Ebbesen, M.F.; Brewer, J.; Gompper, G.; Crassous, J.J.; Sparr, E. Wrapping anisotropic microgel particles in lipid membranes: Effects of particle shape and membrane rigidity. Proc. Natl. Acad. Sci. USA 2023, 120, e2217534120. [Google Scholar] [CrossRef]
- Burmistrova, A.; Richter, M.; Eisele, M.; Üzüm, C.; Von Klitzing, R. The Effect of Co-Monomer Content on the Swelling/Shrinking and Mechanical Behaviour of Individually Adsorbed PNIPAM Microgel Particles. Polymers 2011, 3, 1575–1590. [Google Scholar] [CrossRef]
- Forg, S.; Guo, X.; Von Klitzing, R. Influence of Dopamine Methacrylamide on Swelling Behavior and Nanomechanical Properties of PNIPAM Microgels. ACS Appl. Mater. Interfaces 2024, 16, 1521–1534. [Google Scholar] [CrossRef] [PubMed]
- McPhee, W.; Tam, K.C.; Pelton, R. Poly(N-isopropulacrylamide) Latices Prepared with Sodium Dodecyl Sulfate. J. Colloid Interface Sci. 1993, 156, 24–30. [Google Scholar] [CrossRef]
- Halperin, A.; Kröger, M.; Winnik, F.M. Poly(N-isopropylacrylamide) Phase Diagrams: Fifty Years of Research. Angew. Cheml Intl Edl 2015, 54, 15342–15367. [Google Scholar] [CrossRef]
- Heskins, M.; Guillet, J.E. Solution Properties of Poly(N-isopropylacrylamide). J. Macromol. Sci.-Chem. 1968, 2, 1441–1455. [Google Scholar] [CrossRef]
- Virtanen, O.L.J.; Mourran, A.; Pinard, P.T.; Richtering, W. Persulfate initiated ultra-low cross-linked poly(N-isopropylacrylamide) microgels possess an unusual inverted cross-linking structure. Soft Matter 2016, 12, 3919–3928. [Google Scholar] [CrossRef]
- Gao, J.; Frisken, B.J. Cross-Linker-Free N-Isopropylacrylamide Gel Nanospheres. Langmuir 2003, 19, 5212–5216. [Google Scholar] [CrossRef]
- Gao, J.; Frisken, B.J. Influence of Reaction Conditions on the Synthesis of Self-Cross-Linked N-Isopropylacrylamide Microgels. Langmuir 2003, 19, 5217–5222. [Google Scholar] [CrossRef]
- Varga, I.; Gilányi, T.; Mészáros, R.; Filipcsei, G.; Zrínyi, M. Effect of Cross-Link Density on the Internal Structure of Poly(N-isopropylacrylamide) Microgels. J. Phys. Chem. B 2001, 105, 9071–9076. [Google Scholar] [CrossRef]
- Brugnoni, M.; Nickel, A.C.; Kröger, L.C.; Scotti, A.; Pich, A.; Leonhard, K.; Richtering, W. Synthesis and structure of deuterated ultra-low cross-linked poly(N-isopropylacrylamide) microgels. Polym. Chem. 2019, 10, 2397–2405. [Google Scholar] [CrossRef]
- Schulte, M.F.; Scotti, A.; Brugnoni, M.; Bochenek, S.; Mourran, A.; Richtering, W. Tuning the Structure and Properties of Ultra-Low Cross-Linked Temperature-Sensitive Microgels at Interfaces via the Adsorption Pathway. Langmuir 2019, 35, 14769–14781. [Google Scholar] [CrossRef] [PubMed]
- Vilgis, T.; Stapper, M. Microgels and fractal structures at interfaces and surfaces. Eur. Phys. J. B 1998, 2, 69–74. [Google Scholar] [CrossRef]
- Schulte, M.F.; Bochenek, S.; Brugnoni, M.; Scotti, A.; Mourran, A.; Richtering, W. Stiffness Tomography of Ultra-Soft Nanogels by Atomic Force Microscopy. Angew. Chem. Int. Ed. 2021, 60, 2280–2287. [Google Scholar] [CrossRef] [PubMed]
- Tennenbaum, M.; Anderson, C.; Hyatt, J.S.; Do, C.; Fernandez-Nieves, A. Internal structure of ultralow-crosslinked microgels: From uniform deswelling to phase separation. Phys. Rev. E 2021, 103. [Google Scholar] [CrossRef]
- Islam, M.R.; Tumbarello, M.; Lyon, L.A. Deswelling induced morphological changes in dual pH- and temperature-responsive ultra-low cross-linked poly(N-isopropyl acrylamide)-co-acrylic acid microgels. Colloid Polym. Sci. 2019, 297, 667–676. [Google Scholar] [CrossRef] [PubMed]
- Berndt, I.; Pedersen, J.S.; Richtering, W. Structure of Multiresponsive “Intelligent” Core-Shell Microgels. J. Am. Chem. Soc. 2005, 127, 9372–9373. [Google Scholar] [CrossRef]
- Brugnoni, M.; Fink, F.; Scotti, A.; Richtering, W. Synthesis and structure of temperature-sensitive nanocapsules. Colloid Polym. Sci. 2020, 298, 1179–1185. [Google Scholar] [CrossRef]
- Crassous, J.J.; Mihut, A.M.; Månsson, L.K.; Schurtenberger, P. Anisotropic responsive microgels with tuneable shape and interactions. Nanoscale 2015, 7, 15971–15982. [Google Scholar] [CrossRef]
- Wypysek, S.K.; Centeno, S.P.; Gronemann, T.; Wöll, D.; Richtering, W. Hollow, pH-Sensitive Microgels as Nanocontainers for the Encapsulation of Proteins. Macromol. Biosci. 2023, 23, 2200456. [Google Scholar] [CrossRef]
- Islam, M.R.; Lyon, L.A. Deswelling studies of pH and temperature-sensitive ultra-low cross-linked microgels with cross-linked cores. Colloid Polym. Sci. 2020, 298, 395–405. [Google Scholar] [CrossRef]
- Kozhunova, E.Y.; Vyshivannaya, O.V.; Nasimova, I.R. “Smart” IPN microgels with different network structures: Self-crosslinked vs. conventionally crosslinked. Polymer 2019, 176, 127–134. [Google Scholar] [CrossRef]
- Rudyak, V.Y.; Gavrilov, A.A.; Kozhunova, E.Y.; Chertovich, A.V. Shell–corona microgels from double interpenetrating networks. Soft Matter 2018, 14, 2777–2781. [Google Scholar] [CrossRef]
- Bungenberg de Jong, H.G.; Kruyt, H.R. Koazervation. Koloid Z. 1930, 50, 39–48. [Google Scholar] [CrossRef]
- Semenov, A.N.; Rubinstein, M. Thermoreversible Gelation in Solutions of Associative Polymers. 1. Statics. Macromolecules 1998, 31, 1373–1385. [Google Scholar] [CrossRef]
- Shin, Y.; Brangwynne, C.P. Liquid phase condensation in cell physiology and disease. Science 2017, 357, eaaf4382. [Google Scholar] [CrossRef]
- Brangwynne, C.P.; Eckmann, C.R.; Courson, D.S.; Rybarska, A.; Hoege, C.; Gharakhani, J.; Jülicher, F.; Hyman, A.A. Germline P Granules Are Liquid Droplets That Localize by Controlled Dissolution/Condensation. Science 2009, 324, 1729–1732. [Google Scholar] [CrossRef]
- Lee, D.S.W.; Choi, C.H.; Sanders, D.W.; Beckers, L.; Riback, J.A.; Brangwynne, C.P.; Wingreen, N.S. Size distributions of intracellular condensates reflect competition between coalescence and nucleation. Nat. Phys. 2023, 19, 586–596. [Google Scholar] [CrossRef]
- Liu, L.; Xu, Y.; Zhang, P.; You, J.; Li, W.; Chen, Y.; Li, R.; Rui, B.; Dou, H. High-Order Assembly toward Polysaccharide-Based Complex Coacervate Nanodroplets Capable of Targeting Cancer Cells. Langmuir 2020, 36, 8580–8588. [Google Scholar] [CrossRef] [PubMed]
- Ambadi Thody, S.; Clements, H.D.; Baniasadi, H.; Lyon, A.S.; Sigman, M.S.; Rosen, M.K. Small-molecule properties define partitioning into biomolecular condensates. Nat. Chem. 2024, 16, 1794–1802. [Google Scholar] [CrossRef] [PubMed]
- McInnes, L.; Healy, J.; Melville, J. UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction. arXiv 2020, arXiv:1802.03426. [Google Scholar] [CrossRef]
- QikProp Release 2022-4; Schrödinger LLC: New York, NY, USA, 2021.
- Banani, S.F.; Rice, A.M.; Peeples, W.B.; Lin, Y.; Jain, S.; Parker, R.; Rosen, M.K. Compositional Control of Phase-Separated Cellular Bodies. Cell 2016, 166, 651–663. [Google Scholar] [CrossRef]
- Kilgore, H.R.; Young, R.A. Learning the chemical grammar of biomolecular condensates. Nat. Chem. Biol. 2022, 18, 1298–1306. [Google Scholar] [CrossRef]
- Li, R.; Yang, X.; Chen, S.; Chen, H.; Lin, L.; Chen, Y.; Xiao, J.; Ma, Y.; Li, W. Engineering DNA Condensate Droplets as a Versatile Nanovector. Nano Lett. 2025, 25, 10225–10232. [Google Scholar] [CrossRef]
- Kelley, F.M.; Ani, A.; Pinlac, E.G.; Linders, B.; Favetta, B.; Barai, M.; Ma, Y.; Singh, A.; Dignon, G.L.; Gu, Y.; et al. Controlled and orthogonal partitioning of large particles into biomolecular condensates. Nat. Commun. 2025, 16, 3521. [Google Scholar] [CrossRef]
- Schmidt, H.; Putnam, A.; Rasoloson, D.; Seydoux, G. Protein-based condensation mechanisms drive the assembly of RNA-rich P granules. eLife 2021, 10, e63698. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, S.; Gong, X.; Chen, J. Toward Accurate Simulation of Coupling between Protein Secondary Structure and Phase Separation. J. Am. Chem. Soc. 2024, 146, 342–357. [Google Scholar] [CrossRef]
- Schneider, M.W.G.; Gibson, B.A.; Otsuka, S.; Spicer, M.F.D.; Petrovic, M.; Blaukopf, C.; Langer, C.C.H.; Batty, P.; Nagaraju, T.; Doolittle, L.K.; et al. A mitotic chromatin phase transition prevents perforation by microtubules. Nature 2022, 609, 183–190. [Google Scholar] [CrossRef] [PubMed]
- Su, X.; Ditlev, J.A.; Hui, E.; Xing, W.; Banjade, S.; Okrut, J.; King, D.S.; Taunton, J.; Rosen, M.K.; Vale, R.D. Phase separation of signaling molecules promotes T cell receptor signal transduction. Science 2016, 352, 595–599. [Google Scholar] [CrossRef] [PubMed]
- Sanders, D.W.; Kedersha, N.; Lee, D.S.; Strom, A.R.; Drake, V.; Riback, J.A.; Bracha, D.; Eeftens, J.M.; Iwanicki, A.; Wang, A.; et al. Competing Protein-RNA Interaction Networks Control Multiphase Intracellular Organization. Cell 2020, 181, 306–324.e28. [Google Scholar] [CrossRef]
- Nakashima, K.K.; Van Haren, M.H.I.; André, A.A.M.; Robu, I.; Spruijt, E. Active coacervate droplets are protocells that grow and resist Ostwald ripening. Nat. Commun. 2021, 12, 3819. [Google Scholar] [CrossRef]
- Jambon-Puillet, E.; Testa, A.; Lorenz, C.; Style, R.W.; Rebane, A.A.; Dufresne, E.R. Phase-separated droplets swim to their dissolution. Nat. Commun. 2024, 15, 3919. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Xu, T.; Li, Y.; Wang, H. Enzyme Induced Solid-Like Condensates Formation of Engineered Peptide in Living Cells for Prostate Cancer Inhibition. Angew. Chem. Int. Ed. 2025, 64, e202504958. [Google Scholar] [CrossRef]
- Aarts, D.G.A.L.; Dullens, R.P.A.; Lekkerkerker, H.N.W.; Bonn, D.; Van Roij, R. Interfacial tension and wetting in colloid–polymer mixtures. J. Chem. Phys. 2004, 120, 1973–1980. [Google Scholar] [CrossRef]
- Holland, J.; Castrejón-Pita, A.A.; Tuinier, R.; Aarts, D.G.A.L.; Nott, T.J. Surface tension measurement and calculation of model biomolecular condensates. Soft Matter 2023, 19, 8706–8716. [Google Scholar] [CrossRef]
- Wang, H.; Kelley, F.M.; Milovanovic, D.; Schuster, B.S.; Shi, Z. Surface tension and viscosity of protein condensates quantified by micropipette aspiration. Biophys. Rep. 2021, 1, 100011. [Google Scholar] [CrossRef]
- Law, J.O.; Jones, C.M.; Stevenson, T.; Williamson, T.A.; Turner, M.S.; Kusumaatmaja, H.; Grellscheid, S.N. A bending rigidity parameter for stress granule condensates. Sci. Adv. 2023, 9, eadg0432. [Google Scholar] [CrossRef] [PubMed]
- Alshareedah, I.; Thurston, G.M.; Banerjee, P.R. Quantifying viscosity and surface tension of multicomponent protein-nucleic acid condensates. Biophys. J. 2021, 120, 1161–1169. [Google Scholar] [CrossRef]
- Jawerth, L.; Fischer-Friedrich, E.; Saha, S.; Wang, J.; Franzmann, T.; Zhang, X.; Sachweh, J.; Ruer, M.; Ijavi, M.; Saha, S.; et al. Protein condensates as aging Maxwell fluids. Science 2020, 370, 1317–1323. [Google Scholar] [CrossRef]
- Kota, D.; Zhou, H.X. Macromolecular Regulation of the Material Properties of Biomolecular Condensates. J. Phys. Chem. Lett. 2022, 13, 5285–5290. [Google Scholar] [CrossRef]
- Jawerth, L.M.; Ijavi, M.; Ruer, M.; Saha, S.; Jahnel, M.; Hyman, A.A.; Jülicher, F.; Fischer-Friedrich, E. Salt-Dependent Rheology and Surface Tension of Protein Condensates Using Optical Traps. Phys. Rev. Lett. 2018, 121, 258101. [Google Scholar] [CrossRef]
- Caragine, C.M.; Haley, S.C.; Zidovska, A. Surface Fluctuations and Coalescence of Nucleolar Droplets in the Human Cell Nucleus. Phys. Rev. Lett. 2018, 121, 148101. [Google Scholar] [CrossRef] [PubMed]
- Santamaria, A.; Hutin, S.; Doucet, C.M.; Zubieta, C.; Milhiet, P.E.; Costa, L. Quantifying surface tension and viscosity in biomolecular condensates by FRAP-ID. Biophys. J. 2024, 123, 3366–3374. [Google Scholar] [CrossRef]
- Shimobayashi, S.F.; Konishi, K.; Ackerman, P.J.; Taniguchi, T.; Brangwynne, C.P. Critical capillary waves of biomolecular condensates. bioRxiv 2023. [Google Scholar] [CrossRef]
- Pickering, S.U. Emulsions. J. Chem. Soc. Trans. 1907, 91, 2001–2021. [Google Scholar] [CrossRef]
- Oh, H.J.; Lee, Y.; Hwang, H.; Hong, K.; Choi, H.; Kang, J.Y.; Jung, Y. Size-controlled assembly of phase separated protein condensates with interfacial protein cages. Nat. Commun. 2025, 16, 1009. [Google Scholar] [CrossRef]
- Cai, D.; Feliciano, D.; Dong, P.; Flores, E.; Gruebele, M.; Porat-Shliom, N.; Sukenik, S.; Liu, Z.; Lippincott-Schwartz, J. Phase separation of YAP reorganizes genome topology for long-term YAP target gene expression. Nat. Cell Biol. 2019, 21, 1578–1589. [Google Scholar] [CrossRef] [PubMed]
- Wen, P.; Ke, W.; Dirisala, A.; Toh, K.; Tanaka, M.; Li, J. Stealth and pseudo-stealth nanocarriers. Adv. Drug Deliv. Rev. 2023, 198, 114895. [Google Scholar] [CrossRef]
- Yoo, J.W.; Chambers, E.; Mitragotri, S. Factors that Control the Circulation Time of Nanoparticles in Blood: Challenges, Solutions and Future Prospects. Curr. Pharm. Des. 2010, 16, 2298–2307. [Google Scholar] [CrossRef]
- Sheng, Y.; Chang, L.; Kuang, T.; Hu, J. PEG/heparin-decorated lipid–polymer hybrid nanoparticles for long-circulating drug delivery. RSC Adv. 2016, 6, 23279–23287. [Google Scholar] [CrossRef]
- Est-Witte, S.E.; Shannon, S.R.; Gong, D.H.; Calabresi, K.G.; Harris, J.J.; Storm, K.; Yoo, E.J.; Isser, A.; Jani, V.P.; Livingston, N.K.; et al. Particle elasticity influences polymeric artificial antigen presenting cell effectiveness in vivo via CD8+ T cell activation, macrophage uptake, and the protein corona. Nano Res. 2024, 17, 9052–9064. [Google Scholar] [CrossRef]
- Kierstead, P.H.; Okochi, H.; Venditto, V.J.; Chuong, T.C.; Kivimae, S.; Fréchet, J.M.; Szoka, F.C. The effect of polymer backbone chemistry on the induction of the accelerated blood clearance in polymer modified liposomes. J. Control. Release 2015, 213, 1–9. [Google Scholar] [CrossRef]
- Son, K.; Ueda, M.; Taguchi, K.; Maruyama, T.; Takeoka, S.; Ito, Y. Evasion of the accelerated blood clearance phenomenon by polysarcosine coating of liposomes. J. Control. Release 2020, 322, 209–216. [Google Scholar] [CrossRef]
- Mohamed, M.; Abu Lila, A.S.; Shimizu, T.; Alaaeldin, E.; Hussein, A.; Sarhan, H.A.; Szebeni, J.; Ishida, T. PEGylated liposomes: Immunological responses. Sci. Technol. Adv. Mater. 2019, 20, 710–724. [Google Scholar] [CrossRef]
- Ishida, T.; Atobe, K.; Wang, X.; Kiwada, H. Accelerated blood clearance of PEGylated liposomes upon repeated injections: Effect of doxorubicin-encapsulation and high-dose first injection. J. Control. Release 2006, 115, 251–258. [Google Scholar] [CrossRef]
- Müller, K.; Fedosov, D.A.; Gompper, G. Understanding particle margination in blood flow—A step toward optimized drug delivery systems. Med. Eng. Phys. 2016, 38, 2–10. [Google Scholar] [CrossRef]
- Müller, K.; Fedosov, D.A.; Gompper, G. Margination of micro- and nano-particles in blood flow and its effect on drug delivery. Sci. Rep. 2014, 4, 4871. [Google Scholar] [CrossRef] [PubMed]
- Anselmo, A.C.; Zhang, M.; Kumar, S.; Vogus, D.R.; Menegatti, S.; Helgeson, M.E.; Mitragotri, S. Elasticity of Nanoparticles Influences Their Blood Circulation, Phagocytosis, Endocytosis, and Targeting. ACS Nano 2015, 9, 3169–3177. [Google Scholar] [CrossRef]
- Desai, P.; Rimal, R.; Florea, A.; Gumerov, R.A.; Santi, M.; Sorokina, A.S.; Sahnoun, S.E.M.; Fischer, T.; Mottaghy, F.M.; Morgenroth, A.; et al. Tuning the Elasticity of Nanogels Improves Their Circulation Time by Evading Immune Cells. Angew. Chem. Int. Ed. 2022, 61, e202116653. [Google Scholar] [CrossRef] [PubMed]
- Anraku, Y.; Kishimura, A.; Oba, M.; Yamasaki, Y.; Kataoka, K. Spontaneous Formation of Nanosized Unilamellar Polyion Complex Vesicles with Tunable Size and Properties. J. Am. Chem. Soc. 2010, 132, 1631–1636. [Google Scholar] [CrossRef]
- Merkel, T.J.; Chen, K.; Jones, S.W.; Pandya, A.A.; Tian, S.; Napier, M.E.; Zamboni, W.E.; DeSimone, J.M. The effect of particle size on the biodistribution of low-modulus hydrogel PRINT particles. J. Control. Release 2012, 162, 37–44. [Google Scholar] [CrossRef]
- Merkel, T.J.; Jones, S.W.; Herlihy, K.P.; Kersey, F.R.; Shields, A.R.; Napier, M.; Luft, J.C.; Wu, H.; Zamboni, W.C.; Wang, A.Z.; et al. Using mechanobiological mimicry of red blood cells to extend circulation times of hydrogel microparticles. Proc. Natl. Acad. Sci. USA 2011, 108, 586–591. [Google Scholar] [CrossRef]
- Haghgooie, R.; Toner, M.; Doyle, P.S. Squishy Non-Spherical Hydrogel Microparticles. Macromol. Rapid Commun. 2010, 31, 128–134. [Google Scholar] [CrossRef]
- Barbul, A.; Singh, K.; Horev-Azaria, L.; Dasgupta, S.; Auth, T.; Korenstein, R.; Gompper, G. Nanoparticle-Decorated Erythrocytes Reveal That Particle Size Controls the Extent of Adsorption, Cell Shape, and Cell Deformability. ACS Appl. Nano Mater. 2018, 1, 3785–3799. [Google Scholar] [CrossRef]
- Sosale, N.G.; Rouhiparkouhi, T.; Bradshaw, A.M.; Dimova, R.; Lipowsky, R.; Discher, D.E. Cell rigidity and shape override CD47’s “self”-signaling in phagocytosis by hyperactivating myosin-II. Blood 2015, 125, 542–552. [Google Scholar] [CrossRef]
- Goswami, R.; Jeon, T.; Nagaraj, H.; Zhai, S.; Rotello, V.M. Accessing Intracellular Targets through Nanocarrier-Mediated Cytosolic Protein Delivery. Trends Pharmacol. Sci. 2020, 41, 743–754. [Google Scholar] [CrossRef] [PubMed]
- Du, S.; Liew, S.S.; Li, L.; Yao, S.Q. Bypassing Endocytosis: Direct Cytosolic Delivery of Proteins. J. Am. Chem. Soc. 2018, 140, 15986–15996. [Google Scholar] [CrossRef] [PubMed]
- Vácha, R.; Martinez-Veracoechea, F.J.; Frenkel, D. Receptor-Mediated Endocytosis of Nanoparticles of Various Shapes. Nano Lett. 2011, 11, 5391–5395. [Google Scholar] [CrossRef]
- Le Bihan, O.; Bonnafous, P.; Marak, L.; Bickel, T.; Trépout, S.; Mornet, S.; De Haas, F.; Talbot, H.; Taveau, J.C.; Lambert, O. Cryo-electron tomography of nanoparticle transmigration into liposome. J. Struct. Biol. 2009, 168, 419–425. [Google Scholar] [CrossRef] [PubMed]
- Canton, I.; Battaglia, G. Endocytosis at the nanoscale. Chem. Soc. Rev. 2012, 41, 2718. [Google Scholar] [CrossRef]
- Switacz, V.K.; Wypysek, S.K.; Degen, R.; Crassous, J.J.; Spehr, M.; Richtering, W. Influence of Size and Cross-Linking Density of Microgels on Cellular Uptake and Uptake Kinetics. Biomacromolecules 2020, 21, 4532–4544. [Google Scholar] [CrossRef]
- Sun, Y.; Wu, X.; Li, J.; Radiom, M.; Mezzenga, R.; Verma, C.S.; Yu, J.; Miserez, A. Phase-separating peptide coacervates with programmable material properties for universal intracellular delivery of macromolecules. Nat. Commun. 2024, 15, 10094. [Google Scholar] [CrossRef]
- Liang, T.; Dong, Y.; Cheng, I.; Wen, P.; Li, F.; Liu, F.; Wu, Q.; Ren, E.; Liu, P.; Li, H.; et al. In situ formation of biomolecular condensates as intracellular drug reservoirs for augmenting chemotherapy. Nat. Biomed. Eng. 2024, 8, 1469–1482. [Google Scholar] [CrossRef] [PubMed]
- Baumgärtner, A.; Skolnick, J. Spontaneous Translocation of a Polymer across a Curved Membrane. Phys. Rev. Lett. 1995, 74, 2142–2145. [Google Scholar] [CrossRef]
- Muthukumar, M.; Baumgaertner, A. Effects of entropic barriers on polymer dynamics. Macromolecules 1989, 22, 1937–1941. [Google Scholar] [CrossRef]
- Polson, J.M.; Dunn, T. Evaluating the Applicability of the Fokker-Planck Equation in Polymer Translocation: A Brownian Dynamics Study. J. Chem. Phys. 2014, 140, 184904. [Google Scholar] [CrossRef]
- Song, X.; Ma, J.; Long, T.; Xu, X.; Zhao, S.; Liu, H. Mechanochemical Cellular Membrane Internalization of Nanohydrogels: A Large-Scale Mesoscopic Simulation. ACS Appl. Mater. Interfaces 2021, 13, 123–134. [Google Scholar] [CrossRef]
- Hoppe Alvarez, L.; Eisold, S.; Gumerov, R.A.; Strauch, M.; Rudov, A.A.; Lenssen, P.; Merhof, D.; Potemkin, I.I.; Simon, U.; Wöll, D. Deformation of Microgels at Solid–Liquid Interfaces Visualized in Three-Dimension. Nano Lett. 2019, 19, 8862–8867. [Google Scholar] [CrossRef] [PubMed]
- Debnath, T. (Forschungszentrum Jülich, Jülich, Germany); Midya, J. (Indian Institute of Technology, Bhubaneswar, India); Gompper, G. (Forschungszentrum Jülich, Jülich, Germany). Personal communication, 2025.
- Moy, V.T.; Jiao, Y.; Hillmann, T.; Lehmann, H.; Sano, T. Adhesion Energy of Receptor-Mediated Interaction Measured by Elastic Deformation. Biophys. J. 1999, 76, 1632–1638. [Google Scholar] [CrossRef]
- Ozmaian, A.; Coalson, R.D.; Ozmaian, M. Adsorption of Polymer-Grafted Nanoparticles on Curved Surfaces. Chemistry 2021, 3, 382–390. [Google Scholar] [CrossRef]
- Wang, M.; Mihut, A.M.; Rieloff, E.; Dabkowska, A.P.; Månsson, L.K.; Immink, J.N.; Sparr, E.; Crassous, J.J. Assembling responsive microgels at responsive lipid membranes. Proc. Natl. Acad. Sci. USA 2019, 116, 5442–5450. [Google Scholar] [CrossRef]
- Forg, S.; Karbacher, A.; Ye, Z.; Guo, X.; Von Klitzing, R. Copolymerization Kinetics of Dopamine Methacrylamide during PNIPAM Microgel Synthesis for Increased Adhesive Properties. Langmuir 2022, 38, 5275–5285. [Google Scholar] [CrossRef] [PubMed]
- Sigolaeva, L.V.; Gladyr, S.Y.; Gelissen, A.P.H.; Mergel, O.; Pergushov, D.V.; Kurochkin, I.N.; Plamper, F.A.; Richtering, W. Dual-Stimuli-Sensitive Microgels as a Tool for Stimulated Spongelike Adsorption of Biomaterials for Biosensor Applications. Biomacromolecules 2014, 15, 3735–3745. [Google Scholar] [CrossRef] [PubMed]
- Dasgupta, S.; Auth, T.; Gompper, G. Shape and Orientation Matter for the Cellular Uptake of Nonspherical Particles. Nano Lett. 2014, 14, 687–693. [Google Scholar] [CrossRef]
- Dasgupta, S.; Auth, T.; Gompper, G. Wrapping of ellipsoidal nano-particles by fluid membranes. Soft Matter 2013, 9, 5473–5482. [Google Scholar] [CrossRef]
- Yi, X.; Gao, H. Cell membrane wrapping of a spherical thin elastic shell. Soft Matter 2015, 11, 1107–1115. [Google Scholar] [CrossRef]
- Sorokina, A.S.; Gumerov, R.A.; Noguchi, H.; Potemkin, I.I. Computer Simulations of Responsive Nanogels at Lipid Membrane. Macromol. Rapid Commun. 2024, 45, 2400406. [Google Scholar] [CrossRef]
- Midya, J.; Auth, T.; Gompper, G. Membrane-Mediated Interactions Between Nonspherical Elastic Particles. ACS Nano 2023, 17, 1935–1945. [Google Scholar] [CrossRef] [PubMed]
- Sahu, A.K.; Malik, R.; Midya, J. Wrapping nonspherical vesicles at bio-membranes. Soft Matter 2025, 21, 4275–4287. [Google Scholar] [CrossRef] [PubMed]
- Shen, Z.; Ye, H.; Yi, X.; Li, Y. Membrane Wrapping Efficiency of Elastic Nanoparticles during Endocytosis: Size and Shape Matter. ACS Nano 2019, 13, 215–228. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Li, X.; Zhang, Y.; Chen, T.; Xiao, S.; Liang, H. Morphological and mechanical determinants of cellular uptake of deformable nanoparticles. Nanoscale 2018, 10, 11969–11979. [Google Scholar] [CrossRef] [PubMed]
- Shen, Z.; Ye, H.; Li, Y. Understanding receptor-mediated endocytosis of elastic nanoparticles through coarse grained molecular dynamic simulation. Phys. Chem. Chem. Phys. 2018, 20, 16372–16385. [Google Scholar] [CrossRef]
- Yi, X.; Shi, X.; Gao, H. Cellular Uptake of Elastic Nanoparticles. Phys. Rev. Lett. 2011, 107, 098101. [Google Scholar] [CrossRef]
- Hui, Y.; Yi, X.; Wibowo, D.; Yang, G.; Middelberg, A.P.J.; Gao, H.; Zhao, C.X. Nanoparticle elasticity regulates phagocytosis and cancer cell uptake. Sci. Adv. 2020, 6, eaaz4316. [Google Scholar] [CrossRef]
- Bahrami, A.H.; Raatz, M.; Agudo-Canalejo, J.; Michel, R.; Curtis, E.M.; Hall, C.K.; Gradzielski, M.; Lipowsky, R.; Weikl, T.R. Wrapping of nanoparticles by membranes. Adv. Colloid Interface Sci. 2014, 208, 214–224. [Google Scholar] [CrossRef]
- Dasgupta, S.; Auth, T.; Gompper, G. Nano- and microparticles at fluid and biological interfaces. J. Phys. Condens. Matter 2017, 29, 373003. [Google Scholar] [CrossRef]
- Azadbakht, A.; Kraft, D.J. Repulsions and attractions between membrane-deforming spheres, Janus-particles, and opposite tube-like deformations in giant unilamellar vesicles. Soft Matter 2025, 21, 4730–4738. [Google Scholar] [CrossRef]
- Spanke, H.T.; Style, R.W.; François-Martin, C.; Feofilova, M.; Eisentraut, M.; Kress, H.; Agudo-Canalejo, J.; Dufresne, E.R. Wrapping of Microparticles by Floppy Lipid Vesicles. Phys. Rev. Lett. 2020, 125, 198102. [Google Scholar] [CrossRef]
- Van Der Wel, C.; Vahid, A.; Šarić, A.; Idema, T.; Heinrich, D.; Kraft, D.J. Lipid membrane-mediated attraction between curvature inducing objects. Sci. Rep. 2016, 6, 32825. [Google Scholar] [CrossRef]
- Sharma, A.; Zhu, Y.; Spangler, E.J.; Carrillo, J.M.Y.; Laradji, M. Membrane-mediated dimerization of spherocylindrical nanoparticles. Soft Matter 2023, 19, 1499–1512. [Google Scholar] [CrossRef]
- Bahrami, A.H.; Lipowsky, R.; Weikl, T.R. Tubulation and Aggregation of Spherical Nanoparticles Adsorbed on Vesicles. Phys. Rev. Lett. 2012, 109, 188102. [Google Scholar] [CrossRef]
- Šarić, A.; Cacciuto, A. Fluid Membranes Can Drive Linear Aggregation of Adsorbed Spherical Nanoparticles. Phys. Rev. Lett. 2012, 108, 118101. [Google Scholar] [CrossRef] [PubMed]
- Deserno, M.; Bickel, T. Wrapping of a spherical colloid by a fluid membrane. Europhys. Lett. (EPL) 2003, 62, 767–774. [Google Scholar] [CrossRef]
- Deserno, M. Elastic deformation of a fluid membrane upon colloid binding. Phys. Rev. E 2004, 69, 031903. [Google Scholar] [CrossRef] [PubMed]
- Kusumaatmaja, H.; Li, Y.; Dimova, R.; Lipowsky, R. Intrinsic Contact Angle of Aqueous Phases at Membranes and Vesicles. Phys. Rev. Lett. 2009, 103, 238103. [Google Scholar] [CrossRef]
- Li, Y.; Kusumaatmaja, H.; Lipowsky, R.; Dimova, R. Wetting-Induced Budding of Vesicles in Contact with Several Aqueous Phases. J. Phys. Chem. B 2012, 116, 1819–1823. [Google Scholar] [CrossRef]
- Mangiarotti, A.; Chen, N.; Zhao, Z.; Lipowsky, R.; Dimova, R. Wetting and complex remodeling of membranes by biomolecular condensates. Nat. Commun. 2023, 14, 2809. [Google Scholar] [CrossRef]
- Mangiarotti, A.; Sabri, E.; Schmidt, K.V.; Hoffmann, C.; Milovanovic, D.; Lipowsky, R.; Dimova, R. Lipid packing and cholesterol content regulate membrane wetting and remodeling by biomolecular condensates. Nat. Commun. 2025, 16, 2756. [Google Scholar] [CrossRef] [PubMed]
- Lu, T.; Liese, S.; Schoenmakers, L.; Weber, C.A.; Suzuki, H.; Huck, W.T.S.; Spruijt, E. Endocytosis of Coacervates into Liposomes. J. Am. Chem. Soc. 2022, 144, 13451–13455. [Google Scholar] [CrossRef]
- Ferreira, T.; Kulkarni, A.; Bretscher, C.; Richter, K.; Ehrlich, M.; Marchini, A. Oncolytic H-1 Parvovirus Enters Cancer Cells through Clathrin-Mediated Endocytosis. Viruses 2020, 12, 1199. [Google Scholar] [CrossRef] [PubMed]
- Den Otter, W.K.; Briels, W.J. The Generation of Curved Clathrin Coats from Flat Plaques. Traffic 2011, 12, 1407–1416. [Google Scholar] [CrossRef]
- Eisentraut, M.; Sabri, A.; Kress, H. The spatial resolution limit of phagocytosis. Biophys. J. 2023, 122, 868–879. [Google Scholar] [CrossRef]
- Richards, D.; Endres, R. The Mechanism of Phagocytosis: Two Stages of Engulfment. Biophys. J. 2014, 107, 1542–1553. [Google Scholar] [CrossRef]
- Korn, E.D.; Weisman, R.A. Phagocytosis of latex beads by {\it Acanthamoeba}. J. Cell Biol. 1967, 34, 219–227. [Google Scholar] [CrossRef] [PubMed]
- Yildirim, M.; Weiss, A.V.; Schneider, M. The Effect of Elasticity of Gelatin Nanoparticles on the Interaction with Macrophages. Pharmaceutics 2023, 15, 199. [Google Scholar] [CrossRef] [PubMed]
- Jaumouillé, V.; Cartagena-Rivera, A.X.; Waterman, C.M. Coupling of β2 integrins to actin by a mechanosensitive molecular clutch drives complement receptor-mediated phagocytosis. Nat. Cell Biol. 2019, 21, 1357–1369. [Google Scholar] [CrossRef]
- Kruger, T.M.; Givens, B.E.; Lansakara, T.I.; Bell, K.J.; Mohapatra, H.; Salem, A.K.; Tivanski, A.V.; Stevens, L.L. Mechanosensitive Endocytosis of High-Stiffness, Submicron Microgels in Macrophage and Hepatocarcinoma Cell Lines. ACS Appl. Bio Mater. 2018, 1, 1254–1265. [Google Scholar] [CrossRef]
- Veltman, D.M.; Williams, T.D.; Bloomfield, G.; Chen, B.C.; Betzig, E.; Insall, R.H.; Kay, R.R. A plasma membrane template for macropinocytic cups. eLife 2016, 5, e20085. [Google Scholar] [CrossRef]
- Palomba, R.; Palange, A.L.; Rizzuti, I.F.; Ferreira, M.; Cervadoro, A.; Barbato, M.G.; Canale, C.; Decuzzi, P. Modulating Phagocytic Cell Sequestration by Tailoring Nanoconstruct Softness. ACS Nano 2018, 12, 1433–1444. [Google Scholar] [CrossRef]
- Lee, J.K.; Guevara, M.; Akanbi, O.D.; Hoff, J.D.; Kupor, D.; Brannon, E.R.; Eniola-Adefeso, O. Deciphering neutrophil dynamics: Enhanced phagocytosis of elastic particles and impact on vascular-targeted carrier performance. Sci. Adv. 2025, 11, eadp1461. [Google Scholar] [CrossRef]
- Gurnani, P.; Sanchez-Cano, C.; Xandri-Monje, H.; Zhang, J.; Ellacott, S.H.; Mansfield, E.D.H.; Hartlieb, M.; Dallmann, R.; Perrier, S. Probing the Effect of Rigidity on the Cellular Uptake of Core-Shell Nanoparticles: Stiffness Effects are Size Dependent. Small 2022, 18, 2203070. [Google Scholar] [CrossRef]
- Anselmo, A.C.; Mitragotri, S. Impact of particle elasticity on particle-based drug delivery systems. Adv. Drug Deliv. Rev. 2017, 108, 51–67. [Google Scholar] [CrossRef] [PubMed]
- Kaksonen, M.; Roux, A. Mechanisms of clathrin-mediated endocytosis. Nat. Rev. Mol. Cell Biol. 2018, 19, 313–326. [Google Scholar] [CrossRef]
- Pelkmans, L.; Helenius, A. Endocytosis Via Caveolae. Traffic 2002, 3, 311–320. [Google Scholar] [CrossRef] [PubMed]
- Mylvaganam, S.; Freeman, S.A.; Grinstein, S. The cytoskeleton in phagocytosis and macropinocytosis. Curr. Biol. 2021, 31, R619–R632. [Google Scholar] [CrossRef] [PubMed]
- Uribe-Querol, E.; Rosales, C. Phagocytosis: Our Current Understanding of a Universal Biological Process. Front. Immunol. 2020, 11, 1066. [Google Scholar] [CrossRef]
- Richards, D.M.; Endres, R.G. How cells engulf: A review of theoretical approaches to phagocytosis. Rep. Prog. Phys. 2017, 80, 126601. [Google Scholar] [CrossRef]
- Palmulli, R.; Machesky, L.M. Is macropinocytosis more than just a passive gulp? Curr. Opin. Cell Biol. 2025, 94, 102513. [Google Scholar] [CrossRef]
- Wu, Y.; Hu, X.; Wei, Z.; Lin, Q. Cellular Regulation of Macropinocytosis. Int. J. Mol. Sci. 2024, 25, 6963. [Google Scholar] [CrossRef]
- Swanson, J.A.; Watts, C. Macropinocytosis. Trends Cell Biol. 1995, 5, 424–428. [Google Scholar] [CrossRef]
- Button, B.; Cai, L.H.; Ehre, C.; Kesimer, M.; Hill, D.B.; Sheehan, J.K.; Boucher, R.C.; Rubinstein, M. A Periciliary Brush Promotes the Lung Health by Separating the Mucus Layer from Airway Epithelia. Science 2012, 337, 937–941. [Google Scholar] [CrossRef]
- Azadi, M.; David, A.E. Enhancing Ocular Drug Delivery: The Effect of Physicochemical Properties of Nanoparticles on the Mechanism of Their Uptake by Human Cornea Epithelial Cells. ACS Biomater. Sci. Eng. 2024, 10, 429–441. [Google Scholar] [CrossRef]
- Ursitti, J.A.; Wade, J.B. Ultrastructure and immunocytochemistry of the isolated human erythrocyte membrane skeleton. Cell Motil. Cytoskeleton 1993, 25, 30–42. [Google Scholar] [CrossRef]
- Klein, I.A.; Boija, A.; Afeyan, L.K.; Hawken, S.W.; Fan, M.; Dall’Agnese, A.; Oksuz, O.; Henninger, J.E.; Shrinivas, K.; Sabari, B.R.; et al. Partitioning of cancer therapeutics in nuclear condensates. Science 2020, 368, 1386–1392. [Google Scholar] [CrossRef]
- Kilgore, H.R.; Mikhael, P.G.; Overholt, K.J.; Boija, A.; Hannett, N.M.; Van Dongen, C.; Lee, T.I.; Chang, Y.T.; Barzilay, R.; Young, R.A. Distinct chemical environments in biomolecular condensates. Nat. Chem. Biol. 2024, 20, 291–301. [Google Scholar] [CrossRef]
- Moeendarbary, E.; Harris, A.R. Cell mechanics: Principles, practices, and prospects. WIREs Mech. Dis. 2014, 6, 371–388. [Google Scholar] [CrossRef] [PubMed]
- Lim, Z.W.; Varma, V.B.; Ramanujan, R.V.; Miserez, A. Magnetically responsive peptide coacervates for dual hyperthermia and chemotherapy treatments of liver cancer. Acta Biomater. 2020, 110, 221–230. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Zhorabek, F.; Zhang, T.; Lam, J.W.Y.; Tang, B.Z.; Chau, Y. Multifaceted Cargo Recruitment and Release from Artificial Membraneless Organelles. Small 2022, 18, 2201721. [Google Scholar] [CrossRef] [PubMed]
- Leppert, A.; Feng, J.; Railaite, V.; Bohn Pessatti, T.; Cerrato, C.P.; Mörman, C.; Osterholz, H.; Lane, D.P.; Maia, F.R.N.C.; Linder, M.B.; et al. Controlling Drug Partitioning in Individual Protein Condensates through Laser-Induced Microscale Phase Transitions. J. Am. Chem. Soc. 2024, 146, 19555–19565. [Google Scholar] [CrossRef]
- Patel, A.; Mitrea, D.; Namasivayam, V.; Murcko, M.A.; Wagner, M.; Klein, I.A. Principles and functions of condensate modifying drugs. Front. Mol. Biosci. 2022, 9, 1007744. [Google Scholar] [CrossRef]
- Wang, J.; Abbas, M.; Huang, Y.; Wang, J.; Li, Y. Redox-responsive peptide-based complex coacervates as delivery vehicles with controlled release of proteinous drugs. Commun. Chem. 2023, 6, 243. [Google Scholar] [CrossRef] [PubMed]
- Yoshikawa, M.; Yoshii, T.; Ikuta, M.; Tsukiji, S. Synthetic Protein Condensates That Inducibly Recruit and Release Protein Activity in Living Cells. J. Am. Chem. Soc. 2021, 143, 6434–6446. [Google Scholar] [CrossRef]
- Chatterjee, S.; Kon, E.; Sharma, P.; Peer, D. Endosomal escape: A bottleneck for LNP-mediated therapeutics. Proc. Natl. Acad. Sci. USA 2024, 121, e2307800120. [Google Scholar] [CrossRef] [PubMed]
- Kongkatigumjorn, N.; Smith, S.A.; Chen, M.; Fang, K.; Yang, S.; Gillies, E.R.; Johnston, A.P.R.; Such, G.K. Controlling Endosomal Escape Using pH-Responsive Nanoparticles with Tunable Disassembly. ACS Appl. Nano Mater. 2018, 1, 3164–3173. [Google Scholar] [CrossRef]
- Zhao, F.; Shen, G.; Chen, C.; Xing, R.; Zou, Q.; Ma, G.; Yan, X. Nanoengineering of Stimuli-Responsive Protein-Based Biomimetic Protocells as Versatile Drug Delivery Tools. Chem. Eur. J. 2014, 20, 6880–6887. [Google Scholar] [CrossRef]
- Wang, J.; Hu, L.; Zhang, H.; Fang, Y.; Wang, T.; Wang, H. Intracellular Condensates of Oligopeptide for Targeting Lysosome and Addressing Multiple Drug Resistance of Cancer. Adv. Mater. 2022, 34, 2104704. [Google Scholar] [CrossRef] [PubMed]

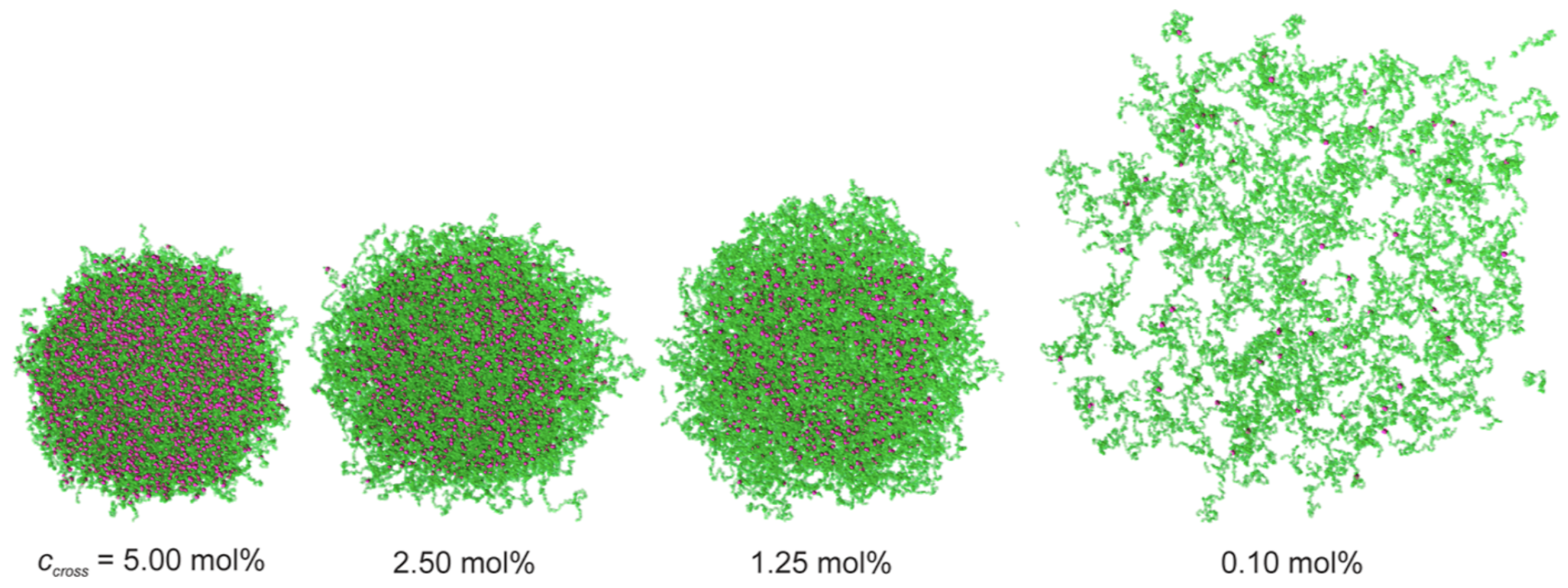
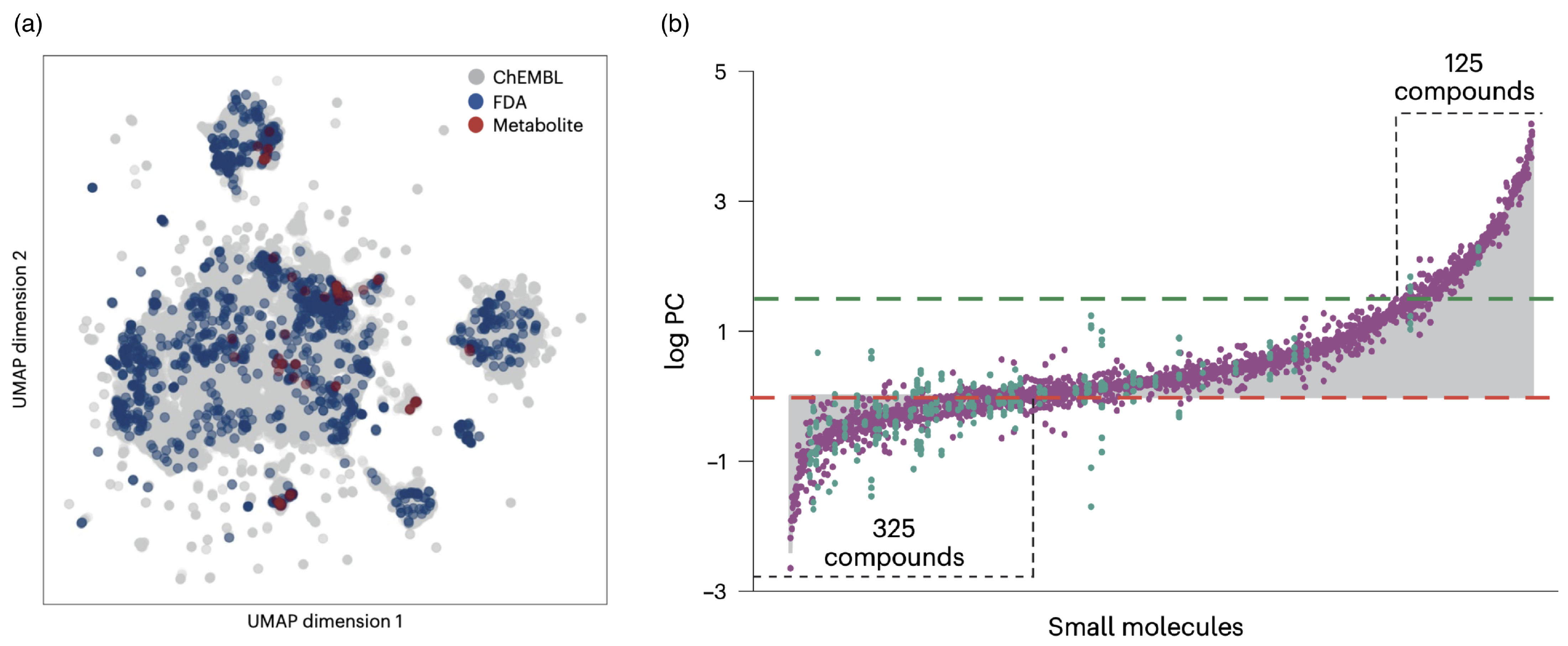
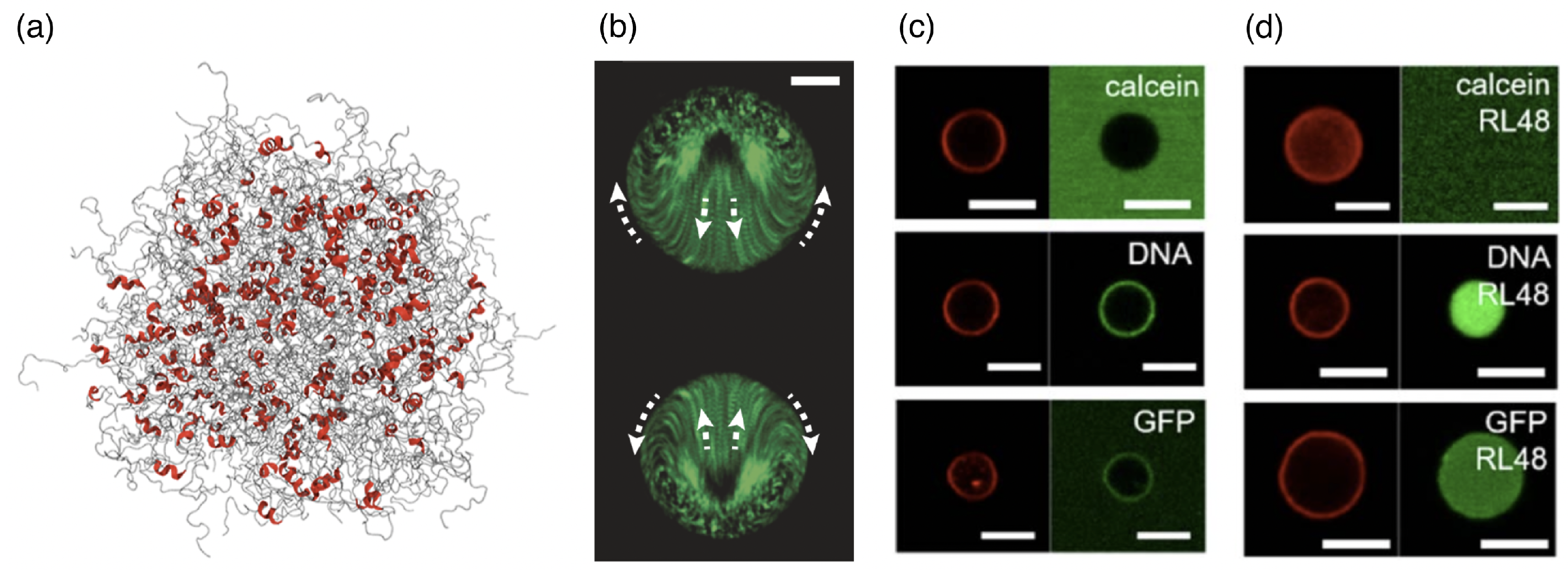
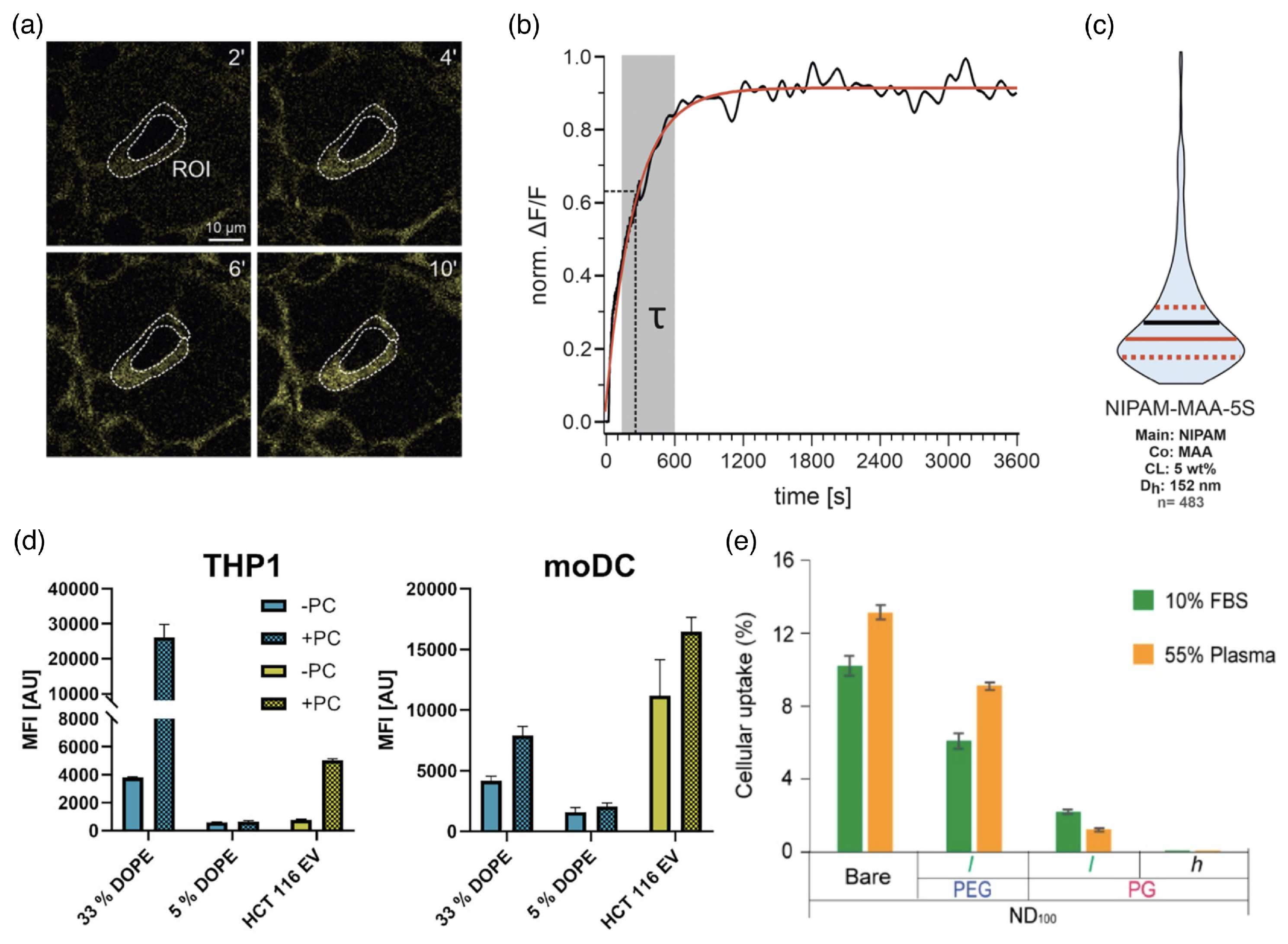

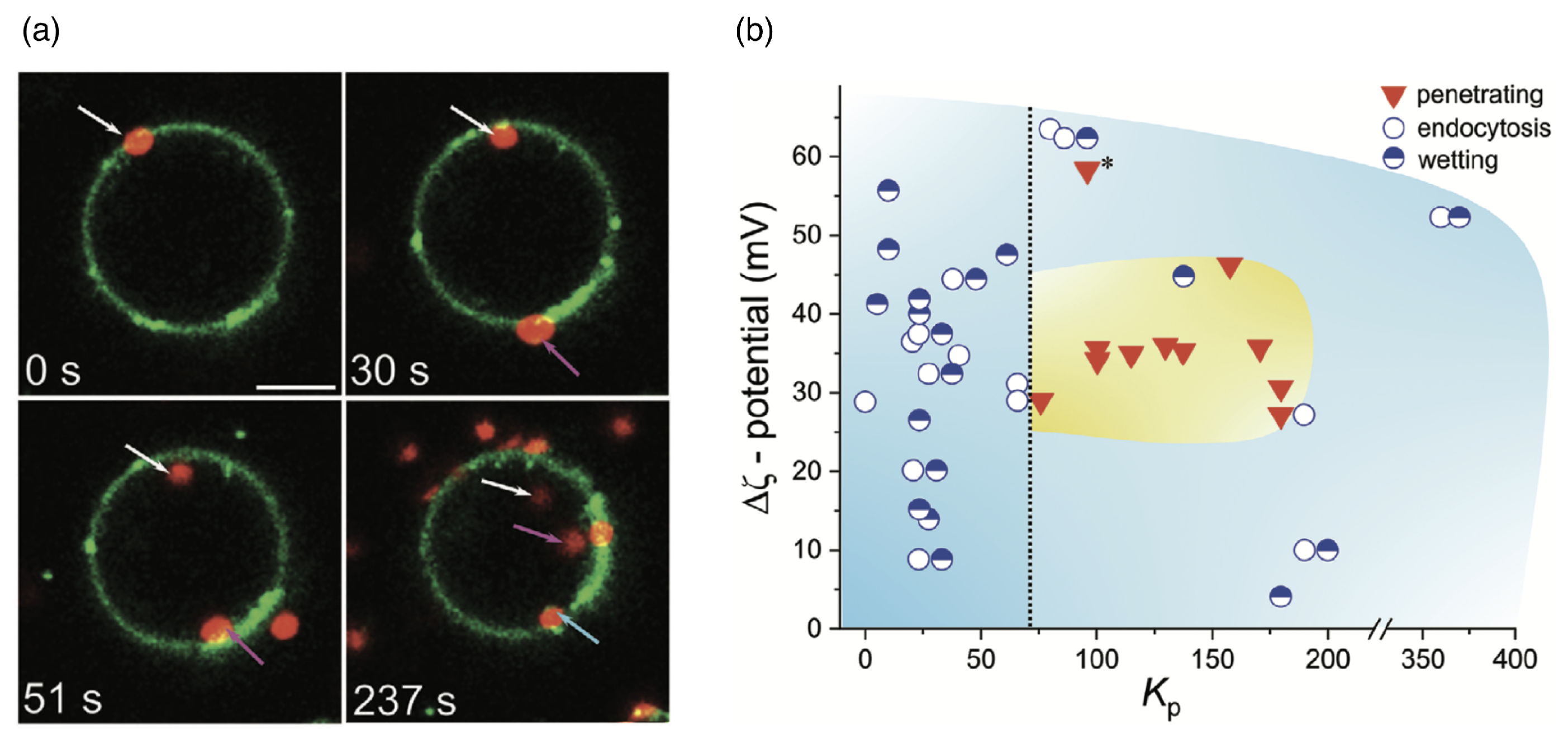

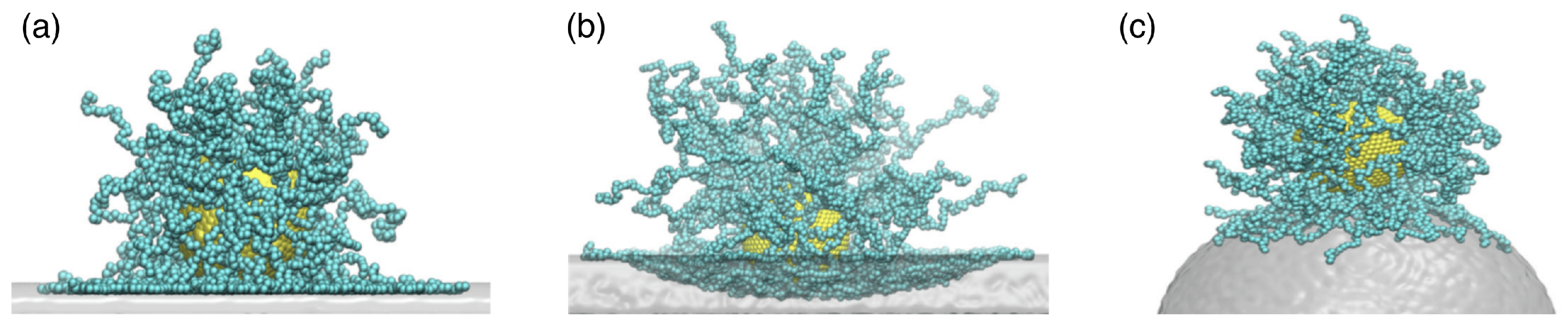


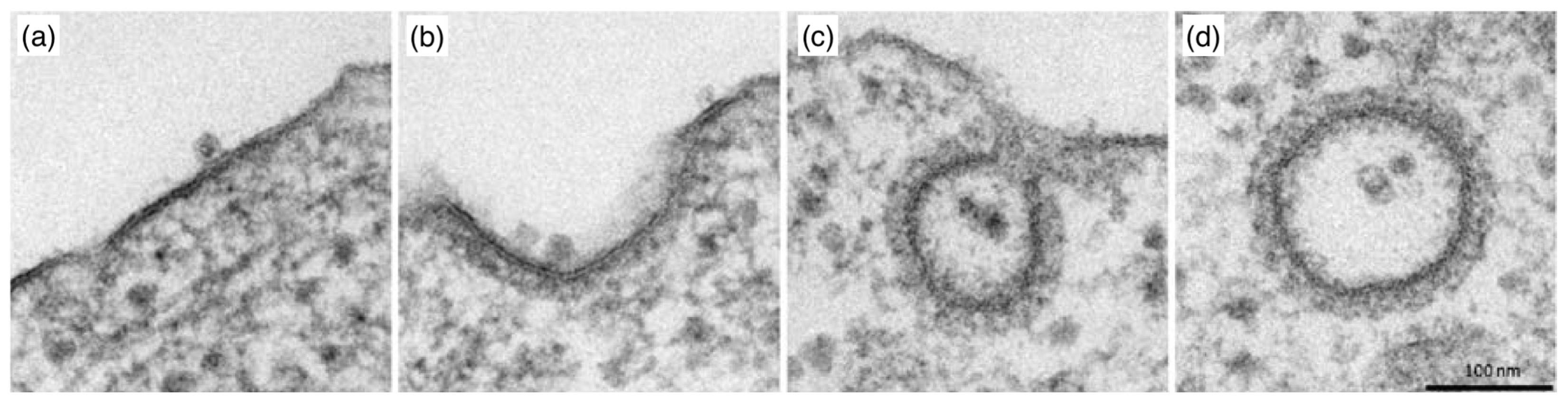

| Particle | Particle Size | References |
|---|---|---|
| star polymers | 3–40 | [12,13,14,15] |
| diblock-copolymer micelles | 25–100 | [16,17] |
| biomolecular condensates | –5 | [18,19,20] |
| nanogels | 10–100 | [21] |
| polymer-grafted nanoparticles | 20–500 | [22,23,24,25] |
| polymersomes 1 | – | [26] |
| DNA and RNA origami particles | 30–400 | [27,28,29,30] |
| stealth liposomes | – | [31] |
| microgels 1 | –100 | [21,32] |
| Polymer | Persistence Length | References |
|---|---|---|
| polyethylene oxide (PEO) | 0.37–0.48 | [35,36] |
| polyethylene glycol (PEG) | [36] | |
| poly(N-isopropylacrylamide) (PNIPAM) | 0.25–1.5 | [37,38] |
| single-stranded RNA and DNA | 1–3 | [39,40] |
| spectrin tetramers | [41] | |
| double-stranded RNA and DNA 1 | 50–65 | [42,43] |
| collagen | 14–180 | [44] |
| intermediate filaments | 0.5–2 | [45] |
| filamentous actin | [46] | |
| microtubules 2 | 80–5000 | [47] |
| Microgel | Young’s Modulus Y (Swollen) | Y (Collapsed) | References |
|---|---|---|---|
| n/a | [146] | ||
| POx-HASH | n/a | [146] | |
| n/a | [142] | ||
| n/a | [142] | ||
| PNIPAM with 20% AAc | ≈150 | ≈400 | [158] |
| PNIPAM with BIS 2 | 0–1000 | 20 times increased | [159] |
| PNIPAM with BIS and DMA 2 | 0–1000 | >100 times increased | [159] |
| -- | n/a | [142] | |
| -- | n/a | [142] | |
| -- | 63,000 | n/a | [142] |
| Condensate | Interface Tension | Bending Rigidity | References |
|---|---|---|---|
| clotrimazole | [204] | ||
| FXR1 overexpression and sodium arsenide | [204] | ||
| sodium arsenite | [204] | ||
| PGL-3 proteins at various KCl concentrations 1 | 1–5 | n/a | [208] |
| nucleoli in HeLa cell nuclei | n/a | [209] | |
| 1–231 in aqueous buffer | n/a | [202] | |
| ELF3 proteins | n/a | [210] | |
| polylysine:heparin mixture and Ficoll70 2 | 70–125 | n/a | [207] |
| 1–229 in aqueous buffer | n/a | [202] | |
| LAF-1 RGG | n/a | [203] | |
| -dT40 at various NaCl concentrations 1 | 0.5–1.6 | n/a | [205] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Auth, T. Polymeric and Polymer-Functionalized Drug Delivery Vectors: From Molecular Architecture and Elasticity to Cellular Uptake. Polymers 2025, 17, 2243. https://doi.org/10.3390/polym17162243
Auth T. Polymeric and Polymer-Functionalized Drug Delivery Vectors: From Molecular Architecture and Elasticity to Cellular Uptake. Polymers. 2025; 17(16):2243. https://doi.org/10.3390/polym17162243
Chicago/Turabian StyleAuth, Thorsten. 2025. "Polymeric and Polymer-Functionalized Drug Delivery Vectors: From Molecular Architecture and Elasticity to Cellular Uptake" Polymers 17, no. 16: 2243. https://doi.org/10.3390/polym17162243
APA StyleAuth, T. (2025). Polymeric and Polymer-Functionalized Drug Delivery Vectors: From Molecular Architecture and Elasticity to Cellular Uptake. Polymers, 17(16), 2243. https://doi.org/10.3390/polym17162243






