Description of Gas Transport in Polymers: Integrated Thermodynamic and Transport Modeling of Refrigerant Gases in Polymeric Membranes
Abstract
1. Introduction
2. Theoretical Background
3. Results
3.1. Model Parameters
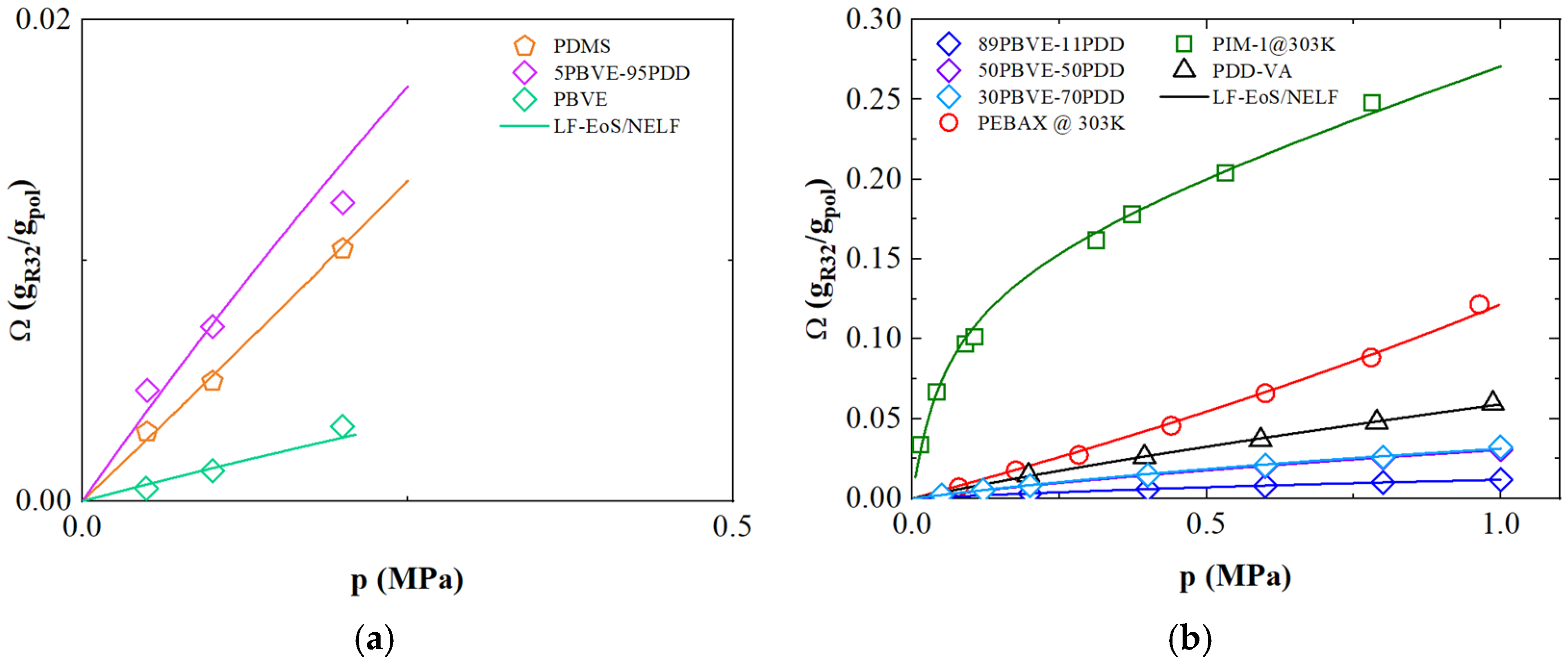
3.2. Solubility of R-32
3.3. Solubility of R-125
3.4. Solubility of R-134a
3.5. Solubility of R-152a
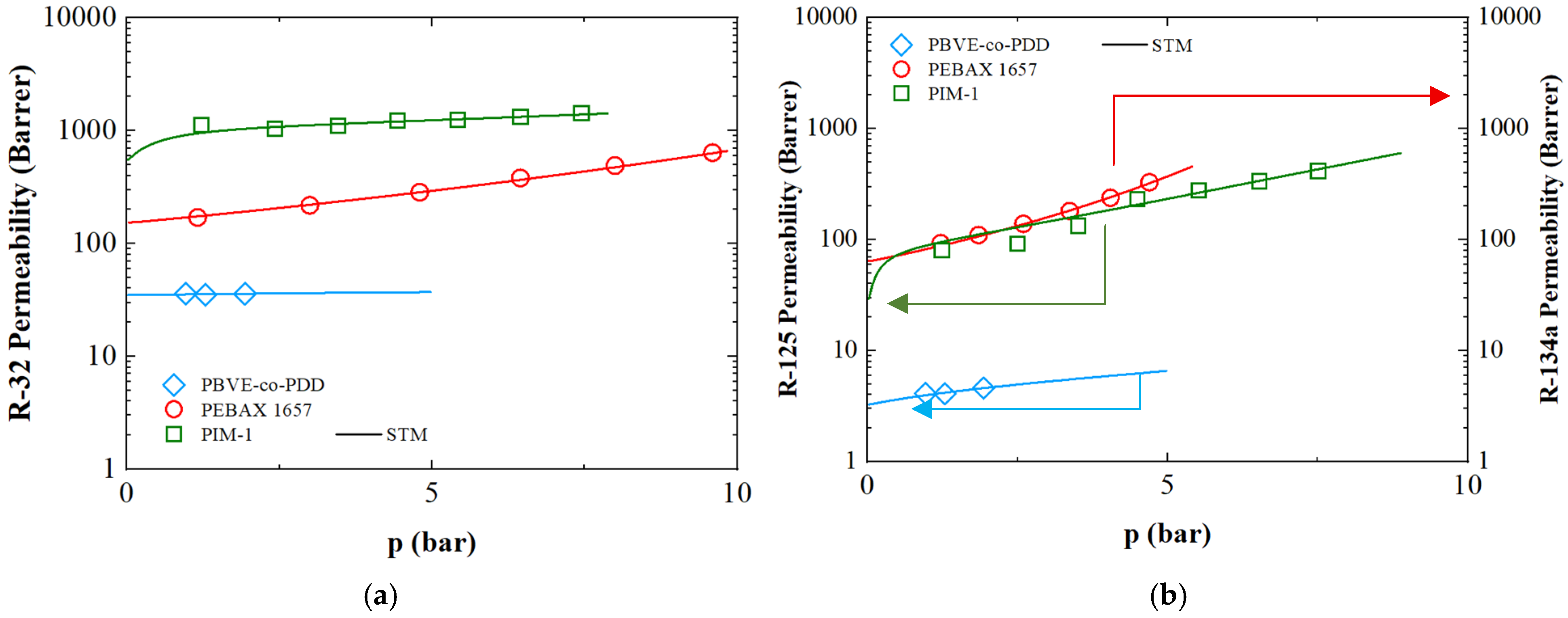
3.6. Refrigerant Gases Transport in Polymers
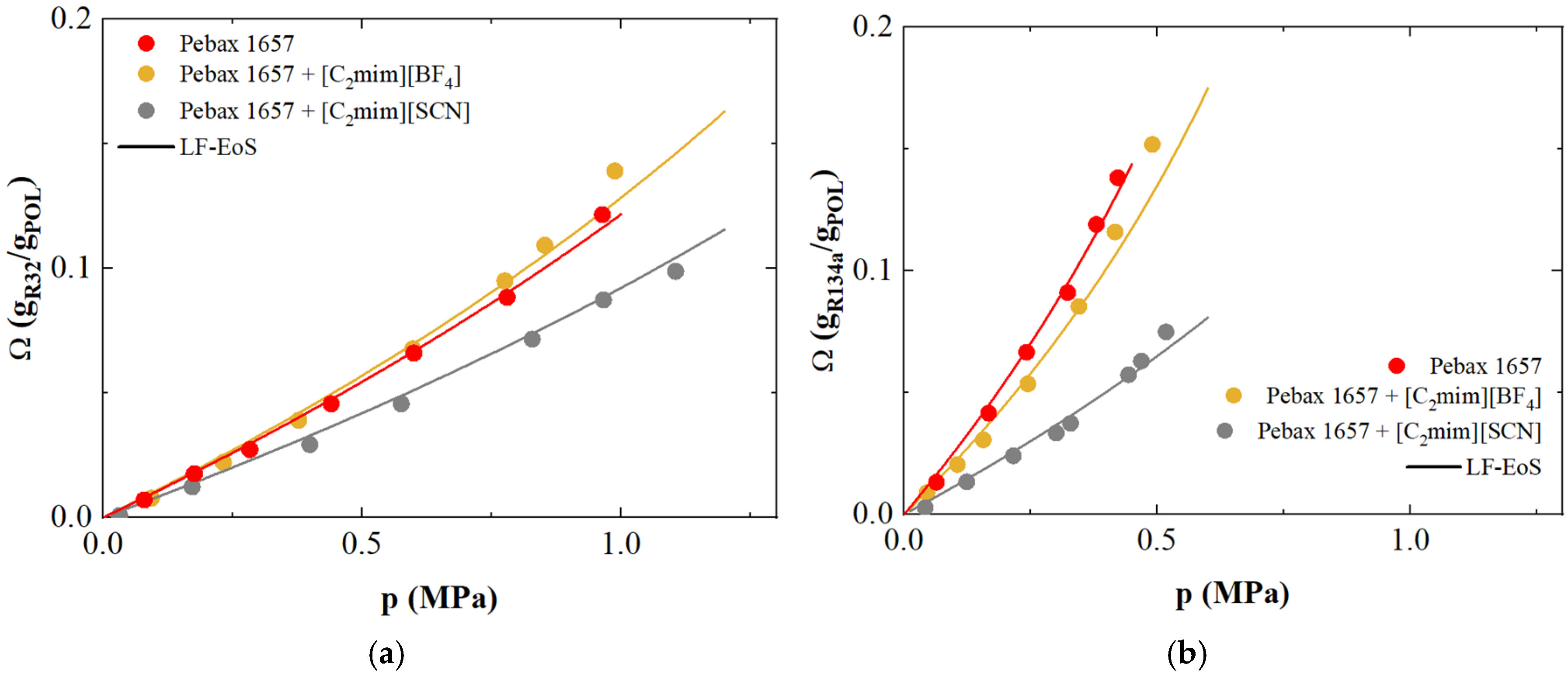
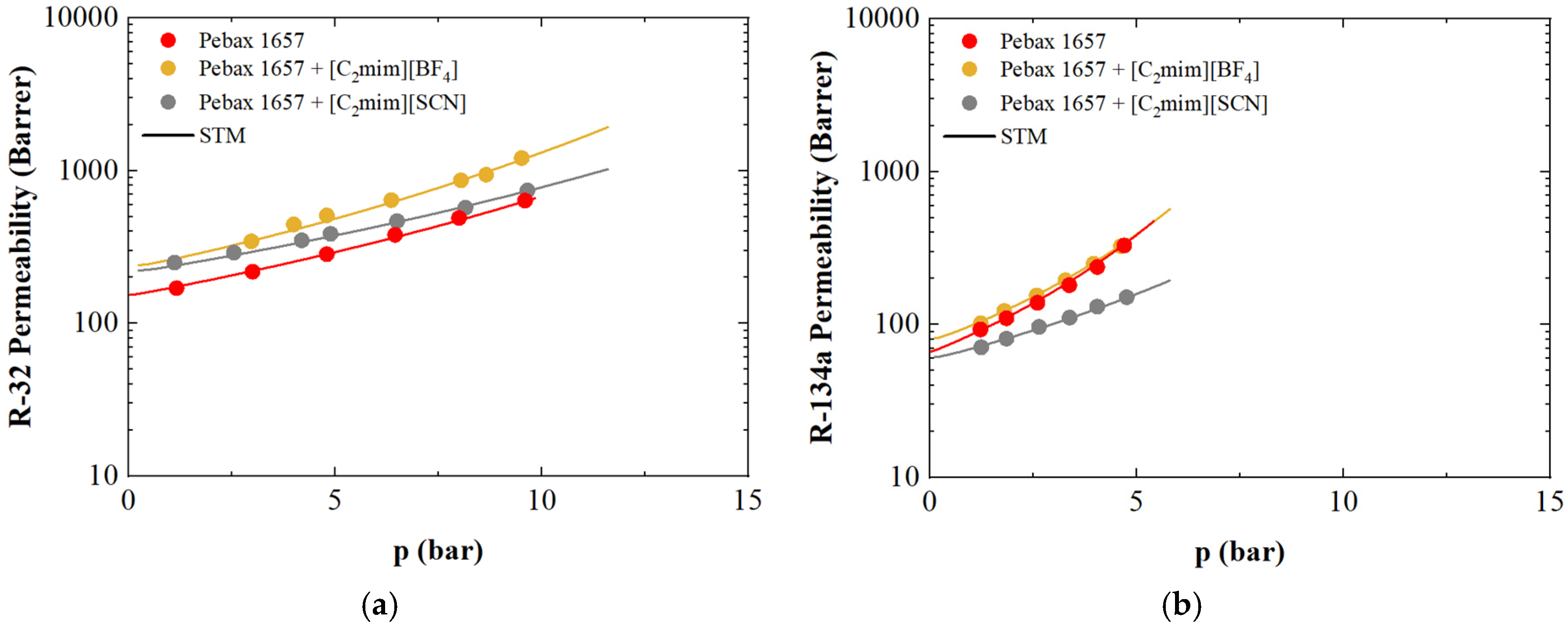
3.7. Refrigerant Gases Sorption and Transport in Supported Ionic Liquid Membranes: A Case Study
4. Conclusions
- Retrieve the main pure components parameters of the models considered (SL EoS or NELF) through the use of a series of experimental data, such as pVT or VLE data, of the pure components, as well as for, the glassy polymers, their density and glass transition temperature and, in case of copolymers, information on chemical composition.
- Fit the Sanchez–Lacombe equation of state or its non-equilibrium extension to a single sorption isotherm to extract polymer-specific parameters and interaction coefficients (kij and ksw).
- Combine these thermodynamic results with the Standard Transport Model (STM)—that incorporates thermodynamic solubility and concentration-dependent mobility coefficients—to estimate permeability, which can be validated against experimental transport data.
- Use the obtained modeling tools to describe and predict gas solubility, diffusivity and permeability in a wide range of experimental conditions, possibly defining general guidelines to describe the expected behavior of the gas-polymer system of interest.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| R-32 | Bifluoromethane |
| R-125 | Pentafluoroethane |
| R-134a | 1,1,1,2-Tetrafluoroethane |
| R-152a | 1-1 Difluoroethane |
| CH4 | Methane |
| C2H6 | Ethane |
| PDMS | Polydimethylsiloxane |
| PIM-1 | Polymer of Intrinsic Microporosity |
| PEBAX | poly(ether-block-amide) |
| PBVE | perfluoro(butenyl vinyl ether) |
| PDD | perfluoro(2,2-dimethyl-1,3-dioxole) |
| VA | Vinyl Acetate |
| SILM | Supported liquid membrane |
| SL-EoS | Sanchez-Lacombe Equation of State |
| NELF | Non-Equilibrium Lattice Fluid |
| STM | Standard Transport Model |
References
- Sicard, A.J.; Baker, R.T. Fluorocarbon Refrigerants and Their Syntheses: Past to Present. Chem. Rev. 2020, 120, 9164–9303. [Google Scholar] [CrossRef]
- The Montreal Protocol on Substances That Deplete the Ozone Layer—United States Department of State. Available online: https://www.state.gov/the-montreal-protocol-on-substances-that-deplete-the-ozone-layer (accessed on 19 February 2025).
- EU. Regulation (EU) No 517/2014 of the European Parliament and of the Council of 16 April 2014 on Fluorinated Greenhouse Gases and Repealing Regulation (EC) No 842/2006. Off. J. Eur. Union 2014, OJ L 150, 195–230. [Google Scholar]
- Abas, N.; Kalair, A.R.; Khan, N.; Haider, A.; Saleem, Z.; Saleem, M.S. Natural and Synthetic Refrigerants, Global Warming: A Review. Renew. Sustain. Energy Rev. 2018, 90, 557–569. [Google Scholar] [CrossRef]
- Bolaji, B.O.; Huan, Z. Ozone Depletion and Global Warming: Case for the Use of Natural Refrigerant—A Review. Renew. Sustain. Energy Rev. 2013, 18, 49–54. [Google Scholar] [CrossRef]
- Proposed Rule—Phasedown of Hydrofluorocarbons: Establishing the Allowance Allocation and Trading Program Under the AIM Act|US EPA. Available online: https://www.epa.gov/climate-hfcs-reduction/ (accessed on 19 February 2025).
- Lin, H.; Van Wagner, E.; Raharjo, R.; Freeman, B.D.; Roman, I. High-Performance Polymer Membranes for Natural-Gas Sweetening. Adv. Mater. 2006, 18, 39–44. [Google Scholar] [CrossRef]
- Baker, R.W.; Lokhandwala, K. Natural Gas Processing with Membranes: An Overview. Ind. Eng. Chem. Res. 2008, 47, 2109–2121. [Google Scholar] [CrossRef]
- Scholes, C.A.; Stevens, G.W.; Kentish, S.E. Membrane Gas Separation Applications in Natural Gas Processing. Fuel 2012, 96, 15–28. [Google Scholar] [CrossRef]
- Pellegrino, J.J.; Giarratano, P.J. Gas Separation Using Ion Exchange Membranes for Producing Hydrogen from Synthesis Gas. Quarterly Report 22 Covering the Period 1 October 1991; Office of Scientific and Technical Information (OSTI): Pittsburgh, PA, USA; Morgantown, WV, USA, 1992; Volume 53. [Google Scholar]
- Turner, J.; Sverdrup, G.; Mann, M.K.; Maness, P.C.; Kroposki, B.; Ghirardi, M.; Evans, R.J.; Blake, D. Renewable Hydrogen Production. Int. J. Energy Res. 2008, 32, 379–407. [Google Scholar] [CrossRef]
- Kayfeci, M.; Keçebaş, A. Hydrogen Storage. In Solar Hydrogen Production: Processes, Systems and Technologies; Academic Press: Cambridge, MA, USA, 2019; pp. 85–110. [Google Scholar] [CrossRef]
- Kato, R.; Nishide, H. Polymers for Carrying and Storing Hydrogen. Polym. J. 2018, 50, 77–82. [Google Scholar] [CrossRef]
- Scholes, C.A.; Ghosh, U.K. Review of Membranes for Helium Separation and Purification. Membranes 2017, 7, 9. [Google Scholar] [CrossRef] [PubMed]
- Sunarso, J.; Hashim, S.S.; Lin, Y.S.; Liu, S.M. Membranes for Helium Recovery: An Overview on the Context, Materials and Future Directions. Sep. Purif. Technol. 2017, 176, 335–383. [Google Scholar] [CrossRef]
- Banerjee, P.; Chowdhury, M.; Das, P.; Nadda, A.K.; Mukhopadhayay, A. Biopolymers for CO2 Capture. In CO2-Philic Polymers, Nanocomposites and Solvents: Capture, Conversion and Industrial Products; Elsevier: Amsterdam, The Netherlands, 2023; pp. 289–320. [Google Scholar] [CrossRef]
- Babamohammadi, S.; Shamiri, A.; Aroua, M.K. A Review of CO2 Capture by Absorption in Ionic Liquid-Based Solvents. Rev. Chem. Eng. 2015, 31, 383–412. [Google Scholar] [CrossRef]
- Comesaña-Gándara, B.; Chen, J.; Bezzu, C.G.; Carta, M.; Rose, I.; Ferrari, M.C.; Esposito, E.; Fuoco, A.; Jansen, J.C.; McKeown, N.B. Redefining the Robeson Upper Bounds for CO2/CH4 and CO2/N2 Separations Using a Series of Ultrapermeable Benzotriptycene-Based Polymers of Intrinsic Microporosity. Energy Environ. Sci. 2019, 12, 2733–2740. [Google Scholar] [CrossRef]
- Chawla, M.; Saulat, H.; Masood Khan, M.; Mahmood Khan, M.; Rafiq, S.; Cheng, L.; Iqbal, T.; Rasheed, M.I.; Farooq, M.Z.; Saeed, M.; et al. Membranes for CO2/CH4 and CO2/N2 Gas Separation. Chem. Eng. Technol. 2020, 43, 184–199. [Google Scholar] [CrossRef]
- Merkel, T.C.; Gupta, R.P.; Turk, B.S.; Freeman, B.D. Mixed-Gas Permeation of Syngas Components in Poly(Dimethylsiloxane) and Poly(1-Trimethylsilyl-1-Propyne) at Elevated Temperatures. J. Membr. Sci. 2001, 191, 85–94. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, X.; Kraslawski, A.; Gao, J.; Cui, P. A Novel Process Design for CO2 Capture and H2S Removal from the Syngas Using Ionic Liquid. J. Clean. Prod. 2019, 213, 480–490. [Google Scholar] [CrossRef]
- Harders, A.N.; Wallisch, L.; White, W.; Shiflett, M.B. Process Design for Separating R-410A Using Fluorinated Membranes. Ind. Eng. Chem. Res. 2024, 63, 16545–16554. [Google Scholar] [CrossRef]
- Harders, A.N.; Sturd, E.R.; Vallier, J.E.; Corbin, D.R.; White, W.R.; Junk, C.P.; Shiflett, M.B. Selective Separation of HFC-32 from R-410A Using Poly(Dimethylsiloxane) and a Copolymer of Perfluoro(Butenyl Vinyl Ether) and Perfluoro(2,2-Dimethyl-1,3-Dioxole). J. Membr. Sci. 2022, 652, 120467. [Google Scholar] [CrossRef]
- Harders, A.N.; Sturd, E.R.; Wallisch, L.; Schmidt, H.; Mendoza-Apodaca, Y.; Corbin, D.R.; White, W.; Junk, C.P.; Shiflett, M.B. Solubility, Diffusivity, and Permeability of HFC-32 and HFC-125 in Amorphous Copolymers of Perfluoro(Butenyl Vinyl Ether) and Perfluoro(2,2-Dimethyl-1,3-Dioxole). Ind. Eng. Chem. Res. 2023, 62, 4054–4063. [Google Scholar] [CrossRef]
- Harders, A.N.; Dixon, S.; Hines, B.; Lundin, M.; White, W.; Shiflett, M.B. Separation of Refrigerant Gases Using a Copolymer of Perfluoro(2,2-Dimethyl-1,3-Dioxole) (PDD) and Vinyl Acetate (VA). Ind. Eng. Chem. Res. 2023, 62, 15148–15156. [Google Scholar] [CrossRef]
- Pardo, F.; Gutiérrez-Hernández, S.V.; Zarca, G.; Urtiaga, A. Toward the Recycling of Low-GWP Hydrofluorocarbon/Hydrofluoroolefin Refrigerant Mixtures Using Composite Ionic Liquid-Polymer Membranes. ACS Sustain. Chem. Eng. 2021, 9, 7012–7021. [Google Scholar] [CrossRef]
- Pardo, F.; Zarca, G.; Urtiaga, A. Separation of Refrigerant Gas Mixtures Containing R32, R134a, and R1234yf through Poly(Ether- Block-Amide) Membranes. ACS Sustain. Chem. Eng. 2020, 8, 2548–2556. [Google Scholar] [CrossRef]
- El-Okazy, M.A.; Liu, L.; Abdellah, M.H.; Goudeli, E.; Kentish, S.E. Gas Sorption and Diffusion in Perfluoro(Butenyl Vinyl Ether) Based Perfluoropolymeric Membranes. J. Membr. Sci. 2022, 644, 120095. [Google Scholar] [CrossRef]
- Okamoto, Y.; Chiang, H.C.; Merkel, T. Perfluoropolymers for Gas Separation Membrane Applications. In Fascinating Fluoropolymers and Their Applications; Elsevier: Amsterdam, The Netherlands, 2020; pp. 143–155. [Google Scholar] [CrossRef]
- De Angelis, M.G.; Merkel, T.C.; Bondar, V.I.; Freeman, B.D.; Doghieri, F.; Sarti, G.C. Gas Sorption and Dilation in Poly(2,2-Bistrifluoromethyl-4,5-Difluoro-1,3-Dioxole-Co-Tetrafluoroethylene): Comparison of Experimental Data with Predictions of the Nonequilibrium Lactice Fluid Model. Macromolecules 2002, 35, 1276–1288. [Google Scholar] [CrossRef]
- El-Okazy, M.A.; Liu, L.; Junk, C.P.; Kathmann, E.; White, W.; Kentish, S.E. Gas Separation Performance of Copolymers of Perfluoro(Butenyl Vinyl Ether) and Perfluoro(2,2-Dimethyl-1,3-Dioxole). J. Membr. Sci. 2021, 634, 119401. [Google Scholar] [CrossRef]
- Gutiérrez-Hernández, S.V.; Pardo, F.; Foster, A.B.; Gorgojo, P.; Budd, P.M.; Zarca, G.; Urtiaga, A. Outstanding Performance of PIM-1 Membranes towards the Separation of Fluorinated Refrigerant Gases. J. Membr. Sci. 2023, 675, 121532. [Google Scholar] [CrossRef]
- Minelli, M.; Sarti, G.C. 110th Anniversary: Gas and Vapor Sorption in Glassy Polymeric Membranes—Critical Review of Different Physical and Mathematical Models. Ind. Eng. Chem. Res. 2020, 59, 341–365. [Google Scholar] [CrossRef]
- Sanchez, I.C. Relationships between Polymer Interaction Parameters. Polymer 1989, 30, 471–475. [Google Scholar] [CrossRef]
- Sanchez, I.C.; Lacombe, R.H. An Elementary Molecular Theory of Classical Fluids. Pure Fluids. J. Phys. Chem. 1976, 80, 2352–2362. [Google Scholar] [CrossRef]
- Lacombe, R.H.; Sanchez, I.C. Statistical Thermodynamics of Fluid Mixtures. J. Phys. Chem. 1976, 80, 2568–2580. [Google Scholar] [CrossRef]
- Doghieri, F.; Sarti, G.C. Nonequilibrium Lattice Fluids: A Predictive Model for the Solubility in Glassy Polymers. Macromolecules 1996, 29, 7885–7896. [Google Scholar] [CrossRef]
- Baschetti, M.G.; Doghieri, F.; Sarti, G.C. Solubility in Glassy Polymers: Correlations through the Nonequilibrium Lattice Fluid Model. Ind. Eng. Chem. Res. 2001, 40, 3027–3037. [Google Scholar] [CrossRef]
- Gross, J.; Sadowski, G. Perturbed-Chain SAFT: An Equation of State Based on a Perturbation Theory for Chain Molecules. Ind. Eng. Chem. Res. 2001, 40, 1244–1260. [Google Scholar] [CrossRef]
- Feng, Z.; Panuganti, S.R.; Chapman, W.G. Predicting Solubility and Swelling Ratio of Blowing Agents in Rubbery Polymers Using PC-SAFT Equation of State. Chem. Eng. Sci. 2018, 183, 306–328. [Google Scholar] [CrossRef]
- Minelli, M.; Doghieri, F. Predictive Model for Gas and Vapor Solubility and Swelling in Glassy Polymers I: Application to Different Polymer/Penetrant Systems. Fluid Phase Equilib. 2014, 381, 1–11. [Google Scholar] [CrossRef]
- Di Carlo, R.; Ricci, E.; Minelli, M. Comprehensive Modelling Strategy for Gas Transport in Polymers: Analysis of Swelling and Non-Swelling Agents at High Pressures. Fluid Phase Equilib. 2025, 591, 114311. [Google Scholar] [CrossRef]
- Signorini, V.; Ansaloni, L.; Peters, T.; Alcock, B.; Baschetti, M.G.; Minelli, M. Characterization and Modeling of CO2 Transport through Fluorinated Thermoplastics. ACS Appl. Polym. Mater. 2023, 6, 379–389. [Google Scholar] [CrossRef]
- Ricci, E.; De Angelis, M.G.; Minelli, M. A Comprehensive Theoretical Framework for the Sub and Supercritical Sorption and Transport of CO2 in Polymers. Chem. Eng. J. 2022, 435, 135013. [Google Scholar] [CrossRef]
- Minelli, M.; De Angelis, M.G. An Equation of State (EoS) Based Model for the Fluid Solubility in Semicrystalline Polymers. Fluid Phase Equilib. 2014, 367, 173–181. [Google Scholar] [CrossRef]
- Earle, M.J.; Seddon, K.R. Ionic Liquids. Green Solvents for the Future. Pure Appl. Chem. 2000, 72, 1391–1398. [Google Scholar] [CrossRef]
- Brennecke, J.F.; Maginn, E.J. Ionic Liquids: Innovative Fluids for Chemical Processing. AIChE J. 2001, 47, 2384–2389. [Google Scholar] [CrossRef]
- Lei, Z.; Dai, C.; Chen, B. Gas Solubility in Ionic Liquids. Chem. Rev. 2014, 114, 1289–1326. [Google Scholar] [CrossRef]
- Zhang, X.; Tu, Z.; Li, H.; Huang, K.; Hu, X.; Wu, Y.; MacFarlane, D.R. Selective Separation of H2S and CO2 from CH4 by Supported Ionic Liquid Membranes. J. Membr. Sci. 2017, 543, 282–287. [Google Scholar] [CrossRef]
- Farahipour, R.; Mehrkesh, A.; Karunanithi, A.T. A Systematic Screening Methodology towards Exploration of Ionic Liquids for CO2 Capture Processes. Chem. Eng. Sci. 2016, 145, 126–132. [Google Scholar] [CrossRef]
- Asensio-Delgado, S.; Pardo, F.; Zarca, G.; Urtiaga, A. Vapor-Liquid Equilibria and Diffusion Coefficients of Difluoromethane, 1,1,1,2-Tetrafluoroethane, and 2,3,3,3-Tetrafluoropropene in Low-Viscosity Ionic Liquids. J. Chem. Eng. Data 2020, 65, 4242–4251. [Google Scholar] [CrossRef]
- Minelli, M.; Sarti, G.C. Gas Permeability in Glassy Polymers: A Thermodynamic Approach. Fluid Phase Equilib. 2016, 424, 44–51. [Google Scholar] [CrossRef]
- Minelli, M.; Paul, D.R.; Sarti, G.C. On the Interpretation of Cryogenic Sorption Isotherms in Glassy Polymers. J. Membr. Sci. 2017, 540, 229–242. [Google Scholar] [CrossRef]
- Wijmans, J.G.; Baker, R.W. The Solution-Diffusion Model: A Review. J. Membr. Sci. 1995, 107, 1–21. [Google Scholar] [CrossRef]
- Flory, P.J. Thermodynamics of Polymer Solutions. Discuss. Daraday Soc. 1970, 49, 683–748. [Google Scholar] [CrossRef]
- Huggins, M.L. Thermodynamic properties of solutions of long-chain compounds. Ann. N. Y. Acad. Sci. 1942, 43, 1–32. [Google Scholar] [CrossRef]
- Flory, P.J. Statistical Thermodynamics of Liquid Mixtures. J. Am. Chem. Soc. 1965, 87, 1833–1838. [Google Scholar] [CrossRef]
- Neau, E. A Consistent Method for Phase Equilibrium Calculation Using the Sanchez–Lacombe Lattice–Fluid Equation-of-State. Fluid Phase Equilib. 2002, 203, 133–140. [Google Scholar] [CrossRef]
- Sanchez, I.C.; Lacombe, R.H. Statistical Thermodynamics of Polymer Solutions. Macromolecules 1978, 11, 1145–1156. [Google Scholar] [CrossRef]
- Green, D.D.W.; Southard, D.M.Z. Perry’s Chemical Engineers’ Handbook; McGraw-Hill Education: New York, NY, USA, 2019; ISBN 9780071834087. [Google Scholar]
- Walsh, D.; Zoller, P. Standard Pressure Volume Temperature Data for Polymers; CRC Press: Boca Raton, FL, USA, 1995. [Google Scholar]
- Eitouni, H.B.; Balsara, N.P. Thermodynamics of Polymer Blends. In Physical Properties of Polymers Handbook; Springer: New York, NY, USA, 2007; Chapter 19; pp. 339–356. [Google Scholar] [CrossRef]
- Sanchez, I.C.; Rodgers, P.A. Solubility of Gases in Polymers. Pure Appl. Chem. 1990, 62, 2107–2114. [Google Scholar] [CrossRef]
- Minelli, M.; Doghieri, F. A Predictive Model for Vapor Solubility and Volume Dilation in Glassy Polymers. Ind. Eng. Chem. Res. 2012, 51, 16505–16516. [Google Scholar] [CrossRef]
- Jordan, S.S.; Koros, W.J. A Free Volume Distribution Model for Gas Sorption and Dilation in Glassy Polymers. Macromolecules 1995, 28, 2228–2235. [Google Scholar] [CrossRef]
- Minelli, M.; Sarti, G.C. Permeability and Solubility of Carbon Dioxide in Different Glassy Polymer Systems with and without Plasticization. J. Membr. Sci. 2013, 444, 429–439. [Google Scholar] [CrossRef]
- Minelli, M.; Campagnoli, S.; De Angelis, M.G.; Doghieri, F.; Sarti, G.C. Predictive Model for the Solubility of Fluid Mixtures in Glassy Polymers. Macromolecules 2011, 44, 4852–4862. [Google Scholar] [CrossRef]
- Grassia, F.; Baschetti, M.G.; Doghieri, F.; Sarti, G.C. Solubility of Gases and Vapors in Glassy Polymer Blends. In Advanced Materials for Membrane Separations; American Chemical Society: Washington, DC, USA, 2004; pp. 55–73. [Google Scholar] [CrossRef]
- Shiflett, M.B.; Maginn, E.J. The Solubility of Gases in Ionic Liquids. AIChE J. 2017, 63, 4722–4737. [Google Scholar] [CrossRef]
- Tang, J.; Shen, Y.; Radosz, M.; Sun, W. Isothermal Carbon Dioxide Sorption in Poly(Ionic Liquid)s. Ind. Eng. Chem. Res. 2009, 48, 9113–9118. [Google Scholar] [CrossRef]
- Santos, D.; Santos, M.; Franceschi, E.; Dariva, C.; Barison, A.; Mattedi, S. Experimental Density of Ionic Liquids and Thermodynamic Modeling with Group Contribution Equation of State Based on the Lattice Fluid Theory. J. Chem. Eng. Data 2016, 61, 348–353. [Google Scholar] [CrossRef]
- Kim, Y.S.; Choi, W.Y.; Jang, J.H.; Yoo, K.P.; Lee, C.S. Solubility Measurement and Prediction of Carbon Dioxide in Ionic Liquids. Fluid Phase Equilib. 2005, 228–229, 439–445. [Google Scholar] [CrossRef]
- Freeman, B.D. Basis of Permeability/Selectivity Tradeoff Relations in Polymeric Gas Separation Membranes. Macromolecules 1999, 32, 375–380. [Google Scholar] [CrossRef]
- Matteucci, S.; Yampolskii, Y.; Freeman, B.D.; Pinnau, I. Transport of Gases and Vapors in Glassy and Rubbery Polymers. In Materials Science of Membranes for Gas and Vapor Separation; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006. [Google Scholar] [CrossRef]
- Crank, J. The Mathematics of Diffusion. J. Am. Chem. Soc. 1957, 79, 1267–1268. [Google Scholar] [CrossRef]
- Giacinti Baschetti, M.; Doghieri, F.; Freeman, B.; Sarti, G.C. Transient and Steady-State Effective Diffusivity in High Free Volume Glassy Polymers. J. Membr. Sci. 2009, 344, 144–154. [Google Scholar] [CrossRef]
- Ghosal, K.; Freeman, B.D. Gas Separation Using Polymer Membranes: An Overview. Polym. Adv. Technol. 1994, 5, 673–697. [Google Scholar] [CrossRef]
- Mulder, M. Basic Principles of Membrane Technology; R. Oldenbourg Verlag: München, Germany, 1991. [Google Scholar] [CrossRef]
- Bernardo, P.; Drioli, E.; Golemme, G. Membrane Gas Separation: A Review/State of the Art. Ind. Eng. Chem. Res. 2009, 48, 4638–4663. [Google Scholar] [CrossRef]
- Vijesh, A.M.; Isloor, A.M. Review on Polymeric Membrane Materials for Gas Separations Which Are Stated above the Robeson’s Trade-off Upper Bound. In Current Trends and Future Developments on (Bio-) Membranes: Modern Approaches in Membrane Technology for Gas Separation and Water Treatment; Elsevier: Amsterdam, The Netherlands, 2024; pp. 3–28. [Google Scholar] [CrossRef]
- Pandey, P.; Chauhan, R.S. Membranes for Gas Separation. Prog. Polym. Sci. 2001, 26, 853–893. [Google Scholar] [CrossRef]
- Stern, S.A. The “Barrer” Permeability Unit. J. Polym. Sci. Part. A-2 Polym. Phys. 1968, 6, 1933–1934. [Google Scholar] [CrossRef]
- Minelli, M.; Sarti, G.C. Permeability and Diffusivity of CO2 in Glassy Polymers with and without Plasticization. J. Membr. Sci. 2013, 435, 176–185. [Google Scholar] [CrossRef]
- Peng, D.Y.; Robinson, D.B. A New Two-Constant Equation of State. Ind. Eng. Chem. Fundam. 1976, 15, 59–64. [Google Scholar] [CrossRef]
- Minelli, M.; Friess, K.; Vopička, O.; De Angelis, M.G. Modeling Gas and Vapor Sorption in a Polymer of Intrinsic Microporosity (PIM-1). Fluid Phase Equilib. 2013, 347, 35–44. [Google Scholar] [CrossRef]
- Pope, D.S.; Sanchez, I.C.; Koros, W.J.; Fleming, G.K. Statistical Thermodynamic Interpretation of Sorption/Dilation Behavior of Gases in Silicone Rubber. Macromolecules 1991, 24, 1779–1783. [Google Scholar] [CrossRef]
- Dlubek, G.; Pionteck, J.; Rätzke, K.; Kruse, J.; Faupel, F. Temperature Dependence of the Free Volume in Amorphous Teflon AF1600 and AF2400: A Pressure-Volume-Temperature and Positron Lifetime Study. Macromolecules 2008, 41, 6125–6133. [Google Scholar] [CrossRef]
- Ismaeel, H.; Gibson, D.; Ricci, E.; De Angelis, M.G. Estimating Gas Sorption In Polymeric Membranes From The Molecular Structure: A Machine Learning Based Group Contribution Method For The Non-Equilibrium Lattice Fluid Model (ML-GC-NELF). J. Membr. Sci. 2024, 691, 122220. [Google Scholar] [CrossRef]
- Gardas, R.L.; Freire, M.G.; Carvalho, P.J.; Marrucho, I.M.; Fonseca, I.M.A.; Ferreira, A.G.M.; Coutinho, J.A.P. PρT Measurements of Imidazolium-Based Ionic Liquids. J. Chem. Eng. Data 2007, 52, 1881–1888. [Google Scholar] [CrossRef]
- Królikowska, M.; Hofman, T. Densities, Isobaric Expansivities and Isothermal Compressibilities of the Thiocyanate-Based Ionic Liquids at Temperatures (298.15–338.15 K) and Pressures up to 10 MPa. Thermochim. Acta 2012, 530, 1–6. [Google Scholar] [CrossRef]
- Boudouris, D.; Prinos, J.; Bridakis, M.; Pantoula, M.; Panayiotou, C. Measurement of HCFC-22 and HFC-152a Sorption by Polymers Using a Quartz Crystal Microbalance. Ind. Eng. Chem. Res. 2001, 40, 604–611. [Google Scholar] [CrossRef]
- Hoff, J.H. van’t XLVII. The Origin of the Theory of Solutions. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1894, 37, 475–491. [Google Scholar] [CrossRef][Green Version]
- Yoon, J.D.; Cha, S.W. Change of Glass Transition Temperature of Polymers Containing Gas. Polym. Test. 2001, 20, 287–293. [Google Scholar] [CrossRef]
- Chow, T.S. Glass Transition Temperature Of Polymer-Diluent Systems. Ferroelectrics 1980, 30, 139–145. [Google Scholar] [CrossRef]
- Harders, A.N.; Wallisch, L.; Lundin, M.D.; Le, C.; Zaher, G.; Atchison, E.; White, W.; Shiflett, M.B. Separation and Recycling of Hydrofluorocarbon Refrigerant Mixtures with Fluoropolymer-Coated Hollow Fiber Membranes. Sci. Adv. 2025, 11, eadp7414. [Google Scholar] [CrossRef] [PubMed]
- Thomas, S.; Pinnau, I.; Du, N.; Guiver, M.D. Pure- and Mixed-Gas Permeation Properties of a Microporous Spirobisindane-Based Ladder Polymer (PIM-1). J. Membr. Sci. 2009, 333, 125–131. [Google Scholar] [CrossRef]
- Starannikova, L.E.; Alentiev, A.Y.; Nikiforov, R.Y.; Ponomarev, I.I.; Blagodatskikh, I.V.; Nikolaev, A.Y.; Shantarovich, V.P.; Yampolskii, Y.P. Effects of Different Treatments of Films of PIM-1 on Its Gas Permeation Parameters and Free Volume. Polymer 2021, 212, 123271. [Google Scholar] [CrossRef]
- Pinnau, I.; He, Z. Pure- and Mixed-Gas Permeation Properties of Polydimethylsiloxane for Hydrocarbon/Methane and Hydrocarbon/Hydrogen Separation. J. Membr. Sci. 2004, 244, 227–233. [Google Scholar] [CrossRef]
- Palomar, J.; Larriba, M.; Lemus, J.; Moreno, D.; Santiago, R.; Moya, C.; de Riva, J.; Pedrosa, G. Demonstrating the Key Role of Kinetics over Thermodynamics in the Selection of Ionic Liquids for CO2 Physical Absorption. Sep. Purif. Technol. 2019, 213, 578–586. [Google Scholar] [CrossRef]
- Chen, Y.; Mutelet, F.; Jaubert, J.N. Modeling the Solubility of Carbon Dioxide in Imidazolium-Based Ionic Liquids with the PC-SAFT Equation of State. J. Phys. Chem. B 2012, 116, 14375–14388. [Google Scholar] [CrossRef]
- Paduszyński, K.; Domańska, U. Thermodynamic Modeling of Ionic Liquid Systems: Development and Detailed Overview of Novel Methodology Based on the PC-SAFT. J. Phys. Chem. B 2012, 116, 5002–5018. [Google Scholar] [CrossRef]
- Pardo, F.; Zarca, G.; Urtiaga, A. Effect of Feed Pressure and Long-Term Separation Performance of Pebax-Ionic Liquid Membranes for the Recovery of Difluoromethane (R32) from Refrigerant Mixture R410A. J. Membr. Sci. 2021, 618, 118744. [Google Scholar] [CrossRef]



| Materials | T* [K] | p* [MPa] | ρ* [g/cm3] | Reference |
|---|---|---|---|---|
| PBVE | 650 | 315 | 2.190 | [28] |
| 89PVBE-11PDD | 649 | 309 | 2.177 | This work |
| 50PBVE-50PDD | 646 | 286 | 2.132 | This work |
| 30PBVE-70PDD | 644 | 274 | 2.108 | This work |
| 5PBVE-95PDD | 642 | 258 | 2.077 | This work |
| 75PDD-25VA | 579 | 287 | 1.854 | This work |
| PDD | 632 | 274 | 2.068 | This work |
| VA | 459 | 415 | 0.955 | [88] |
| PIM-1 | 872 | 523 | 1.438 | [85] |
| PS | 750 | 360 | 1.090 | [68] |
| PMMA | 695 | 560 | 1.270 | [53] |
| PDMS | 560 | 355 | 1.200 | [61] |
| PEBAX 1657 | 664 | 684 | 1.200 | This work, pVT data from [61] |
| C2mim [BF4] | 650 | 580 | 1.385 | This work, pVT data from [89] |
| C2mim [SCN] | 700 | 540 | 1.175 | This work, pVT data from [90] |
| R32 | 339 | 633 | 1.46 | This work, VLE data from [60] |
| R125 | 324 | 342 | 1.91 | This work, VLE data from [60] |
| R134a | 349 | 460 | 1.78 | This work, VLE data from [60] |
| R152a | 360 | 495 | 1.27 | This work, VLE data from [60] |
| R-32 | R-125 | R-134a | R-152a | |||||
|---|---|---|---|---|---|---|---|---|
| kij | ksw [MPa−1] | kij | ksw [MPa−1] | kij | ksw [MPa−1] | kij | ksw [MPa−1] | |
| PBVE | 0.100 | 0.010 | 0.160 | 0.01 | - | - | - | - |
| 89PVBE-11PDD | 0.095 | 0.015 | 0.150 | 0.05 | - | - | - | - |
| 50PBVE-50PDD | 0.080 | 0.030 | 0.070 | 0.08 | - | - | - | - |
| 30PBVE-70PDD | 0.075 | 0.030 | 0.060 | 0.08 | - | - | - | - |
| 5PBVE-95PDD | 0.049 | 0.050 | 0.054 | 0.09 | - | - | - | - |
| 75PDD-25VA | 0.057 | 0.058 | 0.051 | 0.110 | 0.071 | 0.250 | - | - |
| PIM-1 * | 0.06 | 0.09 | 0.080 | 0.20 | - | - | - | - |
| PS | - | - | - | - | - | - | −7.8 × 10−4 T + 0.29 | −9.9 × 10−5 T + 0.12 |
| PMMA | - | - | - | - | - | - | −5.7 × 10−4 T + 0.21 | −2.5 × 10−3 T + 1.03 |
| PDMS | 0.040 | (0.020) # | 0.055 | (0.070) # | - | - | - | - |
| PEBAX1657 * | 0.048 | (0.120) # | - | - | −0.002 | (0.200) # | - | - |
| Materials | 30%PBVE-70%PDD | PIM-1 | ||
|---|---|---|---|---|
| R-32 | R-125 | R-32 | R-125 | |
| L∞ [cm2/s] | 7.7 × 10−8 | 2.5 × 10−9 | 3.0 × 10−8 | 3.5 × 10−10 |
| β | 21 | 24 | 19 | 25.5 |
| Materials | Pebax 1657 | Pebax + 40 wt.% [C2mim][BF4] | Pebax + 40 wt.% [C2mim][SCN] | |||
|---|---|---|---|---|---|---|
| R-32 | R-134a | R-32 | R-134a | R-32 | R-134a | |
| kij | 0.048 | −0.002 | 0.001 | 0.008 | 0.02 | 0.038 |
| L∞ [cm2/s] | 2.3 × 10−7 | 7.5 × 10−8 | 3.0 × 10−7 | 1.0 × 10−7 | 4.0 × 10−7 | 1.5 × 10−7 |
| β | 23 | 20 | 25 | 22 | 26 | 28 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Minelli, M.; Giacinti Baschetti, M.; Signorini, V. Description of Gas Transport in Polymers: Integrated Thermodynamic and Transport Modeling of Refrigerant Gases in Polymeric Membranes. Polymers 2025, 17, 2169. https://doi.org/10.3390/polym17162169
Minelli M, Giacinti Baschetti M, Signorini V. Description of Gas Transport in Polymers: Integrated Thermodynamic and Transport Modeling of Refrigerant Gases in Polymeric Membranes. Polymers. 2025; 17(16):2169. https://doi.org/10.3390/polym17162169
Chicago/Turabian StyleMinelli, Matteo, Marco Giacinti Baschetti, and Virginia Signorini. 2025. "Description of Gas Transport in Polymers: Integrated Thermodynamic and Transport Modeling of Refrigerant Gases in Polymeric Membranes" Polymers 17, no. 16: 2169. https://doi.org/10.3390/polym17162169
APA StyleMinelli, M., Giacinti Baschetti, M., & Signorini, V. (2025). Description of Gas Transport in Polymers: Integrated Thermodynamic and Transport Modeling of Refrigerant Gases in Polymeric Membranes. Polymers, 17(16), 2169. https://doi.org/10.3390/polym17162169









