Microscale Flow Simulation of Resin in RTM Process for Optical Fiber-Embedded Composites
Abstract
1. Introduction
2. Steady-State Analysis
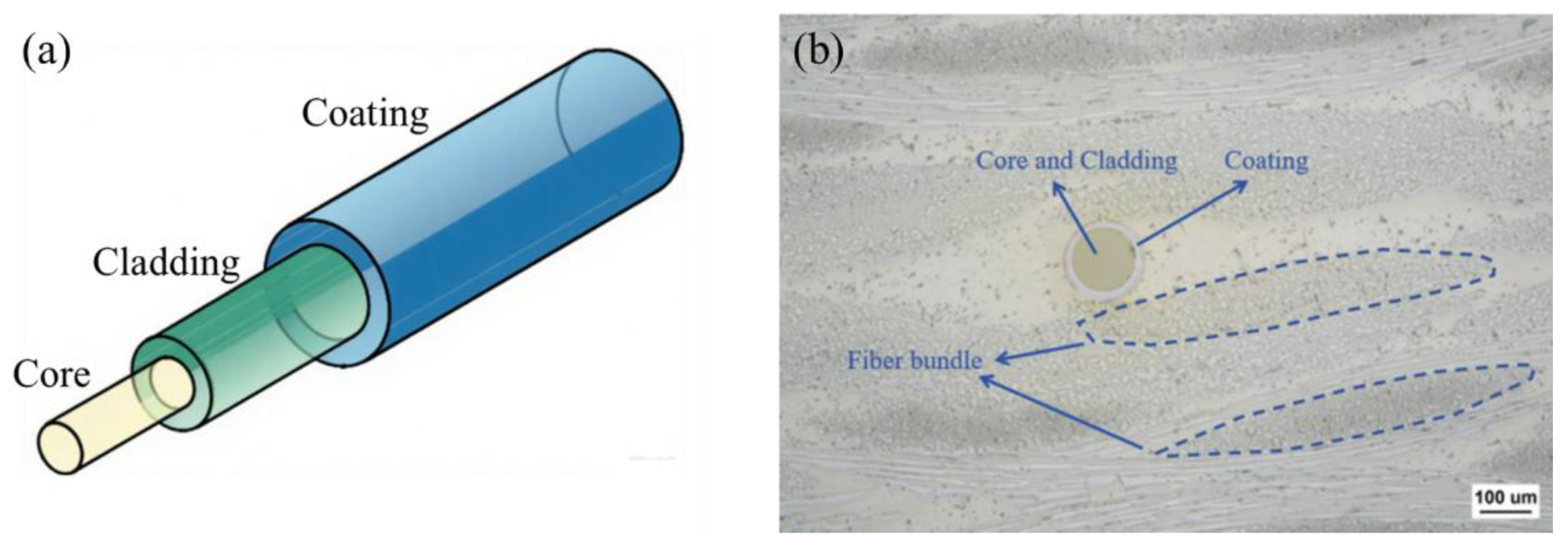
2.1. Model Establishment
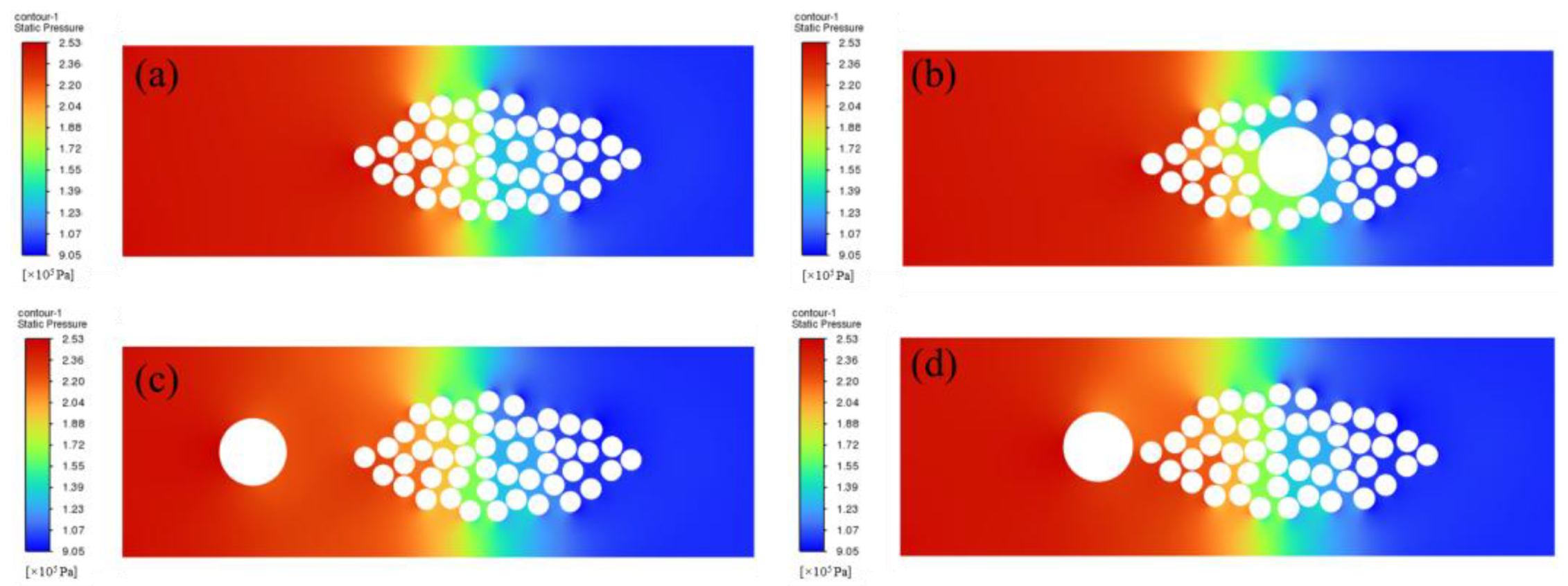
2.2. Calculation Results and Analysis
3. Transient-State Analysis
3.1. Transient Model
3.2. Grid Independence Verification
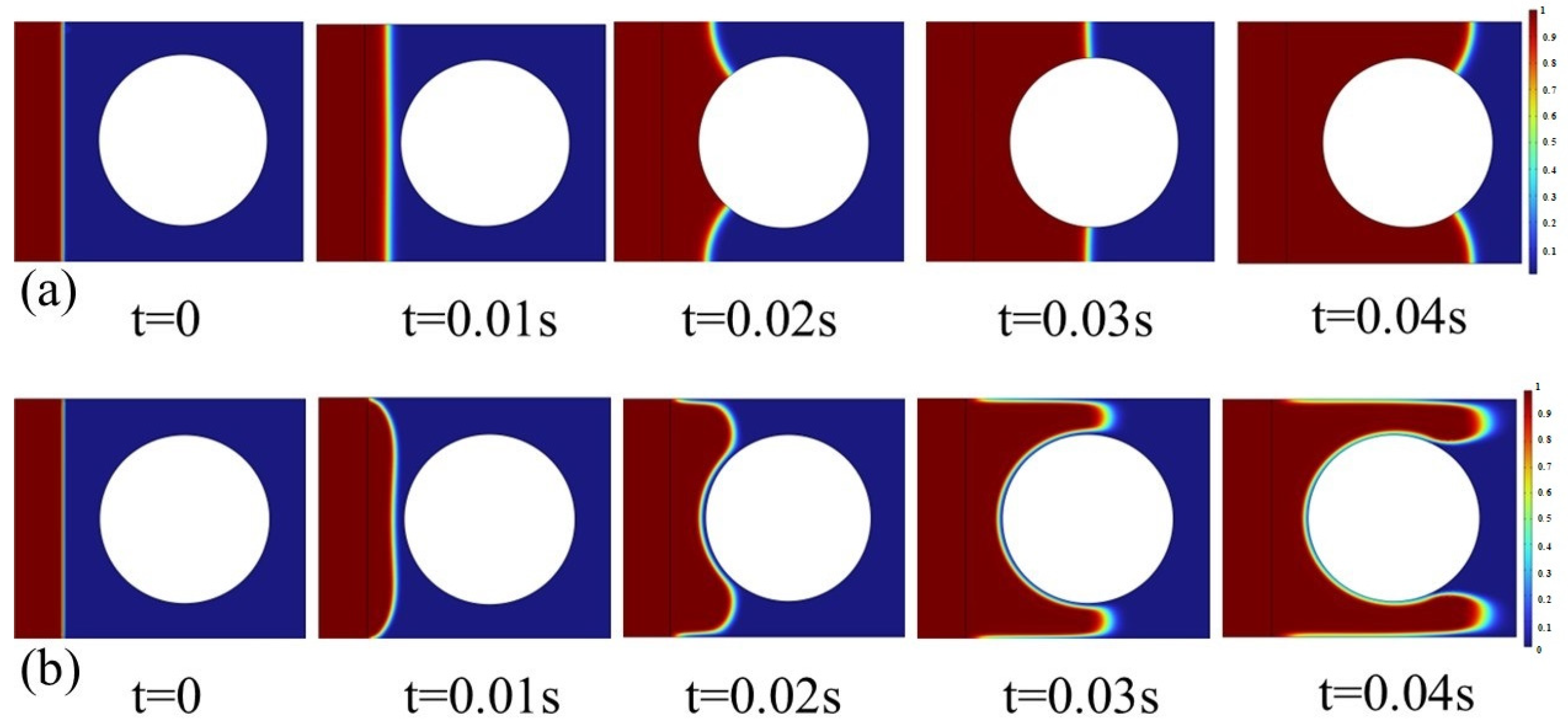
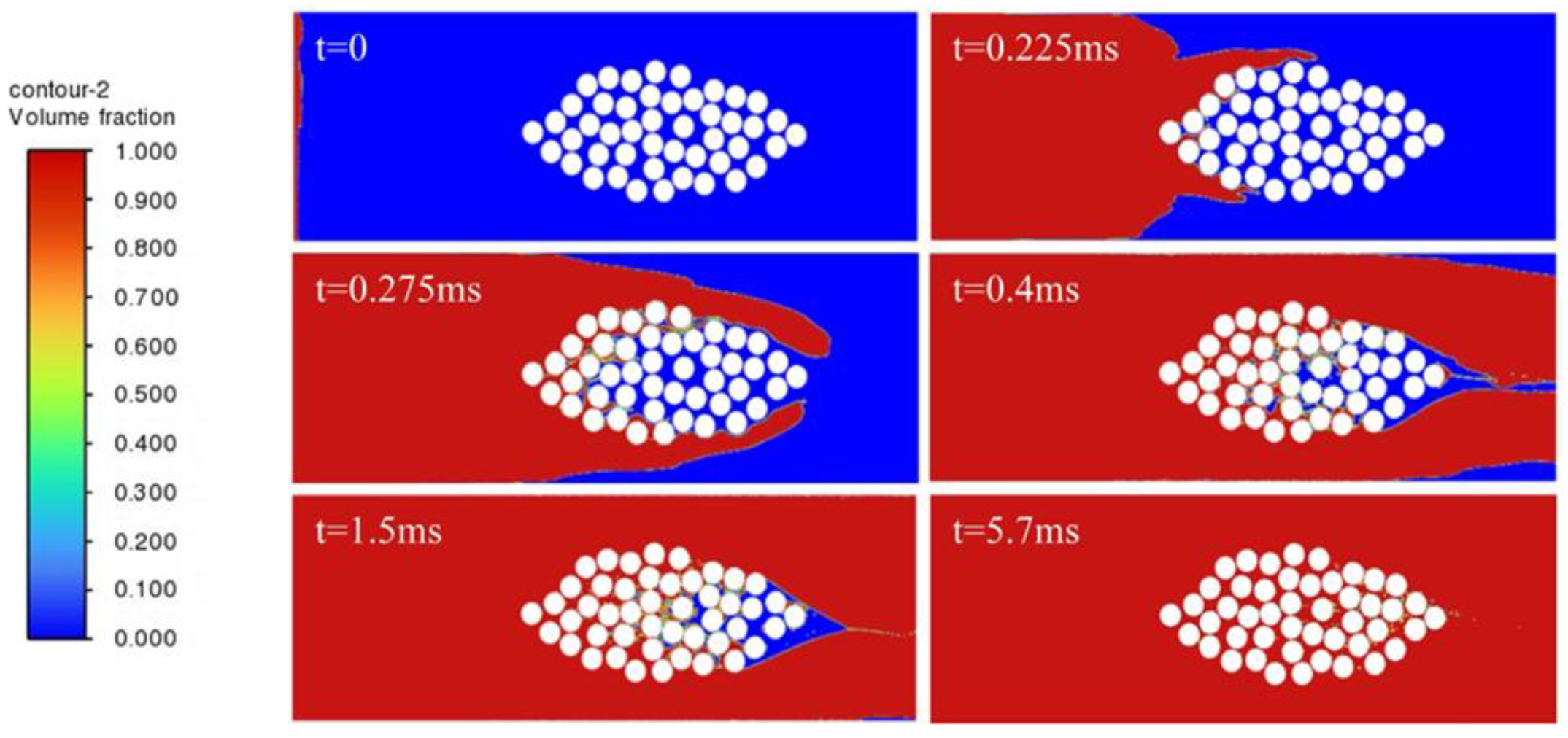
3.3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Li, C.; Cantarel, A.; Gong, X. Influence of structural parameters at microscale on the fiber reinforcement. J. Compos. Mater. 2019, 53, 863–872. [Google Scholar] [CrossRef]
- Kong, L.; Zuo, X.; Zhu, S.; Li, Z.; Shi, J.; Li, L.; Feng, Z.; Zhang, D.; Deng, D.; Yu, J. Novel carbon-poly (silacetylene) composites as advanced thermal protection material in aerospace applications. Compos. Sci. Technol. 2018, 162, 163–169. [Google Scholar] [CrossRef]
- Kim, J.I.; Hwang, Y.T.; Choi, K.H.; Kim, H.-J.; Kim, H.-S. Prediction of the vacuum assisted resin transfer molding (VARTM) process considering the directional permeability of sheared woven fabric. Compos. Struct. 2019, 211, 236–243. [Google Scholar] [CrossRef]
- Magagnato, D.; Seuffert, J.; Bernath, A.; Kärger, L.; Henning, F. Experimental and numerical study of the influence of integrated load transmission elements on filling behavior in resin transfer molding. Compos. Struct. 2018, 198, 135–143. [Google Scholar] [CrossRef]
- Aziz, A.R.; Ali, M.A.; Zeng, X.; Umer, R.; Schubel, P.; Cantwell, W. Transverse permeability of dry fiber preforms manufactured by automated fiber placement. Compos. Sci. Technol. 2017, 152, 57–67. [Google Scholar] [CrossRef]
- Amirkhosravi, M.; Pishvar, M.; Altan, M.C. Fabricating high-quality VARTM laminates by magnetic consolidation: Experiments and process model. Compos. Part A Appl. Sci. Manuf. 2018, 114, 398–406. [Google Scholar] [CrossRef]
- Zhang, K.; Gu, Y.; Li, M.; Wang, S.; Zhang, Z. Effects of curing time and de-molding temperature on the deformation of glass fiber/epoxy resin prepreg laminates fabricated by rapid hot press. Polym. Polym. Compos. 2019, 27, 301–313. [Google Scholar] [CrossRef]
- Yang, H.; Zhou, Z.; Ou, J. A novel smart steel strand based on optical-electrical co-sensing for full-process and full-scale monitoring of prestressing concrete structures. Int. J. Smart Nano Mater. 2023, 14, 337–368. [Google Scholar] [CrossRef]
- Lau, K.T. Structural health monitoring for smart composites using embedded FBG sensor technology. Mater. Sci. Technol. 2014, 30, 1642–1654. [Google Scholar] [CrossRef]
- Kim, P.J. Surface quality and shrinkage of the composite bus housing panel manufactured by RTM. Compos. Struct. 2002, 57, 211–220. [Google Scholar] [CrossRef]
- Johnson, R.J.; Pitchumani, R. Flow control using localized induction heating in a VARTM process. Compos. Sci. Technol. 2007, 67, 669–684. [Google Scholar] [CrossRef]
- Bertling, D.; Kaps, R.; Mulugeta, E. Analysis of dry-spot behavior in the pressure field of a liquid composite molding process. CEAS Aeronaut. J. 2016, 7, 577–585. [Google Scholar] [CrossRef]
- Han, K.; Lee, L.J. Dry spot formation and changes in liquid composite molding: I—Experimental. J. Compos. Mater. 1996, 30, 1458–1474. [Google Scholar] [CrossRef]
- Han, K.; Lee, L.J.; Nakamura, S.; Shafi, A.; White, D. Dry spot formation and changes in liquid composite molding: II—Modeling and simulation. J. Compos. Mater. 1996, 30, 1475–1493. [Google Scholar] [CrossRef]
- Chen, X.; Papathanasiou, T.D. Micro-scale modeling of axial flow through unidirectional disordered fiber arrays. Compos. Sci. Technol. 2007, 67, 1286–1293. [Google Scholar] [CrossRef]
- Chen, X.; Papathanasiou, T.D. The transverse permeability of disordered fiber arrays: A statistical correlation in terms of the mean nearest interfiber spacing. Transp. Porous Media 2008, 71, 233–251. [Google Scholar] [CrossRef]
- Hiremath, P.; Ambiger, K.D.; Jayashree, P.K.; Heckadka, S.S.; Deepak, G.D.; Murthy, B.R.N.; Kowshik, S.; Naik, N. Computational Approach for Optimizing Resin Flow Behavior in Resin Transfer Molding with Variations in Injection Pressure, Fiber Permeability, and Resin Sorption. J. Compos. Sci. 2025, 9, 129. [Google Scholar] [CrossRef]
- Bechtold, G.; Ye, L. Influence of fibre distribution on the transverse flow permeability in fibre bundles. Compos. Sci. Technol. 2003, 63, 2069–2079. [Google Scholar] [CrossRef]
- Yang, B.; Jin, T. Micro-geometry modeling based on monte carlo and permeability prediction of yarn. Polym. Polym. Compos. 2014, 22, 253–260. [Google Scholar] [CrossRef]
- Dong, S.; Liu, G.; Jia, Y.; Li, W.D.; Jiao, X.J. Study on correlation between permeability and structural parameters of non-crimped fabrics. J. Compos. Mater. 2016, 50, 2661–2668. [Google Scholar] [CrossRef]
- Tan, H.; Pillai, K.M. Multiscale modeling of unsaturated flow of dual-scale fiber preform in liquid composite molding II: Non-isothermal flows. Compos. Part A Appl. Sci. Manuf. 2012, 43, 14–28. [Google Scholar] [CrossRef]
- Xiao, Y.; Xu, J.; Wang, M.; Wang, B.; Yuan, S.; Yang, C. Multiscale model of the RTM process: From mesoscale anisotropic permeability of woven structures to macroscale resin impregnation. Ind. Eng. Chem. Res. 2021, 60, 8269–8279. [Google Scholar] [CrossRef]
- Meghdadi Isfahani, A.H. Parametric study of rarefaction effects on micro-and nanoscale thermal flows in porous structures. J. Heat Transf. 2017, 139, 092601. [Google Scholar] [CrossRef]
- Chui, W.K.; Glimm, J.; Tangerman, F.M.; Jardine, A.P.; Madsen, J.S.; Donnellan, T.M.; Leek, R. Case study from industry: Process modeling in resin transfer molding as a method to enhance product quality. SIAM Rev. 1997, 39, 714–727. [Google Scholar] [CrossRef]
- Park, C.H.; Lebel, A.; Saouab, A.; Bréard, J.; Lee, W.I. Modeling and simulation of voids and saturation in liquid composite molding processes. Compos. Part A Appl. Sci. Manuf. 2011, 42, 658–668. [Google Scholar] [CrossRef]
- Madsen, B.; Lilholt, H. Physical and mechanical properties of unidirectional plant fibre composites—An evaluation of the influence of porosity. Compos. Sci. Technol. 2003, 63, 1265–1272. [Google Scholar] [CrossRef]
- Liu, Y.N.; Yuan, C.; Liu, C.; Pan, J.; Dong, Q. Study on the resin infusion process based on automated fiber placement fabricated dry fiber preform. Sci. Rep. 2019, 9, 7440. [Google Scholar] [CrossRef]
- Gebart, B.R. Permeability of unidirectional reinforcements for RTM. J. Compos. Mater. 1992, 26, 1100–1133. [Google Scholar] [CrossRef]
- Li, C.; Cantarel, A.; Gong, X. A study on resin infusion and effects of reinforcement structure at dual scales by a quasi-realistic numerical simulation method. J. Compos. Mater. 2020, 54, 4157–4171. [Google Scholar] [CrossRef]
- Nam, B.W.; Hong, S.Y.; Sung, H.G. Numerical Simulation of Diffracted Wave by a Vertical Cylinder Using VOF Method. In Proceedings of the ISOPE International Ocean and Polar Engineering Conference, Beijing, China, 20–25 June 2010. [Google Scholar]
- Gueyffier, D.; Li, J.; Nadim, A.; Scardovelli, R.; Zaleski, S. Volume-of-fluid interface tracking with smoothed surface stress methods for three-dimensional flows. J. Comput. Phys. 1999, 152, 423–456. [Google Scholar] [CrossRef]










Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, T.; Ruan, B.; Wu, Z.; Yang, L. Microscale Flow Simulation of Resin in RTM Process for Optical Fiber-Embedded Composites. Polymers 2025, 17, 2076. https://doi.org/10.3390/polym17152076
Lu T, Ruan B, Wu Z, Yang L. Microscale Flow Simulation of Resin in RTM Process for Optical Fiber-Embedded Composites. Polymers. 2025; 17(15):2076. https://doi.org/10.3390/polym17152076
Chicago/Turabian StyleLu, Tianyou, Bo Ruan, Zhanjun Wu, and Lei Yang. 2025. "Microscale Flow Simulation of Resin in RTM Process for Optical Fiber-Embedded Composites" Polymers 17, no. 15: 2076. https://doi.org/10.3390/polym17152076
APA StyleLu, T., Ruan, B., Wu, Z., & Yang, L. (2025). Microscale Flow Simulation of Resin in RTM Process for Optical Fiber-Embedded Composites. Polymers, 17(15), 2076. https://doi.org/10.3390/polym17152076







