Temperature/Stress-Dependent Fractional Creep Models of Thermoplastic Polymers
Abstract
1. Introduction
2. Fractional Creep Model
2.1. Temperature/Stress-Dependent Fractional Creep/Creep–Recovery Model
2.2. Temperature/Stress-Dependent Fractional Accelerated Creep Damage Model
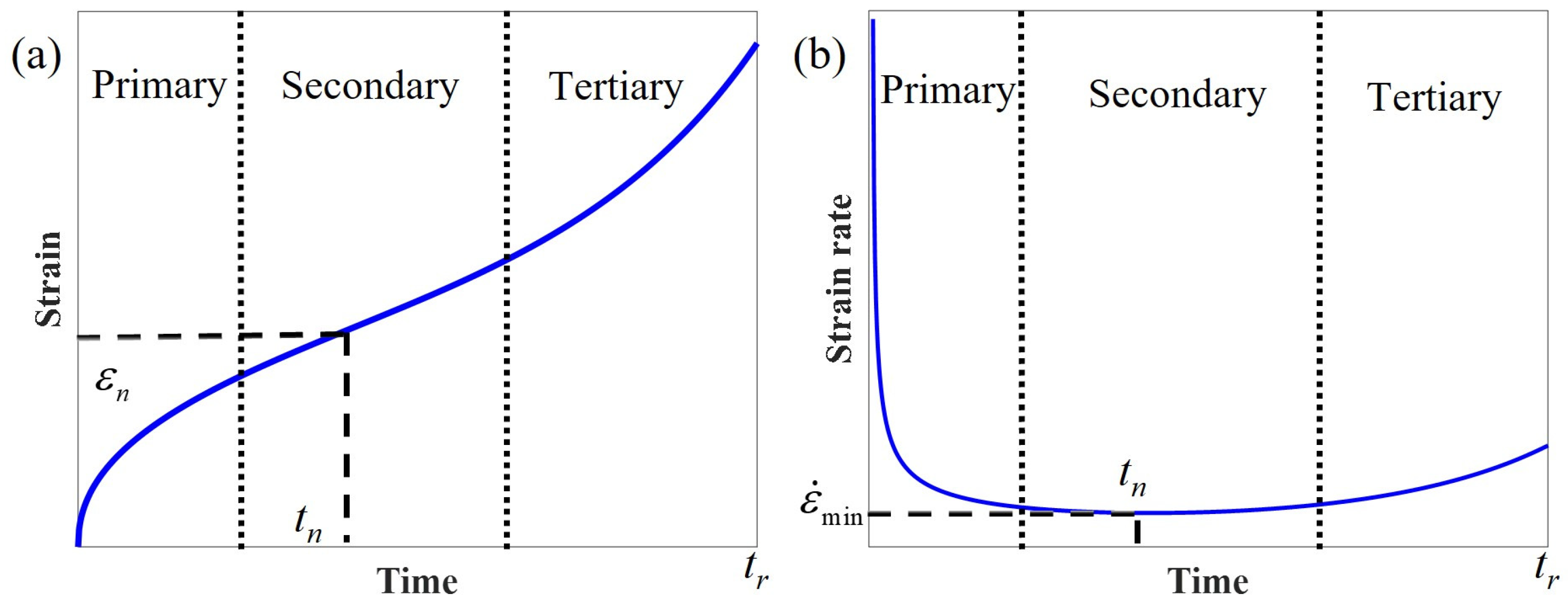
3. Application of Fractional Creep–Recovery Model
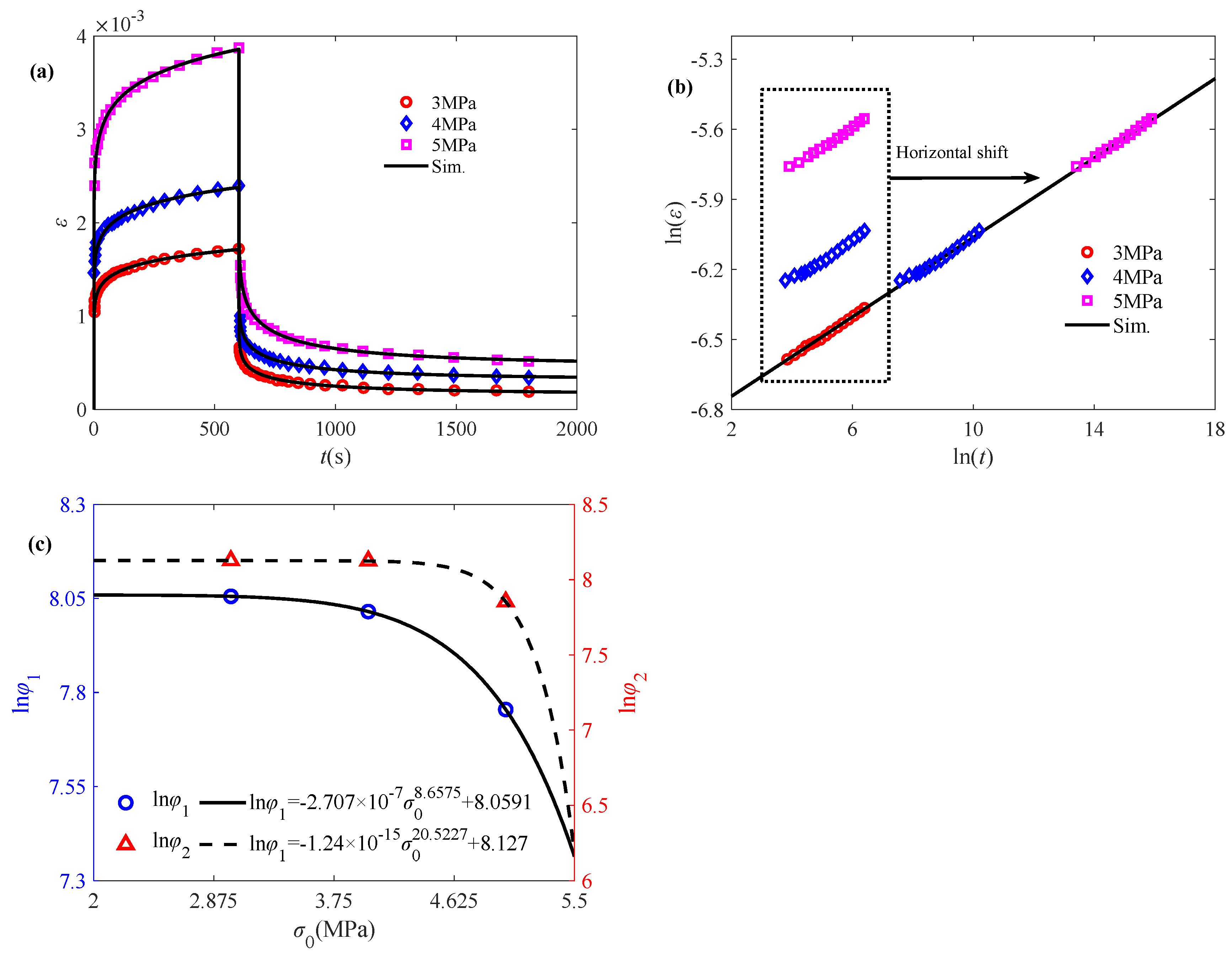
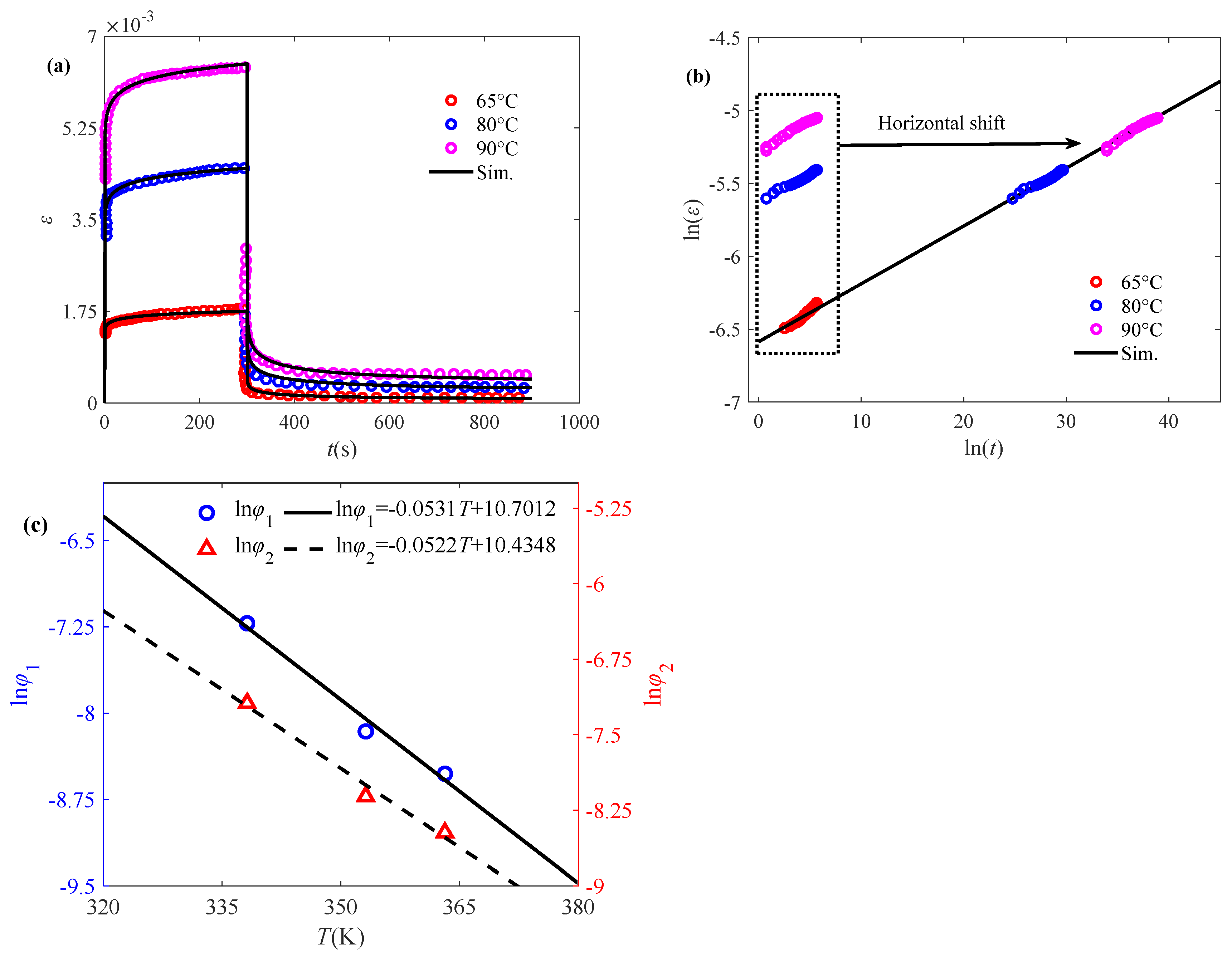
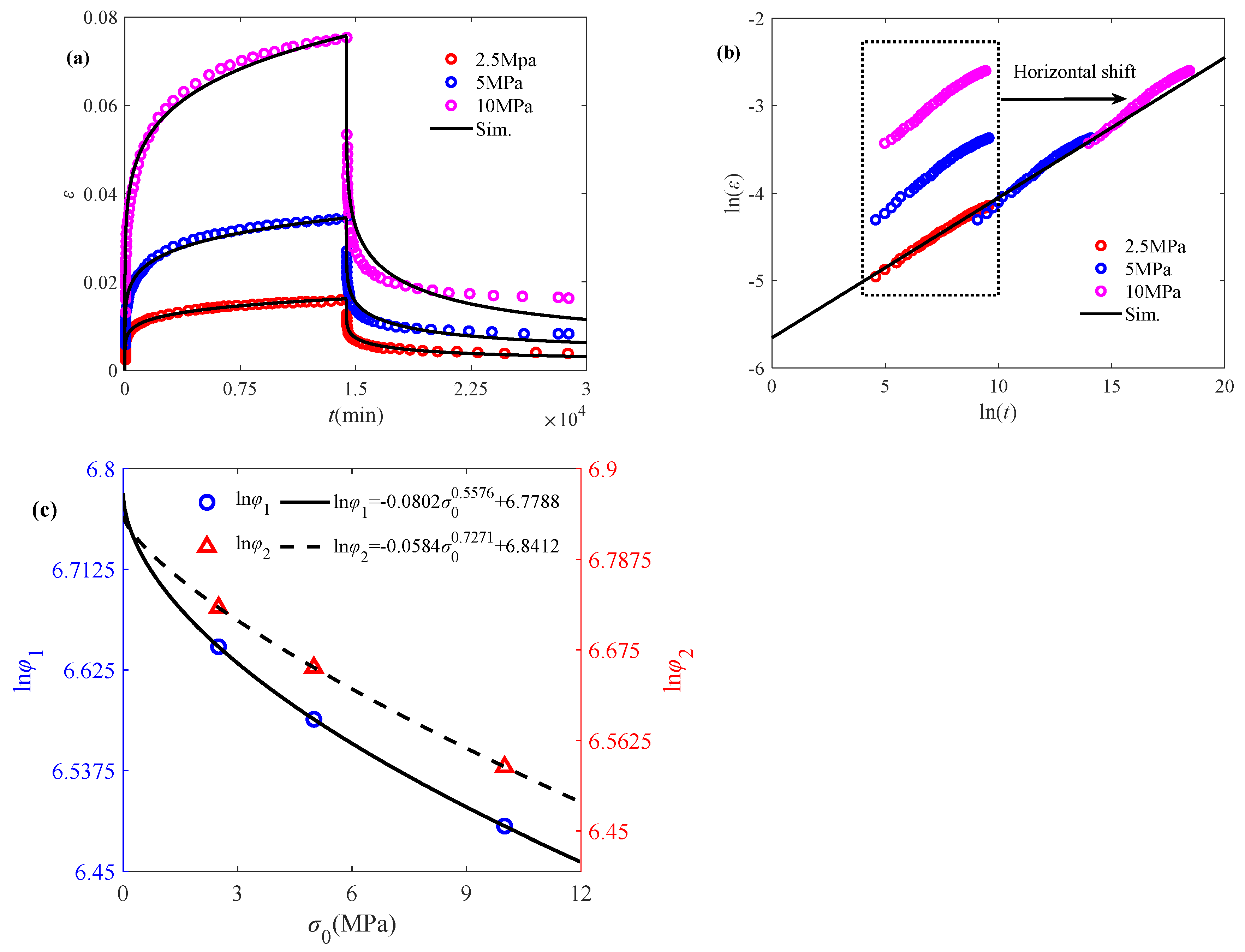
3.1. Modeling Creep/Creep-Recovery Behaviors Affected by Temperature and Initial Stress
3.2. Validation of the Proposed Model
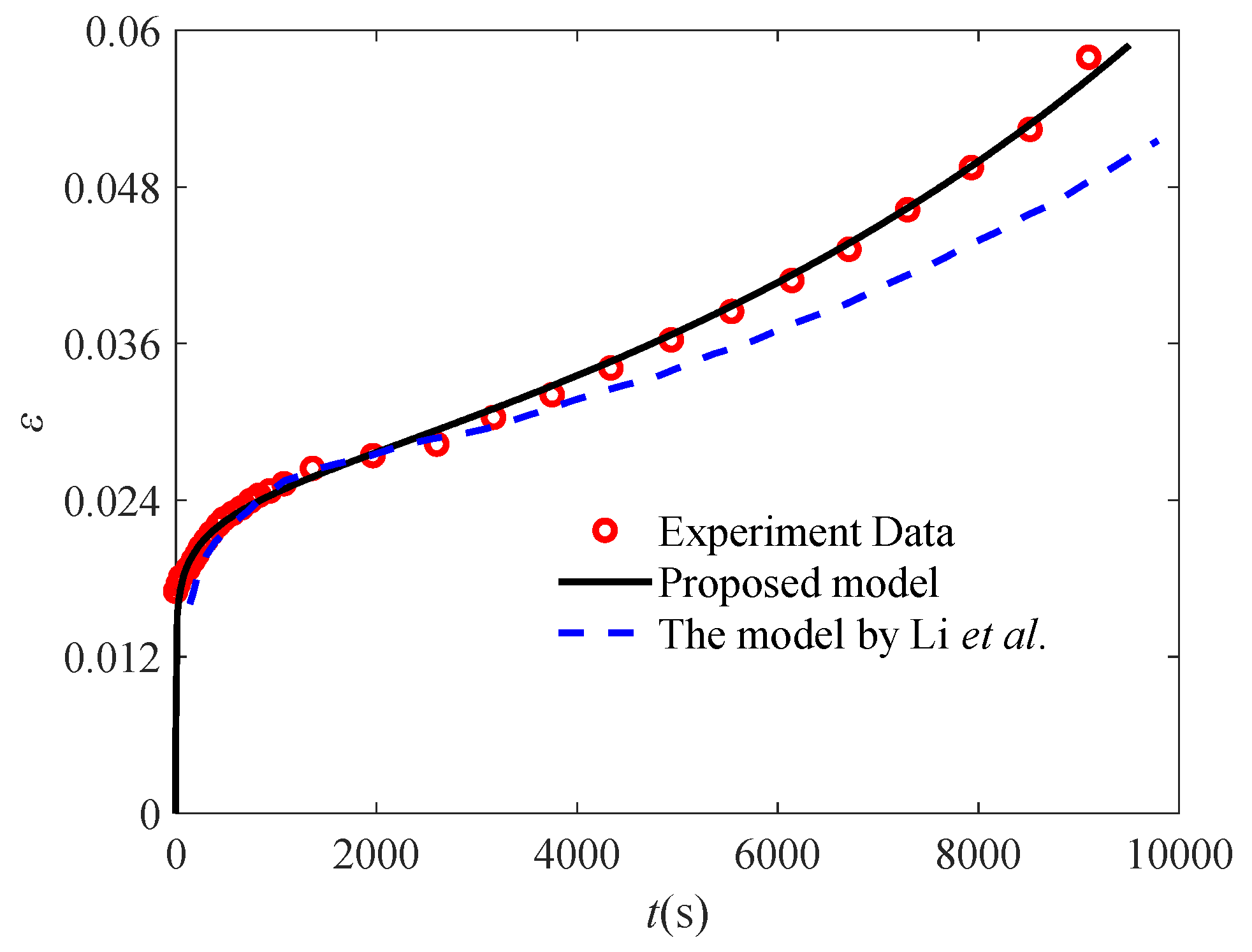
3.3. Model Comparison
4. Fractional Accelerated Creep Damage Model
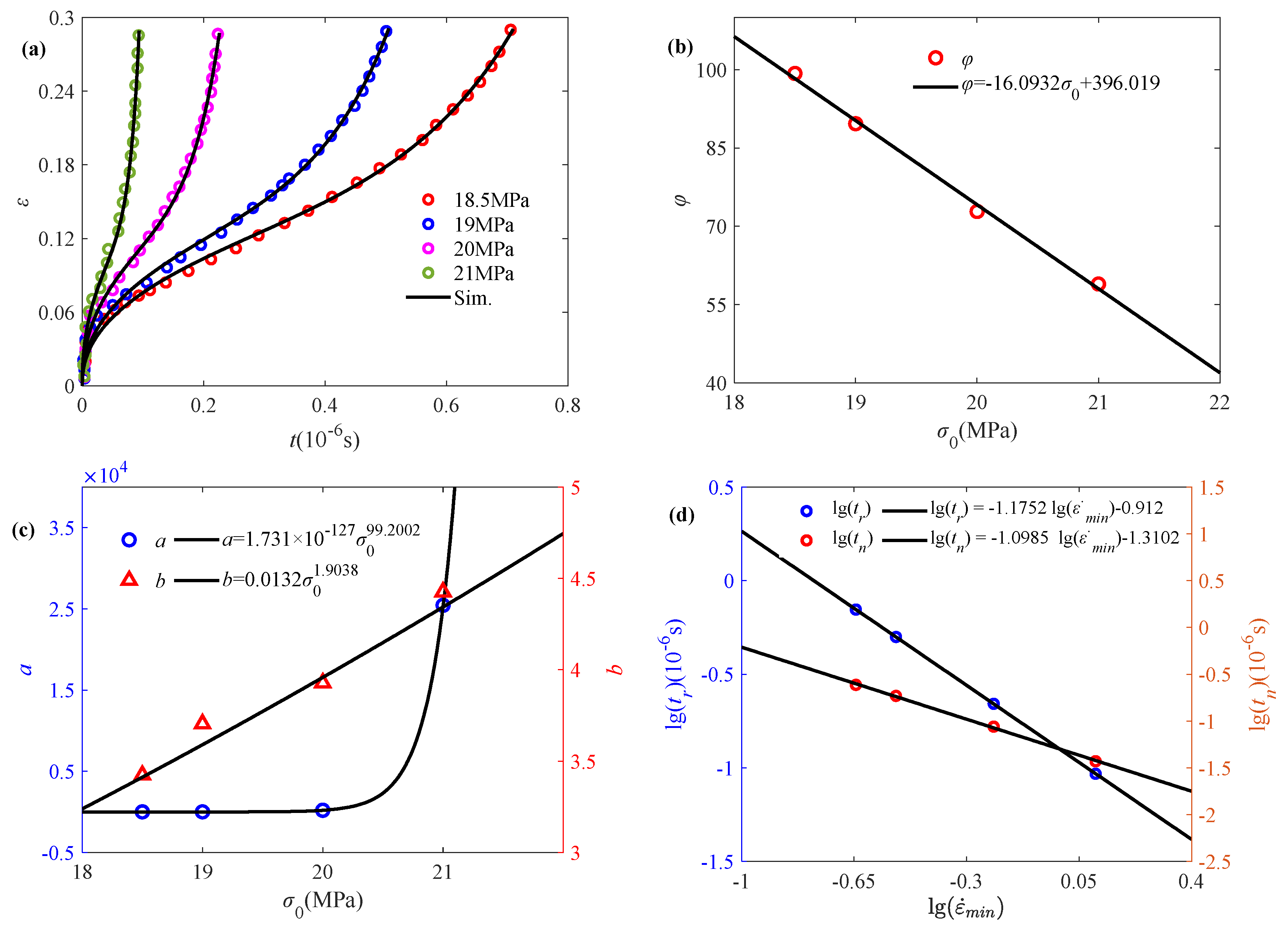
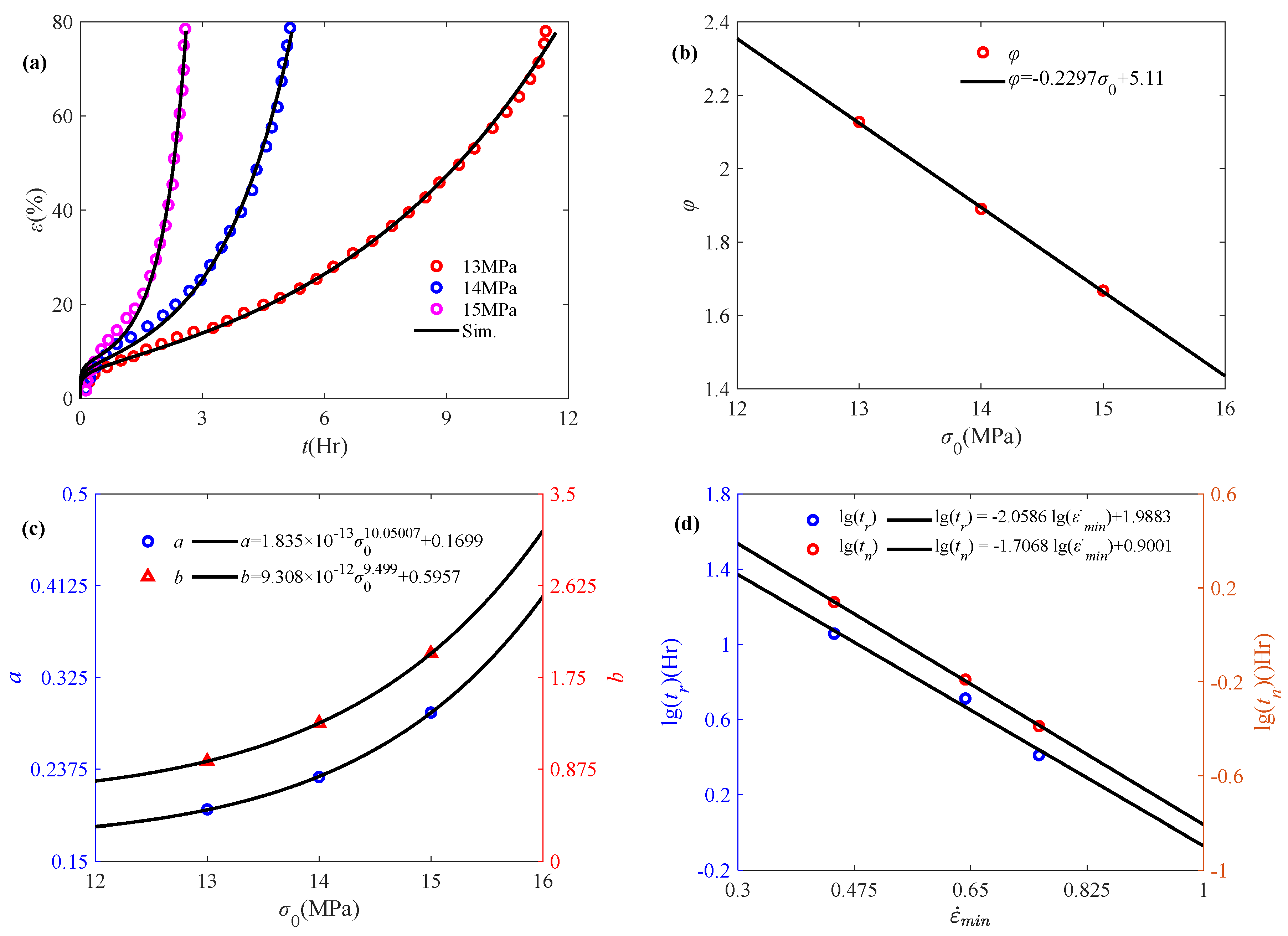
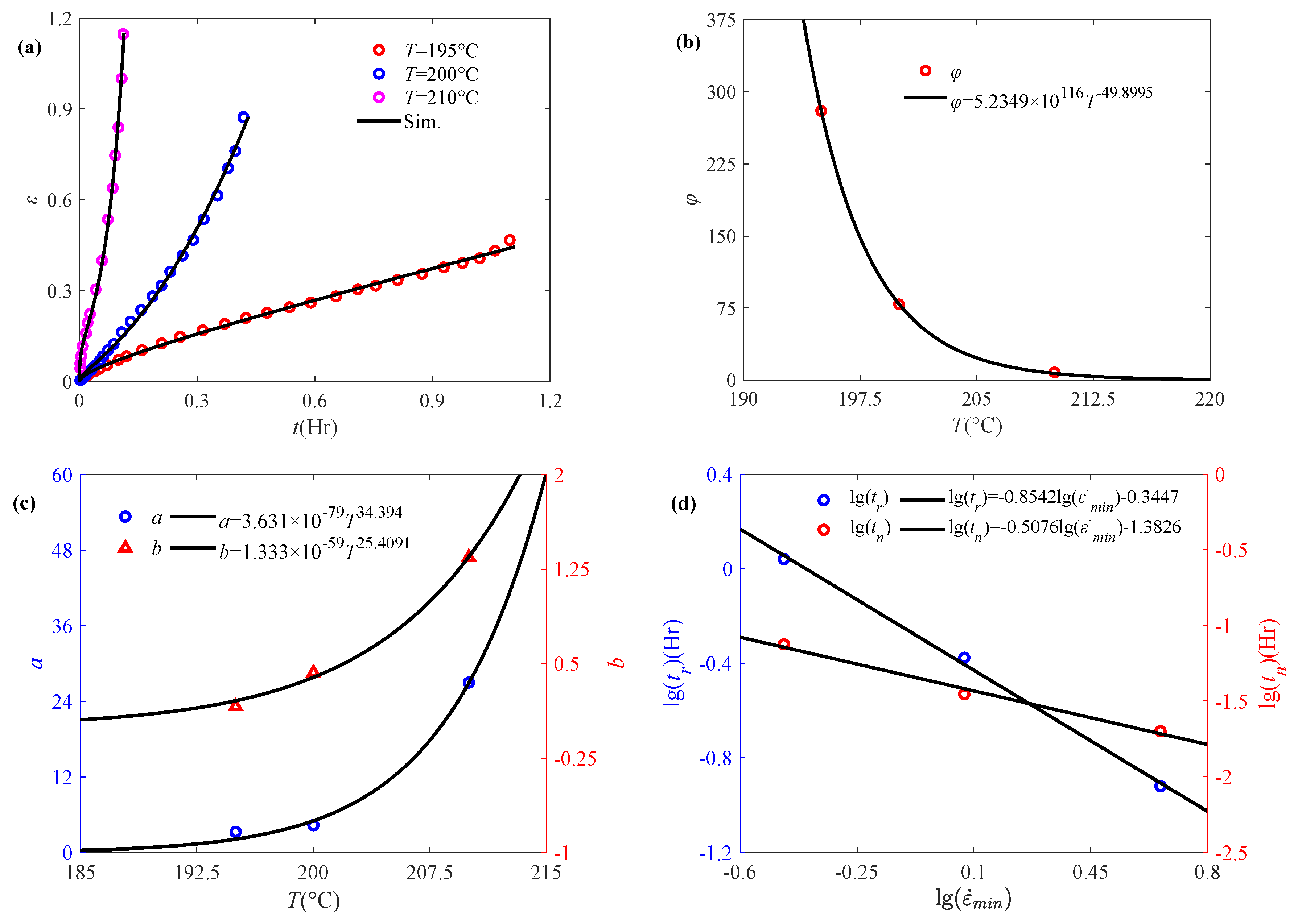
4.1. Application of Accelerated Creep Damage Model
4.2. Validation of the Proposed Model
4.3. Model Comparison
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Charitidis, C.; Sebastiani, M.; Goldbeck, G. Fostering research and innovation in materials manufacturing for industry 5.0: The key role of domain intertwining between materials characterization, modelling and data science. Mater. Design 2022, 223, 111229. [Google Scholar] [CrossRef]
- Lazaridou, A.; Duta, D.; Papageorgiou, M.; Belc, N.; Biliaderis, C.G. Effects of hydrocolloids on dough rheology and bread quality parameters in gluten-free formulations. J. Food Eng. 2007, 79, 1033–1047. [Google Scholar] [CrossRef]
- Siengchin, S.; Rungsardthong, V. Hdpe reinforced with nanoparticle, natural and animal fibers: Morphology, thermal, mechanical, stress relaxation, water absorption and impact properties. J. Thermoplast. Compos. 2013, 26, 1025–1040. [Google Scholar] [CrossRef]
- Xu, Y.J.; Wu, Q.L.; Lei, Y.; Yao, F. Creep behavior of bagasse fiber reinforced polymer composites. Bioresource technol. 2010, 101, 3280–3286. [Google Scholar] [CrossRef] [PubMed]
- Siengchin, S.; Dangtungee, R. Polyethylene and polypropylene hybrid composites based on nano silicon dioxide and different flax structures. J. Thermoplast. Compos. 2014, 27, 1428–1447. [Google Scholar] [CrossRef]
- Pedrazzoli, D.; Pegoretti, A. Long-term creep behavior of polypropylene/fumed silica nanocomposites estimated by time-temperature and time-strain superposition approaches. Polym. Bull. 2014, 71, 2247–2268. [Google Scholar] [CrossRef]
- Mishnev, M.; Korolev, A.; Zadorin, A. Effect of thermal aging on viscoelastic behavior of thermosetting polymers under mechanical and cyclic temperature impact. Polymers 2024, 16, 391. [Google Scholar] [CrossRef] [PubMed]
- Qiu, J.F.; Ma, S.Q.; Wang, S.; Tang, Z.B.; Li, Q.; Tian, A.P.; Xu, X.W.; Wang, B.B.; Lu, N.; Zhu, J. Upcycling of polyethylene terephthalate to continuously reprocessable vitrimers through reactive extrusion. Macromolecules 2021, 54, 703–712. [Google Scholar] [CrossRef]
- Gao, Y.F.; Zhao, B.; Yin, D.S.; Yuan, L.L. A general fractional model of creep response for polymer materials: Simulation and model comparison. J. Appl. Polym. Sci. 2022, 139, 51577. [Google Scholar] [CrossRef]
- Grelle, T.; Wolff, D.; Jaunich, M. Temperature-dependent leak tightness of elastomer seals after partial and rapid. release of compression. Polym. Test. 2015, 48, 44–49. [Google Scholar] [CrossRef]
- Grelle, T.; Wolff, D.; Jaunich, M. Leakage behaviour of elastomer seals under dynamic unloading conditions at low temperatures. Polym. Test. 2017, 58, 219–226. [Google Scholar] [CrossRef]
- Morra, P.V.; Radelaar, S.; Yandouzi, M.; Chen, J.; Bottger, A.J. Precipitate coarsening-induced plasticity: Low temperature creep behaviour of tempered sae 52100. Int. J. Plasticity 2009, 25, 2331–2348. [Google Scholar] [CrossRef]
- Holzapfel, G.A.; Gasser, T.C. A viscoelastic model for fiber-reinforced composites at finite strains: Continuum basis, computational aspects and applications. Comput. Methods Appl. Mech. Eng. 2001, 190, 4379–4403. [Google Scholar] [CrossRef]
- Lai, J.; Bakker, A. Analysis of the non-linear creep of high-density polyethylene. Polymer 1995, 36, 93–99. [Google Scholar] [CrossRef]
- Drozdov, A.; Lejre, A.-L.H.; Christiansen, J.D. Viscoelasticity, viscoplasticity, and creep failure of polypropylene/clay nanocomposites. Compos. Sci. Technol. 2009, 69, 2596–2603. [Google Scholar] [CrossRef]
- Medvedev, G.A.; Caruthers, J.M. Stochastic model prediction of nonlinear creep in glassy polymers. Polymer 2015, 74, 235–253. [Google Scholar] [CrossRef]
- Wang, X.; Pan, Y.; Qin, Y.; Voigt, M.; Liu, X.; Zheng, G.; Chen, Q.; Schubert, D.W.; Liu, C.; Shen, C. Creep and recovery behavior of injection-molded isotactic polypropylene with controllable skin-core structure. Polym. Test. 2018, 69, 478–484. [Google Scholar] [CrossRef]
- Wu, C.; Wu, R.; Tam, L.-H. The creep behavior of semicrystalline carbon nanotube/polypropylene nanocomposite: A coarse-grained molecular study. Polym. Degrad. Stab. 2022, 196, 109834. [Google Scholar] [CrossRef]
- Jorik, S.; Lion, A.; Johlitz, M. Design of the novel tensile creep experimental setup, characterisation and description of the long-term creep performance of polycarbonate. Polym. Test. 2019, 75, 151–158. [Google Scholar] [CrossRef]
- Smit, W.; de Vries, H. Rheological models containing fractional derivatives. Rheol. Acta 1970, 9, 525–534. [Google Scholar] [CrossRef]
- Cai, W.; Wang, Z.; Wang, F. Temperature and strain-rate dependent fractional constitutive model for glassy polymers. Chaos, Solitons Fractals 2024, 185, 115116. [Google Scholar] [CrossRef]
- Cai, W.; Wang, P. Fractional modeling of temperature-dependent mechanical behaviors for glassy polymers. Int. J. Mech. Sci. 2022, 232, 107607. [Google Scholar] [CrossRef]
- Ribeiro, J.G.T.; de Castro, J.T.P.; Meggiolaro, M.A. Modeling concrete and polymer creep using fractional calculus. J. Mater. Res. Technol. 2021, 12, 1184–1193. [Google Scholar] [CrossRef]
- Di Paola, M.; Pirrotta, A.; Valenza, A. Visco-elastic behavior through fractional calculus: An easier method for best fitting experimental results. Mech. Mater. 2011, 43, 799–806. [Google Scholar] [CrossRef]
- Cai, W.; Wang, P.; Zhang, Y. Fractional-order model for temperature-dependent rheological behaviors of polymeric materials. Mech. Adv. Mater. Struct. 2023, 31, 4069–4080. [Google Scholar] [CrossRef]
- Cai, W.; Liu, C.; Zhang, Y. Fractional damage model of cyclic behaviors for nano-silver paste. Eur. J. Mech. A/Solids 2024, 107, 105370. [Google Scholar] [CrossRef]
- Cai, W.; Wang, P.; Fan, J. A variable-order fractional model of tensile and shear behaviors for sintered nano-silver paste used in high power electronics. Mech. Mater. 2020, 145, 103391. [Google Scholar] [CrossRef]
- Lorenzo, C.F.; Hartley, T.T. Variable order and distributed order fractional operators. Nonlinear Dyn. 2002, 29, 57–98. [Google Scholar] [CrossRef]
- Brito-Oliveira, T.C.; Moraes, I.C.; Pinho, S.C.; Campanella, O.H. Modeling creep/recovery behavior of cold-set gels using different approaches. Food Hydrocoll. 2022, 123, 107183. [Google Scholar] [CrossRef]
- Yu, P.; Yao, X.; Han, Q.; Zang, S.; Gu, Y. A visco-elastoplastic constitutive model for large deformation response of polycarbonate over a wide range of strain rates and temperatures. Polymer 2014, 55, 6577–6593. [Google Scholar] [CrossRef]
- Aniskevich, K.; Starkova, O. Evaluation of the viscoplastic strain of high-density polyethylene/multiwall carbon nanotube composites using the reaction rate relation. Mech. Compos. Mater. 2021, 57, 577–586. [Google Scholar] [CrossRef]
- Duan, X.; Yuan, H.; Tang, W.; He, J.; Guan, X. A phenomenological primary–secondary–tertiary creep model for polymer-bonded composite materials. Polymers 2021, 13, 2353. [Google Scholar] [CrossRef] [PubMed]
- Lemaitre, J. Evaluation of dissipation and damage in metals submitted to dynamic loading. In Proceedings of the International Conference of Mechanical Behavior of Materials, Kyoto, Japan, 15–20 August 1971. [Google Scholar]
- Li, Y.; Sun, X.; Zhang, S.; Han, S. A fractal crazing constitutive model of glassy polymers considering damage and toughening. Eng. Fract. Mech. 2022, 267, 108354. [Google Scholar] [CrossRef]
- Izer, A.; Barany, T. Effect of consolidation on the flexural creep behaviour of all-polypropylene composite. Express Polym. Lett. 2010, 4, 210–216. [Google Scholar] [CrossRef]
- Tanaka, Y.; Kashiwabara, S.; Okuya, Y. Time-temperature superposition in the enthalpy relaxation study of polystyrene. Polym. Eng. Sci. 2016, 56, 561–565. [Google Scholar] [CrossRef]
- Di Lorenzo, S.; Di Paola, M.; La Mantia, F.P.; Pirrotta, A. Non-linear viscoelastic behavior of polymer melts interpreted by fractional viscoelastic model. Meccanica 2016, 52, 1843–1850. [Google Scholar] [CrossRef]
- Kodaira, Y.; Takano, Y.; Yonezu, A. Characterization of creep deformation behavior of porous polymer membrane under Small-Punch test. Eng. Fail. Anal. 2022, 135, 106149. [Google Scholar] [CrossRef]
- Zhao, X.; Li, D.; Wang, L.-J.; Wang, Y. Role of gelation temperature in rheological behavior and microstructure of high elastic starch-based emulsion-filled gel. Food Hydrocoll. 2022, 135, 108208. [Google Scholar] [CrossRef]
- Mourad, A.-H.; Fouad, H.; Elleithy, R. Impact of some environmental conditions on the tensile, creep-recovery, relaxation, melting and crystallinity behaviour of UHMWPE-GUR 410-medical grade. Mater. Des. 2009, 30, 4112–4119. [Google Scholar] [CrossRef]
- Findley, W.N.; Davis, F.A. Creep and relaxation of nonlinear viscoelastic materials, 3rd ed.; Courier corporation: North Chelmsford, MA, USA, 2008; pp. 154–196. [Google Scholar]
- Mei, S.Q.; Tang, G.; Yang, B.; Wang, Y.F. Creep/recovery behavior analysis of wood-plastic composites based on fractional order viscoelastic model. Acta Materiae Compositae Sinica 2020, 37, 2055–2064. [Google Scholar]
- Liu, X.; Zhang, S.; Xu, X.J.; Zhang, Z.; Zhou, L.; Zhang, G. Study on the creep and recovery behaviors of UHMWPE/CNTs composite fiber. Fibers Polym. 2013, 14, 1635–1640. [Google Scholar] [CrossRef]
- Starkova, O.; Gagani, A.I.; Karl, C.W.; Rocha, I.B.C.M.; Burlakovs, J.; Krauklis, A.E. Modelling of environmental ageing of polymers and polymer composites-durability prediction methods. Polymers 2022, 14, 907. [Google Scholar] [CrossRef] [PubMed]
- Otsuki, Y.; Hashimoto, K.; Kobayashi, Y.; Nishitsuji, S.; Matsuno, H.; Ito, H. Analyzing the tensile creep behavior of different types of polypropylenes using a simple fractional differential viscoelastic model. Polymers 2025, 17, 1095. [Google Scholar] [CrossRef] [PubMed]
- Guedes, R.M. Lifetime predictions of polymer matrix composites under constant or monotonic load. Compos. Part A: Appl. Sci. Manuf. 2006, 37, 703–715. [Google Scholar] [CrossRef]
- Amjadi, M.; Fatemi, A. Creep behavior and modeling of high-density polyethylene (HDPE). Polym. Test. 2021, 94, 107031. [Google Scholar] [CrossRef]
- Nuñez, A.J.; Marcovich, N.E.; Aranguren, M.I. Analysis of the creep behavior of polypropylene-woodflour composites. Polym. Eng. Sci. 2004, 44, 1594–1603. [Google Scholar] [CrossRef]
- Zhang, Y.-Y.; Sun, Z.; Li, Y.-Q.; Huang, P.; Chen, Q.; Fu, S.-Y. Tensile creep behavior of short-carbon-fiber reinforced polyetherimide composites. Compos. Part B: Eng. 2021, 212, 108717. [Google Scholar] [CrossRef]
- Yang, X.; Steck, J.; Yang, J.; Wang, Y.; Suo, Z. Degradable plastics are vulnerable to cracks. Engineering 2021, 7, 624–629. [Google Scholar] [CrossRef]

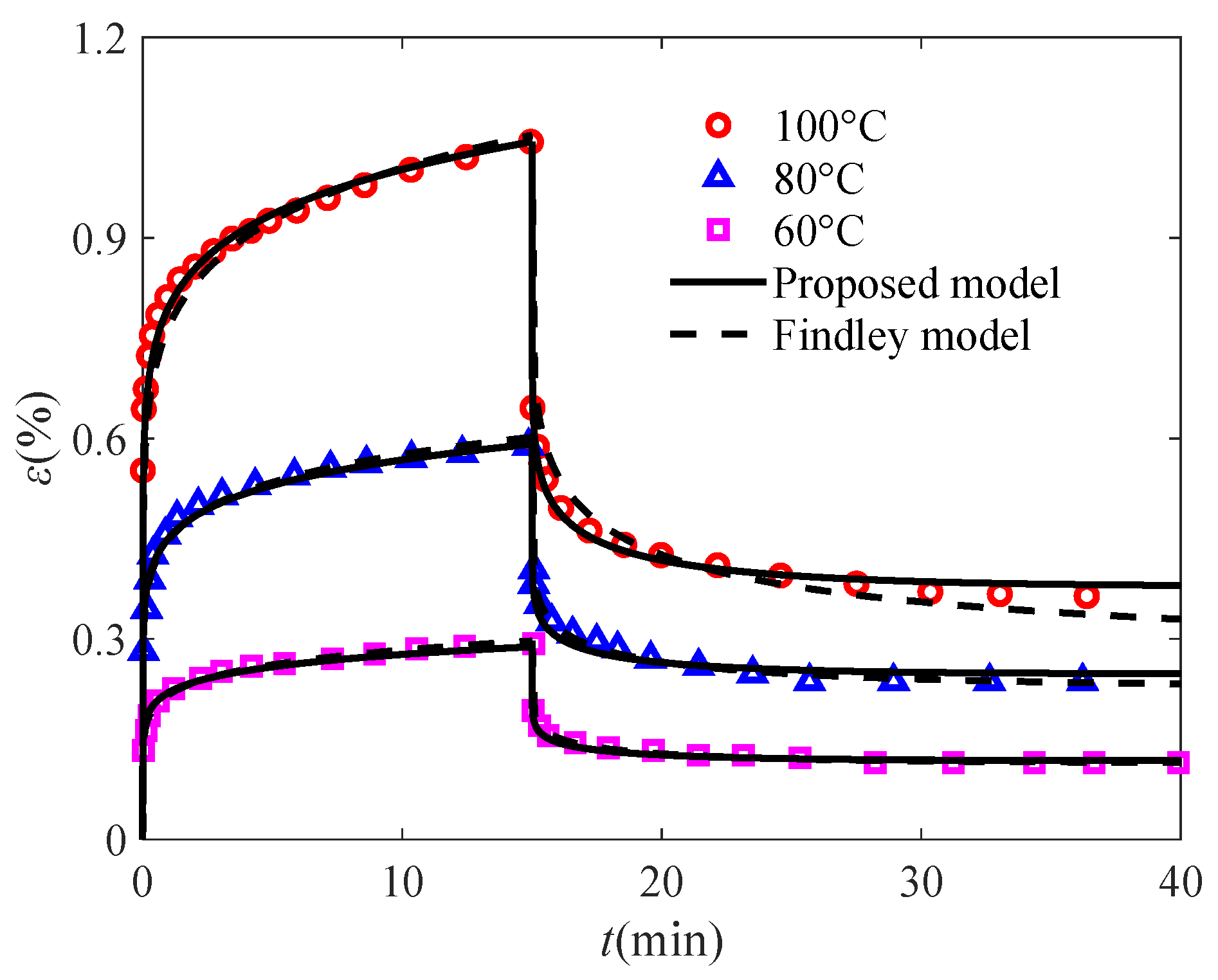


| T (°C) | 100 °C | 80 °C | 60 °C | |
|---|---|---|---|---|
| R2 | ||||
| Proposed model | 0.9842 | 0.9773 | 0.9854 | |
| Findley model | 0.9127 | 0.9750 | 0.9810 | |
| σ0 (MPa) | α | φ | a | b |
|---|---|---|---|---|
| 41.67 | 0.11 | 3917.8 | 9.3428e-7 | 1.4687 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, L.; Cai, W.; Yang, J. Temperature/Stress-Dependent Fractional Creep Models of Thermoplastic Polymers. Polymers 2025, 17, 1984. https://doi.org/10.3390/polym17141984
Wu L, Cai W, Yang J. Temperature/Stress-Dependent Fractional Creep Models of Thermoplastic Polymers. Polymers. 2025; 17(14):1984. https://doi.org/10.3390/polym17141984
Chicago/Turabian StyleWu, Leixiao, Wei Cai, and Jie Yang. 2025. "Temperature/Stress-Dependent Fractional Creep Models of Thermoplastic Polymers" Polymers 17, no. 14: 1984. https://doi.org/10.3390/polym17141984
APA StyleWu, L., Cai, W., & Yang, J. (2025). Temperature/Stress-Dependent Fractional Creep Models of Thermoplastic Polymers. Polymers, 17(14), 1984. https://doi.org/10.3390/polym17141984







