Effect of Printing Parameters on the Dynamic Characteristics of Additively Manufactured ABS Beams: An Experimental Modal Analysis and Response Surface Methodology
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Design and 3D-Printed Specimen Fabrication
2.2. Experimental Modal Analysis Setup and Procedures
2.3. Experimental Data Process
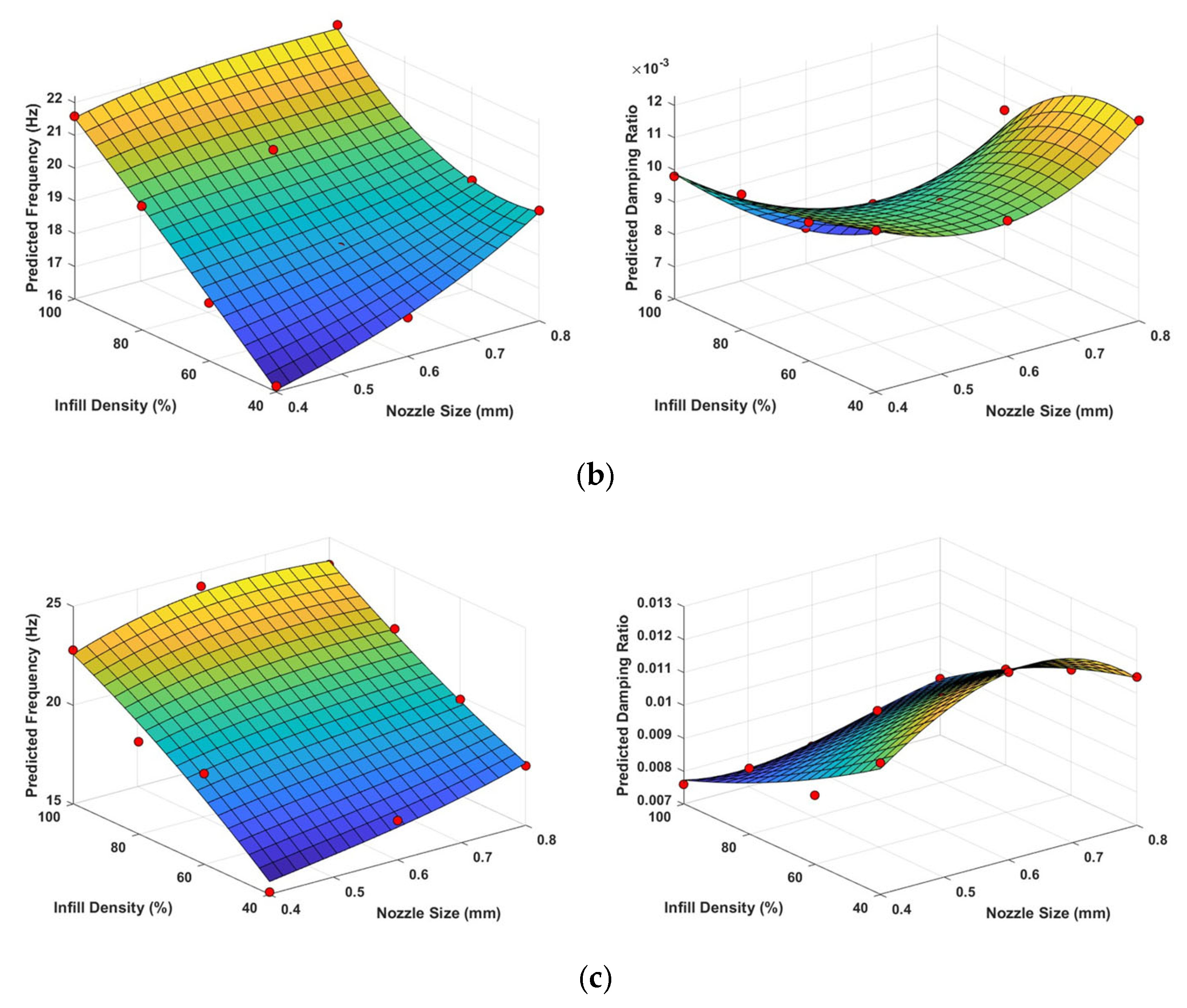
2.4. Response Surface Method (RSM)
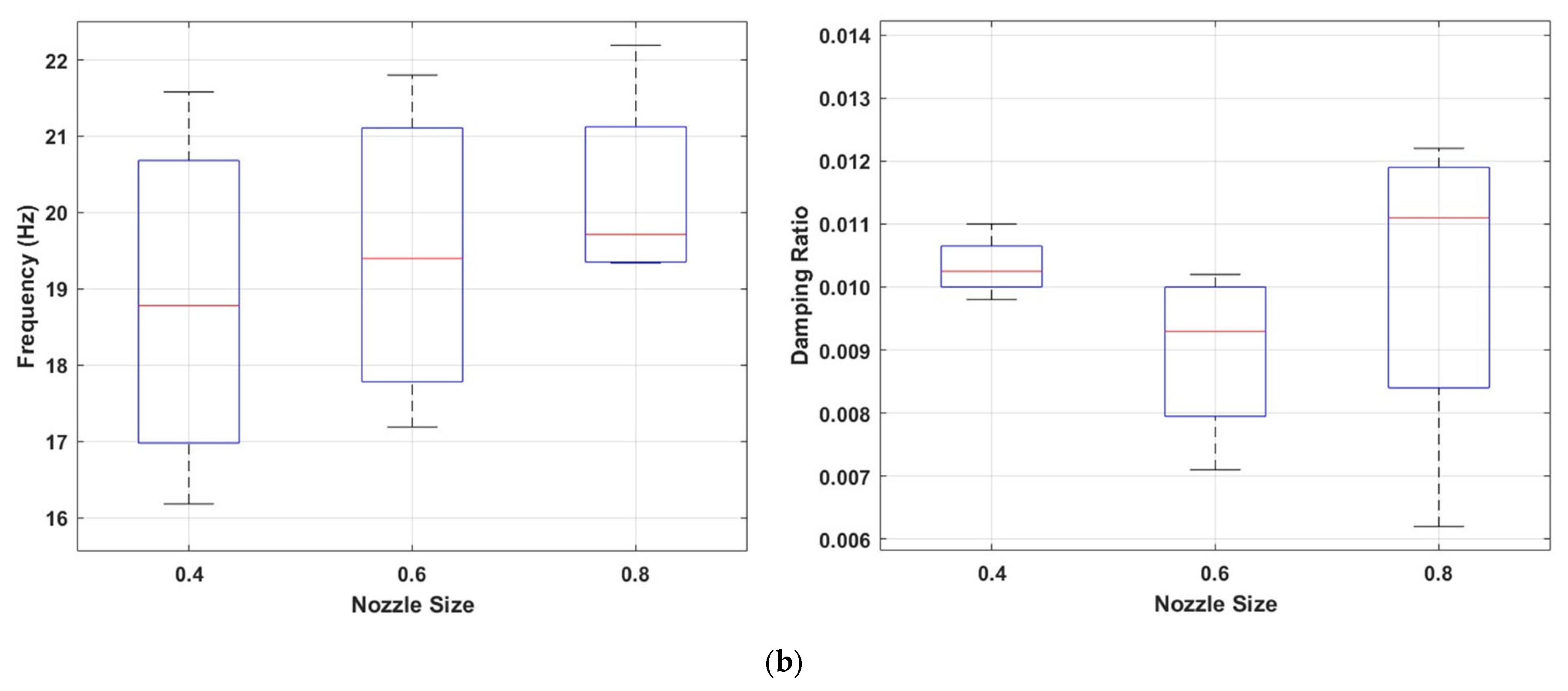
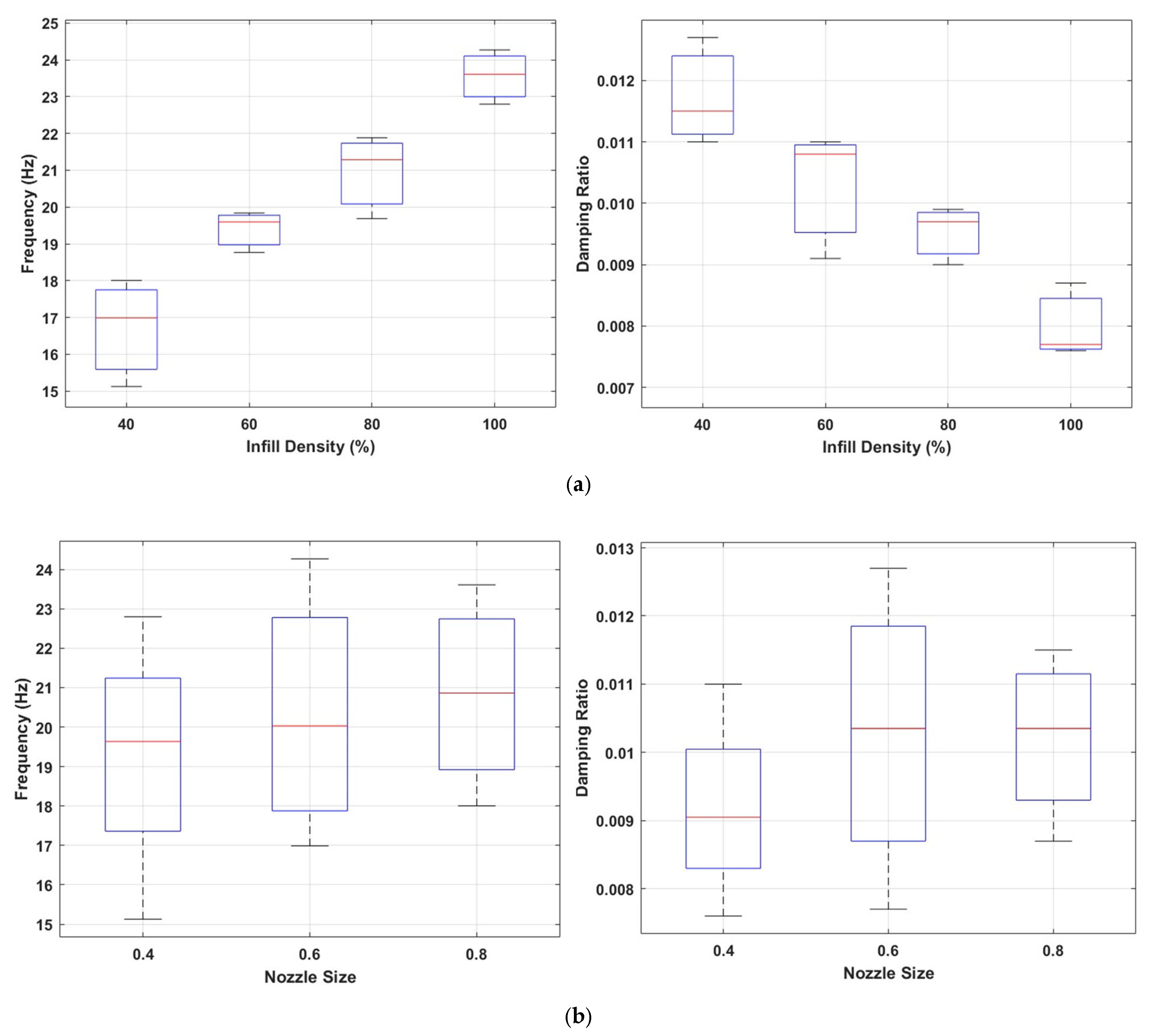
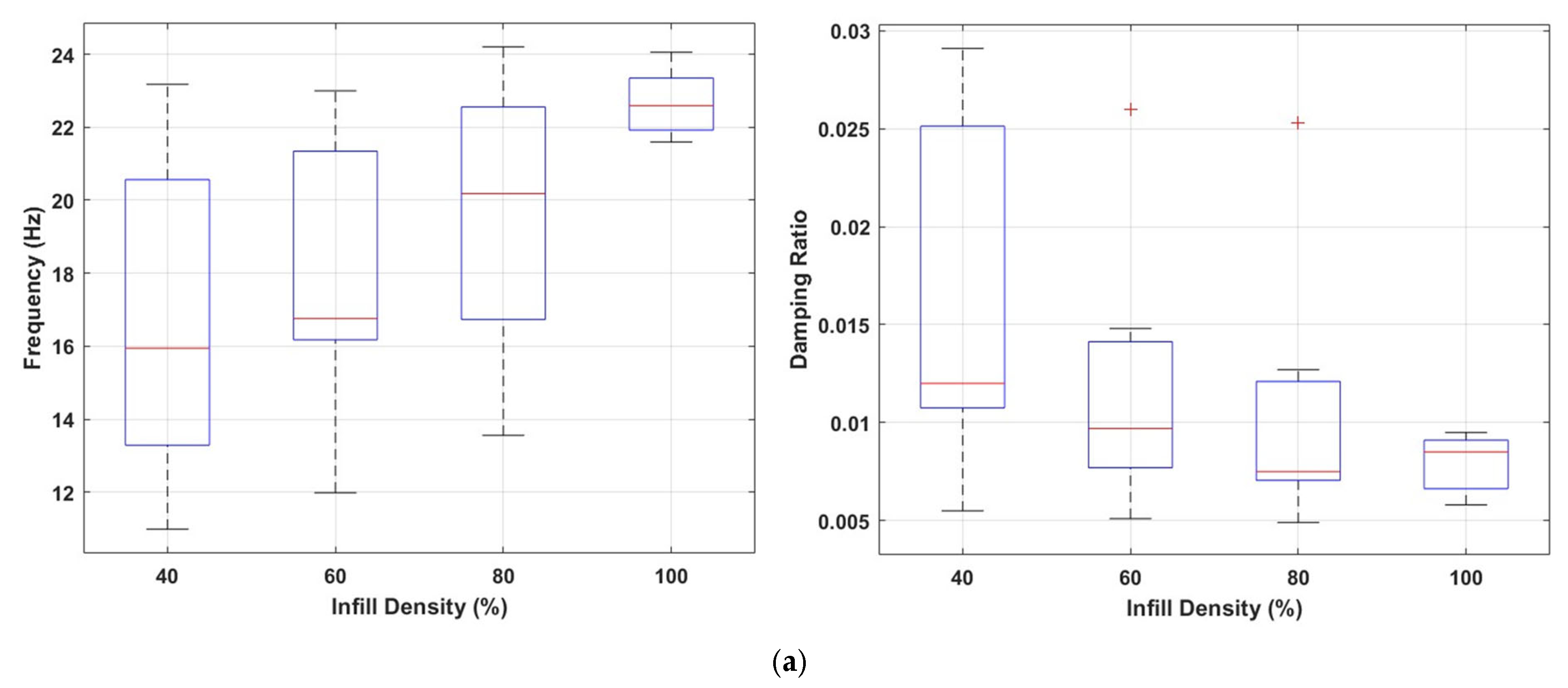
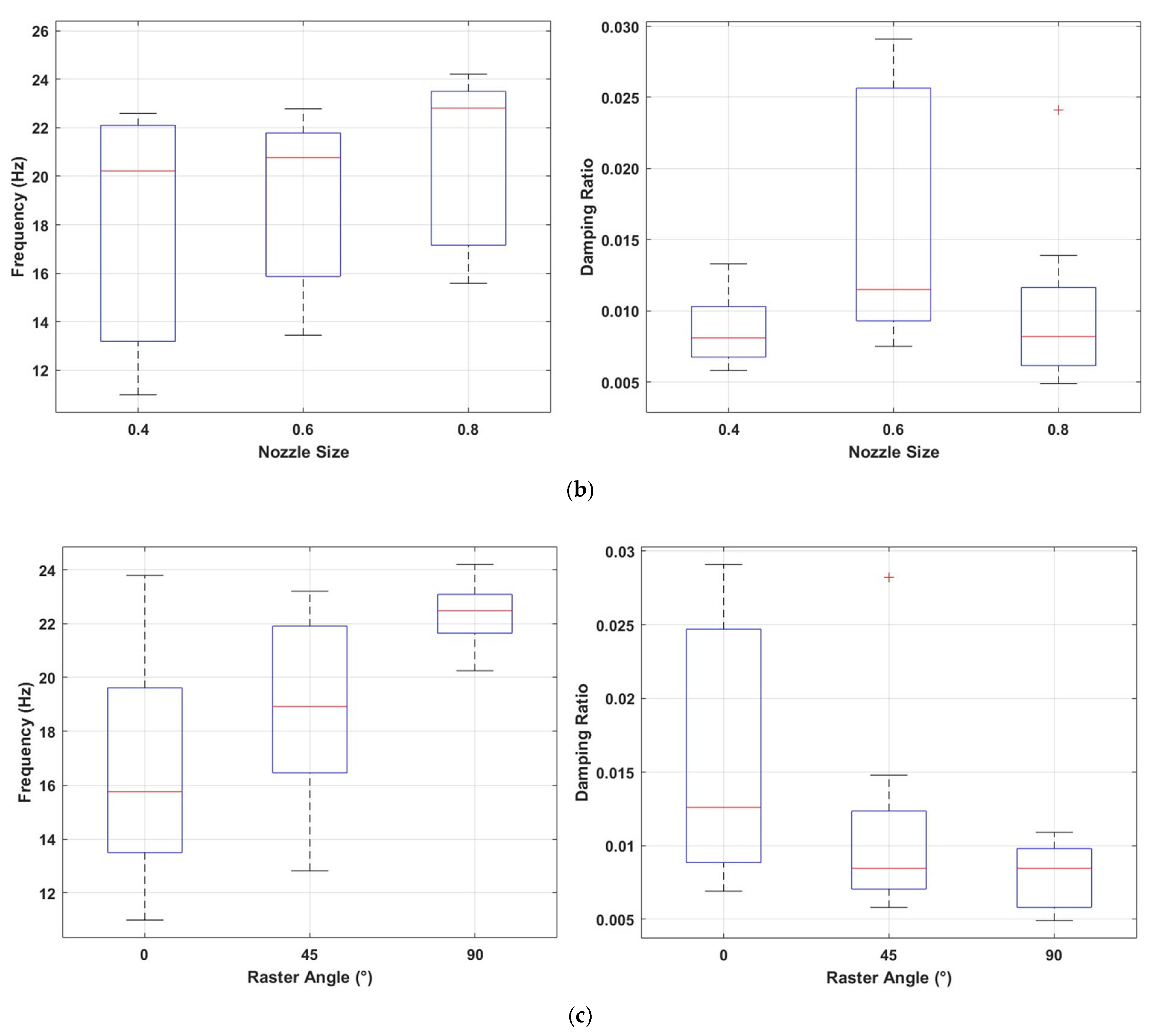
3. Results and Discussion
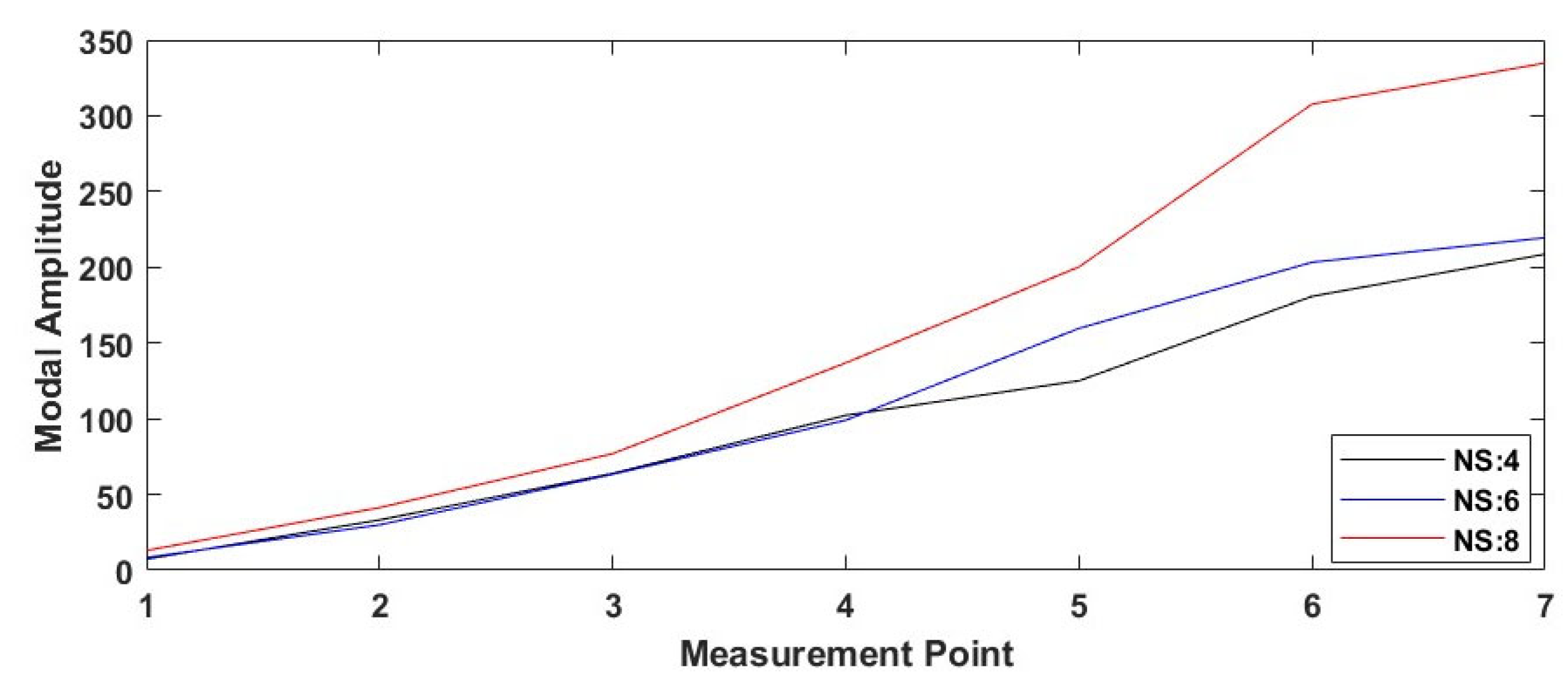
3.1. Influence of the Infill Pattern
3.1.1. Cubic Infill Pattern
3.1.2. Triangle Infill Pattern
3.1.3. Gyroid Infill Pattern
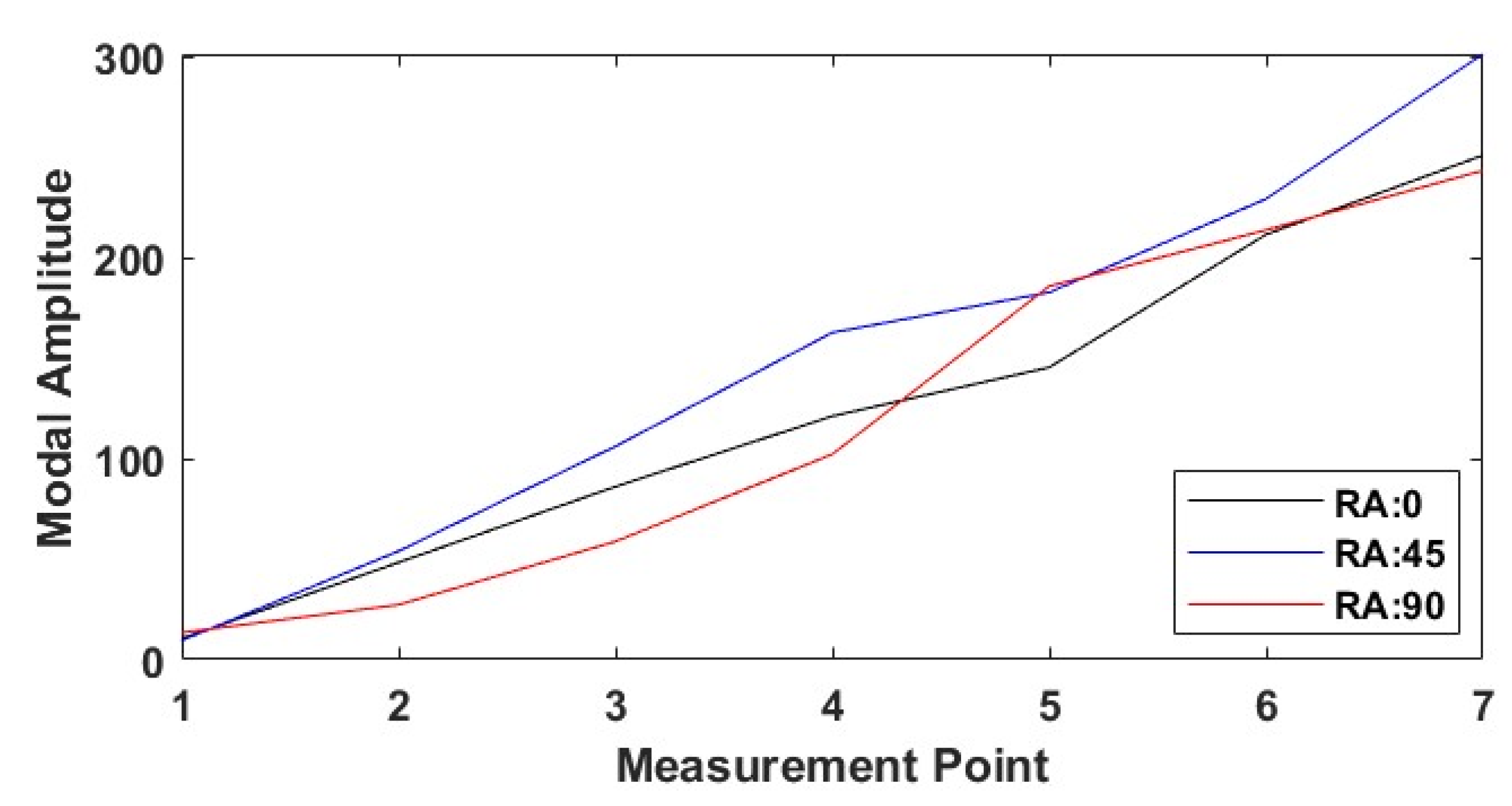
3.1.4. Line Infill Patterns
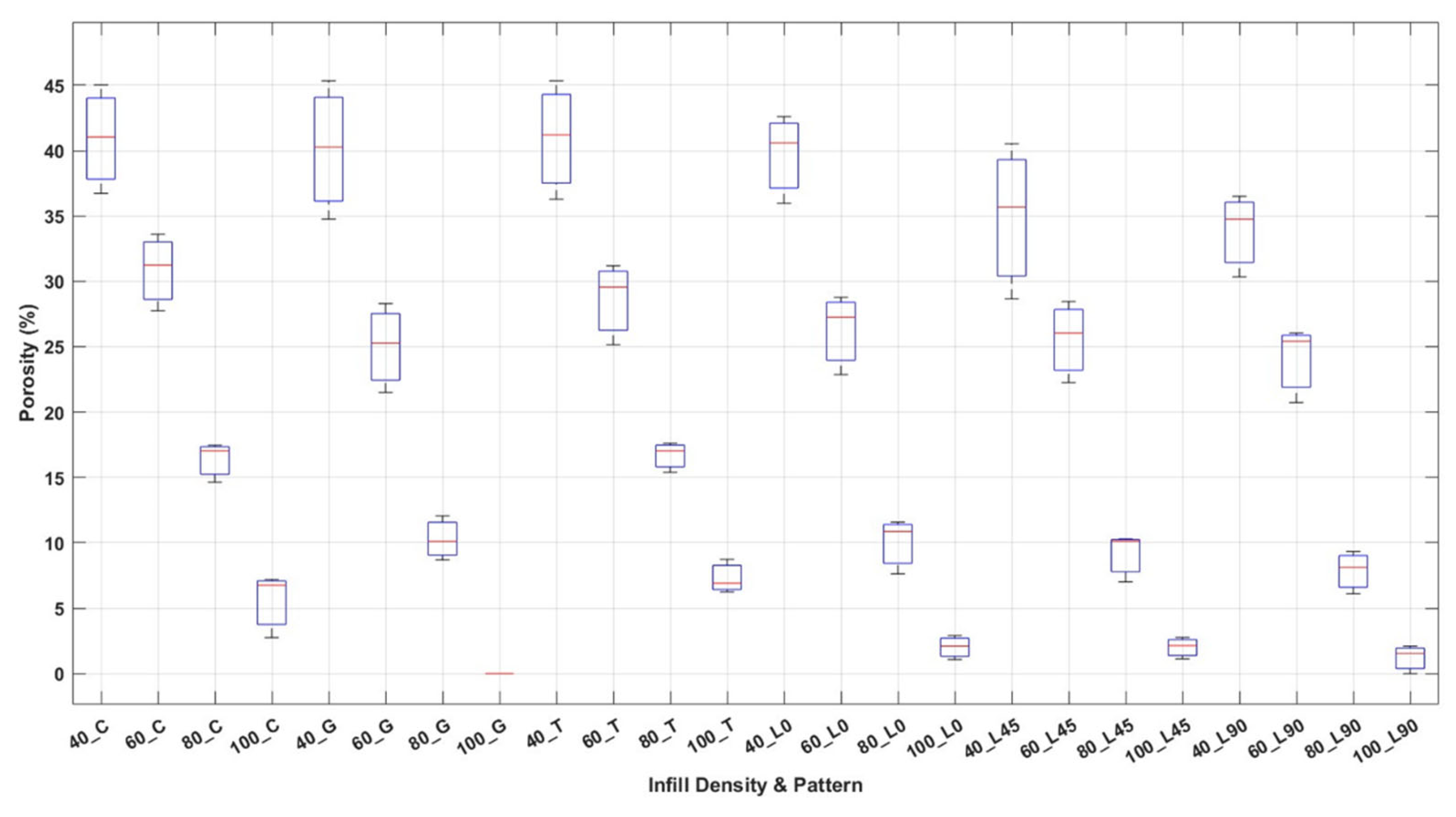
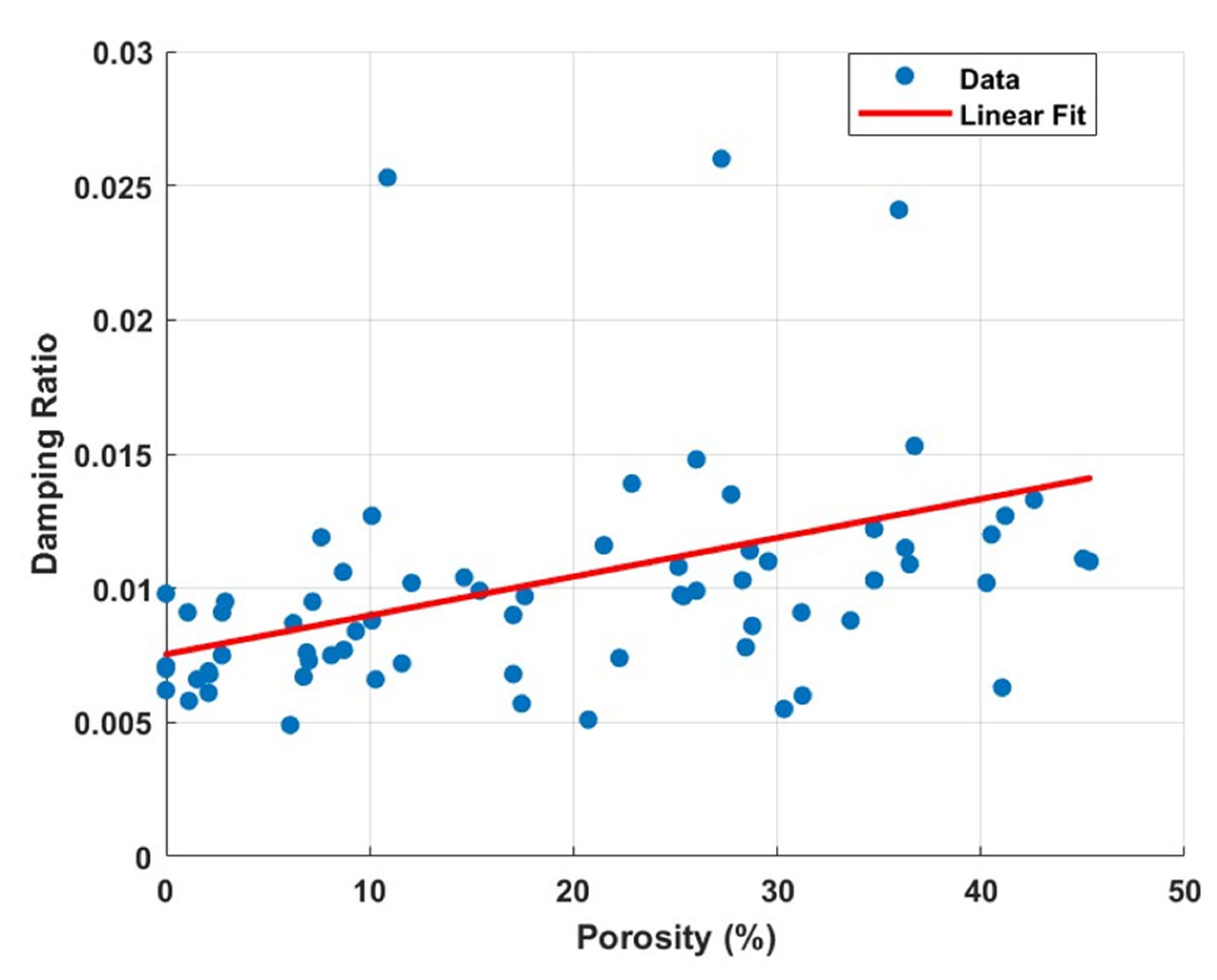
3.2. Influence of Porosity
- : The actual measured mass of the printed part.
- : The mass the part would have if it were printed solid (100% infill).
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Pattern | Component | Natural Frequencies | Damping Ratios | ||||
|---|---|---|---|---|---|---|---|
| SumSq | DF | MeanSq | SumSq | DF | MeanSq | ||
| Cubic | Model | 35.506 | 7 | 5.0723 | 0.00010297 | 7 | 1.4709 × 10−5 |
| Linear | 31.669 | 2 | 15.834 | 3.9607 × 10−5 | 2 | 1.9804 × 10−5 | |
| Nonlinear | 3.8373 | 5 | 0.7675 | 6.3358 × 10−5 | 5 | 1.2672 × 10−5 | |
| Residual | 0.82285 | 4 | 0.2057 | 3.1814 × 10−6 | 4 | 7.9535 × 10−7 | |
| Triangle | Model | 38.456 | 7 | 5.4938 | 3.2372 × 10−5 | 7 | 4.6246 × 10−6 |
| Linear | 35.223 | 2 | 17.612 | 1.8211 × 10−5 | 2 | 9.1056 × 10−6 | |
| Nonlinear | 3.2332 | 5 | 0.64664 | 1.4161 × 10−5 | 5 | 2.8321 × 10−6 | |
| Residual | 0.31612 | 4 | 0.07903 | 5.2475 × 10−7 | 4 | 1.3119 × 10−7 | |
| Gyroid | Model | 79.189 | 7 | 11.313 | 2.6133 × 10−5 | 7 | 3.7332 × 10−6 |
| Linear | 77.974 | 2 | 38.987 | 2.3685 × 10−5 | 2 | 1.1843 × 10−5 | |
| Nonlinear | 1.2149 | 5 | 0.24298 | 2.4475 × 10−6 | 5 | 4.895 × 10−7 | |
| Residual | 3.3814 | 4 | 0.84535 | 5.565 × 10−7 | 4 | 1.3912 × 10−7 | |
| Line | Model | 480.56 | 9 | 53.396 | 0.0012023 | 9 | 0.00013359 |
| Linear | 418.85 | 3 | 139.62 | 0.00064058 | 3 | 0.00021353 | |
| Nonlinear | 61.712 | 6 | 10.285 | 0.00056173 | 6 | 9.3621 × 10−5 | |
| Residual | 57.985 | 26 | 2.2302 | 0.00035568 | 26 | 1.368 × 10−5 | |
References
- Aliheidari, N.; Tripuraneni, R.; Ameli, A.; Nadimpalli, S. Fracture Resistance Measurement of Fused Deposition Modeling 3D Printed Polymers. Polym. Test. 2017, 60, 94–101. [Google Scholar] [CrossRef]
- Khorasani, M.; Ghasemi, A.; Rolfe, B.; Gibson, I. Additive Manufacturing a Powerful Tool for the Aerospace Industry. Rapid Prototyp. J. 2022, 28, 87–100. [Google Scholar] [CrossRef]
- Rojek, I.; Mikołajewski, D.; Dostatni, E.; Macko, M. AI-Optimized Technological Aspects of the Material Used in 3D Printing Processes for Selected Medical Applications. Materials 2020, 13, 5437. [Google Scholar] [CrossRef] [PubMed]
- Yang, Q.; Wang, S.; Chen, A.; Zhao, M.; Zhang, X.; Sheng, L.; Zhang, C.; Wu, Z. A Poly(Ether-Ketone-Ketone) Composite Scaffold Simulating the Immune-Osteogenic Cascade for in Situ Bone Regeneration. J. Mater. Chem. B 2025, 13, 4641–4656. [Google Scholar] [CrossRef]
- O’Donnell, J.; Kim, M.; Yoon, H.-S. A Review on Electromechanical Devices Fabricated by Additive Manufacturing. J. Manuf. Sci. Eng. 2017, 139, 010801. [Google Scholar] [CrossRef]
- Böckin, D.; Tillman, A.-M. Environmental Assessment of Additive Manufacturing in the Automotive Industry. J. Clean. Prod. 2019, 226, 977–987. [Google Scholar] [CrossRef]
- Qu, J.; Wu, Q.; Clancy, T.; Fan, Q.; Wang, X.; Liu, X. 3D-Printed Strain-Gauge Micro Force Sensors. IEEE Sens. J. 2020, 20, 6971–6978. [Google Scholar] [CrossRef]
- Mofidian, S.M.M.; Davani, S.; Momeni, K.; Bardaweel, H. 3D-Printed Strain Sensors: Electro-Mechanical Simulation and Design Analysis Using Nonlinear Material Model and Experimental Investigation. IEEE Sens. J. 2021, 21, 1675–1685. [Google Scholar] [CrossRef]
- Smith, A.; Mofidian, S.M.; Bardaweel, H. Three-Dimensional Printed Embedded Channel–Based Resistive Strain Sensor: Fabrication and Experimental Characterization. J. Intell. Mater. Syst. Struct. 2019, 30, 1518–1526. [Google Scholar] [CrossRef]
- Tilton, M.; Lewis, G.S.; Bok Wee, H.; Armstrong, A.; Hast, M.W.; Manogharan, G. Additive Manufacturing of Fracture Fixation Implants: Design, Material Characterization, Biomechanical Modeling and Experimentation. Addit. Manuf. 2020, 33, 101137. [Google Scholar] [CrossRef]
- Wang, C.; Wu, J.; Liu, L.; Xu, D.; Liu, Y.; Li, S.; Hou, W.; Wang, J.; Chen, X.; Sheng, L.; et al. Improving Osteoinduction and Osteogenesis of Ti6Al4V Alloy Porous Scaffold by Regulating the Pore Structure. Front. Chem. 2023, 11, 1190630. [Google Scholar] [CrossRef] [PubMed]
- Turner, B.N.; Strong, R.; Gold, S.A. A Review of Melt Extrusion Additive Manufacturing Processes: I. Process Design and Modeling. Rapid Prototyp. J. 2014, 20, 192–204. [Google Scholar] [CrossRef]
- Alshammari, Y.L.A.; He, F.; Khan, M.A. Modelling and Investigation of Crack Growth for 3D-Printed Acrylonitrile Butadiene Styrene (ABS) with Various Printing Parameters and Ambient Temperatures. Polymers 2021, 13, 3737. [Google Scholar] [CrossRef]
- Vyavahare, S.; Teraiya, S.; Panghal, D.; Kumar, S. Fused Deposition Modelling: A Review. Rapid Prototyp. J. 2020, 26, 176–201. [Google Scholar] [CrossRef]
- Zai, B.A.; Khan, M.A.; Khan, S.Z.; Asif, M.; Khan, K.A.; Saquib, A.N.; Mansoor, A.; Shahzad, M.; Mujtaba, A. Prediction of Crack Depth and Fatigue Life of an Acrylonitrile Butadiene Styrene Cantilever Beam Using Dynamic Response. J. Test. Eval. 2020, 48, 1520–1536. [Google Scholar] [CrossRef]
- Gómez-Gras, G.; Abad, M.D.; Pérez, M.A. Mechanical Performance of 3D-Printed Biocompatible Polycarbonate for Biomechanical Applications. Polymers 2021, 13, 3669. [Google Scholar] [CrossRef]
- Jayakumar, N. Effect of Printing Parameters of 3D Printed PLA Parts on Mechanical Properties. J. Eng. Res. 2021. [Google Scholar] [CrossRef]
- Saenz, F.; Otarola, C.; Valladares, K.; Rojas, J. Influence of 3D Printing Settings on Mechanical Properties of ABS at Room Temperature and 77 K. Addit. Manuf. 2021, 39, 101841. [Google Scholar] [CrossRef]
- Lee, D.; Wu, G.-Y. Parameters Affecting the Mechanical Properties of Three-Dimensional (3D) Printed Carbon Fiber-Reinforced Polylactide Composites. Polymers 2020, 12, 2456. [Google Scholar] [CrossRef]
- Camargo, J.C.; Machado, Á.R.; Almeida, E.C.; Silva, E.F.M.S. Mechanical Properties of PLA-Graphene Filament for FDM 3D Printing. Int. J. Adv. Manuf. Technol. 2019, 103, 2423–2443. [Google Scholar] [CrossRef]
- Sanei, S.H.R.; Popescu, D. 3D-Printed Carbon Fiber Reinforced Polymer Composites: A Systematic Review. J. Compos. Sci. 2020, 4, 98. [Google Scholar] [CrossRef]
- Paggi, R.A.; Salmoria, G.V.; Ghizoni, G.B.; de Medeiros Back, H.; de Mello Gindri, I. Structure and Mechanical Properties of 3D-Printed Cellulose Tablets by Fused Deposition Modeling. Int. J. Adv. Manuf. Technol. 2019, 100, 2767–2774. [Google Scholar] [CrossRef]
- Bárnik, F.; Vaško, M.; Sága, M.; Handrik, M.; Sapietová, A. Mechanical Properties of Structures Produced by 3D Printing from Composite Materials. MATEC Web Conf. 2019, 254, 01018. [Google Scholar] [CrossRef]
- Gordelier, T.J.; Thies, P.R.; Turner, L.; Johanning, L. Optimising the FDM Additive Manufacturing Process to Achieve Maximum Tensile Strength: A State-of-the-Art Review. Rapid Prototyp. J. 2019, 25, 953–971. [Google Scholar] [CrossRef]
- Popescu, D.; Zapciu, A.; Amza, C.; Baciu, F.; Marinescu, R. FDM Process Parameters Influence over the Mechanical Properties of Polymer Specimens: A Review. Polym. Test 2018, 69, 157–166. [Google Scholar] [CrossRef]
- He, F.; Ning, H.; Khan, M. Effect of 3D Printing Process Parameters on Damping Characteristic of Cantilever Beams Fabricated Using Material Extrusion. Polymers 2023, 15, 257. [Google Scholar] [CrossRef]
- Sood, A.K.; Ohdar, R.K.; Mahapatra, S.S. Experimental Investigation and Empirical Modelling of FDM Process for Compressive Strength Improvement. J. Adv. Res. 2012, 3, 81–90. [Google Scholar] [CrossRef]
- Padhi, S.K.; Sahu, R.K.; Mahapatra, S.S.; Das, H.C.; Sood, A.K.; Patro, B.; Mondal, A.K. Optimization of Fused Deposition Modeling Process Parameters Using a Fuzzy Inference System Coupled with Taguchi Philosophy. Adv. Manuf. 2017, 5, 231–242. [Google Scholar] [CrossRef]
- Sood, A.K.; Ohdar, R.K.; Mahapatra, S.S. Parametric Appraisal of Mechanical Property of Fused Deposition Modelling Processed Parts. Mater. Des. 2010, 31, 287–295. [Google Scholar] [CrossRef]
- Durgun, I.; Ertan, R. Experimental Investigation of FDM Process for Improvement of Mechanical Properties and Production Cost. Rapid Prototyp. J. 2014, 20, 228–235. [Google Scholar] [CrossRef]
- Ziemian, C.; Sharma, M.; Ziemian, S. Anisotropic Mechanical Properties of ABS Parts Fabricated by Fused Deposition Modelling. In Mechanical Engineering; Intechopen: London, UK, 2012. [Google Scholar]
- Aloyaydi, B.; Sivasankaran, S.; Mustafa, A. Investigation of Infill-Patterns on Mechanical Response of 3D Printed Poly-Lactic-Acid. Polym. Test 2020, 87, 106557. [Google Scholar] [CrossRef]
- Kannan, S.; Vezhavendhan, R.; Kishore, S.; Kanumuru, K.V. Investigating the Effect of Orientation, Infill Density with Triple Raster Pattern on the Tensile Properties for 3D Printed Samples. IOP SciNotes 2020, 1, 024405. [Google Scholar] [CrossRef]
- Beattie, N.; Bock, N.; Anderson, T.; Edgeworth, T.; Kloss, T.; Swanson, J. Effects of Build Orientation on Mechanical Properties of Fused Deposition Modeling Parts. J. Mater. Eng. Perform. 2021, 30, 5059–5065. [Google Scholar] [CrossRef]
- Raza, A.; Rimašauskienė, R.; Jūrėnas, V.; Rimašauskas, M. An Experimental Study on the Dynamic Properties of 3D-Printed Structures with Different Layer Orientations. J. Vib. Eng. Technol. 2024, 12, 321–334. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Crittenden, K.; Weiss, L.; Bardaweel, H. Experimental Modal Analysis and Characterization of Additively Manufactured Polymers. Polymers 2022, 14, 2071. [Google Scholar] [CrossRef]
- Kamei, K.; Khan, M.A. Current Challenges in Modelling Vibrational Fatigue and Fracture of Structures: A Review. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 77. [Google Scholar] [CrossRef]
- Zai, B.A.; Khan, M.A.; Khan, K.; Mansoor, A.; Shahzad, M.; Shah, A. The Role of Dynamic Response Parameters in Damage Prediction. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 233, 4620–4636. [Google Scholar] [CrossRef]
- Baqasah, H.; He, F.; Zai, B.A.; Asif, M.; Khan, K.A.; Thakur, V.K.; Khan, M.A. In-Situ Dynamic Response Measurement for Damage Quantification of 3D Printed ABS Cantilever Beam under Thermomechanical Load. Polymers 2019, 11, 2079. [Google Scholar] [CrossRef]
- Sbriglia, L.R.; Baker, A.M.; Thompson, J.M.; Morgan, R.V.; Wachtor, A.J.; Bernardin, J.D. Embedding Sensors in FDM Plastic Parts During Additive Manufacturing. In Modal Analysis & Testing, Proceedings of the 34th IMAC, A Conference and Exposition on Structural Dynamics 2016, Orlando, FL, USA, 25–28 January 2016; Springer: Cham, Switzerland, 2016; Volume 10, pp. 205–214. [Google Scholar]
- Ozcanli, O. Modal Analysis of 3D Printed Parts. Master’s Thesis, Coventry University, Coventry, UK, January 2017. [Google Scholar] [CrossRef]
- İyibilgin, O.; Dal, H.; Gepek, E. Experimental Modal Analysis of 3D Printed Beams. In Proceedings of the 4th International Congress on 3D Printing (Additive Manufacturing) Technologies and Digital Industry, Antalya, Turkey, 11–14 April 2019. [Google Scholar]
- Kannan, S.; Ramamoorthy, M. Mechanical Characterization and Experimental Modal Analysis of 3D Printed ABS, PC and PC-ABS Materials. Mater. Res. Express 2020, 7, 015341. [Google Scholar] [CrossRef]
- Kannan, S.; Ramamoorthy, M.; Sudhagar, E.; Gunji, B. Mechanical Characterization and Vibrational Analysis of 3D Printed PETG and PETG Reinforced with Short Carbon Fiber. AIP Conf. Proc. 2020, 2270, 030004. [Google Scholar]
- Rajkumar, S. Effect Of Infill Pattern and Build Orientation on Mechanical Properties of FDM Printed Parts: An Experimental Modal Analysis Approach. arXiv 2022, arXiv:2202.05692. [Google Scholar]
- Pandya, K. An Experimental and Numerical Investigation into Vibration of Delaminated 3D Printed PLA Beams. Master’s Thesis, Toronto Metropolitan University, Toronto, ON, Canada, December 2023. [Google Scholar] [CrossRef]
- Medel, F.; Abad, J.; Esteban, V. Stiffness and Damping Behavior of 3D Printed Specimens. Polym. Test. 2022, 109, 107529. [Google Scholar] [CrossRef]
- Öteyaka, M.Ö.; Çakir, F.H.; Sofuoğlu, M.A. Effect of Infill Pattern and Ratio on the Flexural and Vibration Damping Characteristics of FDM Printed PLA Specimens. Mater. Today Commun. 2022, 33, 104912. [Google Scholar] [CrossRef]
- Atwah, A.A.; Almutairi, M.D.; He, F.; Khan, M.A. Influence of Printing Parameters on Self-Cleaning Properties of 3D Printed Polymeric Fabrics. Polymers 2022, 14, 3128. [Google Scholar] [CrossRef]
- He, F.; Khan, M.; Aldosari, S. Interdependencies between Dynamic Response and Crack Growth in a 3D-Printed Acrylonitrile Butadiene Styrene (ABS) Cantilever Beam under Thermo-Mechanical Loads. Polymers 2022, 14, 982. [Google Scholar] [CrossRef]
- Yang, Z.; He, F.; Khan, M. An Empirical Torsional Spring Model for the Inclined Crack in a 3D-Printed Acrylonitrile Butadiene Styrene (ABS) Cantilever Beam. Polymers 2023, 15, 496. [Google Scholar] [CrossRef]
- Francese, A.; Khan, M.; He, F. Role of Dynamic Response in Inclined Transverse Crack Inspection for 3D-Printed Polymeric Beam with Metal Stiffener. Materials 2023, 16, 3095. [Google Scholar] [CrossRef]
- Chan, K.P.; He, F.; Atwah, A.A.; Khan, M. Experimental Investigation of Self-Cleaning Behaviour of 3D-Printed Textile Fabrics with Various Printing Parameters. Polym. Test. 2023, 119, 107941. [Google Scholar] [CrossRef]
- Almutairi, M.D.; Mascarenhas, T.A.; Alnahdi, S.S.; He, F.; Khan, M.A. Modal Response of Hybrid Raster Orientation on Material Extrusion Printed Acrylonitrile Butadiene Styrene and Polyethylene Terephthalate Glycol under Thermo-Mechanical Loads. Polym. Test. 2023, 120, 107953. [Google Scholar] [CrossRef]
- Katı, H.D. Vibration Analysis of Beams with Tip Mass Using Differential Transform Method. Ph.D. Thesis, Bursa Technical University, Bursa, Turkey, 2018. [Google Scholar]
- Ewins, D.J. Modal Testing: Theory, Practice and Application, 2nd ed.; Research Studies Press: Brookline, MA, USA, 2000. [Google Scholar]
- He, J.; Fu, Z.-F. Modal Analysis; Elsevier: Amsterdam, The Netherlands, 2001; ISBN 9780750650793. [Google Scholar]
- Mukhopadhyay, T.; Dey, T.K.; Chowdhury, R.; Chakrabarti, A. Structural Damage Identification Using Response Surface-Based Multi-Objective Optimization: A Comparative Study. Arab. J. Sci. Eng. 2015, 40, 1027–1044. [Google Scholar] [CrossRef]
- Papageorgiou, V.; Tsongas, K.; Mansour, M.T.; Tzetzis, D.; Mansour, G. Mechanical Properties and Vibrational Behavior of 3D-Printed Carbon Fiber-Reinforced Polyphenylene Sulfide and Polyamide-6 Composites with Different Infill Types. J. Compos. Sci. 2025, 9, 59. [Google Scholar] [CrossRef]
- Cojocaru, V.; Frunzaverde, D.; Miclosina, C.-O. On the Behavior of Honeycomb, Grid and Triangular PLA Structures under Symmetric and Asymmetric Bending. Micromachines 2022, 14, 120. [Google Scholar] [CrossRef]
- Khaliq, J.; Gurrapu, D.R.; Elfakhri, F. Effects of Infill Line Multiplier and Patterns on Mechanical Properties of Lightweight and Resilient Hollow Section Products Manufactured Using Fused Filament Fabrication. Polymers 2023, 15, 2585. [Google Scholar] [CrossRef]
- Gonabadi, H.; Yadav, A.; Bull, S.J. The Effect of Processing Parameters on the Mechanical Characteristics of PLA Produced by a 3D FFF Printer. Int. J. Adv. Manuf. Technol. 2020, 111, 695–709. [Google Scholar] [CrossRef]
- Lobov, E.; Dobrydneva, A.; Vindokurov, I.; Tashkinov, M. Effect of Short Carbon Fiber Reinforcement on Mechanical Properties of 3D-Printed Acrylonitrile Butadiene Styrene. Polymers 2023, 15, 2011. [Google Scholar] [CrossRef]
- Lakshman Sri, S.V.; Karthick, A.; Dinesh, C. Evaluation of Mechanical Properties of 3D Printed PETG and Polyamide (6) Polymers. Chem. Phys. Impact 2024, 8, 100491. [Google Scholar] [CrossRef]
- Patel, R.; Jani, S.; Joshi, A. Review on Multi-Objective Optimization of FDM Process Parameters for Composite Materials. Int. J. Interact. Des. Manuf. (IJIDeM) 2023, 17, 2115–2125. [Google Scholar] [CrossRef]
- Parodo, G.; Sorrentino, L.; Turchetta, S.; Moffa, G. Evaluation of the Accuracy of a Fused Deposition Modeling Process in the Production of Low-Density ABS Lattice Structures. Materials 2025, 18, 1679. [Google Scholar] [CrossRef]
- Yin, J.; Zhang, J.; Zhang, Y.; Wang, W. Porosity, Mechanical Properties, and Damping Ratio of Particulate-filled Polymer Composite for Precision Machine Tools. J. Appl. Polym. Sci. 2017, 134, 44435. [Google Scholar] [CrossRef]
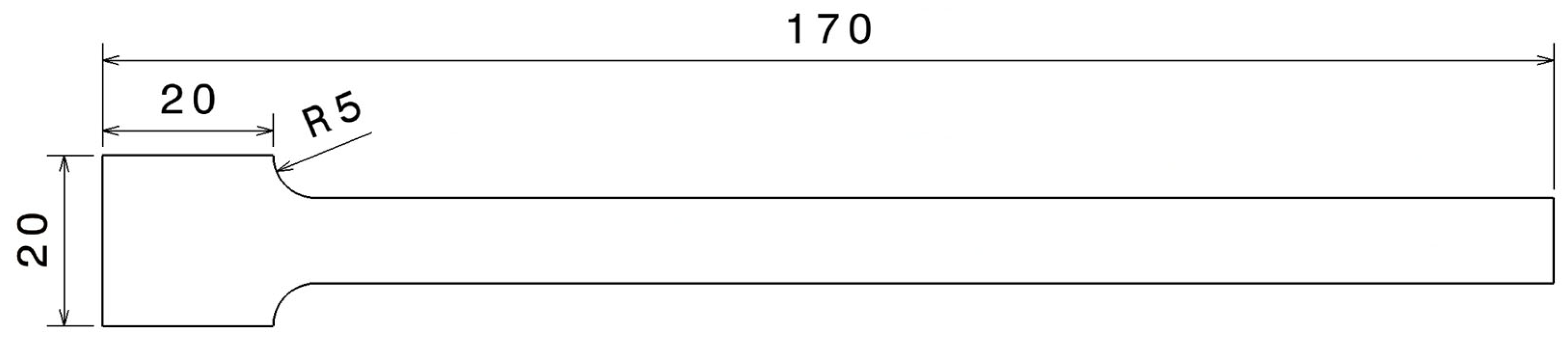


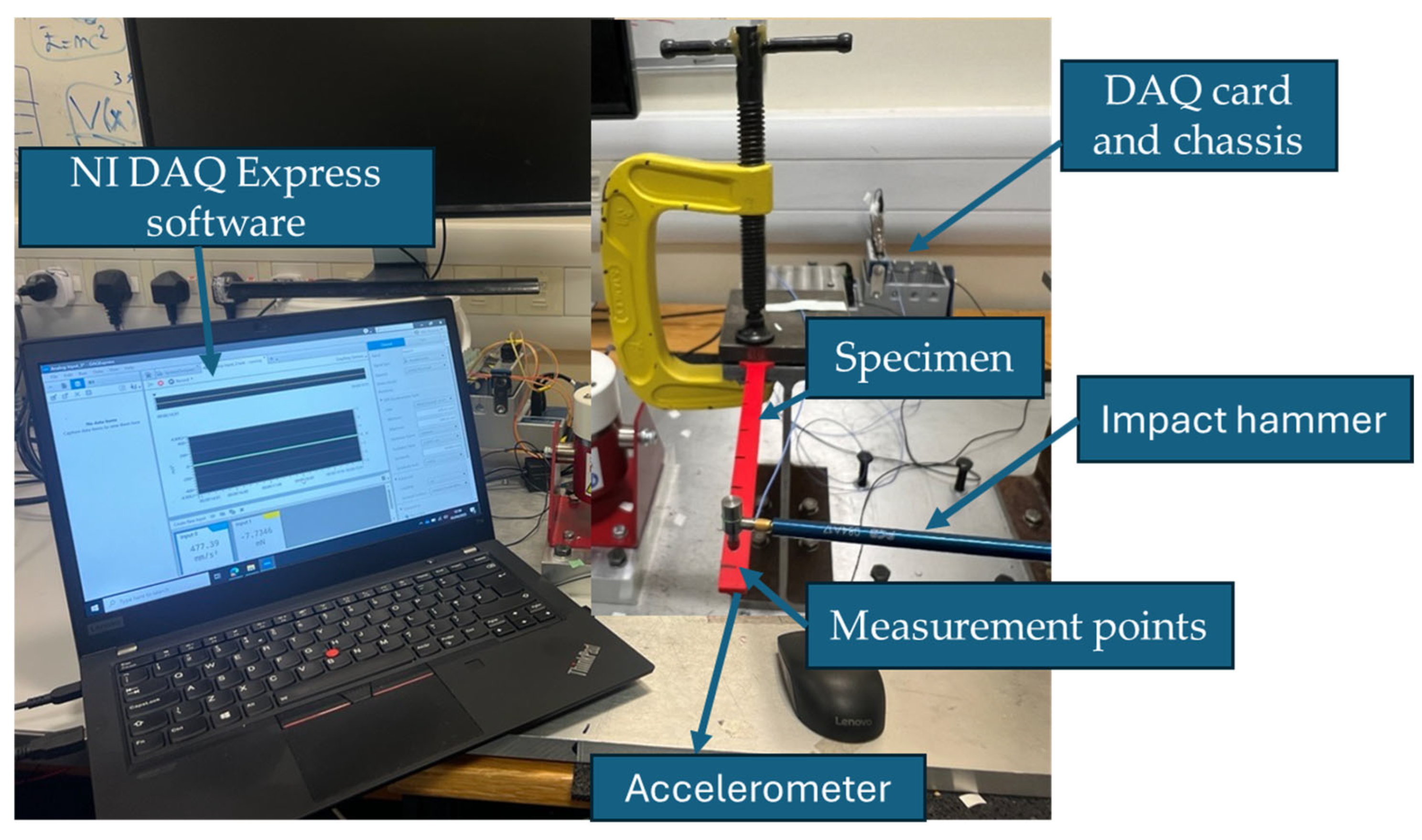
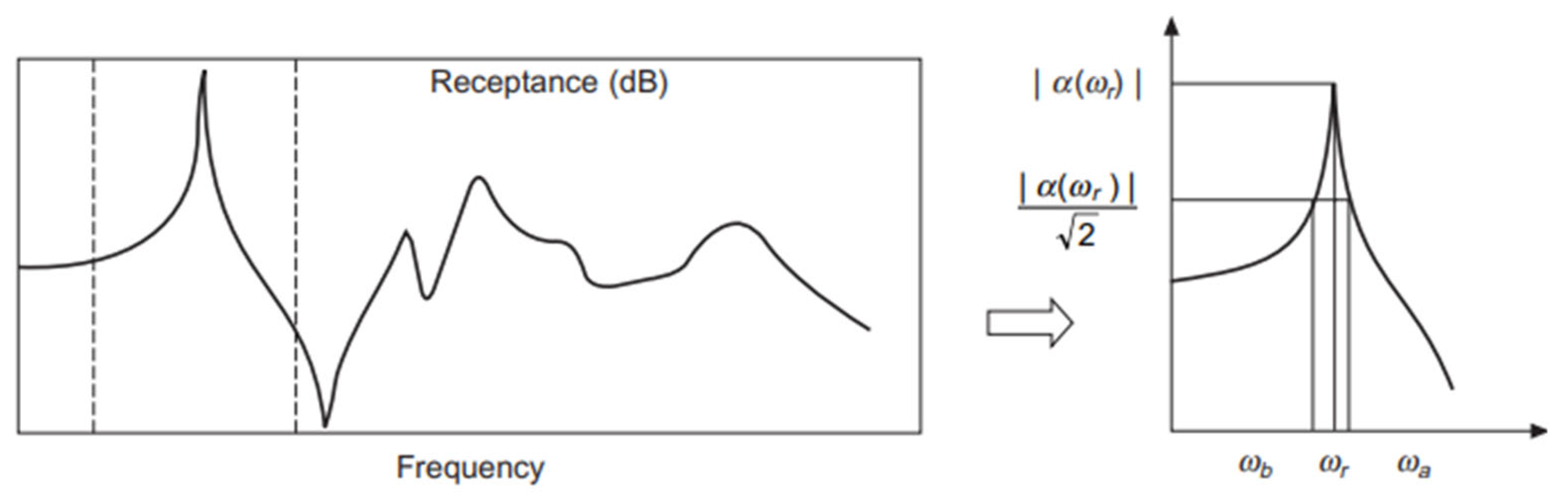


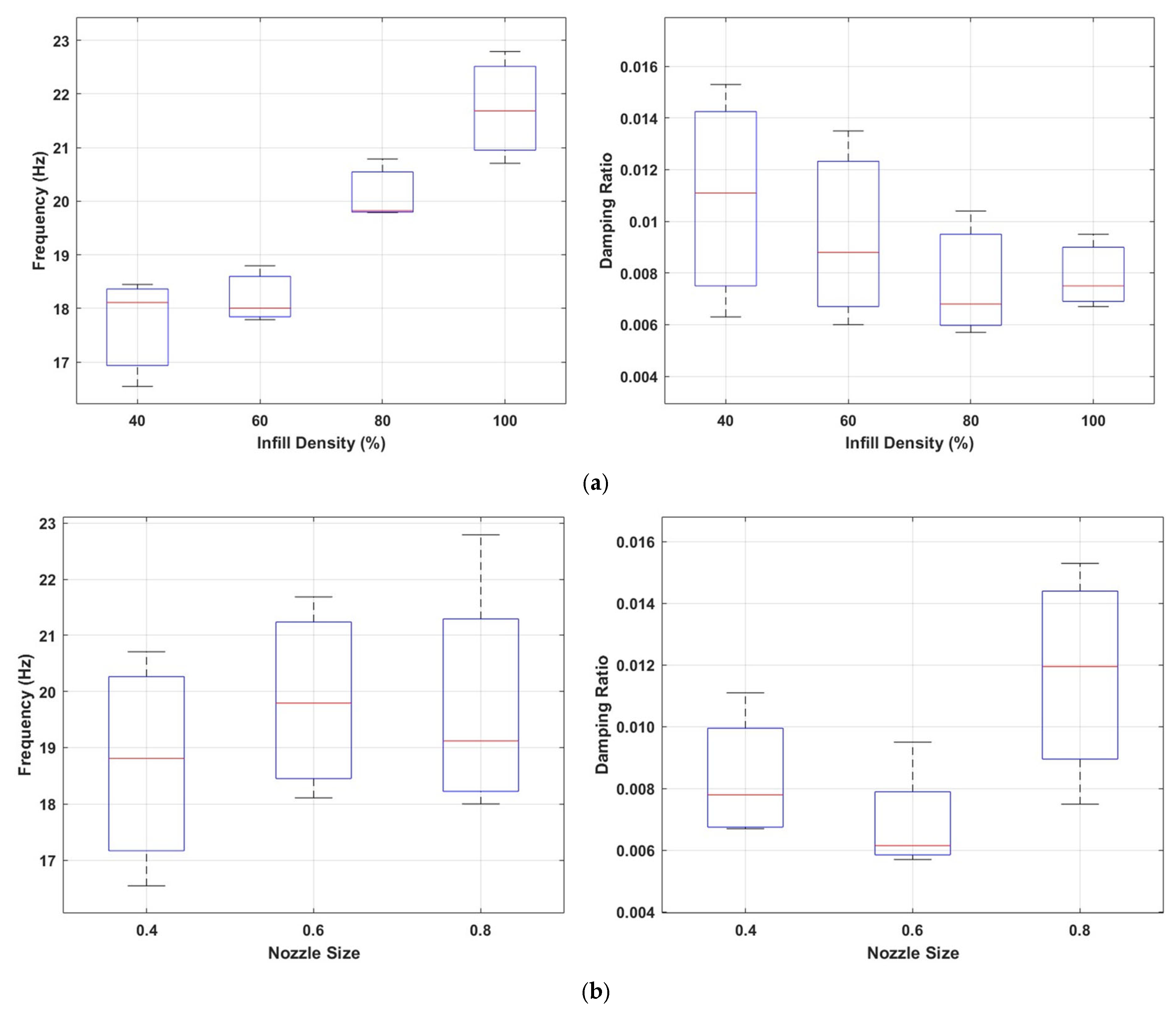



| Parameter | Levels/Variations |
|---|---|
| Nozzle Size (mm) | 0.4, 0.6, 0.8 |
| Infill Density (%) | 40, 60, 80, 100 |
| Infill Pattern | Line, Gyroid, Cubic, Triangular |
| Raster Angles for Line Pattern (°) | 0, ±45, 90 |
| Parameter | Ultimaker® ABS Red |
|---|---|
| Tensile modulus | 1618.5 MPa |
| Tensile stress at yield | 39.0 MPa |
| Tensile stress at break | 33.9 MPa |
| Flexural modulus | 2070.0 MPa |
| Flexural strength | 70.5 MPa |
| Melting temperature Density | 225–245 °C 1.1 g/cm3 |
| NS (mm) | ID (%) | Cubic (C) | Triangle (T) | Gyroid (G) | |||
|---|---|---|---|---|---|---|---|
| 1st Frequency | Damping Ratio | 1st Frequency | Damping Ratio | 1st Frequency | Damping Ratio | ||
| 0.4 | 40 | 16.543 | 0.0111 | 16.179 | 0.0110 | 15.126 | 0.0110 |
| 0.4 | 60 | 17.790 | 0.0088 | 17.775 | 0.0103 | 19.595 | 0.0091 |
| 0.4 | 80 | 19.823 | 0.0068 | 19.782 | 0.0102 | 19.684 | 0.0090 |
| 0.4 | 100 | 20.708 | 0.0067 | 21.581 | 0.0098 | 22.795 | 0.0076 |
| 0.6 | 40 | 18.111 | 0.0063 | 17.186 | 0.0102 | 16.989 | 0.0127 |
| 0.6 | 60 | 18.796 | 0.0060 | 18.378 | 0.0097 | 18.768 | 0.0110 |
| 0.6 | 80 | 20.789 | 0.0057 | 20.416 | 0.0088 | 21.289 | 0.0097 |
| 0.6 | 100 | 21.686 | 0.0095 | 21.803 | 0.0071 | 24.268 | 0.0077 |
| 0.8 | 40 | 18.448 | 0.0153 | 19.364 | 0.0122 | 18.004 | 0.0115 |
| 0.8 | 60 | 18.003 | 0.0135 | 19.339 | 0.0116 | 19.838 | 0.0108 |
| 0.8 | 80 | 19.790 | 0.0104 | 20.057 | 0.0106 | 21.883 | 0.0099 |
| 0.8 | 100 | 22.793 | 0.0075 | 22.192 | 0.0062 | 23.607 | 0.0087 |
| IP | Natural Frequencies | Damping Ratios | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
Value | Value | Value | Value | |||||||
| C1 | 0.924 | 0.86 | 0.554 | 0.00265 | 14.6 | 0.672 | 0.398 | −0.875 | 0.1500 | 2.46 |
| C2 | 0.977 | 0.94 | 0.630 | 0.00389 | 24.7 | 0.970 | 0.918 | 0.365 | 0.0067 | 18.5 |
| IP | Natural Frequencies | Damping Ratios | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
Value | Value | Value | Value | |||||||
| T1 | 0.975 | 0.955 | 0.860 | 9.49 × 10−5 | 47.6 | 0.919 | 0.852 | 0.468 | 0.00317 | 13.6 |
| T2 | 0.992 | 0.978 | 0.851 | 0.00052 | 69.5 | 0.984 | 0.956 | 0.738 | 0.00195 | 35.3 |
| IP | Natural Frequencies | Damping Ratios | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
Value | Value | Value | Value | |||||||
| G1 | 0.952 | 0.912 | 0.832 | 0.00068 | 23.8 | 0.922 | 0.856 | 0.642 | 0.00288 | 14.1 |
| G2 | 0.959 | 0.887 | 0.263 | 0.0123 | 13.4 | 0.979 | 0.943 | 0.692 | 0.00331 | 26.8 |
| IP | Natural Frequencies | Damping Ratios | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
Value | Value | Value | Value | |||||||
| L | 0.892 | 0.855 | 0.801 | 2.14 × 10−10 | 23.9 | 0.772 | 0.693 | 0.565 | 2.35 × 10−6 | 9.77 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Doğanay Kati, H.; He, F.; Khan, M.; Gökdağ, H.; Alshammari, Y.L.A. Effect of Printing Parameters on the Dynamic Characteristics of Additively Manufactured ABS Beams: An Experimental Modal Analysis and Response Surface Methodology. Polymers 2025, 17, 1615. https://doi.org/10.3390/polym17121615
Doğanay Kati H, He F, Khan M, Gökdağ H, Alshammari YLA. Effect of Printing Parameters on the Dynamic Characteristics of Additively Manufactured ABS Beams: An Experimental Modal Analysis and Response Surface Methodology. Polymers. 2025; 17(12):1615. https://doi.org/10.3390/polym17121615
Chicago/Turabian StyleDoğanay Kati, Hilal, Feiyang He, Muhammad Khan, Hakan Gökdağ, and Yousef Lafi A. Alshammari. 2025. "Effect of Printing Parameters on the Dynamic Characteristics of Additively Manufactured ABS Beams: An Experimental Modal Analysis and Response Surface Methodology" Polymers 17, no. 12: 1615. https://doi.org/10.3390/polym17121615
APA StyleDoğanay Kati, H., He, F., Khan, M., Gökdağ, H., & Alshammari, Y. L. A. (2025). Effect of Printing Parameters on the Dynamic Characteristics of Additively Manufactured ABS Beams: An Experimental Modal Analysis and Response Surface Methodology. Polymers, 17(12), 1615. https://doi.org/10.3390/polym17121615







