Multi-Objective Optimization of Injection Molding Process Parameters of Car Lamp Shell Based on Grey Correlation Analysis
Abstract
1. Introduction
2. Product Model and Initial Injection Molding Simulation Analysis
2.1. Car Lamp Shell Model and Grid Division
2.2. Setting of Forming Materials
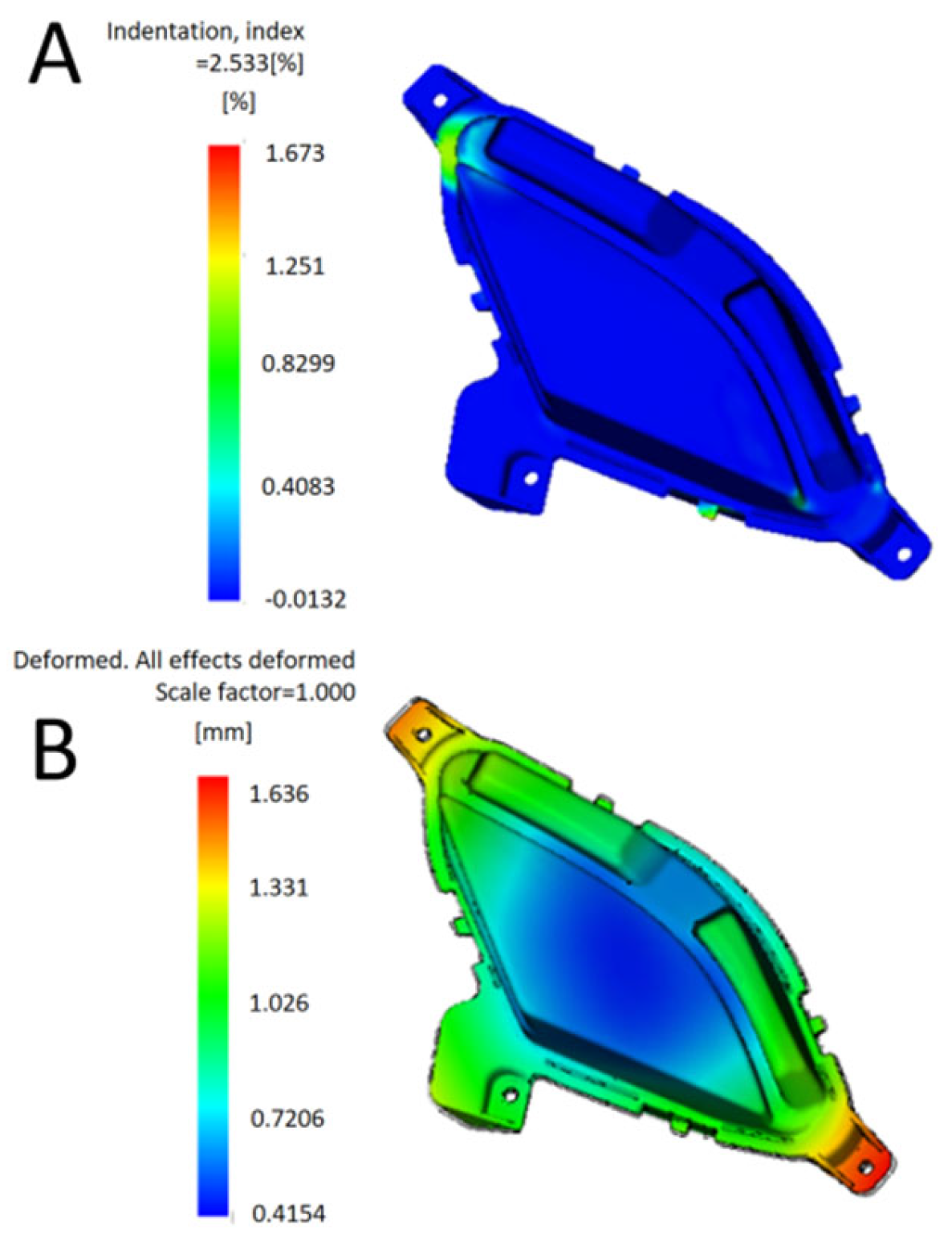
2.3. Initial Injection Molding Simulation Analysis
3. Test Scheme
3.1. Orthogonal Experimental Design
3.2. Orthogonal Test Results
4. Multi-Objective Grey Correlation Analysis
4.1. Signal-to-Noise Ratio Processing
4.2. Calculation of Grey Relational Degree
4.2.1. Non-Dimensional Processing
4.2.2. Grey Correlation Coefficient
4.2.3. Grey Correlation Degree
4.3. CRITIC Method to Calculate Weight
- Obtain data
- 2.
- Data standardization
- 3.
- Calculate information-bearing capacity
- 4.
- Information volume
- 5.
- Objective weight
5. Optimization of Process Parameters and Verification of Test Results
5.1. Optimization of Process Parameters
5.2. Verification of Test Results
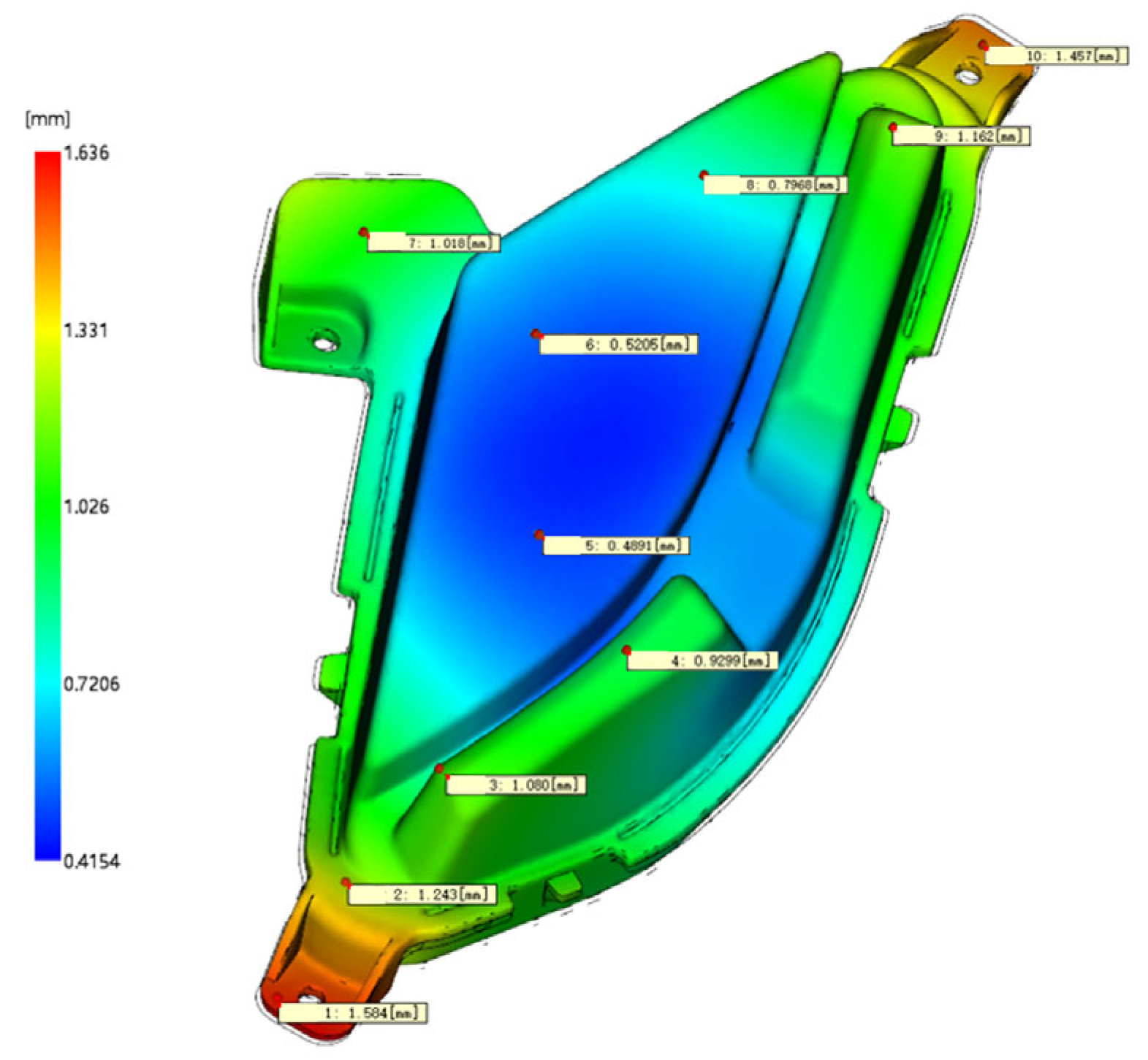
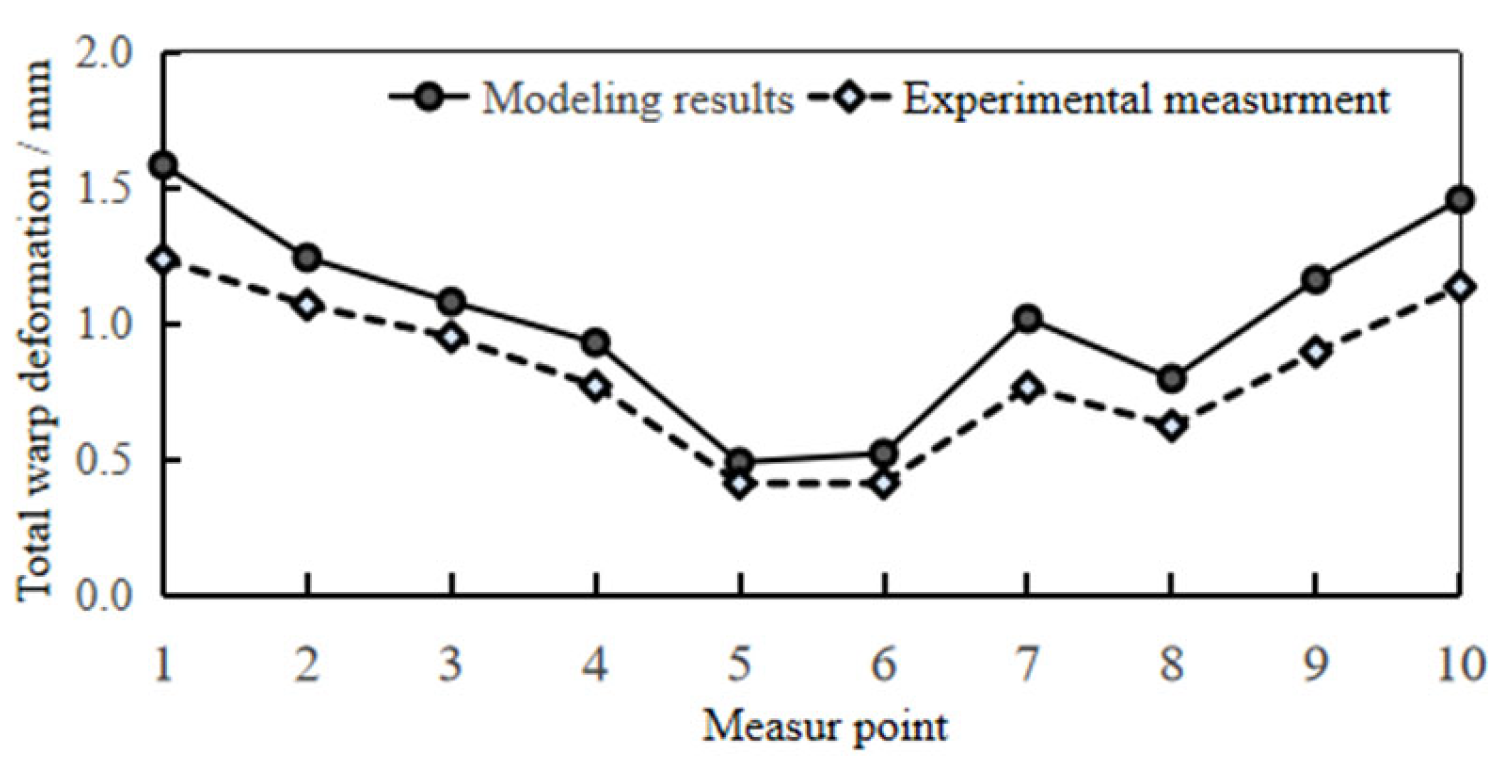
5.3. Production Verification
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Pang, L.F. Optimization of injection molding parameters for car headlight based on orthogonal test. China Plast. Ind. 2018, 46, 27–30+40. [Google Scholar]
- Yin, L.; Su, X.P.; Pan, J.; Qin, X. Optimization of injection molding process parameters for automotive lamp body based on response surface model and ASA algorithm. China Plast. Ind. 2021, 49, 82–85. [Google Scholar]
- Ding, H.F.; Jin, X.Z.; Gu, Y.Y.; Wan, J.X. Optimization of injection molding process for rear cover of lamp based on orthogonal test. China Synth. Resin Plast. 2022, 39, 55–59. [Google Scholar]
- Liu, X.; Fan, X.Y.; Guo, Y.H.; Li, C.X. Research status and development trend of injection molding process parameter optimization. Plast. Sci. Technol. 2021, 49, 106–110. [Google Scholar]
- Li, C.X.; Fan, X.Y.; Guo, Y.H.; Liu, X.; Cao, Y.L.; Li, L.L. Multi-objective optimization of injection molded parts with insert based on GRNN-NSGA. China Plast. Ind. 2021, 49, 84–88. [Google Scholar] [CrossRef]
- Ouyang, Y.; Liu, H.B. Injection molding of PPO/PA fender based on principal component analysis and grey relational analysis. China Plast. 2022, 36, 99–103. [Google Scholar]
- Wang, X.D.; Wang, Q.; Chen, T.; Zheng, Y. Optimization of multi-objective parameters for double color injection⁃molding based on grey relational analysis and entropy weight method. China Plast. 2022, 36, 115–120. [Google Scholar]
- Chen, Z.Y.; Zhu, J.Z.; Zhuang, Y. Study on Polypropylene Filled with Talc. Plast. Sci. Technol. 1992, 3, 7–10. [Google Scholar]
- Yao, J.L.; Hu, Q.L.; Gao, L. Toughening and Reinforcement of Polypropylene with Modified Talc. J. Jianghan Univ. (Nat. Sci. Ed.) 2014, 42, 45–48. [Google Scholar]
- Wu, S.T.; Liu, H.B.; Li, X.F. Multi-objective optimization of injection molding process of automobile bumper based on orthogonal experimental method. China Plast. Ind. 2012, 40, 60–64. [Google Scholar]
- Xue, M.Y.; Mei, Y.; Tang, F.Y.; Xiao, Z.K.; Luo, N.K. Multi-objective optimization of injection molding process based on grey relational analysis and establishment of PSO–SVM prediction model. Eng. Plast. Appl. 2021, 49, 58–64. [Google Scholar]
- Liang, Q.; Zhang, X.M.; Jia, Y.Y. Parameter optimization in cold extrusion process for spur gear based on grey relational analysis. J. Plast. Eng. 2021, 28, 69–76. [Google Scholar]
- Lü, Z.P.; Wu, M.; Song, Z.H.; Zhao, T.; Du, G. Comprehensive evaluation of power quality on CRITIC-TOPSIS method. Electr. Mach. Control. 2020, 24, 137–144. [Google Scholar]
- Roslan, N.; Abd Rahim, S.Z.; Abdellah, A.E.H.; Abdullah, M.M.A.B.; Błoch, K.; Pietrusiewicz, P.; Nabiałek, M.; Szmidla, J.; Kwiatkowski, D.; Correia Vasco, J.O.; et al. Optimisation of shrinkage and strength on thick plate part using recycled LDPE materials. Materials 2021, 14, 1795. [Google Scholar] [CrossRef] [PubMed]



| Processing Property | Parameter |
|---|---|
| Mold surface temperature/°C | 50 |
| Melt temperature/°C | 230 |
| MFI/g·(10 min)−1 | 1.62 |
| Melting range/°C | 165–180 |
| Mold temperature range/°C | 20–80 |
| Melt temperature range/°C | 200–280 |
| Ejection temperature/°C | 93 |
| Maximum shear stress/MPa | 0.26 |
| Maximum shear rate/s−1 | 24,000 |
| Level | Technological Parameter | |||||
|---|---|---|---|---|---|---|
| Mold Temperature (A)/°C | Melt Temperature (B)/°C | Injection Time (C)/s | Velocity to Pressure Control (D)/% | Dwell Pressure (E)/MPa | Dwell Time (F)/s | |
| 1 | 40 | 210 | 0.7 | 96 | 9 | 4 |
| 2 | 45 | 220 | 0.8 | 97 | 12 | 4.5 |
| 3 | 50 | 230 | 0.9 | 98 | 15 | 5 |
| 4 | 55 | 240 | 1 | 99 | 18 | 5.5 |
| 5 | 60 | 250 | 1.1 | 100 | 21 | 6 |
| Number | Technological Parameter | Evaluation Parameter | ||||||
|---|---|---|---|---|---|---|---|---|
| A | B | C | D | E | F | X | Y | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 3.236 | 2.429 |
| 2 | 1 | 2 | 3 | 4 | 5 | 2 | 1.875 | 1.584 |
| 3 | 1 | 3 | 5 | 2 | 4 | 3 | 2.212 | 1.678 |
| 4 | 1 | 4 | 2 | 5 | 3 | 4 | 2.674 | 1.791 |
| 5 | 1 | 5 | 4 | 3 | 2 | 5 | 3.040 | 1.86 |
| 6 | 2 | 1 | 5 | 4 | 3 | 5 | 1.923 | 1.879 |
| 7 | 2 | 2 | 2 | 2 | 2 | 1 | 2.462 | 2.019 |
| 8 | 2 | 3 | 4 | 5 | 1 | 2 | 2.931 | 2.072 |
| 9 | 2 | 4 | 1 | 3 | 5 | 3 | 2.446 | 1.655 |
| 10 | 2 | 5 | 3 | 1 | 4 | 4 | 2.726 | 1.708 |
| 11 | 3 | 1 | 4 | 2 | 5 | 4 | 1.691 | 1.645 |
| 12 | 3 | 2 | 1 | 5 | 4 | 5 | 2.066 | 1.726 |
| 13 | 3 | 3 | 3 | 3 | 3 | 1 | 2.553 | 1.918 |
| 14 | 3 | 4 | 5 | 1 | 2 | 2 | 2.881 | 1.949 |
| 15 | 3 | 5 | 2 | 4 | 1 | 3 | 3.445 | 2.015 |
| 16 | 4 | 1 | 3 | 5 | 2 | 3 | 2.126 | 2.029 |
| 17 | 4 | 2 | 5 | 3 | 1 | 4 | 3.371 | 2.362 |
| 18 | 4 | 3 | 2 | 1 | 5 | 5 | 2.194 | 1.669 |
| 19 | 4 | 4 | 4 | 4 | 4 | 1 | 2.637 | 1.819 |
| 20 | 4 | 5 | 1 | 2 | 3 | 2 | 3.057 | 1.873 |
| 21 | 5 | 1 | 2 | 3 | 4 | 2 | 1.868 | 1.802 |
| 22 | 5 | 2 | 4 | 1 | 3 | 3 | 2.209 | 1.894 |
| 23 | 5 | 3 | 1 | 4 | 2 | 4 | 2.649 | 1.964 |
| 24 | 5 | 4 | 3 | 2 | 1 | 5 | 3.136 | 2.034 |
| 25 | 5 | 5 | 5 | 5 | 5 | 1 | 2.702 | 1.738 |
| Number | Signal-to-Noise Ratio Processing | Dimensionless Processing | Grey Correlation Coefficient | Grey Relational Degree ƞ | |||
|---|---|---|---|---|---|---|---|
| αx | αy | βx | βy | γx | γy | ||
| 1 | −10.200 | −7.708 | 0.088 | 0 | 0.362 | 0.509 | 0.430 |
| 2 | −5.460 | −3.995 | 0.855 | 1 | 0.827 | 1 | 0.907 |
| 3 | −6.895 | −4.495 | 0.623 | 0.865 | 0.627 | 0.903 | 0.755 |
| 4 | −8.543 | −5.061 | 0.356 | 0.713 | 0.472 | 0.809 | 0.628 |
| 5 | −9.657 | −5.390 | 0.176 | 0.624 | 0.394 | 0.761 | 0.564 |
| 6 | −5.679 | −5.478 | 0.819 | 0.601 | 0.791 | 0.748 | 0.771 |
| 7 | −7.825 | −6.102 | 0.472 | 0.432 | 0.532 | 0.668 | 0.595 |
| 8 | −9.340 | −6.327 | 0.227 | 0.372 | 0.414 | 0.642 | 0.520 |
| 9 | −7.769 | −4.375 | 0.481 | 0.897 | 0.537 | 0.925 | 0.717 |
| 10 | −8.710 | −4.649 | 0.329 | 0.824 | 0.459 | 0.876 | 0.652 |
| 11 | −4.562 | −4.323 | 1 | 0.912 | 1 | 0.935 | 0.970 |
| 12 | −6.302 | −4.740 | 0.719 | 0.799 | 0.700 | 0.861 | 0.775 |
| 13 | −8.141 | −5.656 | 0.421 | 0.552 | 0.504 | 0.724 | 0.606 |
| 14 | −9.190 | −5.796 | 0.251 | 0.515 | 0.424 | 0.706 | 0.555 |
| 15 | −10.743 | −6.085 | 0 | 0.437 | 0.333 | 0.670 | 0.489 |
| 16 | −6.551 | −6.145 | 0.678 | 0.421 | 0.668 | 0.663 | 0.666 |
| 17 | −10.555 | −7.465 | 0.031 | 0.065 | 0.343 | 0.530 | 0.430 |
| 18 | −6.824 | −4.449 | 0.634 | 0.878 | 0.636 | 0.912 | 0.764 |
| 19 | −8.422 | −5.196 | 0.376 | 0.676 | 0.481 | 0.789 | 0.624 |
| 20 | −9.705 | −5.450 | 0.168 | 0.608 | 0.391 | 0.752 | 0.559 |
| 21 | −5.427 | −5.115 | 0.860 | 0.698 | 0.832 | 0.801 | 0.818 |
| 22 | −6.883 | −5.547 | 0.624 | 0.582 | 0.629 | 0.739 | 0.680 |
| 23 | −8.461 | −5.862 | 0.369 | 0.497 | 0.478 | 0.698 | 0.580 |
| 24 | −9.927 | −6.167 | 0.132 | 0.415 | 0.378 | 0.661 | 0.509 |
| 25 | −8.633 | −4.800 | 0.341 | 0.783 | 0.465 | 0.851 | 0.644 |
| Evaluation Parameter | Volatility Indicator Sj | Conflict Index Aj | Information Content Cj | Weight Wj |
|---|---|---|---|---|
| X | 0.284 | 0.348 | 0.099 | 53.60% |
| Y | 0.246 | 0.348 | 0.086 | 46.40% |
| Level | Grey Relational Proportion | |||||
|---|---|---|---|---|---|---|
| Mold Temperature (A) | Melt Temperature (B) | Injection Time (C) | Velocity to Pressure Control (D) | Dwell Pressure (E) | Dwell Time (F) | |
| 1 | 0.657 | 0.73 | 0.612 | 0.616 | 0.476 | 0.58 |
| 2 | 0.651 | 0.677 | 0.659 | 0.677 | 0.592 | 0.672 |
| 3 | 0.679 | 0.645 | 0.668 | 0.627 | 0.649 | 0.661 |
| 4 | 0.608 | 0.607 | 0.672 | 0.674 | 0.725 | 0.652 |
| 5 | 0.646 | 0.582 | 0.631 | 0.647 | 0.800 | 0.677 |
| Range | 0.071 | 0.148 | 0.06 | 0.061 | 0.324 | 0.097 |
| Sort | 4 | 2 | 6 | 5 | 1 | 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shan, R.; Liu, A.; Jia, S.; Liu, C.; Yang, W. Multi-Objective Optimization of Injection Molding Process Parameters of Car Lamp Shell Based on Grey Correlation Analysis. Polymers 2025, 17, 1524. https://doi.org/10.3390/polym17111524
Shan R, Liu A, Jia S, Liu C, Yang W. Multi-Objective Optimization of Injection Molding Process Parameters of Car Lamp Shell Based on Grey Correlation Analysis. Polymers. 2025; 17(11):1524. https://doi.org/10.3390/polym17111524
Chicago/Turabian StyleShan, Ruixia, Anqin Liu, Sen Jia, Changyou Liu, and Wenguang Yang. 2025. "Multi-Objective Optimization of Injection Molding Process Parameters of Car Lamp Shell Based on Grey Correlation Analysis" Polymers 17, no. 11: 1524. https://doi.org/10.3390/polym17111524
APA StyleShan, R., Liu, A., Jia, S., Liu, C., & Yang, W. (2025). Multi-Objective Optimization of Injection Molding Process Parameters of Car Lamp Shell Based on Grey Correlation Analysis. Polymers, 17(11), 1524. https://doi.org/10.3390/polym17111524






