Unraveling the Print–Structure–Property Relationships in the FFF of PEEK: A Critical Assessment of Print Parameters
Abstract
1. Introduction
2. The Theoretical Background on Design of Experiments (DoE)
2.1. Full Factorial Design
2.2. Fractional Factorial Design
2.3. Response Surface Methodology (RSM)
2.4. Taguchi Methods
3. Materials and Methods
3.1. Materials
3.2. The Experimental Design Using DoE
3.2.1. Tensile Tests
3.2.2. Two-Dimensional X-Ray Diffraction (WAXS)
3.2.3. X-Ray Computed Micro-Tomography
3.2.4. The Dynamic Mechanical Thermal Analysis (DMTA)
4. Results
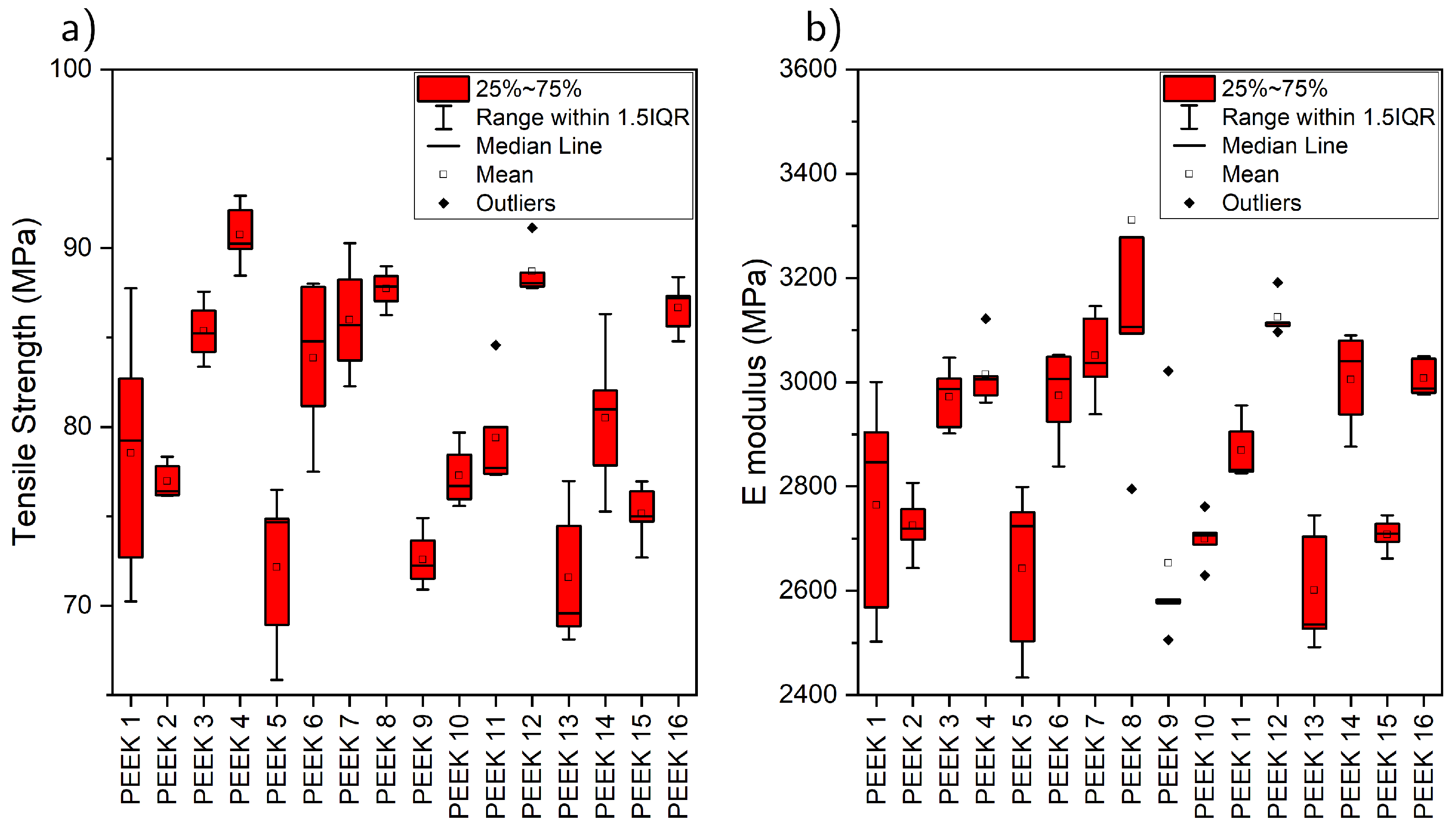
4.1. Mechanical Behavior
| TNozzle | nozzle temperature (°C) |
| TBed | bed temperature (°C) |
| VPrint | printing speed (mm/s) |
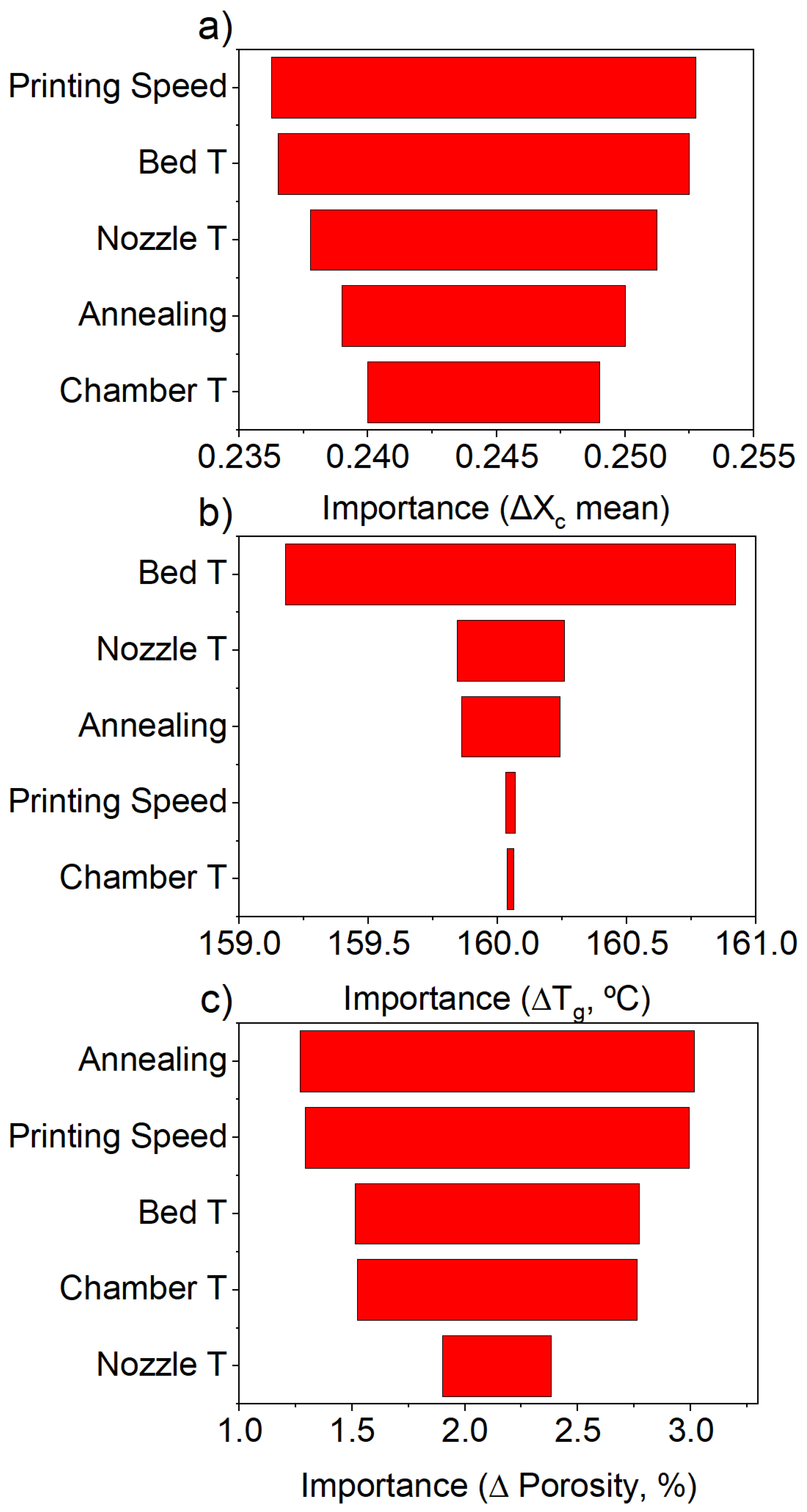
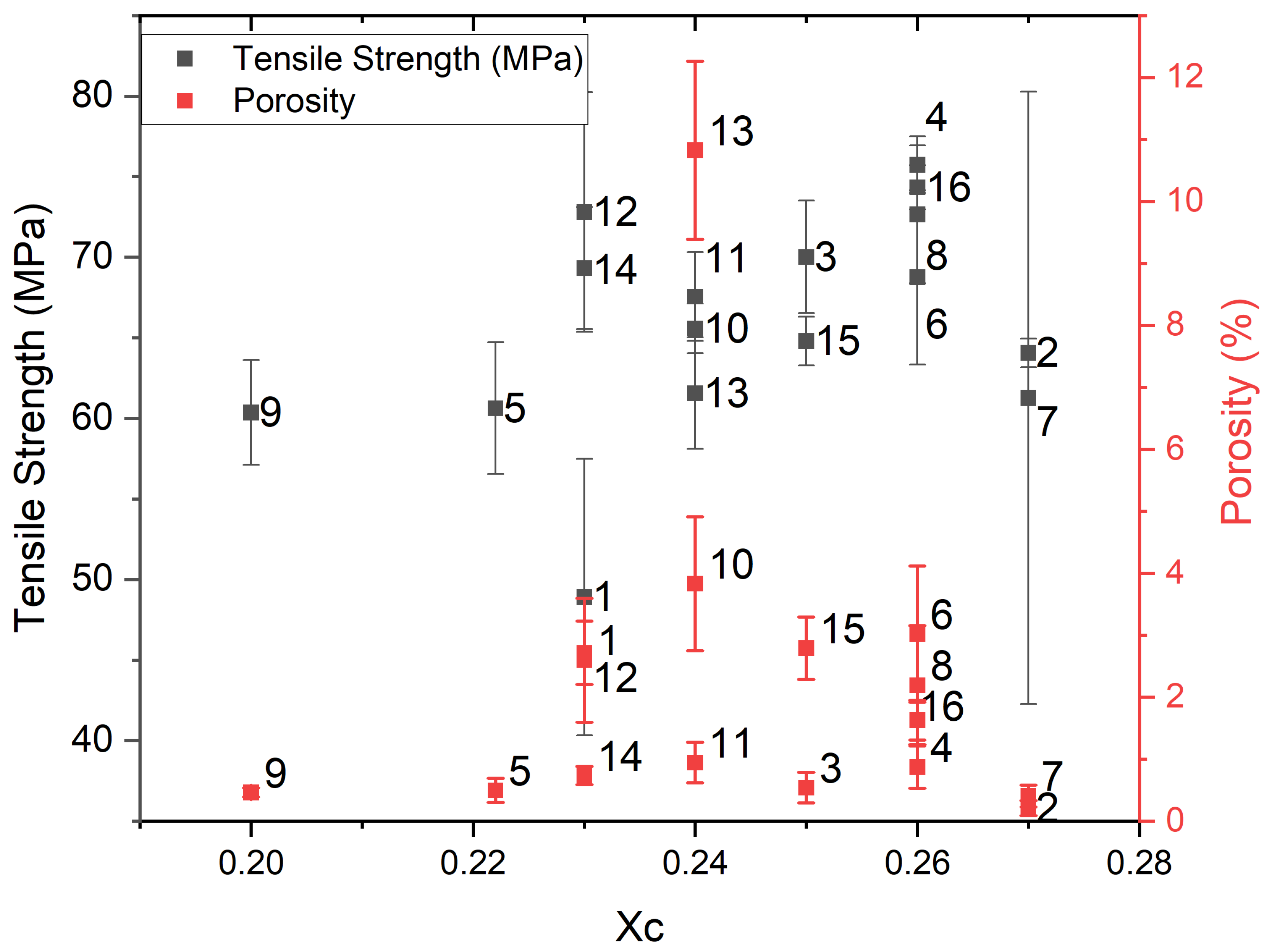
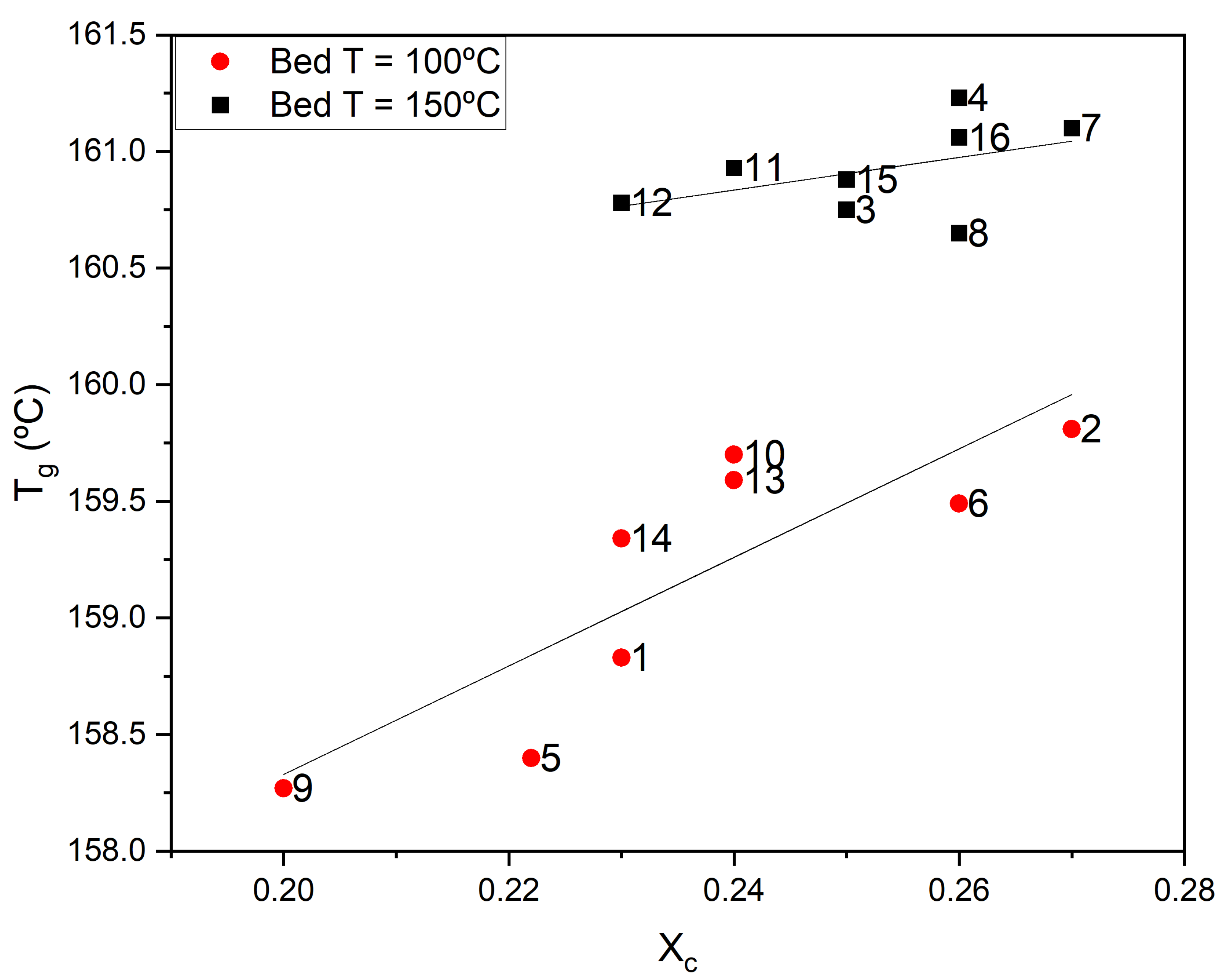
4.2. The Microstructural Analysis
5. Discussion
5.1. Model Validation
5.2. Process–Structure–Property Relationships in FFF of PEEK
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kalra, S.; Munjal, B.S.; Singh, V.R.; Mahajan, M.; Bhattacharya, B. Investigations on the suitability of PEEK material under space environment conditions and its application in a parabolic space antenna. Adv. Space Res. 2019, 63, 4039–4045. [Google Scholar] [CrossRef]
- Bashandeh, K.; Tsigkis, V.; Lan, P.; Polycarpou, A.A. Extreme environment tribological study of advanced bearing polymers for space applications. Tribol. Int. 2021, 153, 106634. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, L.; Hou, X.; Wu, J. Investigation on dielectrical and space charge characteristics of peek insulation used in aerospace high-voltage system. IEEJ Trans. Electr. Electron. Eng. 2020, 15, 172–178. [Google Scholar] [CrossRef]
- Luo, M.; Tian, X.; Shang, J.; Yun, J.; Zhu, W.; Li, D.; Qin, Y. Bi-scale interfacial bond behaviors of CCF/PEEK composites by plasma-laser cooperatively assisted 3D printing process. Compos. Part A Appl. Sci. Manuf. 2020, 131, 105812. [Google Scholar] [CrossRef]
- Shekar, R.I.; Kotresh, T.M.; Rao, P.M.D.; Kumar, K. Properties of high modulus PEEK yarns for aerospace applications. J. Appl. Polym. Sci. 2009, 112, 2497–2510. [Google Scholar] [CrossRef]
- Oladapo, B.I.; Zahedi, S.A.; Ismail, S.O. Mechanical performances of hip implant design and fabrication with PEEK composite. Polymer 2021, 227, 123865. [Google Scholar] [CrossRef]
- Chen, P.; Wang, H.; Su, J.; Tian, Y.; Wen, S.; Su, B.; Yang, C.; Chen, B.; Zhou, K.; Yan, C.; et al. Recent Advances on High-Performance Polyaryletherketone Materials for Additive Manufacturing. Adv. Mater. 2022, 34, e2200750. [Google Scholar] [CrossRef]
- Zhang, H.; Guo, Z.; Zhang, Z.; Wu, G.; Sang, L. Biomimetic design and fabrication of PEEK and PEEK/CF cage with minimal surface structures by fused filament fabrication. J. Mater. Res. Technol. 2023, 26, 5001–5015. [Google Scholar] [CrossRef]
- Li, S.; Wang, T.; Chen, S.; Li, Y.; Zou, Y.; Cao, B.; Hu, J.; Tan, X.; Wang, B. Compressive properties and biocompatibility of additively manufactured lattice structures by using bioactive materials. Thin-Walled Struct. 2024, 205, 112469. [Google Scholar] [CrossRef]
- Mishra, S.; Chowdhary, R. PEEK materials as an alternative to titanium in dental implants: A systematic review. Clin. Implant. Dent. Relat. Res. 2019, 21, 208–222. [Google Scholar] [CrossRef]
- Francis, J.N.; Banerjee, I.; Chugh, A.; Singh, J. Additive manufacturing of polyetheretherketone and its composites: A review. Polym. Compos. 2022, 43, 5802–5819. [Google Scholar] [CrossRef]
- Rahman, K.M.; Letcher, T.; Reese, R. (Eds.) Mechanical Properties of Additively Manufactured PEEK Components Using Fused Filament Fabrication. In Proceedings of the ASME 2015 International Mechanical Engineering Congress and Exposition. Volume 2A: Advanced Manufacturing, Houston, TX, USA, 13–19 November 2015; V02AT02A009. ASME: New York, NY, USA, 2015. [Google Scholar] [CrossRef]
- Valentan, B.; Kadivink, Z.; Brajlih, T.; Anderson, A. Drstvensek, I. Processing Poly(ether etherketone) on a 3D printer for thermoplastic modelling. Mater. Technol. 2013, 47, 715–721. [Google Scholar]
- Picard, M.; Mohanty, A.K.; Misra, M. Recent advances in additive manufacturing of engineering thermoplastics: Challenges and opportunities. RSC Adv. 2020, 10, 36058–36089. [Google Scholar] [CrossRef]
- Das, A.; Chatham, C.A.; Fallon, J.J.; Zawaski, C.E.; Gilmer, E.L.; Williams, C.B.; Bortner, M.J. Current understanding and challenges in high temperature additive manufacturing of engineering thermoplastic polymers. Addit. Manuf. 2020, 34, 101218. [Google Scholar] [CrossRef]
- Pu, J.; McIlroy, C.; Jones, A.; Ashcroft, I. Understanding mechanical properties in fused filament fabrication of polyether ether ketone. Addit. Manuf. 2021, 37, 101673. [Google Scholar] [CrossRef]
- Liaw, C.Y.; Tolbert, J.W.; Chow, L.W.; Guvendiren, M. Interlayer bonding strength of 3D printed PEEK specimens. Soft Matter 2021, 17, 4775–4789. [Google Scholar] [CrossRef]
- Wu, W.; Geng, P.; Li, G.; Zhao, D.; Zhang, H.; Zhao, J. Influence of Layer Thickness and Raster Angle on the Mechanical Properties of 3D-Printed PEEK and a Comparative Mechanical Study between PEEK and ABS. Materials 2015, 8, 5834–5846. [Google Scholar] [CrossRef] [PubMed]
- Deng, X.; Zeng, Z.; Peng, B.; Yan, S.; Ke, W. Mechanical Properties Optimization of Poly-Ether-Ether-Ketone via Fused Deposition Modeling. Materials 2018, 11, 216. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F. Cellular Solids; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar] [CrossRef]
- El Magri, A.; El Mabrouk, K.; Vaudreuil, S.; Chibane, H.; Touhami, M.E. Optimization of printing parameters for improvement of mechanical and thermal performances of 3D printed poly(ether ether ketone) parts. J. Appl. Polym. Sci. 2020, 137, 49087. [Google Scholar] [CrossRef]
- Pulipaka, A.; Gide, K.M.; Beheshti, A.; Bagheri, Z.S. Effect of 3D printing process parameters on surface and mechanical properties of FFF-printed PEEK. J. Manuf. Process. 2023, 85, 368–386. [Google Scholar] [CrossRef]
- Ree, B.J.; Zheng, B.; Abbott, A.; Smieska, L.M.; Page, K.A.; Woll, A.R.; Renwick, Z.; Koerner, H. Mapping Crystallization Kinetics during 3D Printing of Poly(ether ether ketone). Macromolecules 2024, 57, 2810–2817. [Google Scholar] [CrossRef]
- Wang, R.; Cheng, K.j.; Advincula, R.C.; Chen, Q. On the thermal processing and mechanical properties of 3D-printed polyether ether ketone. MRS Commun. 2019, 9, 1046–1052. [Google Scholar] [CrossRef]
- Fischer, R.A. The Design of Experiments; Oliver & Boyd: Edinburgh, UK; London, UK, 1937. [Google Scholar]
- Plackett, R.L.; Burman, J.P. The Design of Optimum Multifactorial Experiments. Biometrika 1946, 33, 305. [Google Scholar] [CrossRef]
- Durakovic, B. Design of experiments application, concepts, examples: State of the art. Period. Eng. Nat. Sci. (PEN) 2017, 5, 421–439. [Google Scholar] [CrossRef]
- ISO 527-2:2012; Plastics—Determination of Tensile Properties: Part 2: Test Conditions for Moulding and Extrusion Plastics. ISO: Geneva, Switzerland, 2012.
- Montgomery, D.C. Design and Analysis of Experiments, 9th ed.; John Wiley & Sons Inc: Hoboken, NJ, USA, 2017. [Google Scholar]
- Alvaredo, A.; Martín, M.I.; Castell, P.; Guzmán de Villoria, R.; Fernández-Bláquez, J.P. Non-Isothermal Crystallization Behavior of PEEK/Graphene Nanoplatelets Composites from Melt and Glass States. Polymers 2019, 11, 124. [Google Scholar] [CrossRef]
- Schindelin, J.; Arganda-Carreras, I.; Frise, E.; Kaynig, V.; Longair, M.; Pietzsch, T.; Preibisch, S.; Rueden, C.; Saalfeld, S.; Schmid, B.; et al. Fiji: An open-source platform for biological-image analysis. Nat. Methods 2012, 9, 676–682. [Google Scholar] [CrossRef]
- Lalegani Dezaki, M.; Mohd Ariffin, M.K.A.; Hatami, S. An overview of fused deposition modelling (FDM): Research, development and process optimisation. Rapid Prototyp. J. 2021, 27, 562–582. [Google Scholar] [CrossRef]
- Medellin-Rodriguez, F.J.; Phillips, P.J. Crystallization and structure–mechanical property relations in poly(aryl ether ether ketone) [PEEK]. Polym. Eng. Sci. 1990, 30, 860–869. [Google Scholar] [CrossRef]
- Cheng, S.Z.D.; Cao, M.Y.; Wunderlich, B. Glass transition and melting behavior of poly(oxy-1,4-phenyleneoxy-1,4-phenylenecarbonyl-1,4-phenylene) (PEEK). Macromolecules 1986, 19, 1868–1876. [Google Scholar] [CrossRef]
- Kida, T.; Yamaguchi, M. Role of Rigid–Amorphous chains on mechanical properties of polypropylene solid using DSC, WAXD, SAXS, and Raman spectroscopy. Polymer 2022, 249, 124834. [Google Scholar] [CrossRef]
- Garcia-Gonzalez, D.; Rusinek, A.; Jankowiak, T.; Arias, A. Mechanical impact behavior of polyether–ether–ketone (PEEK). Compos. Struct. 2015, 124, 88–99. [Google Scholar] [CrossRef]
- Venkatram, S.; McCollum, J.; Stingelin, N.; Brettmann, B. A close look at polymer degree of crystallinity versus polymer crystalline quality. Polym. Int. 2023, 72, 855–860. [Google Scholar] [CrossRef]
- Yi, N.; Davies, R.; Chaplin, A.; McCutchion, P.; Ghita, O. Slow and fast crystallising poly aryl ether ketones (PAEKs) in 3D printing: Crystallisation kinetics, morphology, and mechanical properties. Addit. Manuf. 2021, 39, 101843. [Google Scholar] [CrossRef]
- Arif, M.F.; Kumar, S.; Varadarajan, K.M.; Cantwell, W.J. Performance of biocompatible PEEK processed by fused deposition additive manufacturing. Mater. Des. 2018, 146, 249–259. [Google Scholar] [CrossRef]
- Vaezi, M.; Yang, S. Extrusion-based additive manufacturing of PEEK for biomedical applications. Virtual Phys. Prototyp. 2015, 10, 123–135. [Google Scholar] [CrossRef]



| Print Experiment | Nozzle T (°C) | Bed T (°C) | Chamber T (°C) | Printing Speed (mm/s) | Annealing T (°C) |
|---|---|---|---|---|---|
| 1 | 420 | 100 | 80 | 15 | 390 |
| 2 | 455 | 100 | 80 | 15 | off |
| 3 | 420 | 150 | 80 | 15 | off |
| 4 | 455 | 150 | 80 | 15 | 390 |
| 5 | 420 | 100 | 100 | 15 | off |
| 6 | 455 | 100 | 100 | 15 | 390 |
| 7 | 420 | 150 | 100 | 15 | 390 |
| 8 | 455 | 150 | 100 | 15 | off |
| 9 | 420 | 100 | 80 | 60 | off |
| 10 | 455 | 100 | 80 | 60 | 390 |
| 11 | 420 | 150 | 80 | 60 | 390 |
| 12 | 455 | 150 | 80 | 60 | off |
| 13 | 420 | 100 | 100 | 60 | 390 |
| 14 | 455 | 100 | 100 | 60 | off |
| 15 | 420 | 150 | 100 | 60 | off |
| 16 | 455 | 150 | 100 | 60 | 390 |
| Experiment | Tensile Strength (MPa) | E Modulus (MPa) | Xc | Tg (°C) | Porosity (%) |
|---|---|---|---|---|---|
| 1 | 79.0 ± 7 | 2800 ± 200 | 0.23 | 158.8 | 2.6 ± 1.0 |
| 2 | 77.0 ± 1.0 | 2730 ± 60 | 0.27 | 159.8 | 0.21 ± 0.12 |
| 3 | 85.0 ± 2 | 2970 ± 60 | 0.25 | 160.8 | 0.5 ± 0.2 |
| 4 | 91.0 ± 2 | 3020 ± 60 | 0.26 | 161.2 | 0.9 ± 0.3 |
| 5 | 72.0 ± 5 | 2600 ± 200 | 0.22 | 158.4 | 0.5 ± 0.2 |
| 6 | 84.0 ± 5 | 2970 ± 90 | 0.26 | 159.5 | 3.0 ± 1.1 |
| 7 | 86.0 ± 3 | 3050 ± 90 | 0.27 | 161.1 | 0.4 ± 0.2 |
| 8 | 87.7 ± 1.1 | 3300 ± 600 | 0.26 | 160.7 | 2.2 ± 1.0 |
| 9 | 73.0 ± 2 | 2700 ± 200 | 0.2 | 158.3 | 0.46 ± 0.07 |
| 10 | 77.0 ± 2 | 2700 ± 50 | 0.24 | 159.7 | 3.8 ± 1.1 |
| 11 | 79.0 ± 3 | 2870 ± 60 | 0.24 | 160.9 | 1.0 ± 0.3 |
| 12 | 88.7 ± 1.4 | 3130 ± 40 | 0.23 | 160.8 | 2.7 ± 0.5 |
| 13 | 72.0 ± 4 | 2600 ± 120 | 0.24 | 159.6 | 10.8 ± 1.4 |
| 14 | 81.0 ± 4 | 3010 ± 90 | 0.23 | 159.3 | 0.7 ± 0.2 |
| 15 | 75.0 ± 2 | 2710 ± 30 | 0.25 | 160.9 | 2.8 ± 0.5 |
| 16 | 86.7 ± 1.4 | 3010 ± 40 | 0.26 | 161.1 | 1.6 ± 0.3 |
| Condition | Nozzle T | Bed T | Chamber T | Printing Speed | Annealing T |
|---|---|---|---|---|---|
| (°C) | (°C) | (°C) | (mm/s) | (°C) | |
| 1 | 440 | 150 | 100 | 15 | Off |
| 2 | 430 | 100 | 100 | 15 | Off |
| Condition | Model Prediction | Experimental Mean ± SD | Distance to Model |
|---|---|---|---|
| E Modulus (MPa, 1) | 2931.91 | 2900 ± 200 | 0.26 |
| E Modulus (MPa, 2) | 2686.31 | 2740 ± 90 | 0.67 |
| Tensile Strength (MPa, 1) | 91.89 | 91.4 ± 0.8 | 0.60 |
| Tensile Strength (MPa, 2) | 79.79 | 80.5 ± 0.8 | 0.87 |
| Reference | Chamber T (°C) |
|---|---|
| Ree et al. (2024) [23] | Not reported, apparently none |
| Pulipaca et al. (2023) [22] | 70 |
| Liaw et al. (2021) [17] | 80 |
| Pu et al. (2021) [16] | 90 |
| Yi et al. (2021) [38] | 60 |
| El Magri et al. (2020) [21] | 30 |
| Arif et al. (2018) [39] | Not reported, apparently none |
| Deng et al. (2018) [19] | Not reported, apparently none |
| Wu et al. (2015) [18] | Not reported, apparently none |
| Vaezi and Yang (2015) [40] | 80 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Doyle, L.; García-Molleja, J.; Fernández-Blázquez, J.P.; González, C. Unraveling the Print–Structure–Property Relationships in the FFF of PEEK: A Critical Assessment of Print Parameters. Polymers 2025, 17, 1444. https://doi.org/10.3390/polym17111444
Doyle L, García-Molleja J, Fernández-Blázquez JP, González C. Unraveling the Print–Structure–Property Relationships in the FFF of PEEK: A Critical Assessment of Print Parameters. Polymers. 2025; 17(11):1444. https://doi.org/10.3390/polym17111444
Chicago/Turabian StyleDoyle, Lucía, Javier García-Molleja, Juan Pedro Fernández-Blázquez, and Carlos González. 2025. "Unraveling the Print–Structure–Property Relationships in the FFF of PEEK: A Critical Assessment of Print Parameters" Polymers 17, no. 11: 1444. https://doi.org/10.3390/polym17111444
APA StyleDoyle, L., García-Molleja, J., Fernández-Blázquez, J. P., & González, C. (2025). Unraveling the Print–Structure–Property Relationships in the FFF of PEEK: A Critical Assessment of Print Parameters. Polymers, 17(11), 1444. https://doi.org/10.3390/polym17111444







