Prerequisites for Developing a Classification of Phase Transitions in Systems Based on Thermosensitive Polymers: Use of a Semi-Empirical Model
Abstract
1. Introduction
2. Methods
3. Results
4. Discussions
4.1. Analysis of Experimental Results
4.2. Proposed Semi-Empirical Model
4.3. Opportunities for Further Development of Proposed Approach
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kojima, H. Studies on the phase transition of hydrogels and aqueous solutions of thermosensitive polymers. Polym. J. 2018, 50, 411–418. [Google Scholar] [CrossRef]
- Koland, M.; Narayanan Vadakkepushpakath, A.; John, A.; Tharamelveliyil Rajendran, A.; Raghunath, I. Thermosensitive In Situ Gels for Joint Disorders: Pharmaceutical Considerations in Intra-Articular Delivery. Gels 2022, 8, 723. [Google Scholar] [CrossRef] [PubMed]
- Quoika, P.K.; Kamenik, A.S.; Fernández-Quintero, M.L.; Zacharias, M.; Liedl, K.R. Water model determines thermosensitive and physicochemical properties of poly(N-isopropylacrylamide) in molecular simulations. Front. Mater. 2023, 10, 1005781. [Google Scholar] [CrossRef]
- Keldibekova, R.; Suleimenova, S.; Nurgozhina, G.; Kopishev, E. Interpolymer Complexes Based on Cellulose Ethers: Application. Polymers 2023, 15, 3326. [Google Scholar] [CrossRef]
- Bakirov, A.; Kopishev, E.; Kadyrzhan, K.; Donbaeva, E.; Zhaxybayeva, A.; Duisembiyev, M.; Suyundikova, F.; Suleimenov, I. The Method of Direct and Reverse Phase Portraits as a Tool for Systematizing the Results of Studies of Phase Transitions in Solutions of Thermosensitive Polymers. Gels 2024, 10, 395. [Google Scholar] [CrossRef]
- Niu, X.; Tian, B.; Zhu, Q.; Dkhil, B.; Duan, C. Ferroelectric polymers for neuromorphic computing. Appl. Phys. Rev. 2022, 9, 021309. [Google Scholar] [CrossRef]
- Mikhaylov, A.N.; Gryaznov, E.G.; Koryazhkina, M.N.; Bordanov, I.A.; Shchanikov, S.A.; Telminov, O.A.; Kazantsev, V.B. Neuromorphic Computing Based on CMOS-Integrated Memristive Arrays: Current State and Perspectives. Supercomput. Front. Innov. 2023, 10, 77–103. [Google Scholar] [CrossRef]
- Lee, H.R.; Won, Y.; Oh, J.H. Neuromorphic bioelectronics based on semiconducting polymers. J. Polym. Sci. 2022, 60, 348–376. [Google Scholar] [CrossRef]
- Shaikhutdinov, R.; Mun, G.; Kopishev, E.; Bakirov, A.; Kabdushev, S.; Baipakbaeva, S.; Suleimenov, I. Effect of the Formation of Hydrophilic and Hydrophobic–Hydrophilic Associates on the Behavior of Copolymers of N-Vinylpyrrolidone with Methyl Acrylate in Aqueous Solutions. Polymers 2024, 16, 584. [Google Scholar] [CrossRef]
- Fu, F.; Wang, J.; Zeng, H.; Yu, J. Functional Conductive Hydrogels for Bioelectronics. ACS Mater. Lett. 2020, 2, 1287–1301. [Google Scholar] [CrossRef]
- Pan, Z.; Wang, Z.Y.; Wang, M.H.; Yang, L.; Yu, S.H. Adhesive aero-hydrogel hybrid conductor assembled from silver nanowire architectures. Sci. China Mater. 2021, 64, 2868–2876. [Google Scholar] [CrossRef]
- Kabdushev, S.; Mun, G.; Suleimenov, I.; Alikulov, A.; Shaikhutdinov, R.; Kopishev, E. Formation of Hydrophobic–Hydrophilic Associates in the N-Vinylpyrrolidone and Vinyl Propyl Ether Copolymer Aqueous Solutions. Polymers 2023, 15, 3578. [Google Scholar] [CrossRef]
- Qiu, Y.; Ye, H.; Zhang, H.; Zheng, Y. Machine learning-driven optimization design of hydrogel-based negative hydration expansion metamaterials. CAD Comput. Aided Des. 2024, 166, 103631. [Google Scholar] [CrossRef]
- Ma, L.H.; Wang, S.D.; Liu, J.; Gao, H.; Zhou, W. The design and investigation of hydrogel-based metamaterials with ultra large negative hygroscopic expansion ratio. Int. J. Smart Nano Mater. 2022, 13, 114–129. [Google Scholar] [CrossRef]
- Wang, B.; Moura, A.G.; Chen, J.; Erturk, A.; Hu, Y. Characterization of hydrogel structural damping. Extrem. Mech. Lett. 2020, 40, 100841. [Google Scholar] [CrossRef]
- Kumar, R.; Jin, Y.; Marre, S.; Poncelet, O.; Brunet, T.; Leng, J.; Mondain-Monval, O. Drying kinetics and acoustic properties of soft porous polymer materials. J. Porous Mater. 2021, 28, 249–259. [Google Scholar] [CrossRef]
- Niu, D.; Jiang, W.; Li, D.; Ye, G.; Luo, F.; Liu, H. Reconfigurable shape-morphing flexible surfaces realized by individually addressable photoactuator arrays. Smart Mater. Struct. 2021, 30, 125032. [Google Scholar] [CrossRef]
- Kuang, X.; Roach, D.J.; Hamel, C.M.; Yu, K.; Jerry Qi, H. Materials, design, and fabrication of shape programmable polymers. Multifunct. Mater. 2020, 3, 032002. [Google Scholar] [CrossRef]
- Ivanov, A.V.; Ferapontov, N.B.; Gagarin, A.N.; Alov, N.V.; Smirnova, M.A.; Tikhanova, O.A. Metamaterials Based on Polyvinyl Alcohol with Metal or Metal Oxide Particles: Synthesis and Study by Nondestructive Physical Methods. Theor. Found. Chem. Eng. 2020, 54, 1068–1073. [Google Scholar] [CrossRef]
- Cui, T. Electromagnetic metamaterials-from effective media to field programmable systems. Sci. Sin. Informationis 2020, 50, 1427–1461. [Google Scholar] [CrossRef]
- Wang, P.; Krasavin, A.V.; Liu, L.; Jiang, Y.; Li, Z.; Guo, X.; Tong, L.; Zayats, A.V. Molecular Plasmonics with Metamaterials. Chem. Rev. 2022, 122, 15031–15081. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.; Bandyopadhyay, S.; Liu, Y.H.; Shao, L.Y. A Review on Metasurface: From Principle to Smart Metadevices. Front. Phys. 2021, 8, 586087. [Google Scholar] [CrossRef]
- Jahani, S.; Jacob, Z. All-dielectric metamaterials. Nat. Nanotechnol. 2016, 11, 23–36. [Google Scholar] [CrossRef] [PubMed]
- Lagar’kov, A.N.; Kisel’, V.N.; Semenenko, V.N. Radar absorbers based on metamaterials. J. Commun. Technol. Electron. 2012, 57, 1122–1129. [Google Scholar] [CrossRef]
- Le-Van, Q.; Le Roux, X.; Aassime, A.; Degiron, A. Electrically driven optical metamaterials. Nat. Commun. 2016, 7, 12017. [Google Scholar] [CrossRef]
- Zhou, Y.C.; Yang, J.; Bai, L.; Bao, R.Y.; Yang, M.B.; Yang, W. Flexible phase change hydrogels for mid-/low-temperature infrared stealth. Chem. Eng. J. 2022, 446, 137463. [Google Scholar] [CrossRef]
- Rezaei, Z.; Yilmaz-Aykut, D.; Tourk, F.M.; Bassous, N.; Barroso-Zuppa, M.; Shawl, A.I.; Ashraf, S.S.; Avci, H.; Hassan, S. Immunomodulating Hydrogels as Stealth Platform for Drug Delivery Applications. Pharmaceutics 2022, 14, 2244. [Google Scholar] [CrossRef] [PubMed]
- Karmali, P.P.; Chao, Y.; Park, J.H.; Sailor, M.J.; Ruoslahti, E.; Esener, S.C.; Simberg, D. Different effect of hydrogelation on antifouling and circulation properties of dextran-iron oxide nanoparticles. Mol. Pharm. 2012, 9, 539–545. [Google Scholar] [CrossRef]
- Qin, M.; Sun, M.; Bai, R.; Mao, Y.; Qian, X.; Sikka, D.; Zhao, Y.; Qi, H.J.; Suo, Z.; He, X. Bioinspired Hydrogel Interferometer for Adaptive Coloration and Chemical Sensing. Adv. Mater. 2018, 30, 1800468. [Google Scholar] [CrossRef]
- Tatum, S.D.; Saudi, S.; Tettey, F.; Bhandari, R.K.; Bhattarai, N. A novel hydrogel-bronchial epithelial cell spheroids for toxicological evaluation. Biomed. Sci. Instrum. 2021, 57, 408–421. [Google Scholar] [CrossRef]
- Pathak, H. Smart’ Textile Materials: A Paradigm Shift. J. Text. Sci. Eng. 2012, 2, 107. [Google Scholar] [CrossRef]
- Aguilera, J.; Gracia-Cazaña, T.; Gilaberte, Y. New developments in sunscreens. Photochem. Photobiol. Sci. 2023, 22, 2473–2482. [Google Scholar] [CrossRef] [PubMed]
- Prasad, S.G.; Lal, C. Spectroscopic Investigations of Optical Bandgap and Search for Reaction Mechanism Chemistry Due to γ-Rays Irradiated PMMA Polymer. Biointerface Res. Appl. Chem. 2023, 13, 184. [Google Scholar] [CrossRef]
- Zhang, W.; Kragt, S.; Schenning, A.P.H.J.; De Haan, L.T.; Zhou, G. Easily Processable Temperature-Responsive Infrared-Reflective Polymer Coatings. ACS Omega 2017, 2, 3475–3482. [Google Scholar] [CrossRef]
- Lee, H.P.; Lokhande, G.; Singh, K.A.; Jaiswal, M.K.; Rajput, S.; Gaharwar, A.K. Light-Triggered In Situ Gelation of Hydrogels using 2D Molybdenum Disulfide (MoS2) Nanoassemblies as Crosslink Epicenter. Adv. Mater. 2021, 33, 2101238. [Google Scholar] [CrossRef]
- Mao, Z.; Huo, M.; Lyu, F.; Zhou, Y.; Bu, Y.; Wan, L.; Pan, L.; Pan, J.; Liu, H.; Lu, J. Nacre-liked material with tough and post-tunable mechanical properties. J. Mater. Sci. Technol. 2022, 114, 172–179. [Google Scholar] [CrossRef]
- Klös, G.; Andersen, A.; Miola, M.; Birkedal, H.; Sutherland, D.S. Oxidation controlled lift-off of 3D chiral plasmonic Au nano-hooks. Nano Res. 2019, 12, 1635–1642. [Google Scholar] [CrossRef]
- Torres-Huerta, A.L.; Antonio-Pérez, A.; García-Huante, Y.; Alcázar-Ramírez, N.J.; Rueda-Silva, J.C. Biomolecule-Based Optical Metamaterials: Design and Applications. Biosensors 2022, 12, 962. [Google Scholar] [CrossRef]
- Teutsch, T.; Mesch, M.; Giessen, H.; Tarín, C. Discrete wavelength selection for the optical readout of a metamaterial biosensing system for glucose concentration estimation via a support vector regression model. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, EMBS 2015, Milan, Italy, 25–29 August 2015; pp. 6421–6424. [Google Scholar] [CrossRef]
- Ruiz, A.L.; Ramirez, A.; McEnnis, K. Single and Multiple Stimuli-Responsive Polymer Particles for Controlled Drug Delivery. Pharmaceutics 2022, 14, 421. [Google Scholar] [CrossRef]
- Wang, Z.; Ye, Q.; Yu, S.; Akhavan, B. Poly Ethylene Glycol (PEG)-Based Hydrogels for Drug Delivery in Cancer Therapy: A Comprehensive Review. Adv. Healthc. Mater. 2023, 12, 2300105. [Google Scholar] [CrossRef]
- Li, D.; Yang, Y.; Yang, J.; Fang, M.; Tang, B.Z.; Li, Z. Completely aqueous processable stimulus responsive organic room temperature phosphorescence materials with tunable afterglow color. Nat. Commun. 2022, 13, 347. [Google Scholar] [CrossRef] [PubMed]
- Rust, T.; Jung, D.; Langer, K.; Kuckling, D. Stimuli-accelerated polymeric drug delivery systems. Polym. Int. 2023, 72, 5–19. [Google Scholar] [CrossRef]
- Chow, T.L. Classical Mechanics, 2nd ed.; Pearson: London, UK, 2013; pp. 1–611. [Google Scholar] [CrossRef]
- Arnold, V.I. Mathematical Methods of Classical Mechanics; Springer: New York, NY, USA, 1989; p. 60. [Google Scholar] [CrossRef]
- Suleimenov, I.E.; Baipakbayeva, S.T.; Mun, G.A.; Kaldybekov, D.B.; Yermukhambetova, B.B.; Bakirov, A.S. Analysis of Phase Transitions of Thermoresponsive Polymer Based on N-Vinylcaprolactam and 2-Hydroxyethyl Acrylate in Solutions from the Information Theory Point of View. Eurasian Chem. Technol. J. 2024, 26, 67–73. [Google Scholar] [CrossRef]
- Radecki, M.; Spěváček, J.; Zhigunov, A.; Sedláková, Z.; Hanyková, L. Temperature-induced phase transition in hydrogels of interpenetrating networks of poly(N-isopropylacrylamide) and polyacrylamide. Eur. Polym. J. 2015, 68, 68–79. [Google Scholar] [CrossRef]
- Kozhunova, E.Y.; Makhaeva, E.E.; Grinberg, N.V.; Burova, T.V.; Grinberg, V.Y.; Khokhlov, A.R. Collapse of hydrogels based on copolymers of N-isopropylacrylamide and sodium vinylsulfonate. Mosc. Univ. Phys. Bull. 2012, 67, 372–376. [Google Scholar] [CrossRef]
- Yan, G.; Chen, G.; Peng, Z.; Shen, Z.; Tang, X.; Sun, Y.; Zeng, X.; Lin, L. The Cross-Linking Mechanism and Applications of Catechol–Metal Polymer Materials. Adv. Mater. Interfaces 2021, 8, 2100239. [Google Scholar] [CrossRef]
- Liubimtsev, N.; Kösterke, T.; Che, Y.; Appelhans, D.; Gaitzsch, J.; Voit, B. Redox-sensitive ferrocene functionalised double cross-linked supramolecular hydrogels. Polym. Chem. 2022, 13, 427–438. [Google Scholar] [CrossRef]
- Denisin, A.K.; Pruitt, B.L. Tuning the Range of Polyacrylamide Gel Stiffness for Mechanobiology Applications. ACS Appl. Mater. Interfaces 2016, 8, 21893–21902. [Google Scholar] [CrossRef]
- Budtova, T.V.; Suleimenov, I.E.; Ya. Frenkel, S. Interpolymer complex formation of some nonionogenic polymers with linear and crosslinked polyacrylic acid. J. Polym. Sci. Part A Polym. Chem. 1994, 32, 281–284. [Google Scholar] [CrossRef]
- Suleimenov, I.; Kadyrzhan, K.; Kabdushev, S.; Bakirov, A.; Kopishev, E. New Equipment for Aromatherapy and Related Mobile App: A Tool to Support Small Peasant Farms in Kazakhstan in Crisis. In Smart Innovation, Systems and Technologies; Shamtsyan, M., Pasetti, M., Beskopylny, A., Eds.; Springer Nature Pte Ltd.: Singapore, 2022; pp. 347–355. [Google Scholar] [CrossRef]
- Ermukhambetova, B.B.; Suleimenov, I.E.; Alikulov, A.Z.; Moldakhan, I.; Baipakbaeva, S.T.; Mun, G.A. On the Question of the Method for Determining the Critical pH Value during the Formation of Complexes between Nonionic Polymers and Polyacid in Aqueous Solutions. Polym. Sci. Ser. A 2021, 63, 8–14. [Google Scholar] [CrossRef]
- Wang, H.; Fu, T.; Du, Y.; Gao, W.; Huang, K.; Liu, Z.; Chandak, P.; Liu, S.; Van Katwyk, P.; Deac, A.; et al. Scientific discovery in the age of artificial intelligence. Nature 2023, 620, 47–60. [Google Scholar] [CrossRef] [PubMed]
- Hatakeyama-Sato, K.; Watanabe, S.; Yamane, N.; Igarashi, Y.; Oyaizu, K. Using GPT-4 in parameter selection of polymer informatics: Improving predictive accuracy amidst data scarcity and ‘Ugly Duckling’ dilemma. Digit. Discov. 2023, 2, 1548–1557. [Google Scholar] [CrossRef]
- Padakanti, S.; Kalva, P.; Reddy Kommidi, V. AI in Scientific Research: Empowering Researchers with Intelligent Tools. Int. J. Sci. Res. Comput. Sci. Eng. Inf. Technol. 2024, 10, 416–422. [Google Scholar] [CrossRef]
- Aydin, O.; Yassikaya, M.Y. Validity and Reliability Analysis of the PlotDigitizer Software Program for Data Extraction from Single-Case Graphs. Perspect. Behav. Sci. 2022, 45, 239–257. [Google Scholar] [CrossRef]
- Suleymenov, I.E.; Sedlakova, Z.Z.; Kopishev, E.E. New Polymer Materials for Optical Sensor Systems. J. Inorg. Organomet. Polym. Mater. 2019, 29, 758–764. [Google Scholar] [CrossRef]
- Shirke, N.; Ghase, V.; Jamdar, V. Recent advances in stealth coating. Polym. Bull. 2024, 81, 9389–9418. [Google Scholar] [CrossRef]
- Jiao, P.; Mueller, J.; Raney, J.R.; Zheng, X.; Alavi, A.H. Mechanical metamaterials and beyond. Nat. Commun. 2023, 14, 6004. [Google Scholar] [CrossRef]
- Suleimenov, I.; Gabrielyan, O.; Kopishev, E.; Kadyrzhan, A.; Bakirov, A.; Vitulyova, Y. Advanced Applications of Polymer Hydrogels in Electronics and Signal Processing. Gels 2024, 10, 715. [Google Scholar] [CrossRef]
- Kadyrzhan, K.; Suleimenov, I.; Tolymbekova, L.; Seitenova, G.; Kopishev, E. Background of New Measurement Electronic Devices with Polyelectrolyte Hydrogel Base. Polymers 2025, 17, 539. [Google Scholar] [CrossRef]





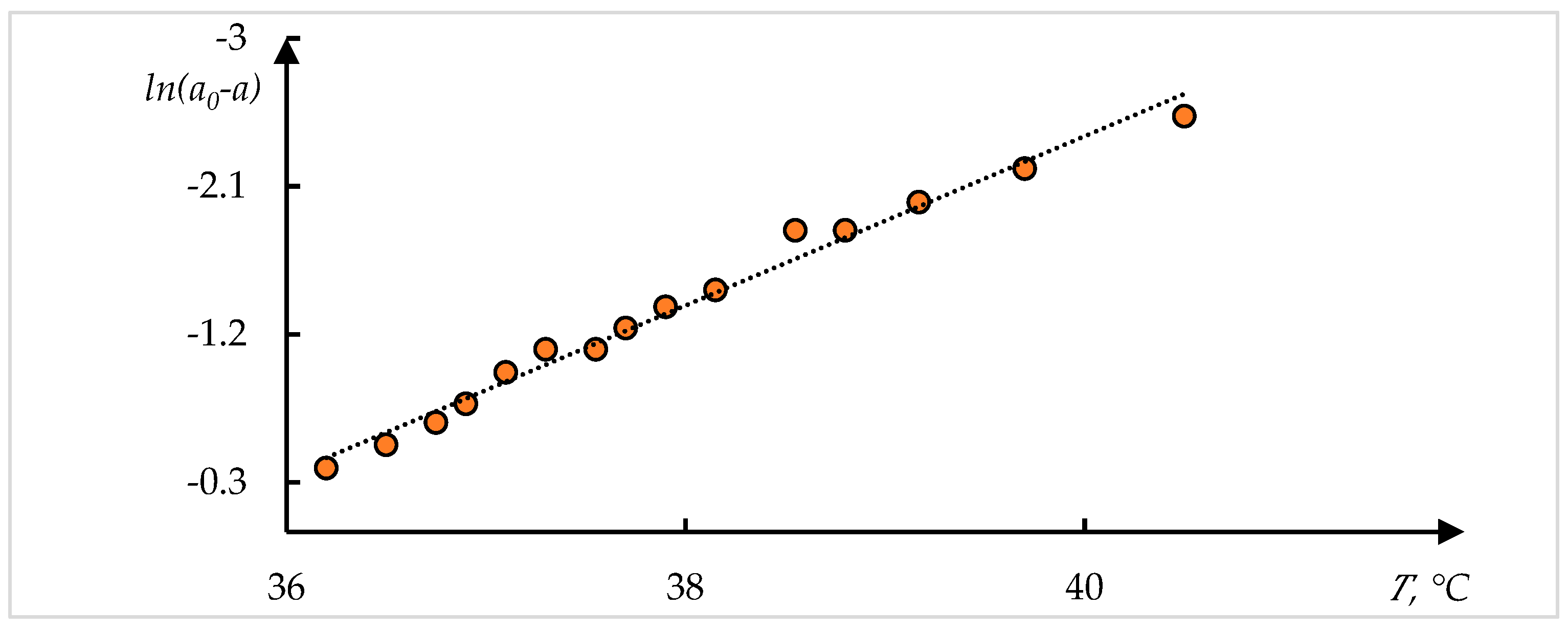
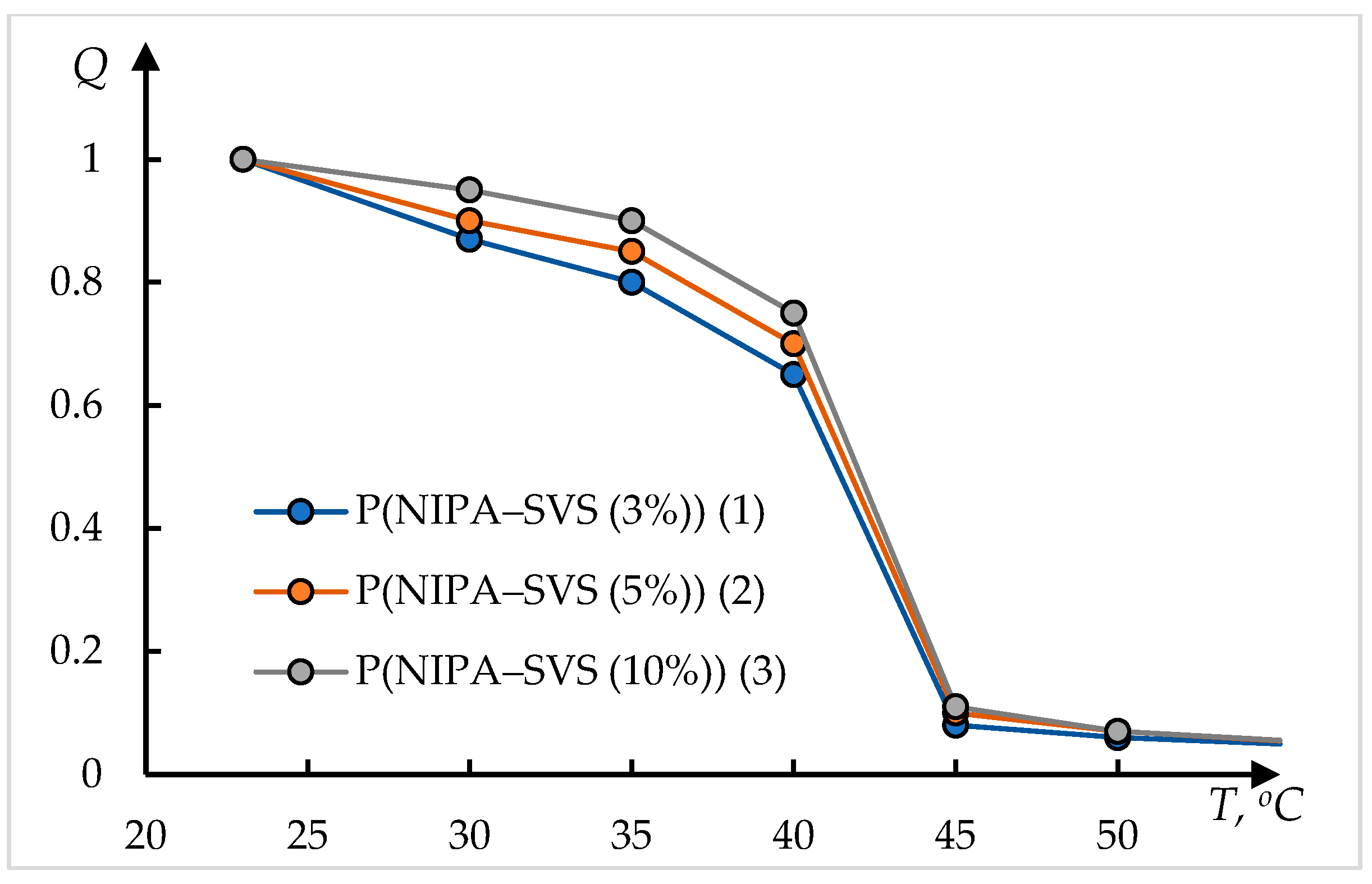






| Curve | , °C | , °C | , °C−1 | ||
|---|---|---|---|---|---|
| 2 | 29.5 ± 0.2 | −0.25 ± 0.03 | 0.46 ± 0.03 | 28.2 ± 0.2 | 3.0 ± 0.3 |
| 3 | 29 ± 0.2 | −0.24 ± 0.03 | 0.52 ± 0.03 | 27 ± 0.2 | 2.9 ± 0.3 |
| 4 | 28.5 ± 0.2 | −0.22 ± 0.03 | 0.62 ± 0.03 | 25.6 ± 0.2 | 2.9 ± 0.3 |
| 5 | 27 ± 0.2 | −0.22 ± 0.03 | 0.69 ± 0.03 | 22.9 ± 0.2 | 2.9 ± 0.3 |
| (a) | (b) | (c) | |
|---|---|---|---|
| τ | 2.3 | 2.3 | 2.3 |
| Q0 | 0.905 | 0.92 | 0.92 |
| T0 | 40 | 40.5 | 40.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suleimenov, I.; Dyussova, R.; Shaltykova, D.; Atasoy, E.; Seitenova, G.; Kopishev, E. Prerequisites for Developing a Classification of Phase Transitions in Systems Based on Thermosensitive Polymers: Use of a Semi-Empirical Model. Polymers 2025, 17, 1441. https://doi.org/10.3390/polym17111441
Suleimenov I, Dyussova R, Shaltykova D, Atasoy E, Seitenova G, Kopishev E. Prerequisites for Developing a Classification of Phase Transitions in Systems Based on Thermosensitive Polymers: Use of a Semi-Empirical Model. Polymers. 2025; 17(11):1441. https://doi.org/10.3390/polym17111441
Chicago/Turabian StyleSuleimenov, Ibragim, Rizagul Dyussova, Dina Shaltykova, Emin Atasoy, Gaini Seitenova, and Eldar Kopishev. 2025. "Prerequisites for Developing a Classification of Phase Transitions in Systems Based on Thermosensitive Polymers: Use of a Semi-Empirical Model" Polymers 17, no. 11: 1441. https://doi.org/10.3390/polym17111441
APA StyleSuleimenov, I., Dyussova, R., Shaltykova, D., Atasoy, E., Seitenova, G., & Kopishev, E. (2025). Prerequisites for Developing a Classification of Phase Transitions in Systems Based on Thermosensitive Polymers: Use of a Semi-Empirical Model. Polymers, 17(11), 1441. https://doi.org/10.3390/polym17111441








