Molecular Simulation Study on the Hydrogen Permeation Behavior and Mechanism of Common Polymers
Abstract
1. Introduction
2. Theoretical Basis of Permeability
3. Model Construction and Parameter Setting
3.1. Selection of Force Field and Simulation Conditions
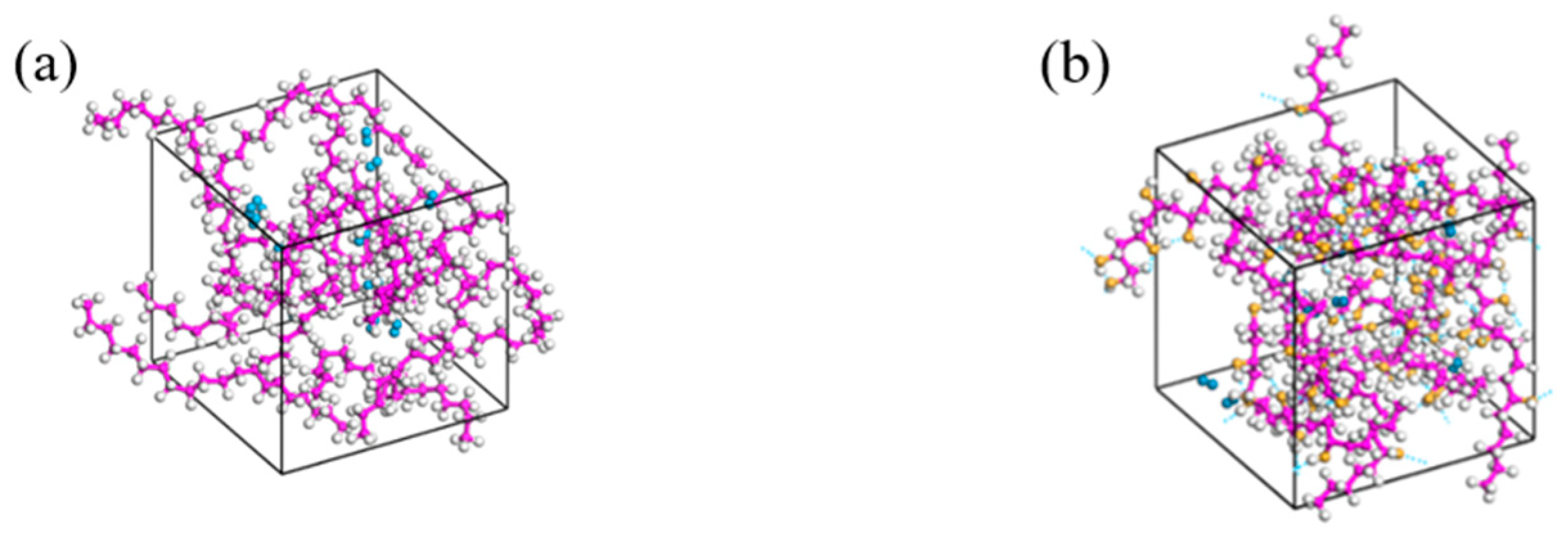
3.2. Model Construction
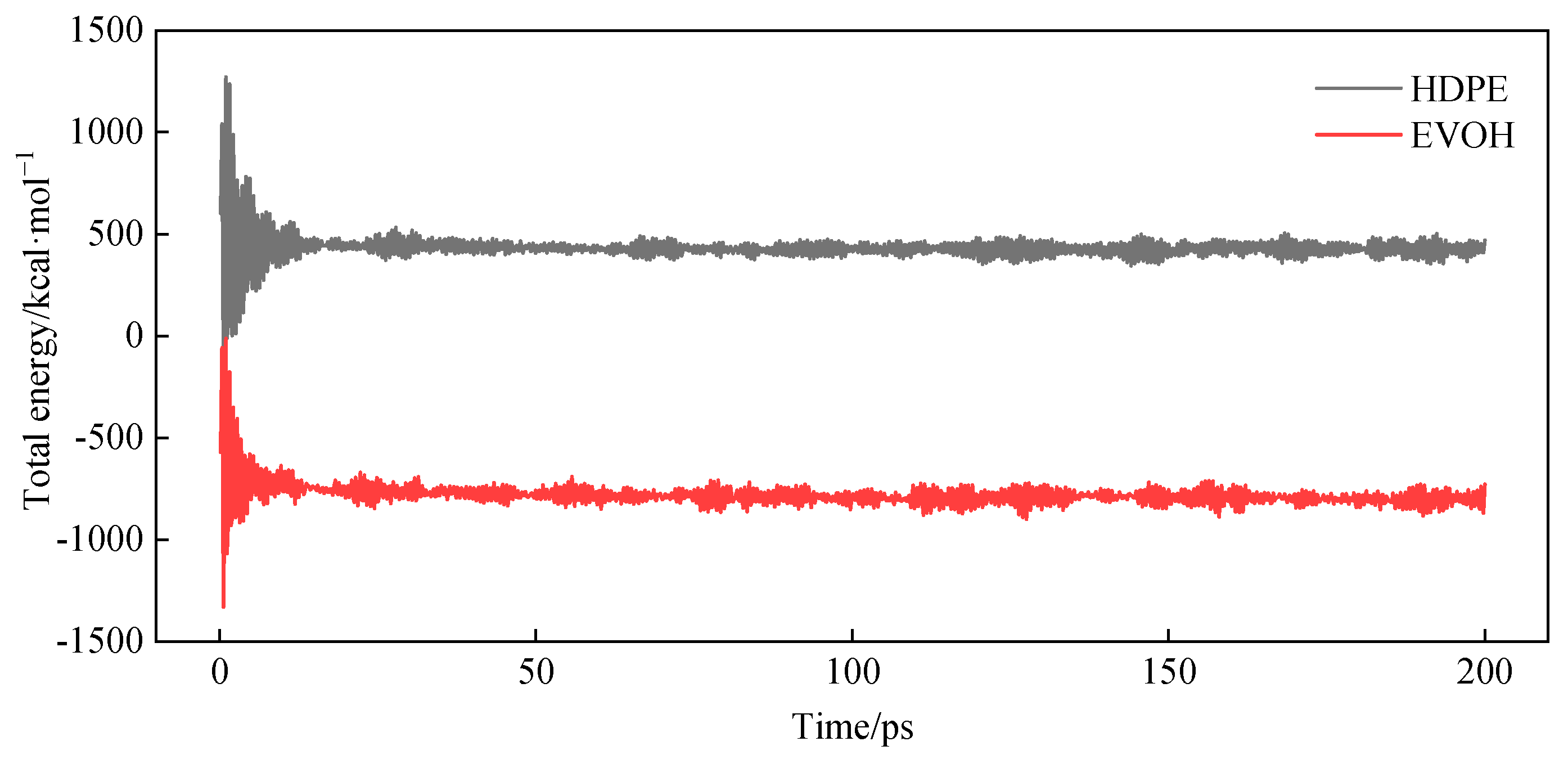
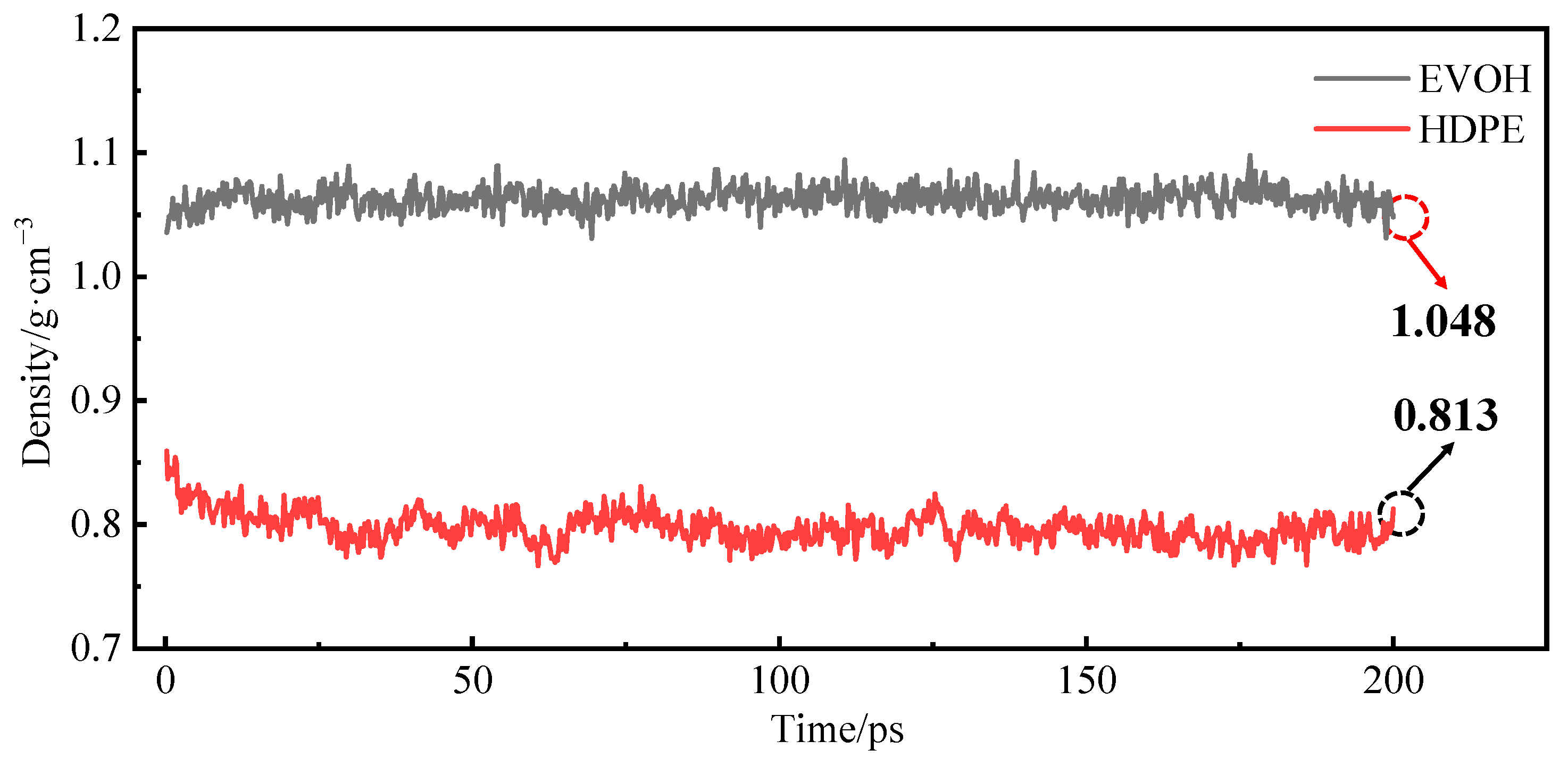
3.3. Relaxation Treatment
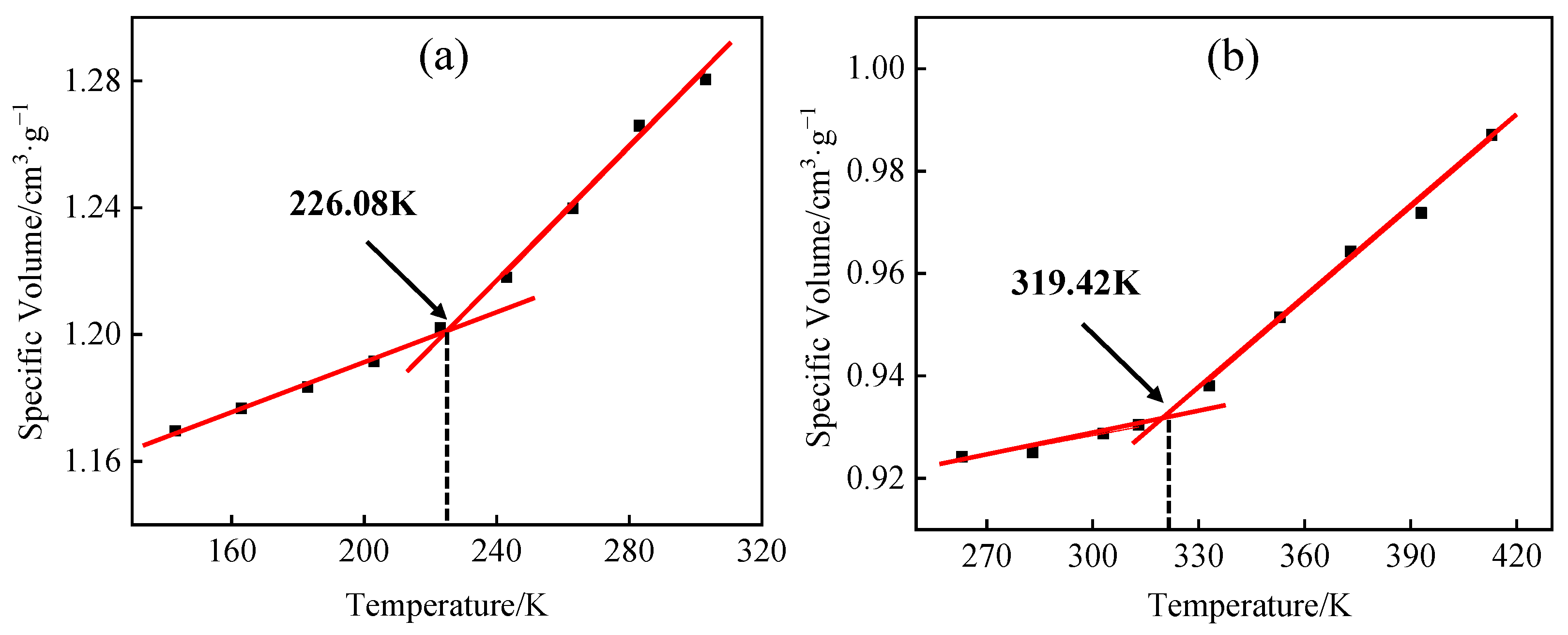
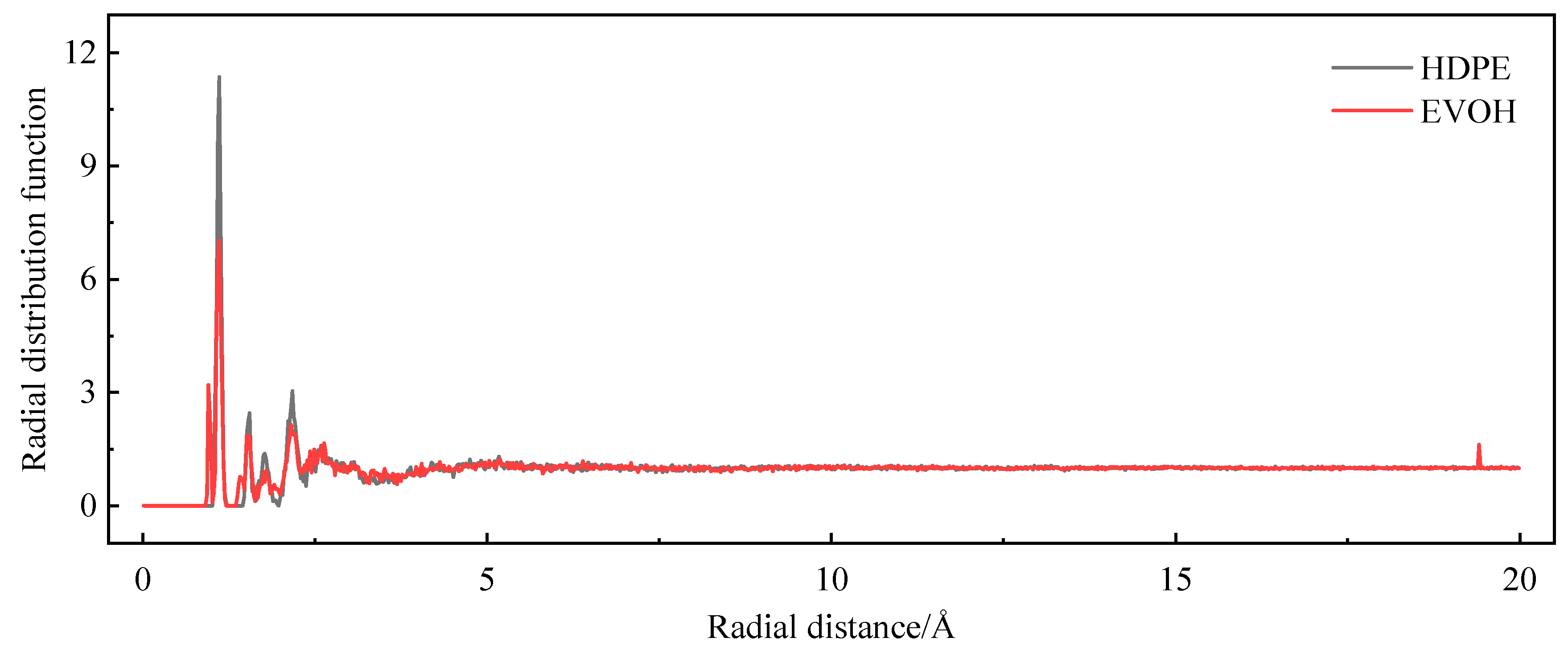
3.4. Model Reliability Verification
4. Results and Discussion
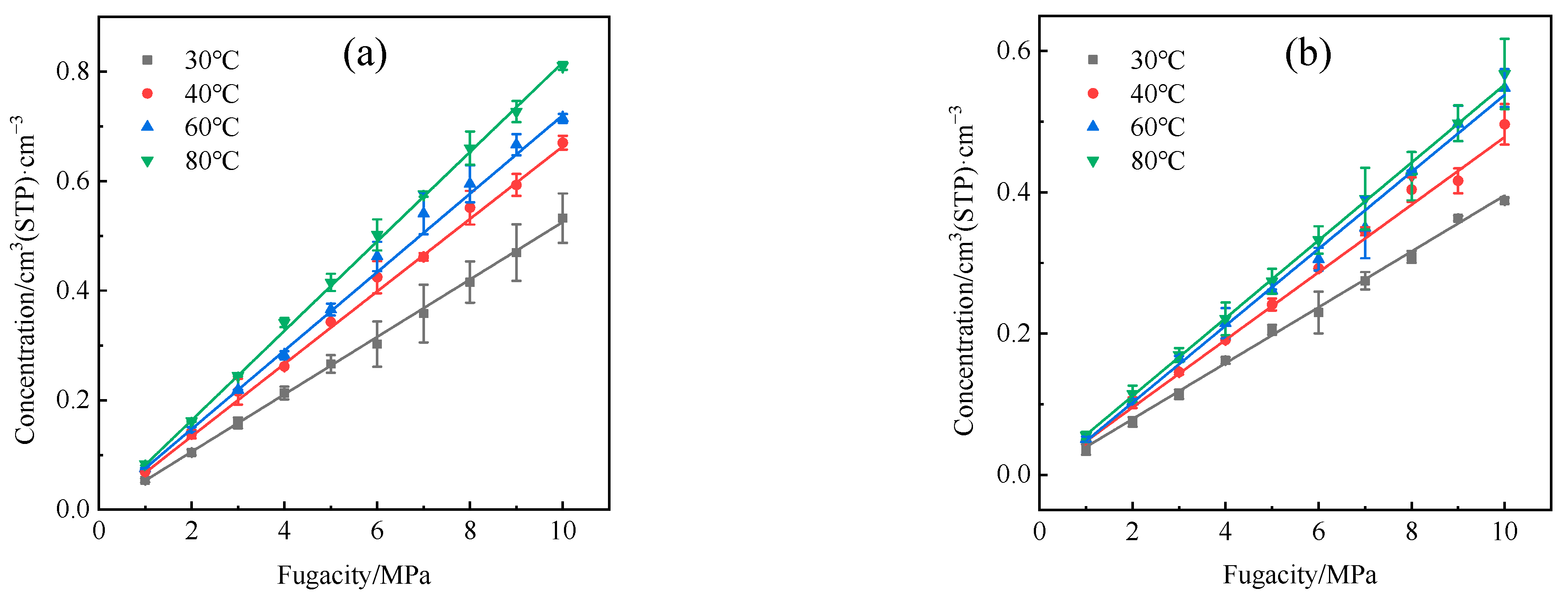
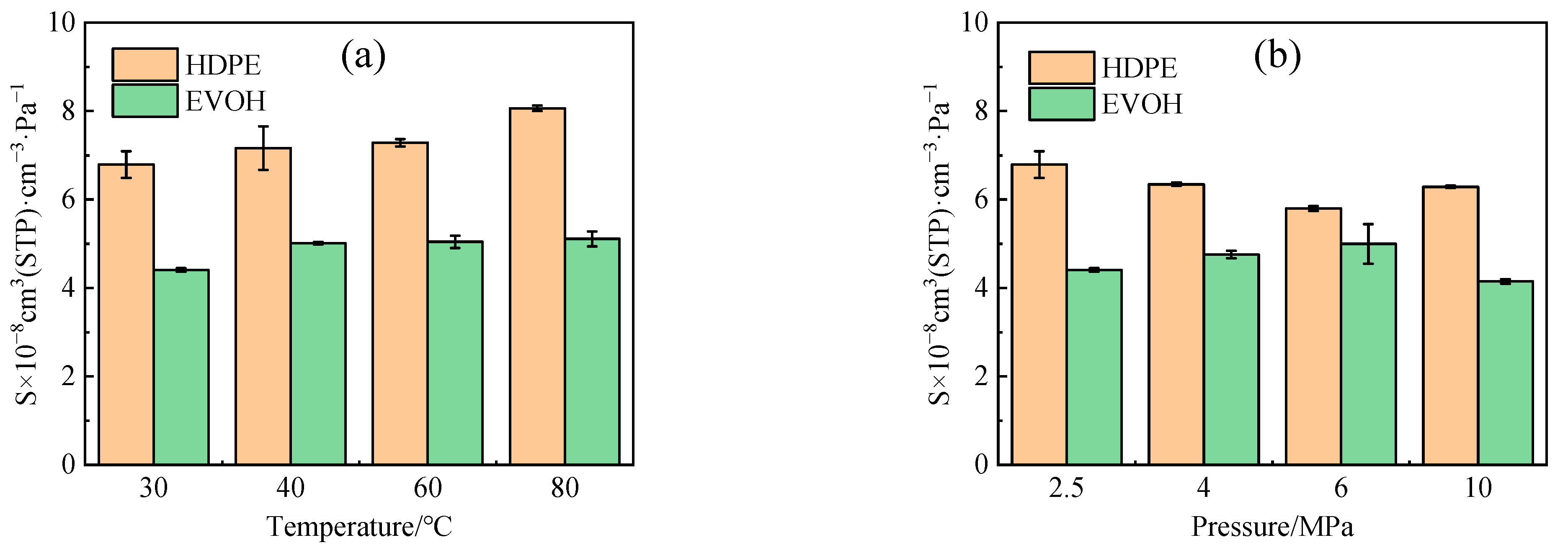
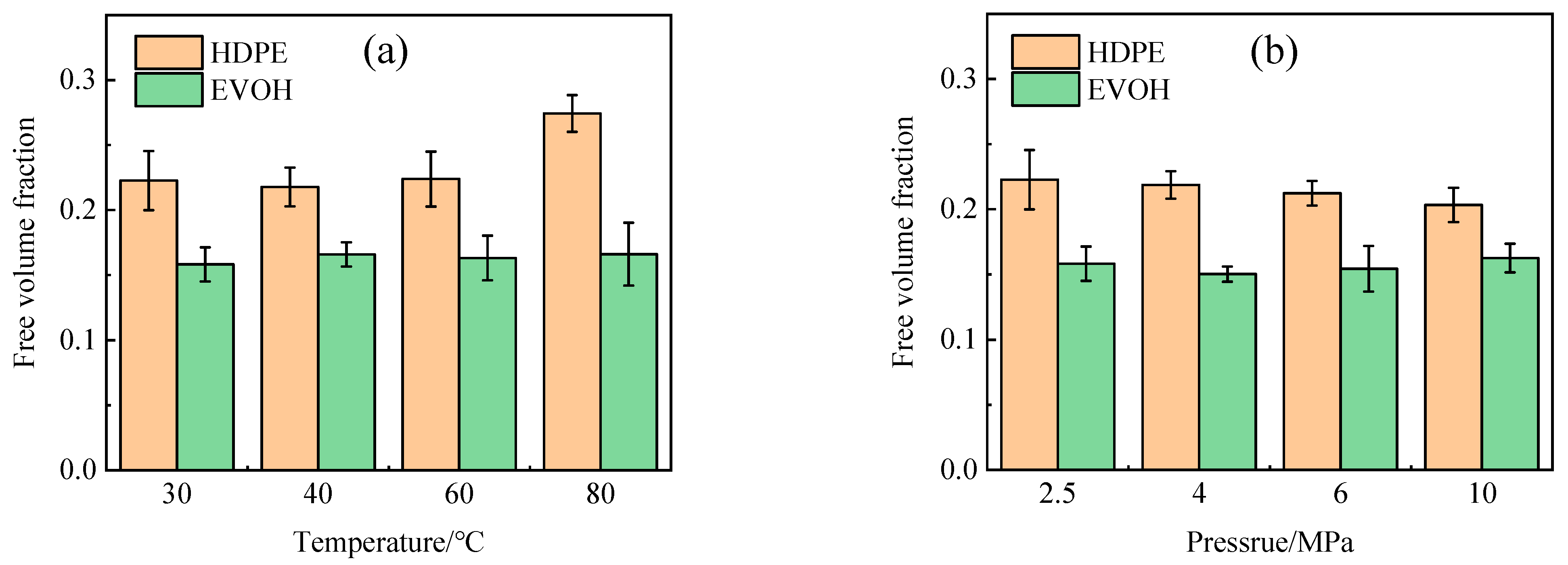
4.1. Solubility Coefficient
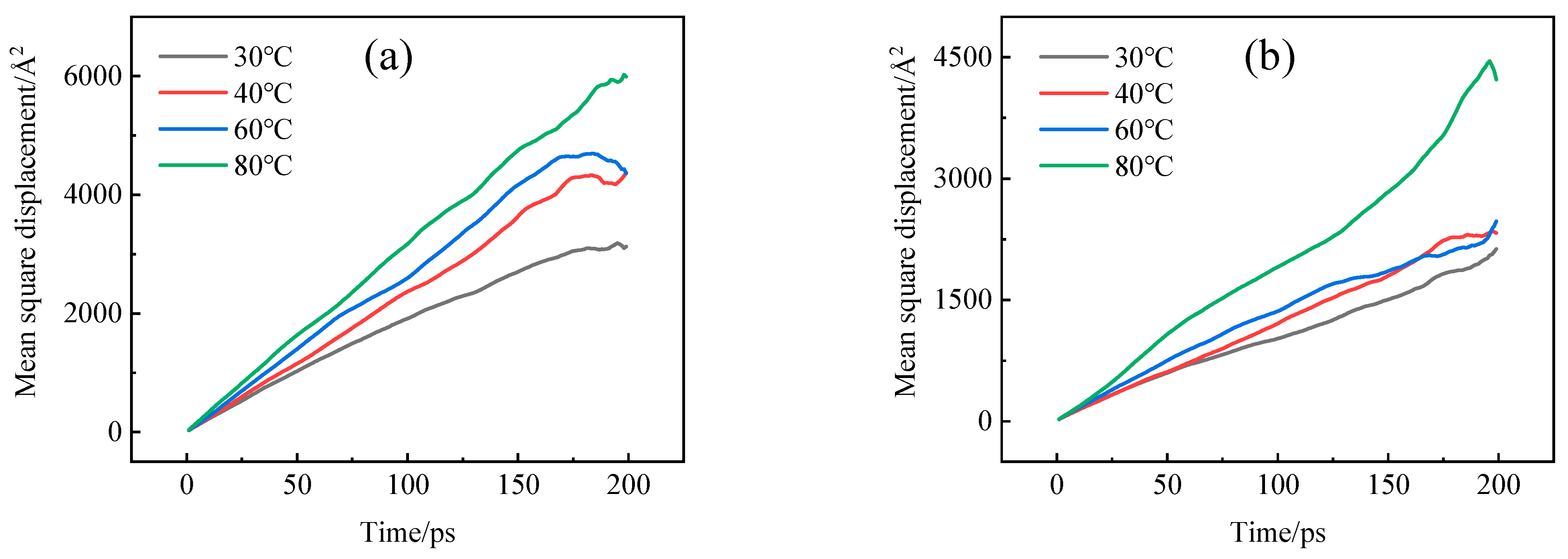
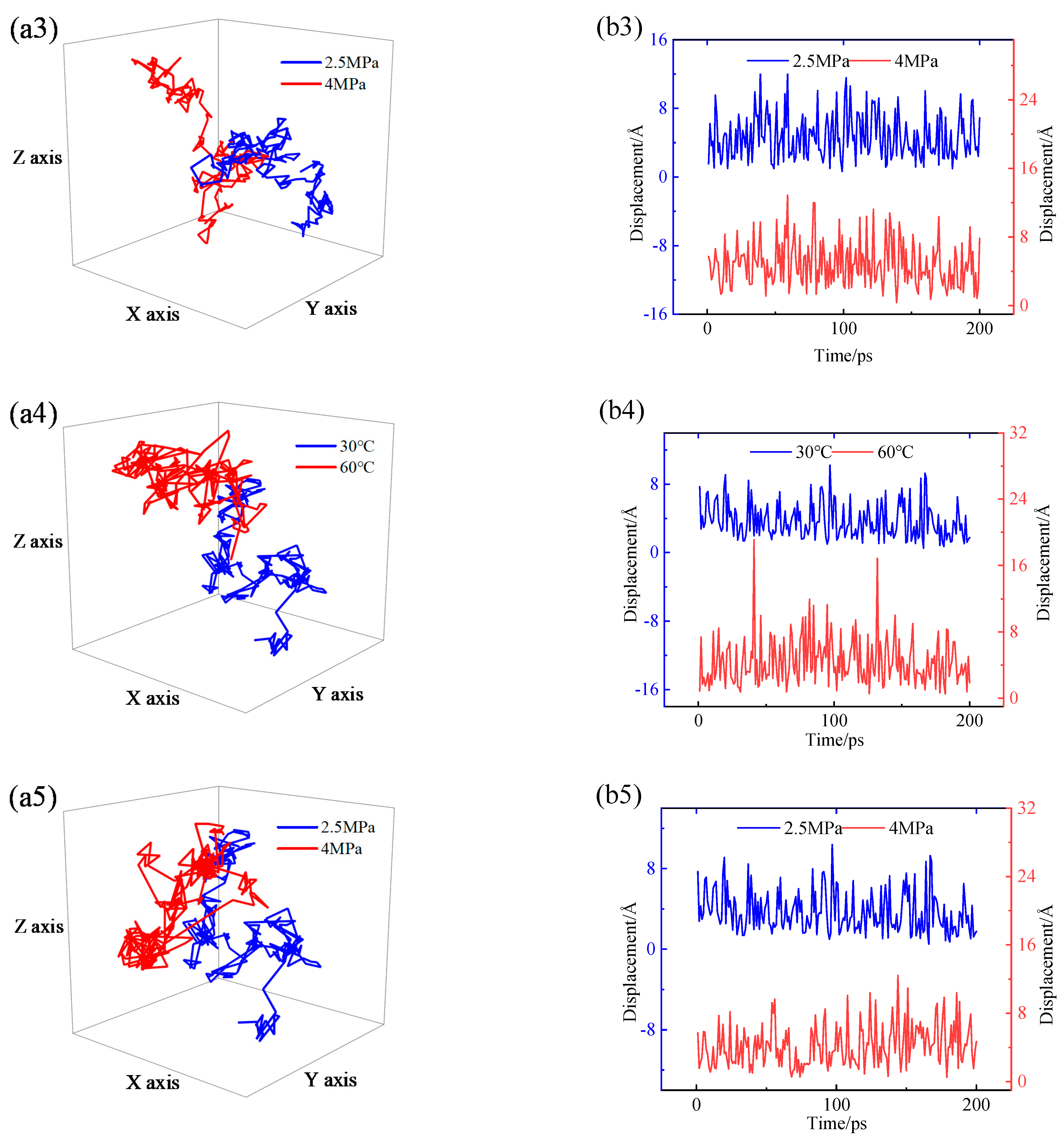
4.2. Diffusion Coefficient
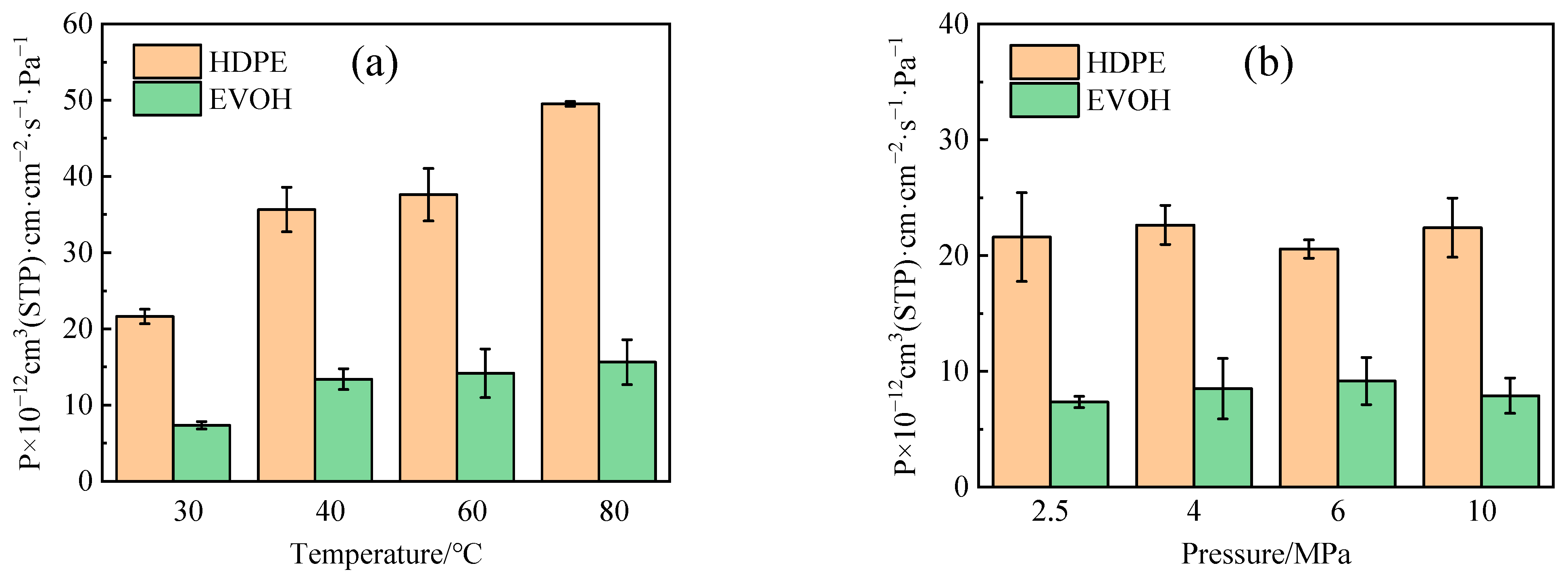
4.3. Permeability Coefficient
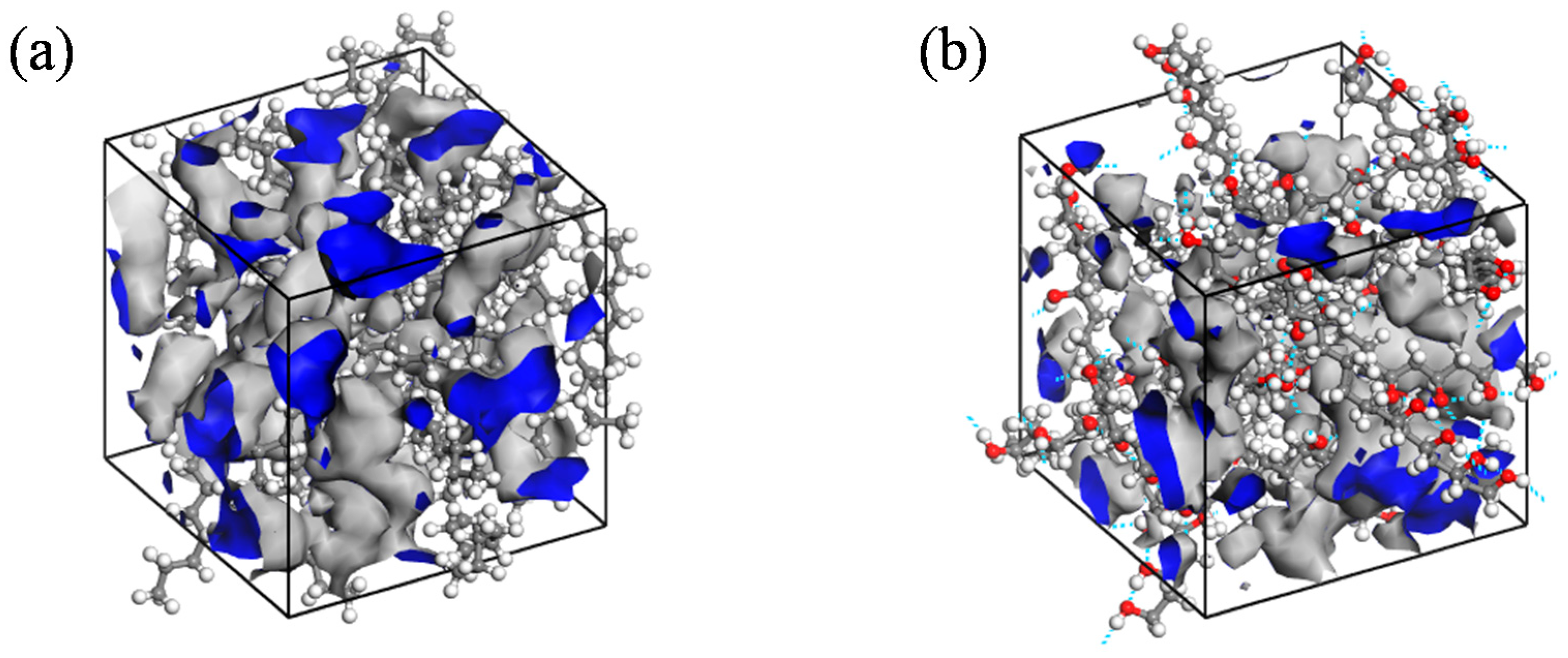
4.4. Permeability Mechanism
5. Conclusions
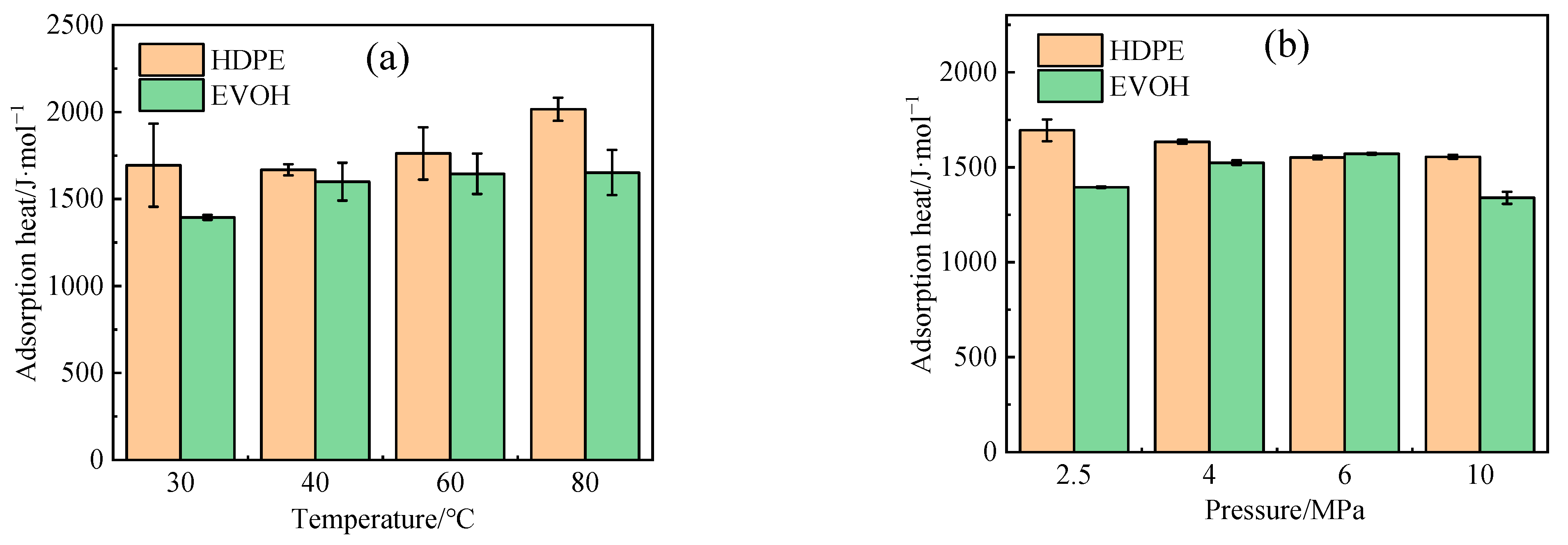
- The adsorption heat and free volume of hydrogen (H2) in high-density polyethylene (HDPE) and ethylene–vinyl alcohol (EVOH) exhibit an increasing trend with rising temperatures, leading to corresponding changes in solubility, diffusion, and permeability coefficients. Specifically, as the temperature increases from 30 °C to 80 °C, the solubility, diffusion, and permeability coefficients of hydrogen in HDPE experience increments of 18.7%, 92.9%, and 129.0%, respectively. In the case of EVOH, the values are 15.9%, 81.6%, and 112.7%. Conversely, the diffusion, solubility, and permeability coefficients of hydrogen in HDPE and EVOH are almost unaffected under low-pressure conditions in the study pressure range (2.5–10 MPa).
- Due to the unique chain segment configuration of EVOH, a robust hydrogen bond is established among the hydroxyl groups, impeding the penetration of hydrogen. Consequently, EVOH exhibits superior hydrogen barrier characteristics compared to HDPE, as evidenced by the significantly lower diffusion, solubility, and permeability coefficients of hydrogen within EVOH.
- The permeability mechanisms of hydrogen (H2) in HDPE and EVOH exhibit similarities, involving an aggregation adsorption process occurring within a low potential energy range and a diffusion process characterized by vibration-induced transitions between holes. During adsorption, hydrogen molecules tend to accumulate in regions of low energy, with EVOH specifically showing a preference for areas lacking hydrogen bonds. During the subsequent diffusion phase, hydrogen molecules exhibit vibrational motion within a hole over a limited range before transitioning to another hole at a greater distance. The hydrogen molecules then vibrate in their new position. Elevated temperatures lead to increases in the motion range and transition frequency of hydrogen molecules.
- The affinity of hydrogen with HDPE is more pronounced compared to that with EVOH, leading to an increased number of adsorption sites and enhanced hydrogen adsorption capacity in HDPE. Hydrogen molecules exhibit higher mobility within HDPE as opposed to EVOH, characterized by greater hole amplitude and a higher number of transitional holes during the diffusion phase. Consequently, EVOH demonstrates superior hydrogen barrier characteristics when compared to HDPE.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vechkinzova, E.; Steblyakova, L.P.; Roslyakova, N.; Omarova, B. Prospects for the Development of Hydrogen Energy: Overview of Global Trends and the Russian Market State. Energies 2022, 15, 8503. [Google Scholar] [CrossRef]
- Meng, X.; Chen, M.; Gu, A.; Wu, X.; Liu, B.; Zhou, J.; Mao, Z. China’s hydrogen development strategy in the context of double carbon targets. Nat. Gas Ind. B 2022, 9, 521–547. [Google Scholar] [CrossRef]
- Tsiklios, C.; Hermesmann, M.; Müller, T.E. Hydrogen transport in large-scale transmission pipeline networks: Thermodynamic and environmental assessment of repurposed and new pipeline configurations. Appl. Energy 2022, 327, 120097. [Google Scholar] [CrossRef]
- Hydrogen and Fuel Cell Technologies Office. Hydrogen Pipelines—Department of Energy. Available online: https://www.energy.gov/eere/fuelcells/hydrogen-pipelines (accessed on 14 November 2018).
- May, L.M.; Matthew, C.; Zachary, N.B.; Peter, E.B.; Damian, L.; Andrew, J.S. Evaluating a natural gas pipeline steel for blended hydrogen service. J. Nat. Gas Sci. Eng. 2022, 101, 104529. [Google Scholar] [CrossRef]
- Amaro, R.L.; Rustagi, N.; Findley, K.O.; Drexler, E.S.; Slifka, A.J. Modeling the fatigue crack growth of X100 pipeline steel in gaseous hydrogen. Int. J. Fatigue 2014, 59, 262–271. [Google Scholar] [CrossRef]
- Siddiqui, R.; Abdullah, H.A. Hydrogen embrittlement in 0.31% carbon steel used for petrochemical applications. J. Mater. Process Technol. 2005, 170, 430–435. [Google Scholar] [CrossRef]
- Capelle, J.; Gilgert, J.; Dmytrakh, I.; Pluvinage, G. Sensitivity of pipelines with steel API X52 to hydrogen embrittlement. Int. J. Hydrogen Energy 2008, 33, 7630–7641. [Google Scholar] [CrossRef]
- Briottet, L.; Moro, I.; Lemoine, P. Quantifying the hydrogen embrittlement of pipeline steels for safety considerations. Int. J. Hydrogem Energy 2012, 37, 17616–17623. [Google Scholar] [CrossRef]
- Li, H.; Niu, R.; Li, W.; Lu, H.; Julie, C.; Chen, Y. Hydrogen in pipeline steels: Recent advances in characterization and embrittlement mitigation. J. Nat. Gas Sci. Eng. 2022, 105, 104709. [Google Scholar] [CrossRef]
- Li, H.; Zhang, X.; Huang, H.; Zhou, T.; Qi, G.; Ding, H. Simulation Analysis of Limit Operating Specifications for Onshore Spoolable Reinforced Thermoplastic Pipes. Polymers 2021, 13, 3480. [Google Scholar] [CrossRef]
- Li, H.; Zhang, X.; Ma, X.; Wang, P.; Yang, X.; Zhang, D. Permeation characteristics and mechanism of CH4 in PVDF. Plastics 2021, 50, 72–76. Available online: https://www.plaschina.com.cn/CN/10.19491/j.issn.1001-9278.2021.03.014 (accessed on 26 March 2021).
- Yersak, T.A.; Baker, D.R.; Yanagisawa, Y.; Slavik, S.; Immel, R.; Mack-Gardner, A.; Herrmann, M.; Cai, M. Predictive model for depressurization-induced blistering of type IV tank liners for hydrogen storage. Int. J. Hydrogen Energy 2017, 42, 28910–28917. [Google Scholar] [CrossRef]
- Cheng, W.; Cheng, Y.F. A techno-economic study of the strategy for hydrogen transport by pipelines in Canada. J. Pipeline Sci. Eng. 2023, 3, 100112. [Google Scholar] [CrossRef]
- Chen, M. Dissolution and Diffusion Behavior of Polyethylene Based on Gravimetric Method and Nuclear Magnetic Resonance Method and Its Application; Zhejiang University: Hangzhou, China, 2014. [Google Scholar]
- Zhang, D.; Ding, N. Study on hydrogen permeation behavior of polyethylene liner material in Type IV bottle. New Energy Prog. 2022, 10, 15–19. Available online: http://www.xnyjz.giec.ac.cn/CN/10.3969/j.issn.2095-560X.2022.01.003 (accessed on 28 February 2022).
- Gay, N.; Lamouchi, T.; Agostini, F.; Davy, C.A.; Skoczylas, F. Hydrogen diffusion through polymer membranes. MATEC Web Conf. 2020, 322, 01044. [Google Scholar] [CrossRef]
- Siracusa, V.; Ingrao, C. Correlation amongst gas barrier behavior, temperature and thickness in BOPP films for food packaging usage: A lab-scale testing experience. Polym. Test. 2017, 59, 277–289. [Google Scholar] [CrossRef]
- Chen, H.; He, J. Numerical simulation of permeation behavior of gas molecules in butyl rubber. J. Wuhan Univ. Technol. 2015, 37, 26–30. [Google Scholar] [CrossRef]
- Zheng, D.; Li, J.; Liu, B.; Yu, B.; Yang, Y.; Han, D.; Li, J.; Huang, Z. Molecular dynamics investigations into the hydrogen permeation mechanism of polyethylene pipeline material. J. Mol. Liq. 2022, 368, 120773. [Google Scholar] [CrossRef]
- Maes, C.; Luyten, W.; Herremans, G.; Peeters, R.; Carleer, R.; Buntinx, M. Recent updates on the barrier properties of Ethylene Vinyl Alcohol Copolymer (EVOH): A Review. Polym. Rev. 2018, 58, 209–246. [Google Scholar] [CrossRef]
- Mozaffari, F.; Eslami, H.; Moghadasi, J. Molecular dynamics simulation of diffusion and permeation of gases in polystyrene. Polymer 2010, 51, 300–307. [Google Scholar] [CrossRef]
- Yoshinori, K.; Yasutoshi, N.; Katsuhiko, T.; Keishin, M.; Akio, T. Volumetric Properties and Interaction Parameters of Dissolved Gases in Poly(dimethylsiloxane) and Polyethylene. Macromolecules 2000, 33, 3111–3119. [Google Scholar] [CrossRef]
- Boyd, R.H.; Pant, P.V.K. Molecular packing and diffusion in polyisobutylene. Macromolecules 1991, 24, 6325–6331. [Google Scholar] [CrossRef]
- He, J. Permeation Behavior of Hydrogen and Isotope in BIIR/CeO2; Southwest University of Science and Technology: Mianyang, China, 2016. [Google Scholar]
- Su, Y.; Lv, H.; Feng, C.; Zhang, C.M. Hydrogen permeability of polyamide 6 as the liner material of Type IV hydrogen storage tanks: A molecular dynamics investigation. Int. J. Hydrog. Energy 2024, 50, 1598–1606. [Google Scholar] [CrossRef]
- Dutta, R.C.; Bhatia, S.K. Transport diffusion of light gases in polyethylene using atomistic simulations. Langmuir 2017, 33, 936–946. [Google Scholar] [CrossRef]
- Flaconneche, B.; Martin, J.; Klopffer, M.H. Permeability.; Diffusion and Solubility of Gases in Polyethylene, Polyamide 11 and Poly (Vinylidene Fluoride). Oil Gas Sci. Technol. 2006, 56, 261–278. [Google Scholar] [CrossRef]
- Kucukpinar, E.; Doruker, P. Effect of absorbed water on oxygen transport in EVOH matrices. A molecular dynamics study. Polym. 2004, 45, 3555–3564. [Google Scholar] [CrossRef]
- Lu, H.; Zhou, Z.; Hao, T.; Ye, X.; Ne, Y. Temperature Dependence of Structural Properties and Chain Configurational Study: A Molecular Dynamics Simulation of Polyethylene Chains. Macromol. Theor. Simul. 2015, 24, 335–343. [Google Scholar] [CrossRef]
- George, W. Handbook of Polymers, 2nd ed.; Chem Tec Publishing: Toronto, ON, Canada, 2016. [Google Scholar]
- Michaels, A.S.; Bixler, H.J. Flow of gases through polyethylene. J. Polym. Sci. 1961, 50, 413–439. [Google Scholar] [CrossRef]
- Pant, P.; Boyd, R.H. Molecular-dynamics simulation of diffusion of small penetrants in polymers. Macromolecules 1993, 26, 679–686. [Google Scholar] [CrossRef]
- Yang, Y.; Nair, A.K.N.; Sun, S. Adsorption and Diffusion of Methane and Carbon Dioxide in Amorphous Regions of Cross-Linked Polyethylene: A Molecular Simulation Study. Ind. Eng. Chem. Res. 2019, 58, 8426–8436. [Google Scholar] [CrossRef]
- He, Q.; Li, Y.; Zhou, Y. Numerical Simulation of Hydrogen permeation Behavior in GO_BIIR Nanocomposites. Funct. Mater. 2018, 49, 103–108. [Google Scholar] [CrossRef]
- Klopffer, M.H.; Flaconneche, B. Transport Properties of Gases in Polymers: Bibliographic Review. Oil Gas Sci. Technol. 2006, 56, 223–244. [Google Scholar] [CrossRef]
- Sato, Y.; Yurugi, M.; Fujiwara, K.; Takishima, S.; Masuoka, H. Solubilities of carbon dioxide and nitrogen in polystyrene under high temperature and pressure. Fluid Phase Equilibria 1996, 125, 129–138. [Google Scholar] [CrossRef]
- Sato, Y.; Fujiwara, K.; Takikawa, T.; Sumarno; Takishima, S.; Masuoka, H. Solubilities and diffusion coefficients of carbon dioxide and nitrogen in polypropylene, high-density polyethylene, and polystyrene under high pressures and temperatures. Fluid Phase Equilibria 1999, 162, 261–276. [Google Scholar] [CrossRef]
- Su, Y.; Lv, H.; Zhou, W.; Zhang, C. Review of the Hydrogen Permeability of the Liner Material of Type IV On-Board Hydrogen Storage Tank. World Electr. Veh. J. 2021, 12, 130. [Google Scholar] [CrossRef]
- Yuan, J.; Liu, X.; Li, X.; Yu, J. Molecular simulation for adsorption and separation of CH4/H2 in zeolites. Acta Phys. Sin. 2021, 70, 156801. [Google Scholar] [CrossRef]
- Yi, Y.; Bi, P.; Zhao, X.; Wang, L. Molecular dynamics simulation of diffusion of hydrogen and its isotopic molecule in polystyrene. J. Polym. Res. 2018, 25, 43. [Google Scholar] [CrossRef]
- Tao, C.; Wang, J.; Zhou, J. Molecular simulation of the effect of humidity on the diffusion of O2 in vinyl-vinyl alcohol copolymer. J. Nanjing Univ. Technol. (Nat. Sci. Ed.) 2009, 31, 70–73. [Google Scholar] [CrossRef]
- Barth, R.R.; Simmons, K.L.; San, M.; Christopher, W. Polymers for Hydrogen Infrastructure and Vehicle Fuel Systems; U.S. Department of Energy: Washington, DC, USA, 2013. [CrossRef]
- Liu, C.; Zhang, R.; Tian, L.; Wang, C.; Xu, X.; Pei, Y.; Li, Y. Research progress on compatibility of nonmetallic pipes in hydrogen environment. Nat. Gas Ind. 2022, 42, 145–156. [Google Scholar] [CrossRef]
- Kane, M. Permeability, Solubility, and Interaction of Hydrogen in Polymers—An Assessment of Materials for Hydrogen Transport: WSRC-STI-2008-00009; Savannah River Site: Aiken, SC, USA, 2008. [Google Scholar] [CrossRef]
- Zhang, X.; Chu, H.; Li, H.; Qi, G.; Feng, J.; Gao, X.; Yang, W. Permeation Characteristics of CH4 in PVDF with Crude Oil-Containing. Polymers 2022, 14, 2723. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Zhai, L.; Li, H.; Qi, G.; Gao, X.; Yang, W. Molecular Simulation Study on the Hydrogen Permeation Behavior and Mechanism of Common Polymers. Polymers 2024, 16, 953. https://doi.org/10.3390/polym16070953
Zhang X, Zhai L, Li H, Qi G, Gao X, Yang W. Molecular Simulation Study on the Hydrogen Permeation Behavior and Mechanism of Common Polymers. Polymers. 2024; 16(7):953. https://doi.org/10.3390/polym16070953
Chicago/Turabian StyleZhang, Xuemin, Lizhen Zhai, Houbu Li, Guoquan Qi, Xiong Gao, and Wenhui Yang. 2024. "Molecular Simulation Study on the Hydrogen Permeation Behavior and Mechanism of Common Polymers" Polymers 16, no. 7: 953. https://doi.org/10.3390/polym16070953
APA StyleZhang, X., Zhai, L., Li, H., Qi, G., Gao, X., & Yang, W. (2024). Molecular Simulation Study on the Hydrogen Permeation Behavior and Mechanism of Common Polymers. Polymers, 16(7), 953. https://doi.org/10.3390/polym16070953





