Modeling Xanthan Gum Foam’s Material Properties Using Machine Learning Methods
Abstract
1. Introduction
2. Material and Methods
2.1. Materials
2.2. Production Process of Foams
2.3. Characterization of Foams
2.4. Machine-Learning-Based Prediction Methods of Foam Properties
2.4.1. Multiple Linear Regression (MLR)
2.4.2. Least Squares Method (LSM)
2.4.3. Support Vector Machine (SVM)
2.4.4. Artificial Neural Networks (ANNs)
2.4.5. Generalized Regression Neural Networks (GRNNs)
3. Results and Discussion
3.1. Effect of Components on the Physical and Mechanical Properties of Foams
3.2. Machine-Learning-Based Prediction of Foam Properties
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yetgin, H.; Ünal, H. Polimer Esasli Köpük Malzemeler. DPÜFBED 2008, 17, 117–128. [Google Scholar]
- Liao, J.; Luan, P.; Zhang, Y.; Chen, L.; Huang, L.; Mo, L.; Li, J.; Xiong, Q. A lightweight, biodegradable, and recyclable cellulose-based bio-foam with good mechanical strength and water stability. J. Environ. Chem. Eng. 2022, 10, 107788. [Google Scholar] [CrossRef]
- Qiu, J.F.; Zhang, M.Q.; Rong, M.Z.; Wu, S.P.; Karger-Kocsis, J. Rigid bio-foam plastics with intrinsic flame retardancy derived from soybean oil. J. Mater. Chem. A 2013, 1, 2533. [Google Scholar] [CrossRef]
- Ozen, E.; Yildirim, N.; Dalkilic, B.; Ergun, M.E. Effects of microcrystalline cellulose on some performance properties of chitosan aerogels. Maderas Cienc. Tecnol. 2021, 23, 1–10. [Google Scholar] [CrossRef]
- Duan, Q.; Zhu, Z.; Chen, Y.; Liu, H.; Yang, M.; Chen, L.; Yu, L. Starch-Based Foams Nucleated and Reinforced by Polysaccharide-Based Crystals. ACS Sustain. Chem. Eng. 2022, 10, 2169–2179. [Google Scholar] [CrossRef]
- Berglund, L.; Nissilä, T.; Sivaraman, D.; Komulainen, S.; Telkki, V.-V.; Oksman, K. Seaweed-Derived Alginate–Cellulose Nanofiber Aerogel for Insulation Applications. ACS Appl. Mater. Interfaces 2021, 13, 34899–34909. [Google Scholar] [CrossRef]
- An, X.; Zhang, X.; Li, M.; Pei, D.; Ma, X.; Li, C. Bubble-Templated Design of Superelastic Cellulose Foam as a Durable Ionotropic Sensor. ACS Sustain. Chem. Eng. 2022, 10, 1714–1721. [Google Scholar] [CrossRef]
- Dong, K.; Wang, X. Development of cost effective ultra-lightweight cellulose-based sound absorbing material over silica sol/natural fiber blended substrate. Carbohydr. Polym. 2021, 255, 117369. [Google Scholar] [CrossRef]
- Sworn, G. Chapter 27—Xanthan gum. In Handbook of Hydrocolloids, 3rd ed.; Phillips, G.O., Williams, P.A., Eds.; Woodhead Publishing Series in Food Science, Technology and Nutrition; Woodhead Publishing: Sawston, UK, 2021; pp. 833–853. ISBN 978-0-12-820104-6. [Google Scholar]
- Katzbauer, B. Properties and applications of xanthan gum. Polym. Degrad. Stab. 1998, 59, 81–84. [Google Scholar] [CrossRef]
- Sheng, Y.; Xue, M.; Zhang, S.; Wang, Y.; Zhai, X.; Ma, L.; Hu, D.; Huang, X. Effect of xanthan gum and silica nanoparticles on improving foam properties of mixed solutions of short-chain fluorocarbon and hydrocarbon surfactants. Chem. Eng. Sci. 2021, 245, 116952. [Google Scholar] [CrossRef]
- Tomé, L.I.N.; Reis, M.S.; de Sousa, H.C.; Braga, M.E.M. Chitosan-xanthan gum PEC-based aerogels: A chemically stable PEC in scCO2. Mater. Chem. Phys. 2022, 287, 126294. [Google Scholar] [CrossRef]
- Xiao, Q.; Zhang, M.; Fan, J.; Li, L.; Xu, T.; Yuan, W. Thermal conductivity enhancement of hydrated salt phase change materials employing copper foam as the supporting material. Sol. Energy Mater. Sol. Cells 2019, 199, 91–98. [Google Scholar] [CrossRef]
- Falusi, F.; Berkó, S.; Kovács, A.; Budai-Szűcs, M. Application of Xanthan Gum and Hyaluronic Acid as Dermal Foam Stabilizers. Gels 2022, 8, 413. [Google Scholar] [CrossRef]
- Riaz, T.; Iqbal, M.W.; Jiang, B.; Chen, J. A review of the enzymatic, physical, and chemical modification techniques of xanthan gum. Int. J. Biol. Macromol. 2021, 186, 472–489. [Google Scholar] [CrossRef] [PubMed]
- Abu Elella, M.H.; Goda, E.S.; Gab-Allah, M.A.; Hong, S.E.; Pandit, B.; Lee, S.; Gamal, H.; ur Rehman, A.; Yoon, K.R. Xanthan gum-derived materials for applications in environment and eco-friendly materials: A review. J. Environ. Chem. Eng. 2021, 9, 104702. [Google Scholar] [CrossRef]
- Kurt, R. Control of system parameters by estimating screw withdrawal strength values of particleboards using artificial neural network-based statistical control charts. J. Wood Sci. 2022, 68, 64. [Google Scholar] [CrossRef]
- Kurt, R.; Karayilmazlar, S. Estimating Modulus of Elasticity (MOE) of Particleboards Using Artificial Neural Networks to Reduce Quality Measurements and Costs. Drv. Ind. 2019, 70, 257–263. [Google Scholar] [CrossRef]
- Hmede, R.; Chapelle, F.; Lapusta, Y. Review of Neural Network Modeling of Shape Memory Alloys. Sensors 2022, 22, 5610. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Bao, W.; Shi, L.; Zuo, B.; Gao, W. General regression neural network for prediction of sound absorption coefficients of sandwich structure nonwoven absorbers. Appl. Acoust. 2014, 76, 128–137. [Google Scholar] [CrossRef]
- Boztoprak, H.; Özbay, Y. Detection of protozoa in wastewater using ann and active contour in image processing. IU-J. Electr. Electron. Eng. 2013, 13, 1661–1666. [Google Scholar]
- Abd, A.M.; Abd, S.M. Modelling the strength of lightweight foamed concrete using support vector machine (SVM). Case Stud. Constr. Mater. 2017, 6, 8–15. [Google Scholar] [CrossRef]
- Mohan, N.; Kalam, S.A.; Mahaveerakannan, R.; Shah, M.; Yadav, J.S.; Sharma, V.; Naik, P.S.; Narasimha, D.B. Statistical Evaluation of Machining Parameters in Drilling of Glass Laminate Aluminum Reinforced Epoxy Composites using Machine Learning Model. Eng. Sci. 2022, 20, 244–251. [Google Scholar] [CrossRef]
- Liu, W.; Fang, Y.; Qiu, H.; Bi, C.; Huang, X.; Lin, S.; Wang, C.; Xu, J. Determinants and performance prediction on photocatalytic properties of hydroxyapatite by machine learning. Opt. Mater. 2023, 146, 114510. [Google Scholar] [CrossRef]
- Mamba, S.; Perry, D.S.; Tsige, M.; Pellicane, G. Toward the Rational Design of Organic Solar Photovoltaics: Application of Molecular Structure Methods to Donor Polymers. J. Phys. Chem. A 2021, 125, 10593–10603. [Google Scholar] [CrossRef]
- Hassan, M.M.; Tucker, N.; Le Guen, M.J. Thermal, mechanical and viscoelastic properties of citric acid-crosslinked starch/cellulose composite foams. Carbohydr. Polym. 2020, 230, 115675. [Google Scholar] [CrossRef]
- ASTM C303; Standard Test Method for Dimensions and Density of Preformed Block and Board–Type Thermal Insulation. American Society for Testing and Materials: West Conshohocken, PA, USA, 2010.
- ASTM C165-07; Standard Test Method for Measuring Compressive Properties of Thermal Insulations. American Society for Testing and Materials: West Conshohocken, PA, USA, 2017.
- ASTM C203-05a; Standard Test Methods for Breaking Load and Flexural Properties of Block-Type Thermal Insulation. American Society for Testing and Materials: West Conshohocken, PA, USA, 2012.
- Tsamardinos, I.; Greasidou, E.; Borboudakis, G. Bootstrapping the out-of-sample predictions for efficient and accurate cross-validation. Mach. Learn. 2018, 107, 1895–1922. [Google Scholar] [CrossRef]
- Mengash, H.A.; Mahmoud, H.H. Brain Cancer Tumor Classification from Motion-Corrected MRI Images Using Convolutional Neural Network. Comput. Mater. Contin. 2021, 68, 1551–1563. [Google Scholar] [CrossRef]
- Rashid, J.; Kanwal, S.; Kim, J.; Wasif Nisar, M.; Naseem, U.; Hussain, A. Heart Disease Diagnosis Using the Brute Force Algorithm and Machine Learning Techniques. Comput. Mater. Contin. 2022, 72, 3195–3211. [Google Scholar] [CrossRef]
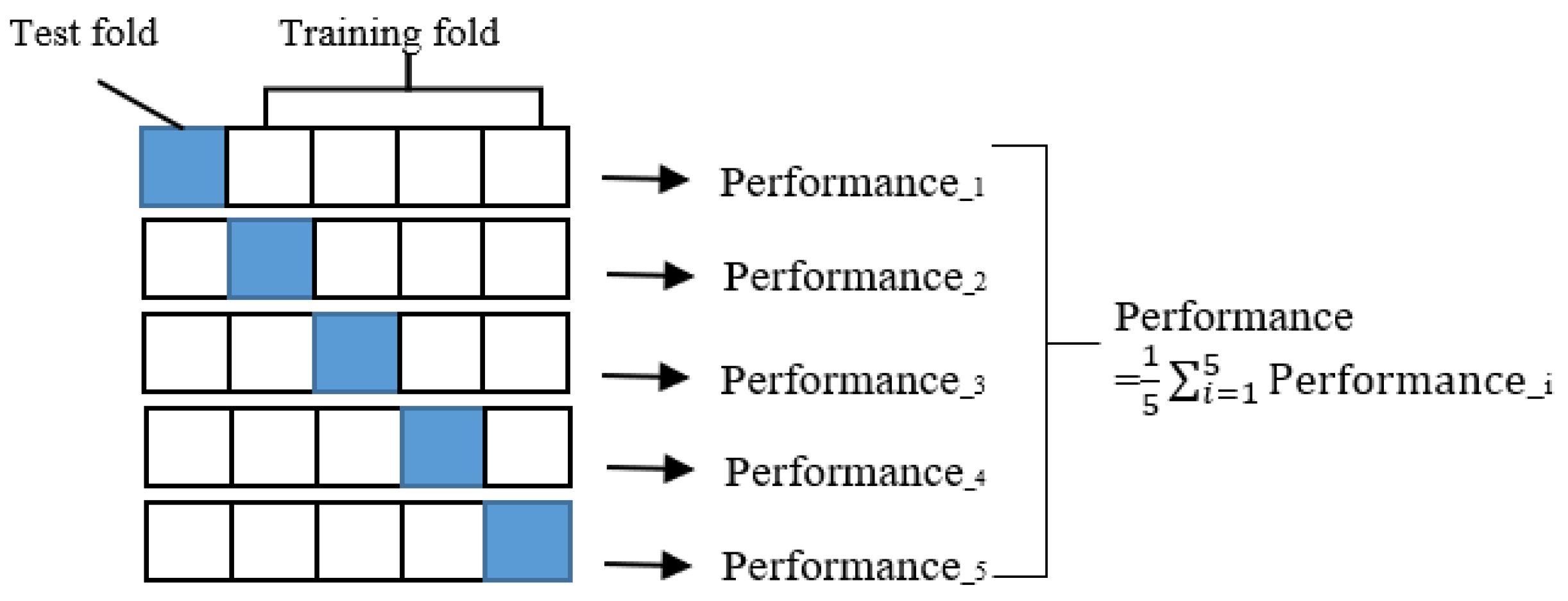
- Refaeilzadeh, P.; Tang, L.; Liu, H. Cross-Validation. In Encyclopedia of Database Systems; Liu, L., Özsu, M.T., Eds.; Springer: Boston, MA, USA, 2009; pp. 532–538. ISBN 978-0-387-35544-3. [Google Scholar]
- Vu, H.L.; Ng, K.T.W.; Richter, A.; An, C. Analysis of input set characteristics and variances on k-fold cross validation for a Recurrent Neural Network model on waste disposal rate estimation. J. Environ. Manag. 2022, 311, 114869. [Google Scholar] [CrossRef] [PubMed]
- Bates, S.; Hastie, T.; Tibshirani, R. Cross-validation: What does it estimate and how well does it do it? J. Am. Stat. Assoc. 2023, 1–12. [Google Scholar] [CrossRef]
- Jiang, P.; Chen, J. Displacement prediction of landslide based on generalized regression neural networks with K-fold cross-validation. Neurocomputing 2016, 198, 40–47. [Google Scholar] [CrossRef]
- Wieczorek, J.; Guerin, C.; McMahon, T. K-fold cross-validation for complex sample surveys. Stat 2022, 11, e454. [Google Scholar] [CrossRef]
- Malebary, S.J.; Khan, Y.D. Identification of Antimicrobial Peptides Using Chou’s 5 Step Rule. Comput. Mater. Contin. 2021, 67, 2863–2881. [Google Scholar] [CrossRef]
- Ajona, M.; Vasanthi, P.; Vijayan, D.S. Application of multiple linear and polynomial regression in the sustainable biodegradation process of crude oil. Sustain. Energy Technol. Assess. 2022, 54, 102797. [Google Scholar] [CrossRef]
- Vinson Joshua, S.; Selwin Mich Priyadharson, A.; Kannadasan, R.; Ahmad Khan, A.; Lawanont, W.; Ahmed Khan, F.; Ur Rehman, A.; Junaid Ali, M. Crop Yield Prediction Using Machine Learning Approaches on a Wide Spectrum. Comput. Mater. Contin 2022, 72, 5663–5679. [Google Scholar] [CrossRef]
- Ryan, T.P. Modern Regression Methods; John Wiley & Sons: Hoboken, NJ, USA, 2008; Volume 655. [Google Scholar]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Tanyildizi, H. Prediction of the Strength Properties of Carbon Fiber-Reinforced Lightweight Concrete Exposed to the High Temperature Using Artificial Neural Network and Support Vector Machine. Adv. Civ. Eng. 2018, 2018, 5140610. [Google Scholar] [CrossRef]
- Masoudi Nejad, R.; Sina, N.; Ma, W.; Liu, Z.; Berto, F.; Gholami, A. Optimization of fatigue life of pearlitic Grade 900A steel based on the combination of genetic algorithm and artificial neural network. Int. J. Fatigue 2022, 162, 106975. [Google Scholar] [CrossRef]
- Specht, D.F. A general regression neural network. IEEE Trans. Neural Netw. 1991, 2, 568–576. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Q.; Xu, H.; Li, T.; Shen, H.; Zhang, L. Estimating surface soil moisture from satellite observations using a generalized regression neural network trained on sparse ground-based measurements in the continental U.S. J. Hydrol. 2020, 580, 124351. [Google Scholar] [CrossRef]
- Kim, B.; Lee, D.W.; Park, K.Y.; Choi, S.R.; Choi, S. Prediction of plasma etching using a randomized generalized regression neural network. Vacuum 2004, 76, 37–43. [Google Scholar] [CrossRef]
- Ghaffari-Razin, S.R.; Rastbood, A.; Hooshangi, N. Regional application of generalized regression neural network in ionosphere spatio-temporal modeling and forecasting. GPS Solut 2023, 27, 51. [Google Scholar] [CrossRef]
- Batayneh, W.; Abdulhay, E.; Alothman, M. Comparing the efficiency of artificial neural networks in sEMG-based simultaneous and continuous estimation of hand kinematics. Digit. Commun. Netw. 2022, 8, 162–173. [Google Scholar] [CrossRef]
- Wasserman, P.D. Advanced Methods in Neural Computing; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1993. [Google Scholar]
- Ergun, M.E. Activated carbon and cellulose-reinforced biodegradable chitosan foams. BioResources 2023, 18, 1215–1231. [Google Scholar] [CrossRef]
- Chen, C.; Zhou, Y.; Xie, W.; Meng, T.; Zhao, X.; Pang, Z.; Chen, Q.; Liu, D.; Wang, R.; Yang, V.; et al. Lightweight, Thermally Insulating, Fire-Proof Graphite-Cellulose Foam. Adv. Funct. Mater. 2023, 33, 2204219. [Google Scholar] [CrossRef]
- Schiavoni, S.; D’Alessandro, F.; Bianchi, F.; Asdrubali, F. Insulation materials for the building sector: A review and comparative analysis. Renew. Sustain. Energy Rev. 2016, 62, 988–1011. [Google Scholar] [CrossRef]
- Yildirim, N.; Ozen, E.; Ergun, M.E.; Dalkilic, B. A Study on Physical, Morphological and Antibacterial Properties of Bio Polymers Reinforced Polyvinyl Acetate Foams. Mat. Res. 2022, 25, e20210579. [Google Scholar] [CrossRef]
- Wang, L.; Schiraldi, D.A.; Sánchez-Soto, M. Foamlike Xanthan Gum/Clay Aerogel Composites and Tailoring Properties by Blending with Agar. Ind. Eng. Chem. Res. 2014, 53, 7680–7687. [Google Scholar] [CrossRef]
- Dehdari, B.; Parsaei, R.; Riazi, M.; Rezaei, N.; Zendehboudi, S. New insight into foam stability enhancement mechanism, using polyvinyl alcohol (PVA) and nanoparticles. J. Mol. Liq. 2020, 307, 112755. [Google Scholar] [CrossRef]
- Campbell, F.C. Introduction to Composite Materials and Processes: Unique Materials that Require Unique Processes. In Manufacturing Processes for Advanced Composites; Elsevier: Amsterdam, The Netherlands, 2004; pp. 1–37. ISBN 978-1-85617-415-2. [Google Scholar]
- Ali, Z.M.; Gibson, L.J. The structure and mechanics of nanofibrillar cellulose foams. Soft Matter 2013, 9, 1580–1588. [Google Scholar] [CrossRef]
- Sun, L.; Liu, L.; Wu, M.; Wang, D.; Shen, R.; Zhao, H.; Lu, J.; Yao, J. Nanocellulose interface enhanced all-cellulose foam with controllable strength via a facile liquid phase exchange route. Carbohydr. Polym. 2023, 299, 120192. [Google Scholar] [CrossRef]
- Ferreira, S.E.; Dobrzanski, E.; Tiwary, P.; Agrawal, P.; Chen, R.; Cranston, D.E. Insulative wood materials templated by wet foams. Mater. Adv. 2023, 4, 641–650. [Google Scholar] [CrossRef]
- Wu, J.-S.; Yeh, T.-M. Studies on the flexural modulus of structural foams. J. Polym. Res. 1994, 1, 61–68. [Google Scholar] [CrossRef]
- Yang, S.-Y.; Yang, H.-X.; Hu, A.-J. Chapter 4—Super Engineering Plastics and Forms. In Advanced Polyimide Materials; Yang, S.-Y., Ed.; Elsevier: Amsterdam, The Netherlands, 2018; pp. 137–193. ISBN 978-0-12-812640-0. [Google Scholar]
- Raymond, A.; Rodrigue, D. Foams and wood composite foams produced by rotomolding. Cell. Polym. 2013, 32, 199–212. [Google Scholar] [CrossRef]
- Moo-Tun, N.M.; Iñiguez-Covarrubias, G.; Valadez-Gonzalez, A. Assessing the effect of PLA, cellulose microfibers and CaCO3 on the properties of starch-based foams using a factorial design. Polym. Test. 2020, 86, 106482. [Google Scholar] [CrossRef]
- Yildirim, N. Performance Comparison of Bio-based Thermal Insulation Foam Board with Petroleum-based Foam Boards on the Market. BioResources 2018, 13, 3395–3403. [Google Scholar] [CrossRef]
- Patel, J.; Maji, B.; Moorthy, N.S.H.N.; Maiti, S. Xanthan gum derivatives: Review of synthesis, properties and diverse applications. RSC Adv. 2020, 10, 27103–27136. [Google Scholar] [CrossRef]
- Shen, J.; Lu, G.; Ruan, D. Compressive behaviour of closed-cell aluminium foams at high strain rates. Compos. B Eng. 2010, 41, 678–685. [Google Scholar] [CrossRef]
- Alava, M.; Niskanen, K. The physics of paper. Rep. Prog. Phys. 2006, 69, 669. [Google Scholar] [CrossRef]
- Murmu, S.B. Alternatives derived from renewable natural fibre to replace conventional polyurethane rigid foam insulation. Clean. Eng. Technol. 2022, 8, 100513. [Google Scholar] [CrossRef]
- Salim, M.H.; Kassab, Z.; Ablouh, E.; Semlali Aouragh Hassani, F.; El Achaby, M. Cellulosic biocomposite foam papers impregnated by crosslinked starch/poly (vinyl alcohol) biopolymers. Ind. Crops Prod. 2023, 192, 116074. [Google Scholar] [CrossRef]
- Ghanbarzadeh, B.; Almasi, H.; Entezami, A.A. Improving the barrier and mechanical properties of corn starch-based edible films: Effect of citric acid and carboxymethyl cellulose. Ind. Crops Prod. 2011, 33, 229–235. [Google Scholar] [CrossRef]
- Priya, B.; Gupta, V.K.; Pathania, D.; Singha, A.S. Synthesis, characterization and antibacterial activity of biodegradable starch/PVA composite films reinforced with cellulosic fibre. Carbohydr. Polym. 2014, 109, 171–179. [Google Scholar] [CrossRef] [PubMed]
- Montaño Moreno, J.J.; Palmer Pol, A.; Sesé Abad, A. Using the R-MAPE index as a resistant measure of forecast accuracy. Psicothema 2013, 25, 500–506. [Google Scholar] [CrossRef] [PubMed]


| Codes | Xanthan Gum (%) | Citric Acid (%) | Cellulose (%) | SDS (%) |
|---|---|---|---|---|
| XCF-1 | 2 | 5 | 5 | 0.1 |
| XCF-2 | 5 | 5 | 5 | 0.1 |
| XCF-3 | 8 | 5 | 5 | 0.1 |
| XCF-4 | 5 | 5 | 2 | 0.1 |
| XCF-5 | 5 | 5 | 8 | 0.1 |
| Codes | Density (kg/m3) | Compression Modulus (KPa) | Flexural Modulus (KPa) |
|---|---|---|---|
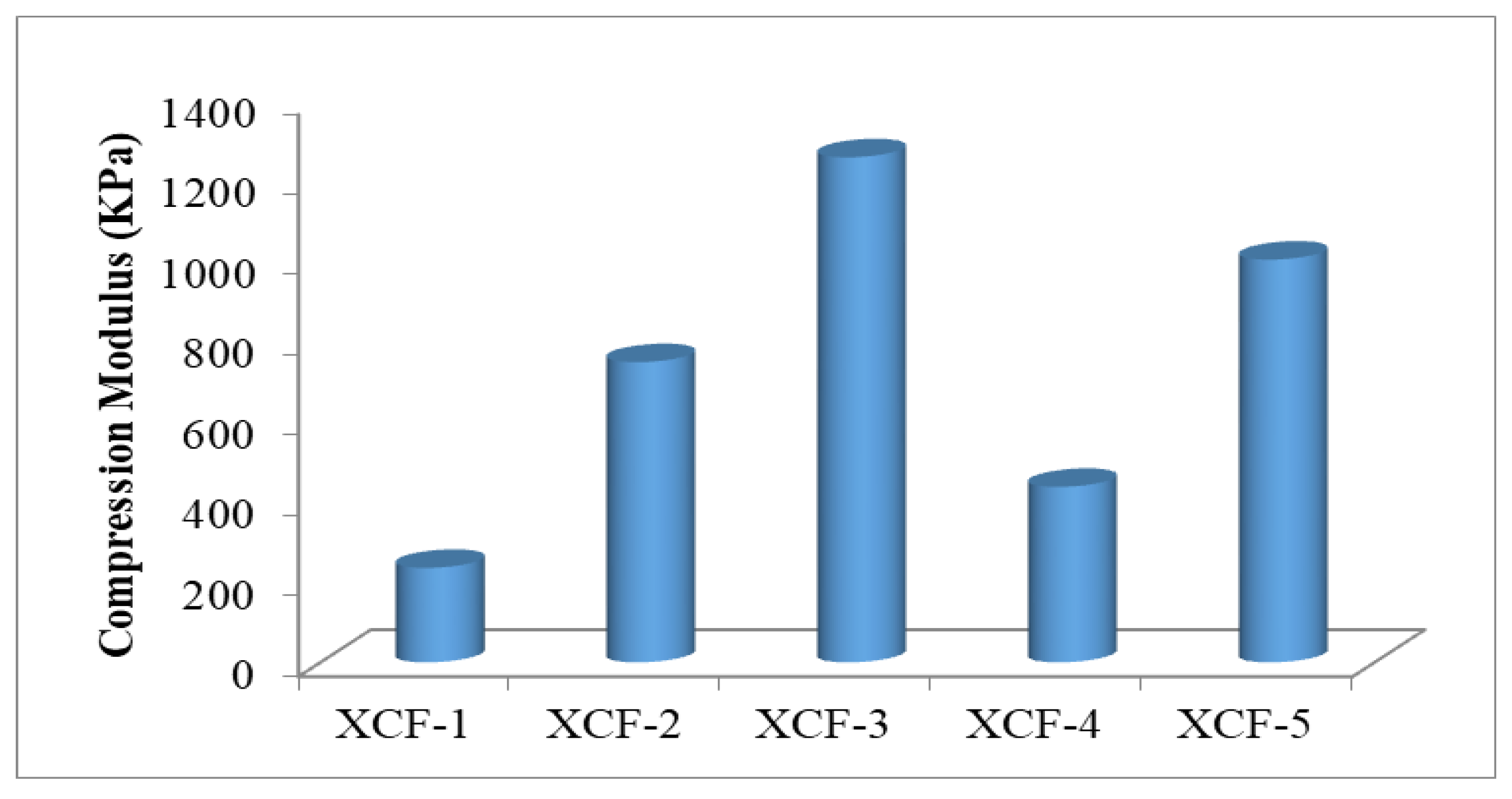
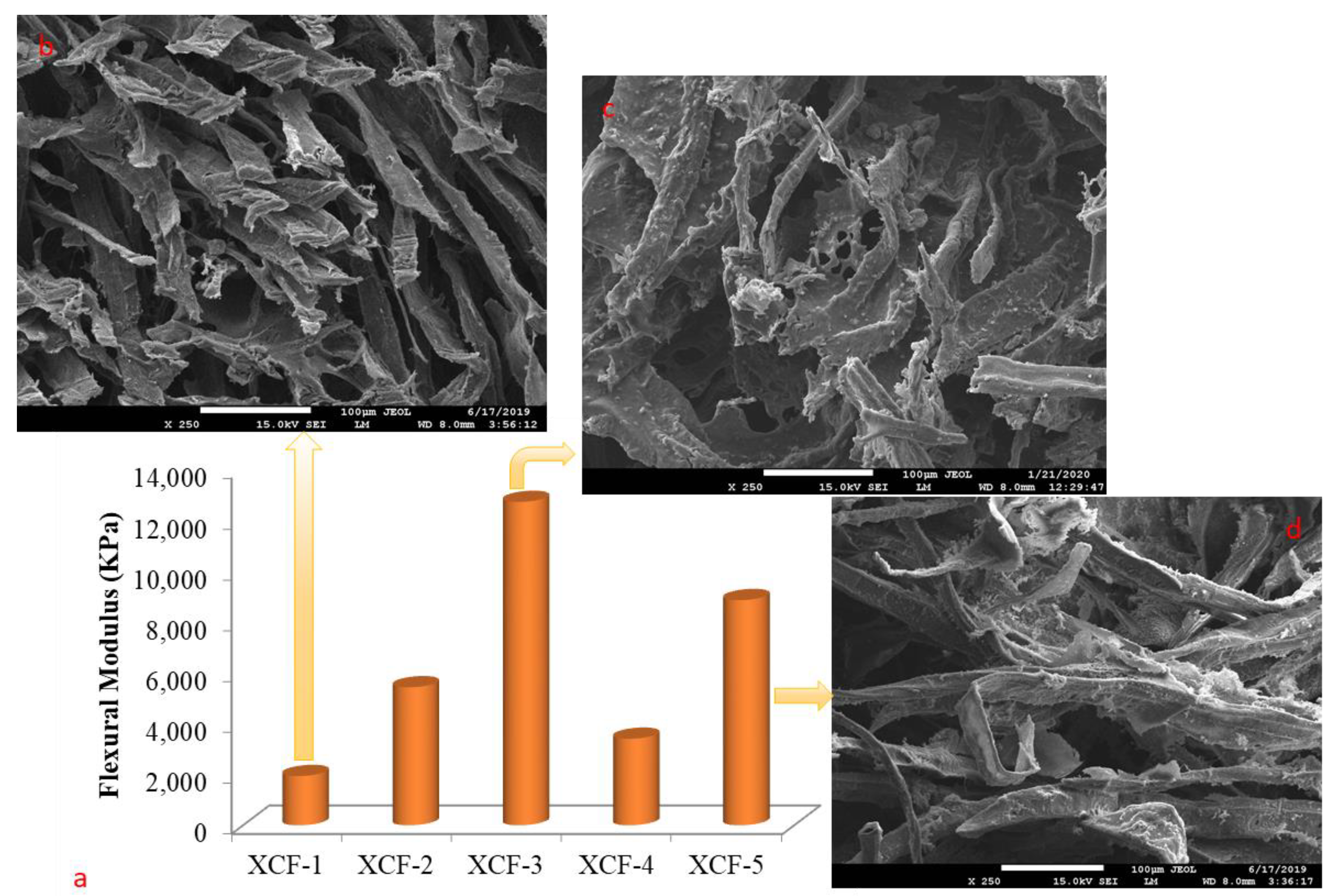
| XCF-1 | 49.42 | 235.25 | 1939.76 |
| XCF-2 | 112.12 | 747.39 | 5436.99 |
| XCF-3 | 172.71 | 1257.52 | 12,736.39 |
| XCF-4 | 76.90 | 436.85 | 3408.63 |
| XCF-5 | 137.52 | 1002.69 | 8869.27 |
| Density | Compression Modulus | Flexural Modulus | ||||
|---|---|---|---|---|---|---|
| MSE | R2 | MSE | R2 | MSE | R2 | |
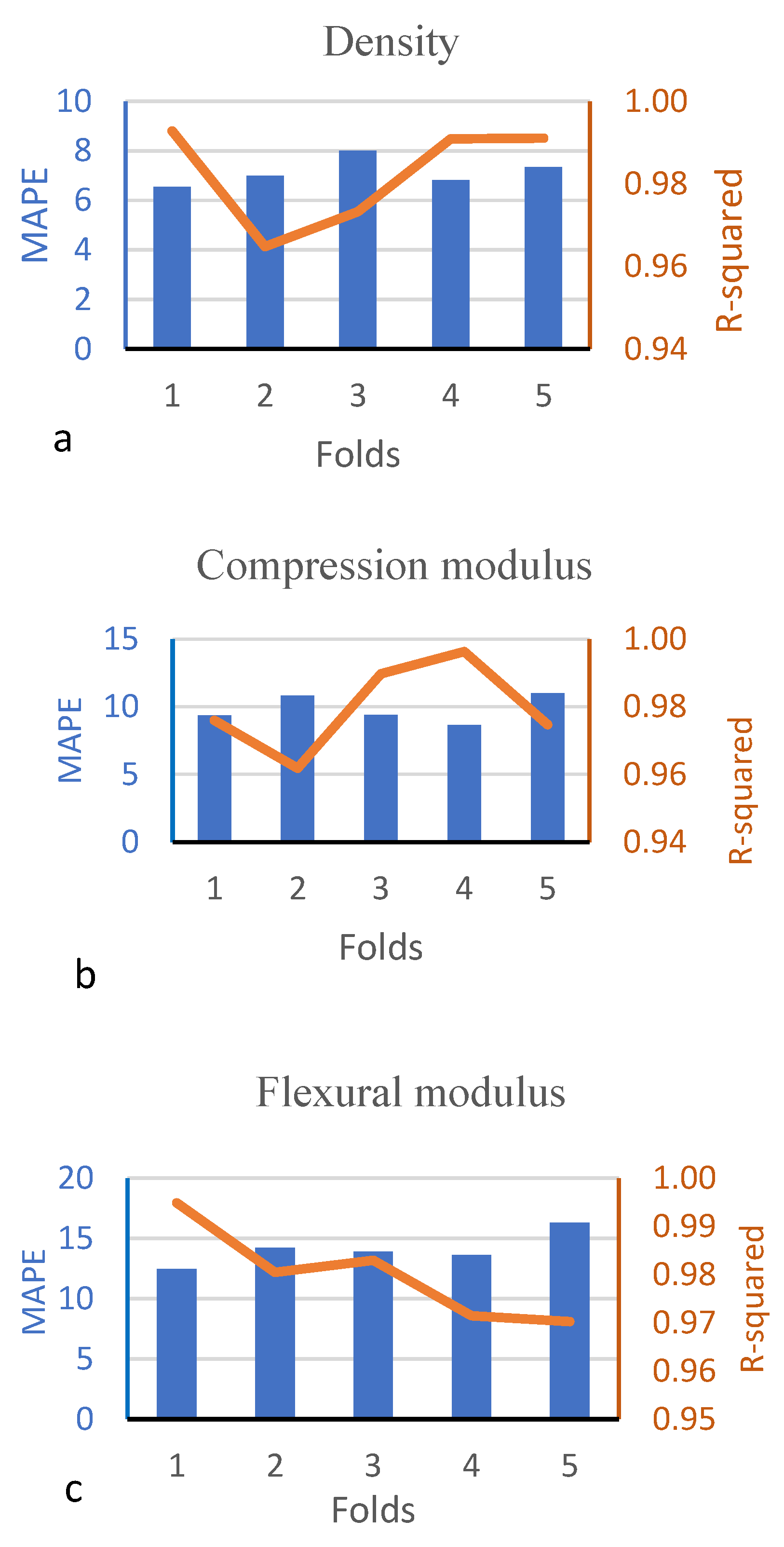
| Neural Network | 69,195 | 0.9642 | 7031.36 | 0.9505 | 791,205 | 0.9501 |
| Linear Regression | 74,763 | 0.9613 | 7271.33 | 0.9489 | 1,373,913 | 0.9473 |
| SVM | 75,326 | 0.9478 | 7624.01 | 0.9463 | 834,695 | 0.9135 |
| Least Squares Method | 14,217 | 0.9398 | 12,971.6 | 0.9094 | 1,467,168 | 0.9074 |
| GRNN | 68,582 | 0.9820 | 7100.18 | 0.9749 | 796,872 | 0.9747 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ergün, H.; Ergün, M.E. Modeling Xanthan Gum Foam’s Material Properties Using Machine Learning Methods. Polymers 2024, 16, 740. https://doi.org/10.3390/polym16060740
Ergün H, Ergün ME. Modeling Xanthan Gum Foam’s Material Properties Using Machine Learning Methods. Polymers. 2024; 16(6):740. https://doi.org/10.3390/polym16060740
Chicago/Turabian StyleErgün, Halime, and Mehmet Emin Ergün. 2024. "Modeling Xanthan Gum Foam’s Material Properties Using Machine Learning Methods" Polymers 16, no. 6: 740. https://doi.org/10.3390/polym16060740
APA StyleErgün, H., & Ergün, M. E. (2024). Modeling Xanthan Gum Foam’s Material Properties Using Machine Learning Methods. Polymers, 16(6), 740. https://doi.org/10.3390/polym16060740






