Structural Optimization of a High-Performance Green Sandwich Made of Sisal Reinforced Epoxy Facings and Balsa Core
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
- (1)
- sisal fibers are supplied by Mellau-Teppich Lotteraner, Wüstner GmbH & Co KG (Mellau, Austria) with a low specific weight of 1.45 g/cm3, tensile strength of 685 MPa, Young’s modulus of about 40 GPa, and ultimate tensile strain of 1.75%;
- (2)
- balsa wood with a specific weight of 150 g/cm3 (the other characteristics are not provided by the vendor and will be determined in the following);
- (3)
- green epoxy resin called SUPERSAP CLR with SuperSap INH Hardener (San Antonio, CA, USA), which, as amply demonstrated in previous studies by the same authors, has an almost linear elastic behavior with a specific weight of 1.05 g/cm3, tensile strength σm,R of about 50 MPa, Young’s modulus Em equal to 2.5 GPa, and an ultimate tensile strain εm,R of 2.5%.
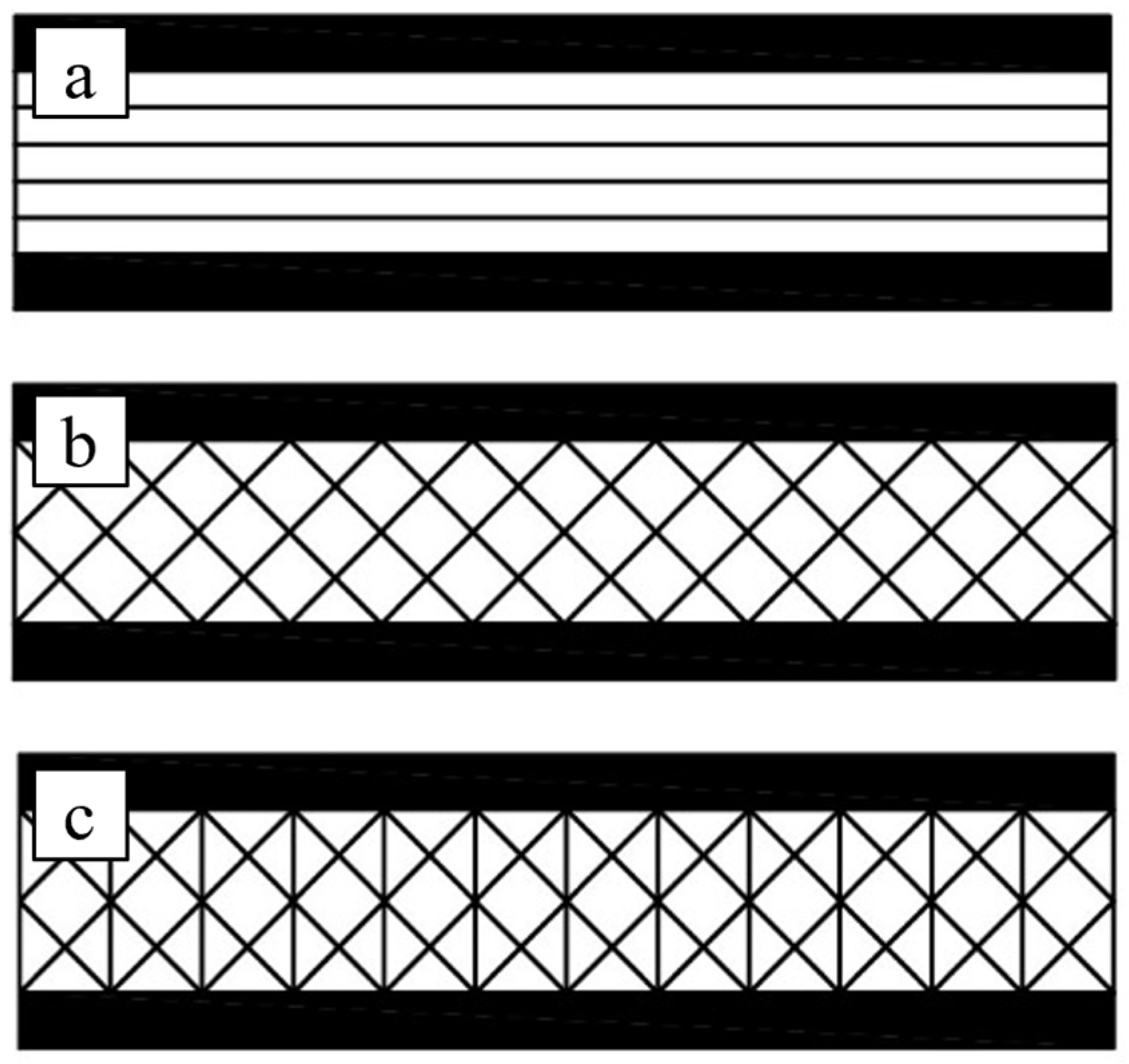
2.2. Cores Manufacture
2.3. Skins Manufacture
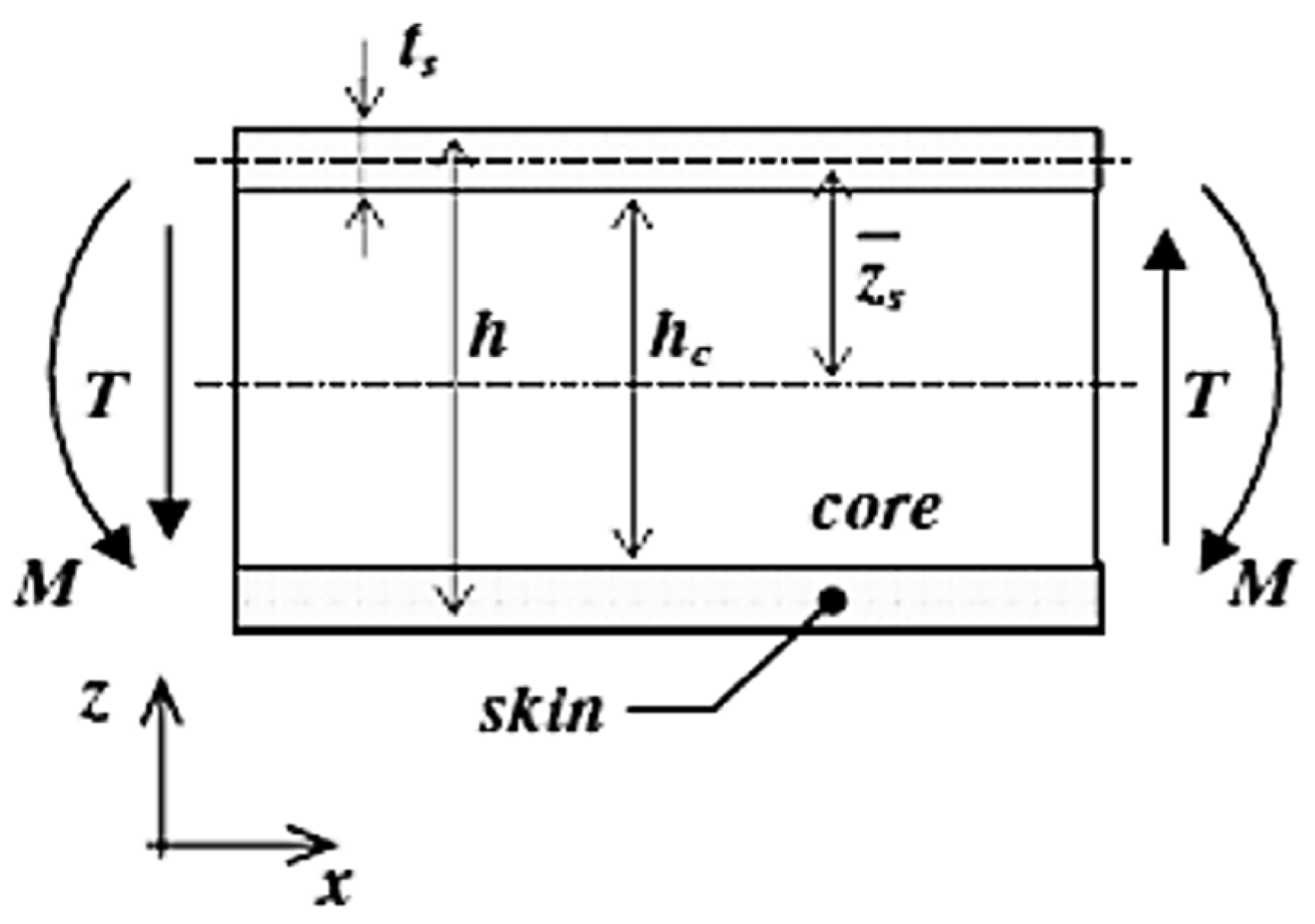
2.4. Sandwichies Manufacture
3. Experimental Results
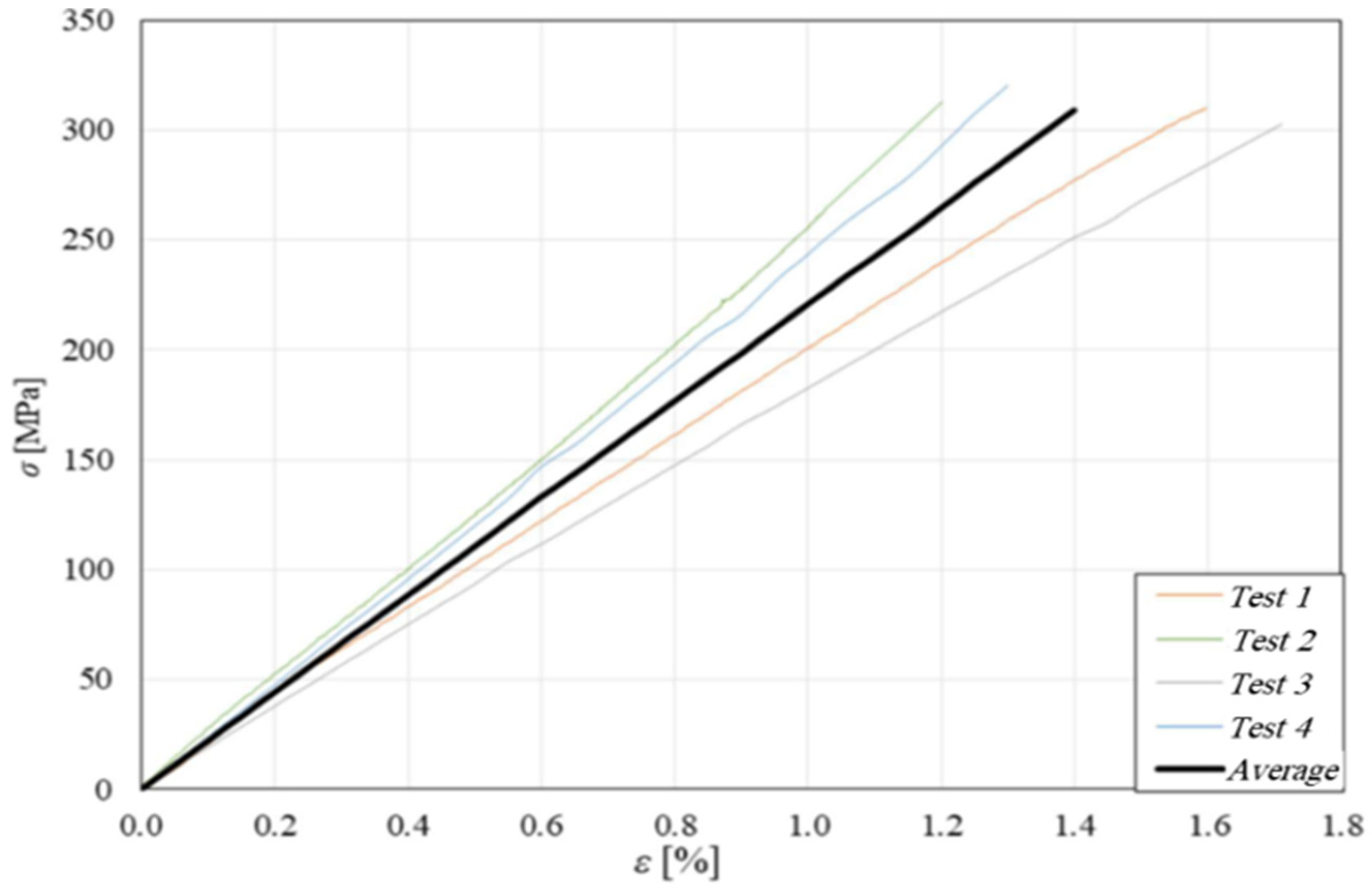
3.1. Tensile Characterization of Skins
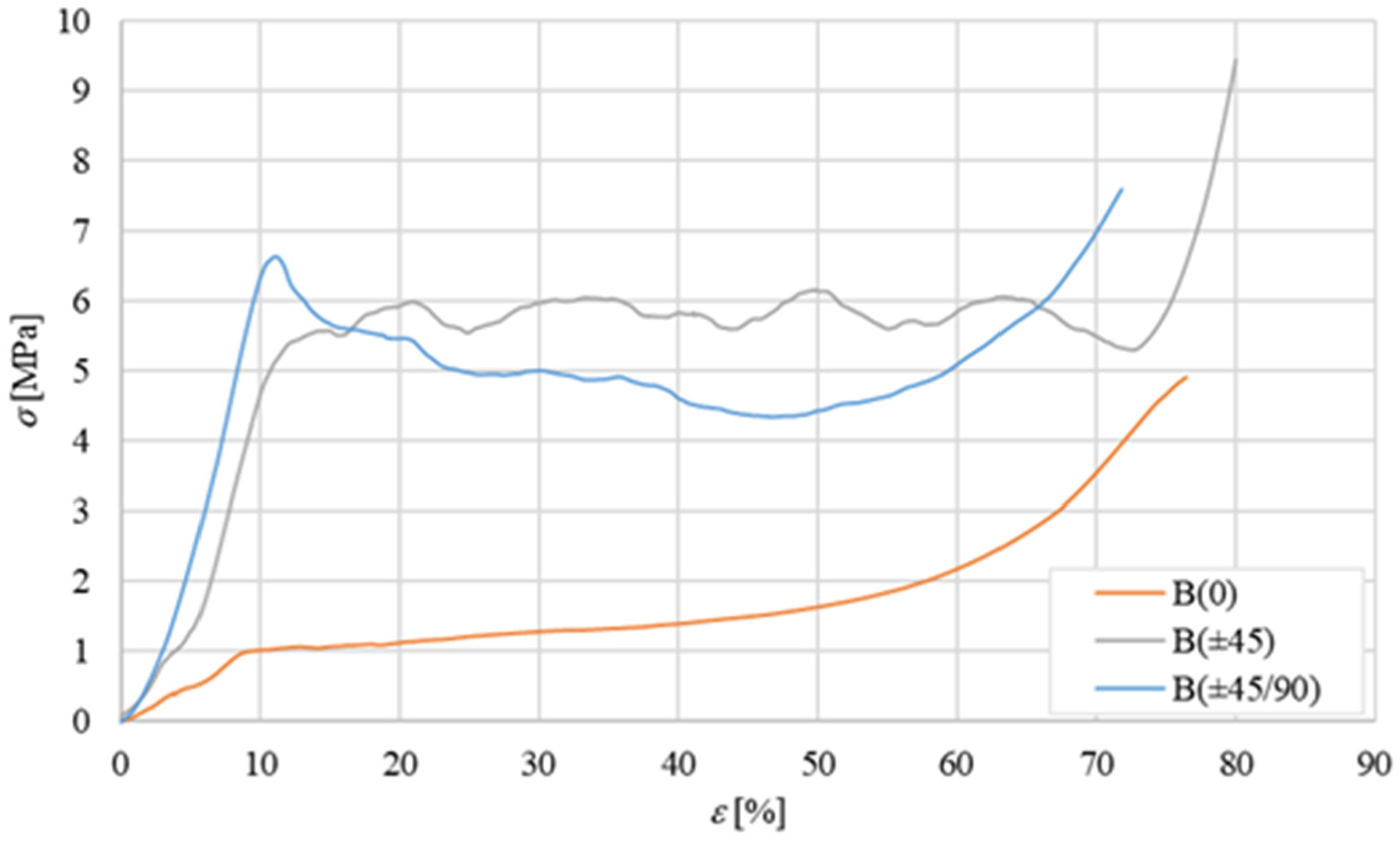
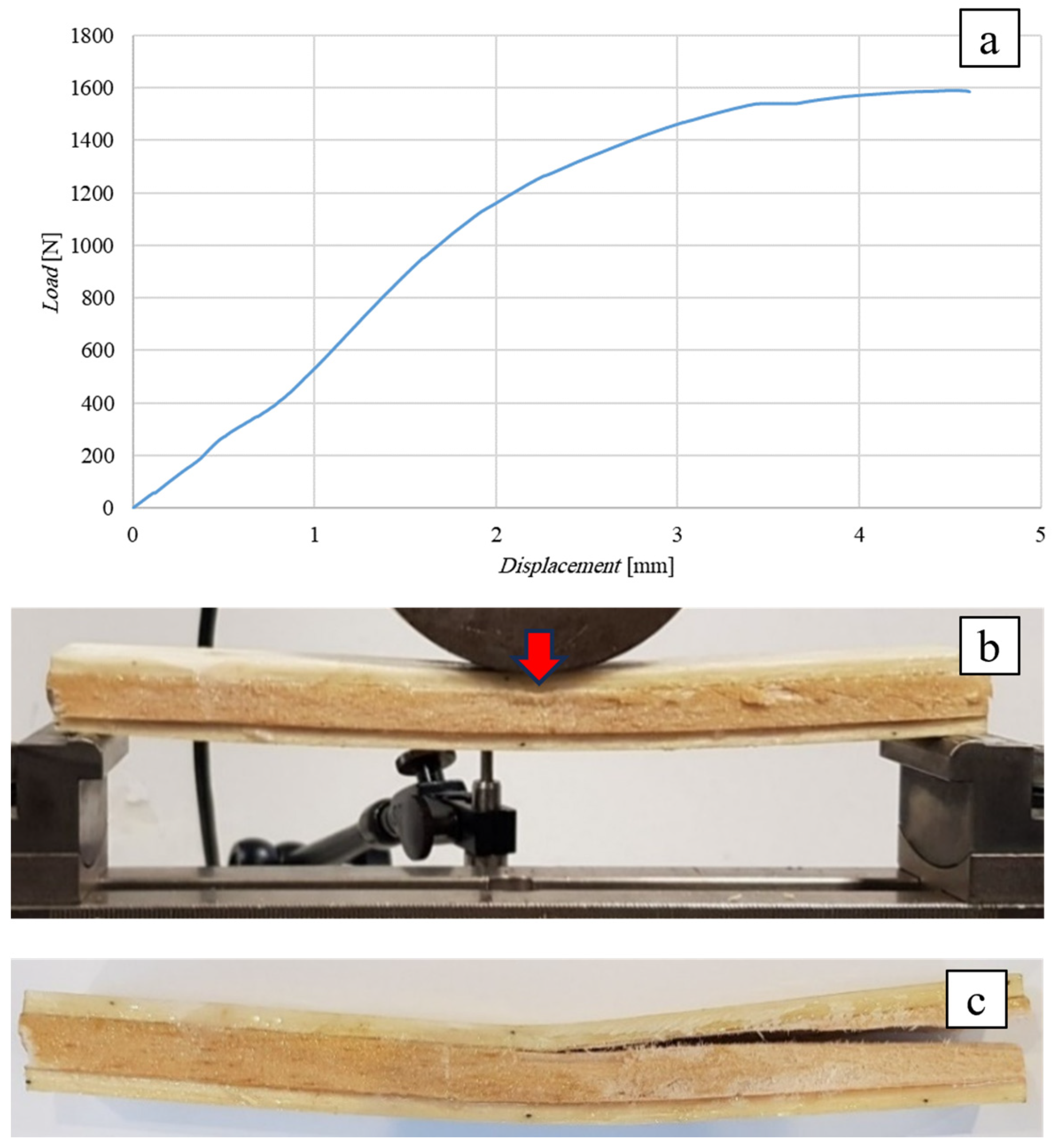
3.2. Transverse Compression Characterization of the Core
3.3. Structural Characterization of the Sandwich
3.3.1. Rail Shear Test
3.3.2. Three-Point Bending Test
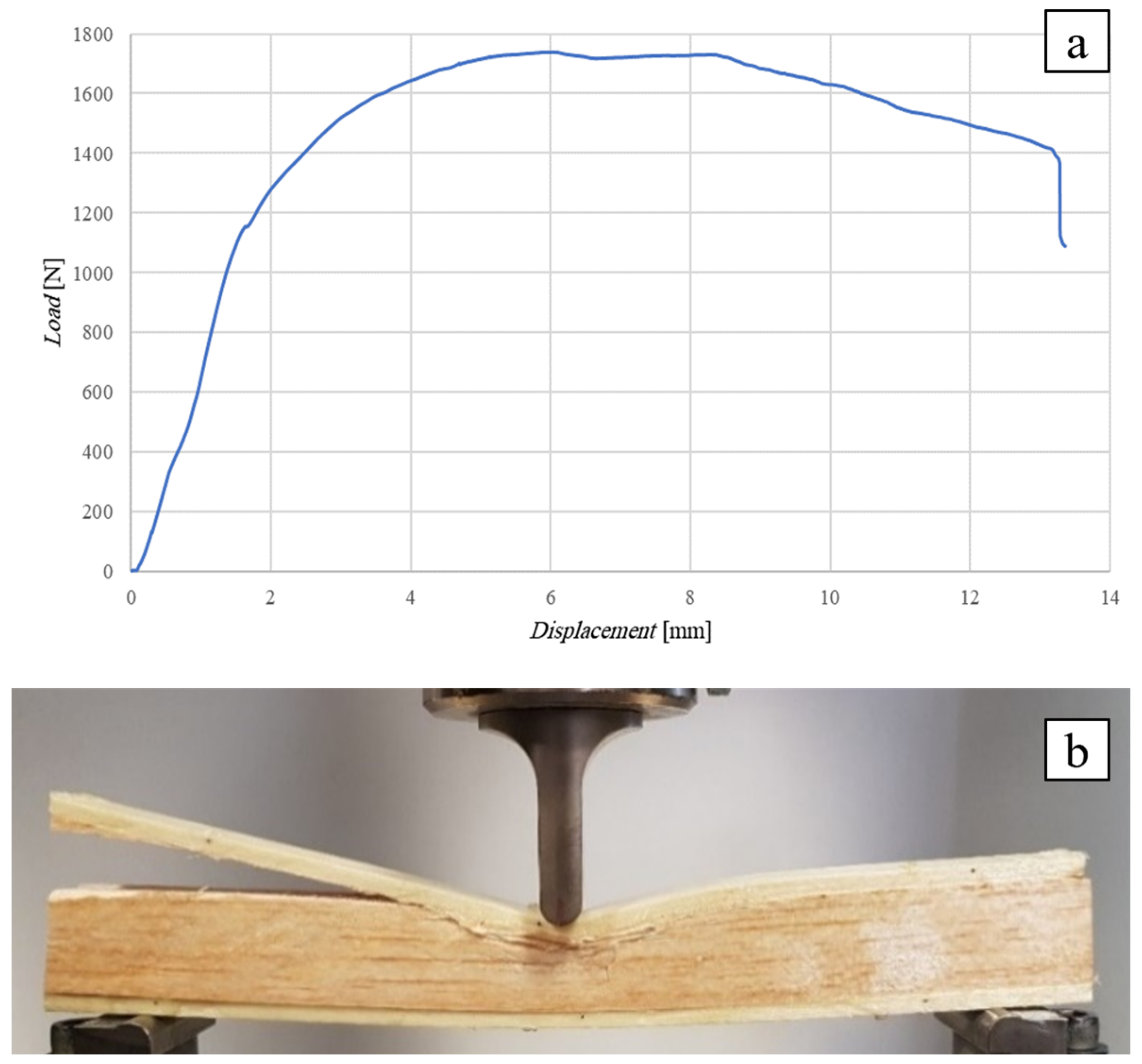
Flexural Test of the SB(0)25 Sandwich
Flexural Test of the SB(0)10 Sandwich
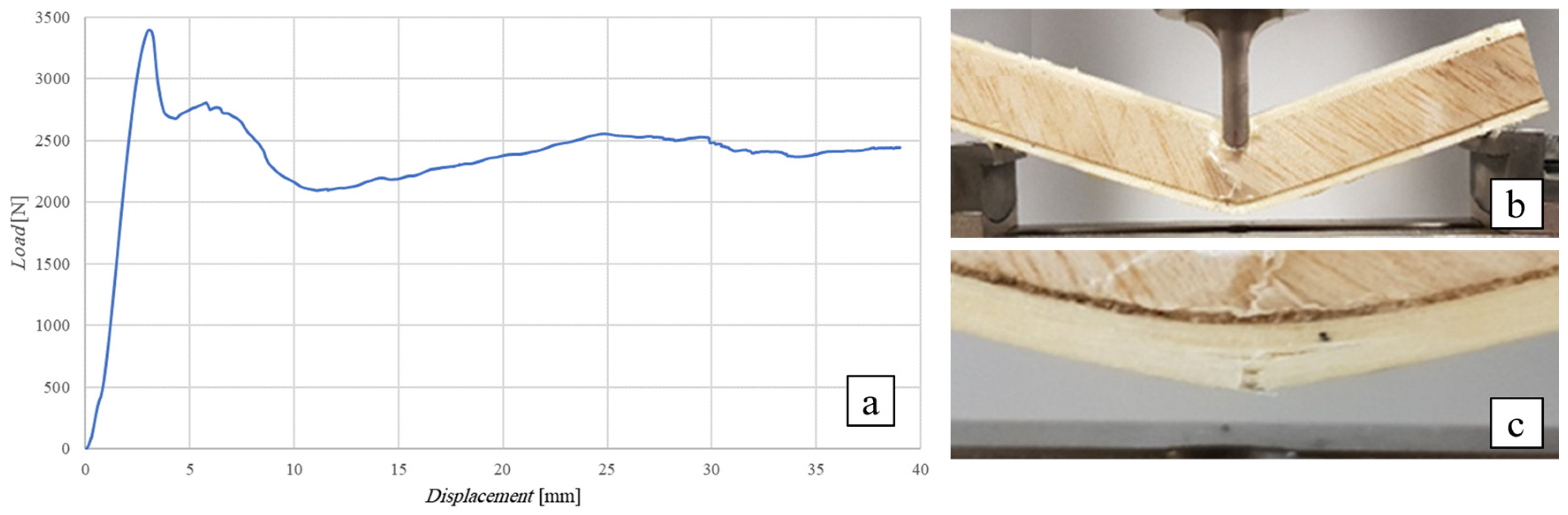
Flexural Test of the SB(±45)25 Sandwich
Flexural Test of the SB(±45)10 Sandwich
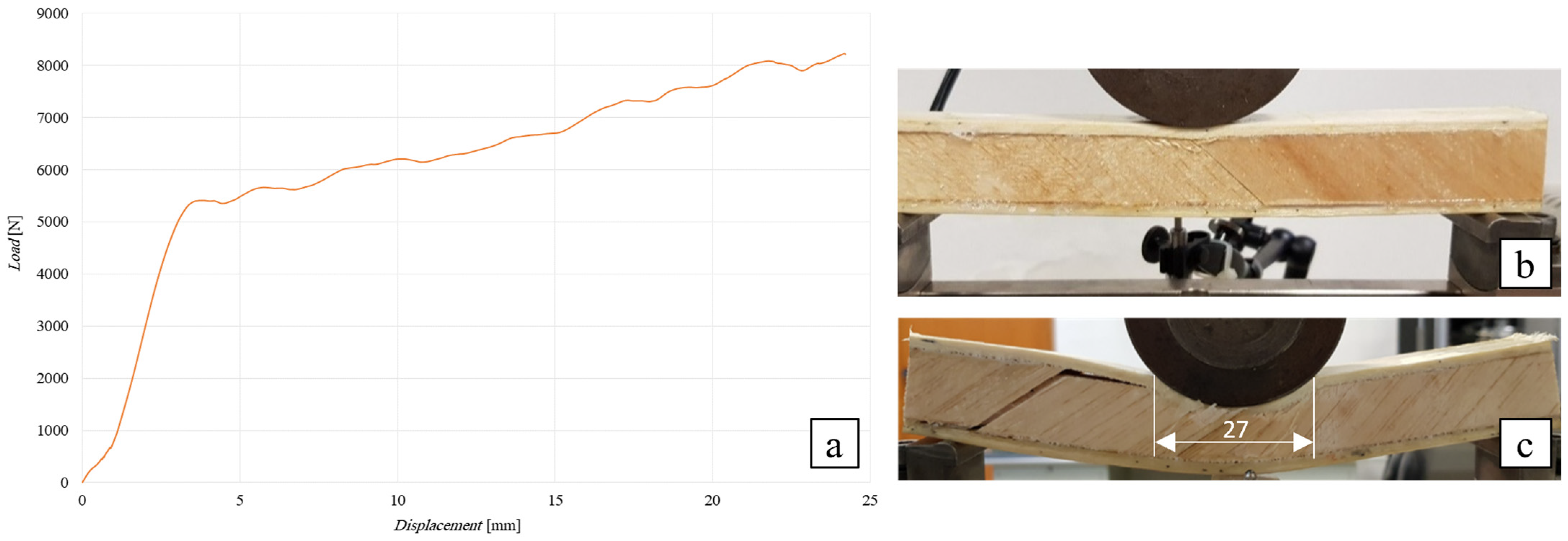
Flexural Test of the SB(±45/90)25 Sandwich
Flexural Test of the SB(±45/90)10 Sandwich
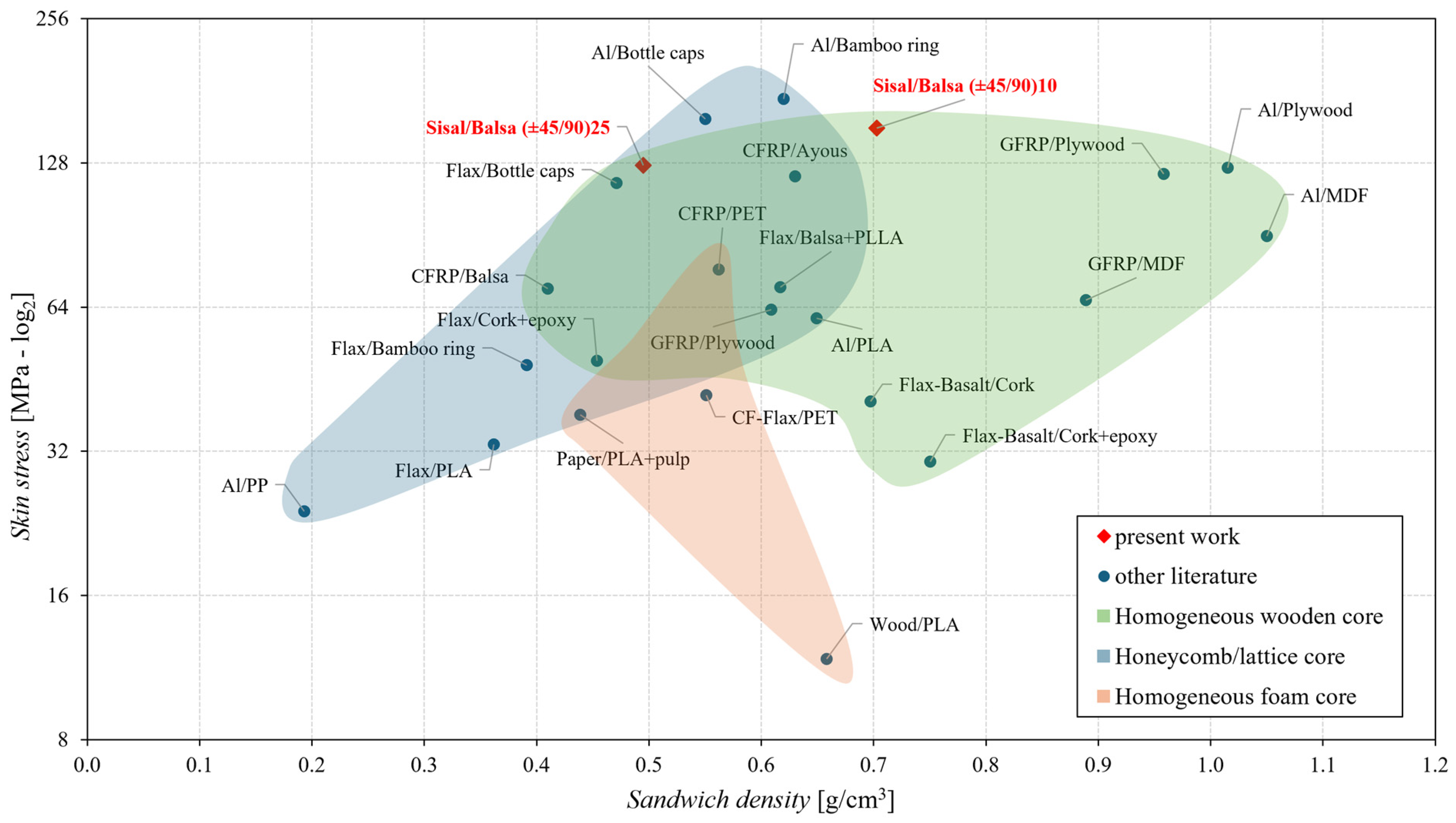
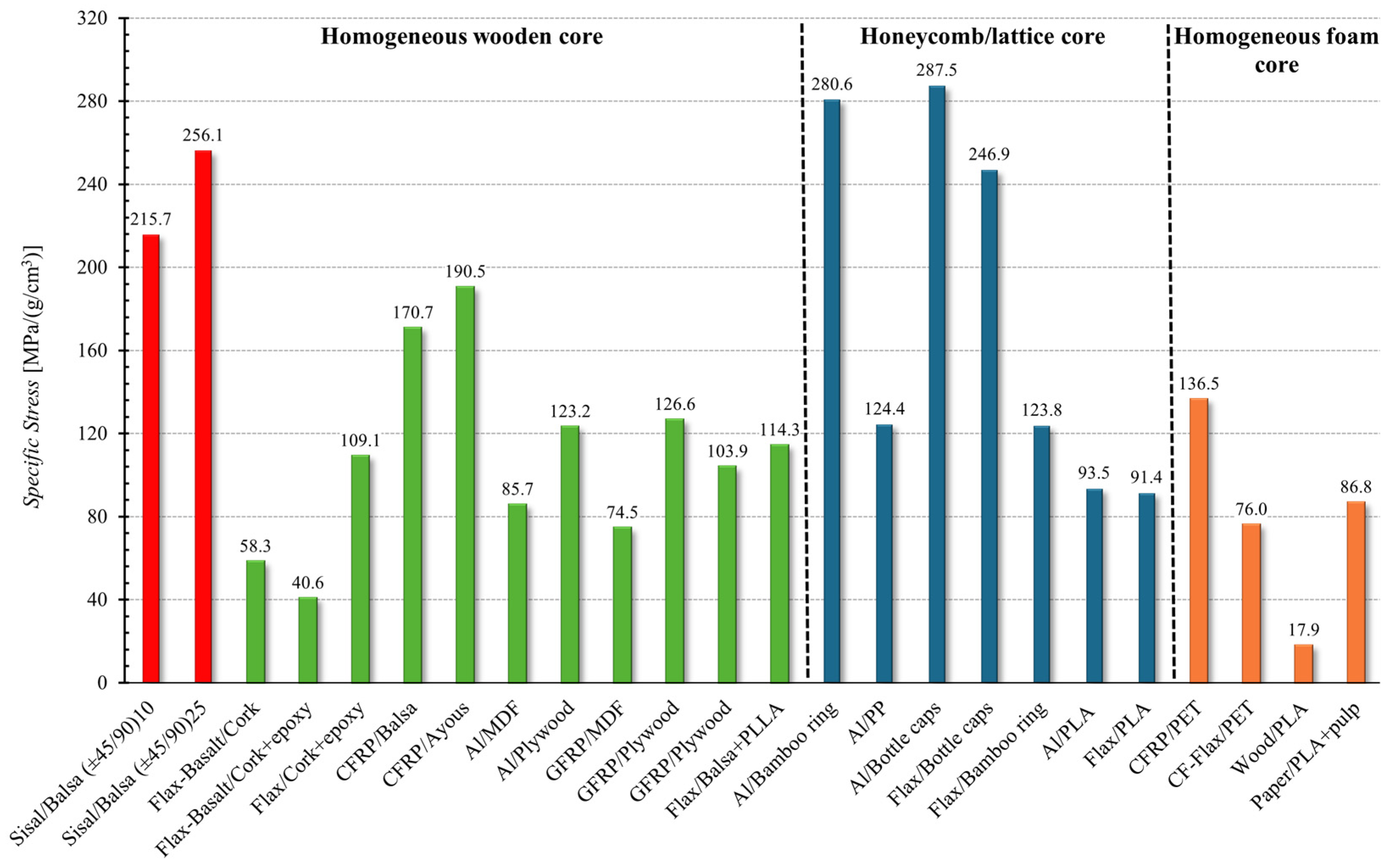
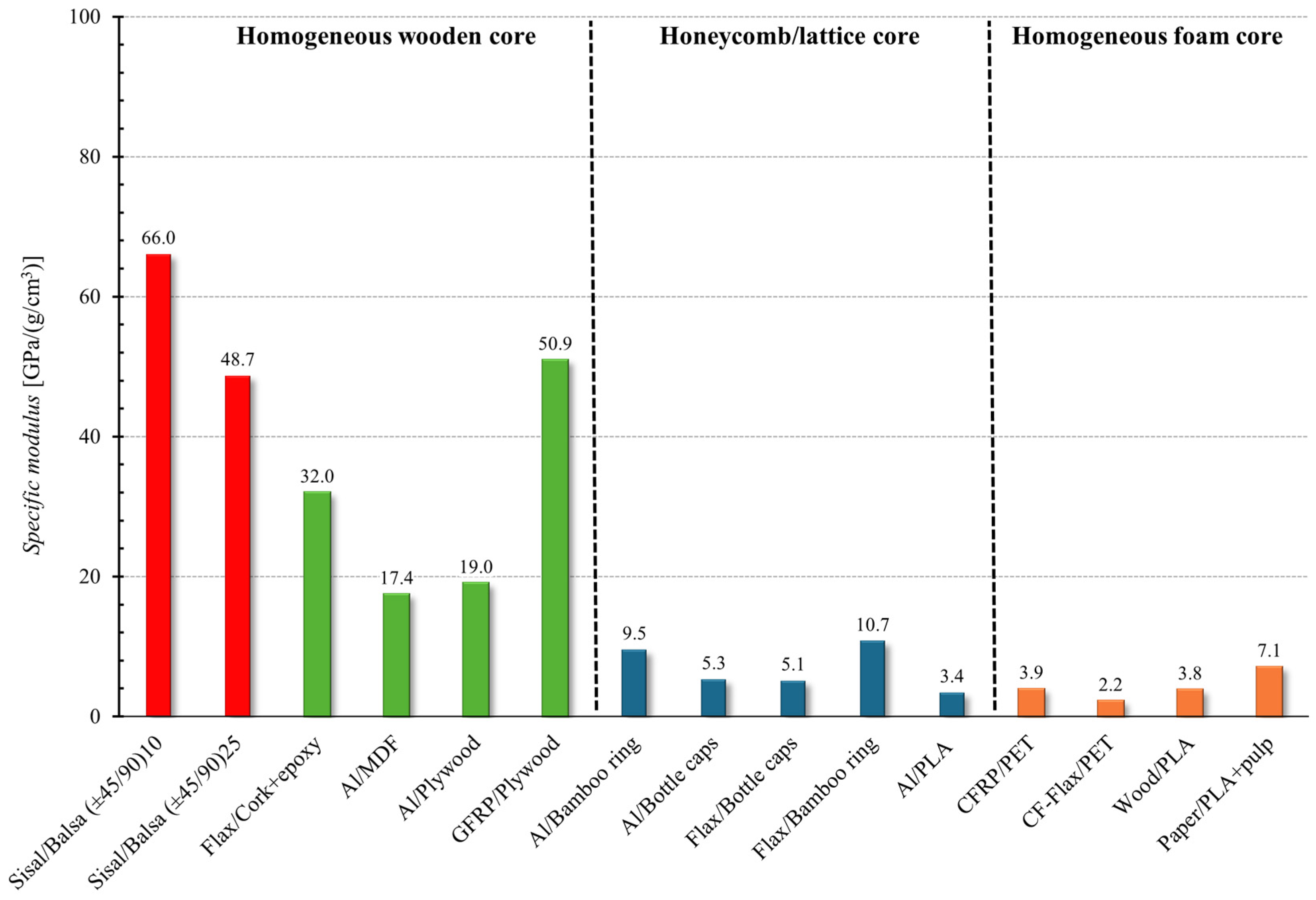
4. Discussion and Comparisons
5. Conclusions
- the use of natural balsa gives rise to inefficient sandwiches, i.e., sandwiches characterized by low load-bearing capacities (included in the range 1590 ÷ 1740 N for sandwiches with core thicknesses of 10 ÷ 25 mm), mainly due to the limited shear strength of common balsa, equal to approximately 1 MPa;
- the mechanical efficiency improves instead significantly by using innovative cross-ply laminar cores with laminae oriented at ±45°; such a configuration in fact permit to increase the load-bearing capacities up to failure loads in the range 2680 ÷ 3440 N (+70% ÷ 100% respect to the simple balsa), although such actual performance are significantly limited respect to the theoretical ones computed by considering the actual core shear strength of 5.5 MPa, due to the unavoidable premature core indentation phenomena and the low transverse compressive strength responsible for significant core indentation effects and the cutting of the compressed skin, or its buckling for core thicknesses of 25 mm and 10 mm respectively;
- however, thanks to the improved transversal compressive strength, the optimization of the sandwich performance is fully obtained by using a core laminate lay-up [(±45/90)n]; indeed, experimentation shows how for such an optimal core configuration, no premature core indentation and/or buckling of the compressed skin no longer occur, and the sandwich strength (8230 N) reaches in practice the theoretical value (8477 N);
- also, such an optimal configuration permits us to quintuple the shear strength (from 1 MPa to about 4.5 MPa) and the transversal compressive strength (from 1 MPa to about 6.5 MPa) of the core, avoiding completely the premature damage phenomena that typically limit the performance of sandwich, such as the indentation of the core around the applied load (indentation that can also lead to the cutting of the compressed skin) and the corrugation/buckling of the upper skin subjected to axial compression, made also easier by the low transversal compressive strength of the common core materials;
- the comparisons with the sandwiches reported in the literature have shown that the skin stress of the proposed optimal sandwich is higher than both the homogeneous foam core and the homogeneous wooden core, and it is comparable with the best sandwiches having a honeycomb/lattice core. Similar results are obtained in terms of specific stress by considering the actual specific sandwich density;
- in terms of absolute and specific flexural modulus, instead, the performance of the proposed sandwich is significantly higher than that of the honeycomb/lattice core and foam core and comparable with the sandwich having a homogeneous wooden core.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Failure Mechanisms and Strength Characterization
References
- Castanie, B.; Christophe, B.; Ginot, M. Review of composite sandwich structure in aeronautic applications. Compos. Part C Open Access 2020, 1, 100004. [Google Scholar] [CrossRef]
- Wang, W.; Li, Z.; Feng, Y.; Luo, C.; Liu, S.; Wang, Y.; Zhu, L. Damage mechanism and bending properties degradation of aviation composite honeycomb sandwich structures under laser irradiation. Opt. Laser Technol. 2025, 181, 111635. [Google Scholar] [CrossRef]
- Oliveira, P.R.; May, M.; Panzera, T.H.; Hiermaier, S. Bio-based/green sandwich structures: A review. Thin-Walled Struct. 2022, 177, 109426. [Google Scholar] [CrossRef]
- Pickering, K.L.; Efendy, M.G.A.; Le, T.M. A review of recent developments in natural fibre composites and their mechanical performance. Compos. Part A Appl. Sci. Manuf. 2016, 83, 98–112. [Google Scholar] [CrossRef]
- Hoto, R.; Furundarena, G.; Torres, J.P.; Muñoz, E.; Andrés, J.; García, J.A. Flexural behavior and water absorption of asymmetrical sandwich composites from natural fibers and cork agglomerate core. Mater. Lett. 2014, 127, 48–52. [Google Scholar] [CrossRef]
- Colomina, S.; Boronat, T.; Fenollar, O.; Sánchez-Nacher, L.; Balart, R. High renewable content sandwich structures based on flax-basalt hybrids and biobased epoxy polymers. AIP Conf. Proc. 2014, 1593, 467–470. [Google Scholar] [CrossRef]
- Mohareb, A.S.O.; Hassanin, A.H.; Badr, A.A.; Hassan, K.T.S.; Farag, R. Novel composite sandwich structure from green materials: Mechanical, physical, and biological evaluation. J. Appl. Polym. Sci. 2015, 132, 4–11. [Google Scholar] [CrossRef]
- Mancuso, A.; Pitarresi, G.; Tumino, D. Mechanical Behaviour of a Green Sandwich Made of Flax Reinforced Polymer Facings and Cork Core. Procedia Eng. 2015, 109, 144–153. [Google Scholar] [CrossRef]
- Jiang, L.; Walczyk, D.; McIntyre, G.; Bucinell, R.; Li, B. Bioresin infused then cured mycelium-based sandwich-structure biocomposites: Resin transfer molding (RTM) process, flexural properties, and simulation. J. Clean. Prod. 2019, 207, 123–135. [Google Scholar] [CrossRef]
- Chan, K.E.; Yong, L.A.; Ko, Y.F.; Mendez, S. Experimental and numerical studies of sustainable sandwich bio-composites derived from plant-based resources. J. Sandw. Struct. Mater. 2017, 19, 192–215. [Google Scholar] [CrossRef]
- Torres, J.P.; Hoto, R.; Andrés, J.; García-Manrique, J.A. Manufacture of green-composite sandwich structures with basalt fiber and bioepoxy resin. Adv. Mater. Sci. Eng. 2013, 1, 214506. [Google Scholar] [CrossRef]
- Zoumaki, M.; Mansour, M.T.; Tsongas, K.; Tzetzis, D.; Mansour, G. Mechanical Characterization and Finite Element Analysis of Hierarchical Sandwich Structures with PLA 3D-Printed Core and Composite Maize Starch Biodegradable Skins. J. Compos. Sci. 2022, 6, 118. [Google Scholar] [CrossRef]
- Zarna, C.; Chinga-Carrasco, G.; Echtermeyer, A.T. Bending properties and numerical modelling of cellular panels manufactured from wood fibre/PLA biocomposite by 3D printing. Compos. Part A Appl. Sci. Manuf. 2023, 165, 107368. [Google Scholar] [CrossRef]
- Galos, J.; Das, R.; Sutcliffe, M.P.; Mouritz, A.P. Review of balsa core sandwich composite structures. Mater. Des. 2022, 221, 111013. [Google Scholar] [CrossRef]
- Zuccarello, B.; Zingales, M. Toward high performance renewable agave reinforced biocomposites: Optimization of fiber performance and fiber-matrix adhesion analysis. Compos. Part B Eng. 2017, 122, 109–120. [Google Scholar] [CrossRef]
- Zuccarello, B.; Scaffaro, R. Experimental analysis and micromechanical models of high performance renewable agave reinforced biocomposites. Compos. Part B Eng. 2017, 119, 141–152. [Google Scholar] [CrossRef]
- Zuccarello, B.; Marannano, G. Random short sisal fiber biocomposites: Optimal manufacturing process and reliable theoretical models. Mater. Des. 2018, 149, 87–100. [Google Scholar] [CrossRef]
- Militello, C.; Bongiorno, F.; Epasto, G.; Zuccarello, B. Low-velocity impact behaviour of green epoxy biocomposite laminates reinforced by sisal fibers. Compos. Struct. 2020, 253, 112744. [Google Scholar] [CrossRef]
- Zuccarello, B.; Bartoli, M.; Bongiorno, F.; Militello, C.; Tagliaferro, A.; Pantano, A. New concept in bioderived composites: Biochar as toughening agent for improving performances and durability of agave-based epoxy biocomposites. Polymers 2021, 13, 198. [Google Scholar] [CrossRef] [PubMed]
- Bongiorno, F.; Militello, C.; Zuccarello, B. Mode I translaminar fracture toughness of high performance laminated biocomposites reinforced by sisal fibers: Accurate measurement approach and lay-up effects. Compos. Sci. Technol. 2022, 217, 109089. [Google Scholar] [CrossRef]
- Zuccarello, B.; Militello, C.; Bongiorno, F. Influence of the anisotropy of sisal fibers on the mechanical properties of high performance unidirectional biocomposite lamina and micromechanical models. Compos. Part A Appl. Sci. Manuf. 2021, 143, 106320. [Google Scholar] [CrossRef]
- Zuccarello, B.; Bongiorno, F.; Militello, C. Basalt Fiber Hybridization Effects on High-Performance Sisal-Reinforced Biocomposites. Polymer 2022, 14, 16. [Google Scholar] [CrossRef]
- Zuccarello, B.; Militello, C.; Bongiorno, F. Environmental aging effects on high-performance biocomposites reinforced by sisal fibers. Polym. Degrad. Stab. 2023, 211, 110319. [Google Scholar] [CrossRef]
- Zuccarello, B.; Militello, C.; Bongiorno, F. Fatigue Behaviour of High-Performance Green Epoxy Biocomposite Laminates Reinforced by Optimized Long Sisal Fibers. Polymers 2024, 16, 18. [Google Scholar] [CrossRef] [PubMed]
- ASTM D3039; Standard Test Method for Tensile Properties of Polymer Matrix Composite Materials. ASTM International: West Conshohocken, PA, USA, 2002.
- ASTM C365; Standard Test Method for Flatwise Compressive Properties of Sandwich Cores. ASTM International: West Conshohocken, PA, USA, 2003.
- Barbero, E.J. Introduction to Composite Materials Design; Taylor & Francis Group: New York, NY, USA, 1999. [Google Scholar]
- ASTM C273; Standard Test Method for Shear Properties of Sandwich Core Materials. ASTM International: West Conshohocken, PA, USA, 2008.
- ASTM C393; Standard Test Method for Flexural Properties of Sandwich Constructions. ASTM International: West Conshohocken, PA, USA, 2008.
- Dogan, A. Low-velocity impact, bending, and compression response of carbon fiber/epoxy-based sandwich composites with different types of core materials. J. Sandw. Struct. Mater. 2021, 23, 1956–1971. [Google Scholar] [CrossRef]
- Segovia, F.; Blanchet, P.; Barbuta, C.; Beauregard, R. Aluminum-laminated panels: Physical and mechanical properties. BioResources 2015, 10, 4751–4767. [Google Scholar] [CrossRef]
- Hussain, M.; Abbas, N.; Zahra, N.; Sajjad, U.; Awan, M.B. Investigating the performance of GFRP/wood-based honeycomb sandwich panels for sustainable prefab building construction. SN Appl. Sci. 2019, 1, 875. [Google Scholar] [CrossRef]
- Susainathan, J.; Eyma, F.; De Luycker, E.; Cantarel, A.; Castanie, B. Manufacturing and quasi-static bending behavior of wood-based sandwich structures. Compos. Struct. 2017, 182, 487–504. [Google Scholar] [CrossRef]
- Le Duigou, A.; Deux, J.M.; Davies, P.; Baley, C. PLLA/flax mat/balsa bio-sandwich manufacture and mechanical properties. Appl. Compos. Mater. 2011, 18, 421–438. [Google Scholar] [CrossRef]
- Ávila de Oliveira, L.; Orth, J.N.; Freire, R.T.S.; Panzera, T.H.; Christoforo, A.L.; Scarpa, F. Sustainable sandwich panels made of aluminium skins and bamboo rings. Mater. Res. 2021, 24, e20200543. [Google Scholar] [CrossRef]
- Cabrera, N.O.; Alcock, B.; Peijs, T. Design and manufacture of all-PP sandwich panels based on co-extruded polypropylene tapes. Compos. Part B Eng. 2008, 39, 1183–1195. [Google Scholar] [CrossRef]
- Oliveira, P.R.; May, M.; Panzera, T.H.; Scarpa, F.; Hiermaier, S. Improved sustainable sandwich panels based on bottle caps core. Compos. Part B Eng. 2020, 199, 108165. [Google Scholar] [CrossRef]
- Oliveira, P.R.; May, M.; Kilchert, S.; Ávila de Oliveira, L.; Panzera, T.H.; Placet, V.; Scarpa, F.; Hiermaier, S. Eco-friendly panels made of autoclaved flax composites and upcycled bottle caps core: Experimental and numerical analysis. Compos. Part C Open Access 2021, 4, 100114. [Google Scholar] [CrossRef]
- Ávila de Oliveira, L.; Coura, G.L.C.; PassaiaTonatto, M.L.; Panzera, T.H.; Placet, V.; Scarpa, F. A novel sandwich panel made of prepreg flax skins and bamboo core. Compos. Part C Open Access 2020, 3, 100048. [Google Scholar] [CrossRef]
- Brischetto, S.; Torre, R. Honeycomb Sandwich Specimens Made of PLA and Produced Via 3D FDM Printing Process: An Experimental Study. J. Aircr. Spacecr. Technol. 2020, 4, 54–69. [Google Scholar] [CrossRef]
- Lascano, D.; Guillen-Pineda, R.; Quiles-Carrillo, L.; Ivorra-Martínez, J.; Balart, R.; Montanes, N.; Boronat, T. Manufacturing and characterization of highly environmentally friendly sandwich composites from polylactide cores and flax-polylactide faces. Polymers 2021, 13, 342. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Q.; Chen, G.; Kumar, A.; Mills, A.; Jani, K.; Rajamohan, V.; Venugopal, B.; Rahatekar, S. Sustainable sandwich composites manufactured from recycled carbon fibers, flax fibers/pp skins, and recycled pet core. J. Compos. Sci. 2021, 5, 2. [Google Scholar] [CrossRef]
- Ayrilmis, N.; Nagarajan, R.; Kuzman, M.K. Effects of the face/core layer ratio on the mechanical properties of 3d printed wood/polylactic acid (Pla) green biocomposite panels with a gyroid core. Polymers 2020, 12, 2929. [Google Scholar] [CrossRef] [PubMed]
- Du, Y.; Yan, N.; Kortschot, M.T. Novel lightweight sandwich-structured bio-fiber-reinforced poly(lactic acid) composites. J. Mater. Sci. 2014, 49, 2018–2026. [Google Scholar] [CrossRef]
- Anderson, M.S. Optimum Proportions of Truss Core and Web-Core Sandwich Plates Loaded in Compression; NASA: Washington, DC, USA, 1959. [Google Scholar]
- Steeves, C.A.; Fleck, N.A. Material selection in sandwich beam construction. Scr. Mater. 2004, 50, 1335–1339. [Google Scholar] [CrossRef]
- Steeves, C.A.; Fleck, N.A. Collapse mechanisms of sandwich beams with composite faces and a foam core, loaded in three-point bending. Part I: Analytical models and minimum weight design. Int. J. Mech. Sci. 2004, 46, 561–583. [Google Scholar] [CrossRef]
- Vaikhanski, L.; Nutt, S.R. Fiber-reinforced composite foam from expandable PVC microspheres. Compos. Part A Appl. Sci. Manuf. 2003, 34, 1245–1253. [Google Scholar] [CrossRef]
- Kim, J.; Swanson, S.R. Design of sandwich structures for concentrated loading. Compos. Struct. 2001, 52, 365–373. [Google Scholar] [CrossRef]
- Belingardi, G.; Cavatorta, M.P.; Duella, R. Material characterization of a composite-foam sandwich for the front structure of a high speed train. Compos. Struct. 2003, 61, 13–25. [Google Scholar] [CrossRef]
- Corigliano, A.; Rizzi, E.; Papa, E. Experimental characterization and numerical simulations of a syntactic-foam/glass-fibre composite sandwich. Compos. Sci. Technol. 2000, 60, 2169–2180. [Google Scholar] [CrossRef]
- Thomson, R.S.; Shah Khan, M.Z.; Mouritz, A.P. Shear properties of a sandwich composite containing defects. Compos. Struct. 1998, 42, 107–118. [Google Scholar] [CrossRef]
- Hadi, B.K.; Matthews, F.L. Development of Benson-Mayers theory on the wrinkling of anisotropic sandwich panels. Compos. Struct. 2000, 49, 425–434. [Google Scholar] [CrossRef]
- Sokolinsky, V.S.; Shen, H.; Vaikhanski, L.; Nutt, S.R. Experimental and analytical study of nonlinear bending response of sandwich beams. Compos. Struct. 2003, 60, 219–229. [Google Scholar] [CrossRef]
- Petras, A.; Sutcliffe, M.P.F. Indentation failure analysis of sandwich beams. Compos. Struct. 2000, 50, 311–318. [Google Scholar] [CrossRef]
- Vinson, J.R. The Behaviour of Sandwich Structures of Isotropic and Composite Materials; Westport Technomic: Chicago, IL, USA, 1999. [Google Scholar]
- Russo, A.; Zuccarello, B. Experimental and numerical evaluation of the mechanical behaviour of GFRP sandwich panels. Compos. Struct. 2007, 81, 575–586. [Google Scholar] [CrossRef]
- Mines, R.A.W.; Alias, A. Numerical simulation of the progressive collapse of polymer composite sandwich beams under static loading. Compos. Part A Appl. Sci. Manuf. 2002, 33, 11–26. [Google Scholar] [CrossRef]
- Borsellino, C.; Calabrese, L.; Valenza, A. Experimental and numerical evaluation of sandwich composite structures. Compos. Sci. Technol. 2004, 64, 1709–1715. [Google Scholar] [CrossRef]








| Material | ρ [g/cm3] | σR [MPa] | τR [MPa] | E [GPa] | εR [%] |
|---|---|---|---|---|---|
| Sisal fiber | 1.45 | 685 | 19.8 | 40 | 1.75 |
| Balsa wood | 0.15 | 4.9 | 1.5 | 0.23 | - |
| Green Epoxy | 1.05 | 50 | 25 | 2.5 | 1.20 |
| Sandwich | τc,R [MPa] | Gc [MPa] | γc,R [%] |
|---|---|---|---|
| SB(0) | 1 | 10 | 11 |
| SB(±45) | 5.5 | 25 | 23 |
| SB(±45/90) | 4.5 | 15 | 45 |
| Skins | Core | Sandwich | ||||||
|---|---|---|---|---|---|---|---|---|
| b [mm] | Es [MPa] | σs [MPa] | Gc [MPa] | τc [MPa] | Mmax [Nmm] | Tmax [N] | 2·rmax [mm] | |
| SB(0)10 | 26 | 22,000 | 310 | 10 | 1 | 521.119 | 1062 | 1960 |
| SB(±45)10 | 22 | 22,000 | 310 | 25 | 5.5 | 440.947 | 4950 | 356 |
| SB(±45°/90)10 | 21.5 | 22,000 | 310 | 15 | 4.5 | 517.800 | 3792 | 420 |
| SB(0)25 | 21.5 | 22,000 | 310 | 10 | 1 | 911.646 | 1446 | 2520 |
| SB(±45)25 | 21.5 | 22,000 | 310 | 25 | 5.5 | 911.646 | 7995 | 458 |
| SB(±45°/90)25 | 28 | 22,000 | 310 | 15 | 4.5 | 1187.260 | 8477 | 560 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zuccarello, B.; Bongiorno, F.; Militello, C. Structural Optimization of a High-Performance Green Sandwich Made of Sisal Reinforced Epoxy Facings and Balsa Core. Polymers 2024, 16, 3341. https://doi.org/10.3390/polym16233341
Zuccarello B, Bongiorno F, Militello C. Structural Optimization of a High-Performance Green Sandwich Made of Sisal Reinforced Epoxy Facings and Balsa Core. Polymers. 2024; 16(23):3341. https://doi.org/10.3390/polym16233341
Chicago/Turabian StyleZuccarello, Bernardo, Francesco Bongiorno, and Carmelo Militello. 2024. "Structural Optimization of a High-Performance Green Sandwich Made of Sisal Reinforced Epoxy Facings and Balsa Core" Polymers 16, no. 23: 3341. https://doi.org/10.3390/polym16233341
APA StyleZuccarello, B., Bongiorno, F., & Militello, C. (2024). Structural Optimization of a High-Performance Green Sandwich Made of Sisal Reinforced Epoxy Facings and Balsa Core. Polymers, 16(23), 3341. https://doi.org/10.3390/polym16233341







