Effect of Part Size, Displacement Rate, and Aging on Compressive Properties of Elastomeric Parts of Different Unit Cell Topologies Formed by Vat Photopolymerization Additive Manufacturing
Abstract
1. Introduction
2. Materials and Methods
2.1. Part Design
2.2. Materials and Manufacturing
2.3. Mechanical Testing
2.4. Simulations
3. Results
3.1. Effect of Part Size
3.2. Effect of Displacement Rate
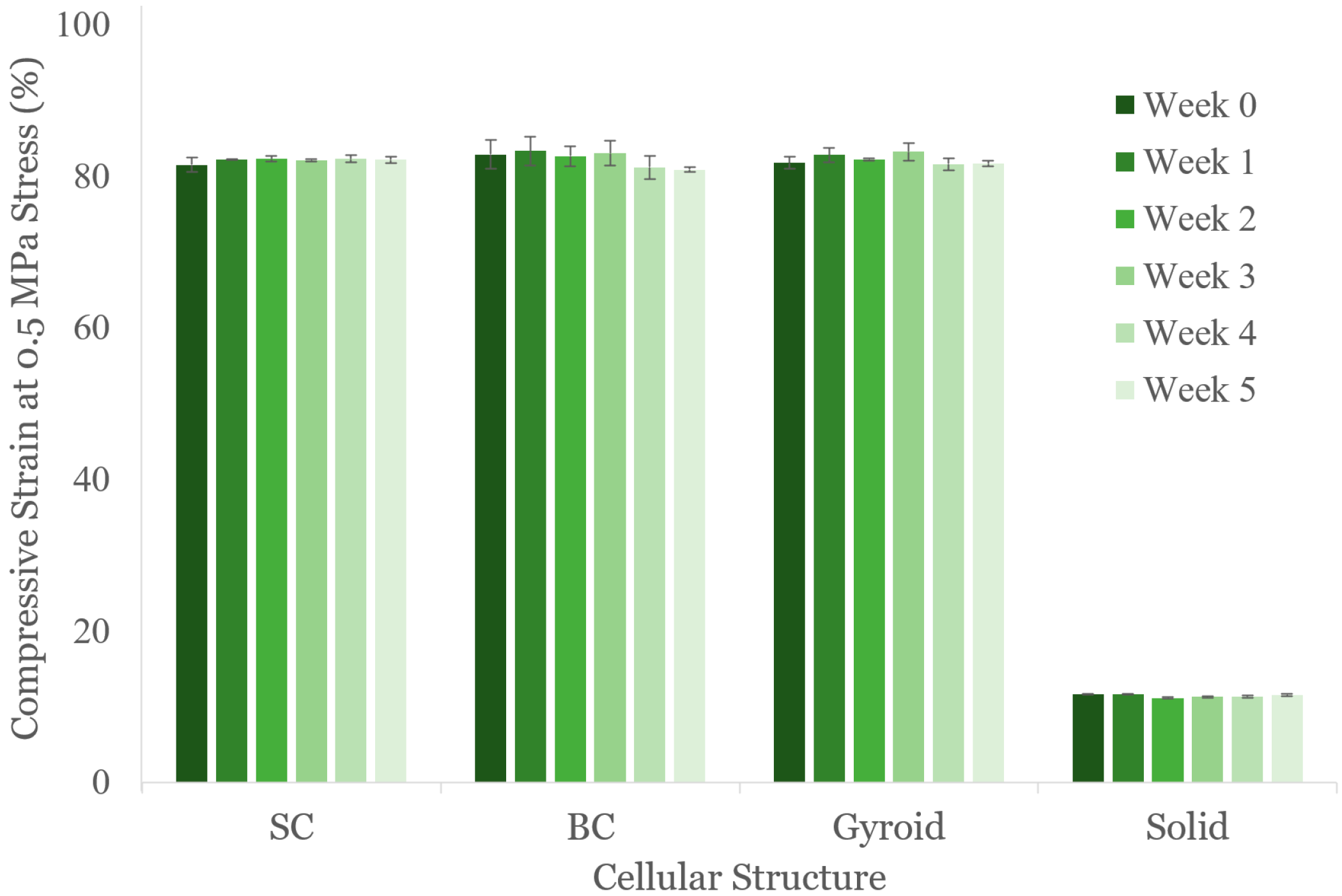
3.3. Effect of Aging
4. Conclusions
- In general, the results from the FE simulations exhibited excellent comparison to experimental data when qualitatively and quantitatively describing the compressive responses of the SC, BC, and G structures at different part sizes.
- Across the part sizes tested, the experiments and simulations consistently showed there were no appreciable differences in stress–strain responses except for the BC structures, which experienced shifts in the densification region.
- The BC, G, and S structures experienced stiffer stress–strain responses at the highest displacement rate tested.
- The tested structures did not show substantial changes in the compressive response over the duration of five weeks of aging time.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
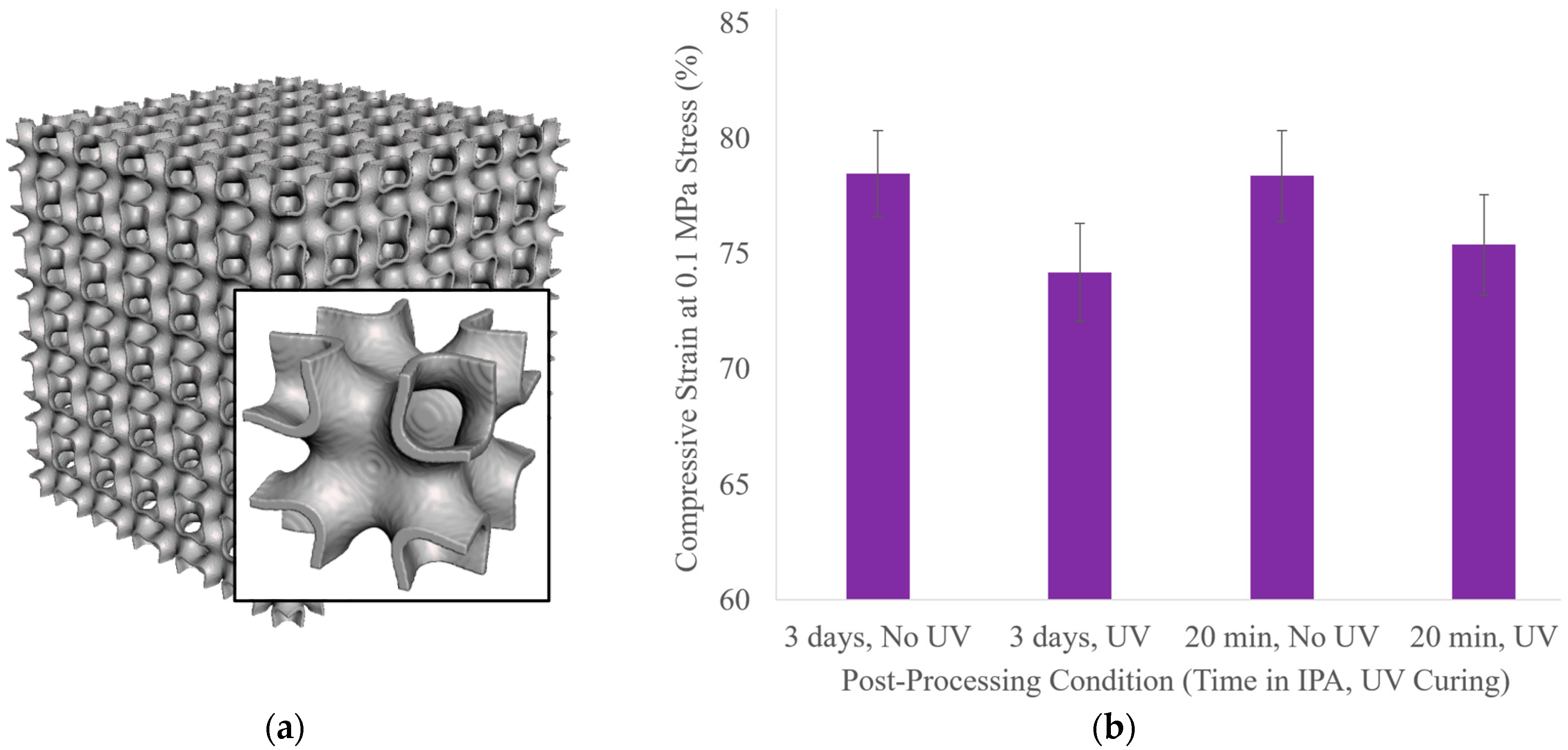
Appendix B
| Sample 1 | Sample 2 | Sample 3 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Length (mm) | Width (mm) | Height (mm) | Length (mm) | Width (mm) | Height (mm) | Length (mm) | Width (mm) | Height (mm) | ||
| Part Size | ||||||||||
| SC | 3 × 3 × 3 | 14.2 | 14.3 | 14.0 | 14.1 | 14.4 | 14.1 | 14.4 | 14.4 | 14.2 |
| 6 × 6 × 6 | 30.3 | 30.1 | 29.3 | 29.9 | 30.0 | 29.5 | 29.7 | 30.1 | 29.2 | |
| 12 × 12 × 12 | 60.5 | 61.2 | 57.6 | 60.1 | 60.3 | 57.7 | 61.0 | 61.0 | 58.2 | |
| BC | 3 × 3 × 3 | 14.4 | 14.1 | 12.8 | 14.1 | 14.4 | 13.0 | 14.2 | 14.2 | 13.4 |
| 6 × 6 × 6 | 30.0 | 30.4 | 26.7 | 30.7 | 30.9 | 27.2 | 30.6 | 31.0 | 27.5 | |
| 12 × 12 × 12 | 61.8 | 61.9 | 55.4 | 61.2 | 60.8 | 55.6 | 62.0 | 62.4 | 55.0 | |
| G | 3 × 3 × 3 | 13.7 | 13.8 | 13.0 | 13.6 | 13.3 | 12.7 | 13.6 | 14.1 | 12.9 |
| 6 × 6 × 6 | 29.8 | 30.1 | 26.7 | 30.1 | 30.1 | 26.6 | 30.0 | 29.9 | 26.9 | |
| 12 × 12 × 12 | 60.9 | 60.7 | 56.7 | 62.0 | 62.2 | 57.5 | 62.7 | 62.8 | 58.9 | |
| Displacement Rate | ||||||||||
| SC | 12 mm/min | 30.1 | 30.3 | 29.3 | 29.9 | 30.1 | 29.3 | 30.0 | 29.7 | 29.0 |
| 120 mm/min | 30.4 | 30.0 | 29.4 | 30.2 | 30.0 | 29.4 | 30.3 | 30.2 | 29.0 | |
| 1000 mm/min | 30.3 | 30.0 | 29.5 | 29.9 | 30.2 | 29.3 | 30.4 | 30.5 | 29.4 | |
| BC | 12 mm/min | 30.9 | 30.8 | 27.5 | 31.0 | 31.1 | 28.0 | 31.1 | 31.0 | 28.1 |
| 120 mm/min | 30.8 | 30.5 | 26.6 | 30.6 | 31.0 | 27.3 | 30.9 | 30.6 | 27.1 | |
| 1000 mm/min | 30.5 | 30.8 | 27.5 | 31.0 | 31.1 | 28.0 | 31.1 | 31.0 | 28.1 | |
| G | 12 mm/min | 33.8 | 32.5 | 30.0 | 33.2 | 32.6 | 30.3 | 32.1 | 32.3 | 29.9 |
| 120 mm/min | 30.8 | 30.7 | 28.2 | 30.8 | 30.4 | 28.0 | 30.3 | 30.6 | 27.5 | |
| 1000 mm/min | 30.4 | 30.3 | 28.4 | 30.3 | 30.4 | 28.2 | 30.5 | 30.4 | 28.1 | |
| S | 12 mm/min | 29.7 | 29.9 | 30.5 | 30.1 | 29.9 | 30.2 | 29.8 | 29.8 | 30.4 |
| 120 mm/min | 29.8 | 30.4 | 30.3 | 29.9 | 29.8 | 30.2 | 30.1 | 30.0 | 30.5 | |
| 1000 mm/min | 29.9 | 29.8 | 30.2 | 30.1 | 29.9 | 30.2 | 29.8 | 29.8 | 30.4 | |
| Aging | ||||||||||
| SC | Week 0 | 32.0 | 32.0 | 30.0 | 31.9 | 31.9 | 30.0 | 31.7 | 31.7 | 30.0 |
| Week 1 | 31.0 | 31.0 | 29.1 | 30.8 | 30.8 | 29.2 | 30.8 | 30.8 | 28.8 | |
| Week 2 | 31.0 | 31.0 | 29.1 | 30.8 | 30.8 | 29.0 | 30.8 | 30.8 | 28.8 | |
| Week 3 | 31.0 | 31.0 | 29.0 | 30.9 | 30.9 | 29.3 | 30.8 | 30.8 | 28.8 | |
| Week 4 | 30.8 | 30.8 | 29.0 | 30.8 | 30.8 | 29.3 | 30.7 | 30.7 | 28.5 | |
| Week 5 | 30.8 | 30.8 | 28.9 | 30.8 | 30.8 | 29.2 | 30.7 | 30.7 | 28.6 | |
| BC | Week 0 | 31.6 | 31.6 | 28.8 | 32.1 | 31.6 | 27.7 | 30.4 | 31.2 | 26.7 |
| Week 1 | 31.9 | 31.3 | 26.7 | 31.0 | 31.4 | 27.7 | 29.7 | 31.4 | 26.2 | |
| Week 2 | 30.3 | 30.2 | 26.3 | 31.4 | 30.2 | 26.6 | 29.5 | 29.7 | 26.6 | |
| Week 3 | 30.2 | 29.4 | 25.7 | 29.5 | 29.1 | 25.8 | 29.2 | 29.6 | 26.4 | |
| Week 4 | 32.1 | 32.1 | 28.0 | 32.0 | 31.6 | 28.1 | 31.8 | 31.8 | 27.9 | |
| Week 5 | 31.9 | 31.9 | 28.0 | 32.0 | 31.6 | 28.1 | 31.8 | 31.8 | 27.9 | |
| G | Week 0 | 33.8 | 32.5 | 30.0 | 33.2 | 32.6 | 30.3 | 32.1 | 32.3 | 29.9 |
| Week 1 | 30.9 | 31.4 | 29.5 | 30.2 | 30.3 | 28.6 | 30.9 | 31.4 | 28.2 | |
| Week 2 | 31.1 | 29.9 | 28.1 | 29.5 | 30.1 | 28.2 | 30.2 | 30.3 | 28.0 | |
| Week 3 | 30.9 | 29.4 | 27.8 | 29.3 | 28.6 | 26.4 | 30.0 | 29.4 | 27.4 | |
| Week 4 | 31.8 | 31.8 | 29.5 | 31.8 | 31.8 | 29.6 | 31.8 | 31.8 | 29.4 | |
| Week 5 | 31.8 | 31.8 | 29.3 | 31.8 | 31.8 | 29.6 | 31.8 | 31.8 | 29.4 | |
| S | Week 0 | 29.7 | 29.8 | 30.0 | 29.7 | 29.8 | 30.0 | 29.5 | 29.7 | 30.1 |
| Week 1 | 29.7 | 29.7 | 30.0 | 29.7 | 29.6 | 30.0 | 29.6 | 29.7 | 30.3 | |
| Week 2 | 29.6 | 29.5 | 30.1 | 29.4 | 29.5 | 29.8 | 29.7 | 29.7 | 30.1 | |
| Week 3 | 29.4 | 29.4 | 30.0 | 29.8 | 29.4 | 29.9 | 29.4 | 29.6 | 30.0 | |
| Week 4 | 29.7 | 29.8 | 30.5 | 29.7 | 29.7 | 30.1 | 29.9 | 29.8 | 30.5 | |
| Week 5 | 30.2 | 30.0 | 30.3 | 29.7 | 29.8 | 30.2 | 29.8 | 29.7 | 30.4 | |
References
- Liravi, F.; Toyserkani, E. Additive manufacturing of silicone structures: A review and prospective. Addit. Manuf. 2018, 24, 232–242. [Google Scholar] [CrossRef]
- Arenas, M.A.A.; Gutkelch, D.; Kosch, O.; Brühl, R.; Wiekhorst, F.; Löwa, N. Development of Phantoms for Multimodal Magnetic Resonance Imaging and Magnetic Particle Imaging. Polymers 2022, 14, 3925. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Honari, M.M.; Fu, Y.; Kumar, A.; Saghlatoon, H.; Mousavi, P.; Chung, H.-Y. Self-reinforcing graphene coatings on 3D printed elastomers for flexible radio frequency antennas and strain sensors. Flex. Print. Electron. 2017, 2, 035001. [Google Scholar] [CrossRef]
- Yirmibesoglu, O.D.; Morrow, J.; Walker, S.; Gosrich, W.; Cañizares, R.; Kim, H.; Daalkhaijav, U.; Fleming, C.; Branyan, C.; Menguc, Y. Direct 3D printing of silicone elastomer soft robots and their performance comparison with molded counterparts. In Proceedings of the 2018 IEEE International Conference on Soft Robotics (RoboSoft), Livorno, Italy, 24–28 April 2018; pp. 295–302. [Google Scholar]
- Zhou, L.; Gao, Q.; Fu, J.-Z.; Chen, Q.-Y.; Zhu, J.-P.; Sun, Y.; He, Y. Multimaterial 3D Printing of Highly Stretchable Silicone Elastomers. ACS Appl. Mater. Interfaces 2019, 11, 23573–23583. [Google Scholar] [CrossRef]
- Al-Ketan, O.; Rowshan, R.; Abu Al-Rub, R.K. Topology-mechanical property relationship of 3D printed strut, skeletal, and sheet based periodic metallic cellular materials. Addit. Manuf. 2018, 19, 167–183. [Google Scholar] [CrossRef]
- Forés-Garriga, A.; Gómez-Gras, G.; Pérez, M.A. Additively manufactured three-dimensional lightweight cellular solids: Experimental and numerical analysis. Mater. Des. 2023, 226, 111641. [Google Scholar] [CrossRef]
- Park, K.-M.; Min, K.-S.; Roh, Y.-S. Design Optimization of Lattice Structures under Compression: Study of Unit Cell Types and Cell Arrangements. Materials 2021, 15, 97. [Google Scholar] [CrossRef]
- Tao, W.; Leu, M.C. Design of lattice structure for additive manufacturing. In Proceedings of the 2016 International Symposium on Flexible Automation (ISFA), Cleveland, OH, USA, 1–3 August 2016; pp. 325–332. [Google Scholar]
- Johnston, R.; Kazancı, Z. Analysis of additively manufactured (3D printed) dual-material auxetic structures under compression. Addit. Manuf. 2021, 38, 101783. [Google Scholar] [CrossRef]
- Higuera, S.; Miralbes, R.; Ranz, D. Mechanical properties and energy–absorption capabilities of thermoplastic sheet gyroid structures. Mech. Adv. Mater. Struct. 2022, 29, 4110–4124. [Google Scholar] [CrossRef]
- Nian, S.; Zhu, J.; Zhang, H.; Gong, Z.; Freychet, G.; Zhernenkov, M.; Xu, B.; Cai, L.-H. Three-Dimensional Printable, Extremely Soft, Stretchable, and Reversible Elastomers from Molecular Architecture-Directed Assembly. Chem. Mater. 2021, 33, 2436–2445. [Google Scholar] [CrossRef]
- Durban, M.M.; Lenhardt, J.M.; Wu, A.S.; Small, W., IV; Bryson, T.M.; Perez-Perez, L.; Nguyen, D.T.; Gammon, S.; Smay, J.E.; Duoss, E.B.; et al. Custom 3D Printable Silicones with Tunable Stiffness. Macromol. Rapid Commun. 2018, 39, 1700563. [Google Scholar] [CrossRef] [PubMed]
- Zheng, R.; Chen, Y.; Chi, H.; Qiu, H.; Xue, H.; Bai, H. 3D Printing of a Polydimethylsiloxane/Polytetrafluoroethylene Composite Elastomer and its Application in a Triboelectric Nanogenerator. ACS Appl. Mater. Interfaces 2020, 12, 57441–57449. [Google Scholar] [CrossRef] [PubMed]
- Jiang, H.; Le Barbenchon, L.; Bednarcyk, B.A.; Scarpa, F.; Chen, Y. Bioinspired multilayered cellular composites with enhanced energy absorption and shape recovery. Addit. Manuf. 2020, 36, 101430. [Google Scholar] [CrossRef]
- He, Y.; Zhou, Y.; Liu, Z.; Liew, K.M. Buckling and pattern transformation of modified periodic lattice structures. Extreme Mech. Lett. 2018, 22, 112–121. [Google Scholar] [CrossRef]
- Dwyer, C.M. Spatially-Graded Elastomeric Lattice Structures with Integrated Electronic Sensors. Master’s Thesis, Youngstown State University, Youngstown, OH, USA, December 2021. [Google Scholar]
- Rodriguez, N.; Ruelas, S.; Forien, J.-B.; Dudukovic, N.; DeOtte, J.; Rodriguez, J.; Moran, B.; Lewicki, J.P.; Duoss, E.B.; Oakdale, J.S. 3D Printing of High Viscosity Reinforced Silicone Elastomers. Polymers 2021, 13, 2239. [Google Scholar] [CrossRef]
- Scott, P.J.; Meenakshisundaram, V.M.; Hedge, M.; Kasprzak, C.R.; Winkler, C.R.; Felller, K.D.; Williams, C.B.; Long, T.E. 3D Printing Latex: A Route to Complex Geometries of High Molecular Weight Polymers. ACS Appl. Mater. Interfaces 2020, 12, 10918–10928. [Google Scholar] [CrossRef]
- Mazzoldi, E.L.; Riva, L.; Ferraro, R.M.; Ginestra, P.S.; Giliani, S.C. 3D Printing of Biocompatible Scaffolds for Eye Tissue Engineering. Procedia CIRP 2022, 110, 213–218. [Google Scholar] [CrossRef]
- Von Steuben, T.; Enzmann, F.K.; Spintzyk, S.; Rupp, F.; Roehler, A. Needle Penetration Simulation: Influence of Penetration Angle and Sample Stress on the Mechanical Behaviors of Polymers Applying a Cast Silicone and a 3D-Printed Resin. Materials 2022, 15, 5575. [Google Scholar] [CrossRef]
- Okutani, C.; Yokota, T.; Miyazako, H.; Someya, T. 3D Printed Spring-Type Electronics with Liquid Metals for Highly Stretchable Conductors and Inductive Strain/Pressure Sensors. Adv. Mater. Technol. 2022, 7, 2101657. [Google Scholar] [CrossRef]
- Cipriani, C.E.; Shu, Y.; Pentzer, E.B.; Benjamin, C.C. Viscoelastic and thixotropic characterization of paraffin/photopolymer composites for extrusion-based printing. Phys. Fluids 2022, 34, 093106. [Google Scholar] [CrossRef]
- Subramanian, A.S.; Peng, E.; Cheng Lau, W.; Chuen Wee Goh, D.; Pramono, S.; Sriramulu, D.; Wu, Y.; Kobayashi, H.; Guo Sheng Moo, J.; Su, P.-C. Morphological Effects of Various Silica Nanostructures on the Mechanical Properties of Printed Parts in Digital Light Projection 3D Printing. ACS Appl. Nano Mater. 2021, 4, 4522–4531. [Google Scholar] [CrossRef]
- Acuna, D.; Gutiérrez, F.; Silva, R.; Palza, H.; Nunez, A.S.; Düring, A.S. Auxetic behavior on demand: A three steps recipe for new designs. arXiv 2021, arXiv:2101.12352. Available online: http://arxiv.org/abs/2101.12352 (accessed on 14 May 2024).
- Zheng, X.; Chen, T.-T.; Guo, X.; Samitsu, S.; Watanabe, I. Controllable inverse design of auxetic metamaterials using deep learning. Mater. Des. 2021, 211, 110178. [Google Scholar] [CrossRef]
- Galea, R.; Farrugia, P.-S.; Dudek, K.K.; Attard, D.; Grima, J.N.; Gatt, R. A novel design method to produce 3D auxetic metamaterials with continuous pores exemplified through 3D rotating auxetic systems. Mater. Des. 2023, 226, 111596. [Google Scholar] [CrossRef]
- Bustamante, M.V.; Jimenez, C.P.; Lara-Padilla, H.; Gavilanes, V.C. Digital design and fabrication of two-dimensional soft lattice structures with genotype patterns. In Proceedings of the 2022 IEEE Sixth Ecuador Technical Chapters Meeting (ETCM), Quito, Ecuador, 11–14 October 2022; pp. 1–5. [Google Scholar]
- Nakarmi, S.; Kim, J.; Bezek, L.B.; Leiding, J.; Lee, K.-S.; Daphalapurkar, N.P. The role of unit cell topology in modulating the compaction response of additively manufactured cellular materials using simulations and validation experiments. Model. Simul. Mater. Sci. Eng. 2024, 32, 055029. [Google Scholar] [CrossRef]
- Davidson, S. Grasshopper-Algorithmic Modeling for Rhino. 2024. Available online: https://www.grasshopper3d.com/ (accessed on 15 October 2024).
- “Form Wash/Form Wash L Time Settings,” Formlabs Support. 2024. Available online: https://support.formlabs.com/s/article/Form-Wash-Time-Settings?language=en_US (accessed on 15 October 2024).
- “Form Cure Time and Temperature Settings,” Formlabs Support. 2024. Available online: https://support.formlabs.com/s/article/Form-Cure-Time-and-Temperature-Settings?language=en_US (accessed on 15 October 2024).
- Abaqus Analysis User’s Manual; Dassault Systèmes: Providence, RI, USA, 2020.
- Owen, S.; Ernst, C.; Stimpson, C. Sculpt: Automatic Parallel Hexahedral Mesh Generation. SAND 2019, 2019, 1762652. [Google Scholar] [CrossRef]
- Bian, Y.; Yang, F.; Zhang, S.; Chen, M.; Song, Y. Similarities of the Mechanical Responses of Body-Centered Cubic Lattice Structures with Different Constituent Materials Under Compression. JOM 2022, 74, 1774–1783. [Google Scholar] [CrossRef]
- Li, P.; Yang, F.; Bian, Y.; Zhang, S.; Wang, L. Designable mechanical properties of modified body-centered cubic lattice materials. Compos. Struct. 2023, 317, 117060. [Google Scholar] [CrossRef]
- Bouteldja, A.; Louar, M.A.; Hemmouche, L.; Gilson, L.; Miranda-Vicario, A.; Rabet, L. Experimental investigation of the quasi-static and dynamic compressive behavior of polymer-based 3D-printed lattice structures. Int. J. Impact Eng. 2023, 180, 104640. [Google Scholar] [CrossRef]
- Bai, L.; Gong, C.; Chen, X.; Sun, Y.; Xin, L.; Pu, H.; Peng, Y.; Luo, J. Mechanical properties and energy absorption capabilities of functionally graded lattice structures: Experiments and simulations. Int. J. Mech. Sci. 2020, 182, 105735. [Google Scholar] [CrossRef]
- Söver, A.; Frormann, L.; Kipscholl, R. High impact-testing machine for elastomers investigation under impact loads. Polym. Test. 2009, 28, 871–874. [Google Scholar] [CrossRef]
- Hong, S.; Park, N.-Y.; Ju, S.; Lee, A.; Shin, Y.; Soo Kim, J.; Um, M.-K.; Woo Yi, J.; Gi Chae, H.; Park, T. Molecular degradation mechanism of segmented polyurethane and life prediction through accelerated aging test. Polym. Test. 2023, 124, 108086. [Google Scholar] [CrossRef]
- Tayefi, M.; Eesaee, M.; Hassanipour, M.; Elkoun, S.; David, E.; Nguyen-Tri, P. Recent progress in the accelerated aging and lifetime prediction of elastomers: A review. Polym. Degrad. Stab. 2023, 214, 110379. [Google Scholar] [CrossRef]
- Kanyanta, V.; Ivankovic, A. Mechanical characterisation of polyurethane elastomer for biomedical applications. J. Mech. Behav. Biomed. Mater. 2010, 3, 51–62. [Google Scholar] [CrossRef]
- Opreni, A.; Mariani, S.; Dossi, M.; Brennan, M. Combined effects of temperature and humidity on the mechanical properties of polyurethane foams. J. Rheol. 2020, 64, 161–176. [Google Scholar] [CrossRef]
- Bezek, L.B.; Williams, C.B. Process-structure-property effects of ultraviolet curing in multi-material jetting additive manufacturing. Addit. Manuf. 2023, 73, 103640. [Google Scholar] [CrossRef]
- Decker, C.; Moussa, K.; Bendaikha, T. Photodegradation of UV-cured coatings II. Polyurethane–acrylate networks. J. Polym. Sci. Part Polym. Chem. 1991, 29, 739–747. [Google Scholar] [CrossRef]
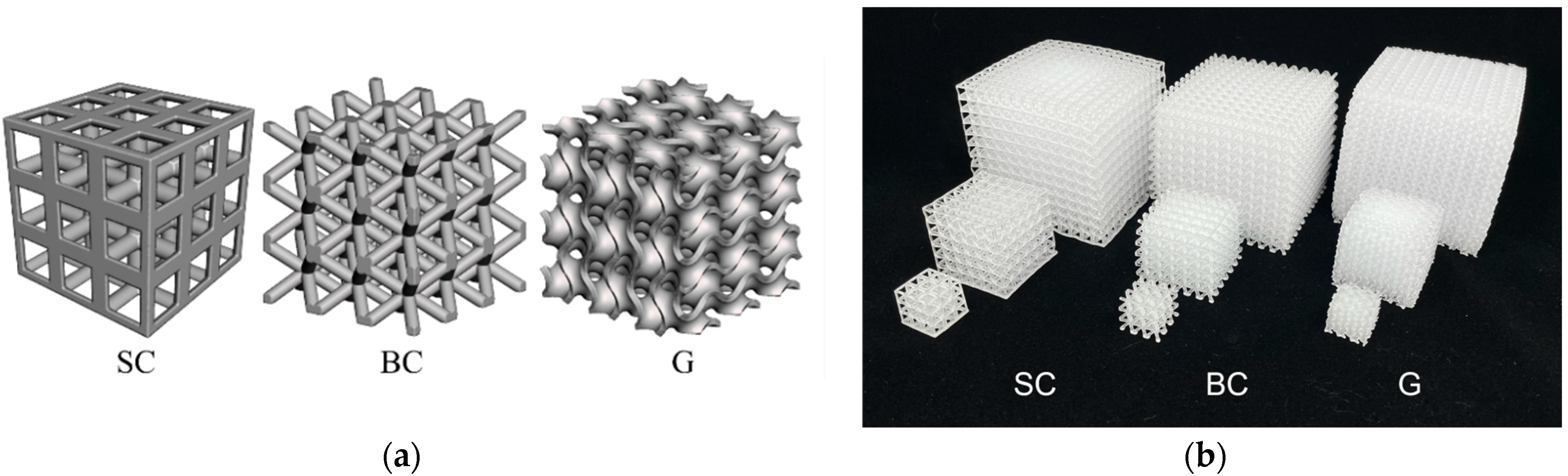

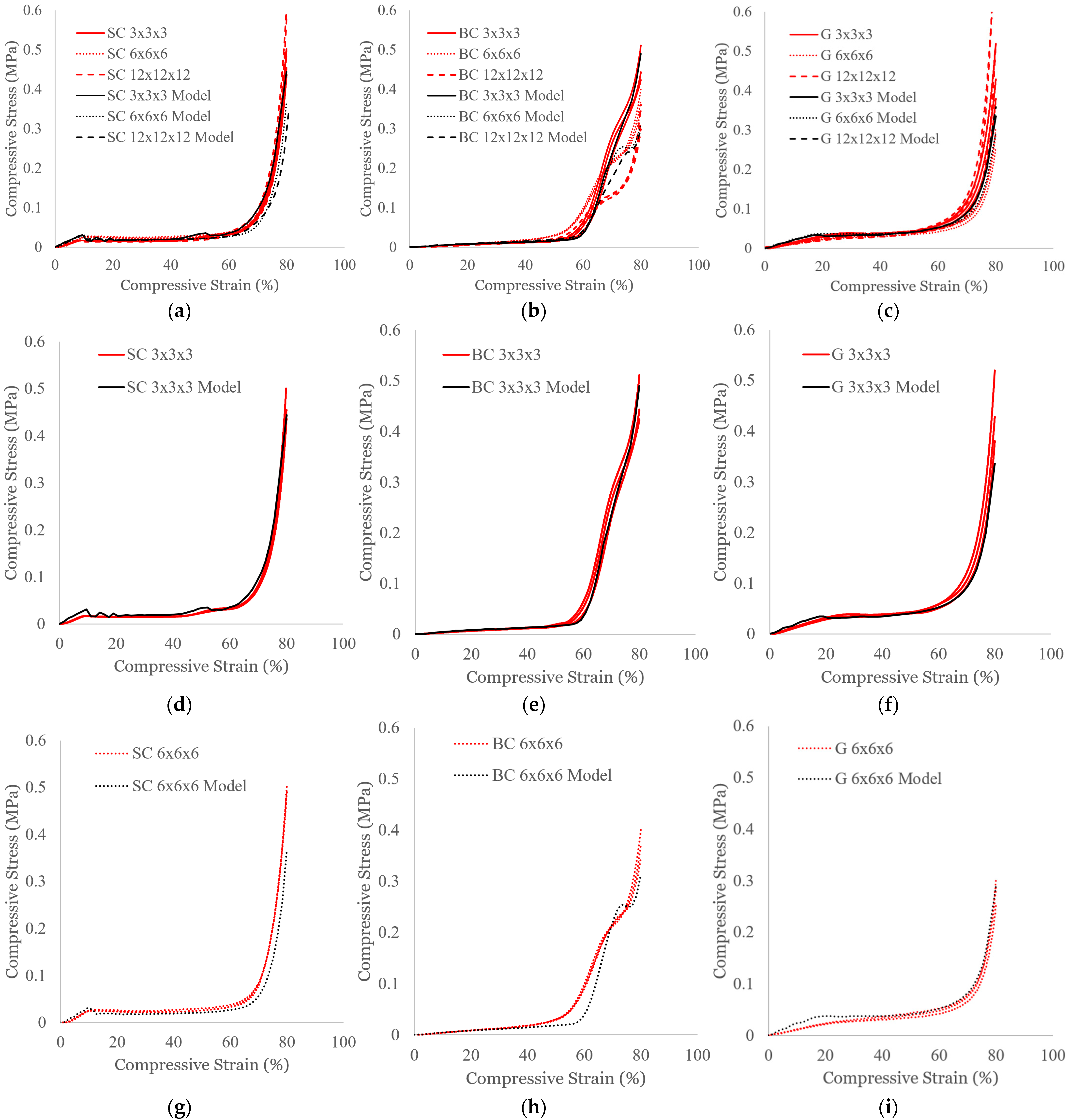
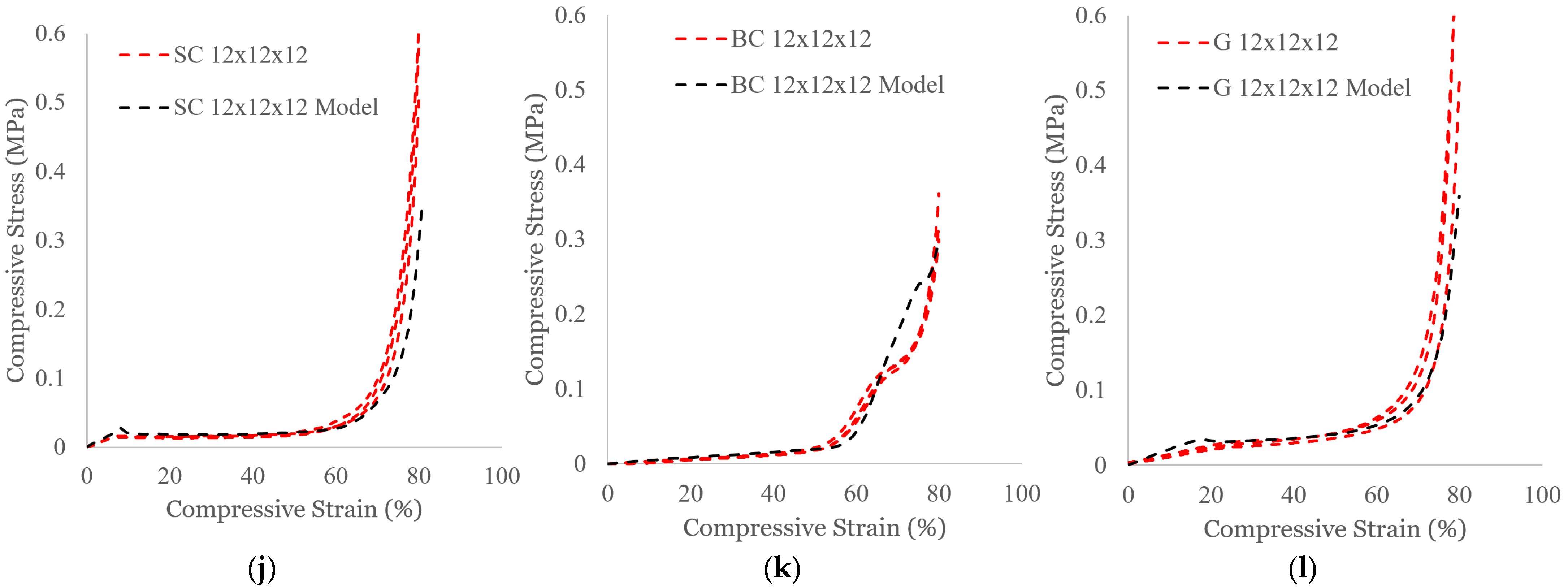

| Experiment | Unit Cell Topology | Part Size (Unit Cells per Length) | Testing Rate | Additional Studies |
|---|---|---|---|---|
| Part size | SC, BC, or G | 3 × 3 × 3, 6 × 6 × 6, or 12 × 12 × 12 | 80%/min to 80% | Compared to simulations |
| Displacement rate | SC, BC, G, or S | 6 × 6 × 6 | 12, 120, or 1000 mm/min to 0.5 MPa | N/A |
| Aging | SC, BC, G, or S | 6 × 6 × 6 | 12 mm/min to 0.5 MPa | Tested weekly for five weeks |
| SC | BC | G | S | |
|---|---|---|---|---|
| 12 mm/min | 78.04 ± 0.41 | 75.98 ± 0.63 | 81.72 ± 0.80 | 11.29 ± 0.15 |
| 120 mm/min | 77.35 ± 0.18 | 75.65 ± 0.44 | 79.75 ± 1.04 | 11.01 ± 0.20 |
| 1000 mm/min | 75.99 ± 0.16 | 69.88 ± 1.33 | 75.48 ± 0.45 | 9.78 ± 0.20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bezek, L.B.; Nakarmi, S.; Pantea, A.C.; Leiding, J.A.; Daphalapurkar, N.P.; Lee, K.-S. Effect of Part Size, Displacement Rate, and Aging on Compressive Properties of Elastomeric Parts of Different Unit Cell Topologies Formed by Vat Photopolymerization Additive Manufacturing. Polymers 2024, 16, 3166. https://doi.org/10.3390/polym16223166
Bezek LB, Nakarmi S, Pantea AC, Leiding JA, Daphalapurkar NP, Lee K-S. Effect of Part Size, Displacement Rate, and Aging on Compressive Properties of Elastomeric Parts of Different Unit Cell Topologies Formed by Vat Photopolymerization Additive Manufacturing. Polymers. 2024; 16(22):3166. https://doi.org/10.3390/polym16223166
Chicago/Turabian StyleBezek, Lindsey B., Sushan Nakarmi, Alexander C. Pantea, Jeffery A. Leiding, Nitin P. Daphalapurkar, and Kwan-Soo Lee. 2024. "Effect of Part Size, Displacement Rate, and Aging on Compressive Properties of Elastomeric Parts of Different Unit Cell Topologies Formed by Vat Photopolymerization Additive Manufacturing" Polymers 16, no. 22: 3166. https://doi.org/10.3390/polym16223166
APA StyleBezek, L. B., Nakarmi, S., Pantea, A. C., Leiding, J. A., Daphalapurkar, N. P., & Lee, K.-S. (2024). Effect of Part Size, Displacement Rate, and Aging on Compressive Properties of Elastomeric Parts of Different Unit Cell Topologies Formed by Vat Photopolymerization Additive Manufacturing. Polymers, 16(22), 3166. https://doi.org/10.3390/polym16223166







