Mechanical Strength of Additive Manufactured and Standard Polymeric Components Joined Through Structural Adhesives
Abstract
1. Introduction
2. Materials and Method
2.1. Pin–Collar Joints
2.1.1. Experimental Test Procedure
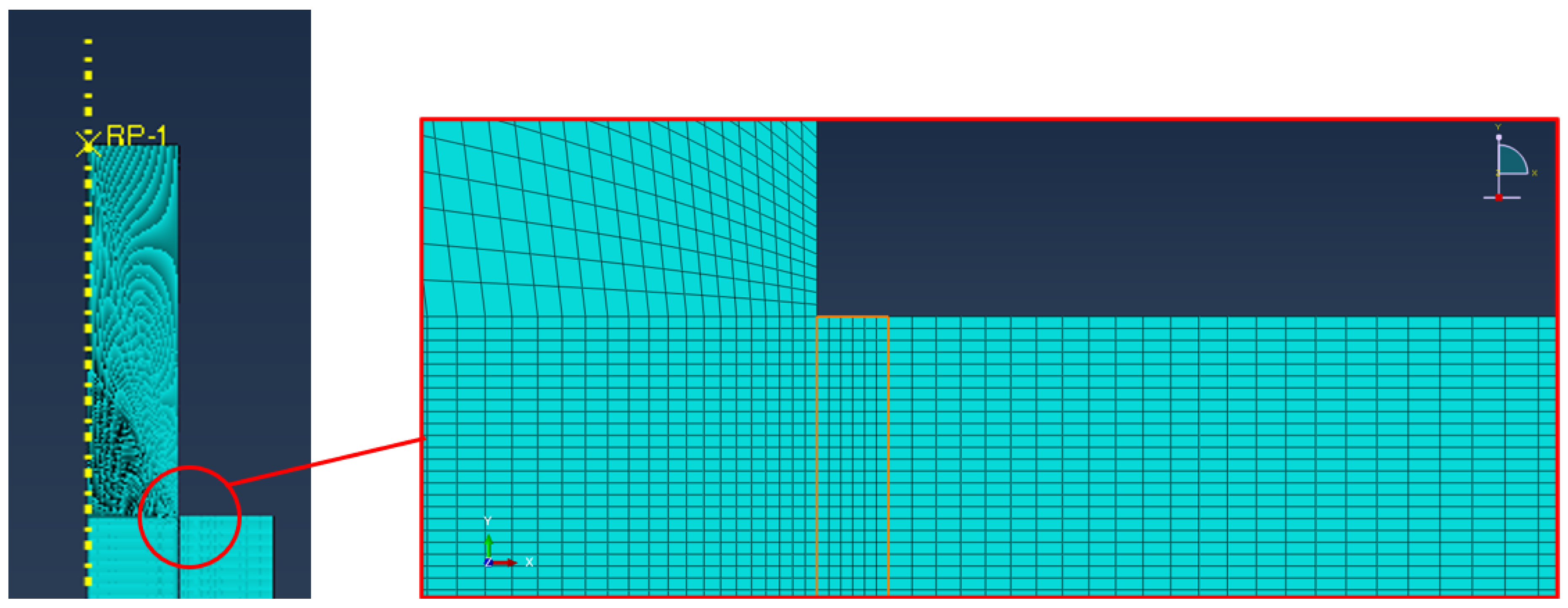
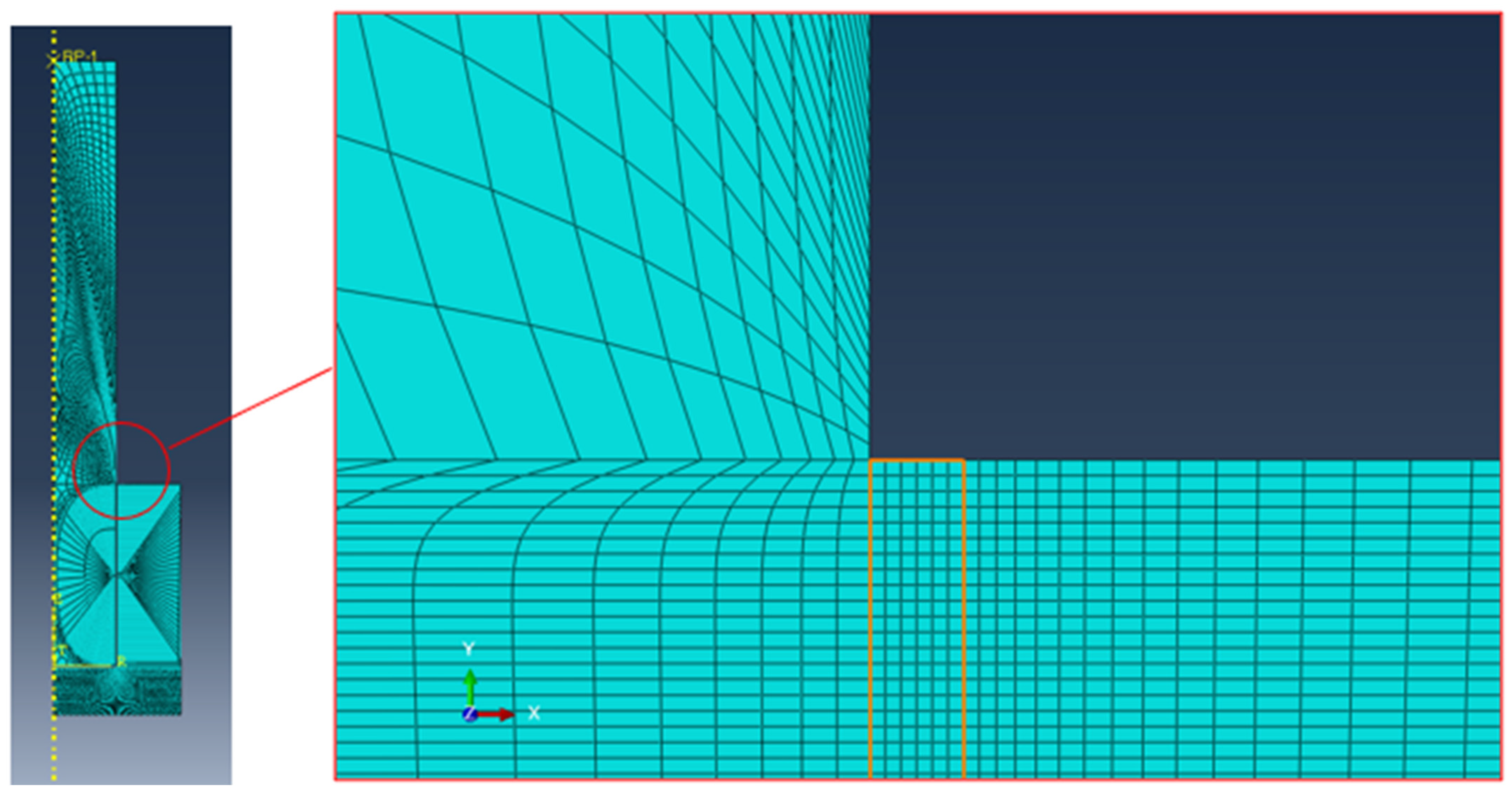
2.1.2. Finite Element Models of Pin–Collar Joints
2.2. Hybrid AM–Traditional Bonded Joints
2.2.1. Cylindrical Double Hub Joint
2.2.2. Prismatic Double Hub Joint
3. Results and Discussion
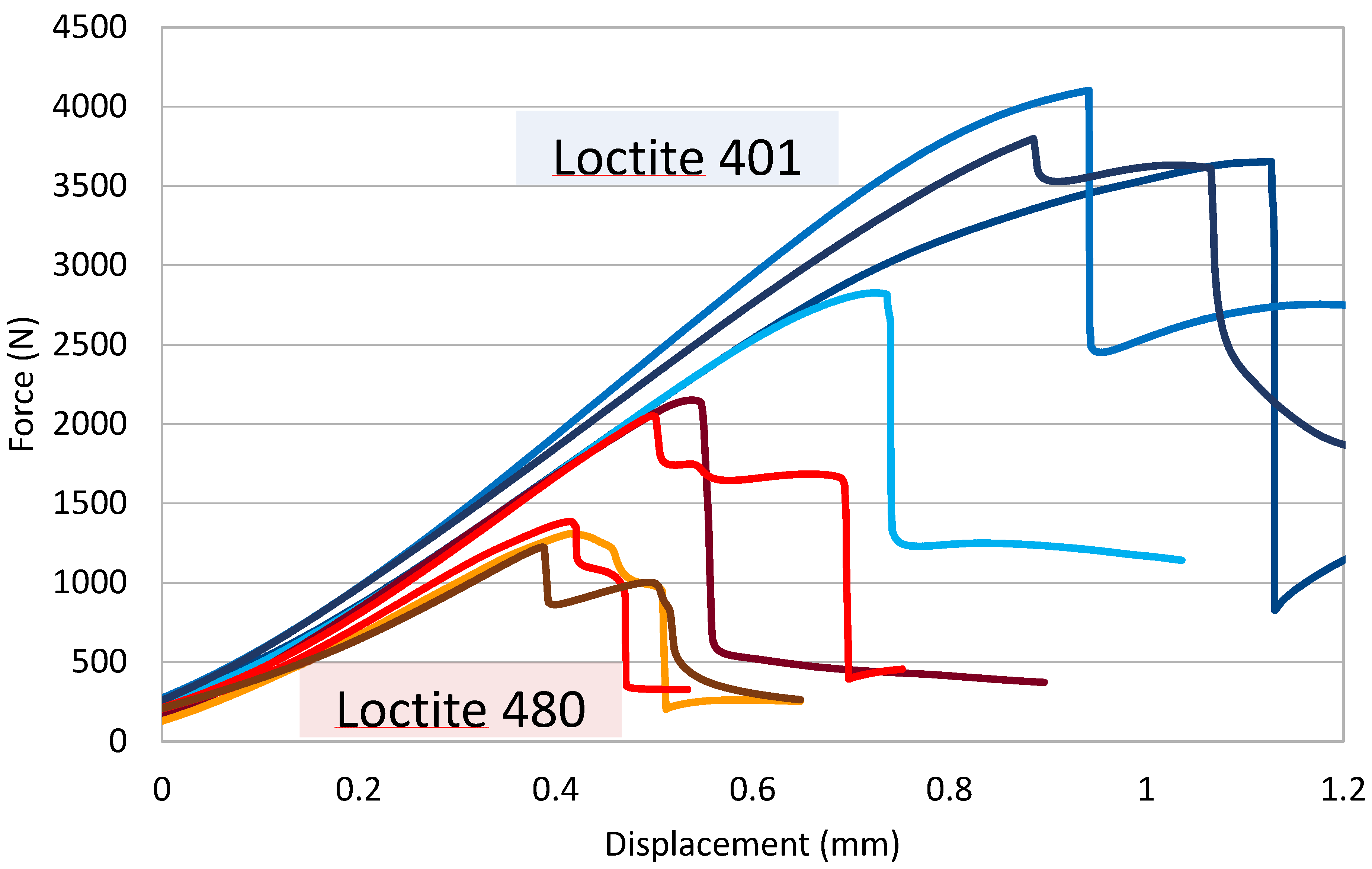
3.1. Pin–Collar Joints: Experimental Tests
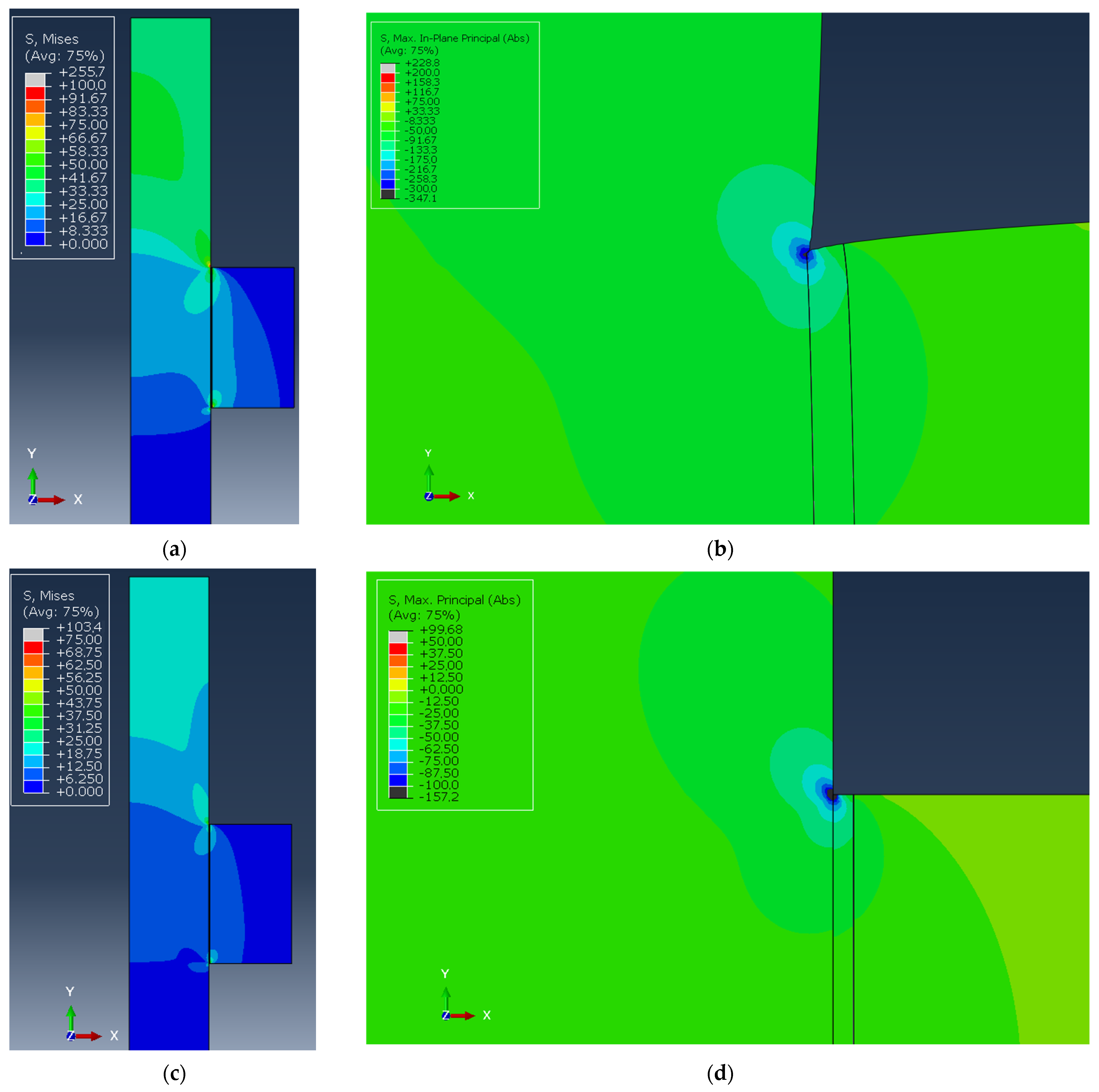
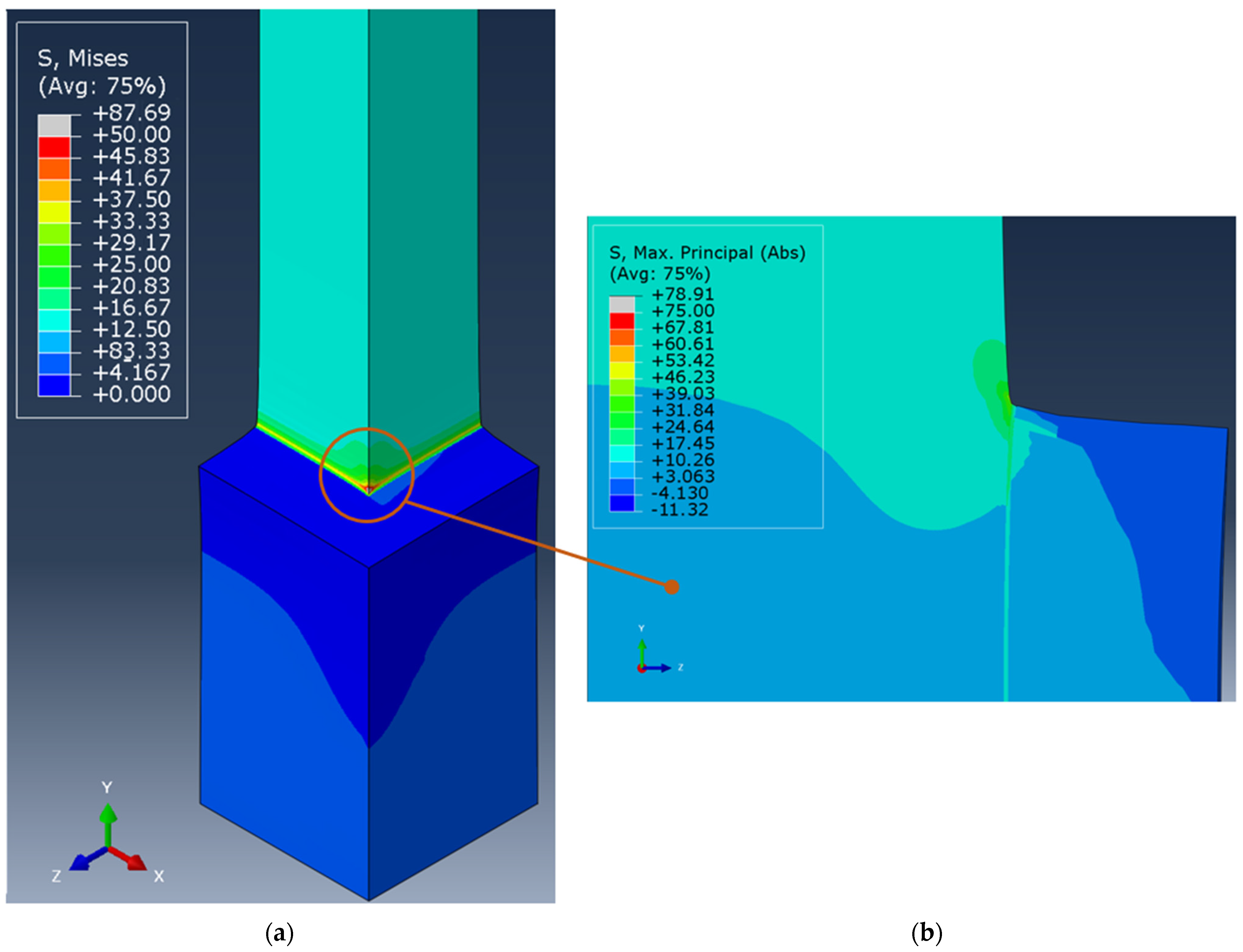
3.2. Pin–Collar Joints: Finite Element Analyses
3.3. Cylindrical Double Hub Joint: Experimental Test
3.4. Cylindrical Double Hub Joint: Finite Element Analyses
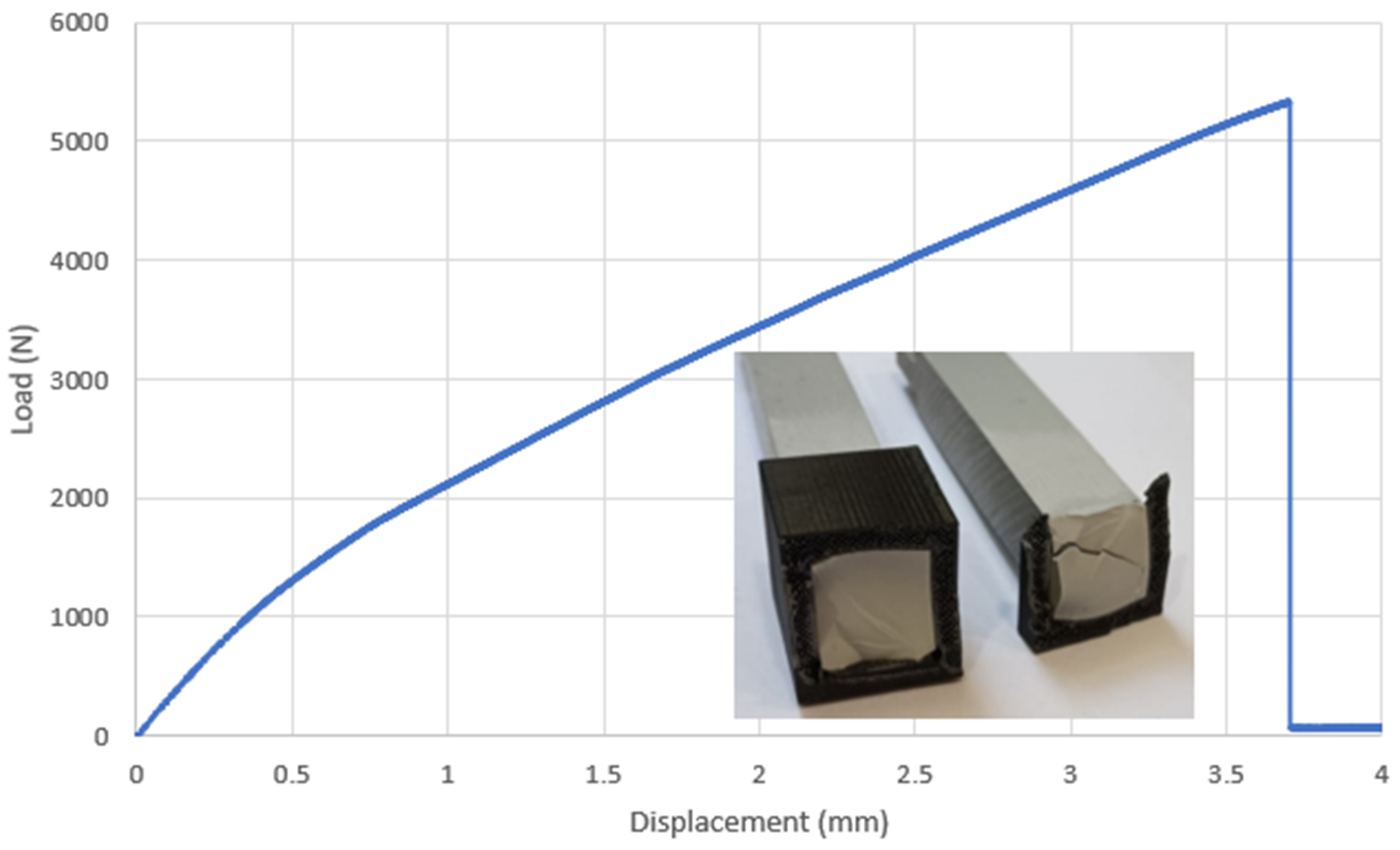
3.5. Prismatic Double Hub Joint: Experimental Test
3.6. Prismatic Double Hub Joint: Finite Element Analyses
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Adams, R.D.; Comyn, J.; Wake, W.C. Structural Adhesive Joints in Engineering; Chapman and Hall: London, UK, 1997. [Google Scholar]
- Adams, R.D. Strength Predictions for Lap Joints, Especially with Composite Adherends. A Review. J. Adhes. 1989, 30, 219–242. [Google Scholar] [CrossRef]
- Jennings, C.W. Surface Roughness and Bond Strength of Adhesives. J. Adhes. 1972, 4, 25–38. [Google Scholar] [CrossRef]
- Broad, R.; French, J.; Sauer, J. CLP new, effective, ecological surface pretreatment for highly durable adhesively bonded metal joints. Int. J. Adhes. Adhes. 1999, 19, 193–198. [Google Scholar] [CrossRef]
- Harris, A.; Beevers, A. The effects of grit-blasting on surface properties for adhesion. Int. J. Adhes. Adhes. 1999, 19, 445–452. [Google Scholar] [CrossRef]
- Shahid, M.; Hashim, S. Effect of surface roughness on the strength of cleavage joints. Int. J. Adhes. Adhes. 2002, 22, 235–244. [Google Scholar] [CrossRef]
- Adams, R.D.; Peppiatt, N.A. Stress Analysis of Adhesive Bonded Tubular Lap Joints. J. Adhes. 1977, 9, 1–18. [Google Scholar] [CrossRef]
- Iosipescu, N. New accurate procedure for single shear testing of metals. J. Mater. 1967, 2, 537–566. [Google Scholar]
- Stojcevski, F.; Hilditch, T.; Henderson, L.C. A modern account of Iosipescu testing. Compos. Part A Appl. Sci. Manuf. 2018, 107, 545–554. [Google Scholar] [CrossRef]
- Spaggiari, A.; Dragoni, E.; Brinson, H.F. Measuring the shear strength of structural adhesives with bonded beams under antisymmetric bending. Int. J. Adhes. Adhes. 2016, 67, 112–120. [Google Scholar] [CrossRef]
- Wycherley, G.; Mestan, S.; Grabovac, I. A Method for uniform shear stress-strain analysis of adhesives. J. Test. Eval. 1990, 18, 203–209. [Google Scholar] [CrossRef]
- Goland, M.; Reissner, E. The stresses in cemented joints. J. Appl. Mech. 1944, 11, A17–A27. [Google Scholar] [CrossRef]
- Carpenter, W.C. Goland and reissner were correct. J. Strain Anal. Eng. Des. 1989, 24, 185–187. [Google Scholar] [CrossRef]
- Crocombe, A.; Bigwood, D.; Richardson, G. Analysing structural adhesive joints for failure. Int. J. Adhes. Adhes. 1990, 10, 167–178. [Google Scholar] [CrossRef]
- da Silva, L.F.M.; Adams, R.D. Techniques to reduce the peel stresses in adhesive joints with composites. Int. J. Adhes. Adhes. 2007, 27, 227–235. [Google Scholar] [CrossRef]
- Hart-Smith, L. Adhesive-Bonded Single-Lap Joints; Douglas Aircraft Company: Santa Monica, CA, USA, 1973. [Google Scholar]
- Wah, T. The adhesive scarf joint in pure bending. Int. J. Mech. Sci. 1976, 18, 223–228. [Google Scholar] [CrossRef]
- Gay, D.; Hoa, S.V.; Tsai, S.W. Composite Materials Design and Applications; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar]
- Tsai, M.; Morton, J. The effect of a spew fillet on adhesive stress distributions in laminated composite single-lap joints. Compos. Struct. 1995, 32, 123–131. [Google Scholar] [CrossRef]
- Alfonso, L.; Badulescu, C.; Carrere, N. Use of the modified Arcan fixture to study the strength of bonded assemblies for automotive applications. Int. J. Adhes. Adhes. 2018, 80, 104–114. [Google Scholar] [CrossRef]
- dos Santos, D.J.; Batalha, G.F. Failure criterion for adhesively bonded joints using Arcan´s experimental method. Polim. E Tecnol. 2014, 24, 441–445. [Google Scholar] [CrossRef][Green Version]
- Cognard, J.; Créac’hcadec, R.; Sohier, L.; Davies, P. Analysis of the nonlinear behavior of adhesives in bonded assemblies—Comparison of TAST and Arcan tests. Int. J. Adhes. Adhes. 2008, 28, 393–404. [Google Scholar] [CrossRef]
- da Silva, L.F.; Ferreira, N.; Richter-Trummer, V.; Marques, E. Effect of grooves on the strength of adhesively bonded joints. Int. J. Adhes. Adhes. 2010, 30, 735–743. [Google Scholar] [CrossRef]
- Spaggiari, A.; Castagnetti, D.; Dragoni, E. Experimental tests on tubular bonded butt specimens: Effect of relief grooves on tensile strength of the adhesive. J. Adhes. 2012, 88, 499–512. [Google Scholar] [CrossRef]
- Spaggiari, A.; Dragoni, E. Regularization of torsional stresses in tubular lap bonded joints by means of functionally graded adhesives. Int. J. Adhes. Adhes. 2014, 53, 23–28. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, M.-J.; Zhang, D. Designing functionally graded materials with superior load-bearing properties. Acta Biomater. 2011, 8, 1101–1108. [Google Scholar] [CrossRef] [PubMed]
- Apalak, M.K. Elastic stresses in an adhesively-bonded functionally-graded tubular single-lap joint in tension. J. Adhes. Sci. Technol. 2006, 20, 1019–1046. [Google Scholar] [CrossRef]
- Stapleton, S.E.; Waas, A.M.; Arnold, S.M. Functionally graded adhesives for composite joints. Int. J. Adhes. Adhes. 2012, 35, 36–49. [Google Scholar] [CrossRef]
- Carbas, R.; da Silva, L.; Critchlow, G. Effect of post-cure on adhesively bonded functionally graded joints by induction heating. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2014, 229, 419–430. [Google Scholar] [CrossRef]
- Gackowski, B.M.; Phua, H.; Sharma, M.; Idapalapati, S. Hybrid additive manufacturing of polymer composites reinforced with buckypapers and short carbon fibres. Compos. Part A Appl. Sci. Manuf. 2022, 154, 106794. [Google Scholar] [CrossRef]
- Sadowski, T.; Golewski, P.; Zarzeka-Raczkowska, E. Damage and failure processes of hybrid joints: Adhesive bonded aluminium plates reinforced by rivets. Comput. Mater. Sci. 2011, 50, 1256–1262. [Google Scholar] [CrossRef]
- Ozel, A.; Yazici, B.; Akpinar, S.; Aydin, M.D.; Temiz, Ş. A study on the strength of adhesively bonded joints with different adherends. Compos. Part B Eng. 2014, 62, 167–174. [Google Scholar] [CrossRef]
- Spaggiari, A.; Denti, F. Mechanical strength of adhesively bonded joints using polymeric additive manufacturing. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 235, 1851–1859. [Google Scholar] [CrossRef]
- Spaggiari, A.; Favali, F. Evaluation of polymeric 3D printed adhesively bonded joints: Effect of joint morphology and mechanical interlocking. Rapid Prototyp. J. 2022, 28, 1437–1451. [Google Scholar] [CrossRef]
- Manoj, I.; Shah, A.K.; Jain, A. Strength and failure assessments of 3D printed PLA single lap joints: Experimental and numerical analysis. Eng. Fail. Anal. 2024, 161, 108257. [Google Scholar] [CrossRef]
- Frascio, M.; de Sousa Marques, E.A.; Carbas, R.J.C.; da Silva, L.F.M.; Monti, M.; Avalle, M. Review of tailoring methods for joints with additively manufactured adherends and adhesives. Materials 2020, 13, 3949. [Google Scholar] [CrossRef] [PubMed]
- Khosravani, M.R.; Soltani, P.; Reinicke, T. Fracture and structural performance of adhesively bonded 3D-printed PETG single lap joints under different printing parameters. Theor. Appl. Fract. Mech. 2021, 116. [Google Scholar] [CrossRef]
- Khosravani, M.R.; Anders, D.; Reinicke, T. Effects of post-processing on the fracture behavior of surface-treated 3D-printed parts. CIRP J. Manuf. Sci. Technol. 2023, 46, 148–156. [Google Scholar] [CrossRef]
- Khosravani, M.R.; Soltani, P.; Reinicke, T. Failure and fracture in adhesively bonded 3D-printed joints: An overview on the current trends. Eng. Fail. Anal. 2023, 153, 107574. [Google Scholar] [CrossRef]
- Khosravani, M.R.; Soltani, P.; Weinberg, K.; Reinicke, T. Structural integrity of adhesively bonded 3D-printed joints. Polym. Test. 2021, 100, 107262. [Google Scholar] [CrossRef]
- ASTM D4562-01; Test Method for Shear Strength of Adhesives Using Pin-And-Collar Specimen. ASTM International: West Conshohocken, PA, USA, 2019.
- ISO 10123; Adhesives—Determination of Shear Strength of Anaerobic Adhesives Using Pin-And-Collar Specimens. ISO: Geneva, Switzerland, 2013.
- Croccolo, D.; De Agostinis, M.; Vincenzi, N. Static and dynamic strength evaluation of interference fit and adhesively bonded cylindrical joints. Int. J. Adhes. Adhes. 2010, 30, 359–366. [Google Scholar] [CrossRef]
- Croccolo, D.; De Agostinis, M.; Vincenzi, N. Design of hybrid steel-composite interference fitted and adhesively bonded connections. Int. J. Adhes. Adhes. 2012, 37, 19–25. [Google Scholar] [CrossRef]
- Stratasys. Fortus 3D Production Systems. 2018. Available online: http://usglobalimages.stratasys.com/Main/Files/Machine_Spec_Sheets/PSS_FDM_FortusSystemsMaterialsOverview.pdf?v=635832637185031244 (accessed on 6 December 2018).
- Stratasys. ABSplus-P430 Mechanical Properties. 2019. Available online: http://usglobalimages.stratasys.com/Main/Files/Material_Spec_Sheets/MSS_FDM_ABSplusP430.pdf (accessed on 4 April 2019).
- Loctite. TDS for New Formulation of Loctite® 401TM. 2012. Available online: www.henkel.com/industrial (accessed on 10 September 2021).
- Loctite. LOCTITE® 480TM TDS. 2017. Available online: www.henkel.com/industrial (accessed on 6 May 2024).
- Cardarelli, F. Polymers and Elastomers. In Materials Handbook; Springer: London, UK, 2018; pp. 1013–1092. [Google Scholar] [CrossRef]
- Montgomery, D.C. Design and Analysis of Experiments, Design and Analysis of Experiments; John Wiley and Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Spaggiari, A.; Dragoni, E. Effect of mechanical surface treatment on the static strength of adhesive lap joints. J. Adhes. 2013, 89, 677–696. [Google Scholar] [CrossRef]
- Dragoni, E.; Goglio, L. Adhesive stresses in axially-loaded tubular bonded joints—Part I: Critical review and finite element assessment of published models. Int. J. Adhes. Adhes. 2013, 47, 35–45. [Google Scholar] [CrossRef]
- Goglio, L.; Paolino, D. Adhesive stresses in axially-loaded tubular bonded joints—Part II: Development of an explicit closed-form solution for the Lubkin and Reissner model. Int. J. Adhes. Adhes. 2014, 48, 35–42. [Google Scholar] [CrossRef]
- Goglio, L.; Rossetto, M.; Dragoni, E. Design of adhesive joints based on peak elastic stresses. Int. J. Adhes. Adhes. 2008, 28, 427–435. [Google Scholar] [CrossRef]





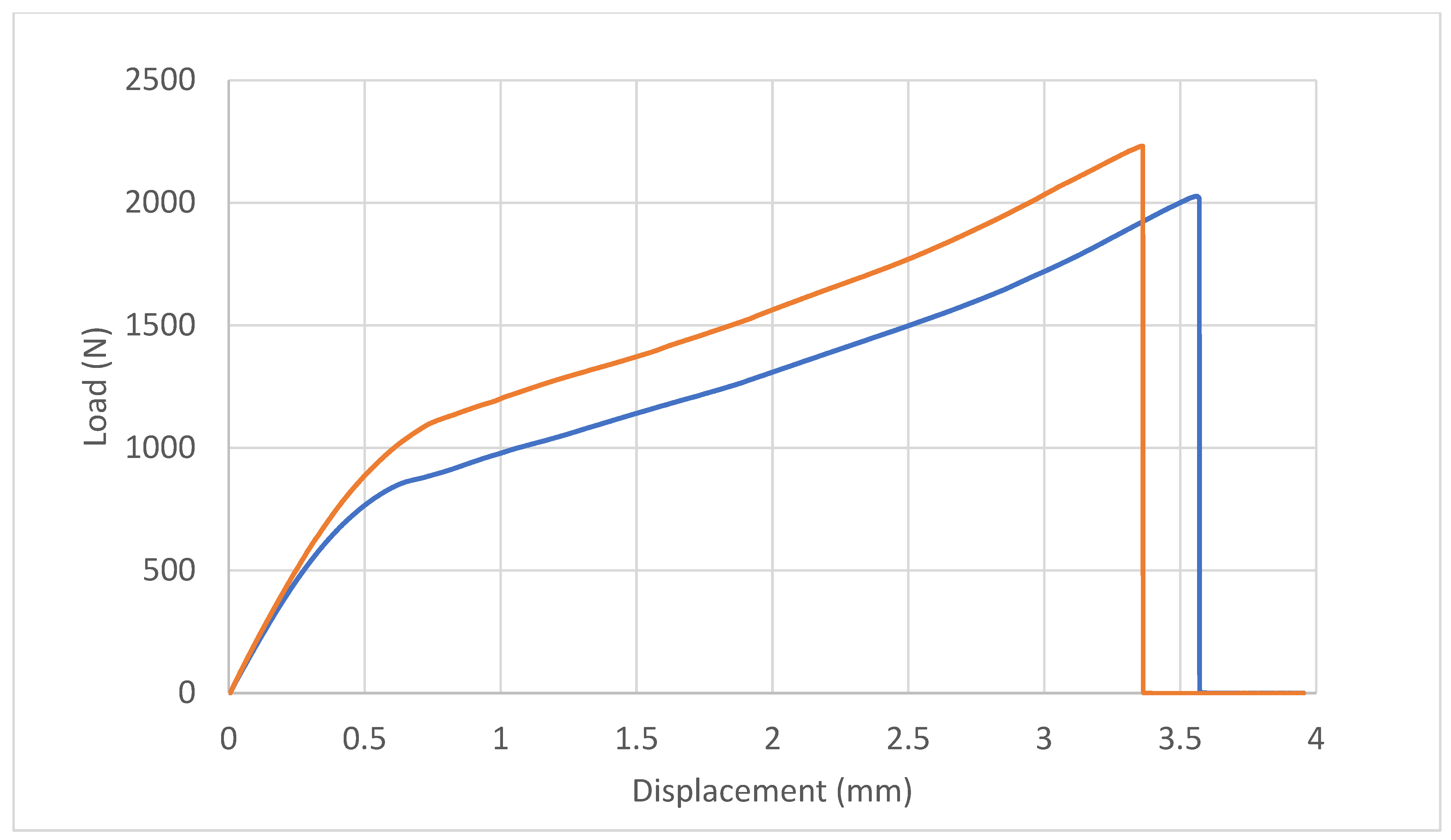


| Exp. Values | Experimental Force | Av. Shear Stress | Stiffness | Displacement at Failure |
|---|---|---|---|---|
| Loctite 401 | 3595.7 N ± 15% | 11.56 MPa ± 15% | 4449 N/mm ± 5% | 0.918 mm ± 18% |
| Loctite 480 | 1723.9 N ± 25% | 5.22 MPa ± 25% | 3649 N/mm ± 11% | 0.466 mm ± 13% |
| Applied Pressure | Max. Principal “Structural” Stress | Pin Max Vertical Displacement | |
|---|---|---|---|
| Loctite 401 | 45.8 MPa | 81.33 MPa | 0.923 mm |
| Loctite 480 | 12.72 MPa | 42.3 MPa | 0.423 mm |
| Peak Load | Displacement at Failure | Adhesive σcritical/σpeak | Adherend σcritical/σaverage | Adherend σcritical/σpeak | |
|---|---|---|---|---|---|
| Experimental tests | 2129 N ± 6.8% | 3.46 mm ± 4.1% | 81.3/51.2 = 1.58 | 33/7.95 = 4.15 | 33/56.8 = 0.58 |
| FE analysis | 2130 N | 3.1 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Spaggiari, A.; Orlandini, S. Mechanical Strength of Additive Manufactured and Standard Polymeric Components Joined Through Structural Adhesives. Polymers 2024, 16, 3036. https://doi.org/10.3390/polym16213036
Spaggiari A, Orlandini S. Mechanical Strength of Additive Manufactured and Standard Polymeric Components Joined Through Structural Adhesives. Polymers. 2024; 16(21):3036. https://doi.org/10.3390/polym16213036
Chicago/Turabian StyleSpaggiari, Andrea, and Simone Orlandini. 2024. "Mechanical Strength of Additive Manufactured and Standard Polymeric Components Joined Through Structural Adhesives" Polymers 16, no. 21: 3036. https://doi.org/10.3390/polym16213036
APA StyleSpaggiari, A., & Orlandini, S. (2024). Mechanical Strength of Additive Manufactured and Standard Polymeric Components Joined Through Structural Adhesives. Polymers, 16(21), 3036. https://doi.org/10.3390/polym16213036







