Molecular Dynamics Simulation of the Viscosity Enhancement Mechanism of P-n Series Vinyl Acetate Polymer–CO2
Abstract
1. Introduction
2. Materials and Methods
2.1. Single-Molecule Modeling and Structure Optimization
2.2. Modeling and Simulation Method for P-n-scCO2 System
3. MD Calculated Equilibrium Determination Method
4. Analysis of MD Calculations
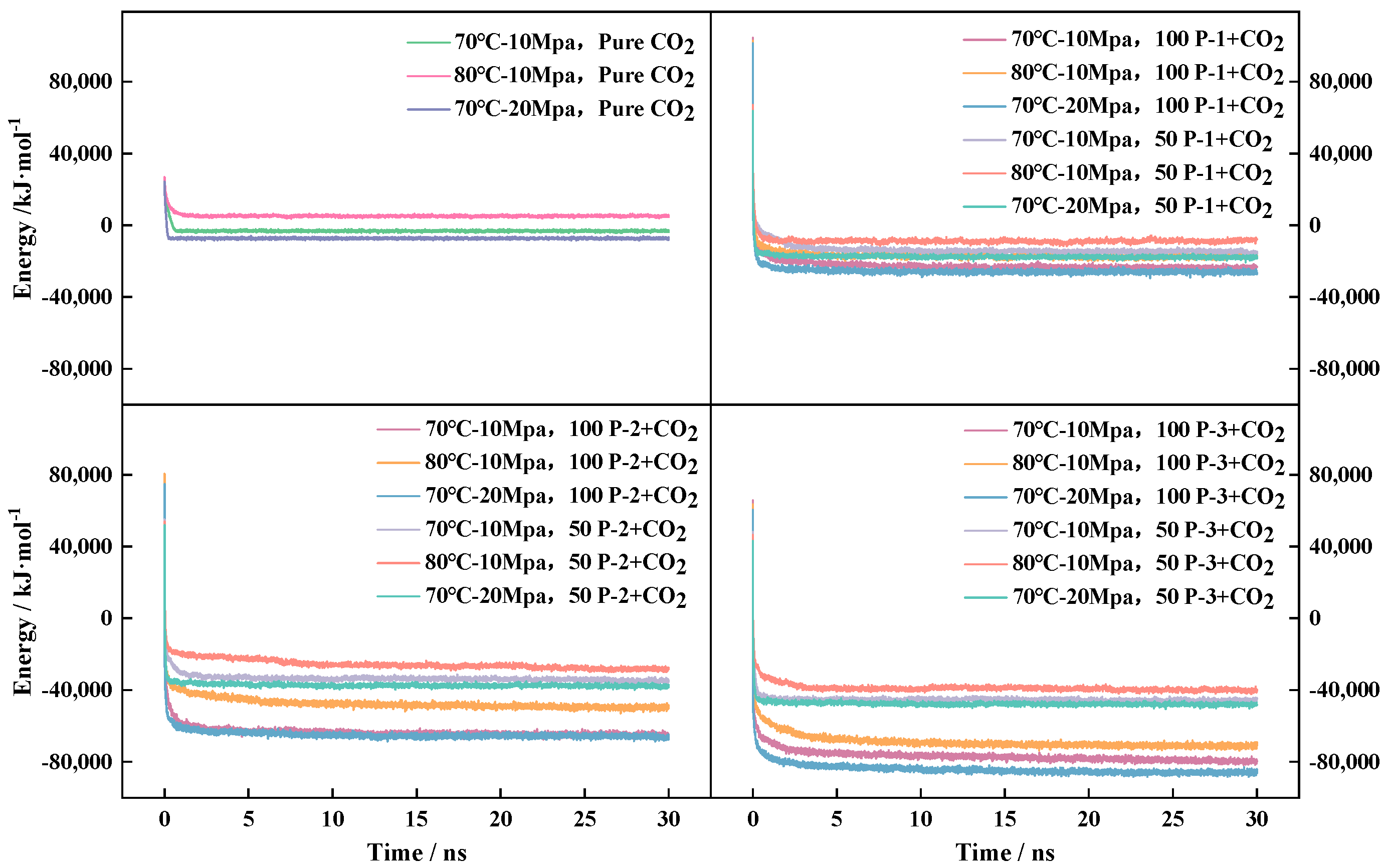
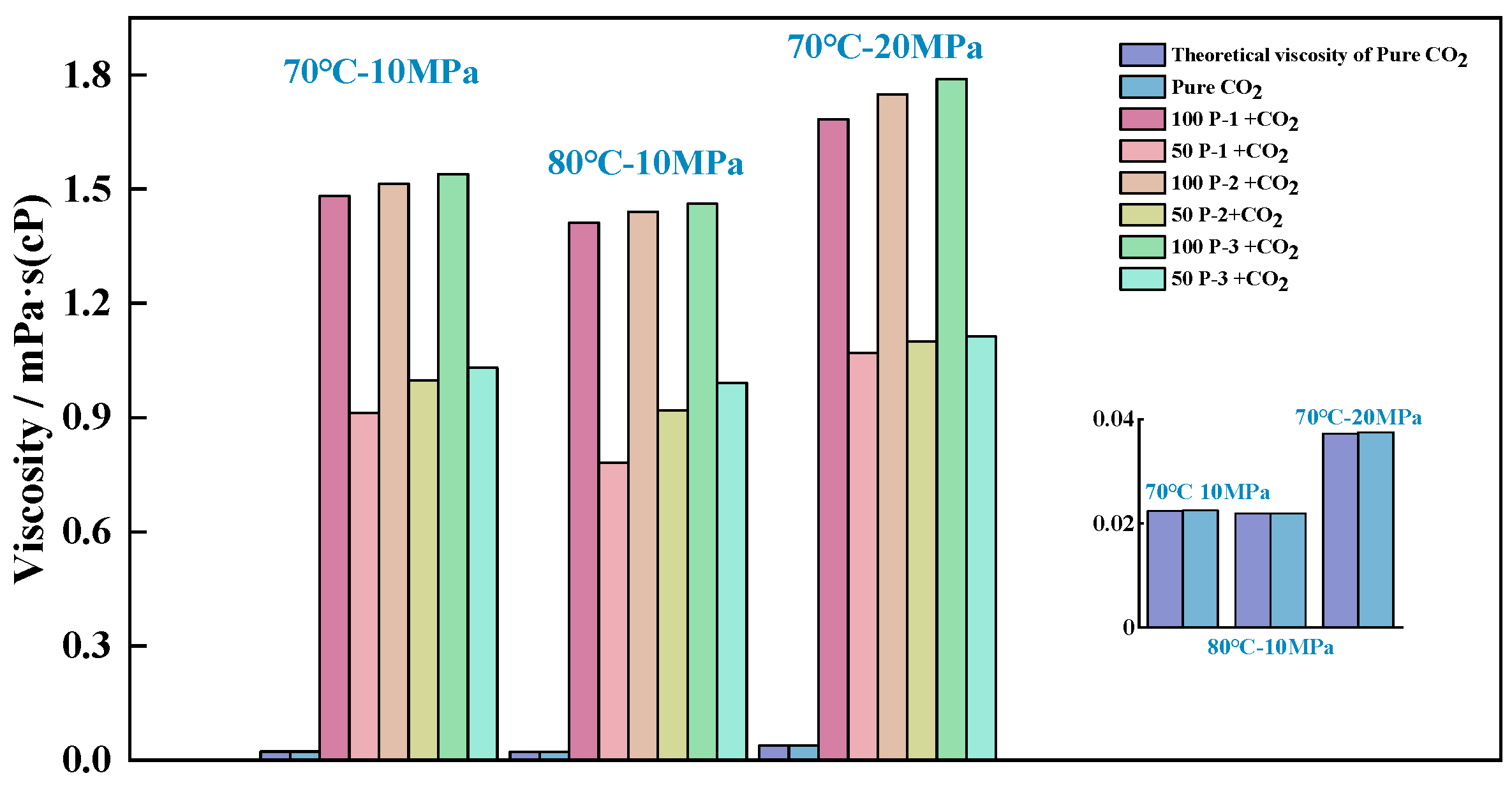
4.1. System Viscosity Study
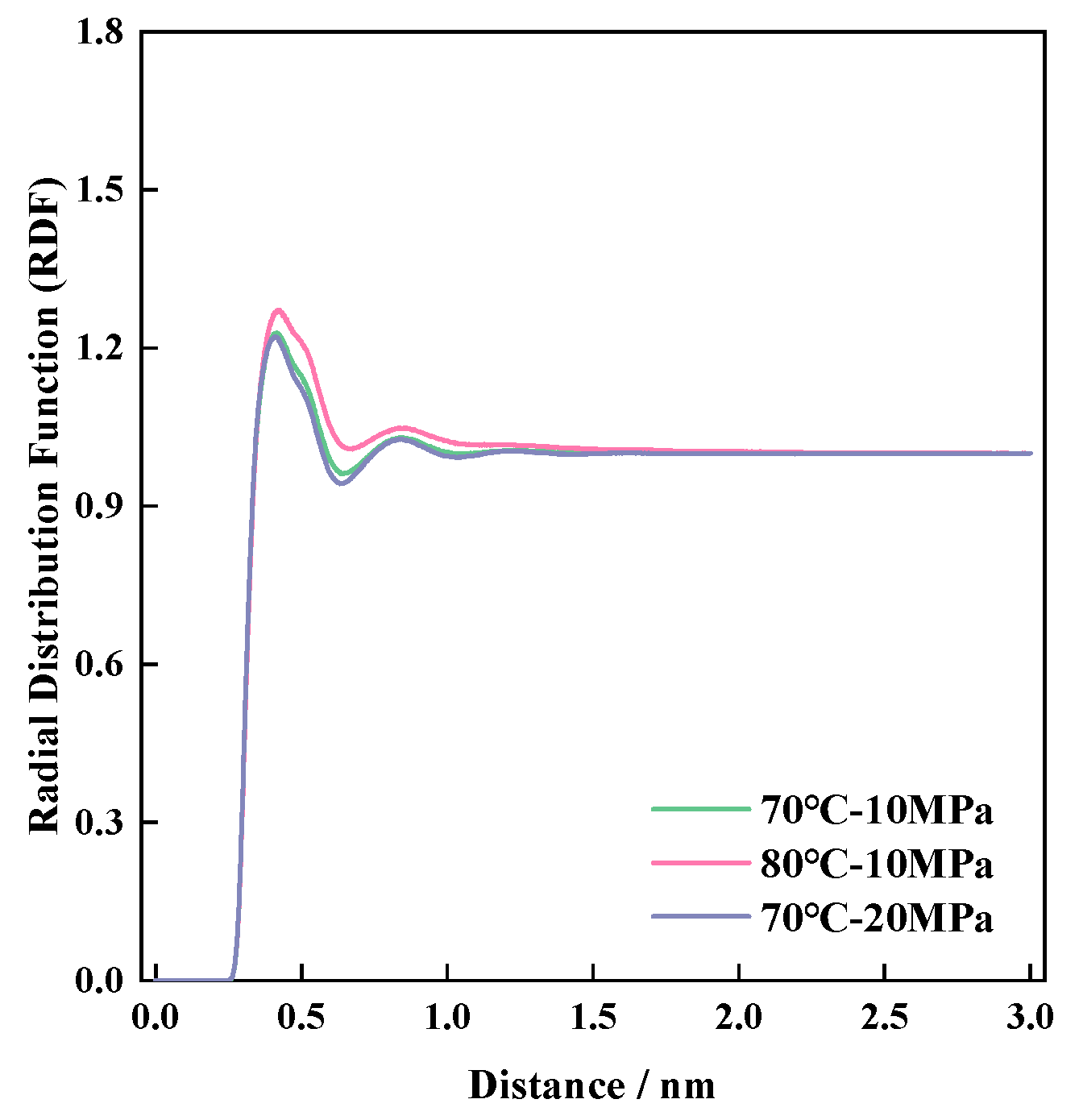
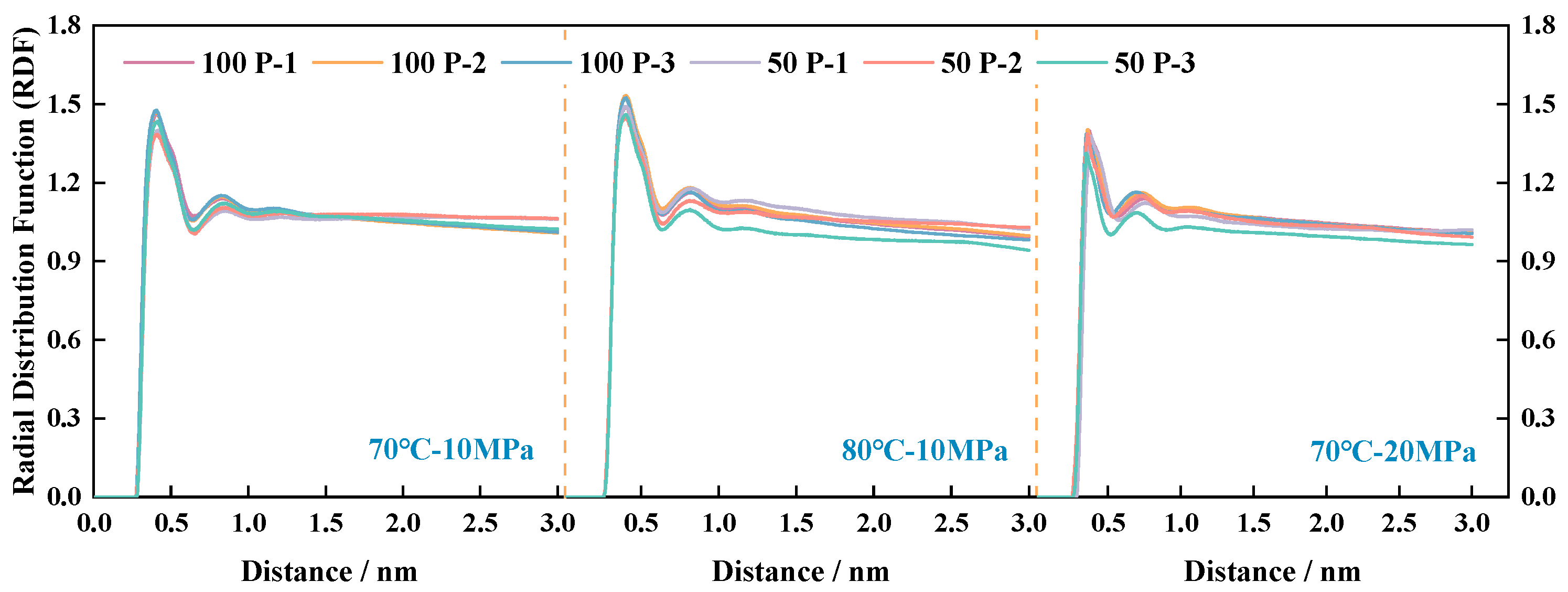
4.2. Visualization of Molecular Distribution Patterns
4.3. Examination of Polymer Molecular Distribution Laws
4.3.1. Solubility of PVE in scCO2
4.3.2. System Density Change Rule
4.3.3. Laws of Change of CO2 and Surface Area Before and After Equilibration
4.4. Examination of Functional Groups and Atoms of Polymer Molecules and CO2 Interaction Law
4.4.1. Analysis of Fluctuations in the Radius of Gyration
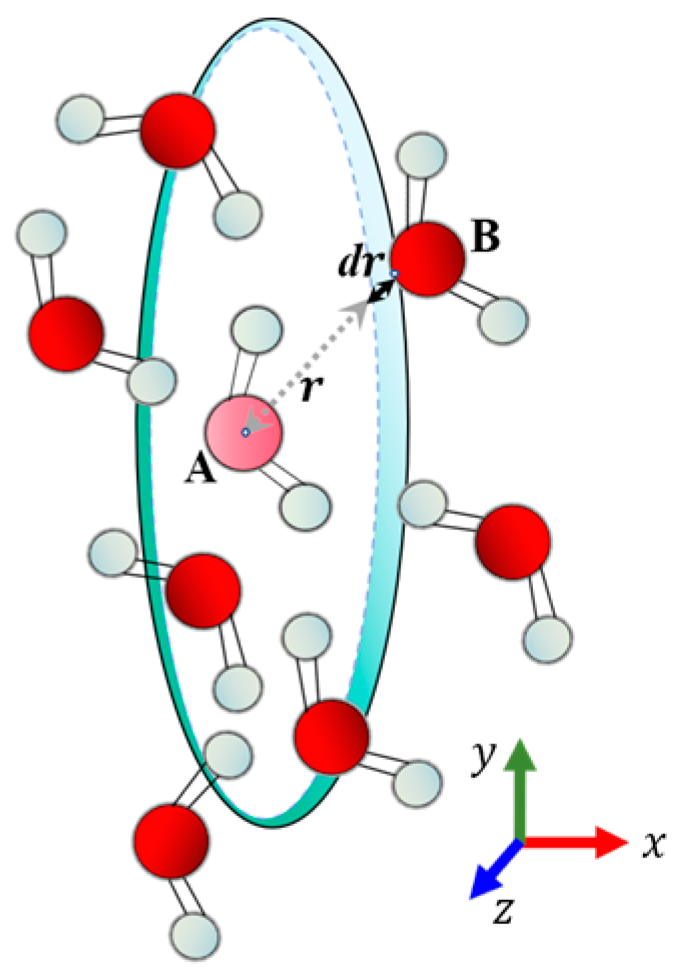
4.4.2. Calculation of the Minimum Intermolecular Contact Distance and the Number of Pairs of Contacting Atoms
5. Conclusions
- The viscosities of the P-n-CO2 systems, in descending order, are Ƞ100-P-3, Ƞ100-P-2, Ƞ100-P-1, Ƞ50-P-3, Ƞ50-P-2, and Ƞ100-P-1.
- All of the above systems achieved effective viscosity enhancement, and the degree of viscosity enhancement of P-n molecules was positively correlated with the contact area of CO2 and the number of P-n molecules.
- The molecules within the equilibrium system did not occur between the phenomena of bond breaking, bridging, etc.; that is, there was no chemical reaction.
- Multi-scale analysis of microscopic interaction patterns between P-n molecular structures and CO2 molecules: the molecular weight was positively correlated with the molecular amplitude, radial distribution peak, molecular radius of gyration, and effective contact area.
- For the molecules containing the total number of atoms, the molecular density distribution of the system tends to be more stabilized, allowing for a greater number of atom contact pairs.
- The minimum space between P-n molecules and CO2 molecules in the system model was calculated to be in the range of 1.699–1.736 Å. The introduction of VAc can promote the dissolution of polymers in CO2.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Turan, G.; Zapantis, A.; Kearns, D.; Tamme, E.; Staib, C.; Zhang, T.; Liu, H. Global status of CCS 2021. In CCS Accelerating to Net Zero; Global CCS Institute: Melbourne, Australia, 2021. [Google Scholar]
- Bera, A.; Babadagli, T. Relative Permeability of Foamy Oil for Different Types of Dissolved Gases. SPE Reserv. Eval. Eng. 2016, 19, 604–619. [Google Scholar] [CrossRef]
- Bai, B.; Sun, X. Development of Swelling-Rate Controllable Particle Gels to Control the Conformance of CO2 Flooding. In Proceedings of the Day 3 Wed, Virtual, 2 September 2020; SPE: Tulsa, OK, USA, 2020; p. D031S045R001. [Google Scholar]
- Tokunaga, T.K. DLVO-based estimates of adsorbed water film thicknesses in geologic CO2 reservoirs. Langmuir 2012, 28, 8001–8009. [Google Scholar] [CrossRef] [PubMed]
- Kuang, N.; Yang, S.; Yuan, Z.; Wang, M.; Zhang, Z.; Zhang, X.; Wang, M.; Zhang, Y.; Li, S.; Wu, J.; et al. Study on Oil and Gas Amphiphilic Surfactants Promoting the Miscibility of CO2 and Crude Oil. ACS Omega 2021, 6, 27170–27182. [Google Scholar] [CrossRef] [PubMed]
- Rognmo, A.U.; Heldal, S.; Fernø, M.A. Silica Nanoparticles to Stabilize CO2-Foam for Improved CO2 Utilization: Enhanced CO2 Storage and Oil Recovery from Mature Oil Reservoirs. Fuel 2018, 216, 621–626. [Google Scholar] [CrossRef]
- Ricky, E.X.; Mwakipunda, G.C.; Nyakilla, E.E.; Kasimu, N.A.; Wang, C.; Xu, X. A Comprehensive Review on CO2 Thickeners for CO2 Mobility Control in Enhanced Oil Recovery: Recent Advances and Future Outlook. J. Ind. Eng. Chem. 2023, 126, 69–91. [Google Scholar] [CrossRef]
- Hsiao, Y.-L.; Maury, E.E.; DeSimone, J.M.; Mawson, S.; Johnston, K.P. Dispersion Polymerization of Methyl Methacrylate Stabilized with Poly(1,1-Dihydroperfluorooctyl Acrylate) in Supercritical Carbon Dioxide. Macromolecules 1995, 28, 8159–8166. [Google Scholar] [CrossRef]
- Shi, C.; Huang, Z.; Beckman, E.J.; Enick, R.M.; Kim, S.-Y.; Curran, D.P. Semi-Fluorinated Trialkyltin Fluorides and Fluorinated Telechelic Ionomers as Viscosity-Enhancing Agents for Carbon Dioxide. Ind. Eng. Chem. Res. 2001, 40, 908–913. [Google Scholar] [CrossRef]
- Afra, S.; Alhosani, M.; Firoozabadi, A. Improvement in CO2 Geo-Sequestration in Saline Aquifers by Viscosification: From Molecular Scale to Core Scale. Int. J. Greenh. Gas Control 2023, 125, 103888. [Google Scholar] [CrossRef]
- AlYousef, Z.; Swaie, O.; Alabdulwahab, A.; Kokal, S. Direct Thickening of Supercritical Carbon Dioxide Using CO2-Soluble Polymer. In Proceedings of the Day 4 Thu, Abu Dhabi, United Arab Emirates, 14 November 2019; SPE: Abu Dhabi, United Arab Emirates (UAE), 2019; p. D041S105R004. [Google Scholar]
- Liu, H.; Song, J.; Bai, Y.X.; Zhang, L.; Mu, M. Study on pressure reduction and injection system for low permeability reservoirs. Petrochem. Technol. 2024, 31, 152–154. [Google Scholar]
- Potluri, V.K.; Hamilton, A.D.; Karanikas, C.F.; Bane, S.E.; Xu, J.; Beckman, E.J.; Enick, R.M. The High CO2-Solubility of per-Acetylated α-, β-, and γ-Cyclodextrin. Fluid Phase Equilibria 2003, 211, 211–217. [Google Scholar] [CrossRef]
- Enick, R.; Beckman, E.; Hamilton, A. Inexpensive CO2 Thickening Agents for Improved Mobility Control of CO2 Floods; University of Pittsburgh: Pittsburgh, PA, USA, 2005; p. 968338. [Google Scholar]
- Li, Y. Molecular Dynamics Simulation of Minimum Mixed-Phase Pressure and Intra-Nanopore Exfoliation for CO2 Driven Oil. Master’s Thesis, Huazhong University of Science and Technology, Wuhan, China, 2022. [Google Scholar]
- Fu, H.; Song, K.; Pan, Y.; Song, H.; Meng, S.; Liu, M.; Bao, R.; Hao, H.; Wang, L.; Fu, X. Application of Polymeric CO2 Thickener Polymer-Viscosity-Enhance in Extraction of Low-Permeability Tight Sandstone. Polymers 2024, 16, 299. [Google Scholar] [CrossRef] [PubMed]
- Xue, P.; Shi, J.; Cao, X.; Yuan, S. Molecular Dynamics Simulation of Thickening Mechanism of Supercritical CO2 Thickener. Chem. Phys. Lett. 2018, 706, 658–664. [Google Scholar] [CrossRef]
- O’Neill, M.L.; Cao, Q.; Fang, M.; Johnston, K.P.; Wilkinson, S.P.; Smith, C.D.; Kerschner, J.L.; Jureller, S.H. Solubility of Homopolymers and Copolymers in Carbon Dioxide. Ind. Eng. Chem. Res. 1998, 37, 3067–3079. [Google Scholar] [CrossRef]
- Wu, K.; Song, L.; Hu, Y.; Lu, H.; Kandola, B.K.; Kandare, E. Synthesis and Characterization of a Functional Polyhedral Oligomeric Silsesquioxane and Its Flame Retardancy in Epoxy Resin. Prog. Org. Coat. 2009, 65, 490–497. [Google Scholar] [CrossRef]
- Jeon, I.; Lee, S.; Yang, S. Hyperthermal Erosion of Thermal Protection Nanocomposites under Atomic Oxygen and N2 Bombardment. Int. J. Mech. Sci. 2023, 240, 107910. [Google Scholar] [CrossRef]
- Guan, J.; Liu, X.; Lai, G.; Luo, Q.; Qian, S.; Zhan, J.; Wang, Z.; Cui, S. Effect of Sulfonation Modification of Polycarboxylate Superplasticizer on Tolerance Enhancement in Sulfate. Constr. Build. Mater. 2021, 273, 122095. [Google Scholar] [CrossRef]
- Gurina, D.L.; Budkov, Y.A.; Kiselev, M.G. A Molecular Insight into Poly(Methyl Methacrylate) Impregnation with Mefenamic Acid in Supercritical Carbon Dioxide: A Computational Simulation. J. Mol. Liq. 2021, 337, 116424. [Google Scholar] [CrossRef]
- Nijjer, J.S.; Hewitt, D.R.; Neufeld, J.A. Horizontal Miscible Displacements Through Porous Media: The Interplay between Viscous Fingering and Gravity Segregation. J. Fluid Mech. 2022, 935, A14. [Google Scholar] [CrossRef]
- Zhan, X.; Jiang, B.; Yi, L.; Zhang, Q.; Chen, B.; Chen, F. Vinyl acetate “reactive”/controlled radical polymerization. J. Zhejiang Univ. (Eng.) 2010, 44, 1014–1018. [Google Scholar]
- Neese, F. Software Update: The ORCA Program System—Version 5.0. WIREs Comput. Mol. Sci. 2022, 12, e1606. [Google Scholar] [CrossRef]
- Neese, F. Software Update: The ORCA Program System, Version 4.0. WIREs Comput. Mol. Sci. 2018, 8, e1327. [Google Scholar] [CrossRef]
- Yuan, S.; Zhang, H.; Zhang, D. Molecular Simulation-Theory and Experiment GitHub; Chemical Industry Press: Beijing, China, 2016; ISBN 9787122277084. [Google Scholar]
- Zhang, Z.; Liu, L.; Zhu, J.; Wang, B. MATLAB and Mathematical Experiments, 2nd ed.; Mechanical Industry Press: Beijing, China, 2004. [Google Scholar]
- Wang, C.; Gao, L.; Liu, M.; Xia, S.; Han, Y. Viscosity Reduction Mechanism of Functionalized Silica Nanoparticles in Heavy Oil-Water System. Fuel Process. Technol. 2022, 237, 107454. [Google Scholar] [CrossRef]
- Wang, C.; Gao, L.; Liu, M.; Nian, Y.; Shu, Q.; Xia, S.; Han, Y. Viscosity Reduction Mechanism of Surface-Functionalized Fe3O4 Nanoparticles in Different Types of Heavy Oil. Fuel 2024, 360, 130535. [Google Scholar] [CrossRef]
- Lu, N.; Dong, X.; Chen, Z.; Liu, H.; Zheng, W.; Zhang, B. Effect of Solvent on the Adsorption Behavior of Asphaltene on Silica Surface: A Molecular Dynamic Simulation Study. J. Pet. Sci. Eng. 2022, 212, 110212. [Google Scholar] [CrossRef]
- Schettino, V.; Bini, R. Constraining Molecules at the Closest Approach: Chemistry at High Pressure. Chem. Soc. Rev. 2007, 36, 869. [Google Scholar] [CrossRef]
- Sun, B.; Sun, W.; Wang, H.; Li, Y.; Fan, H.; Li, H.; Chen, X. Molecular Simulation Aided Design of Copolymer Thickeners for Supercritical CO2 as Non-Aqueous Fracturing Fluid. J. CO2 Util. 2018, 28, 107–116. [Google Scholar] [CrossRef]
- Hess, B. Determining the Shear Viscosity of Model Liquids from Molecular Dynamics Simulations. J. Chem. Phys. 2002, 116, 209–217. [Google Scholar] [CrossRef]
- Wang, F.; Lai, R.; Zhang, D. New progress of CCUS-EOR technology research and practice in Jilin Oilfield. Nat. Gas Ind. 2024, 44, 76–82. [Google Scholar]
- Li, M.; Shan, W.; Liu, X.; Shang, G. Experimental study on the mechanism of supercritical carbon dioxide mixed-phase oil drive. J. Pet. 2006, 80–83. [Google Scholar] [CrossRef]
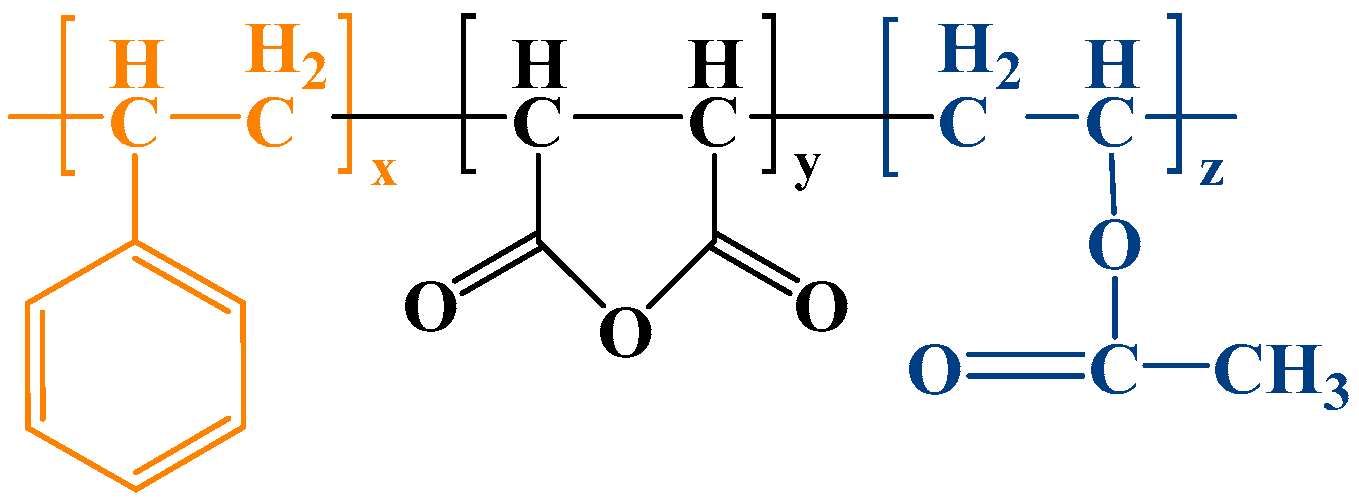
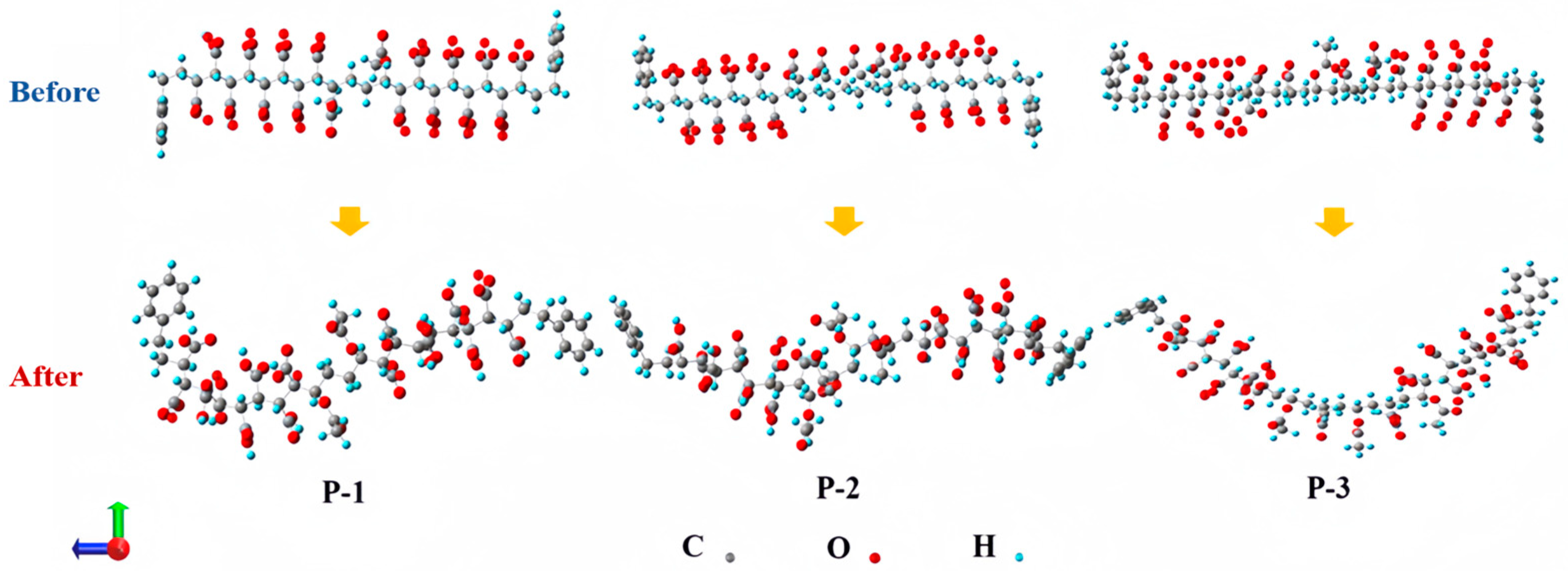
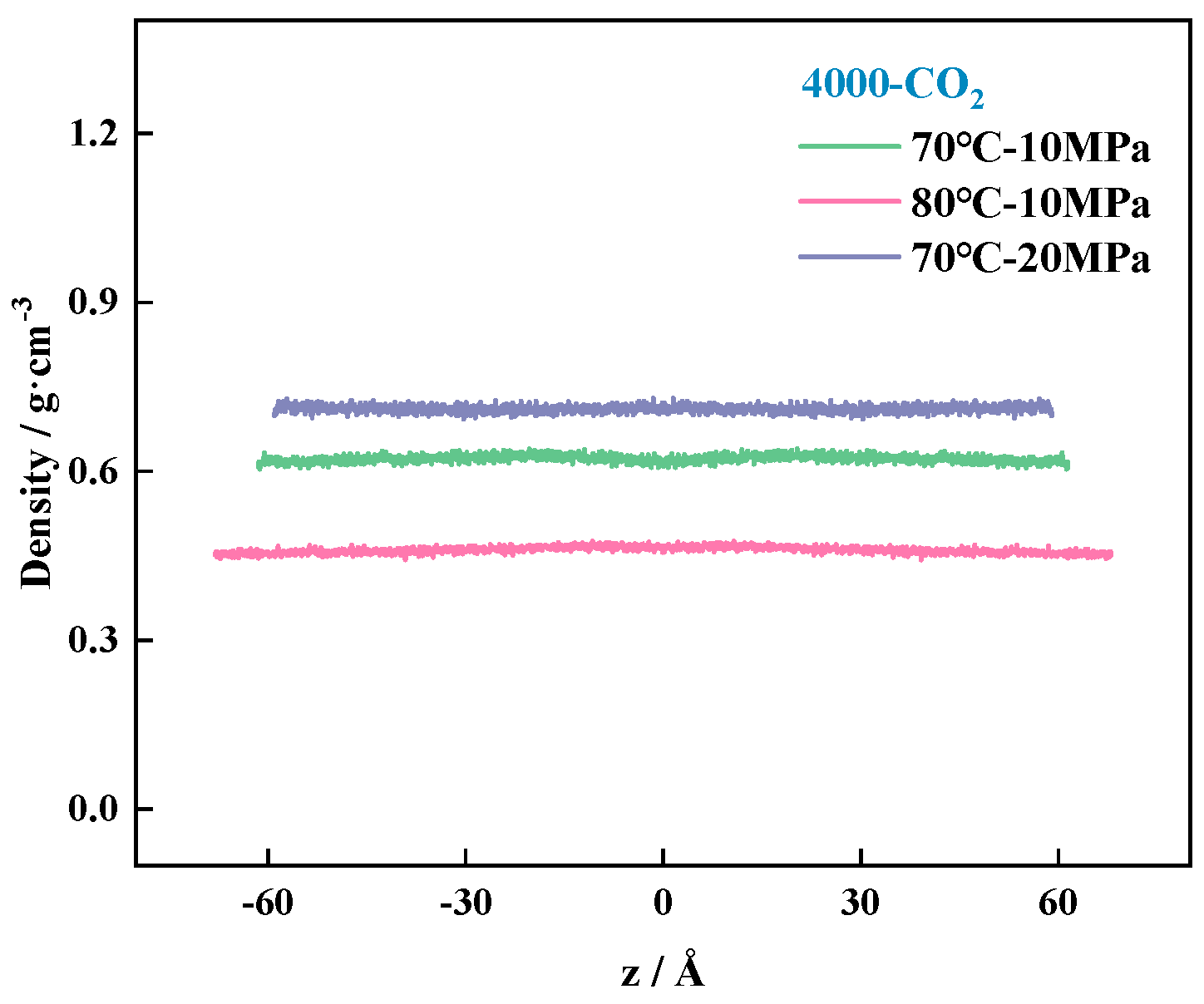
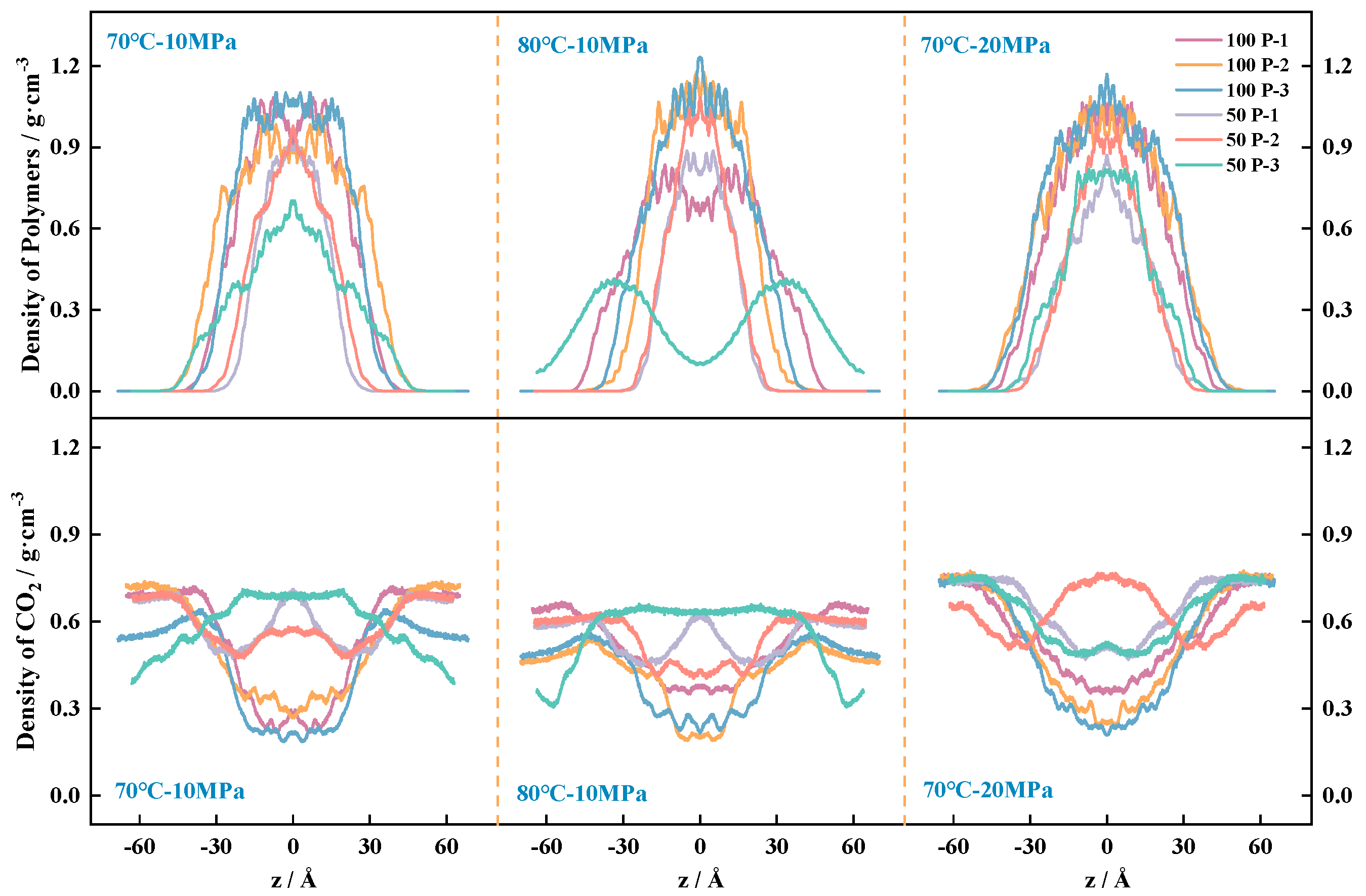
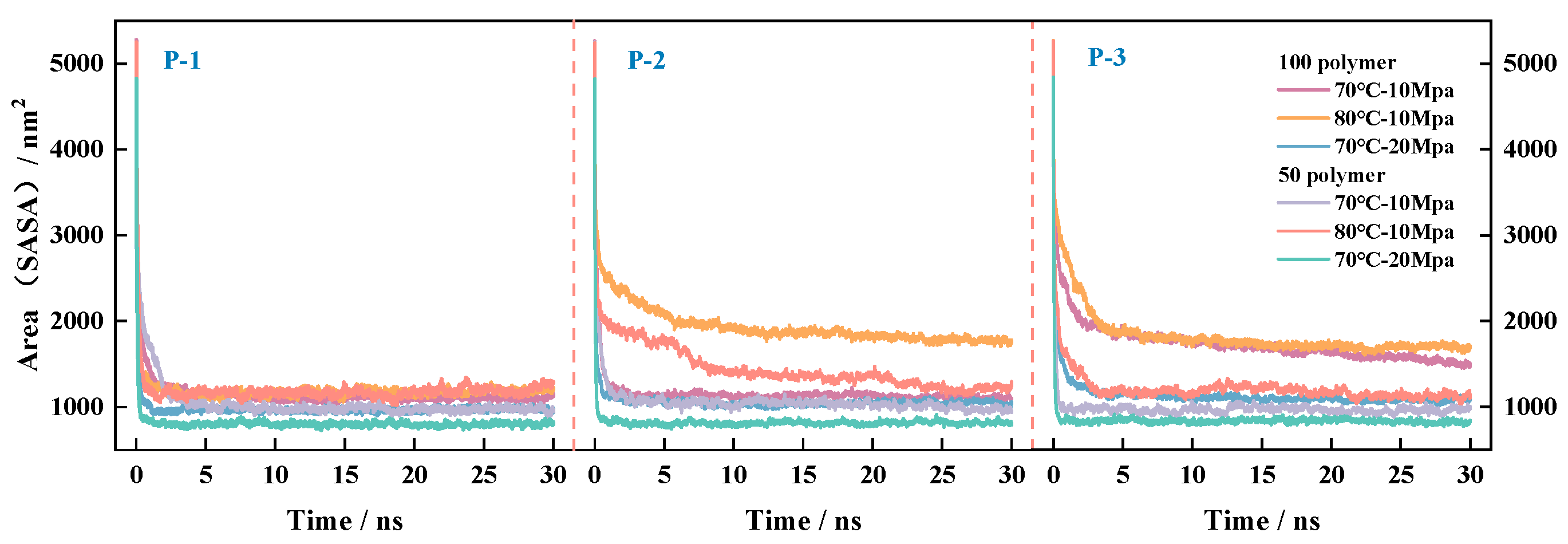
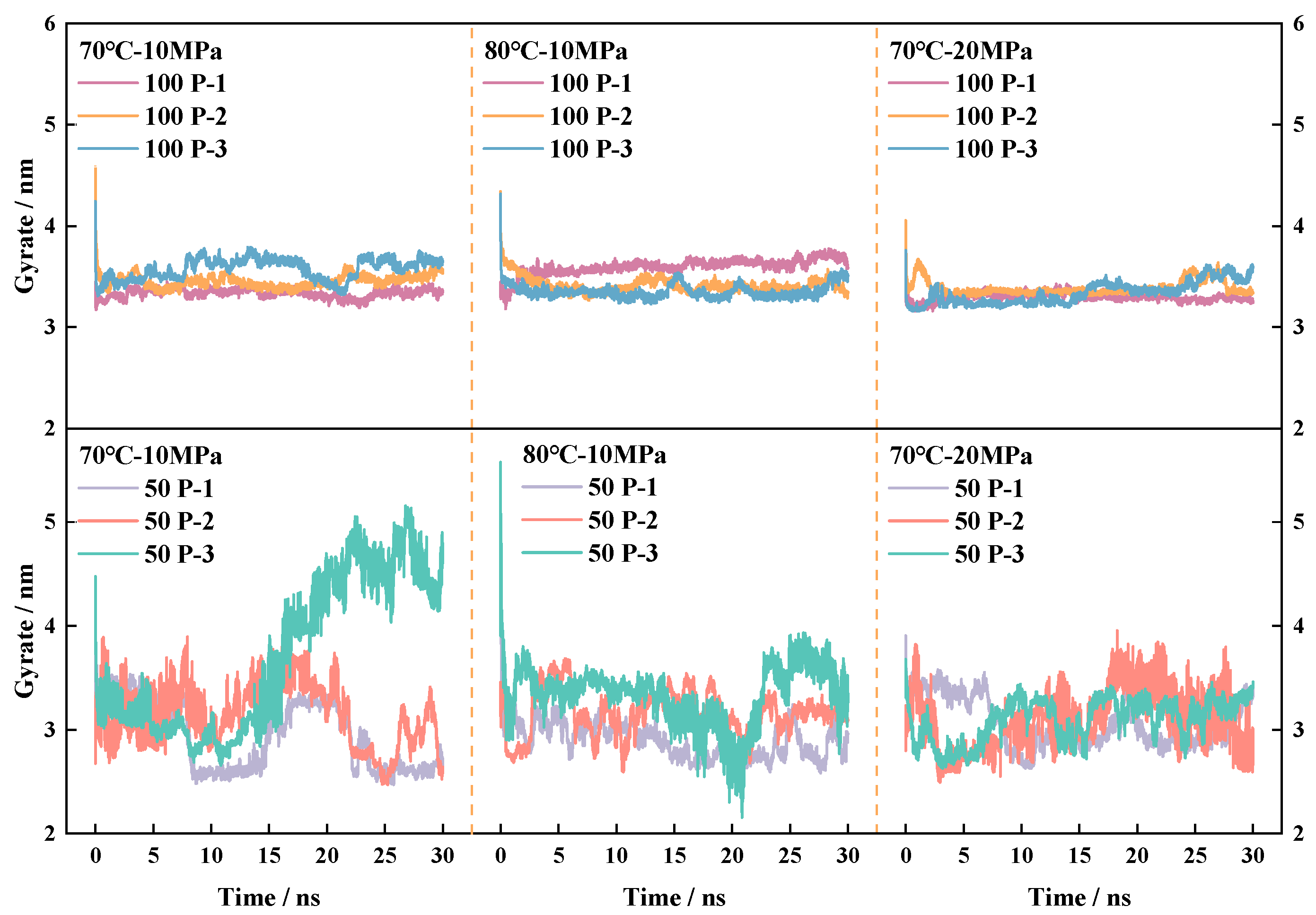

| Name of Polymer | Component Mole Ratio St/MA/VAc | Atomic Number Ratio C/H/O | Total Number of Atoms |
|---|---|---|---|
| P-1 | 1:4:1 | 56:60:28 | 144 |
| P-2 | 1:4:2 | 64:78:44 | 168 |
| P-3 1 | 1:4:2.5 | 68:78:44 | 190 |
| Two-Sided Angle | Molecular Conformation | Initial Drawing of Structures/° | P-1 | P-2 | P-3 |
|---|---|---|---|---|---|
| C-Phenyl | 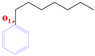 | 65.61 | 109.78 | 63.87 | 120.22 |
| C- Carboxy |  | 128.45 | 94.26 | 100.17 | 126.26 |
| C-Ester |  | 125.24 | 108.29 | 109.31 | 114.67 |
| Environmental Settings | 50 Polymers-CO2 | 100 Polymers-CO2 | CO2 | ||||
|---|---|---|---|---|---|---|---|
| P-1 | P-2 | P-3 | P-1 | P-2 | P-3 | ||
| 70 °C-10 MPa | 483.68 | 490.30 | 499.38 | 554.37 | 553.18 | 640.51 | 464.78 |
| 80 °C-10 MPa | 542.43 | 541.10 | 520.02 | 563.91 | 689.79 | 686.48 | 631.29 |
| 70 °C-15 MPa | 455.40 | 462.68 | 472.00 | 521.06 | 543.80 | 563.15 | 411.76 |
| Theoretical Viscosity | 100 | 50 | ||||
|---|---|---|---|---|---|---|
| Environmental Settings | P-1 | P-2 | P-3 | P-1 | P-2 | P-3 |
| 70 °C-10 MPa | 1.706 | 1.670 | 1.709 | 1.736 | 1.730 | 1.735 |
| 80 °C-10 MPa | 1.704 | 1.708 | 1.709 | 1.735 | 1.736 | 1.736 |
| 70 °C-15 MPa | 1.703 | 1.699 | 1.703 | 1.727 | 1.731 | 1.730 |
| Theoretical Viscosity | 100 | 50 | ||||
|---|---|---|---|---|---|---|
| Environmental Settings | P-1 | P-2 | P-3 | P-1 | P-2 | P-3 |
| 70 °C-10 MPa | 202,189 | 217,560 | 225,079 | 105,411 | 121,834 | 134,987 |
| 80 °C-10 MPa | 208,187 | 208,932 | 213,365 | 106,011 | 116,343 | 129,021 |
| 70 °C-15 MPa | 207,601 | 246,558 | 248,779 | 127,586 | 137,326 | 143,336 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, H.; Pan, Y.; Song, H.; Xing, C.; Bao, R.; Song, K.; Fu, X. Molecular Dynamics Simulation of the Viscosity Enhancement Mechanism of P-n Series Vinyl Acetate Polymer–CO2. Polymers 2024, 16, 3034. https://doi.org/10.3390/polym16213034
Fu H, Pan Y, Song H, Xing C, Bao R, Song K, Fu X. Molecular Dynamics Simulation of the Viscosity Enhancement Mechanism of P-n Series Vinyl Acetate Polymer–CO2. Polymers. 2024; 16(21):3034. https://doi.org/10.3390/polym16213034
Chicago/Turabian StyleFu, Hong, Yiqi Pan, Hanxuan Song, Changtong Xing, Runfei Bao, Kaoping Song, and Xindong Fu. 2024. "Molecular Dynamics Simulation of the Viscosity Enhancement Mechanism of P-n Series Vinyl Acetate Polymer–CO2" Polymers 16, no. 21: 3034. https://doi.org/10.3390/polym16213034
APA StyleFu, H., Pan, Y., Song, H., Xing, C., Bao, R., Song, K., & Fu, X. (2024). Molecular Dynamics Simulation of the Viscosity Enhancement Mechanism of P-n Series Vinyl Acetate Polymer–CO2. Polymers, 16(21), 3034. https://doi.org/10.3390/polym16213034






