The Kinetics of Polymer Brush Growth in the Frame of the Reaction Diffusion Front Formalism
Abstract
1. Introduction
- (i)
- The chain initiation reaction
- (ii)
- The chain propagation reaction
2. The Model and the Simulation Method
- (i)
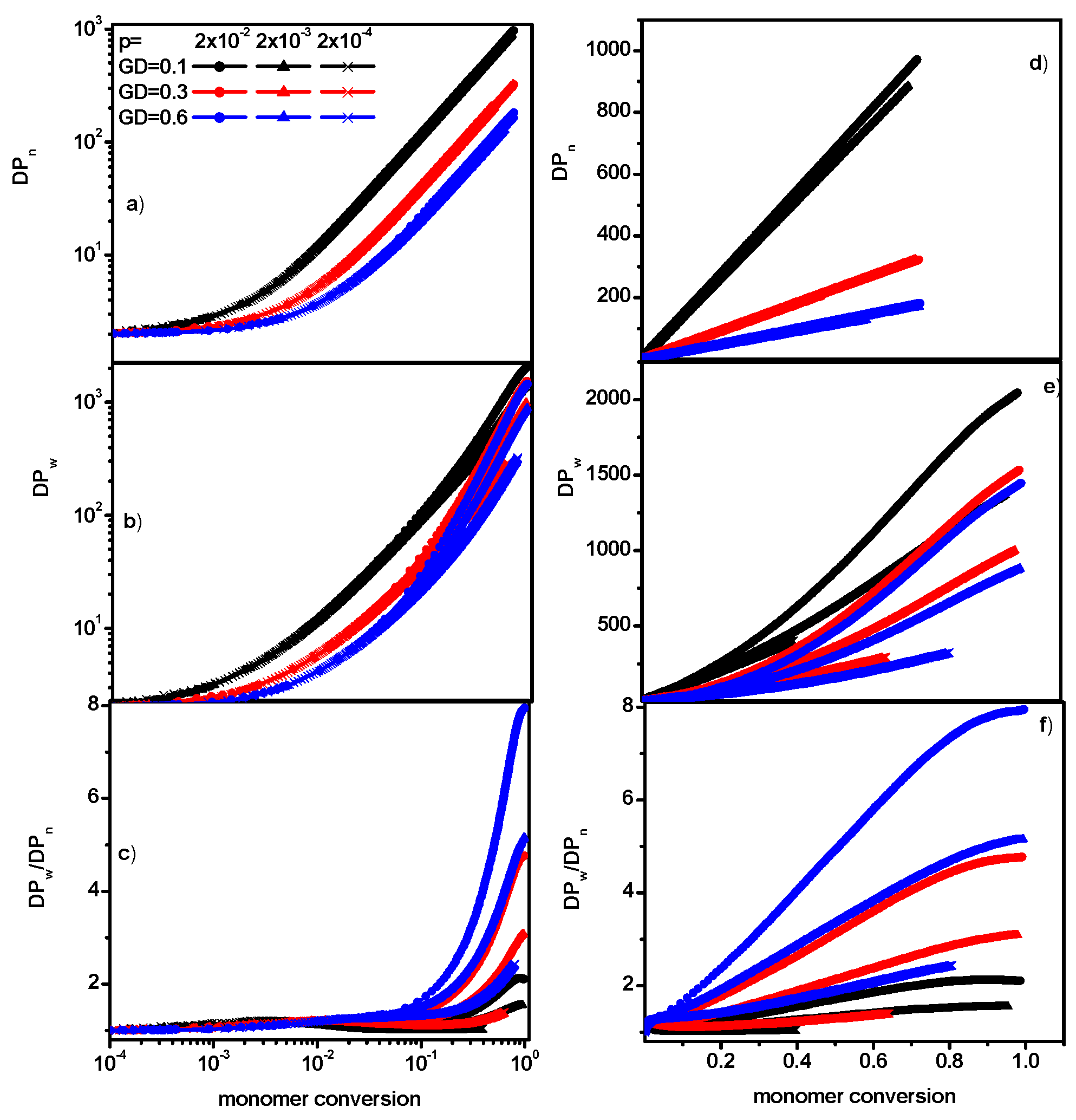
- The averaged degree of polymerization
- (ii)
- The weight-averaged degree of polymerization defined asn
- (iii)
- The distribution of the chain length is characterized by the dispersity D that is defined as the ratio .
- (iv)
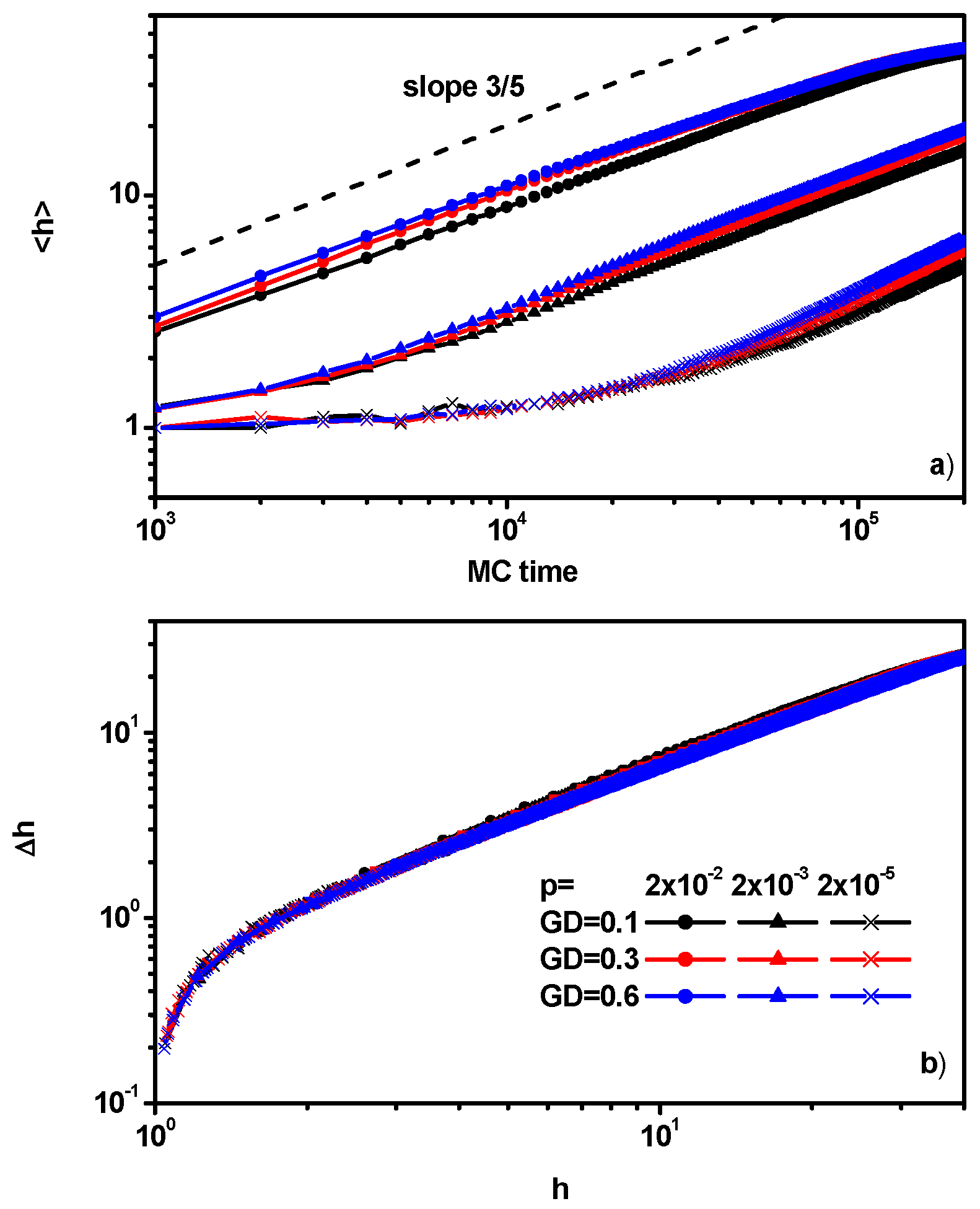
- The parameter that describes the structure of the entire brush is the mean brush thickness <x>, defined as [87]
3. Results and Discussion
3.1. The Properties of the Obtained Brushes
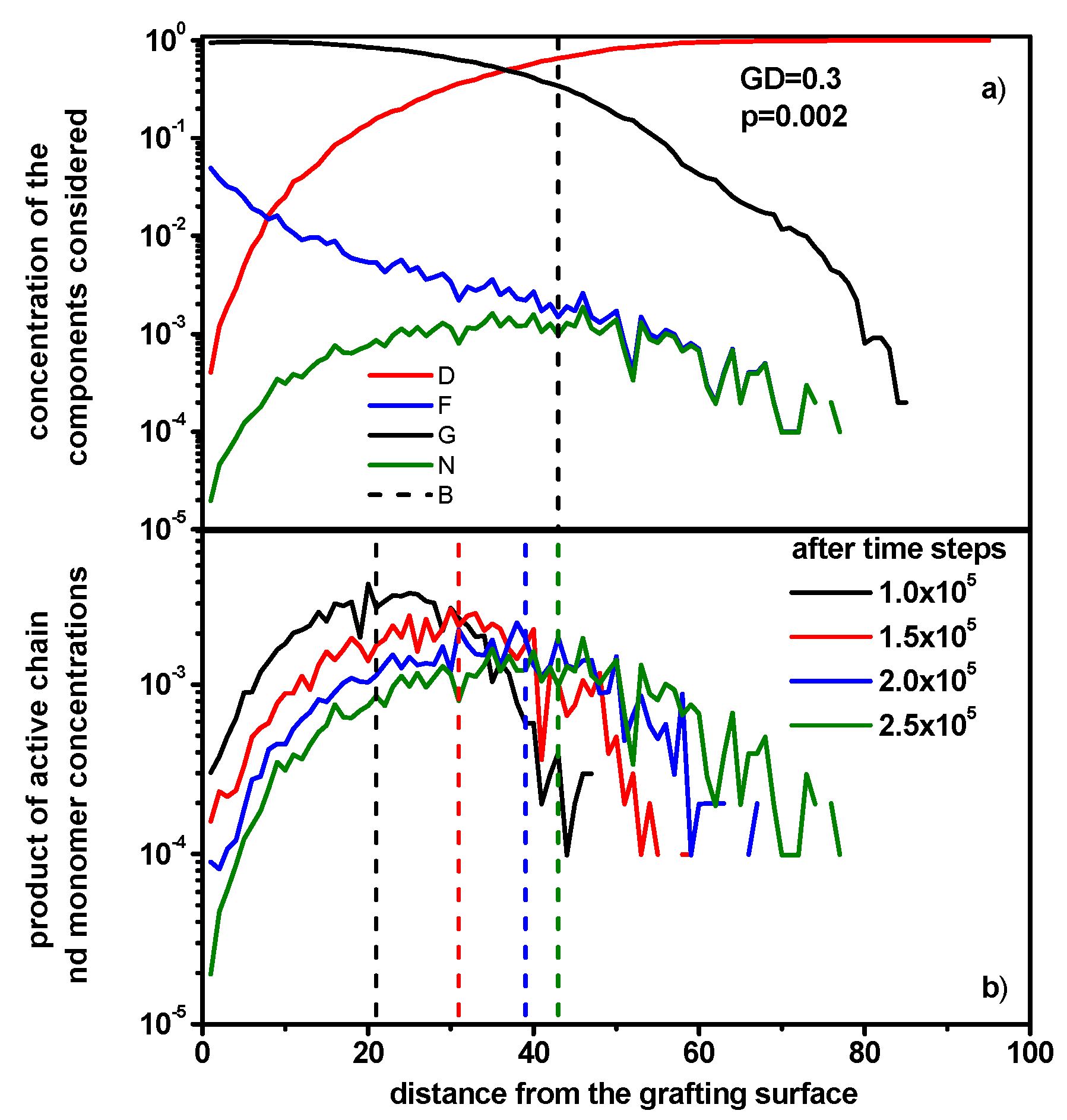
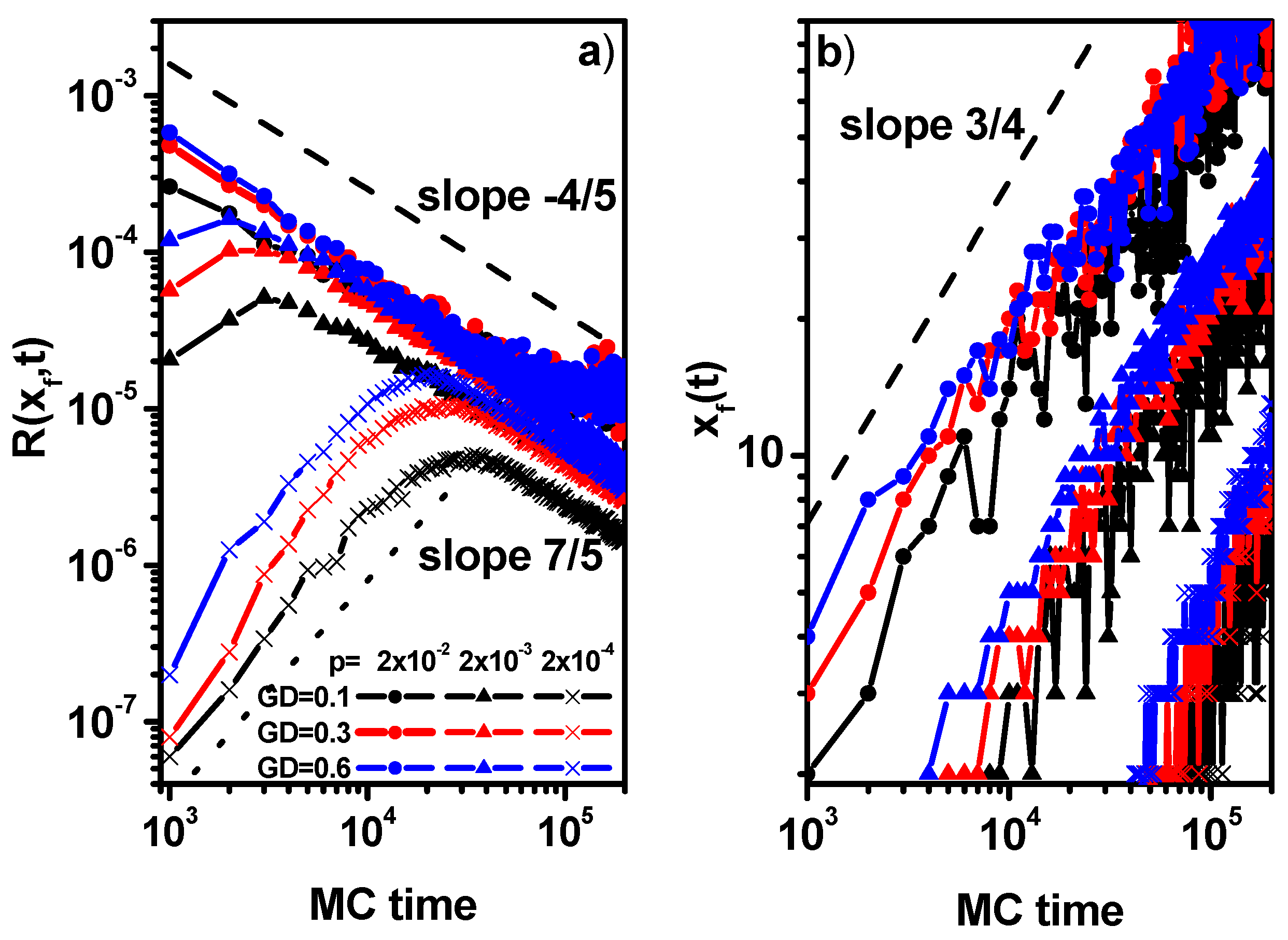
3.2. Reaction–Diffusion Front
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Correction Statement
References
- Teraoka, I. Polymer solutions in confining geometries. Prog. Polym. Sci. 1996, 21, 89–149. [Google Scholar] [CrossRef]
- Chen, W.-L.; Cordero, R.; Tran, H.; Ober, C.K. 50th anniversary perspective: Polymer brushes: Novel surfaces for future materials. Macromolecules 2017, 50, 4089–4113. [Google Scholar] [CrossRef]
- Brittain, W.J.; Minko, S. A structural definition of polymer brushes. J. Polym. Sci. Part A Polym. Chem. 2007, 45, 3505–3512. [Google Scholar] [CrossRef]
- Binder, K.; Milchev, A. Polymer brushes on flat and curved surfaces: How computer simulations can help to test theories and to interpret experiments. J. Polym. Sci. Part B Polym. Phys. 2012, 50, 1515–1555. [Google Scholar] [CrossRef]
- Zhao, B.; Brittain, W.J. Polymer brushes: Surface-immobilized macromolecules. Prog. Polym. Sci. 2000, 25, 677–710. [Google Scholar] [CrossRef]
- Zoppe, J.O.; Ataman, N.C.; Mocny, P.; Wang, J.; Moraes, J.; Klok, H.-A. Surface-initiated controlled radical polymerization: State-of-art, opportunities, and challenges in surface and interface engineering with polymer brushes. Chem. Rev. 2017, 117, 1105–1318. [Google Scholar] [CrossRef]
- Yan, J.; Bockstaller, M.R.; Matyjaszewski, K. Brush-modified materials: Control of molecular architecture, assembly behavior, properties and applications. Prog. Polym. Sci. 2020, 100, 101180. [Google Scholar] [CrossRef]
- Matyjaszewski, K.; Dong, H.; Jakubowski, W.; Pietrasik, J.; Kusumo, A. Grafting from surfaces for “everyone”: ARGET ATRP in the presence of air. Langmuir 2007, 23, 4528–4531. [Google Scholar] [CrossRef]
- Tsuji, Y.; Ohno, K.; Yamamoto, S.; Goto, A.; Fukuda, T. Structure and properties of high-density polymer brushes prepared by surface-initiated living radical polymerization. Adv. Polym. Sci. 2006, 197, 1–45. [Google Scholar]
- Khabibullin, A.; Mastan, E.; Matyjaszewski, K.; Zhu, S. Surface-initiated atom transfer radical polymerization. Adv. Polym. Sci. 2016, 270, 29–76. [Google Scholar]
- Milchev, A.; Wittmer, J.P.; Landau, D.P. Formation and equilibrium properties of living polymer brushes. J. Chem. Phys. 2000, 112, 1606–1615. [Google Scholar] [CrossRef]
- Binder, K. Scaling concepts for polymer brushes and their test with computer simulation. Eur. Phys. J. E 2002, 9, 293–298. [Google Scholar] [CrossRef] [PubMed]
- Netz, R.R.; Schick, M. Polymer brushes: From self-consistent field theory to classical theory. Macromolecules 1998, 31, 5105–5122. [Google Scholar] [CrossRef] [PubMed]
- Milner, S.T.; Witten, T.A.; Cates, M.E. Theory of the grafted polymer brush. Macromolecules 1988, 21, 2610–2619. [Google Scholar] [CrossRef]
- Zhulina, E.B.; Borisov, O.V.; Pryamitsyn, V.A.; Birshtein, T.M. Coil globule type transitions in polymers. 1. Collapse of layers of grafted polymer-chains. Macromolecules 1991, 24, 140–149. [Google Scholar] [CrossRef]
- Wittmer, J.; Johner, A.; Joanny, J.F.; Binder, K. Some dynamic properties of grafted polymer layers. Colloids Surf. A 1994, 86, 85–89. [Google Scholar] [CrossRef]
- de Vos, W.M.; Leermakers, F.A.M. Modeling the structure of a polydisperse polymer brush. Polymer 2009, 50, 305–316. [Google Scholar] [CrossRef]
- Matsen, M.W. Field theoretic approach for block polymer melts: SCFT and FTS. J. Chem. Phys. 2020, 152, 110901. [Google Scholar] [CrossRef]
- Milner, S.T. Polymer brushes. Science 1991, 251, 905–914. [Google Scholar] [CrossRef]
- Milner, S.T.; Witten, T.A.; Cates, M.E. Effects of polydispersity in the end-grafted polymer brush. Macromolecules 1989, 22, 853–861. [Google Scholar] [CrossRef]
- Reith, D.; Milchev, A.; Virnau, P.; Binder, K. Computer simulation studies of chain dynamics in polymer brushes. Macromolecules 2012, 45, 4381–4393. [Google Scholar] [CrossRef]
- Deng, B.; Palermo, E.F.; Shi, Y. Comparison of chain-growth polymerization in solution versus on surface using reactive coarse-grained simulations. Polymer 2017, 129, 105–118. [Google Scholar] [CrossRef]
- Elliot, I.G.; Kuhl, T.L.; Faller, R. Molecular simulation study of the structure of high density polymer brushes in good solvent. Macromolecules 2010, 43, 9131–9138. [Google Scholar] [CrossRef]
- Murat, M.; Grest, G.S. Structure of a grafted polymer brush: A molecular dynamics simulation. Macromolecules 1989, 22, 4054–4059. [Google Scholar] [CrossRef]
- Malfreyt, P.; Tildesley, D.J. Dissipative Particle Dynamics simulations of grafted polymer chains between two walls. Langmuir 2000, 16, 4732–4740. [Google Scholar] [CrossRef]
- Pakula, T.; Zhulina, E.B. Computer simulations of polymers in thin layers. II. Structure of polymer melt layers consisting of end-to-end grafted chains. J. Chem. Phys. 1991, 95, 4691–4697. [Google Scholar] [CrossRef]
- Zhulina, E.B.; Pakula, T. Structure of dense polymer layers between end-grafting and end-adsorbing walls. Macromolecules 1992, 25, 754–758. [Google Scholar] [CrossRef]
- Kuznetsov, D.V.; Balazs, A.C. Phase behavior of end-functionalized polymers confined between two surfaces. J. Chem. Phys. 2000, 113, 2479–2483. [Google Scholar] [CrossRef]
- Lai, P.Y.; Binder, K. Structure and dynamics of grafted polymer layers—A Monte Carlo simulation. J. Chem. Phys. 1991, 95, 9288–9299. [Google Scholar] [CrossRef]
- Lai, P.Y.; Binder, K. Structure and dynamics of polymer brushes near the theta point—A Monte Carlo simulation. J. Chem. Phys. 1992, 97, 586–595. [Google Scholar] [CrossRef]
- Stadler, C.; Schmid, F. Phase behavior of grafted chain molecules: Influence of head size and chain length. J. Chem. Phys. 1999, 110, 9697–9705. [Google Scholar] [CrossRef]
- Stadler, C.; Lange, H.; Schmid, F. Short grafted chains: Monte Carlo simulations of a model for monolayers of amphiphiles. Phys. Rev. E 1999, 59, 4248–4257. [Google Scholar] [CrossRef][Green Version]
- Huang, J.; Jiang, W.; Han, S. Dynamic Monte Carlo simulation on the polymer chain with one end grafted on a flat surface. Macromol. Theory Simul. 2001, 10, 339–342. [Google Scholar] [CrossRef]
- Polanowski, P.; Hałagan, K.; Pietrasik, J.; Jeszka, J.K.; Matyjaszewski, K. Growth of polymer brushes by “grafting from” via ATRP—Monte Carlo simulations. Polymer 2017, 130, 267–279. [Google Scholar] [CrossRef]
- Genzer, J. In silico polymerization: Computer simulation of controlled radical polymerization in bulk and on flat surfaces. Macromolecules 2006, 39, 7157–7169. [Google Scholar] [CrossRef]
- Turgman-Cohen, S.; Genzer, J. Computer simulation of controlled radical polymerization: Effect of chain confinement due to initiator grafting density and solvent quality in “grafting from” method. Macromolecules 2010, 43, 9567–9577. [Google Scholar] [CrossRef]
- Turgman-Cohen, S.; Genzer, J. Computer simulation of concurrent bulk- and surface initiated living polymerization. Macromolecules 2012, 45, 2128–2137. [Google Scholar] [CrossRef]
- Jalili, K.; Abbasi, F.; Milchev, A. Dynamic compression of in situ grown living polymer brush: Simulation and experiment. Macromolecules 2012, 45, 9827–9840. [Google Scholar] [CrossRef]
- Shrivastava, S.; Saha, S.; Singh, A. Dissipative particle dynamics simulation study on ATRP-brush modification of variably shaped surfaces and biopolymer adsorption. Phys. Chem. Chem. Phys. 2022, 24, 17986–18003. [Google Scholar] [CrossRef]
- Tang, Y.; Liu, Y.; Zhang, D.; Zheng, J. Perspectives on theoretical models and molecular simulations of polymer brushes. Langmuir 2024, 40, 1487–1502. [Google Scholar] [CrossRef]
- Hałagan, K.; Banaszak, M.; Jung, J.; Polanowski, P.; Sikorski, A. Dynamics of opposing polymer brushes. A computer simulation study. Polymers 2021, 13, 2758. [Google Scholar] [CrossRef] [PubMed]
- Hałagan, K.; Banaszak, M.; Jung, J.; Polanowski, P.; Sikorski, A. Polymerization and structure of opposing polymer brushes studied by computer simulation. Polymers 2021, 13, 4294. [Google Scholar] [CrossRef] [PubMed]
- Avnir, D.; Kagan, M. Spatial structures generated by chemical reactions at interfaces. Nature 1984, 307, 717–720. [Google Scholar] [CrossRef]
- Dee, G.T. Patterns produced by precipitation at a moving reaction front. Phys. Rev. Lett. 1986, 57, 275–278. [Google Scholar] [CrossRef] [PubMed]
- Henisch, H.K. Periodic Precipitation; Pergamon: Oxford, UK, 1991. [Google Scholar]
- Rice, S.A. Diffusion Limited Reactions; Elsevier: Amsterdam, The Netherlands, 1985. [Google Scholar]
- Ben Avraham, D.; Havlin, S. Diffusion and Reactions in Fractals and Disordered Systems; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Galfi, L.; Racz, Z. Properties of the reaction front in an A + B → C type reaction-diffusion process. Phys. Rev. A 1988, 38, 3151–3154. [Google Scholar] [CrossRef] [PubMed]
- Taitelbaum, H.; Vilensky, B.; Lin, A.L.; Yen, A.; Koo, Y.L.; Kopelman, R. Competing reactions with initially separated components. Phys. Rev. Lett. 1996, 77, 1640–1643. [Google Scholar] [CrossRef]
- Yen, A.; Lin, A.L.; Koo, Y.L.; Vilensky, B.; Taitelbaum, H.; Kopelman, R. Spatiotemporal patterns and nonclassical kinetics of competing elementary reactions: Chromium complex formation with xylenol orange in a capillary. J. Phys. Chem. 1997, 101, 2819–2837. [Google Scholar] [CrossRef]
- Yen, A.; Kopelman, R. Experimental study of a ternary A + 2B → C reaction-diffusion system with a propagating reaction front: Scaling exponents. Phys. Rev. E 1997, 56, 3694–3696. [Google Scholar] [CrossRef]
- Koza, Z. The long-time behavior of initially separated A + B → 0 reaction-diffusion systems with arbitrary diffusion constants. J. Stat. Phys. 1996, 85, 179–191. [Google Scholar] [CrossRef]
- Havlin, S.; Araujo, M.; Larralde, H.; Shehter, A.; Stanley, H.E. Anomalous kinetics in A + B → C with initially-separated reactants. Solitons Fractals 1995, 6, 157–169. [Google Scholar] [CrossRef]
- Araujo, M. Scaling of reaction fronts under quenched disorder. Physica A 1995, 219, 239–245. [Google Scholar] [CrossRef]
- Lee, B.P.; Cardy, J. Scaling of reaction zones in the A + B → 0 diffusion-limited reaction. Phys. Rev. E 1994, 50, R3287–R3290. [Google Scholar] [CrossRef]
- Araujo, M.; Larralde, H.; Havlin, S.; Stanley, H.E. Scaling anomalies in reaction front dynamics of confined systems. Phys. Rev. Lett. 1993, 71, 3592–3595. [Google Scholar] [CrossRef] [PubMed]
- Larralde, H.; Araujo, M.; Havlin, S.; Stanley, H.E. Diffusion-reaction kinetics for A + B (static) → C (inert) for one-dimensional systems with initially separated reactants. Phys. Rev. A 1992, 46, R6121–R6123. [Google Scholar] [CrossRef] [PubMed]
- Bazant, M.Z.; Stone, H.A. Asymptotics of reaction-diffusion fronts with one static and one diffusing reactant. Physica D 2000, 147, 95–121. [Google Scholar] [CrossRef]
- Larralde, H.; Araujo, M.; Havlin, S.; Stanley, H.E. Reaction front for A + B → C diffusion-reaction systems with initially separated reactants. Phys. Rev. A 1992, 46, 855–859. [Google Scholar] [CrossRef]
- Cornell, S.; Droz, M.; Chopard, B. Role of fluctuations for inhomogeneous reaction-diffusion phenomena. Phys. Rev. A 1991, 44, 4826–4832. [Google Scholar] [CrossRef]
- Cornell, S.; Droz, M. Steady-state reaction-diffusion front scaling for mA + nB → [inert]. Phys. Rev. Lett. 1993, 70, 3824–3827. [Google Scholar] [CrossRef]
- Krapivsky, P.L. Diffusion-limited annihilation with initially separated reactants. Phys. Rev. E 1995, 51, 4774–4777. [Google Scholar] [CrossRef]
- Taitelbaum, H.; Koza, Z. Anomalous kinetics of reaction-diffusion fronts. Phil. Mag. B 1998, 77, 1389–1400. [Google Scholar] [CrossRef]
- Taitelbaum, H.; Koo, Y.E.L.; Havlin, S.; Kopelman, R.; Weiss, G.H. Exotic behavior of the reaction front in the A + B → C reaction-diffusion system. Phys. Rev. A 1992, 46, 2151–2154. [Google Scholar] [CrossRef] [PubMed]
- Taitelbaum, H.; Koza, Z. Reaction-diffusion processes: Exotic phenomena in simple systems. Physica A 2000, 285, 166–175. [Google Scholar] [CrossRef]
- Taitelbaum, H.; Yen, A.; Kopelman, R.; Havlin, S.; Weiss, G.H. Effects of bias on the kinetics of A + B → C with initially separated reactants. Phys. Rev. E 1996, 54, 5942–5947. [Google Scholar] [CrossRef]
- Howard, M.; Cardy, J. Fluctuation effects and multiscaling of the reaction-diffusion front for A + B → 0. J. Phys. A 1995, 28, 3599–3621. [Google Scholar] [CrossRef]
- Jiang, Z.; Ebner, C. Simulation study of reaction fronts. Phys. Rev. A 1990, 42, 7483–7486. [Google Scholar] [CrossRef]
- Cornell, S.; Droz, M. Exotic reaction fronts in the steady state. Physica D 1997, 103, 348–356. [Google Scholar] [CrossRef]
- Cornell, S.J. Refined simulations of the reaction front for diffusion-limited two-species annihilation in one dimension. Phys. Rev. E 1995, 51, 4055–4064. [Google Scholar] [CrossRef]
- Chopard, B.; Droz, M. Microscopic Study of the properties of the reaction front in an A + B → C reaction-diffusion process. Europhys. Lett. 1991, 15, 459–464. [Google Scholar] [CrossRef]
- Taitelbaum, H.; Havlin, S.; Kiefer, J.E.; Trus, B.; Weiss, G.H. Some properties of the a + b → C reaction-diffusion system with initially separated components. J. Stat. Phys. 1991, 65, 873–891. [Google Scholar] [CrossRef]
- Lemarchand, A.; Lesne, A.; Perera, A.; Moreau, M.; Mareschal, M. Chemical wave front in two dimensions. Phys. Rev. E 1993, 48, 1568–1571. [Google Scholar] [CrossRef]
- Koza, Z.; Taitelbaum, H. Motion of the reaction front in the A + B → C reaction-diffusion system. Phys. Rev. E 1996, 54, R1040–R1043. [Google Scholar] [CrossRef] [PubMed]
- Koza, Z.; Taitelbaum, H. Reaction-diffusion front in a system with strong quenched disorder. Phys. Rev. E 1997, 56, 6387–6392. [Google Scholar] [CrossRef]
- Polanowski, P.; Koza, Z. Reaction-diffusion fronts in system with concentration dependent diffusivities. Phys. Rev. E 2006, 74, 036103. [Google Scholar] [CrossRef] [PubMed]
- Pakula, T. Simulation on the completely occupied lattices. In Simulation Methods for Polymers; Kotelyanskii, M., Theodorou, D.N., Eds.; Marcel Dekker: New York, NY, USA; Basel, Switzerland, 2004. [Google Scholar]
- Polanowski, P.; Sikorski, A. Simulation of diffusion in a crowded environment. Soft Matter 2014, 10, 3597–3607. [Google Scholar] [CrossRef]
- Pakula, T. Collective dynamics in simple supercooled and polymer liquids. J. Mol. Liq. 2000, 86, 109–121. [Google Scholar] [CrossRef]
- Polanowski, P.; Pakula, T. Studies of polymer conformation and dynamics in two dimensions using simulations based on the Dynamic Lattice Liquid (DLL) model. J. Chem. Phys. 2002, 117, 4022–4029. [Google Scholar] [CrossRef]
- Polanowski, P.; Sikorski, A. The concept of cooperative dynamics in simulations of soft matter. Front. Phys. 2020, 8, 607480. [Google Scholar] [CrossRef]
- Polanowski, P.; Pakula, T. Studies of mobility, interdiffusion, and self-diffusion in two-component mixtures using the dynamic lattice liquid model. J. Chem. Phys. 2003, 118, 11139–11146. [Google Scholar] [CrossRef]
- Polanowski, P.; Pakula, T. Simulation of polymer–polymer interdiffusion using the dynamic lattice liquid model. J. Chem. Phys. 2004, 120, 6306–6311. [Google Scholar] [CrossRef]
- Polanowski, P.; Jeszka, J.K.; Matyjaszewski, K. Polymer brush relaxation during and after polymerization—Monte Carlo simulation study. Polymer 2019, 173, 190–196. [Google Scholar] [CrossRef]
- Polanowski, P.; Jeszka, J.K.; Matyjaszewski, K. Polymer brushes in pores by ATRP: Monte Carlo simulations. Polymer 2020, 211, 123124. [Google Scholar] [CrossRef]
- Polanowski, P.; Sikorski, A. The influence of constraints on gelation in a controlling/living copolymerization process. Int. J. Mol. Sci. 2023, 24, 2701. [Google Scholar] [CrossRef] [PubMed]
- Nickel, B.G. One-parameter recursion model for flexible-chain polymers. Macromolecules 1991, 24, 1358–1366. [Google Scholar] [CrossRef]
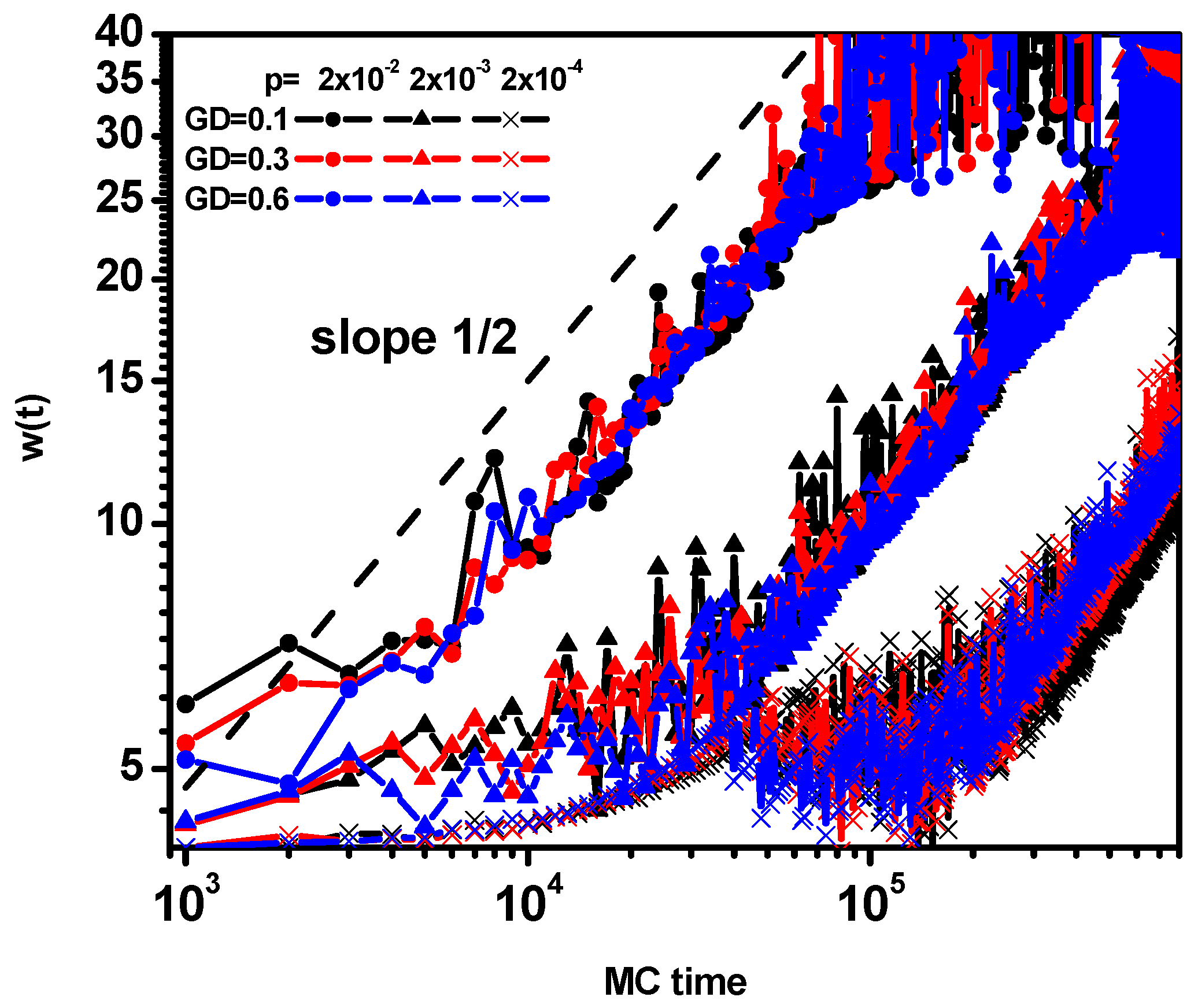
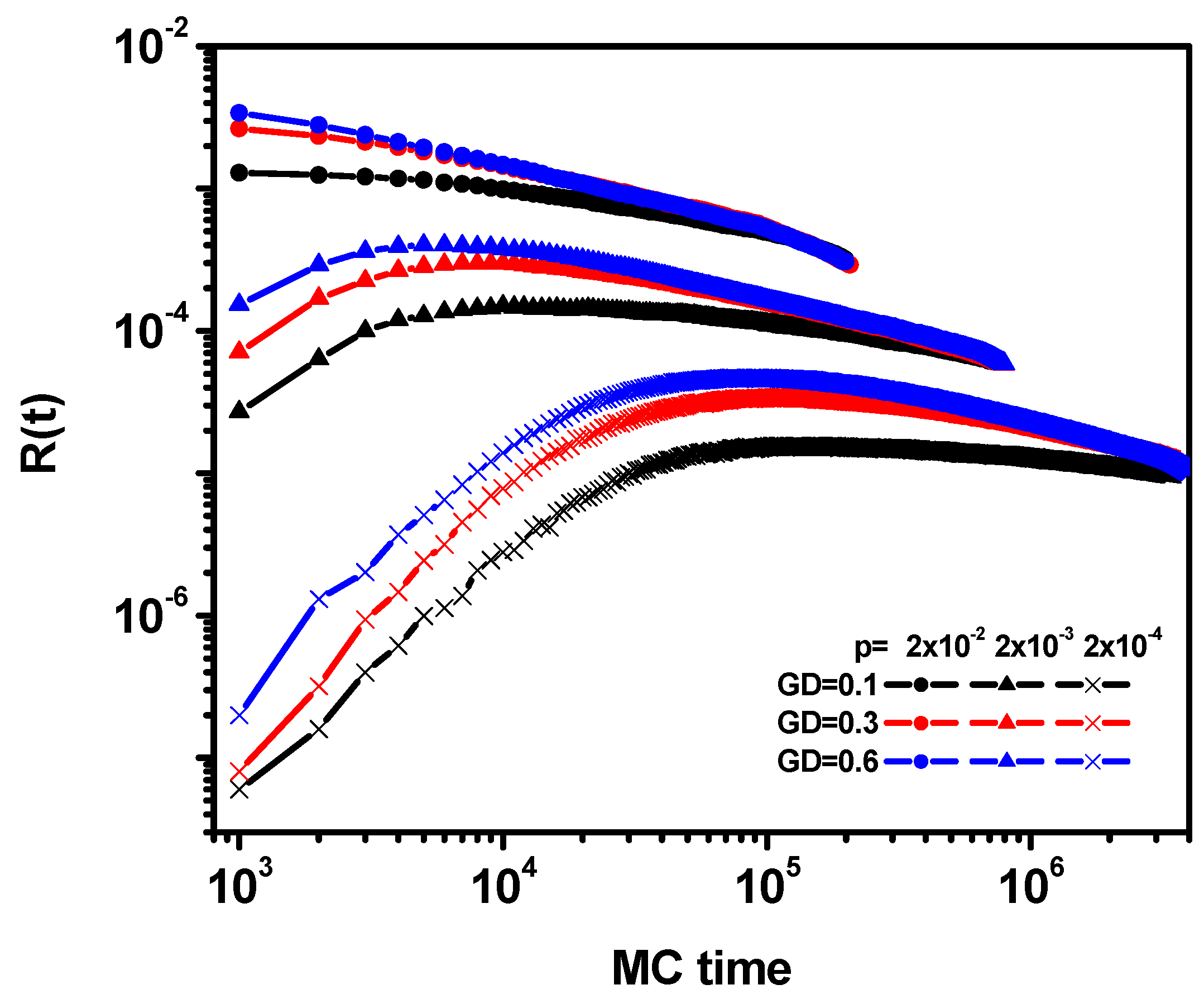
| Quantity | Short-Time Behavior | Long-Time Behavior |
|---|---|---|
| R(t) | t1/2 | t−1/2 |
| W(t) | t1/2 | t1/6 |
| R(xf, t) | const | t−2/3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Polanowski, P.; Sikorski, A. The Kinetics of Polymer Brush Growth in the Frame of the Reaction Diffusion Front Formalism. Polymers 2024, 16, 2963. https://doi.org/10.3390/polym16212963
Polanowski P, Sikorski A. The Kinetics of Polymer Brush Growth in the Frame of the Reaction Diffusion Front Formalism. Polymers. 2024; 16(21):2963. https://doi.org/10.3390/polym16212963
Chicago/Turabian StylePolanowski, Piotr, and Andrzej Sikorski. 2024. "The Kinetics of Polymer Brush Growth in the Frame of the Reaction Diffusion Front Formalism" Polymers 16, no. 21: 2963. https://doi.org/10.3390/polym16212963
APA StylePolanowski, P., & Sikorski, A. (2024). The Kinetics of Polymer Brush Growth in the Frame of the Reaction Diffusion Front Formalism. Polymers, 16(21), 2963. https://doi.org/10.3390/polym16212963







