Classification of the Crosslink Density Level of Para Rubber Thick Film of Medical Glove by Using Near-Infrared Spectral Data
Abstract
1. Introduction
2. Materials and Methods
2.1. Sample Preparation
2.2. NIR Spectroscopy
2.3. Toluene Swelling
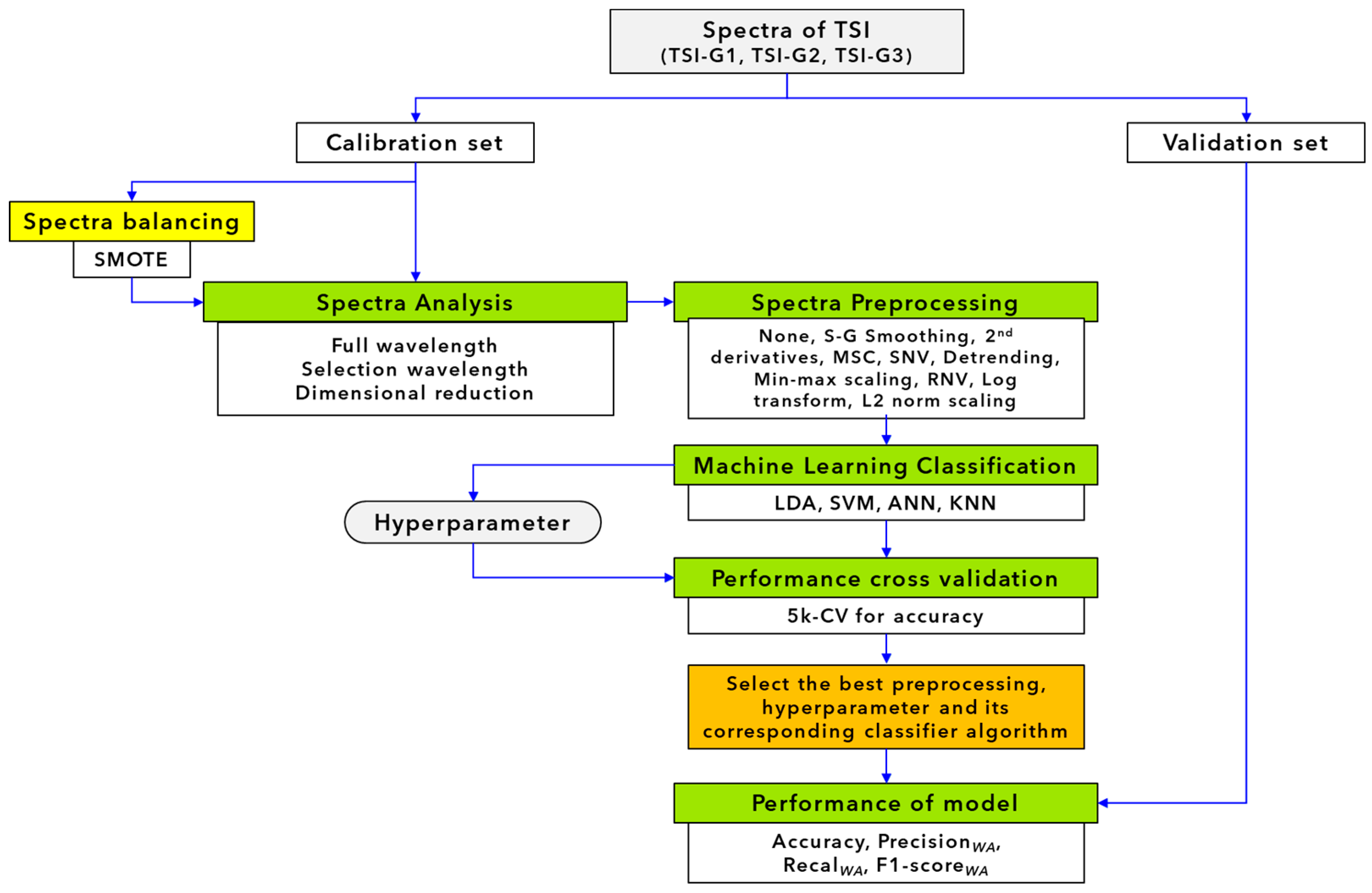
2.4. Near Infrared Spectroscopy Classification Modelling
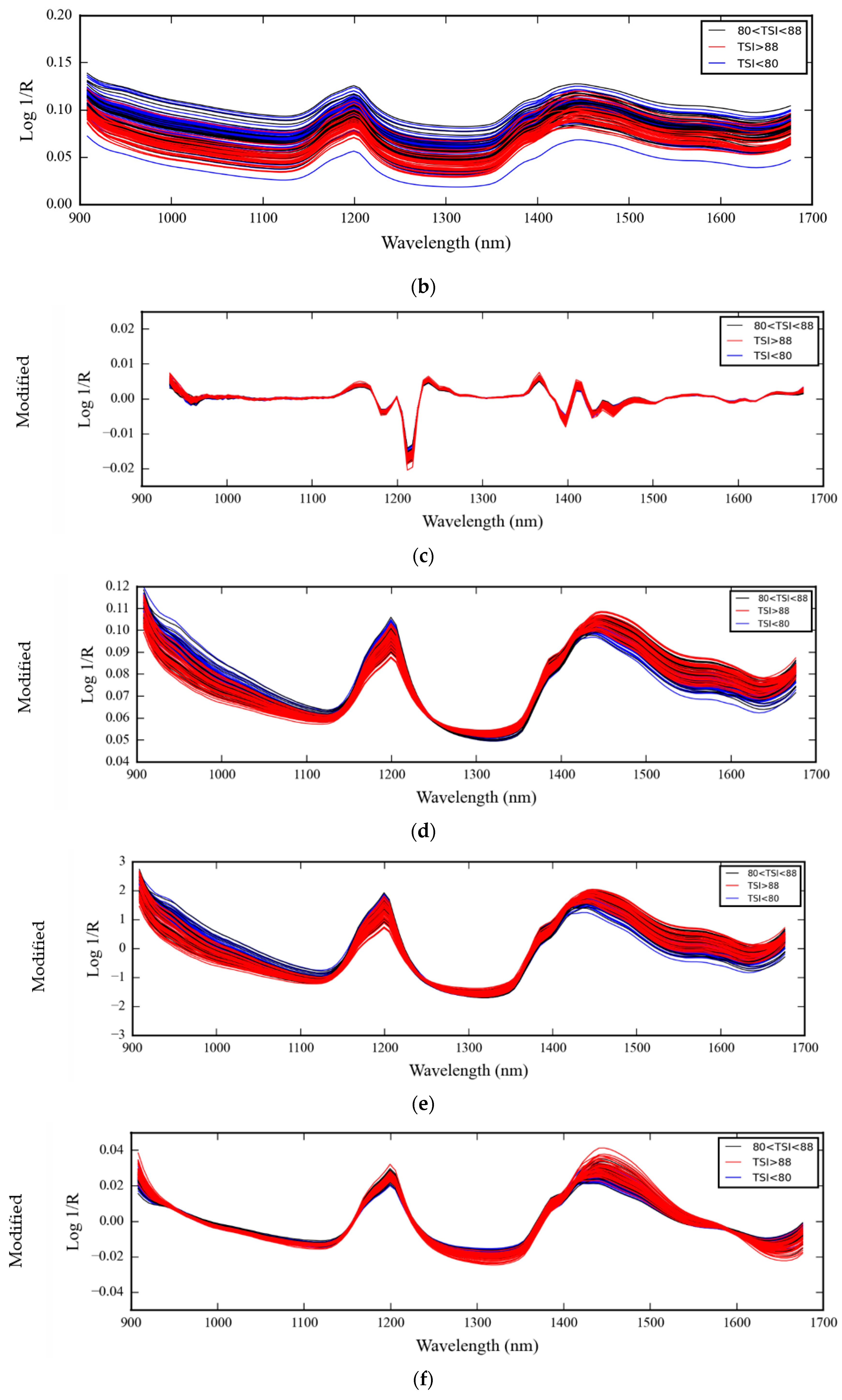
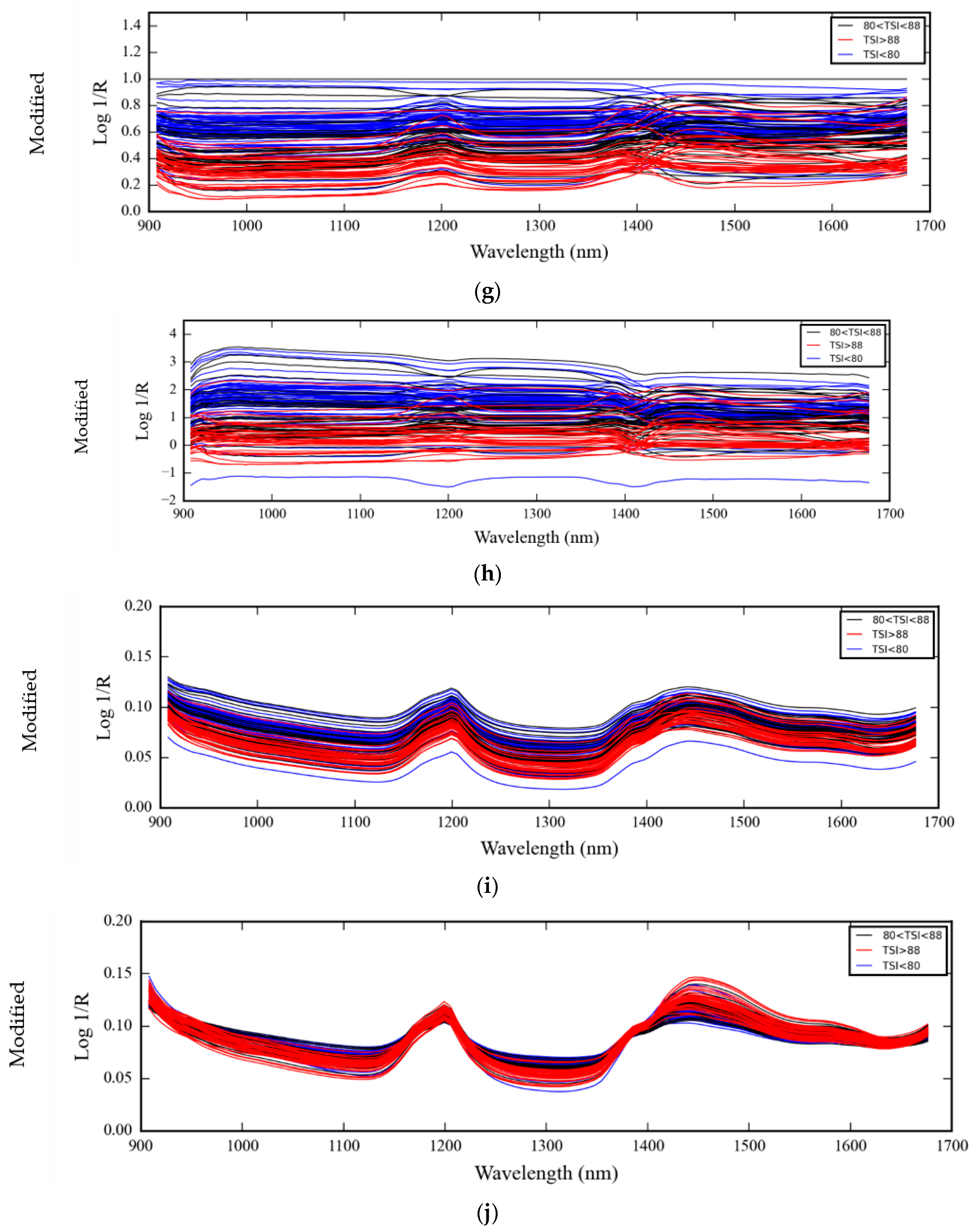
2.4.1. Spectral Pretreatment
2.4.2. Classification Analysis
2.5. Classification Model Performance Determination
2.6. Validation by Unknown Real Sample Set form Factories
3. Results
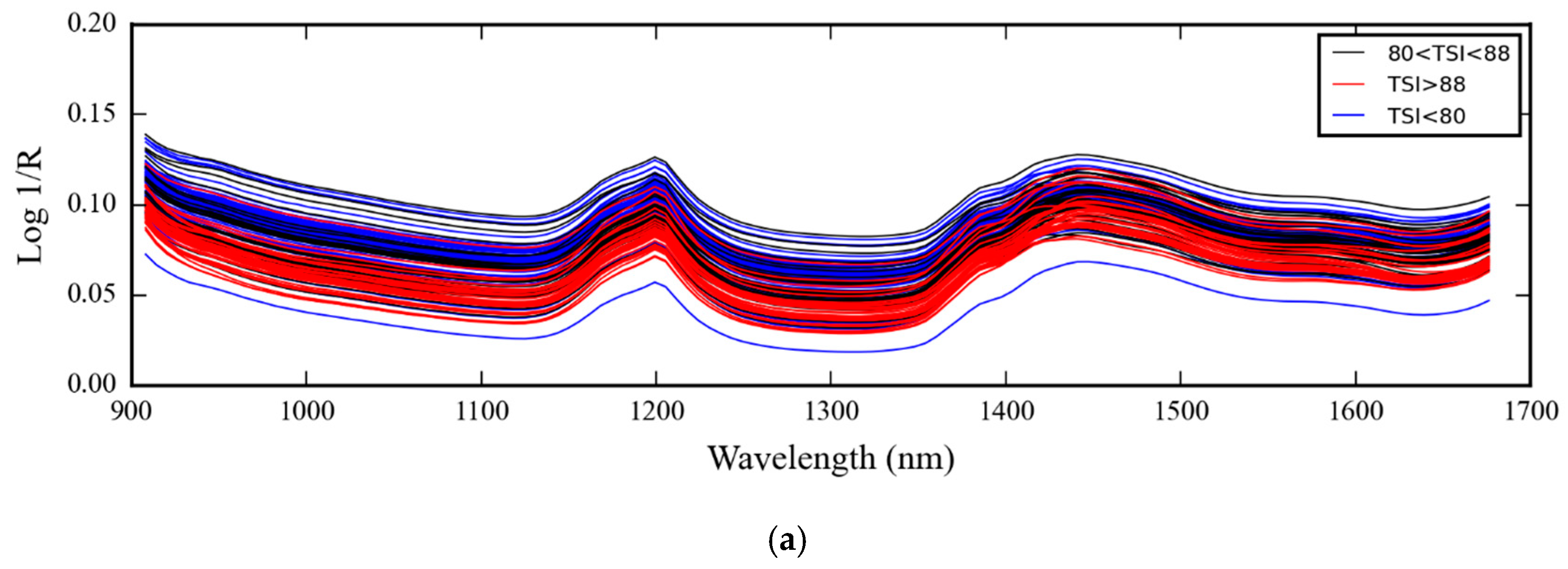
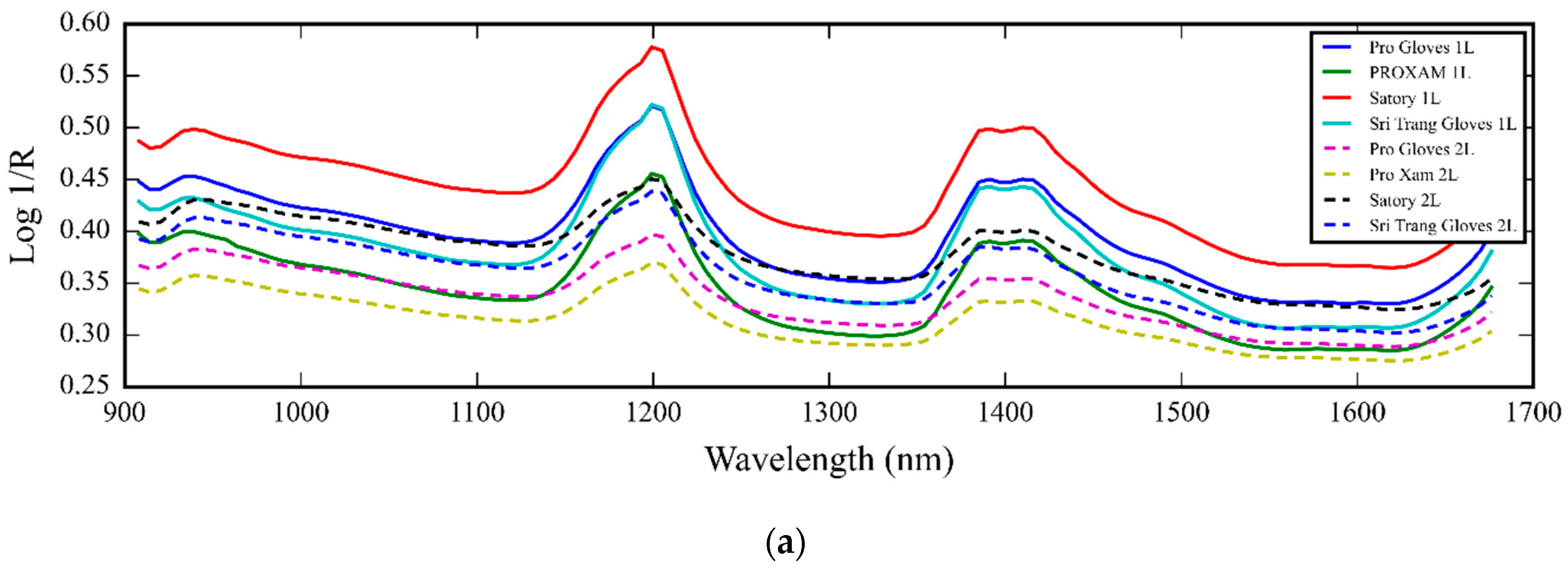
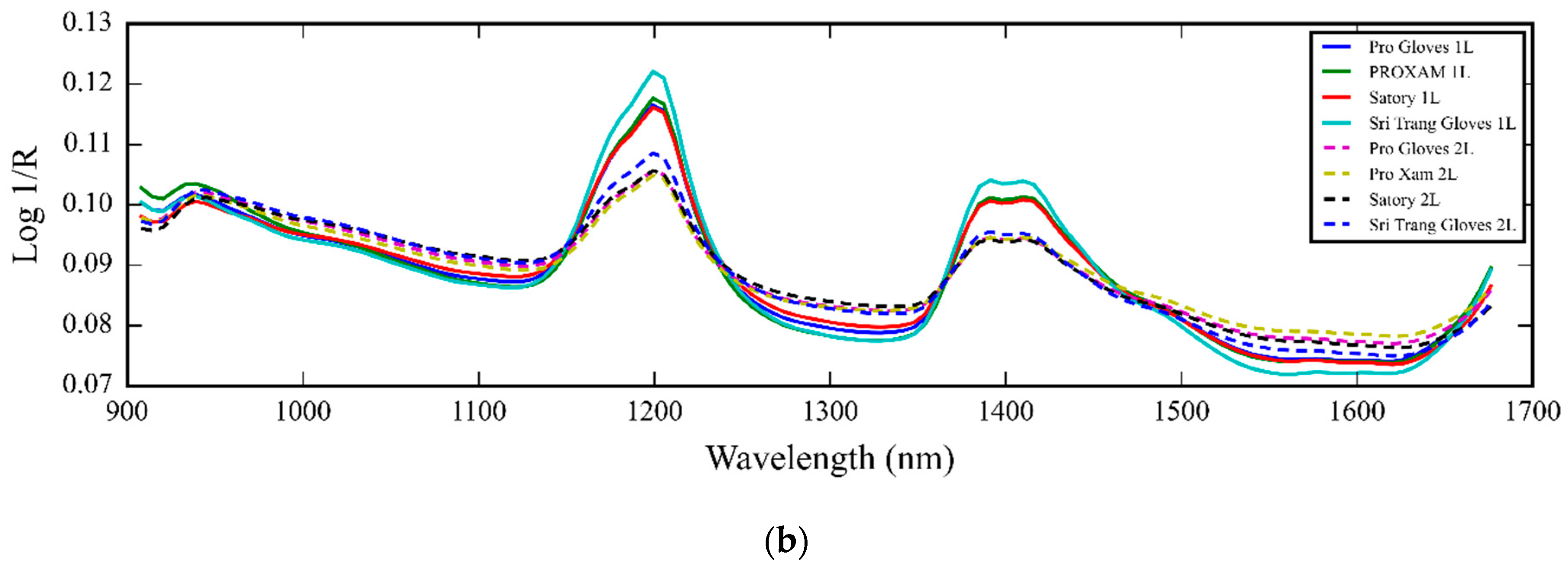
3.1. NIR Spectra of Medical Glove Samples Measured by MicroNIR Spectrometer
3.2. Statistics of Toluene Swell Index of Thick Film Samples for Modelling
3.3. Performance of Classification Models
3.3.1. Full Spectra
3.3.2. Selective Spectra by k-Best and GA Method
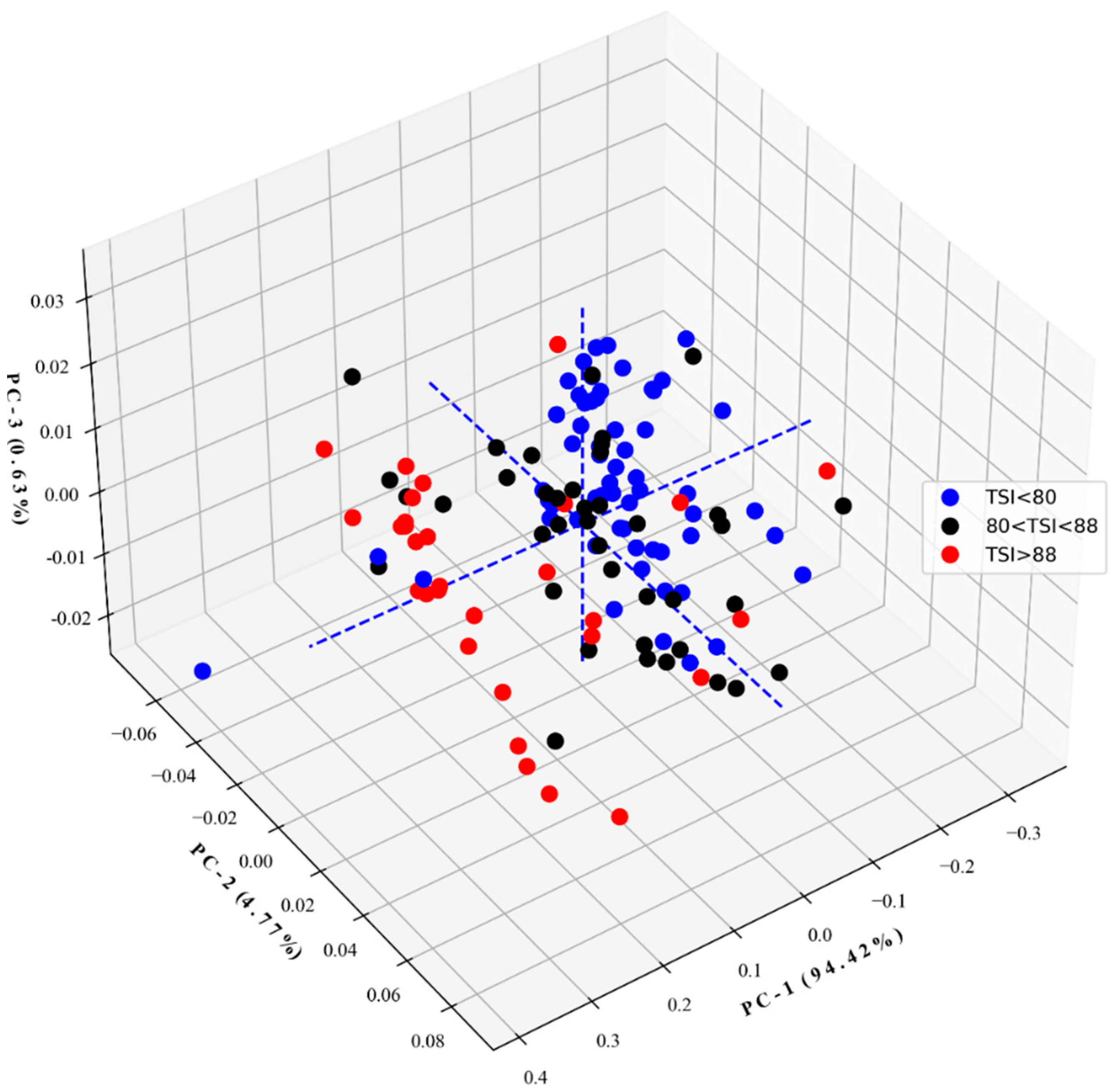
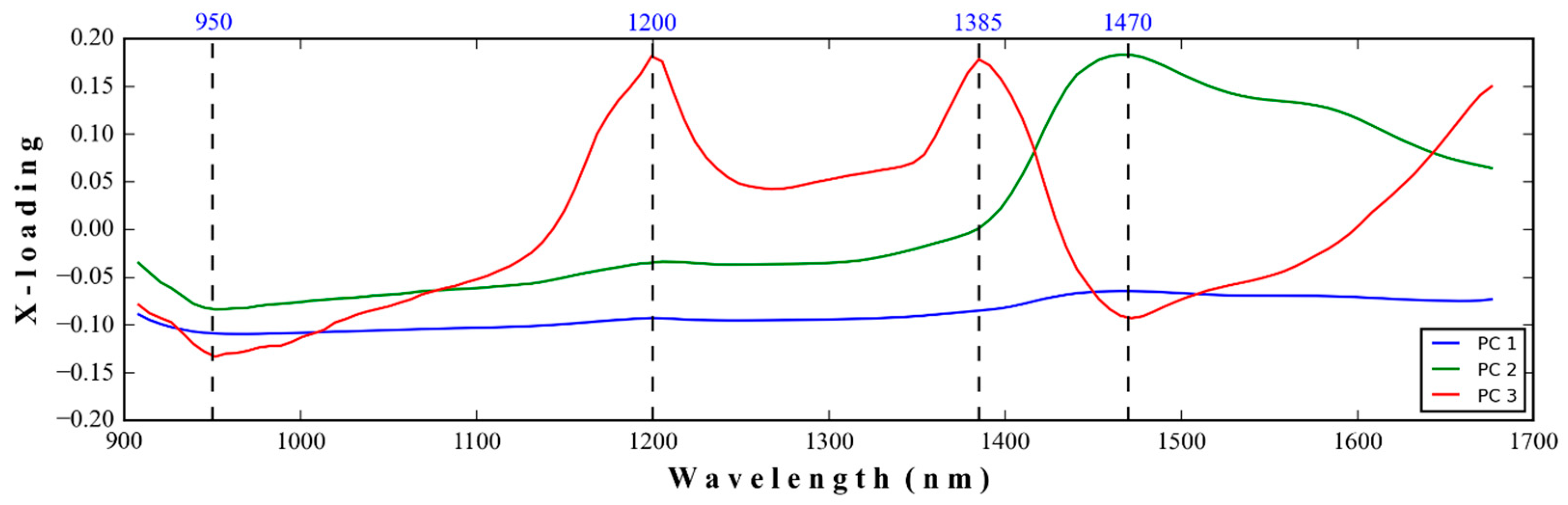
3.3.3. Dimensional Reduction by PCA
3.3.4. Validation Result by Unknown Real Sample Set from Factories
4. Discussion
4.1. NIR Spectra of Medical Glove Samples Measured by MicroNIR Spectrometer
4.2. Statistics of Toluene Swell Index of Thick Film Samples for Modelling
4.3. Performance of Classification Models
4.3.1. Full Spectra
4.3.2. Selective Wavelengths by k-Best and GA Method
4.3.3. Dimensional Reduction by PCA
4.4. Effect of Sample Number
4.5. Effect of SMOTE
4.6. The Merit of This Study
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- US Food and Drug Administration. Medical Device Shortages during the COVID-19 Public Health Emergency. Available online: https://www.myast.org/medical-device-shortages-during-covid-19-public-health-emergency (accessed on 25 October 2023).
- ISO 11193-1; International Standard. Single-Use Medical Examination Gloves—Part 1: Specification for Gloves Made from Rubber Latex or Rubber Solution. ISO: London, UK, 2020.
- Lim, C.H.; Sirisomboon, P. Near infrared spectroscopy as an alternative method for rapid evaluation of toluene swell of natural rubber latex and its products. J. Near Infrared Spectrosc. 2018, 26, 159–168. [Google Scholar] [CrossRef]
- Lim, C.H.; Sirisomboon, P. Evaluation of prevulcanisate relaxed modulus of prevulcanised natural rubber latex using Fourier transform near infrared spectroscopy. J. Near Infrared Spectrosc. 2017, 25, 407–415. [Google Scholar] [CrossRef]
- Sirisomboon, P.; Kaewkuptong, A.; Williams, P. Feasibility study on the evaluation of the dry rubber content of field and concentrated latex of Para rubber by diffuse reflectance near infrared spectroscopy. J. Near Infrared Spectrosc. 2013, 21, 149–156. [Google Scholar] [CrossRef]
- Sirisomboon, P.; Posom, J. On-line measurement of activation energy of ground bamboo using near infrared spectroscopy. Renew. Energy 2019, 133, 480–488. [Google Scholar] [CrossRef]
- Risoluti, R.; Gullifa, G.; Battistini, A.; Materazzi, S. “Lab-on-click” detection of illicit drugs in oral fluids by microNIR–chemometrics. Anal. Chem. 2019, 91, 6435–6439. [Google Scholar] [CrossRef]
- Pakhomova, S.; Zhdanov, I.; Bavel, B.v. Polymer type identification of marine plastic litter using a miniature near-infrared spectrometer (MicroNIR). Appl. Sci. 2020, 10, 8707. [Google Scholar] [CrossRef]
- Yu, D.-x.; Guo, S.; Zhang, X.; Yan, H.; Zhang, Z.-y.; Chen, X.; Chen, J.-y.; Jin, S.-j.; Yang, J.; Duan, J.-a. Rapid detection of adulteration in powder of ginger (Zingiber officinale Roscoe) by FT-NIR spectroscopy combined with chemometrics. Food Chem. X 2022, 15, 100450. [Google Scholar] [CrossRef]
- Torniainen, J.; Afara, I.O.; Prakash, M.; Sarin, J.K.; Stenroth, L.; Töyräs, J. Open-source python module for automated preprocessing of near infrared spectroscopic data. Anal. Chim. Acta 2022, 1108, 1–9. [Google Scholar] [CrossRef]
- Engel, J.; Gerretzen, J.; Szymańska, E.; Jansen, J.J.; Downey, G.; Blanchet, L.; Buydens, L.M.C. Breaking with trends in pre-processing? TrAC Trends in Analytical Chemistry. TrAC Trends Anal. Chem. 2013, 50, 96–106. [Google Scholar] [CrossRef]
- Mallet, A.; Tsenkova, R.; Muncan, J.; Charnier, C.; Latrille, É.; Bendoula, R.; Steyer, J.-P.; Roger, J.-M. Relating Near-Infrared Light Path-Length Modifications to the Water Content of Scattering Media in Near-Infrared Spectroscopy: Toward a New Bouguer–Beer–Lambert Law. Anal. Chem. 2021, 93, 6817–6823. [Google Scholar] [CrossRef]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic Minority Over-sampling Technique. J. Artif. Intell. Res. 2002, 2, 321–357. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learningin Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Chu, X.; Huang, Y.; Yun, Y.-H.; Bian, X. Chemometric Methods in Analytical Spectroscopy Technology; Springer: Singapore, 2022. [Google Scholar]
- Amirruddin, A.D.; Muharam, F.M.; Ismail, M.H.; Tan, N.P.; Ismail, M.F. Synthetic Minority Over-sampling TEchnique (SMOTE) and Logistic Model Tree (LMT)-Adaptive Boosting algorithms for classifying imbalanced datasets of nutrient and chlorophyll sufficiency levels of oil palm (Elaeis guineensis) using spectroradiometers and unmanned aerial vehicles. Comput. Electron. Agric. 2022, 193, 106646. [Google Scholar] [CrossRef]
- Phanomsophon, T.; Jaisue, N.; Worphet, A.; Tawinteung, N.; Shrestha, B.; Posom, J.; Khurnpoon, L.; Sirisomboon, P. Rapid measurement of classification levels of primary macronutrients in durian (Durio zibethinus Murray CV. Mon Thong) leaves using FT-NIR spectrometer and comparing the effect of imbalanced and balanced data for modelling. Measurement 2022, 203, 111975. [Google Scholar] [CrossRef]
- Wang, S.; Liu, S.; Zhang, J.; Che, X.; Yuan, Y.; Wang, Z.; Kong, D. A new method of diesel fuel brands identification: SMOTE oversampling combined with XGBoost ensemble learning. Fuel 2020, 282, 118848. [Google Scholar] [CrossRef]
- Brownlee, J. SMOTE for Imbalanced Classification with Python. Available online: https://machinelearningmastery.com/smote-oversampling-for-imbalanced-classification (accessed on 6 September 2023).
- Walczak, S. Artificial Neural Networks. In Encyclopedia of Physical Science and Technology; Elsevier Science Ltd.: Amsterdam, The Netherlands, 2003. [Google Scholar]
- Mohseni-Dargah, M.; Falahati, Z.; Dabirmanesh, B.; Nasrollahi, P.; Khajeh, K. Machine learning in surface plasmon resonance for environmental monitoring. In Machine Learning in Surface Plasmon Resonance for Environmental Monitoring, in Artificial Intelligence and Data Science in Environmental Sensing; Elsevier Inc.: Amsterdam, The Netherlands, 2022. [Google Scholar]
- Sadiq, R.; Rodriguez, M.J.; Mian, H.R. Empirical Models to Predict Disinfection By-Products (DBPs) in Drinking Water: An Updated Review. In Encyclopedia of Environmental Health (Second Edition), 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2019; pp. 324–338. [Google Scholar]
- Whittingham, H.; Ashenden, S.K. Hit discovery. In The Era of Artificial Intelligence, Machine Learning, and Data Science in the Pharmaceutical Industry; Elsevier Inc.: Amsterdam, The Netherlands, 2021. [Google Scholar]
- Gove, R.; Faytong, J. Machine Learning and Event-Based Software Testing: Classifiers for Identifying Infeasible GUI Event Sequences. In Advances in Computers; Elsevier Inc.: Amsterdam, The Netherlands, 2012; pp. 109–135. [Google Scholar]
- Jeffers, J.; Reinders, J.; Sodani, A. Machine learning. In Intel Xeon Phi Processor High Performance Programming; Elsevier Inc.: Amsterdam, The Netherlands, 2016; pp. 527–548. [Google Scholar]
- Shi, Y.; Yang, K.; Yang, Z.; Zhou, Y. Primer on artificial intelligence. In Mobile Edge Artificial Intelligence; Elsevier Inc.: Amsterdam, The Netherlands, 2021. [Google Scholar]
- Mohanty, N.; Lee-St.john, A.; Manmatha, R.; Rath, T.M. Shape-Based Image Classification and Retrieval. In Handbook of Statistics; Elsevier: Amsterdam, The Netherlands, 2013; pp. 249–267. [Google Scholar]
- Vaibhaw; Sarraf, J.; Pattnaik, P.K. Brain–computer interfaces and their applications. In An Industrial IoT Approach for Pharmaceutical Industry Growth; Elsevier Inc.: Amsterdam, The Netherlands, 2020; pp. 31–54. [Google Scholar]
- The MathWorks Inc. MATLAB Version: 9.13.0 (R2022b). Available online: https://www.mathworks.com (accessed on 15 September 2023).
- Ludwig, B.; Murugan, R.; Parama, V.R.R.; Vohland, M. Accuracy of estimating soil properties with mid-infrared spectroscopy: Implications of different chemometric approaches and software packages related to calibration sample size. Nutr. Manag. Soil Plant Anal. 2019, 83, 1542–1552. [Google Scholar] [CrossRef]
- Cawley, G.C.; Talbot, N.L.C. On over-fitting in model selection and subsequent selection bias in performance evaluation. J. Mach. Learn. Res. 2010, 11, 2079–2107. [Google Scholar]
- Conzen, J.-P. Multivariate calibration. In A Practical Guide for Developing Methods in the Quantitative Analytical Chemistry, 2nd ed.; Bruker Optics: Ettlingen, Germany, 2006. [Google Scholar]
- Blanco, M.; Coello, J.; Iturriaga, H.; Maspoch, S.; Pagès, J. NIR calibration in non-linear systems: Different PLS approaches and artificial neural networks. Chemom. Intell. Lab. Syst. 2000, 50, 75–82. [Google Scholar] [CrossRef]
- Sharabiani, V.R.; Nazarloo, A.S.; Taghinezhad, E.; Veza, I.; Szumny, A.; Figiel, A. Prediction of winter wheat leaf chlorophyll content based on VIS/NIR spectroscopy using ANN and PLSR. Food Sci. Nutr. 2023, 11, 2166–2175. [Google Scholar] [CrossRef]
- Ni, W.; Nørgaard, L.; Mørup, M. Non-linear calibration models for near infrared spectroscopy. Anal. Chim. Acta 2014, 813, 1–14. [Google Scholar] [CrossRef]
- Hao, Y.; Li, X.; Zhang, C. Improving prediction model robustness with virtual sample construction for near-infrared spectra analysis. Anal. Chim. Acta 2023, 1279, 341763. [Google Scholar] [CrossRef] [PubMed]
- Kawahara, S. Discovery of island-nanomatrix structure in natural rubber. Polym. J. 2023, 55, 1007–1021. [Google Scholar] [CrossRef]
- de Lima, D.R.; Vieira, I.R.S.; Rocha, E.B.D.d.; Sousa, A.M.F.d.; Costa, A.C.A.d.; Furtado, C.R.G. Biodegradation of natural rubber latex films by highlighting the crosslinked bond. Ind. Crops Prod. 2023, 204, 117290. [Google Scholar] [CrossRef]
- Sirisomboon, P.; Deeprommit, M.; Suchaiboonsiri, W.; Lertsri, W. Shortwave near infrared spectroscopy for determination of dry rubber content and total solids content of Para rubber (Hevea brasiliensis) latex. J. Near Infrared Spectrosc. 2013, 21, 269–279. [Google Scholar] [CrossRef]
- Maraphum, K.; Wanjantuk, P.; Hanpinitsak, P.; Paisarnsrisomsuk, S.; Lim, C.H.; Posom, J. Fast determination of total solids content (TSC) and dry rubber content (DRC) of para rubber latex using near-infrared spectroscopy. Ind. Crops Prod. 2022, 187, 115507. [Google Scholar] [CrossRef]
- Narongwongwattana, S.; Rittiron, R.; Hock, L.C. Rapid determination of alkalinity (ammonia content) in Para rubber latex using portable and Fourier transform-near infrared spectrometers. J. Near Infrared Spectrosc. 2015, 23, 181–188. [Google Scholar] [CrossRef]
- Sirisomboon, P.; Chowbankrang, R.; Williams, P. Evaluation of apparent viscosity of Para rubber latex by diffuse reflection near-infrared spectroscopy. Appl. Spectrosc. 2012, 66, 595–599. [Google Scholar] [CrossRef]
- Lim, C.H.; Sirisomboon, P. Measurement of cross link densities of prevulcanized natural rubber latex and latex products using low-cost near infrared spectrometer. Ind. Crops Prod. 2021, 159, 113016. [Google Scholar] [CrossRef]
- Amirruddin, A.D.; Muharam, F.M.; Ismail, M.H.; Ismail, M.F.; Tan, N.P.; Karam, D.S. Hyperspectral remote sensing for assessment of chlorophyll sufficiency levels in mature oil palm (Elaeis guineensis) based on frond numbers: Analysis of decision tree and random forest. Comput. Electron. Agric. 2020, 169, 105221. [Google Scholar] [CrossRef]

| Algorithm | Hyperparameter | Range of Tuning |
|---|---|---|
| ANN | Hidden layer size (HLZ) | (3), (4), (5), (10), (11), (12), (16), (19), (20), (100), (3, 2), (5, 4), (100, 100), (4, 3, 2), (100, 100, 100) |
| Activation function (AF) | identity, logistic, tanh, relu | |
| SVM | Pinalty factor (C) | 1–50 |
| Degree (D) | 2, 3, 4 | |
| Gamma (G) | scale, auto | |
| kNN | n-neighbor (n) | 1–20 |
| LDA | n-component | 1–20 |
| Parameter | Meaning | Formula |
|---|---|---|
| Accuracy | the proportion of correct predictions | |
| Precision | Correctly predicting positive outcomes when the model predicts them as positive. | |
| Recall | the model’s capability of predicting positive cases | |
| F1-score | the harmonic means between precision and sensitivity |
| TSI Range (%) | Calibration Set | Prediction Set | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Number of Samples before SMOTE | Number of Samples after SMOTE | True TSI Range (%) | Mean (%) | SD (%) | Number of Samples | True TSI Range (%) | Mean (%) | SD (%) | |
| less than 80 | 42 | 42 | 71.00–79.17 | 75.42 | 2.22 | 17 | 72.92–79.17 | 75.90 | 2.01 |
| 80–88 | 29 | 42 | 80.00–88.00 | 83.39 | 2.67 | 12 | 81.25–88.00 | 84.42 | 2.49 |
| more than 88 | 22 | 42 | 89.58–108.00 | 92.46 | 3.92 | 8 | 90.63–98.96 | 93.20 | 3.03 |
| Algorithm (WL) | Pre-Treatment | Hyper-Parameter | Calibration Set | Prediction Set | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Weighted Average | A | Weighted Average | A | |||||||
| P | R | F1 | P | R | F1 | |||||
| ANN (125) | Savitzky–Golay smoothing + RNV | HLZ = (100, 100, 100) AF = Identity | 0.70 | 0.70 | 0.69 | 0.70 | 0.84 | 0.84 | 0.83 | 0.84 |
| SVM (125) | Savitzky–Golay smoothing + RNV | C = 1 D = 2 G = scale | 0.75 | 0.74 | 0.74 | 0.74 | 0.70 | 0.70 | 0.70 | 0.70 |
| kNN (125) | Savitzky–Golay smoothing + log transform | n = 6 | 0.77 | 0.77 | 0.76 | 0.77 | 0.69 | 0.70 | 0.69 | 0.70 |
| LDA (125) | Second derivative | n = 1 | 0.99 | 0.99 | 0.99 | 0.99 | 0.49 | 0.46 | 0.44 | 0.46 |
| Algorithm (WL) | Pre-Treatment | Hyper-Parameter | Calibration Set | Prediction Set | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Weighted Average | A | Weighted Average | A | |||||||
| P | R | F1 | P | R | F1 | |||||
| ANN (125) | Min-max normalization | HLZ = (100) AF = logistic | 0.78 | 0.78 | 0.78 | 0.78 | 0.74 | 0.73 | 0.73 | 0.73 |
| SVM (125) | Savitzky–Golay smoothing + L2 norm scaling | C = 3 D = 2 G = Scale | 0.78 | 0.78 | 0.78 | 0.78 | 0.74 | 0.73 | 0.73 | 0.73 |
| kNN (125) | Savitzky–Golay smoothing + L2 norm scaling | n = 13 | 0.76 | 0.75 | 0.75 | 0.75 | 0.73 | 0.73 | 0.73 | 0.73 |
| LDA (125) | Savitzky–Golay smoothing + L2 norm scaling | n = 1 | 0.99 | 0.99 | 0.99 | 0.99 | 0.45 | 0.43 | 0.43 | 0.43 |
| Selection Method | Algorithm (WL) | Pre-Treatment | Hyper-Parameter | Calibration Set | Prediction Set | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Weighted Average | A | Weighted Average | A | ||||||||
| P | R | F1 | P | R | F1 | ||||||
| k-Best | ANN (41) | Savitzky–Golay smoothing + RNV | HLZ = (100) AF = relu k-best = f_classif | 0.74 | 0.74 | 0.74 | 0.74 | 0.67 | 0.68 | 0.66 | 0.68 |
| SVM (14) | Savitzky–Golay smoothing + RNV | C = 27 D = 2 G = scale k-best = mutual_info_classif | 0.79 | 0.78 | 0.78 | 0.78 | 0.64 | 0.65 | 0.63 | 0.65 | |
| kNN (19) | Savitzky–Golay smoothing + log transform | n = 4 k-best = mutual_info_classif | 0.75 | 0.75 | 0.74 | 0.75 | 0.67 | 0.68 | 0.65 | 0.68 | |
| LDA (15) | Second derivative | n = 1 k-best = f_classif | 0.72 | 0.72 | 0.72 | 0.72 | 0.76 | 0.76 | 0.76 | 0.76 | |
| GA | ANN (60) | Savitzky–Golay smoothing + RNV | HLZ = (10) AF = relu | 0.71 | 0.71 | 0.70 | 0.71 | 0.66 | 0.65 | 0.63 | 0.65 |
| SVM (55) | Savitzky–Golay smoothing + RNV | C = 1 D = 2 G = scale | 0.75 | 0.74 | 0.74 | 0.74 | 0.70 | 0.70 | 0.70 | 0.70 | |
| kNN (62) | Savitzky–Golay smoothing + log transform | n = 6 | 0.76 | 0.76 | 0.75 | 0.76 | 0.69 | 0.70 | 0.69 | 0.70 | |
| LDA (60) | Second derivative | n = 1 | 0.91 | 0.91 | 0.91 | 0.91 | 0.64 | 0.65 | 0.64 | 0.65 | |
| Selection Method | Algorithm (WL) | Pre-Treatment | Hyper-Parameter | Calibration Set | Prediction Set | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Weighted Average | A | Weighted Average | A | ||||||||
| P | R | F1 | P | R | F1 | ||||||
| k-best | ANN (22) | Min-max scaling | HLZ = (100, 100) AF = relu k-best = chi2 | 0.75 | 0.75 | 0.74 | 0.75 | 0.70 | 0.70 | 0.70 | 0.70 |
| SVM (43) | Savitzky–Golay smoothing + L2 norm scaling | C = 1, D = 2 G = Scale k-best = mutual_info_classif | 0.80 | 0.79 | 0.79 | 0.79 | 0.68 | 0.65 | 0.66 | 0.65 | |
| kNN (1) | Savitzky–Golay smoothing + L2 norm scaling | n = 7 k-best = chi2 | 0.80 | 0.79 | 0.79 | 0.80 | 0.68 | 0.65 | 0.66 | 0.68 | |
| LDA (2) | Savitzky–Golay smoothing + L2 norm scaling | n = 1 k-best = mutual_info_classif | 0.75 | 0.75 | 0.75 | 0.75 | 0.70 | 0.70 | 0.70 | 0.70 | |
| GA | ANN (61) | Min-max scaling | HLZ = (100, 100) AF = relu | 0.80 | 0.80 | 0.80 | 0.80 | 0.74 | 0.73 | 0.73 | 0.73 |
| SVM (69) | Savitzky–Golay smoothing + L2 norm scaling | C = 2, D = 2 G = Scale | 0.78 | 0.78 | 0.78 | 0.78 | 0.73 | 0.70 | 0.71 | 0.70 | |
| kNN (63) | Savitzky–Golay smoothing + L2 norm scaling | n = 19 | 0.75 | 0.75 | 0.75 | 0.75 | 0.72 | 0.73 | 0.72 | 0.73 | |
| LDA (74) | Savitzky–Golay smoothing + L2 norm scaling | n = 1 | 0.99 | 0.99 | 0.99 | 0.99 | 0.57 | 0.57 | 0.57 | 0.57 | |
| Algorithm | Pretreatment | Hyper- Parameter | Calibration Set | Prediction Set | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Weighted Average | A | Weighted Average | A | |||||||
| P | R | F1 | P | R | F1 | |||||
| 10PC-ANN | Savitzky–Golay smoothing + Mean scaling | HLZ = (100) AF = relu | 0.74 | 0.74 | 0.74 | 0.74 | 0.75 | 0.76 | 0.75 | 0.76 |
| 10PC-SVM | Savitzky–Golay smoothing | C = 1 D = 2 G = scale | 0.75 | 0.74 | 0.74 | 0.74 | 0.70 | 0.70 | 0.70 | 0.70 |
| 10PC-kNN | Savitzky–Golay smoothing + Log transform | n = 6 | 0.77 | 0.77 | 0.76 | 0.77 | 0.69 | 0.70 | 0.69 | 0.70 |
| 10PC-LDA | Savitzky–Golay smoothing + Detrending | n = 1 | 0.76 | 0.76 | 0.76 | 0.76 | 0.75 | 0.76 | 0.75 | 0.75 |
| Algorithm | Pretreatment | Hyper- Parameter | Calibration Set | Prediction Set | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Weighted Average | A | Weighted Average | A | |||||||
| P | R | F1 | P | R | F1 | |||||
| 10PC-ANN | Savitzky–Golay smoothing + RNV | HLZ = (100, 100, 100) AF = relu | 0.94 | 0.94 | 0.94 | 0.94 | 0.61 | 0.62 | 0.61 | 0.62 |
| 10PC-SVM | Second derivative | C = 25 D = 2 G = Scale | 0.98 | 0.98 | 0.98 | 0.98 | 0.70 | 0.68 | 0.68 | 0.68 |
| 10PC-kNN | Savitzky–Golay smoothing + Log transform | n = 3 | 0.83 | 0.83 | 0.83 | 0.83 | 0.66 | 0.68 | 0.65 | 0.68 |
| 10PC-LDA | Savitzky–Golay smoothing + Robust normal variate | n = 1 | 0.76 | 0.76 | 0.76 | 0.76 | 0.75 | 0.76 | 0.75 | 0.76 |
| Factory | Production Date | Expired Date | Initial Diameter (mm) | % TSI |
|---|---|---|---|---|
| sl1 | August 2022 | August 2025 | 40 | 60 |
| sl2 | August 2022 | August 2025 | 40 | 60 |
| sl3 | August 2022 | August 2025 | 40 | 60 |
| sl4 | August 2022 | August 2025 | 40 | 60 |
| PO1 | May 2023 | May 2026 | 40 | 60 |
| PO2 | May 2023 | May 2026 | 40 | 60 |
| PO3 | May 2023 | May 2026 | 40 | 60 |
| PO4 | May 2023 | May 2026 | 40 | 60 |
| PX 1 | October 2023 | October 2026 | 40 | 60 |
| PX 2 | October 2023 | October 2026 | 40 | 60 |
| PX 3 | October 2023 | October 2026 | 40 | 60 |
| PX 4 | October 2023 | October 2026 | 40 | 60 |
| St1 | September 2023 | September 2026 | 43 | 72 |
| St2 | September 2023 | September 2026 | 40 | 60 |
| St3 | September 2023 | September 2026 | 40 | 60 |
| St4 | September 2023 | September 2026 | 40 | 60 |
| Full Spectrum | Best Preprocessing + Algorithm | Scanning Method | Group | ||
|---|---|---|---|---|---|
| G1 (TSI < 80) | G2 (80 < TSI < 88) | G3 (TSI > 88) | |||
| Before SMOTE | (Savitzky–Golay smoothing + RNV) + SVM | One-layer scan | 288 | 12 | 20 |
| Two-layer scan | 276 | 21 | 23 | ||
| After SMOTE | (Savitzky–Golay smoothing + L2 norm scaling) + kNN | One-layer scan | 320 | 0 | 0 |
| Two-layer scan | 320 | 0 | 0 | ||
| Selection Wavelength | Best Preprocessing + Algorithm | Scanning Method | Group | ||
| G1 (TSI < 80) | G2 (80 < TSI < 88) | G3 (TSI > 88) | |||
| Before SMOTE | (Second derivative) + k-best + LDA | One-layer scan | 55 | 1 | 264 |
| Two-layer scan | 263 | 45 | 12 | ||
| After SMOTE | (Savitzky–Golay smoothing + L2 norm scaling) + GA + kNN | One-layer scan | 320 | 0 | 0 |
| Two-layer scan | 320 | 0 | 0 | ||
| Reduction Features | Best Preprocessing + Algorithm | Scanning Method | Group | ||
| G1 (TSI < 80) | G2 (80 < TSI < 88) | G3 (TSI > 88) | |||
| Before SMOTE | (Savitzky–Golay smoothing + Detrending) + 10-PC + LDA | One-layer scan | 128 | 104 | 88 |
| Two-layer scan | 137 | 104 | 79 | ||
| After SMOTE | (Savitzky–Golay smoothing + RNV) + 10-PC + LDA | One-layer scan | 141 | 69 | 110 |
| Two-layer scan | 127 | 92 | 101 | ||
| Algorithm | Selection Method | Calibration | Validation | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Before SMOTE | After SMOTE | Before SMOTE | After SMOTE | ||||||||||
| <80% | 80–88% | >80% | <80% | 80–88% | >80% | <80% | 80–88% | >80% | <80% | 80–88% | >80% | ||
| ANN | Full | 0.78 | 0.62 | 0.63 | 0.80 | 0.75 | 0.78 | 0.89 | 0.73 | 0.88 | 0.79 | 0.62 | 0.80 |
| k-best | 0.83 | 0.66 | 0.67 | 0.79 | 0.68 | 0.77 | 0.79 | 0.45 | 0.71 | 0.78 | 0.52 | 0.88 | |
| GA | 0.86 | 0.65 | 0.46 | 0.86 | 0.75 | 0.80 | 0.83 | 0.52 | 0.36 | 0.79 | 0.62 | 0.80 | |
| SVM | Full | 0.81 | 0.69 | 0.65 | 0.83 | 0.74 | 0.77 | 0.81 | 0.52 | 0.71 | 0.79 | 0.62 | 0.80 |
| k-best | 0.84 | 0.74 | 0.72 | 0.82 | 0.76 | 0.78 | 0.77 | 0.38 | 0.71 | 0.73 | 0.52 | 0.71 | |
| GA | 0.81 | 0.69 | 0.65 | 0.83 | 0.74 | 0.77 | 0.81 | 0.52 | 0.71 | 0.71 | 0.67 | 0.80 | |
| kNN | Full | 0.87 | 0.70 | 0.65 | 0.82 | 0.70 | 0.74 | 0.82 | 0.48 | 0.71 | 0.80 | 0.58 | 0.80 |
| k-best | 0.83 | 0.68 | 0.67 | 0.81 | 0.78 | 0.78 | 0.78 | 0.42 | 0.71 | 0.73 | 0.52 | 0.71 | |
| GA | 0.86 | 0.68 | 0.65 | 0.82 | 0.70 | 0.74 | 0.82 | 0.48 | 0.71 | 0.81 | 0.55 | 0.75 | |
| LDA | Full | 1.00 | 0.98 | 0.98 | 1.00 | 0.99 | 0.99 | 0.50 | 0.29 | 0.56 | 0.47 | 0.36 | 0.45 |
| k-best | 0.81 | 0.63 | 0.67 | 0.81 | 0.68 | 0.77 | 0.79 | 0.64 | 0.88 | 0.78 | 0.52 | 0.80 | |
| GA | 0.95 | 0.88 | 0.88 | 1.00 | 0.99 | 0.99 | 0.73 | 0.45 | 0.74 | 0.69 | 0.61 | 0.25 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jongyingcharoen, J.S.; Howimanporn, S.; Sitorus, A.; Phanomsophon, T.; Posom, J.; Salubsi, T.; Kongwaree, A.; Lim, C.H.; Phetpan, K.; Sirisomboon, P.; et al. Classification of the Crosslink Density Level of Para Rubber Thick Film of Medical Glove by Using Near-Infrared Spectral Data. Polymers 2024, 16, 184. https://doi.org/10.3390/polym16020184
Jongyingcharoen JS, Howimanporn S, Sitorus A, Phanomsophon T, Posom J, Salubsi T, Kongwaree A, Lim CH, Phetpan K, Sirisomboon P, et al. Classification of the Crosslink Density Level of Para Rubber Thick Film of Medical Glove by Using Near-Infrared Spectral Data. Polymers. 2024; 16(2):184. https://doi.org/10.3390/polym16020184
Chicago/Turabian StyleJongyingcharoen, Jiraporn Sripinyowanich, Suppakit Howimanporn, Agustami Sitorus, Thitima Phanomsophon, Jetsada Posom, Thanapol Salubsi, Adisak Kongwaree, Chin Hock Lim, Kittisak Phetpan, Panmanas Sirisomboon, and et al. 2024. "Classification of the Crosslink Density Level of Para Rubber Thick Film of Medical Glove by Using Near-Infrared Spectral Data" Polymers 16, no. 2: 184. https://doi.org/10.3390/polym16020184
APA StyleJongyingcharoen, J. S., Howimanporn, S., Sitorus, A., Phanomsophon, T., Posom, J., Salubsi, T., Kongwaree, A., Lim, C. H., Phetpan, K., Sirisomboon, P., & Tsuchikawa, S. (2024). Classification of the Crosslink Density Level of Para Rubber Thick Film of Medical Glove by Using Near-Infrared Spectral Data. Polymers, 16(2), 184. https://doi.org/10.3390/polym16020184







