Using the Herschel–Bulkley Consistency Index to Characterise Complex Biopolymer Systems—The Effect of Screening
Abstract
1. Introduction
2. The Herschel–Bulkley Approach
3. Materials and Methods
3.1. Materials
3.2. Methods
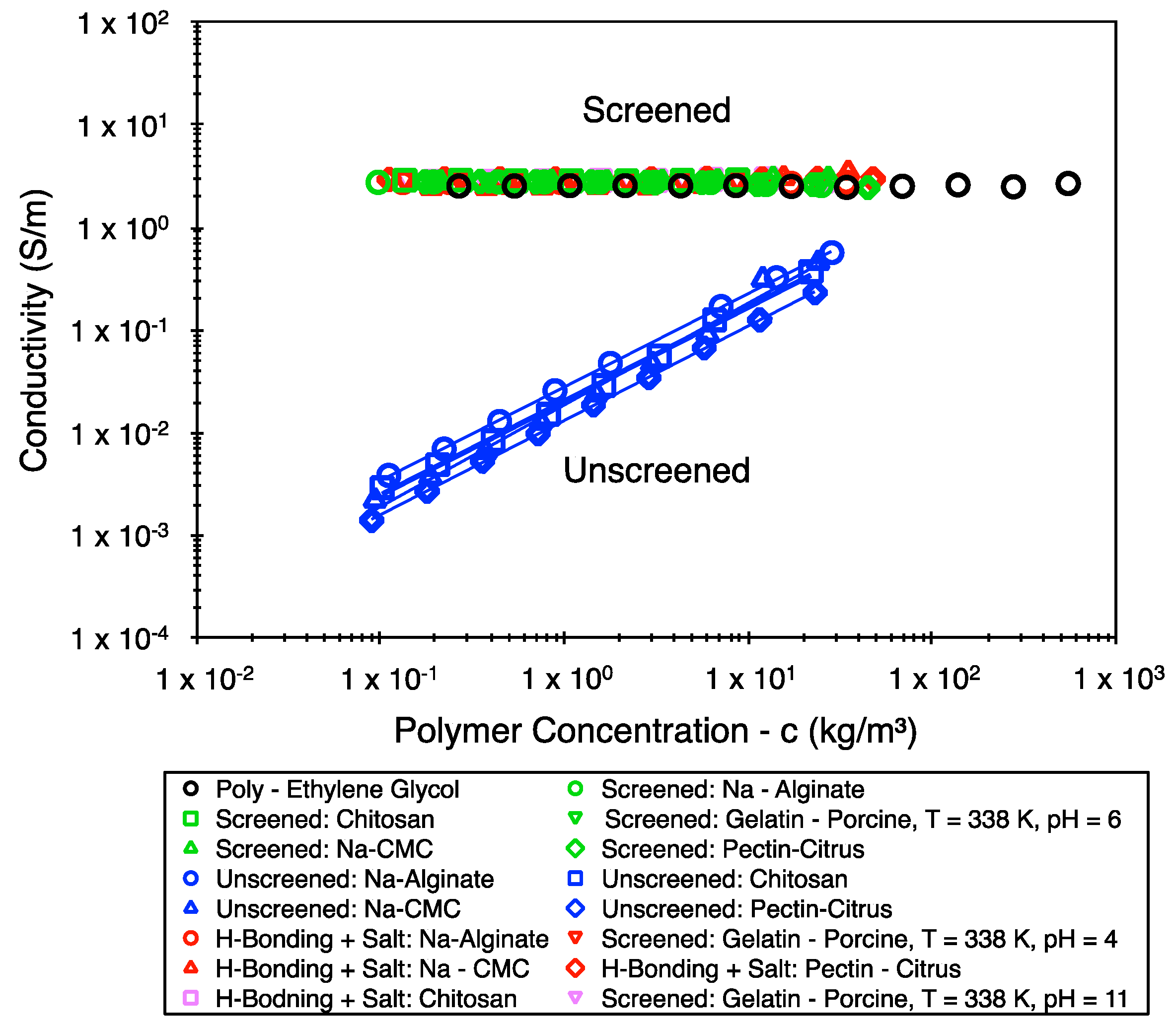
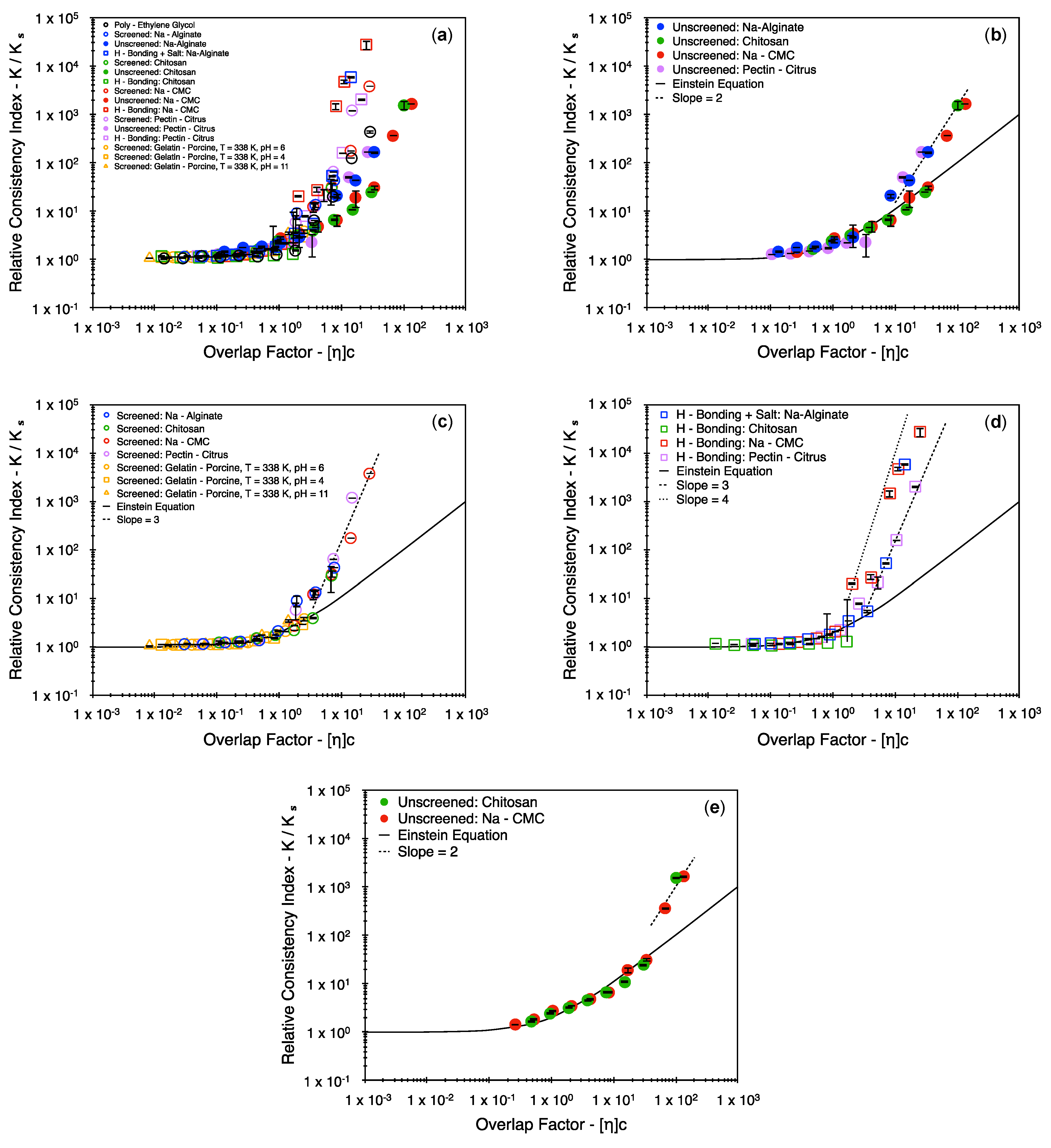
4. Results
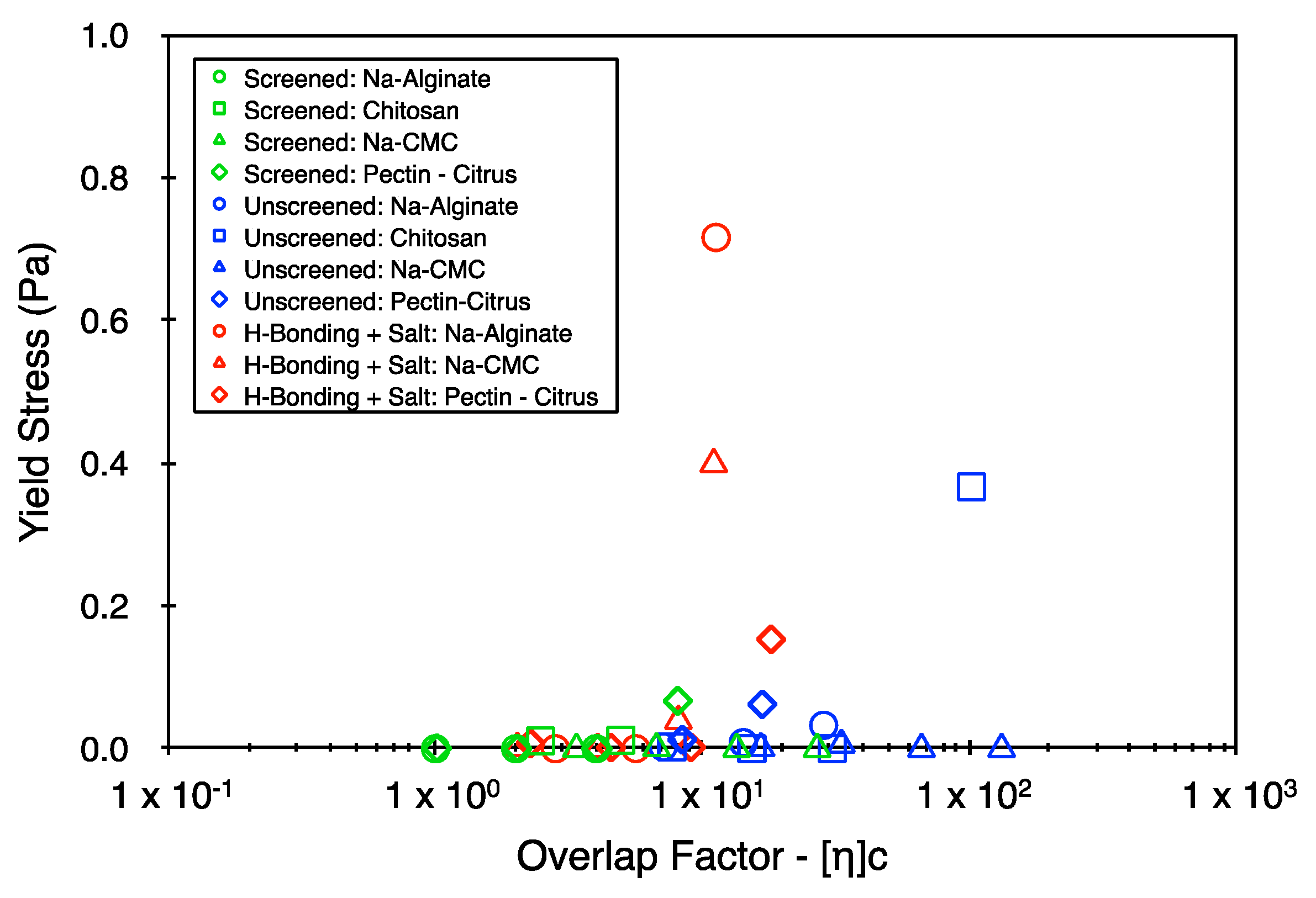
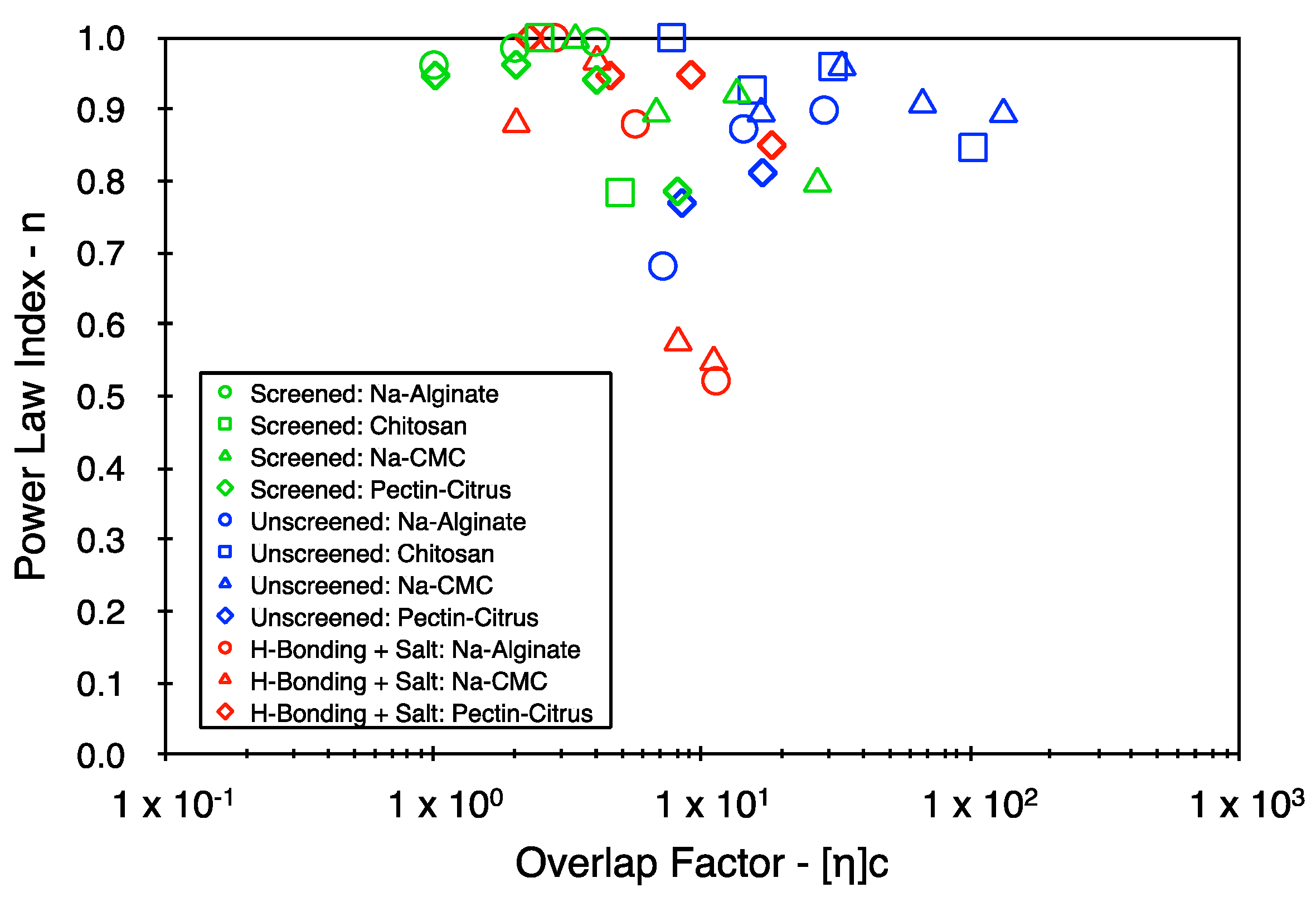
5. Discussion
5.1. Exploring the Theoretical Premise
5.2. Yield Stress and Power Law Indices
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shivu, B.; Seshadri, S.; Li, J.; Oberg, K.A.; Uversky, V.N.; Fink, A.L. Distinct β-sheet structure in protein aggregates determined by ATR–FTIR spectroscopy. Biochemistry 2013, 52, 5176–5183. [Google Scholar] [CrossRef] [PubMed]
- Gómez-Ordóñez, E.; Rupérez, P. FTIR-ATR spectroscopy as a tool for polysaccharide identification in edible brown and red seaweeds. Food Hydrocoll. 2011, 25, 1514–1520. [Google Scholar] [CrossRef]
- Jackson, M.; Mantsch, H.H. The use and misuse of FTIR spectroscopy in the determination of protein structure. Crit. Rev. Biochem. Mol. Biol. 1995, 30, 95–120. [Google Scholar] [CrossRef]
- Cheng, H.; Neiss, T.G. Solution NMR spectroscopy of food polysaccharides. Polym. Rev. 2012, 52, 81–114. [Google Scholar] [CrossRef]
- Seviour, T.; Lambert, L.K.; Pijuan, M.; Yuan, Z. Structural determination of a key exopolysaccharide in mixed culture aerobic sludge granules using NMR spectroscopy. Environ. Sci. Technol. 2010, 44, 8964–8970. [Google Scholar] [CrossRef]
- Patterson, S.D.; Aebersold, R.H. Proteomics: The first decade and beyond. Nat. Genet. 2003, 33, 311–323. [Google Scholar] [CrossRef] [PubMed]
- Beranova-Giorgianni, S. Proteome analysis by two-dimensional gel electrophoresis and mass spectrometry: Strengths and limitations. TrAC 2003, 22, 273–281. [Google Scholar] [CrossRef]
- Tyers, M.; Mann, M. From genomics to proteomics. Nature 2003, 422, 193–197. [Google Scholar] [CrossRef] [PubMed]
- Lawrie, G.; Keen, I.; Drew, B.; Chandler-Temple, A.; Rintoul, L.; Fredericks, P.; Grondahl, L. Interactions between alginate and chitosan biopolymers characterized using FTIR and XPS. Biomacromolecules 2007, 8, 2533–2541. [Google Scholar] [CrossRef] [PubMed]
- Kontogiorgos, V. Pectin: Technological and Physiological Properties; Springer International: Cham, Switzerland, 2020. [Google Scholar]
- Seviour, T.; Derlon, N.; Dueholm, M.S.; Flemming, H.-C.; Girbal-Neuhauser, E.; Horn, H.; Kjelleberg, S.; van Loosdrecht, M.C.; Lotti, T.; Malpei, M.F. Extracellular polymeric substances of biofilms: Suffering from an identity crisis. Water Res. 2019, 151, 1–7. [Google Scholar] [CrossRef]
- O’Mahony, J.A.; Fox, P. Milk proteins: Introduction and historical aspects. In Advanced Dairy Chemistry: Volume 1A: Proteins: Basic Aspects, 4th ed.; Springer: New York, NY, USA, 2013; pp. 43–85. [Google Scholar]
- Van Vlierberghe, S.; Dubruel, P.; Schacht, E. Biopolymer-based hydrogels as scaffolds for tissue engineering applications: A review. Biomacromolecules 2011, 12, 1387–1408. [Google Scholar] [CrossRef]
- Zhao, S.; Malfait, W.J.; Guerrero-Alburquerque, N.; Koebel, M.M.; Nyström, G. Biopolymer aerogels and foams: Chemistry, properties, and applications. Angew. Chem. Int. Ed. 2018, 57, 7580–7608. [Google Scholar] [CrossRef]
- Xu, T.; Ma, C.; Aytac, Z.; Hu, X.; Ng, K.W.; White, J.C.; Demokritou, P. Enhancing agrichemical delivery and seedling development with biodegradable, tunable, biopolymer-based nanofiber seed coatings. ACS Sustain. Chem. Eng. 2020, 8, 9537–9548. [Google Scholar] [CrossRef]
- Zlopasa, J.; Norder, B.; Koenders, E.A.; Picken, S.J. Origin of highly ordered sodium alginate/montmorillonite bionanocomposites. Macromolecules 2015, 48, 1204–1209. [Google Scholar] [CrossRef]
- Kanmani, P.; Rhim, J.-W. Properties and characterization of bionanocomposite films prepared with various biopolymers and ZnO nanoparticles. Carbohyd. Polym. 2014, 106, 190–199. [Google Scholar] [CrossRef] [PubMed]
- Fulcher, G.S. Analysis of recent measurements of the viscosity of glasses. JACerS 1925, 8, 339–355. [Google Scholar] [CrossRef]
- Korson, L.; Drost-Hansen, W.; Millero, F.J. Viscosity of water at various temperatures. J. Phys. Chem. 1969, 73, 34–39. [Google Scholar] [CrossRef]
- Rubinstein, M.; Colby, R.H. Polymer Physics; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Rubinstein, M.; Colby, R.H.; Dobrynin, A.V. Dynamics of semidilute polyelectrolyte solutions. PRL 1994, 73, 2776. [Google Scholar] [CrossRef] [PubMed]
- Sayko, R.; Jacobs, M.; Dobrynin, A.V. Quantifying properties of polysaccharide solutions. ACS Polym. Au 2021, 1, 196–205. [Google Scholar] [CrossRef] [PubMed]
- Pathak, J.A.; Nugent, S.; Bender, M.F.; Roberts, C.J.; Curtis, R.J.; Douglas, J.F. Comparison of huggins coefficients and osmotic second virial coefficients of buffered solutions of monoclonal antibodies. Polymers 2021, 13, 601. [Google Scholar] [CrossRef] [PubMed]
- Raja, A.; Wilfert, P.K.; Picken, S.J. Charge Mediated Changes to The Intrinsic Viscosity of Biopolymer Systems. Polymers 2024. submitted. [Google Scholar]
- Osswald, T.A.; Rudolph, N.S. Polymer Rheology: Fundamentals and Applications; Carl Hanser Verlag GmbH: Munich, Germany, 2015. [Google Scholar]
- Sprakel, J.; van der Gucht, J.; Stuart, M.A.C.; Besseling, N.A. Brownian particles in transient polymer networks. PRE 2008, 77, 061502. [Google Scholar] [CrossRef] [PubMed]
- Van der Gucht, J.; Besseling, N.; Knoben, W.; Bouteiller, L.; Stuart, M.C. Brownian particles in supramolecular polymer solutions. PRE 2003, 67, 051106. [Google Scholar] [CrossRef] [PubMed]
- Bicerano, J.; Douglas, J.F.; Brune, D.A. Model for the viscosity of particle dispersions. J. Macromol. Sci. Part C Polym. Rev. 1999, 39, 561–642. [Google Scholar] [CrossRef]
- Lewandowska, K.; Staszewska, D.U.; Bohdanecký, M. The Huggins viscosity coefficient of aqueous solution of poly (vinyl alcohol). Eur. Polym. J. 2001, 37, 25–32. [Google Scholar] [CrossRef]
- Likhtman, A.E.; McLeish, T.C. Quantitative theory for linear dynamics of linear entangled polymers. Macromolecules 2002, 35, 6332–6343. [Google Scholar] [CrossRef]
- te Nijenhuis, K. On the nature of crosslinks in thermoreversible gels. Polym. Bull. 2007, 58, 27–42. [Google Scholar] [CrossRef]
- De Gennes, P.-G. Scaling Concepts in Polymer Physics; Cornell University Press: Ithaca, NY, USA, 1979. [Google Scholar]


| Polymer Name | Salient Properties |
|---|---|
| Poly-Ethylene Glycol (PEG) | End functionalization with hydroxyl group, = 20 kg/mol. |
| Sodium Alginate (Na–Alginate) | Polyanion: Carboxyl group, High mannuronic acid content. Linear copolymer. |
| Chitosan | Polycation: Amine group, Linear homopolymer, ~50 to 190 kg/mol. |
| Sodium Carboxy Methyl Cellulose (Na–CMC) | Polyanion: Carboxyl group, Degree of substitution = 0.9, Linearly substituted homopolymer, ~250 kg/mol. |
| Pectin from Citrus Peels (Pectin–Citrus) | Polyanion: Carboxyl group, Galacturonic acid ≥ 74.0%, degree of methylation ≥ 6.7%, Branched heteropolymer. |
| Gelatin from Porcine Skin (Porcine–Gelatin) | Polyampholyte: Carboxyl group and amine group, Linear–collagen derivative. |
| Biopolymer System | (m3/kg) ± S.D. 1 |
|---|---|
| Poly–Ethylene Glycol | 0.053 ± 0.007 |
| Screened: Na-Alginate | 0.308 ± 0.065 |
| Screened: Chitosan | 0.795 ± 0.100 |
| Screened: Gelatin–Porcine, T = 338 K, pH = 6 | 0.102 ± 0.024 |
| Screened: Na-CMC | 1.034 ± 0.037 |
| Screened: Pectin–Citrus | 0.332 ± 0.064 |
| Unscreened: Na-Alginate | 1.183 ± 0.157 |
| Unscreened: Chitosan | 4.636 ± 0.379 |
| Unscreened: Na-CMC | 5.624 ± 0.626 |
| Unscreened: Pectin–Citrus | 1.152 ± 0.175 |
| H-Bonding + Salt: Na–Alginate | 0.420 ± 0.042 |
| Screened: Gelatin–Porcine, T = 338 K, pH = 4 | 0.095 ± 0.017 |
| H-Bonding + Salt: Na-CMC | 0.719 ± 0.016 |
| H-Bonding + Salt: Pectin–Citrus | 0.440 ± 0.027 |
| H-Bonding + Salt: Chitosan | 0.066 ± 0.027 |
| Screened: Gelatin–Porcine, T = 338 K, pH = 11 | 0.060 ± 0.017 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Raja, A.; Wilfert, P.K.; Picken, S.J. Using the Herschel–Bulkley Consistency Index to Characterise Complex Biopolymer Systems—The Effect of Screening. Polymers 2024, 16, 2822. https://doi.org/10.3390/polym16192822
Raja A, Wilfert PK, Picken SJ. Using the Herschel–Bulkley Consistency Index to Characterise Complex Biopolymer Systems—The Effect of Screening. Polymers. 2024; 16(19):2822. https://doi.org/10.3390/polym16192822
Chicago/Turabian StyleRaja, Anand, Philipp K. Wilfert, and Stephen J. Picken. 2024. "Using the Herschel–Bulkley Consistency Index to Characterise Complex Biopolymer Systems—The Effect of Screening" Polymers 16, no. 19: 2822. https://doi.org/10.3390/polym16192822
APA StyleRaja, A., Wilfert, P. K., & Picken, S. J. (2024). Using the Herschel–Bulkley Consistency Index to Characterise Complex Biopolymer Systems—The Effect of Screening. Polymers, 16(19), 2822. https://doi.org/10.3390/polym16192822







