Prediction of Dielectric Constant in Series of Polymers by Quantitative Structure-Property Relationship (QSPR)
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Data Collection
2.2. Generation of Descriptors
2.3. Model Assembly
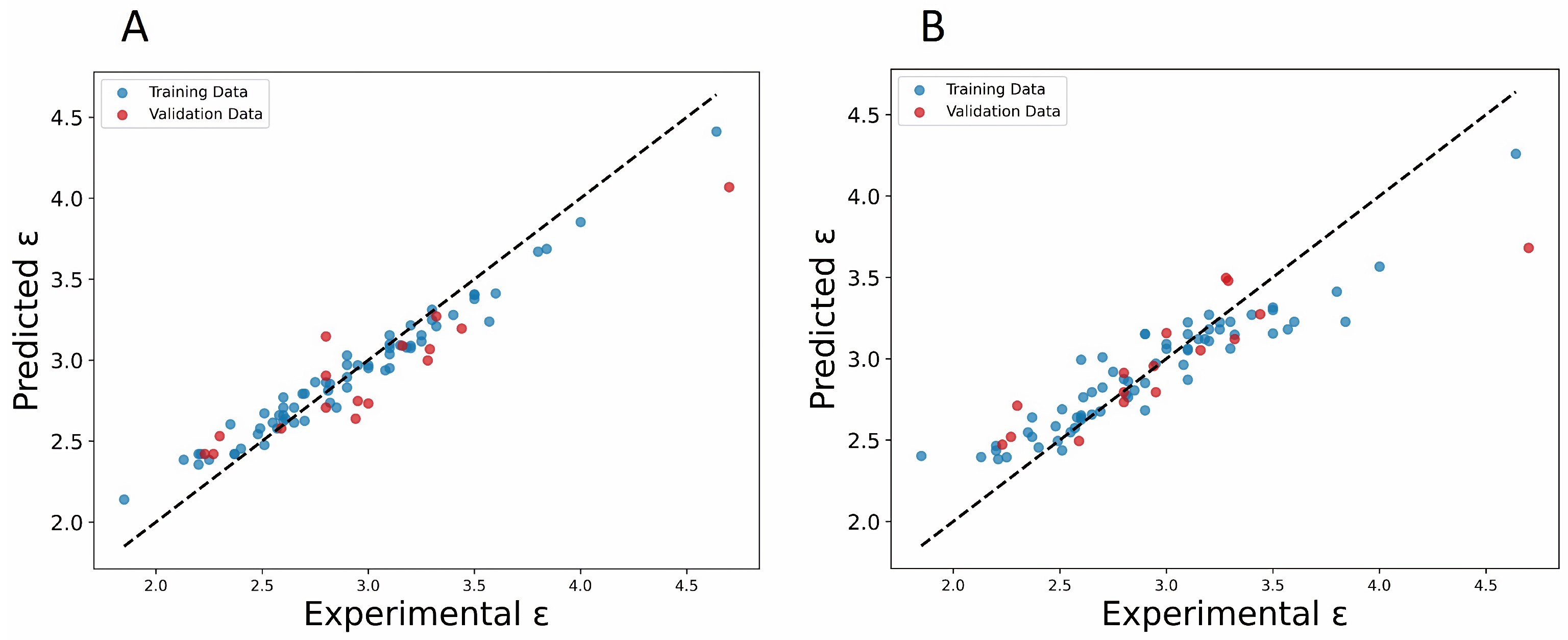
2.4. Gradient Boosting Regressor Model Modeling and Validation
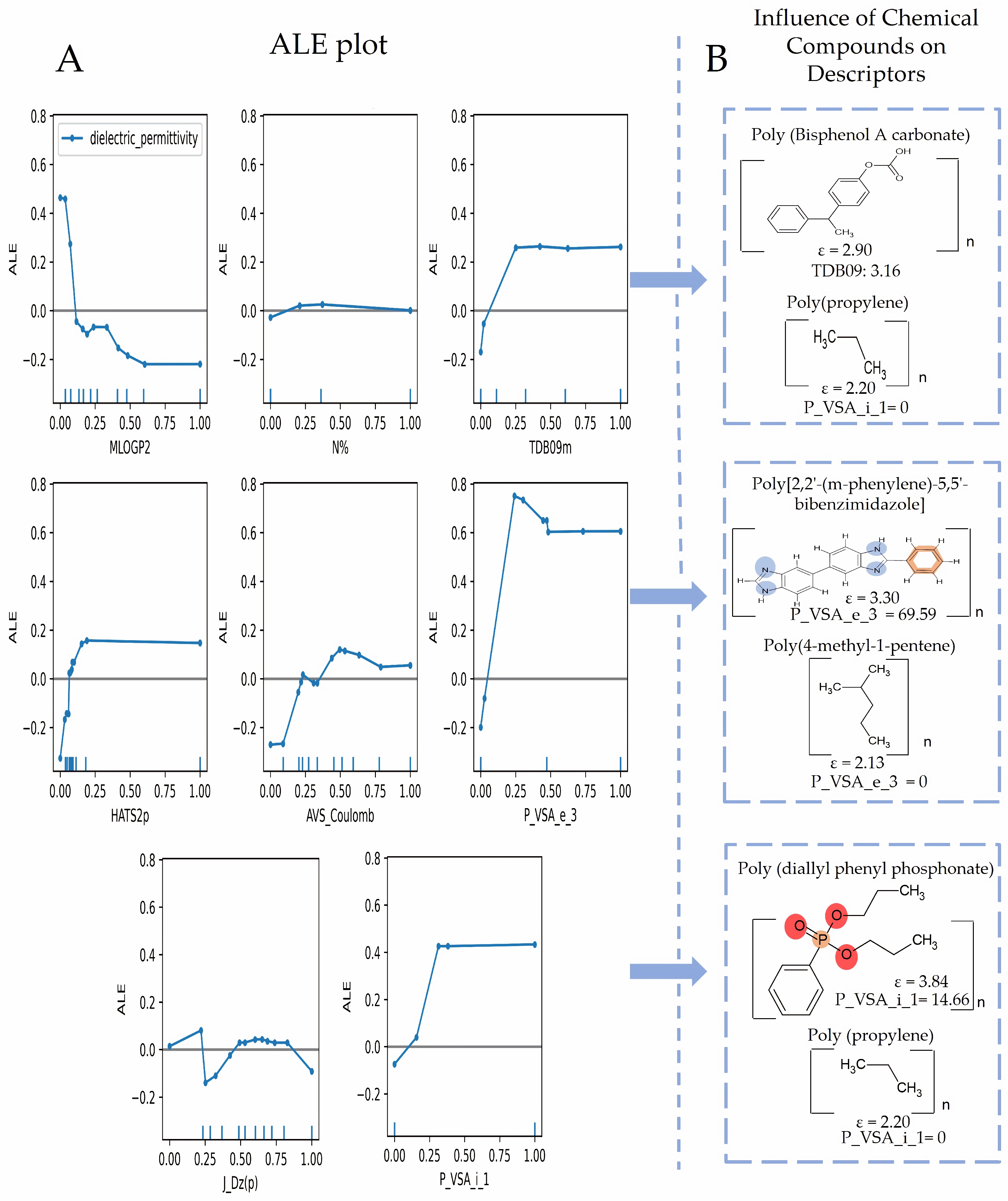
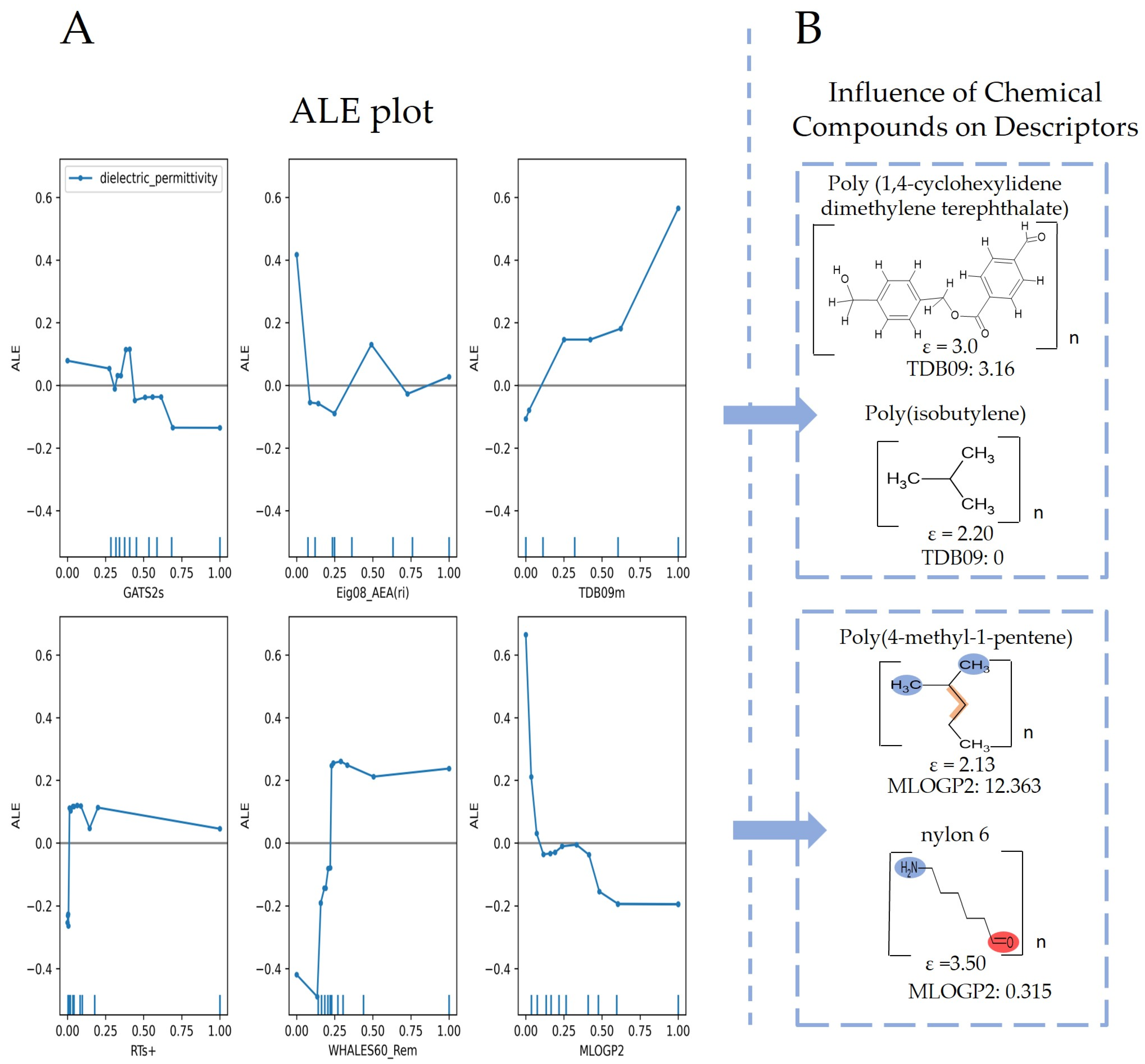
2.5. Analysis of Descriptors in Models
3. Results and Discussion
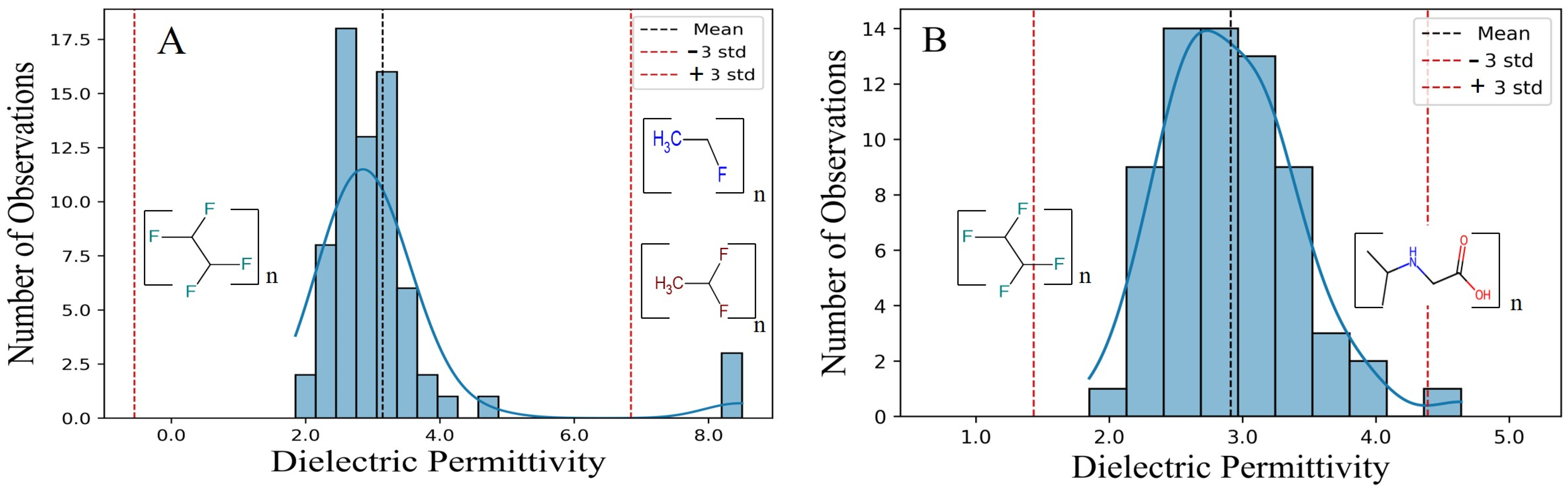
3.1. Exploratory Data Analysis
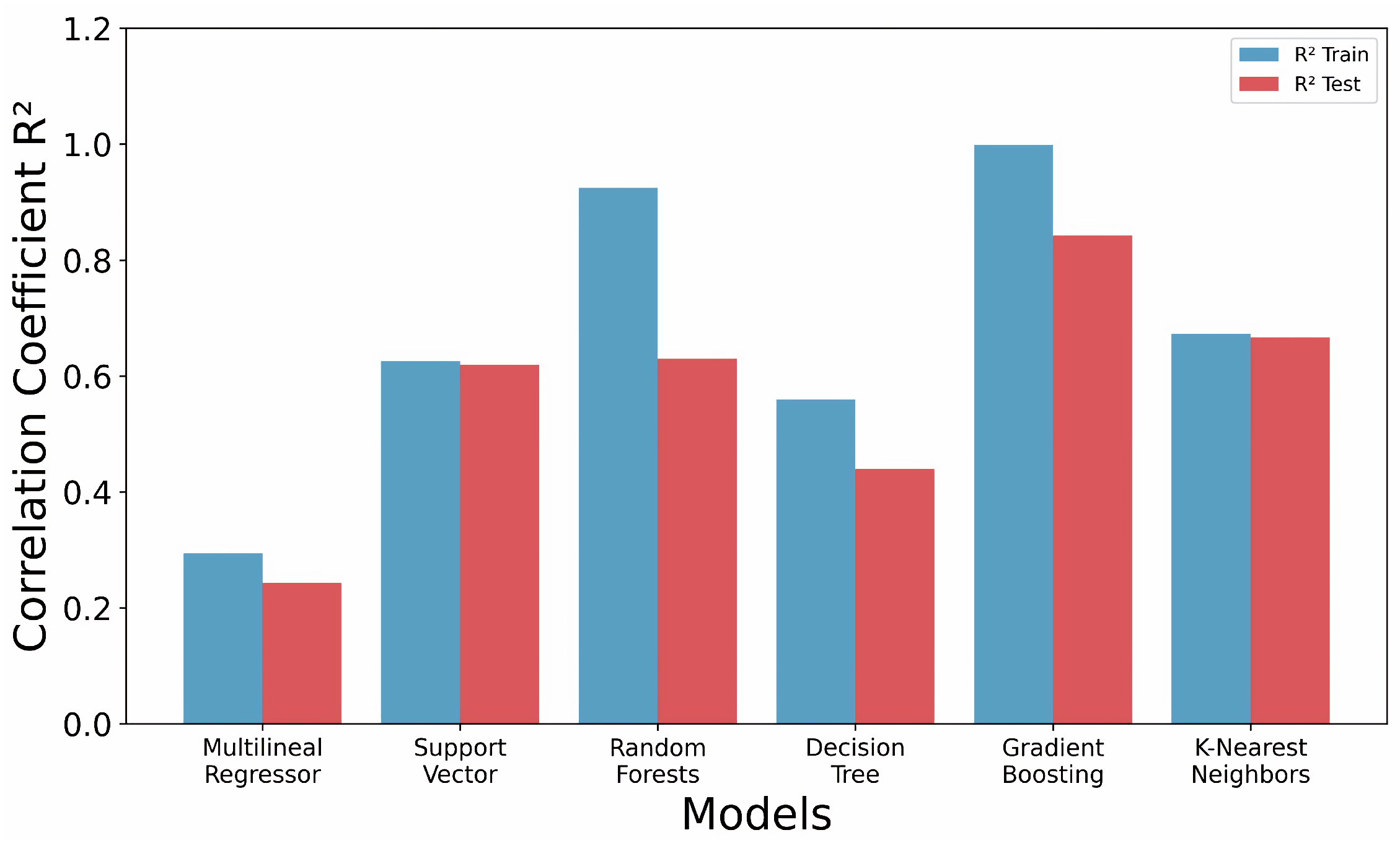
3.2. Ensemble Model
3.3. ML-QSPR Models Explanation
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Zhuravskyi, Y.; Iduoku, K.; Erickson, M.E.; Karuth, A.; Usmanov, D.; Casanola-Martin, G.; Sayfiyev, M.N.D.; Ziyaev, A.; Smanova, Z.; Mikolajczyk, A.; et al. Quantitative Structure Permittivity Relationship Study of a Series of Polymers. ACS Mater. Au 2024, 4, 195–203. [Google Scholar] [CrossRef] [PubMed]
- Zahidul, M.D.; Fu, Y.; Deb, H.; Khalid, M.D.; Dong, Y.; Shi, S. Polymer-based low dielectric constant and loss materials for high-speed communication network: Dielectric constants and challenges. Eur. Polym. J. 2023, 200, 112543. [Google Scholar] [CrossRef]
- Borkar, H.; Rao, V.; Tomar, M.; Gupta, V.; Scott, J.F.; Kumar, A. Experimental Evidence of Electronic Polarization in a Family of Photo-Ferroelectrics. RSC Adv. 2017, 7, 12842–12855. [Google Scholar] [CrossRef]
- Talebian, E.; Talebian, M. A General Review on the Derivation of Clausius-Mossotti Relation. Optik 2013, 124, 2324–2326. [Google Scholar] [CrossRef]
- Baker-Fales, M.; Gutiérrez-Cano, J.D.; Catalá-Civera, J.M.; Vlachos, D.G. Temperature-Dependent Complex Dielectric Permittivity: A Simple Measurement Strategy for Liquid-Phase Samples. Sci. Rep. 2023, 13, 18171. [Google Scholar] [CrossRef]
- Afantitis, A.; Melagraki, G.; Makridima, K.; Alexandridis, A.; Sarimveis, H.; Iglessi-Markopoulou, O. Prediction of high weight polymers glass transition temperature using RBF neural networks. J. Mol. Struct. Theochem. 2004, 716, 193–198. [Google Scholar] [CrossRef]
- Bicerano, J. Prediction of Polymer Properties, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2002; pp. 1–784. [Google Scholar]
- Chen, L.; Kim, C.; Batra, R.; Lightstone, J.P.; Wu, C.; Li, Z.; Deshmukh, A.A.; Wang, Y. Frequency-dependent dielectric constant prediction of polymers using machine learning. NPJ Comput. Mater. 2020, 6, 61. [Google Scholar] [CrossRef]
- Ma, R.; Baldwin, A.F.; Wang, C.; Offenbach, I.; Cakmak, M.; Ramprasad, R.; Sotzing, G.A. Rationally designed polyimides for high-energy density capacitor applications. ACS Appl. Mater. Interfaces 2014, 6, 10445–10451. [Google Scholar] [CrossRef]
- Maier, G. Low dielectric constant polymers for microelectronics. Prog. Polym. Sci. 2001, 26, 3–65. [Google Scholar] [CrossRef]
- Dang, M.T.; Hirsch, L.; Wantz, G. P3HT: PCBM, best seller in polymer photovoltaic research. Adv. Mater. 2011, 23, 3597–3602. [Google Scholar] [CrossRef]
- Facchetti, A. π-Conjugated polymers for organic electronics and photovoltaic cell applications. J. Mater. Chem. 2011, 23, 733–758. [Google Scholar] [CrossRef]
- Kim, J.H.; Kim, S.Y.; Moore, J.A.; Mason, J.F. Dielectric Properties of Poly(enaminonitrile)s. Polym. J. 2000, 32, 57–61. [Google Scholar] [CrossRef]
- Le, T.; Epa, V.C.; Burden, F.R.; Winkler, D.A. Quantitative structure-property relationship modeling of diverse materials properties. Chem. Rev. 2012, 112, 2889–2919. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.; Jabeen, M.F.; Rasulev, B.; Ossowski, M.; Boudjouk, P. A computational structure–property relationship study of glass transition temperatures for a diverse set of polymers. J. Polym. Sci. 2018, 56, 877–885. [Google Scholar] [CrossRef]
- Karuth, A.; Alesadi, A.; Xia, W.; Rasulev, B. Predicting glass transition of amorphous polymers by application of cheminformatics and molecular dynamics simulations. Polym. J. 2021, 218, 123495. [Google Scholar] [CrossRef]
- Petrosyan, L.S.; Sizochenko, N.; Leszczynski, J.; Rasulev, B. Modeling of Glass Transition Temperatures for Polymeric Coating Materials: Application of QSPR Mixture-based Approach. Mol. Inform. 2019, 38, 8–9. [Google Scholar] [CrossRef]
- Xu, J.; Wang, L.; Liang, G.; Wang, L.; Shen, X. A general quantitative structure-property relationship treatment for dielectric constants of polymers. Polym. Eng. Sci. 2011, 51, 2408–2416. [Google Scholar] [CrossRef]
- Wu, K.; Sukumar, N.; Lanzillo, N.A.; Wang, C.; Ramamurthy, R.; Ma, R.; Baldwin, A.F.; Sotzing, G.; Breneman, C. Prediction of polymer properties using infinite chain descriptors (ICD) and machine learning: Toward optimized dielectric polymeric materials. J. Polym. Sci. 2016, 54, 2082–2091. [Google Scholar] [CrossRef]
- Liu, A.; Wang, X.; Wang, L.; Wang, H.; Wang, H. Prediction of dielectric constants and glass transition temperatures of polymers by quantitative structure property relationships. Eur. Polym. J. 2007, 43, 989–995. [Google Scholar] [CrossRef]
- Cramer, R.D. Partial Least Squares (PLS): Its Strengths and Limitations. Perspect. Drug Discov. Des. 1993, 1, 269–278. [Google Scholar] [CrossRef]
- Maxwell, A.E. Limitations on the Use of the Multiple Linear Regression Model. Br. J. Math. Stat. Psychol. 1975, 28, 51–62. [Google Scholar] [CrossRef]
- Erkoç, A.; Tez, M.; Akay, K.U. On Multicollinearity in Nonlinear Regression. Mod. Appl. Math. 2010, 65–72. [Google Scholar]
- Zhou, G.; Ni, Z.; Zhao, Y.; Luan, J. Identification of Bamboo Species Based on Extreme Gradient Boosting (XGBoost) Using Zhuhai-1 Orbita Hyperspectral Remote Sensing Imagery. Sensors 2022, 22, 5434. [Google Scholar] [CrossRef] [PubMed]
- Guillen, M.D.; Aparicio, J.; Esteve, M. Gradient tree boosting and the estimation of production frontiers. Expert Syst. Appl. 2023, 214, 119134. [Google Scholar] [CrossRef]
- Sipper, M.; Moore, J.H. AddGBoost: A gradient boosting-style algorithm based on strong learners. Mach. Learn. Appl. 2021, 7, 100243. [Google Scholar] [CrossRef]
- Goh, K.L.; Goto, A.; Lu, Y. LGB-Stack: Stacked Generalization with LightGBM for Highly Accurate Predictions of Polymer Bandgap. ACS Omega 2022, 7, 29787–29793. [Google Scholar] [CrossRef]
- Tao, L.; Varshney, V.; Li, Y. Benchmarking Machine Learning Models for Polymer Informatics: An Example of Glass Transition Temperature. J. Chem. Inf. Model. 2021, 61, 5395–5413. [Google Scholar] [CrossRef]
- Malashin, I.P.; Tynchenko, V.S.; Nelyub, V.A.; Borodulin, A.S.; Gantimurov, A.P. Estimation and Prediction of the Polymers. Physical Characteristics Using the Machine Learning Models. Polymers 2023, 16, 115. [Google Scholar] [CrossRef]
- Yang, Y.; Yang, C.; Wang, L.; Cao, S.; Li, X.; Bai, Y.; Hu, X. Research on Early Identification Model of Intravenous Immunoglobulin Resistant Kawasaki Disease Based on Gradient Boosting Decision Tree. Pediatr. Infect. Dis. J. 2023, 42, 537–542. [Google Scholar] [CrossRef]
- Nematzadeh, S.; Kiani, F.; Torkamanian-Afshar, M.; Aydin, N. Tuning Hyperparameters of Machine Learning Algorithms and Deep Neural Networks Using Metaheuristics: A Bioinformatics Study on Biomedical and Biological Cases. Comput. Biol. Chem. 2022, 97, 107619. [Google Scholar] [CrossRef]
- Naseri, H.; Waygood, E.O.D.; Wang, B.; Patterson, Z. Application of Machine Learning to Child Mode Choice with a Novel Technique to Optimize Hyperparameters. Int. J. Environ. Res. Public Health 2022, 19, 16844. [Google Scholar] [CrossRef] [PubMed]
- Daghighi, A.; Casanola-Martin, G.M.; Timmerman, T.; Milenković, D.; Lučić, B.; Rasulev, B. In Silico Prediction of the Toxicity of Nitroaromatic Compounds: Application of Ensemble Learning QSAR Approach. Toxics 2022, 10, 746. [Google Scholar] [CrossRef] [PubMed]
- Friedman, J.H.; Meulman, J.J. Multiple additive regression trees with application in epidemiology. Stat. Med. 2003, 22, 1365–1381. [Google Scholar] [CrossRef] [PubMed]
- Chan, M.C.; Pai, K.C.; Su, S.A.; Wang, M.S.; Wu, C.L.; Chao, W.C. Explainable Machine Learning to Predict Long-Term Mortality in Critically Ill Ventilated Patients: A Retrospective Study in Central Taiwan. BMC Med. Inform. Decis. Mak. 2022, 22, 75. [Google Scholar] [CrossRef]
- Welchowski, T.; Maloney, K.O.; Mitchell, R.; Schmid, M. Techniques to Improve Ecological Interpretability of Black-Box Machine Learning Models: Case Study on Biological Health of Streams in the United States with Gradient Boosted Trees. J. Agric. Biol. Environ. Stat. 2022, 27, 175–197. [Google Scholar] [CrossRef]
- Angelini, M.; Blasilli, G.; Lenti, S.; Santucci, G. A Visual Analytics Conceptual Framework for Explorable and Steerable Partial Dependence Analysis. IEEE Trans. Vis. Comput. Graph. 2024, 30, 4497–4513. [Google Scholar] [CrossRef]
- Zha, J.W.; Zheng, M.S.; Fan, B.H.; Dang, Z.M. Polymer-based dielectrics with high permittivity for electric energy storage: A review. Nano Energy 2021, 89, 106438. [Google Scholar] [CrossRef]
- Ho, J.S.; Greenbaum, S.G. Polymer Capacitor Dielectrics for High Temperature Applications. ACS Appl. Mater. Interfaces 2018, 10, 29189–29218. [Google Scholar] [CrossRef]
- Ničkčović, V.P.; Nikolić, G.R.; Nedeljković, B.M.; Mitić, N.; Danić, S.F.; Mitić, J.; Marčetić, Z.; Sokolović, D.; Veselinović, A.M. In Silico Approach for the Development of Novel Antiviral Compounds Based on SARS-CoV-2 Protease Inhibition. Chem. Zvesti. 2022, 76, 4393–4404. [Google Scholar] [CrossRef]
- Kim, S.; Thiessen, P.A.; Bolton, E.E.; Chen, J.; Fu, G.; Gindulyte, A.; Han, L.; He, J.; He, S.; Shoemaker, B.A.; et al. PubChem substance and compound databases. Nucleic Acids Res. 2016, 44, D1202–D1213. [Google Scholar] [CrossRef]
- Cousins, K.R. ChemDraw Ultra 9.0. CambridgeSoft, 100 CambridgePark Drive, Cambridge, MA 02140. www.cambridgesoft.com. See Web site for pricing options. J. Am. Chem. Soc. 2005, 127, 4115–4116. [Google Scholar] [CrossRef]
- Hanwell, M.D.; Curtis, D.E.; Lonie, D.C.; Vandermeersch, T.; Zurek, E.; Hutchison, G.R. Avogadro: An advanced semantic chemical editor, visualization, and analysis platform. J. Cheminform. 2012, 4, 17. [Google Scholar] [CrossRef] [PubMed]
- Jász, Á.; Rák, Á.; Ladjánszki, I.; Cserey, G. Optimized GPU implementation of Merck Molecular Force Field and Universal Force Field. J. Mol. Struct. 2019, 1188, 227–233. [Google Scholar] [CrossRef]
- Zhao, Y.; Mulder, R.J.; Houshyar, S.; Le, T.C. A review on the application of molecular descriptors and machine learning in polymer design. Polym. Chem. 2023, 14, 3325–3346. [Google Scholar] [CrossRef]
- Mauri, A. alvaDesc: A Tool to Calculate and Analyze Molecular Descriptors and Fingerprints. In Ecotoxicological QSARs; Roy, K., Ed.; Methods in Pharmacology and Toxicology; Humana: New York, NY, USA, 2020. [Google Scholar]
- Sun, L.; Zhou, L.; Yu, Y.; Lan, Y.; Li, Z. QSPR study of polychlorinated diphenyl ethers by molecular electronegativity distance vector (MEDV-4). Chemosphere 2007, 66, 1039–1051. [Google Scholar] [CrossRef]
- Witte, R.S.; Witte, J.S. Statistics, 11th ed.; Wiley: Hoboken, NJ, USA, 2021; pp. 1–496. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. 2011, 12, 2825–2830. [Google Scholar]
- Katoch, S.S.; Chauhan, S.; Kumar, V. A review on genetic algorithm: Past, present, and future. Multimed. Tools Appl. 2021, 80, 8091–8126. [Google Scholar] [CrossRef] [PubMed]
- Gad, A.F. PyGAD: An Intuitive Genetic Algorithm Python Library. Multimed. Tools Appl. 2024, 83, 58029–58042. [Google Scholar] [CrossRef]
- Gramatica, P.; Sangion, A. A Historical Excursus on the Statistical Validation Parameters for QSAR Models: A Clarification Concerning Metrics and Terminology. J. Chem. Inf. Model. 2016, 56, 1127–1131. [Google Scholar] [CrossRef]
- Apley, D.W.; Zhu, J. Visualizing the Effects of Predictor Variables in Black Box Supervised Learning Models. J. R. Stat. Soc. Ser. Methodol. 2020, 82, 1059–1086. [Google Scholar] [CrossRef]
- Boels, L.; Bakker, A.; Van Dooren, W.; Drijvers, P. Conceptual difficulties when interpreting histograms: A review. Educ. Res. Rev. 2019, 28, 100291. [Google Scholar] [CrossRef]
- Wand, M.P. Data-Based Choice of Histogram Bin Width. Am. Stat. 1997, 51, 59–64. [Google Scholar] [CrossRef]
- Diwekar, U.; David, A. BONUS Algorithm for Large Scale Stochastic Nonlinear Programming Problems; Springer: Berlin/Heidelberg, Germany, 2015; Volume 1, pp. 27–34. [Google Scholar]
- Bardenet, R.; Brendel, M.; Kégl, B.; Sebag, M. Collaborative Hyperparameter Tuning. In Proceedings of the 30th International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013; PMLR: London, UK, 2013; Volume 28, pp. 199–207. [Google Scholar]
- Xue, L.; Bajorath, J. Molecular descriptors in chemoinformatics, computational combinatorial chemistry, and virtual screening. Comb. Chem. High Throughput Screen. 2000, 3, 363–372. [Google Scholar] [CrossRef] [PubMed]
- Todeschini, R.; Consonni, V. Handbook of Molecular Descriptors; WILEY-VCH: Weinheim, Germany, 2000; pp. 154–196. [Google Scholar]
- Khan, K.; Kumar, V.; Colombo, E.; Lombardo, A.; Benfenati, E.; Roy, K. Intelligent consensus predictions of bioconcentration factor of pharmaceuticals using 2D and fragment-based descriptors. Environ. Int. 2022, 170, 107625. [Google Scholar] [CrossRef]
- Consonni, V.; Todeschini, R.; Pavan, M. Structure/response correlations and similarity/diversity analysis by GETAWAY descriptors. 1. Theory of the novel 3D molecular descriptors. J. Chem. Inf. Comput. Sci. 2002, 42, 682–692. [Google Scholar] [CrossRef]
- Labute, P. A widely applicable set of descriptors. J. Mol. Graph. Model. 2000, 18, 464–477. [Google Scholar] [CrossRef]
- Guha, R.; Willighagen, E. A Survey of Quantitative Descriptions of Molecular Structure. Curr. Top. Med. Chem. 2012, 18, 1946–1956. [Google Scholar] [CrossRef]
- Sun, G.; Fan, T.; Sun, X.; Hao, Y.; Cui, X.; Zhao, L.; Ren, T.; Zhou, Y.; Zhong, R.; Peng, Y. In Silico Prediction of O⁶-Methylguanine-DNA Methyltransferase Inhibitory Potency of Base Analogs with QSAR and Machine Learning Methods. Molecules 2018, 23, 2892. [Google Scholar] [CrossRef] [PubMed]
- Rao, H.; Zhu, Z.; Le, Z.; Xu, Z. QSPR models for the critical temperature and pressure of cycloalkanes. Chem. Phys. Lett. 2022, 808, 140088. [Google Scholar]
- Velázquez-Libera, J.L.; Caballero, J.; Toropova, A.P.; Toropov, A.A. Estimation of 2D autocorrelation descriptors and 2D Monte Carlo descriptors as a tool to build up predictive models for acetylcholinesterase (AChE) inhibitory activity. Chemom. Intell. Lab. Syst. 2019, 184, 14–21. [Google Scholar] [CrossRef]
- Dehmer, M.; Emmert-Streib, F.; Tripathi, S. Large-scale evaluation of molecular descriptors by means of clustering. PLoS ONE 2013, 8, e83956. [Google Scholar] [CrossRef] [PubMed]
- Qiu, J.; Gu, Q.; Sha, Y.; Huang, Y.; Zhang, M.; Luo, Z. Preparation and application of dielectric polymers with high permittivity and low energy loss: A mini review. J. Appl. Polym. Sci. 2022, 139, 52367. [Google Scholar] [CrossRef]
- Wang, Q.; Che, J.; Wu, W.; Hu, Z.; Liu, X.; Ren, T.; Chen, Y.; Zhang, J. Contributing Factors of Dielectric Properties for Polymer Matrix Composites. Polymers 2023, 15, 590. [Google Scholar] [CrossRef] [PubMed]
- Grisoni, F.; Merk, D.; Byrne, R.; Schneider, G. Scaffold-Hopping from Synthetic Drugs by Holistic Molecular Representation. Sci. Rep. 2018, 8, 16469. [Google Scholar] [CrossRef]
| Model Type | Common Values | Unique Values |
|---|---|---|
| Gradient Boosting Regressor_A | alpha: 0.9; ccp_alpha: 0.0; criterion:friedman_mse; init: None; learning_rate: 0.2; loss: squared_error; | max depth: 4; n estimators: 10 |
| max_features: None; max_leaf_nodes: None; min_impurity_decrease: 0.0; min_samples_leaf: 1; | ||
| Gradient Boosting Regressor_B | min_samples_split: 2; min_weight_fraction_leaf: 0.0; n_iter_no_change: None; random_state: 42; | max depth’: 2; n estimators: 13 |
| subsample: 1.0; ‘tol’: 0.0001; validation_fraction: 0.1; verbose: 0; warm_start: False. |
| Descriptor | GBR_A | GBR_B | Definition and Scope | Descriptor Type |
|---|---|---|---|---|
| N% | X | percentage of N atoms | Constitutional Indices | |
| J_Dz(p) | X | Balaban-like index from Barysz matrix weighted by polarizability | 2D matrix-based descriptors | |
| P_VSA_e_3 | X | P_VSA-like on Sanderson electronegativity, bin 3 | P_VSA-like descriptors | |
| P_VSA_i_1 | X | P_VSA-like on ionization potential, bin 1 | P_VSA-like descriptors | |
| AVS_Coulomb | X | Average vertex sum from Coulomb matrix | 3D matrix-based descriptors | |
| TDB09m | X | X | 3D Topological distance-based descriptors lag 9 weighted by mass | 3D autocorrelations |
| HATS2p | X | leverage-weighted autocorrelation of lag 2/weighted by polarizability | GETAWAY descriptors | |
| MLOGP2 | X | X | squared Moriguchi octanol–water partition coeff. (logP^2) | Molecular properties |
| GATS2s | X | Geary autocorrelation of lag 2 weighted by I-state | 2D autocorrelations | |
| Eig08_AEA (ri) | X | Eigen value n. 8 from augmented edge adjacency mat. weighted by resonance integral | Edge adjacency indices | |
| RTs+ | X | R maximal index/ weighted by I-state | GETAWAY descriptors | |
| WHALES60_Rem | X | WHALES Remoteness (Rem) (percentile 60) | WHALES descriptors |
| Model | R2 (Train) | RMSE (Train) | MAE (Train) | MAECV | R2 (Test) | RMSE (Test) | MAE (Test) | CCC (Test) | Q2F1 | Q2F2 | k | k′ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| GBR_A | 0.938 | 0.123 | 0.100 | 0.261 | 0.802 | 0.256 | 0.212 | 0.869 | 0.805 | 0.802 | 1.035 | 0.961 |
| GBR_B | 0.822 | 0.208 | 0.155 | 0.273 | 0.704 | 0.313 | 0.213 | 0.787 | 0.710 | 0.704 | 0.101 | 0.980 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ascencio-Medina, E.; He, S.; Daghighi, A.; Iduoku, K.; Casanola-Martin, G.M.; Arrasate, S.; González-Díaz, H.; Rasulev, B. Prediction of Dielectric Constant in Series of Polymers by Quantitative Structure-Property Relationship (QSPR). Polymers 2024, 16, 2731. https://doi.org/10.3390/polym16192731
Ascencio-Medina E, He S, Daghighi A, Iduoku K, Casanola-Martin GM, Arrasate S, González-Díaz H, Rasulev B. Prediction of Dielectric Constant in Series of Polymers by Quantitative Structure-Property Relationship (QSPR). Polymers. 2024; 16(19):2731. https://doi.org/10.3390/polym16192731
Chicago/Turabian StyleAscencio-Medina, Estefania, Shan He, Amirreza Daghighi, Kweeni Iduoku, Gerardo M. Casanola-Martin, Sonia Arrasate, Humberto González-Díaz, and Bakhtiyor Rasulev. 2024. "Prediction of Dielectric Constant in Series of Polymers by Quantitative Structure-Property Relationship (QSPR)" Polymers 16, no. 19: 2731. https://doi.org/10.3390/polym16192731
APA StyleAscencio-Medina, E., He, S., Daghighi, A., Iduoku, K., Casanola-Martin, G. M., Arrasate, S., González-Díaz, H., & Rasulev, B. (2024). Prediction of Dielectric Constant in Series of Polymers by Quantitative Structure-Property Relationship (QSPR). Polymers, 16(19), 2731. https://doi.org/10.3390/polym16192731








