Systematic Investigation on the Swelling Response and Oil Resistance of NBR Using the Prediction Models Determined by the Modified Flory–Huggins Interaction Parameter
Abstract
1. Introduction
2. Experimental Section
2.1. Materials
2.2. Equilibrium Swelling Test
3. Results and Discussion
3.1. Correlation of Swelling Ratio with Solubility Parameter
3.2. Flory–Huggins Interaction Parameters of NBR/Solvent
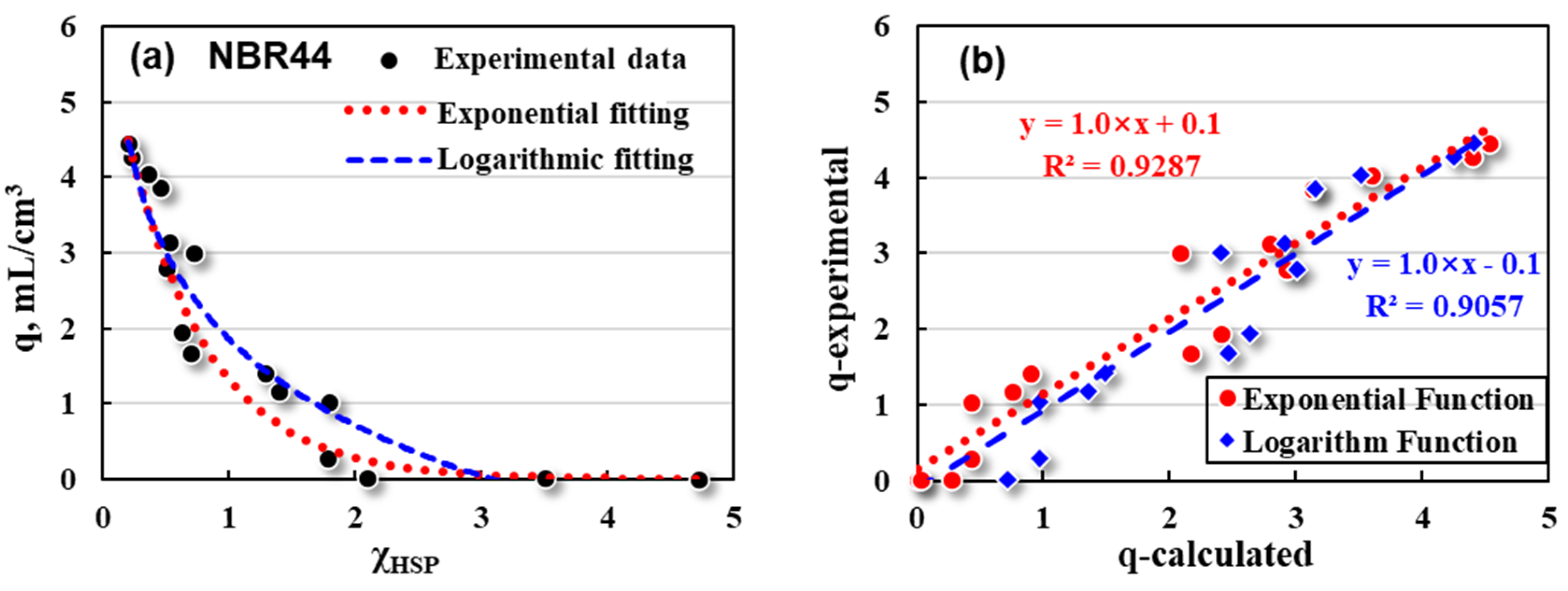
3.3. Prediction Model for the Swelling Response of NBR
3.4. Basic Prediction Models of Swelling Responses
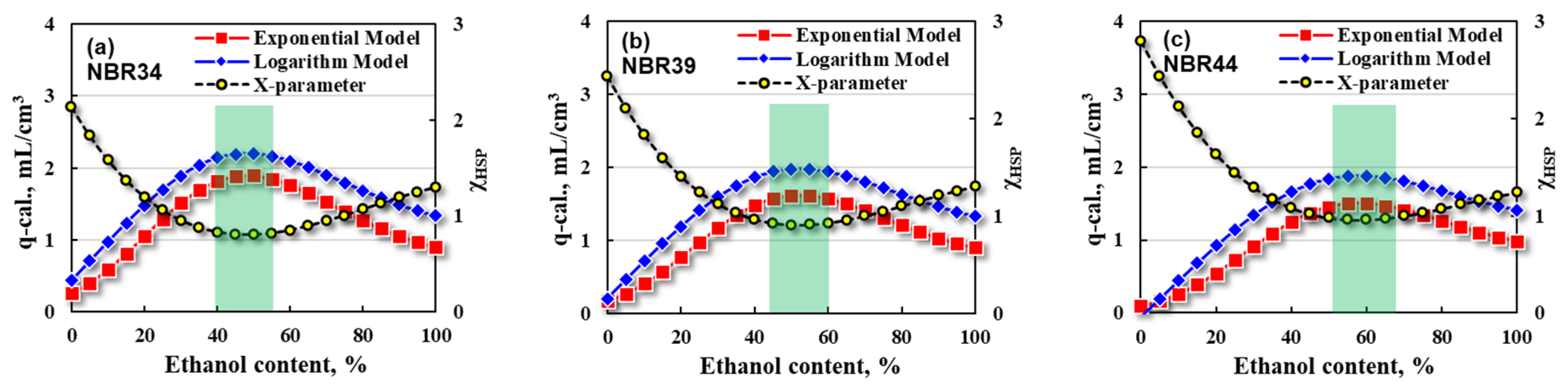
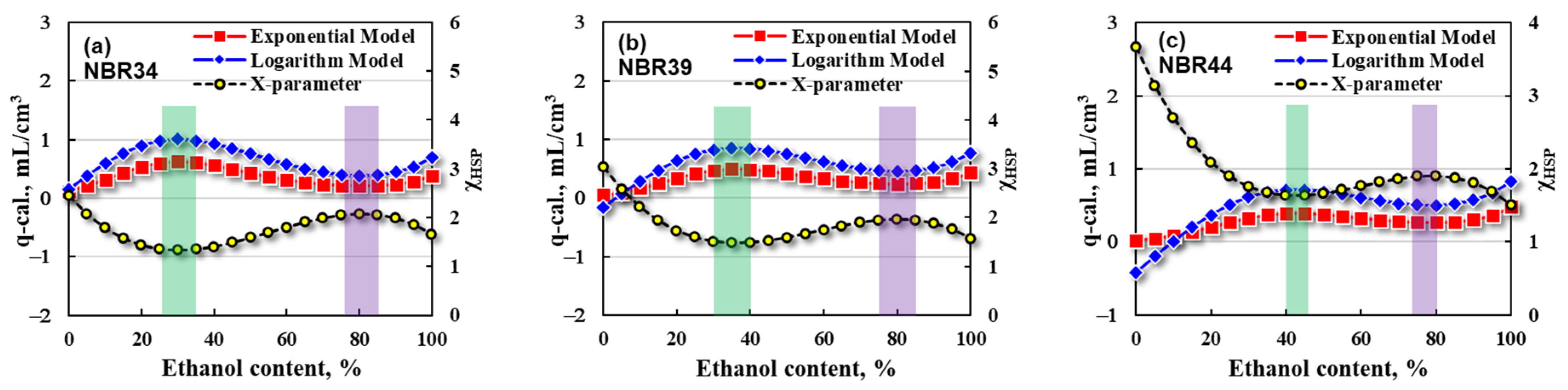
3.5. Application of Prediction Model in Oil Resistance of NBR
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Yang, S.; Che, R.; Chen, J.; He, Z.; Lai, T.; Liang, Y.; Bian, X. A Feasible Way to Modify Microcrystalline Cellulose Powder and Its Reinforcing Effect for NBR Composites. Polym. Compos. 2024, 45, 4709–4724. [Google Scholar] [CrossRef]
- Yang, T.; Han, C.; Deng, Q.; Wen, F. Optimized Tribological Performance of Nitrogen-Doped Diamond-like Carbon Films on NBR: Influence of Bias Voltage of DC Magnetron Sputtering. Nanomaterials 2024, 14, 564. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Li, Y.; Qian, C.; Wang, S.; Liu, D. Relationship between the Aging Thermal Oxygen and Mechanical Properties of Nitrile Butadiene Rubber Reinforced by RD-Loaded Carboxylated Carbon Nanotubes. Appl. Surf. Sci. 2024, 655, 159569. [Google Scholar] [CrossRef]
- Xie, X.; Yang, D. Simultaneously Improved Thermal Conductivity and Dielectric Properties of NBR Composites by Constructing 3D Hybrid Filler Networks. Macromol. Mater. Eng. 2023, 308, 2300016. [Google Scholar] [CrossRef]
- Hao, X.; Wang, G.; Wang, X.; Li, K.; He, Q. The Thermal Stability and Flame Retardant Effect of Al(OH)3 on NBR Containing Intumescent Flame Retardant. J. Polym. Res. 2023, 30, 410. [Google Scholar] [CrossRef]
- Ammineni, S.P.; Nagaraju, C.; Lingaraju, D. Thermal Degradation of Naturally Aged NBR with Time and Temperature. Mater. Res. Express 2022, 9, 065305. [Google Scholar] [CrossRef]
- Ghowsi, M.A.; Jamshidi, M. Using a Facile Method to Predict Properties of Recycled Waste Nitrile Rubber (NBR) through Devulcanization. Sci. Rep. 2023, 13, 15361. [Google Scholar] [CrossRef]
- Da Silva Ruiz, N.M.; de Sousa, A.M.F.; Da Costa Marques Calderari, M.R.; de Figueiredo, M.A.G.; Lima, A.P.; de Azevedo, E.R. Time Domain NMR Evaluation of Thermal and Thermochemical Aging of Nitrile Rubber on Crosslinking and Mechanical Properties. Polym. Degrad. Stab. 2024, 224, 110727. [Google Scholar] [CrossRef]
- Schmidt, F.C. The Solubility of Nonelectrolytes (Hildebrand, Joel H.). J. Chem. Educ. 1952, 29, 51. [Google Scholar] [CrossRef][Green Version]
- Jiang, X.; Yuan, X.; Guo, X.; Zeng, F.; Liu, G. Determination of three-dimensional solubility parameters of HNBR/EPDM blends and the transport behaviors in ester solvents. J. Appl. Polym. Sci. 2022, 139, e52881. [Google Scholar] [CrossRef]
- Jing, Y.; Cui, Z.; Zou, H.; Tu, J.; Jiang, X.; Shi, X.; Yong, Z.; Liu, S.; Liu, G. Three-dimensional solubility parameters of natural rubber and its predictive power in diffusion coefficients. J. Appl. Polym. Sci. 2022, 139, 51473. [Google Scholar] [CrossRef]
- Seymour, R.B.; Sosa, J.M. Estimation of Solubility Parameters of Nonelectrolytes. Nature 1974, 248, 759–761. [Google Scholar] [CrossRef]
- Nielsen, T.B.; Hansen, C.M. Elastomer Swelling and Hansen Solubility Parameters. Polym. Test. 2005, 24, 1054–1061. [Google Scholar] [CrossRef]
- Murase, M.; Ohta, R.; Iseki, T. Liquid-Repellent Films Comprising Octamethylsilsesquioxane Selected Based on Three-Dimensional Solubility Parameters. Langmuir 2020, 36, 2247–2254. [Google Scholar] [CrossRef]
- Wang, Y.Z.; Bi, L.Y.; Zhang, H.J.; Zhu, X.T.; Liu, G.Y.; Qiu, G.X.; Liu, S.S. Predictive power in oil resistance of fluororubber and fluorosilicone rubbers based on three-dimensional solubility parameter theory. Polym. Test. 2019, 75, 380–386. [Google Scholar] [CrossRef]
- Liu, G.; Hoch, M.; Liu, S.; Kulbaba, K.; Qiu, G. Quantitative exploration of the swelling response for carbon black filled hydrogenated nitrile rubber with three-dimensional solubility parameters. Polym. Bull. 2015, 72, 1961–1974. [Google Scholar] [CrossRef]
- Wiśniewski, R.; Śmieszek, E.; Kamińska, E. Three-Dimensional Solubility Parameters: Simple and Effective Determination of Compatibility Regions. Prog. Org. Coat. 1995, 26, 265–274. [Google Scholar] [CrossRef]
- Huang, J.-C.; Lin, K.-T.; Deanin, R.D. Three-Dimensional Solubility Parameters of Poly(ε-Caprolactone). J. Appl. Polym. Sci. 2006, 100, 2002–2009. [Google Scholar] [CrossRef]
- Larson, B.K.; Hess, J.M.; Williams, J.M. Procedure for Estimating Oil Three-Dimensional Solubility Parameters. Rubber Chem. Technol. 2017, 90, 621–632. [Google Scholar] [CrossRef]
- Su, R.; Liu, G.; Sun, H.; Yong, Z. A new method to measure the three-dimensional solubility parameters of acrylate rubber and predict its oil resistance. Polym. Bull. 2022, 79, 971–984. [Google Scholar] [CrossRef]
- Jiang, X.; Hao, Y.; Wang, H.; Tu, J.; Liu, G. Application of Three-Dimensional Solubility Parameter in Diffusion Behavior of Rubber-Solvent System and Its Predictive Power in Calculating the Key Parameters. Macromol. Res. 2022, 30, 271–278. [Google Scholar] [CrossRef]
- Wang, H.; Liu, S.; Liu, G. Investigation on the Thermo-Oxidative Aging Resistance of Nitrile-Butadiene Rubber/Polyamide Elastomer Blend and the Swelling Behaviors in Fuels Predicted via Hansen Solubility Parameter Method. Polym. Degrad. Stab. 2023, 217, 110512. [Google Scholar] [CrossRef]
- Mieczkowski, R. The Determination of the Solubility Parameter Components of Polystyrene. Eur. Polym. J. 1989, 25, 1055–1057. [Google Scholar] [CrossRef]
- Chen, J.; Farajtabar, A.; Jouyban, A.; Acree, W.E., Jr.; Zhao, H. Solubility, Three-Dimensional Hansen Solubility Parameters, and Solution Thermodynamics of 3,3′-Diaminodiphenyl Sulfone in 14 Neat Solvents from 283.15 to 328.15 K. J. Chem. Eng. Data 2021, 66, 2167–2176. [Google Scholar] [CrossRef]
- Koenhen, D.M.; Smolders, C.A. The Determination of Solubility Parameters of Solvents and Polymers by Means of Correlations with Other Physical Quantities. J. Appl. Polym. Sci. 1975, 19, 1163–1179. [Google Scholar] [CrossRef]
- Marco, C.; Bello, A.; Fatou, J.G.; Garza, J. Solubility Parameter of Poly(1,3-Dioxepane). Die Makromol. Chem. 1986, 187, 177–185. [Google Scholar] [CrossRef]
- DiPaola-Baranyi, G. Estimation of Polymer Solubility Parameters by Inverse Gas Chromatography. Macromolecules 1982, 15, 622–624. [Google Scholar] [CrossRef]
- Siemann, U. The Solubility Parameter of Poly (Dl-Lactic Acid). Eur. Polym. J. 1992, 28, 293–297. [Google Scholar] [CrossRef]
- Flory, P.J.; Rehner, J., Jr. Statistical Mechanics of Cross-Linked Polymer Networks II. Swelling. J. Chem. Phys. 1943, 11, 521–526. [Google Scholar] [CrossRef]
- Liu, G.; Hoch, M.; Wrana, C.; Kulbaba, K.; Liu, S.; Bi, W.; Zhao, S. Investigation of the swelling response and quantitative prediction for hydrogenated nitrile rubber. Polym. Test. 2014, 34, 72–77. [Google Scholar] [CrossRef]
- Hashimoto, I. Relation Between the Swelling and Solution Behaviors and the Three Dimensional Solubility Parameters for Various Polymers in Organic Solvents. Sen’i Gakkaishi 1978, 34, T469–T473. [Google Scholar] [CrossRef]
- Liu, S.; Jing, Y.; Tu, J.; Zou, H.; Yong, Z.; Liu, G. Systematic Investigation on the Swelling Behaviors of Acrylonitrile-butadiene Rubber via Solubility Parameter and Flory-Huggins Interaction Parameter. J. App. Polym. Sci. 2022, 139, 52172. [Google Scholar] [CrossRef]
- Tang, S.; Zhang, R.; Liu, F.; Liu, X. Hansen Solubility Parameters of Polyglycolic Acid and Interaction Parameters between Polyglycolic Acid and Solvents. Eur. Polym. J. 2015, 72, 83–88. [Google Scholar] [CrossRef]
- Pajula, K.; Taskinen, M.; Lehto, V.-P.; Ketolainen, J.; Korhonen, O. Predicting the Formation and Stability of Amorphous Small Molecule Binary Mixtures from Computationally Determined Flory−Huggins Interaction Parameter and Phase Diagram. Mol. Pharm. 2010, 7, 795–804. [Google Scholar] [CrossRef] [PubMed]
- Lindvig, T.; Michelsen, M.L.; Kontogeorgis, G.M.A. Flory–Huggins Model Based on the Hansen Solubility Parameters. Fluid Phase Equilibria 2002, 203, 247–260. [Google Scholar] [CrossRef]
- Clarke, C.J.; Eisenberg, A.; La Scala, J.; Rafailovich, M.H.; Sokolov, J.; Li, Z.; Qu, S.; Nguyen, D.; Schwarz, S.A.; Strzhemechny, Y.; et al. Measurements of the Flory−Huggins Interaction Parameter for Polystyrene−Poly(4-Vinylpyridine) Blends. Macromolecules 1997, 30, 4184–4188. [Google Scholar] [CrossRef]
- Huang, J. Probe Dependency of Flory–Huggins Interaction Parameters between Solvents: Cases of Hydrocarbons and Isosteric Derivatives. J. Appl. Polym. Sci. 2013, 127, 5000–5006. [Google Scholar] [CrossRef]
- Liu, S.; Jing, Y.; Tu, J.; Zou, H.; Yong, Z.; Gao, Y.; Tang, Z.; Liu, G. New Flory-Huggins Interaction Parameter between SBR and P-phenylenediamine Antioxidants and the Predictive Power in Molecular Structure and Rubber Formula Design. J. Appl. Polym. Sci. 2022, 139, 51840. [Google Scholar] [CrossRef]
- Jiang, X.; Yuan, X.; Guo, X.; Zeng, F.; Wang, H.; Liu, G. Study on the Application of Flory–Huggins Interaction Parameters in Swelling Behavior and Crosslink Density of HNBR/EPDM Blend. Fluid Phase Equilibria 2023, 563, 113589. [Google Scholar] [CrossRef]
- Chu, H.Z.; Liu, D.; Cui, Z.W.; Wang, K.; Qiu, G.X.; Liu, G.Y. Effect of Crosslink Density on Solubility Parameters of Styrene Butadiene Rubber and the Application in Pre-Screening of New Potential Additives. Polym. Test. 2020, 81, 106253. [Google Scholar] [CrossRef]
- Liu, S.S.; Li, X.P.; Qi, P.J.; Song, Z.J.; Zhang, Z.; Wang, K.; Qiu, G.X.; Liu, G.Y. Determination of Three-Dimensional Solubility Parameters of Styrene Butadiene Rubber and the Potential Application in Tire Tread Formula Design. Polym. Test. 2020, 81, 106170. [Google Scholar] [CrossRef]


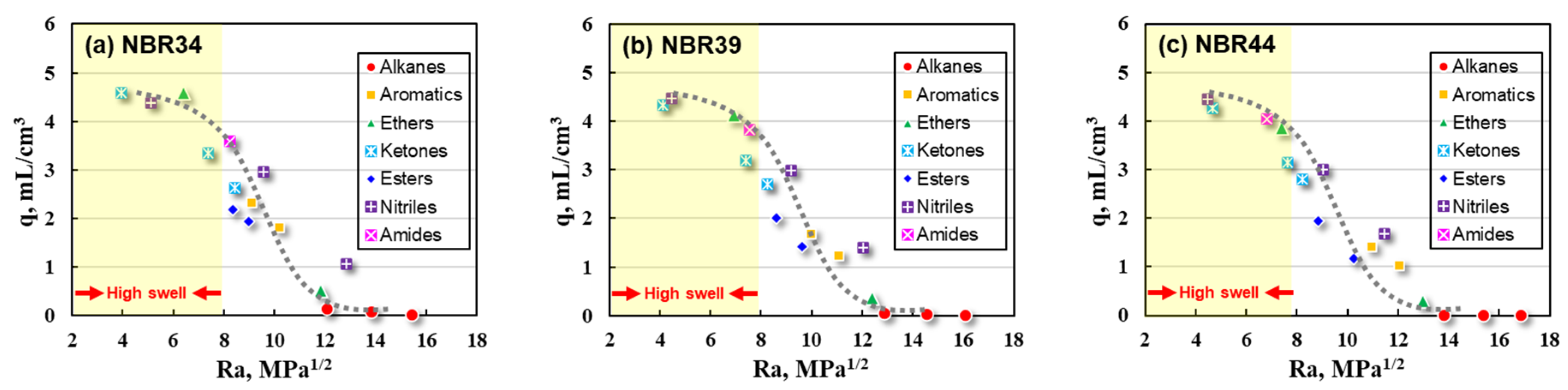
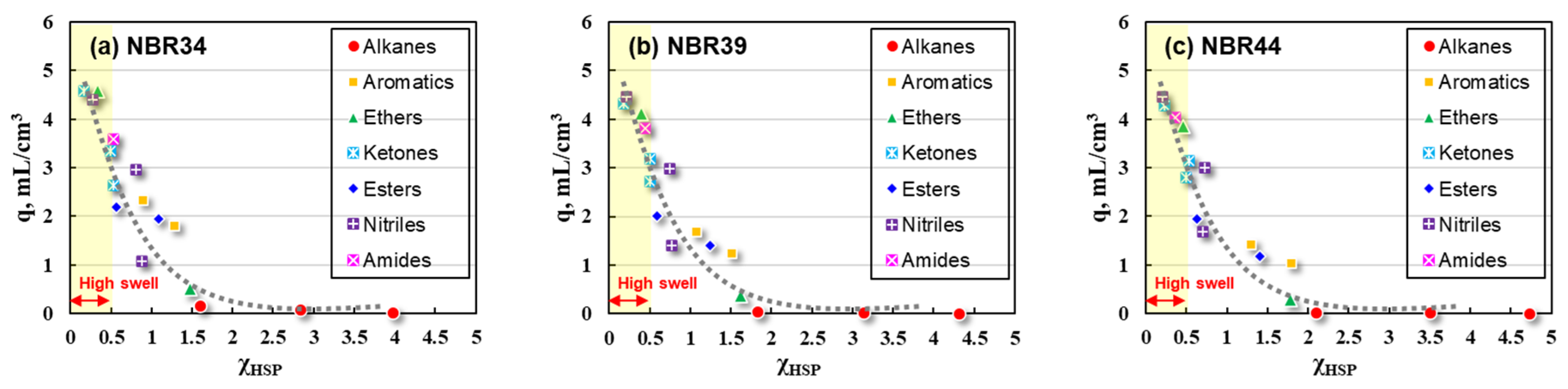




| Solvents | δd, MPa1/2 | δp, MPa1/2 | δh, MPa1/2 | q, NBR34 | q, NBR39 | q, NBR44 | |
|---|---|---|---|---|---|---|---|
| Alkanes | Isooctane | 14.10 | 0.00 | 0.00 | 0.03 | 0.01 | 0.01 |
| Heptane | 15.30 | 0.00 | 0.00 | 0.09 | 0.03 | 0.02 | |
| Cyclohexane | 16.80 | 0.00 | 0.20 | 0.16 | 0.05 | 0.02 | |
| Aromatics | Ethylbenzene | 17.80 | 0.60 | 1.40 | 1.81 | 1.24 | 1.03 |
| Toluene | 18.00 | 1.40 | 2.00 | 2.33 | 1.68 | 1.42 | |
| Ethers | Diethyl ether | 14.50 | 2.90 | 4.60 | 0.51 | 0.36 | 0.29 |
| THF | 16.80 | 5.70 | 8.00 | 4.59 | 4.12 | 3.86 | |
| Esters | Butyl acetate | 15.60 | 6.20 | 4.90 | 3.35 | 3.19 | 3.14 |
| Methyl acetate | 15.50 | 7.20 | 7.60 | 2.63 | 2.71 | 2.79 | |
| Ketones | 2-butanone | 16.00 | 9.00 | 5.10 | 4.58 | 4.33 | 4.27 |
| Acetone | 15.50 | 10.40 | 7.00 | 1.94 | 1.41 | 1.17 | |
| Cyclohexanone | 17.80 | 8.40 | 5.10 | 2.19 | 2.01 | 1.95 | |
| Nitriles | Butyronitrile | 15.30 | 12.40 | 5.10 | 2.96 | 2.98 | 3 |
| Benzonitrile | 18.80 | 12.00 | 3.30 | 4.39 | 4.46 | 4.45 | |
| Acetonitrile | 15.30 | 18.00 | 6.10 | 1.07 | 1.4 | 1.68 | |
| Amides | DMF | 17.40 | 13.70 | 11.30 | 3.59 | 3.82 | 4.04 |
| NBR | δd, MPa1/2 | δp, MPa1/2 | δh, MPa1/2 | δt, MPa1/2 |
|---|---|---|---|---|
| NBR34 | 19.6 | 8.5 | 6.7 | 22.4 |
| NBR39 | 19.6 | 9.6 | 6.7 | 22.8 |
| NBR44 | 19.6 | 10.5 | 7.2 | 23.4 |
| Fluids | δd, MPa1/2 | δp, MPa1/2 | δh, MPa1/2 | δt, MPa1/2 | Vmol, mL/mol |
|---|---|---|---|---|---|
| IRM 903 | 17.9 | 0.7 | 1.8 | 18.0 | 350 |
| Bio-diesel | 16.5 | 0.3 | 0.9 | 16.5 | 152 |
| Ethanol | 15.8 | 8.8 | 19.4 | 26.5 | 59 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jing, Y.; Liu, G. Systematic Investigation on the Swelling Response and Oil Resistance of NBR Using the Prediction Models Determined by the Modified Flory–Huggins Interaction Parameter. Polymers 2024, 16, 2696. https://doi.org/10.3390/polym16192696
Jing Y, Liu G. Systematic Investigation on the Swelling Response and Oil Resistance of NBR Using the Prediction Models Determined by the Modified Flory–Huggins Interaction Parameter. Polymers. 2024; 16(19):2696. https://doi.org/10.3390/polym16192696
Chicago/Turabian StyleJing, Yiran, and Guangyong Liu. 2024. "Systematic Investigation on the Swelling Response and Oil Resistance of NBR Using the Prediction Models Determined by the Modified Flory–Huggins Interaction Parameter" Polymers 16, no. 19: 2696. https://doi.org/10.3390/polym16192696
APA StyleJing, Y., & Liu, G. (2024). Systematic Investigation on the Swelling Response and Oil Resistance of NBR Using the Prediction Models Determined by the Modified Flory–Huggins Interaction Parameter. Polymers, 16(19), 2696. https://doi.org/10.3390/polym16192696






