Prediction of Glass Transition Temperature of Polymers Using Simple Machine Learning
Abstract
1. Introduction
2. Materials and Methods
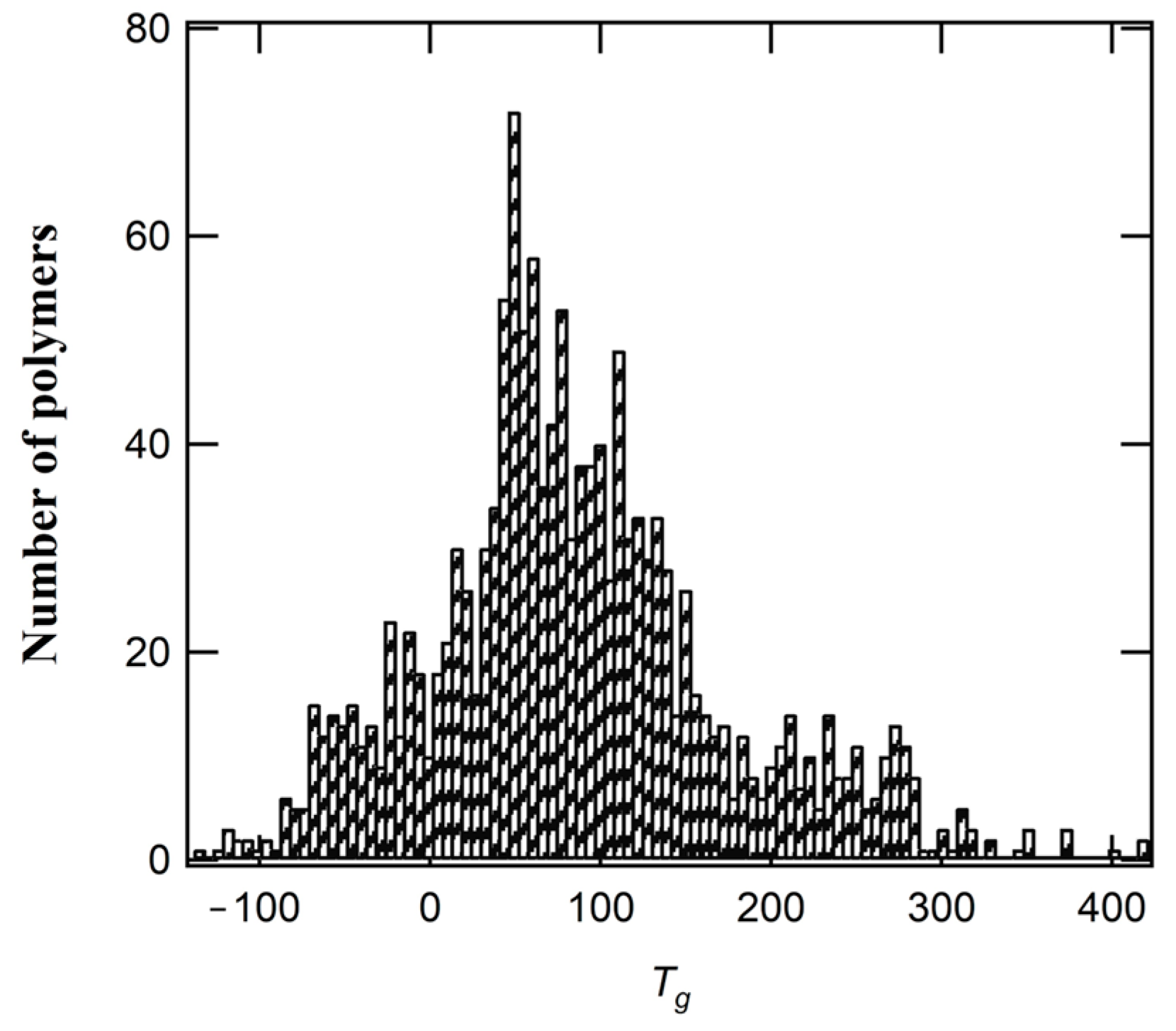
2.1. Data Collection and Preparation
2.2. Machine Learning Modeling
2.3. Model Performance Evaluation
3. Results
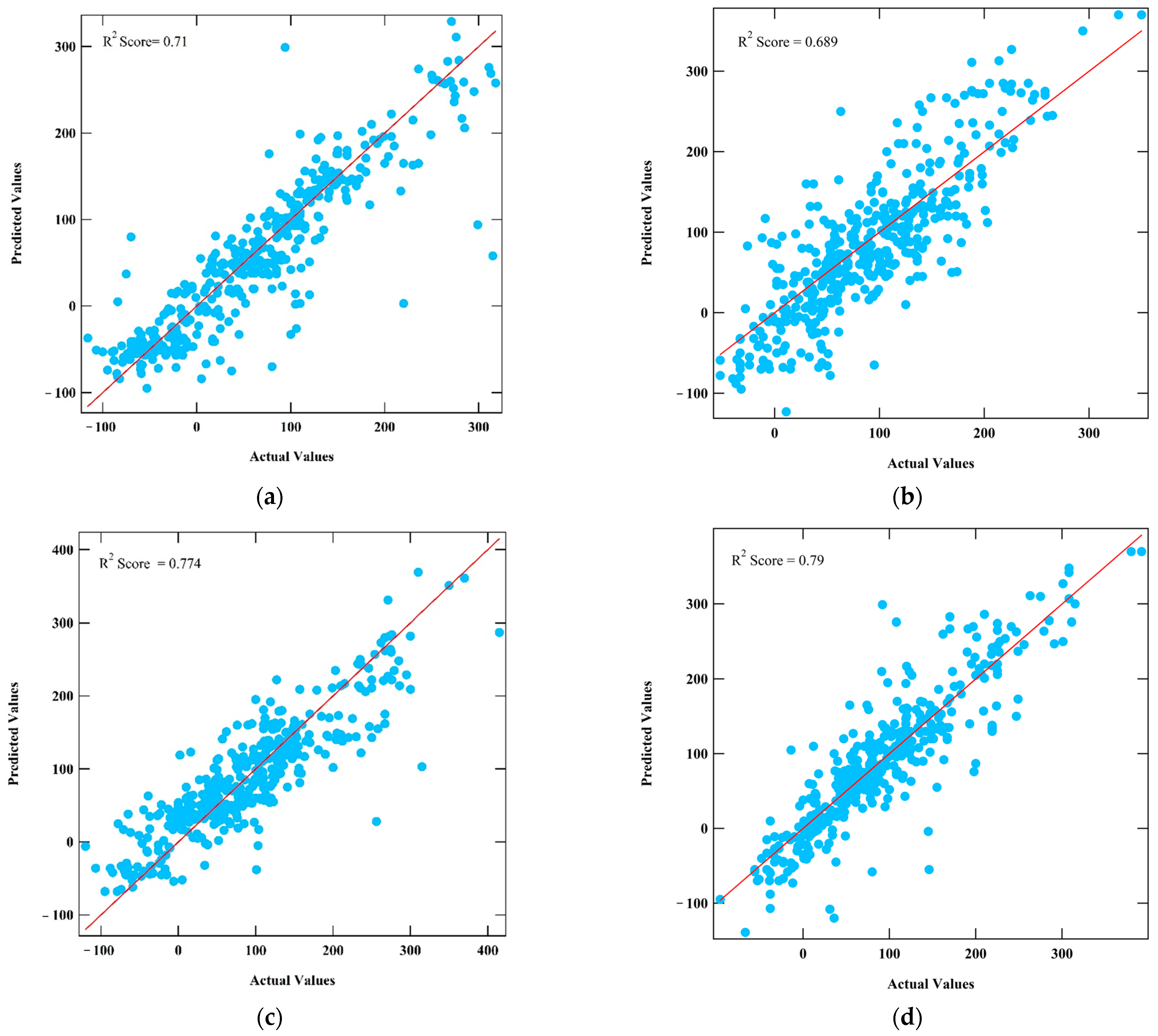
3.1. Machine Learning Model Prediction Performance
3.2. Model Validation for Predicting the Tg of Polymers Using SMILES Descriptors
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Yuan, L.; Shen, Y. A review of research on recyclable polymer materials. MATEC Web Conf. 2022, 363, 01025. [Google Scholar] [CrossRef]
- Chalid, M.; Fikri, A.I.; Satrio, H.H.; Joshua, M.; Fatriansyah, J.F. An investigation of the melting temperature effect on the rate of solidification in polymer using a modified phase field model. Int. J. Technol. 2017, 8, 1321–1328. [Google Scholar] [CrossRef][Green Version]
- Fatriansyah, J.F.; Orihara, H. Dynamical properties of nematic liquid crystal subjected tp shear flow and magnetic fields: Tumbling instability and nonequilibrium fluctuations. Phys. Rev. E 2013, 88, 012510–012518. [Google Scholar] [CrossRef] [PubMed]
- Goswami, S.; Ghosh, R.; Neog, A.; Das, B. Deep learning based approach for prediction of glass transition temperature in polymers. Mater. Today Proc. 2021, 46, 5838–5843. [Google Scholar] [CrossRef]
- Xie, R.; Weisen, A.R.; Lee, Y.; Aplan, M.A.; Fenton, A.M.; Masucci, A.E.; Kempe, F.; Sommer, M.; Pester, C.W.; Colby, R.H.; et al. Glass transition temperature from the chemical structure of conjugated polymers. Nat. Commun. 2020, 11, 893. [Google Scholar] [CrossRef]
- Jha, A.; Chandrasekaran, A.; Kim, C.; Ramprasad, R. Impact of dataset uncertainties on machine learning model predictions: The example of polymer glass transition temperatures. Model. Simul. Mater. Sci. Eng. 2019, 27, 024002. [Google Scholar] [CrossRef]
- Ilmiati, S.; Hafiza, J.; Fatriansyah, J.F.; Kustiyah, E.; Chalid, M. Synthesis and characteristics of lignin-based polyurethane as a potential compatibilizer. Indones. J. Chem. 2018, 18, 390–396. [Google Scholar] [CrossRef]
- Fatriansyah, J.F.; Matari, T.; Harjanto, S. The preparation of activated carbon from coconut shell charcoal by novel mehano-chemical activation. Mater. Sci. Forum 2018, 929, 50–55. [Google Scholar] [CrossRef]
- Cassar, D.R.; Carvalho, A.C.P.L.F.; Zanotto, E.D. Predicting glass transition temperatures using neural networks. Acta Mater. 2018, 159, 249–256. [Google Scholar] [CrossRef]
- Fatriansyah, J.F.; Dhaneswara, D.; Abdurrahman, M.H.; Kuskendrianto, F.R.; Yusuf, M.B. Molecular dynamics simulation of hydrogen adsorption on silica. IOP Conf. Ser. Mater. Sci. Eng. 2019, 478, 012034. [Google Scholar] [CrossRef]
- Fatriansyah, J.F.; Sasaki, Y.; Orihara, H. Nonequilibrium steady-state response of a nematic liquid crystal under simple shear flow and electric fields. Phys. Rev. E 2014, 90, 032504–032511. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Friedrich, K. Artificial neural networks applied to polymer composited: A review. Compos. Sci. Technol. 2003, 63, 2029–2044. [Google Scholar] [CrossRef]
- Chen, G.; Tao, L.; Li, Y. Predicting polymers’ glass transition temperature by a chemical language processing model. Polymers 2021, 13, 1898. [Google Scholar] [CrossRef]
- Lo, S.-C.B.; Chan, H.-P.; Lin, J.-S.; Li, H.; Freedman, M.T.; Mun, S.K. Artificial convolution neural network for medical image pattern recognition. Neural Netw. 1995, 8, 1201–1214. [Google Scholar] [CrossRef]
- Imandoust, S.B.; Bolandraftar, M. Application of k-nearest neighbor (knn) approach for predicting economic events: Theoretical background. Int. J. Eng. Res. Appl. 2013, 3, 605–610. [Google Scholar]
- Zhang, F.; O’Donnell, L.J. Support Vector Machine. In Machine Learning; Mecheli, A., Vieira, S., Eds.; Academic Press: Cambridge, MA, USA, 2020; pp. 123–140. [Google Scholar]
- Zhang, Z. Introduction to machine learning: K-nearest neighbors. Ann. Transl. Med. 2016, 4, 218. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.-C.; Kuo, P.-H.; Chen, G.-Y. Machine learning prediction of turning precision using optimized XGBoost model. Appl. Sci. 2022, 12, 7739. [Google Scholar] [CrossRef]
- Pathy, A.; Meher, S.; Paramasivan, B. Predicting algal biochar yield using eXtreme Gradient Boosting (XGB) algorithm of machine learning methods. Agal Res. 2020, 50, 102006. [Google Scholar] [CrossRef]
- Joshi, A.V. Deep Learning. In Machine Learning and Artificial Intelligence, 2nd ed.; Springer International Publishing: Cham, Switzerland, 2023; pp. 149–169. [Google Scholar]
- Di Bucchianico, A. Coefficient of determination (R2). In Encyclopedia of Statistics in Quality and Reliability; Wiley: Hoboken, NJ, USA, 2007. [Google Scholar]
- Steurer, M.; Hill, R.J.; Pfeifer, N. Metrics for evaluating the performance of machine learning based automated valuation models. J. Prop. Res. 2021, 38, 99–129. [Google Scholar] [CrossRef]
- Turchetti, C. Stochastic Models of Neural Networks; IOS Press: Amsterdam, The Netherlands, 2004; Volume 102. [Google Scholar]
- Diebold, F.X.; Mariano, R.S. Comparing predictive accuracy. J. Bus. Econ. Stat. 2002, 20, 134–144. [Google Scholar] [CrossRef]
- Harrell, F.E., Jr.; Lee, K.L.; Califf, R.M.; Pryor, D.B.; Rosati, R.A. Regression modelling strategies for improved prognostic prediction. Stat. Med. 1984, 3, 143–152. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Li, Y.; Ma, Y. Comparison of XGBoost and the neural network model on the class-balanced datasets. In Proceedings of the 2021 IEEE 3rd International Conference on Frontiers Technology of Information and Computer (ICFTIC), Greenville, SC, USA, 12–14 November 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 457–461. [Google Scholar]



| Data | Min | Max | Average | Std. Dev. |
|---|---|---|---|---|
| Character length | 3 | 170 | 48.22 | 27.8 |
| Tg value | −139 | 420 | 85.40 | 88.82 |
| Model | Parameter | Optimal Value |
|---|---|---|
| KNN | Character length | 200 |
| n_neighbors | 8 | |
| SVR | Character length | 200 |
| Kernel | RBF | |
| C | 1 | |
| gamma | 0.01 | |
| XGB | Character length | 200 |
| max_depth | 10 | |
| learning_rate | 0.1509741801833367 | |
| n_estimators | 2.095 | |
| min_child_weight | 20 | |
| gamma | 0.010500376855063191 | |
| reg_lambda | 0.007188240690305372 | |
| reg_alpha | 2.4700851023872214 × 10−6 | |
| ANN | Character length | 200 |
| Number of hidden layers | 3 | |
| Number of nodes per hidden layer | 512, 256, 128 | |
| Activation function for input layer | ReLU | |
| Activation function for hidden layer | ReLU | |
| Activation function for output layer | Linear | |
| Optimizer | Adam | |
| Loss function | MSE | |
| Epoch | 100 | |
| Batch size | 479 | |
| Learning rate | 0.0001 | |
| RNN | Input dim | 45 |
| Input len | 200 | |
| Activation function for input layer | ReLU | |
| Activation function for hidden layer | ReLU | |
| Activation function for output layer | Linear | |
| Optimizer | Adam | |
| Loss function | MSE | |
| Epoch | 500 | |
| Batch size | 479 | |
| Patience | 50 |
| Model | Training Time |
|---|---|
| KNN | 4 s |
| SVR | 18 s |
| XGB | 7 s |
| ANN | 30 s |
| RNN | 14 h 12 min |
| Model | Diebold–Mariano Test Statistic Value | p-Value |
|---|---|---|
| XGBoost-ANN | 1.12 | 0.78 |
| XGBoost-RNN | 1.56 | 0.27 |
| ANN-RNN | 0.48 | 0.45 |
| Polymer Compounds | SMILES | Tg Actual | Tg Predicted | Delta |
|---|---|---|---|---|
| poly(ethyl 2-fluoroacrylate) | CCOC(=O)C(C*)(F)* | 94 | 97.3 | 3.3 |
| poly[(phenylarsandiyl)(1-phenylethene-1,2-diyl)] | *C=C([As](c1ccccc1)*)c1ccccc1 | 92.9 | 97 | 4.1 |
| poly{1-[(2,2-difluoroethane-1,1,2-triyl-1-oxy)methoxy]-2,2-difluoroethylene} | *C(C(F)(F)*)OCOC(C(F)(F)*)* | 122 | 122.7 | 0.7 |
| poly(2-phenylacetate) | *CC(C(=O)c1ccc(cc1)C)* | 71 | 69.5 | 1.5 |
| poly[(4,4′-methylenedianiline)-alt-(terephthaloyl dichloride)] | *Nc1ccc(cc1)Cc1ccc(cc1)NC(=O)c1ccc(cc1)C(=O)* | 300 | 260.8 | 39.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fatriansyah, J.F.; Linuwih, B.D.P.; Andreano, Y.; Sari, I.S.; Federico, A.; Anis, M.; Surip, S.N.; Jaafar, M. Prediction of Glass Transition Temperature of Polymers Using Simple Machine Learning. Polymers 2024, 16, 2464. https://doi.org/10.3390/polym16172464
Fatriansyah JF, Linuwih BDP, Andreano Y, Sari IS, Federico A, Anis M, Surip SN, Jaafar M. Prediction of Glass Transition Temperature of Polymers Using Simple Machine Learning. Polymers. 2024; 16(17):2464. https://doi.org/10.3390/polym16172464
Chicago/Turabian StyleFatriansyah, Jaka Fajar, Baiq Diffa Pakarti Linuwih, Yossi Andreano, Intan Septia Sari, Andreas Federico, Muhammad Anis, Siti Norasmah Surip, and Mariatti Jaafar. 2024. "Prediction of Glass Transition Temperature of Polymers Using Simple Machine Learning" Polymers 16, no. 17: 2464. https://doi.org/10.3390/polym16172464
APA StyleFatriansyah, J. F., Linuwih, B. D. P., Andreano, Y., Sari, I. S., Federico, A., Anis, M., Surip, S. N., & Jaafar, M. (2024). Prediction of Glass Transition Temperature of Polymers Using Simple Machine Learning. Polymers, 16(17), 2464. https://doi.org/10.3390/polym16172464






