Molecular Dynamics Simulation of Effect of Carbon Nanotube Diameter on Properties of Crosslinked Epichlorohydrin Rubbers
Abstract
1. Introduction
2. Model Construction
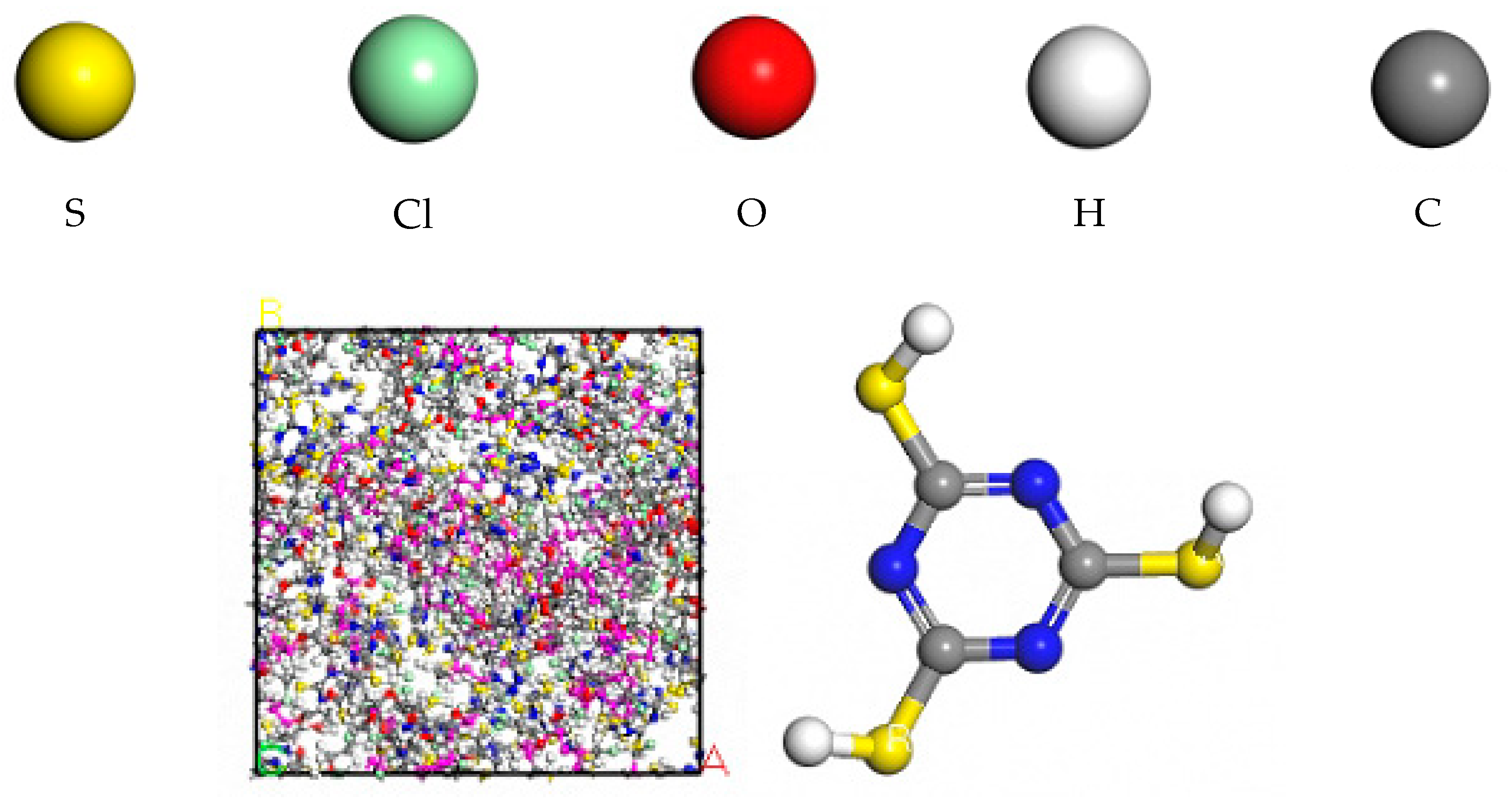
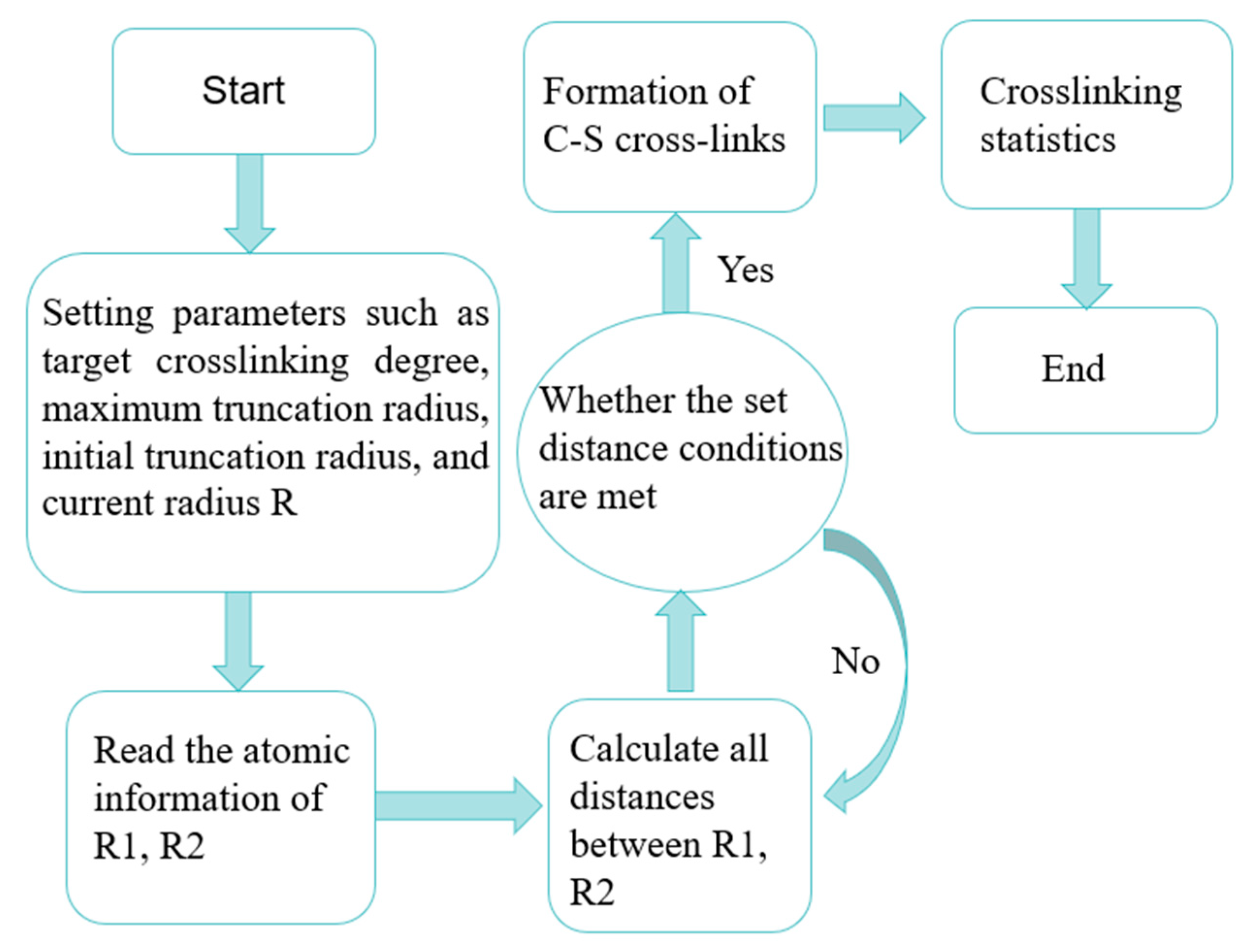
2.1. Crosslinking ECO Model Construction
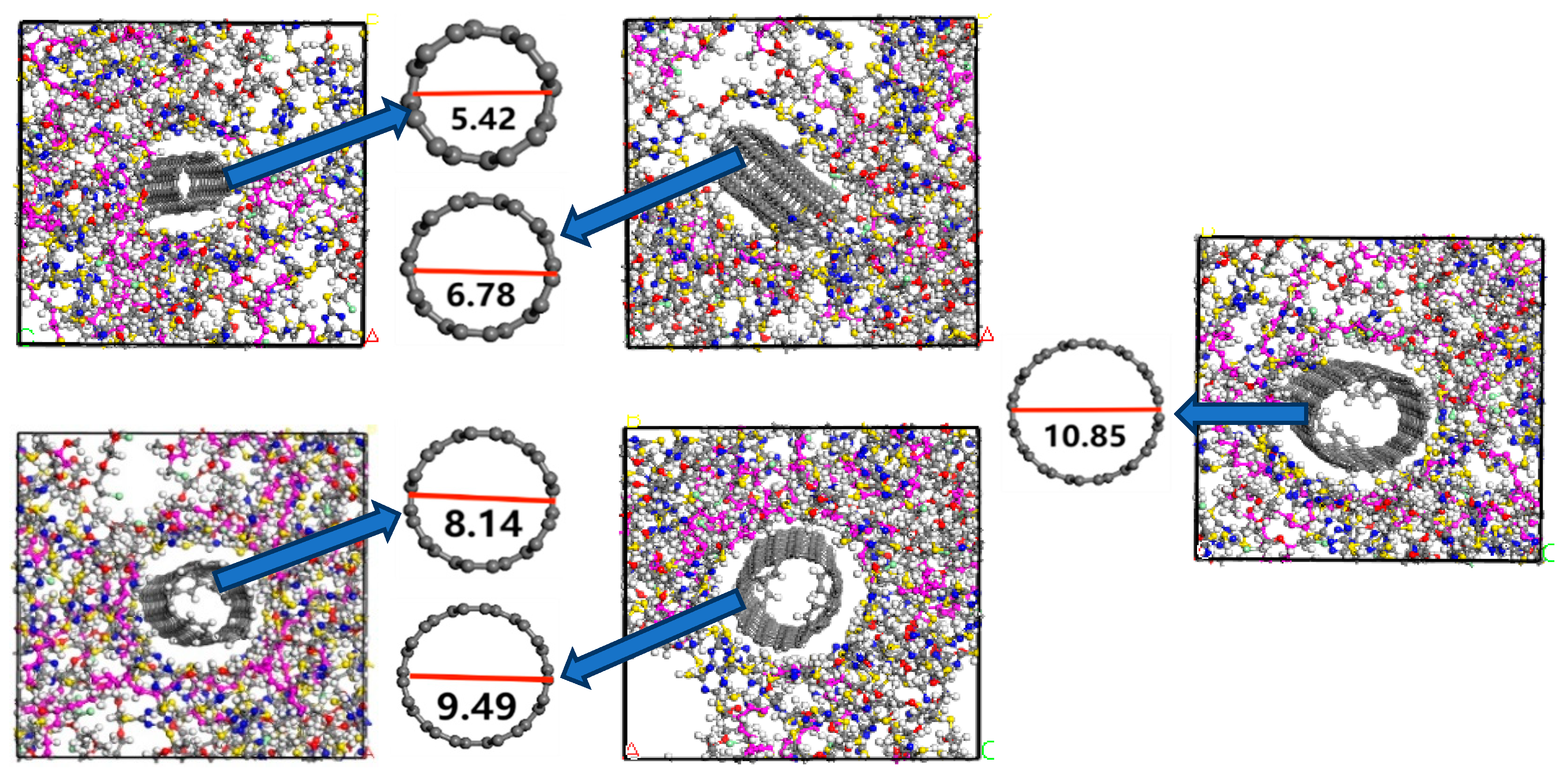
2.2. Construction of CNTs/ECO Models for Different Pipe Sizes
3. Results and Discussion
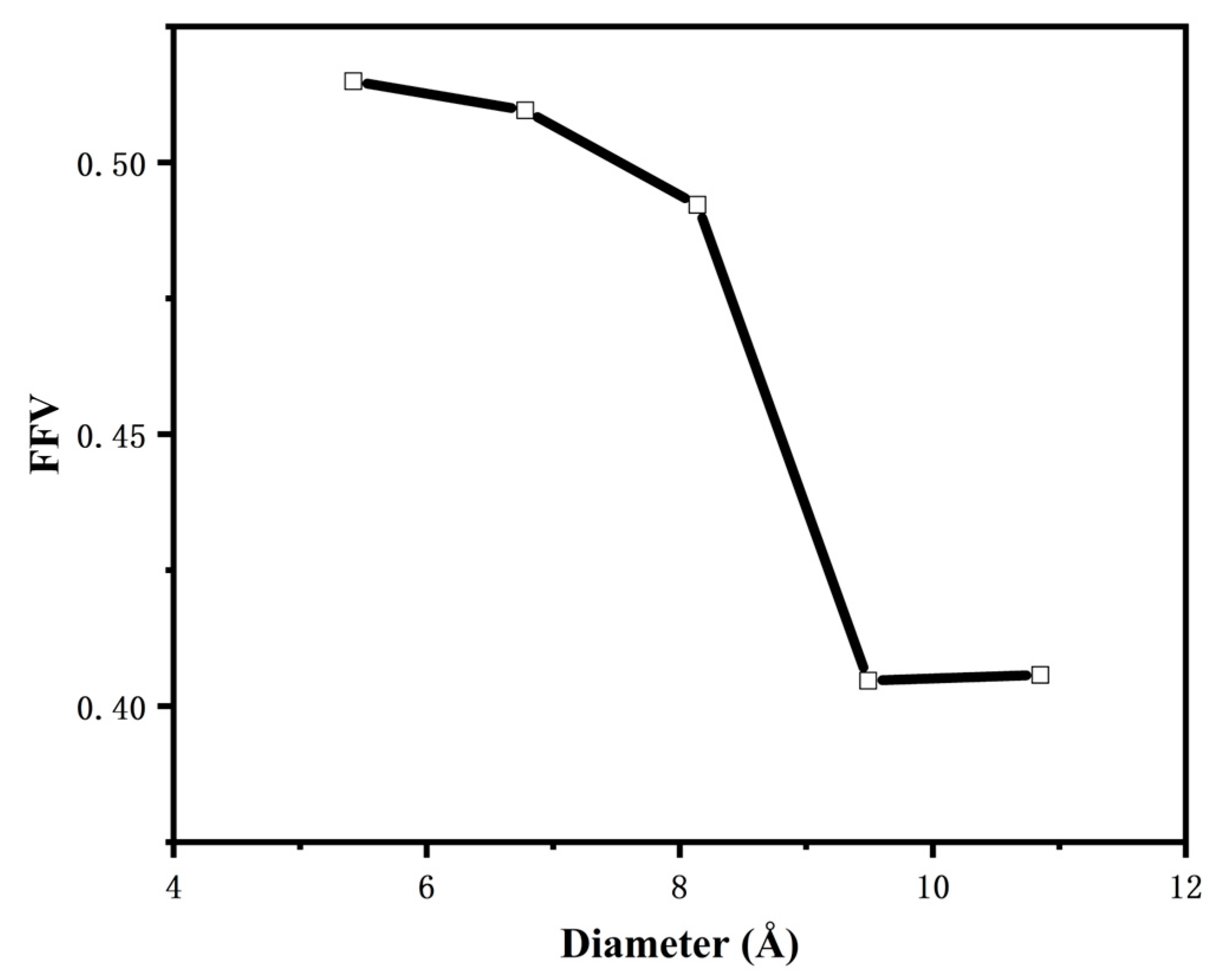
3.1. Free Volume Fraction
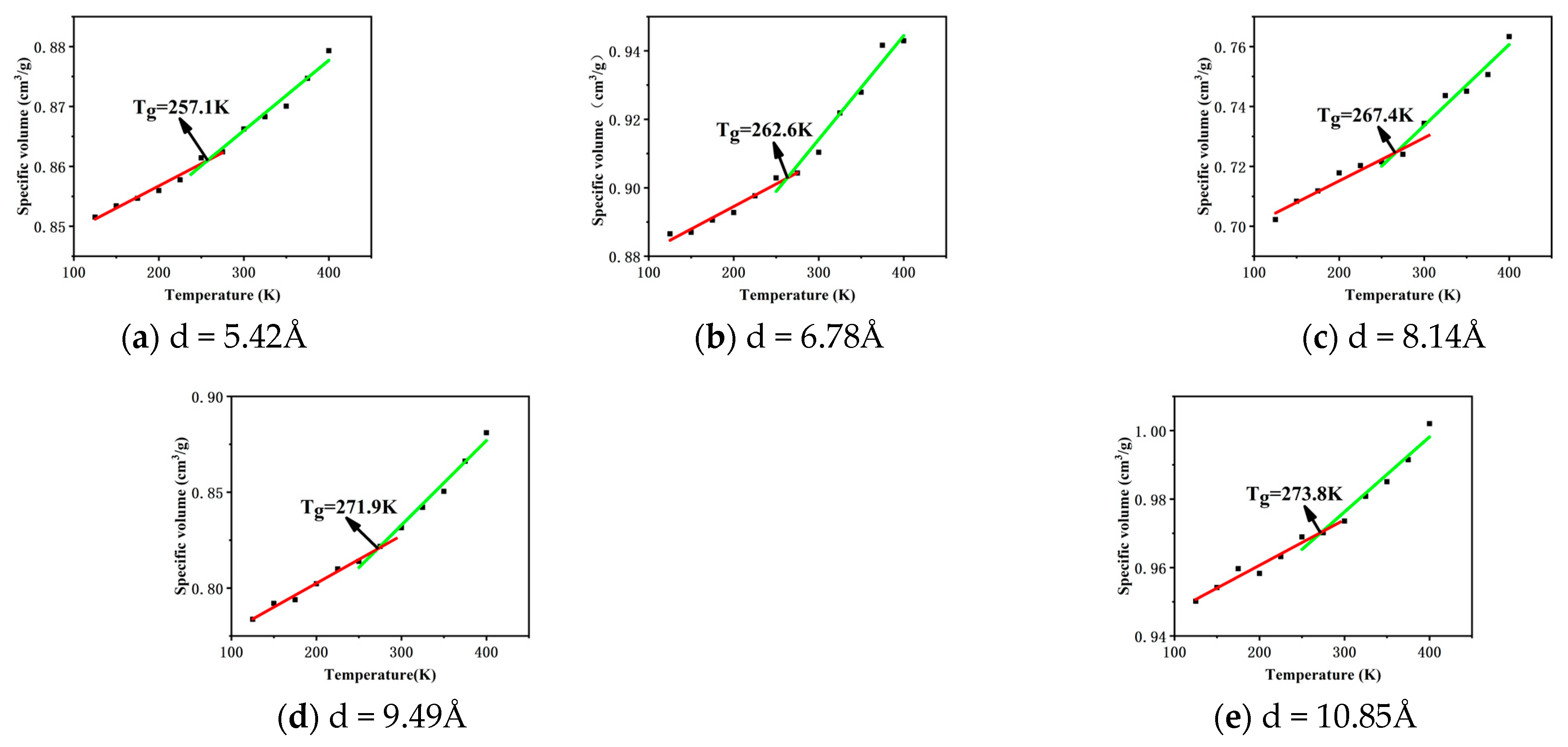
3.2. Glass Transition Temperature
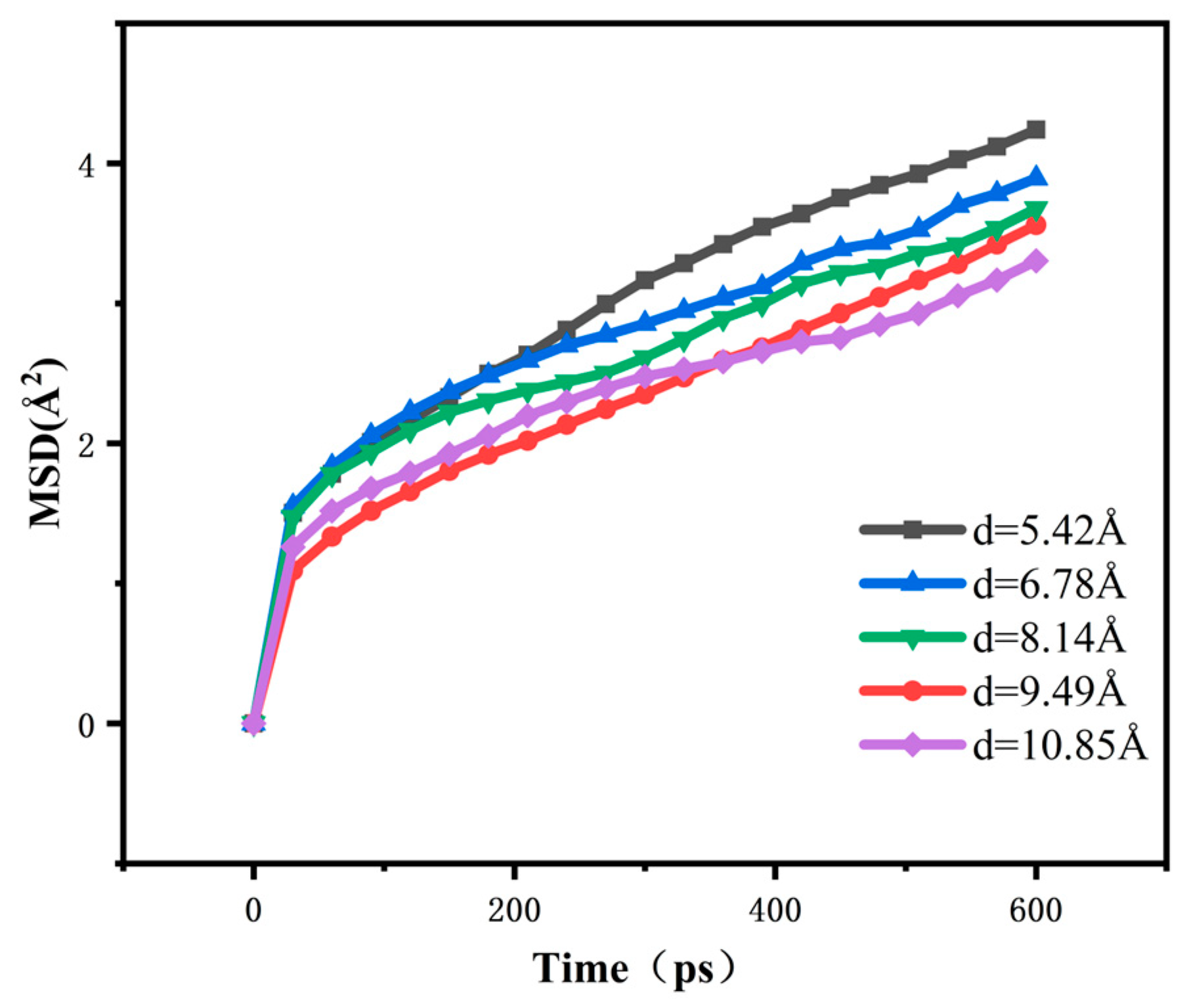
3.3. Mean Square Displacement
3.4. Turning Radius
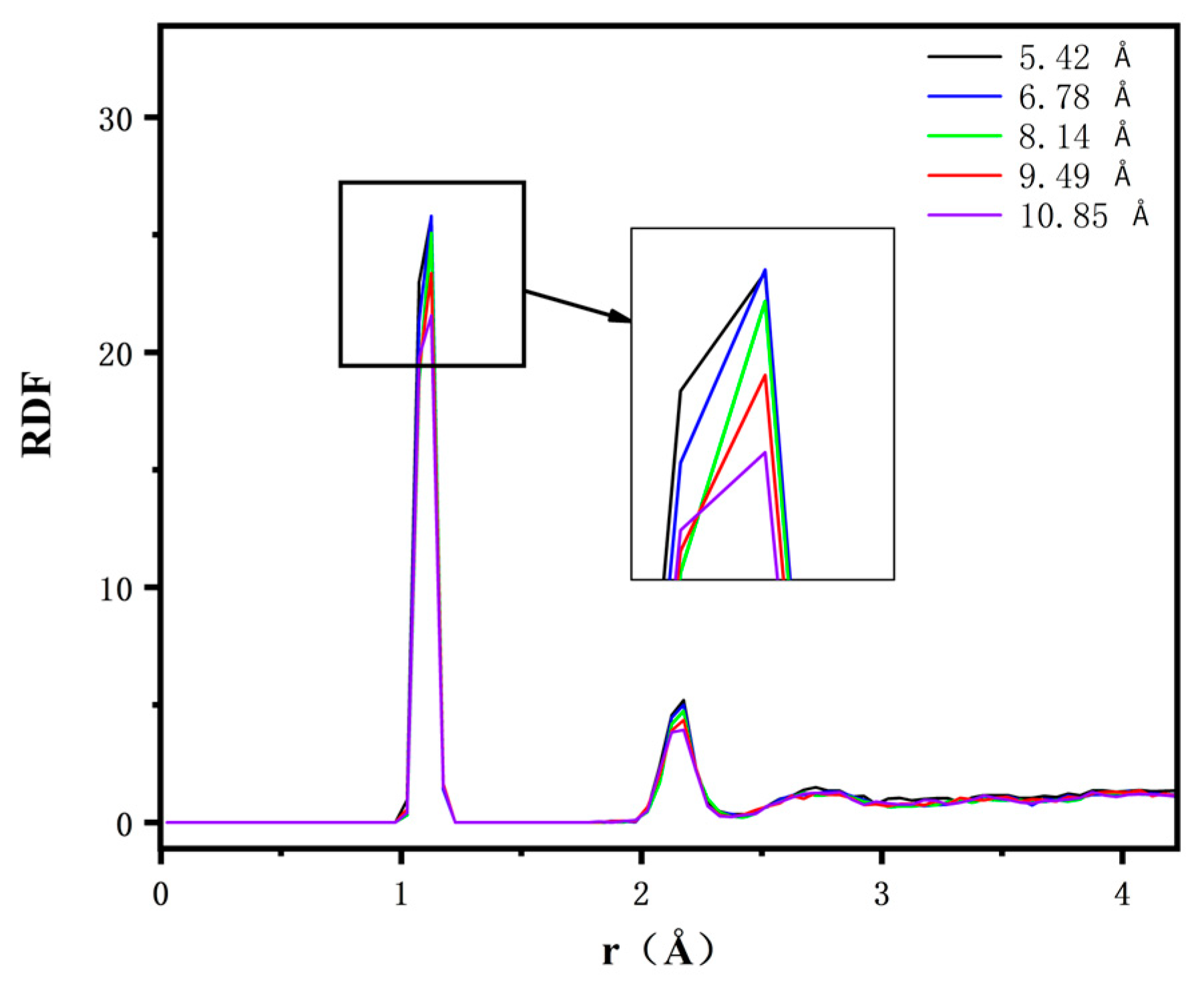
3.5. Radial Distribution Function
3.6. Binding Energy
4. Conclusions
- The free volume fraction and glass transition temperature of different carbon nanotube diameter composites were analysed and compared: with the increase in tube diameter, the free volume fraction of the composites decreased by 21.36%, and the Tg of the composites increased by 6.5%. The reason was that with the increase in CNT tube diameter, the contact area with epichlorohydrin rubber also increased, which made the interaction between CNTs and epichlorohydrin rubber molecules closer, enhanced the force between them, and increased the constraint of the movement of molecular chains, thus reducing the free volume fraction, increasing the stiffness of molecular chains, and increasing Tg.
- The mean square displacement and radius of gyration of different carbon nanotube diameter composites were analysed and compared. With the increase in the tube diameter, the rms displacement of the composites decreases, and the radius of gyration decreases by 3.18 Å. The reason is that the increase in the carbon nanotube diameter strengthens the molecular interactions in the system, which results in a stronger restriction of the molecular chains, and so the rms displacement and the radius of gyration of the composites both decrease.
- The binding energy and the radial distribution function between the C and H atom groups of the five carbon nanotube diameter composites were analysed and compared, and the results show that with the increase in the tube diameter, the radial distribution function of the C and H atom groups in the system decreases gradually, and the binding energy increases gradually. The increase in the binding energy proves that the interaction force in the system is enhanced, which validates the previous results.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhong, X. Current status and expansion of epichlorohydrin rubber. World Rubber Ind. 2016, 43, 52–59. (In Chinese) [Google Scholar]
- Guo, W.; Xian, G. Application of ECO recycled rubber in automotive hose. Rubber Ind. 2007, 232–233. (In Chinese) [Google Scholar]
- Hong, Z.; Hong, W.; Dong, L. Effect of carbon black type and dosage on epichlorohydrin rubber. In Proceedings of the 2019 China Automotive Materials (Xiqing) International Forum, Shanghai, China, 16–18 April 2019. [Google Scholar]
- Yu, Z.; Tan, Y.; Luo, Q.; Wang, X.; Su, S. Effects of Black Liquor-Montmorillonite Complexes on the Mechanical and Thermal Properties of Epichlorohydrin Rubber. Clays Clay Miner. 2019, 67, 334–339. [Google Scholar] [CrossRef]
- Timofeeva, E.N.; Petrova, N.N.; Nikolaeva, K.N.; Kuzmina, E.S. The Research of the Effect of Single-Walled Carbon Nanotubes on the Properties of Epichlorohydrin Rubber. Mater. Sci. Forum 2019, 945, 428–432. [Google Scholar] [CrossRef]
- Ya, T. Research on the Vulcanisation System of Epichlorohydrin Rubber. Ph.D. Thesis, Hunan Normal University, Changsha, China, 2014. [Google Scholar]
- Akkermans, R.L.C.; Spenley, N.A.; Robertson, S.H. Monte Carlo methods in Materials Studio. Mol. Simul. 2013, 39, 1153–1164. [Google Scholar] [CrossRef]
- Xiao, H. Molecular Dynamics Simulation of Corrosion Resistance and Mechanical Properties of Rubber Materials under High Pressure and Low Temperature Conditions. Ph.D. Thesis, Qingdao University of Science and Technology, Qingdao, China, 2023. [Google Scholar]
- Ronova, I.A.; Rozhkov, E.M.; Alentiev, A.Y.; Yampolskii, Y.P. Occupied and accessible volumes in glassy polymers and their relationship with gas permeation parameters. Macromol. Theory Simul. 2003, 12, 425–439. [Google Scholar] [CrossRef]
- Shi, H.; Hui, W.; Shi, W. Molecular simulation of the effect of crosslink density on the properties of nitrile rubber. Synth. Rubber Ind. 2021, 44, 379–383. [Google Scholar]
- Jian, Y. Molecular Dynamics Simulation Study on the Effect of Nano-Reinforcement Materials on the Friction and thermomechanical Properties of Smooth-Butadiene Rubber. Ph.D. Thesis, Qingdao University of Science and Technology, Qingdao, China, 2023. [Google Scholar]




| CNTs Pipe Diameter (Å) | Rg (Å) |
|---|---|
| 5.42 | 18.43 |
| 6.78 | 18.88 |
| 8.14 | 18.39 |
| 9.49 | 17.43 |
| 10.85 | 15.25 |
| CNT Tube Diameter (Å) | (Kcal/mol) | (Kcal/mol) | (Kcal/mol) | |
|---|---|---|---|---|
| 5.42 | 284.14 | 74.75 | 11,165.59 | −10,806.70 |
| 6.78 | 301.11 | 3051.43 | 13,764.73 | −10,412.20 |
| 8.14 | 370.92 | 5381.51 | 16,472.72 | −10,720.29 |
| 9.49 | 391.91 | 9723.28 | 19,146.15 | −9030.96 |
| 10.85 | 425.33 | 11,893.71 | 21,805.09 | −9486.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Li, X.; Yu, L.; Song, J. Molecular Dynamics Simulation of Effect of Carbon Nanotube Diameter on Properties of Crosslinked Epichlorohydrin Rubbers. Polymers 2024, 16, 2419. https://doi.org/10.3390/polym16172419
Wang Z, Li X, Yu L, Song J. Molecular Dynamics Simulation of Effect of Carbon Nanotube Diameter on Properties of Crosslinked Epichlorohydrin Rubbers. Polymers. 2024; 16(17):2419. https://doi.org/10.3390/polym16172419
Chicago/Turabian StyleWang, Zepeng, Xinyan Li, Liangchen Yu, and Junping Song. 2024. "Molecular Dynamics Simulation of Effect of Carbon Nanotube Diameter on Properties of Crosslinked Epichlorohydrin Rubbers" Polymers 16, no. 17: 2419. https://doi.org/10.3390/polym16172419
APA StyleWang, Z., Li, X., Yu, L., & Song, J. (2024). Molecular Dynamics Simulation of Effect of Carbon Nanotube Diameter on Properties of Crosslinked Epichlorohydrin Rubbers. Polymers, 16(17), 2419. https://doi.org/10.3390/polym16172419





