Storage Life of Particle-Filled Polymer Composites Considering Aging Effects
Abstract
1. Introduction
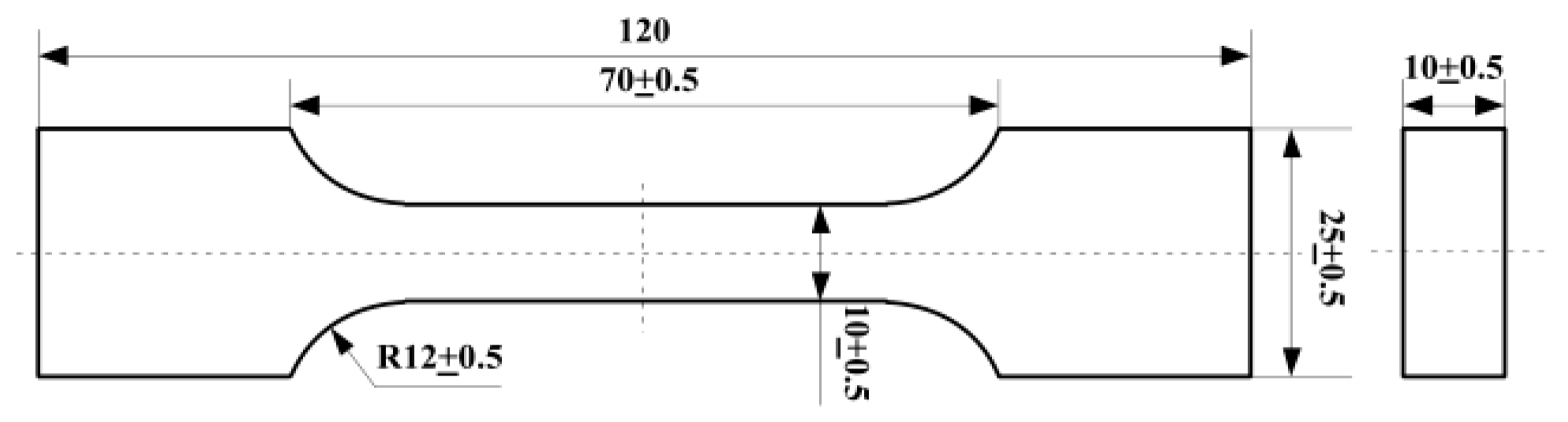
2. Materials and Methods
3. Aging Viscoelastic Constitutive Model
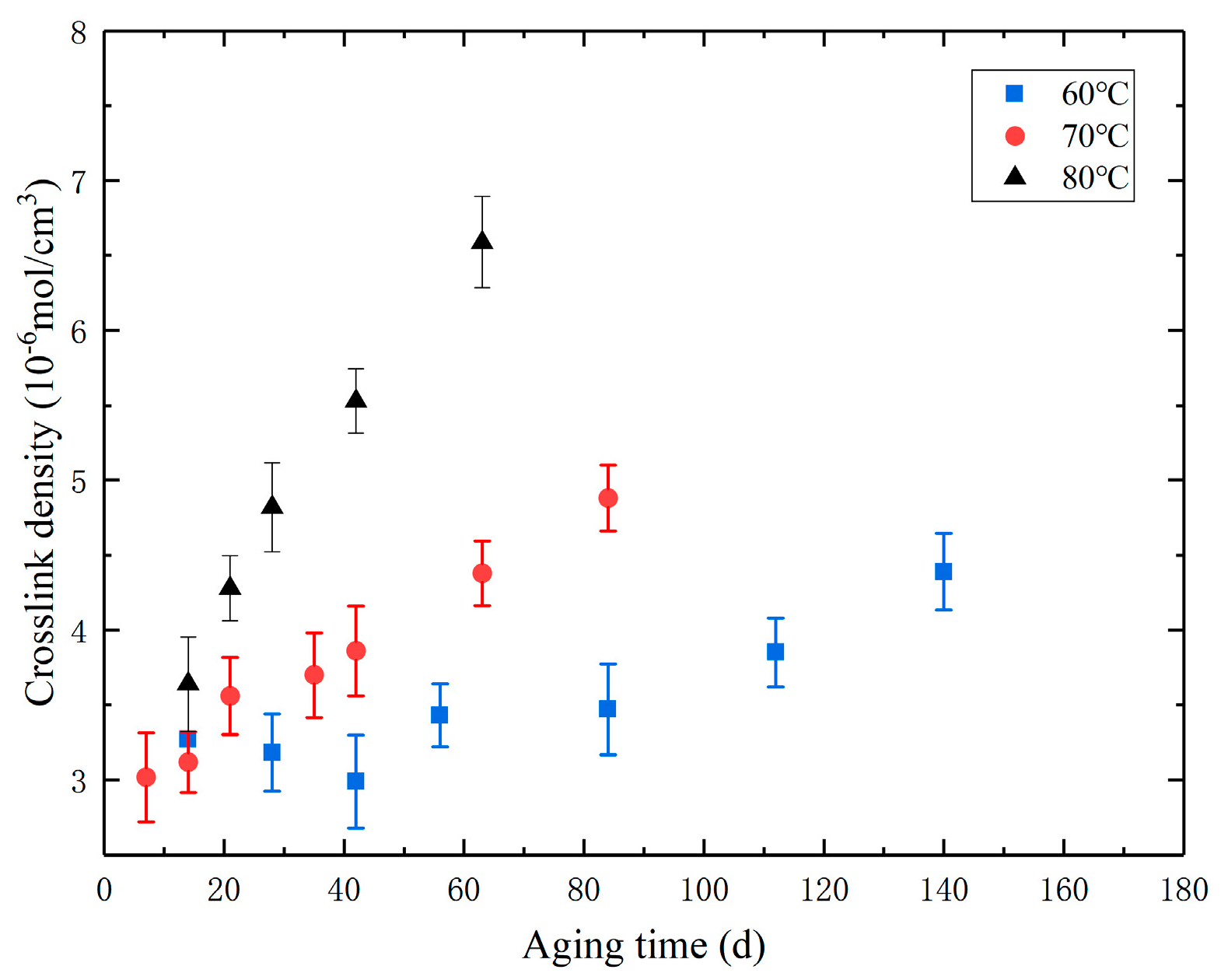
3.1. Crosslink Density Prediction Model
3.2. Aging Viscoelastic Constitutive Model Based on Crosslink Density
3.3. Discretization of the Aging Viscoelastic Constitutive Model
3.4. The Verification of the Model
4. Estimation Method for the Storage Life of PFPCs
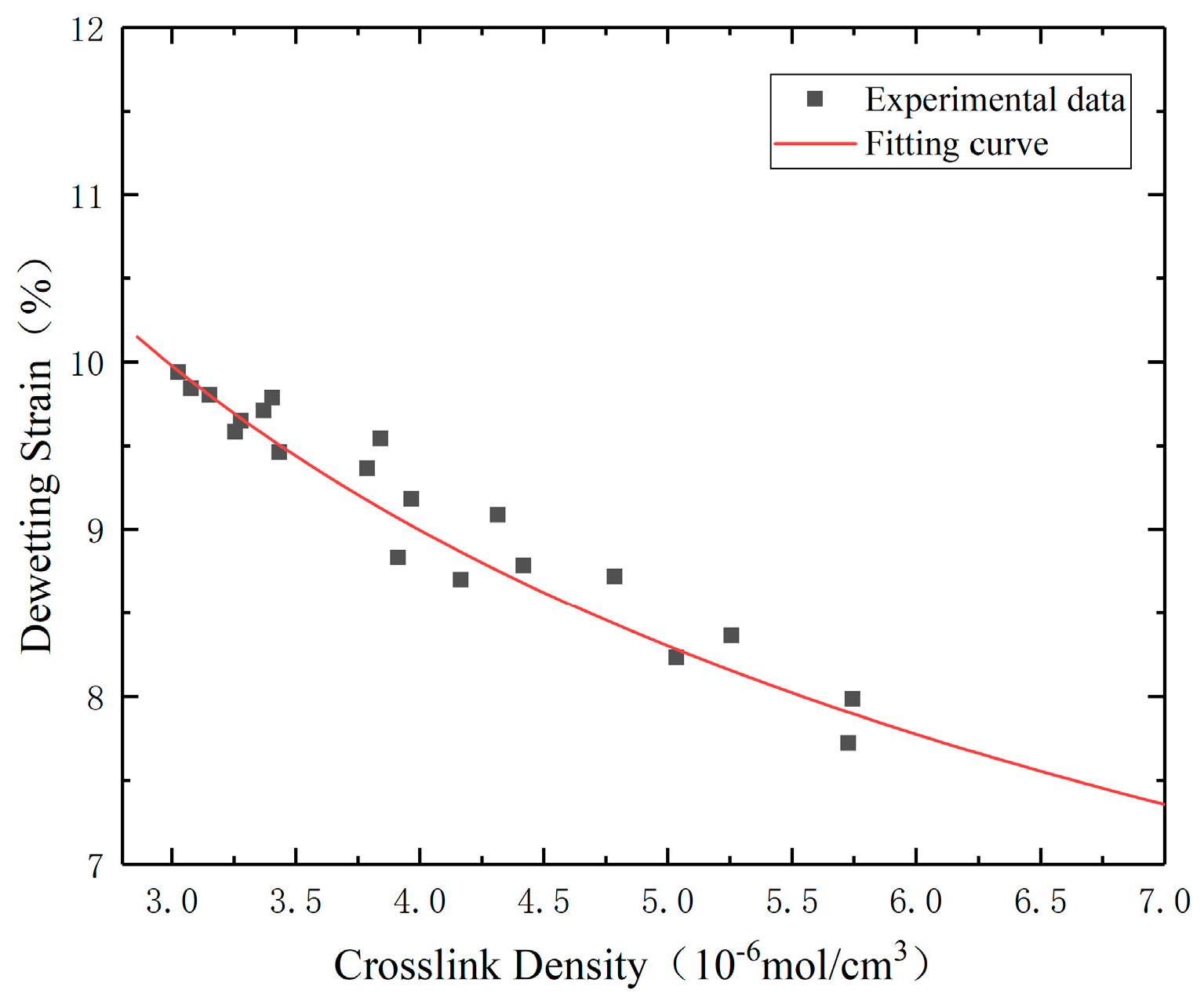
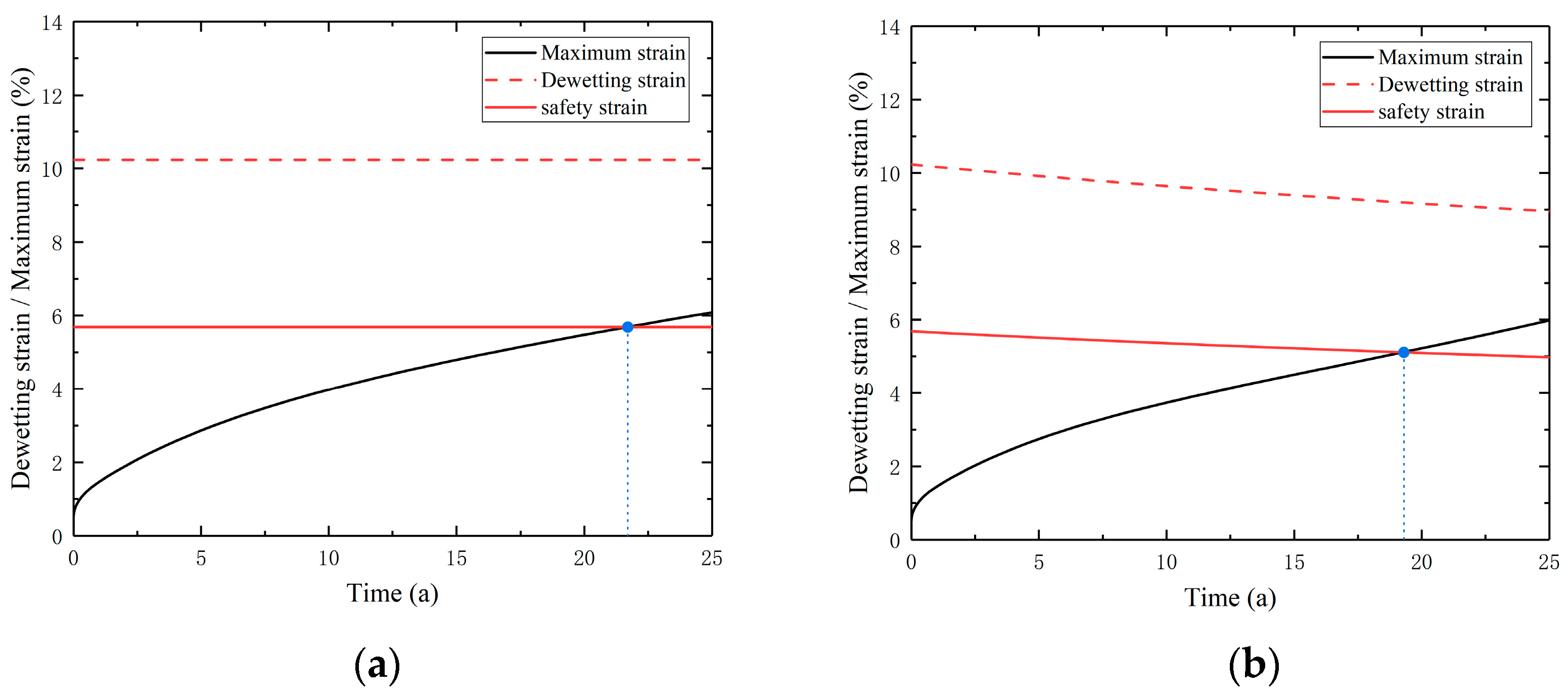
4.1. Safety Margin Assessment
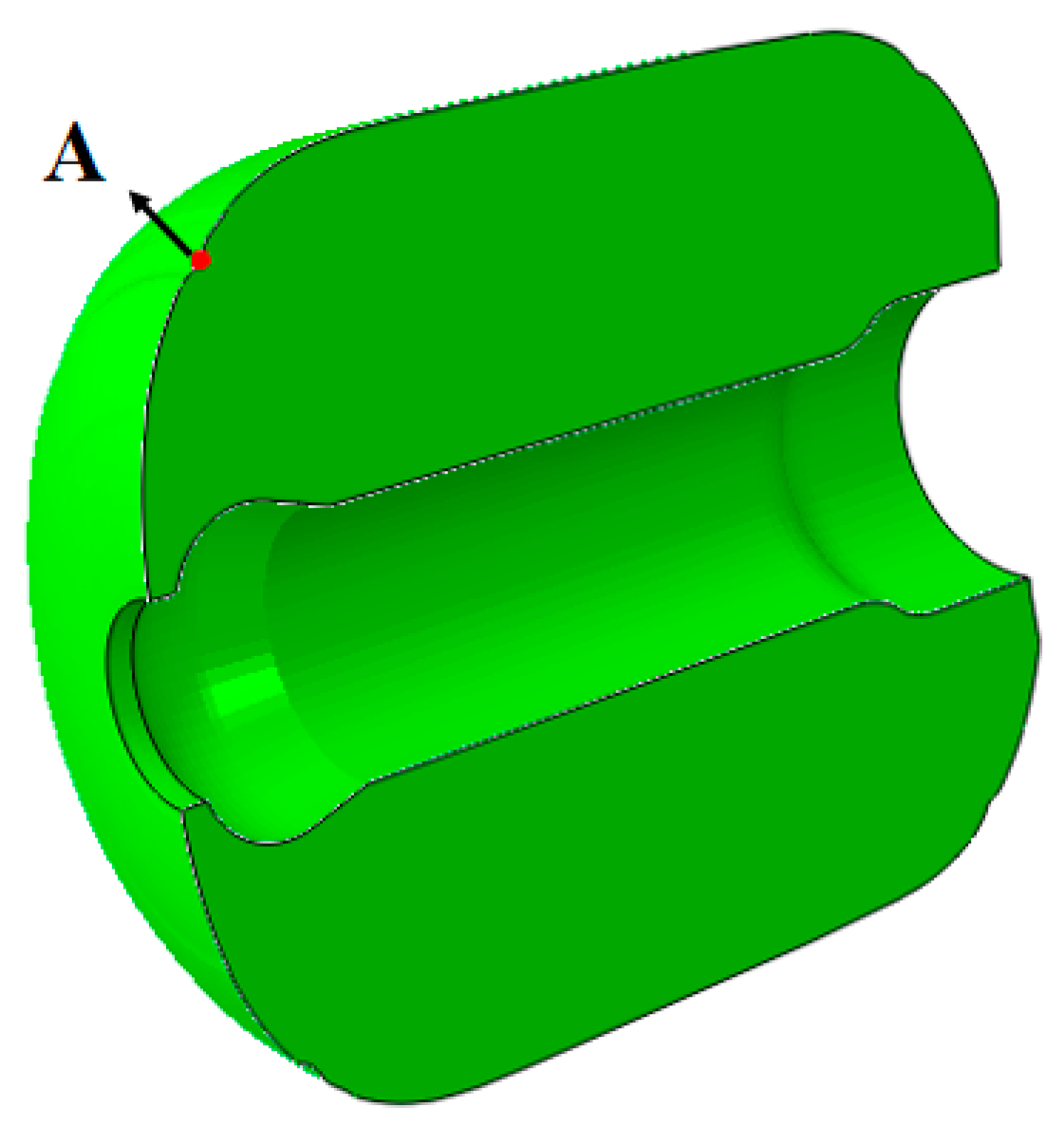
4.2. Case Analysis of PFPC Column
5. Conclusions
- (1)
- The degree of aging of the PFPCs was characterized using crosslink density. Combined with the Arrhenius equation, a crosslink density prediction model was established. This model can be used to determine the crosslink density of samples at different aging stages. Then, based on the mathematical relationship between crosslink density and relaxation modulus, an aging model for the relaxation modulus was developed, as well as an aging viscoelastic constitutive model.
- (2)
- Based on the aging relaxation modulus, an aging viscoelastic constitutive model was established. An integral algorithm was used for the numerical discretization of this constitutive model. The UMAT subroutine of ABAQUS was employed to compute the stress and strain behavior of the PFPC column in a horizontal storage condition. The results show that stress values are increased while strain values are reduced when considering aging effects. Compared to the constitutive model that ignores aging, the hardening effect of the PFPCs caused by aging can be characterized by the aging viscoelastic constitutive.
- (3)
- Based on the maximum stress and the safety margin assessment method using dewetting strain, the PFPC column with a length of 2.3 m and outer diameter of 1.8 m storage life is estimated. The results show that when aging effects are ignored, the estimated storage life is 22 years, and when aging effects are considered, the estimated storage life is 19 years. The predicted storage life of the PFPC column is reduced when considering aging effects. This method provides a reference for predicting the storage life of PFPCs.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Colin, X.; Verdu, J. Strategy for studying thermal oxidation of organic matrix composites. Compos. Sci. Technol. 2005, 65, 411–419. [Google Scholar] [CrossRef]
- Moumen, A.; Saouab, A.; Imad, A.; Kanit, T. Towards a numerical modeling of the coupling between RTM process and induced mechanical properties for rigid particle-filled composites. Int. J. Adv. Manuf. Technol. 2023, 125, 1251–1270. [Google Scholar] [CrossRef]
- Lakshmi Narayana, S.; Gopalan, V. Mechanical characterization of particle reinforced jute fiber composite and development of hybrid Grey-ANFIS predictive model. J. Nat. Fibers 2023, 20, 2167033. [Google Scholar] [CrossRef]
- Tandon, G.; Pochiraju, K.; Schoeppner, G. Modeling of oxidative development in PMR-15 resin. Polym. Degrad. Stab. 2006, 91, 1861–1869. [Google Scholar] [CrossRef]
- Yang, Z.; Kang, G.; Liu, R.; Chen, P. Effect of Particle Morphology on Mechanical Behaviour of Highly Particle-Filled Composites. Int. J. Mech. Sci. 2022, 227, 107446. [Google Scholar] [CrossRef]
- Lu, T.; Solis-Ramos, E.; Yi, Y.B.; Kumosa, M. Particle removal mechanisms in synergistic aging of polymers and glass reinforced polymer composites under combined UV and water. Compos. Sci. Technol. 2017, 153, 273–281. [Google Scholar] [CrossRef]
- Li, D.; Li, X.; Dai, J. Process modelling of curing process-induced internal stress and deformation of composite laminate structure with elastic and viscoelastic models. Appl. Compos. Mater. 2018, 25, 527–544. [Google Scholar] [CrossRef]
- Hussein, R.M.; Chandrashekhara, K. Thermo-oxidative induced damage in polymer composites: Microstructure image-based multi-scale modeling and experimental validation. Appl. Compos. Mater. 2018, 25, 1183–1203. [Google Scholar] [CrossRef]
- Fielding, S.M. Elastoviscoplastic rheology and aging in a simplified soft glassy constitutive model. J. Rheol. 2020, 64, 723–738. [Google Scholar] [CrossRef]
- Singh, B.; Kumar, P. Viscoelastic and morphological evaluation of aged polymer modified asphalt binders. Int. J. Civ. Eng. 2020, 18, 1077–1096. [Google Scholar] [CrossRef]
- Yang, J.; Ma, X.; Wang, H.; Shang, F.; Hou, D. Characterization of nonlinear viscoelastic behaviors of CF/EP laminates with consideration to physical aging effect under thermo-mechanical loading. Mech. Mater. 2023, 180, 104615. [Google Scholar] [CrossRef]
- Rahmani, E.; Darabi, M.K.; Little, D.N.; Masad, E.A. Constitutive modeling of coupled aging-viscoelastic response of asphalt concrete. Constr. Build. Mater. 2017, 131, 1–15. [Google Scholar] [CrossRef]
- Ozer, H.; Yousefi, S.S.; Al-Qadi, I.L.; Elizalde-Castro, G. Field aging and development of aging model for hot-poured crack sealants. Transport. Res. Rec. 2015, 2481, 90–99. [Google Scholar] [CrossRef]
- Guo, Q.; Zaïri, F. A micromechanics-based model for deformation-induced damage and failure in elastomeric media. Int. J. Plasticity 2021, 140, 102976. [Google Scholar] [CrossRef]
- Najmeddine, A.; Shakiba, M. Physics and chemistry-based phase-field constitutive framework for thermo-chemically aged elastomer. Int. J. Mech. Sci. 2024, 262, 108721. [Google Scholar] [CrossRef]
- Zhang, P.; Tan, W.; Zhang, X.; Chen, J.; Yuan, J.; Deng, J. Chemical modification of hydroxyl-terminated polybutadiene and its application in composite propellants. Ind. Eng. Chem. Res. 2021, 60, 3819–3829. [Google Scholar] [CrossRef]
- Chen, C.; Pan, H.; Tu, J.; Chen, J.; Zhang, X.; Mao, C.; Zhou, X. Thermal aging mechanism of PBT energetic elastomer based on the evolution of microstructure. Mater. Today Chem. 2023, 32, 101655. [Google Scholar] [CrossRef]
- Choi, S.S. Influence of internal strain on change of crosslink density of natural rubber vulcanizates by thermal ageing. Polym. Int. 2001, 50, 107–112. [Google Scholar] [CrossRef]
- Du, Y.; Zheng, J.; Xiong, C. Cross-linking density and aging constitutive model of HTPB coating under prestrain thermal accelerated aging. Def. Technol. 2020, 16, 439–446. [Google Scholar] [CrossRef]
- Bahrololoumi, A.; Mohammadi, H.; Moravati, V.; Dargazany, R. A physically-based model for thermo-oxidative and hydrolytic aging of elastomers. Int. J. Mech. Sci. 2021, 194, 106193. [Google Scholar] [CrossRef]
- Pochiraju, K.V. Modeling Thermo-Oxidative Aging and Degradation of Composites. In Long-Term Durability of Polymeric Matrix Composites; Springer US: Boston, MA, USA, 2012; pp. 383–425. [Google Scholar]
- Shakiba, M.; Najmeddine, A. Physics-based constitutive equation for thermochemically aged elastomers based on crosslink density evolution. J. Mech. Mater. Struct. 2023, 17, 229–246. [Google Scholar] [CrossRef]
- Mohammadi, H.; Morovati, V.; Korayem, A.E.; Poshtan, E.; Dargazany, R. Constitutive modeling of elastomers during photo-and thermo-oxidative aging. Polym. Degrad. Stab. 2021, 191, 109663. [Google Scholar] [CrossRef]
- Fang, C.; Wang, H.; Zhang, Y.; Zhang, M.; Shen, T.; Du, J. Multi-Scale Model for the Aging Performance of Particle-Filled Polymer Composites. Polymers 2023, 15, 3158. [Google Scholar] [CrossRef] [PubMed]
- Hu, R.; Prakash, C.; Tomar, V.; Harr, M.; Gunduz, I.E.; Oskay, C. Experimentally-validated mesoscale modeling of the coupled mechanical–thermal response of AP–HTPB energetic material under dynamic loading. Int. J. Fracture 2017, 203, 277–298. [Google Scholar] [CrossRef]
- Supriya, S.; Selwinrajadurai, J.; Anshul, P. Microstructure based finite element analysis of particle filled polymer composite. Trans. Can. Soc. Mech. Eng. 2017, 41, 681–690. [Google Scholar] [CrossRef]
- Chaudhary, N.; Dikshit, M.K. Study of the cross-linking density effect on the mechanical properties of h-BNNS reinforced epoxy nanocomposite part-1: A molecular dynamics simulation. J. Mol. Model. 2023, 29, 146. [Google Scholar] [CrossRef] [PubMed]
- Aziz, S.A.A.; Mazlan, S.A.; Ubaidillah, U.; Mohamad, N.; Choi, S.B.; Che Aziz, M.A.; Homma, K. Thermal aging rheological behavior of magnetorheological elastomers based on silicone rubber. Int. J. Mol. Sci. 2020, 21, 9007. [Google Scholar] [CrossRef] [PubMed]
- Pochiraju, K.V.; Tandon, G.P.; Schoeppner, G.A. Evolution of stress and deformations in high-temperature polymer matrix composites during thermo-oxidative aging. Mech. Time Depend. Mater. 2008, 12, 45–68. [Google Scholar] [CrossRef]
- Bahrololoumi, A.; Morovati, V.; Poshtan, E.A.; Dargazany, R. A multi-physics constitutive model to predict hydrolytic aging in quasi-static behaviour of thin cross-linked polymers. Int. J. Plasticity 2020, 130, 102676. [Google Scholar] [CrossRef]
- Ma, Z.; Pu, Y.; Huang, Y.; Liu, L.; Yuan, C. Preparation of self-emulsifying waterborne polyamide-imide sizing for carbon fiber and improvement on mechanical performances of carbon fiber reinforced thermoplastic polymer. Polym. Compos. 2022, 43, 6560–6570. [Google Scholar] [CrossRef]
- Zheng, T.; Zheng, X.; Zhan, S.; Zhou, J.; Liao, S. Study on the ozone aging mechanism of Natural Rubber. Polym. Degrad. Stabil. 2021, 186, 109514. [Google Scholar] [CrossRef]
- Naseem, H.; Yerra, J.; Murthy, H.; Ramakrishna, P.A. Ageing studies on AP/HTPB based composites solid propellants. Energetic Mater. Front. 2021, 2, 111–124. [Google Scholar] [CrossRef]
- Kohout, J. Modified Arrhenius equation in materials science, chemistry and biology. Molecules 2021, 26, 7162. [Google Scholar] [CrossRef] [PubMed]
- Manha, W.D. Propellant systems safety. In Safety Design for Space Systems; Butterworth-Heinemann: Oxford, UK, 2009; pp. 473–511. [Google Scholar]
- Dalby, B.; Caraës, A. Lifetime numerical prediction of solid rocket motors with HTPB binder based propellants using a multiscale model. In Proceedings of the 51st AIAA/SAE/ASEE Joint Propulsion Conference, Orlando, FL, USA, 27–29 July 2015. [Google Scholar]
- Zheng, J.Y. Applied safety factor in design of composite material structures Acta Aeronaut. Astronaut. Sin. 1998, 9, 1–10. [Google Scholar]









| Temperature (°C) | Aging Time (d) | |||||||
|---|---|---|---|---|---|---|---|---|
| 60 | 14 | 28 | 42 | 56 | 84 | 112 | 140 | 168 |
| 70 | 7 | 14 | 21 | 35 | 42 | 63 | 84 | 112 |
| 80 | 7 | 14 | 21 | 28 | 35 | 42 | 63 | 84 |
| Temperature (°C) | Aging Time (d) | |
|---|---|---|
| 60 | 42 | 84 |
| 70 | 42 | 84 |
| 80 | 42 | 84 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ∞ | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Ei/MPa | 7.2 | 2.11 | 1.43 | 0.98 | 0.41 | 0.19 | 0.71 | 0.85 | 0.93 | 0.28 | 0.13 |
| τi/s | 0.5 | 5 | 5 × 10 | 5 × 102 | 5 × 103 | 5 × 104 | 5 × 105 | 5 × 106 | 5 × 107 | 5 × 108 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Fang, C.; Wang, H.; Zhang, M.; Shen, T.; Du, J. Storage Life of Particle-Filled Polymer Composites Considering Aging Effects. Polymers 2024, 16, 1893. https://doi.org/10.3390/polym16131893
Zhang Y, Fang C, Wang H, Zhang M, Shen T, Du J. Storage Life of Particle-Filled Polymer Composites Considering Aging Effects. Polymers. 2024; 16(13):1893. https://doi.org/10.3390/polym16131893
Chicago/Turabian StyleZhang, Yujiao, Congli Fang, Huizhen Wang, Minghua Zhang, Tao Shen, and Jianke Du. 2024. "Storage Life of Particle-Filled Polymer Composites Considering Aging Effects" Polymers 16, no. 13: 1893. https://doi.org/10.3390/polym16131893
APA StyleZhang, Y., Fang, C., Wang, H., Zhang, M., Shen, T., & Du, J. (2024). Storage Life of Particle-Filled Polymer Composites Considering Aging Effects. Polymers, 16(13), 1893. https://doi.org/10.3390/polym16131893






