Molecular Dynamics Simulation of Cumulative Microscopic Damage in a Thermosetting Polymer under Cyclic Loading
Abstract
1. Introduction
2. Simulation Method
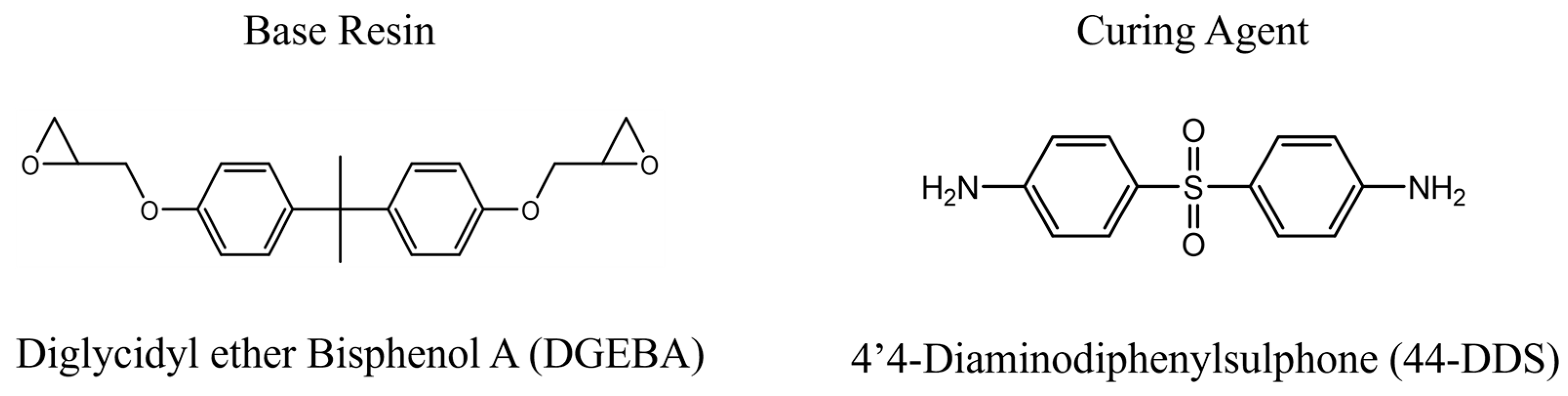
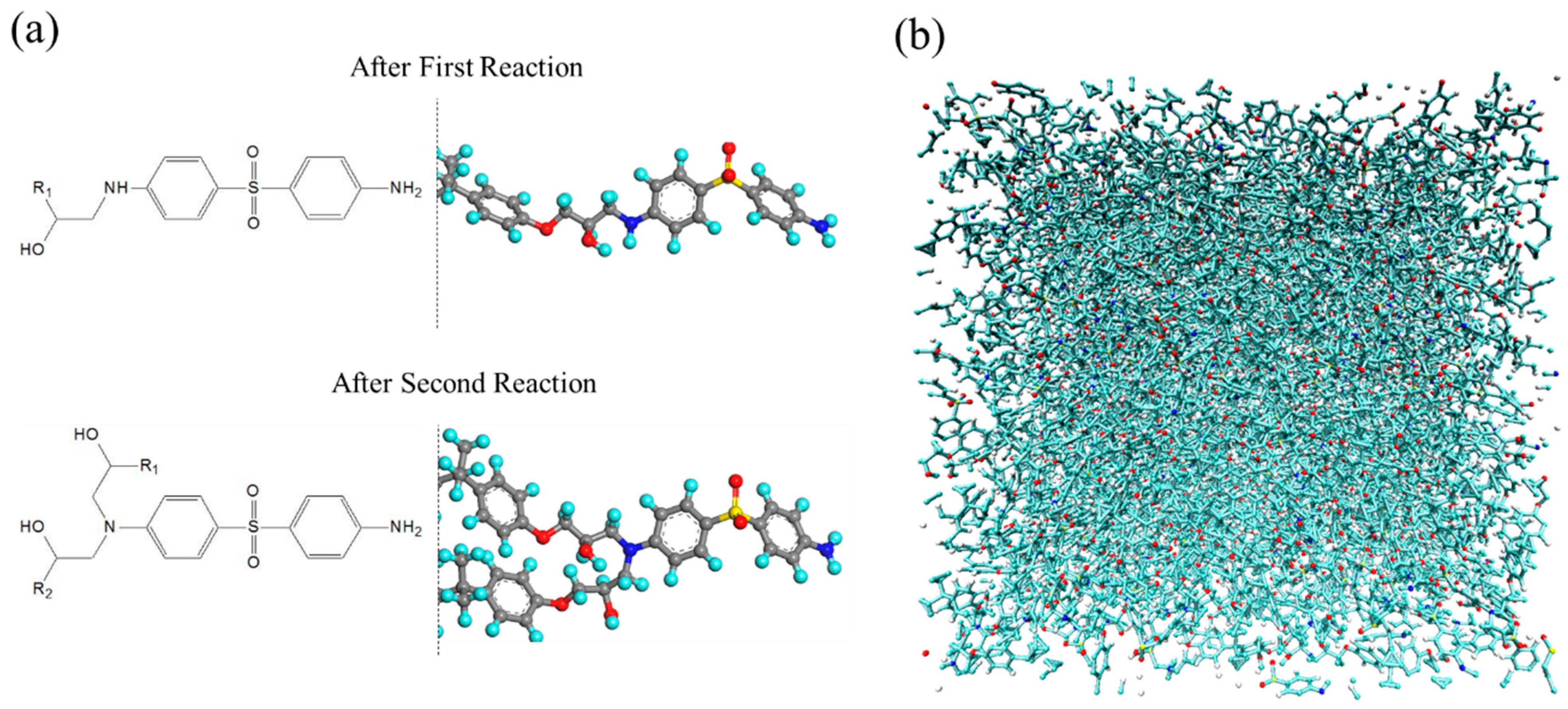
2.1. Molecular Structure Construction
2.2. Curing Simulation
2.3. Cyclic Loading Simulation
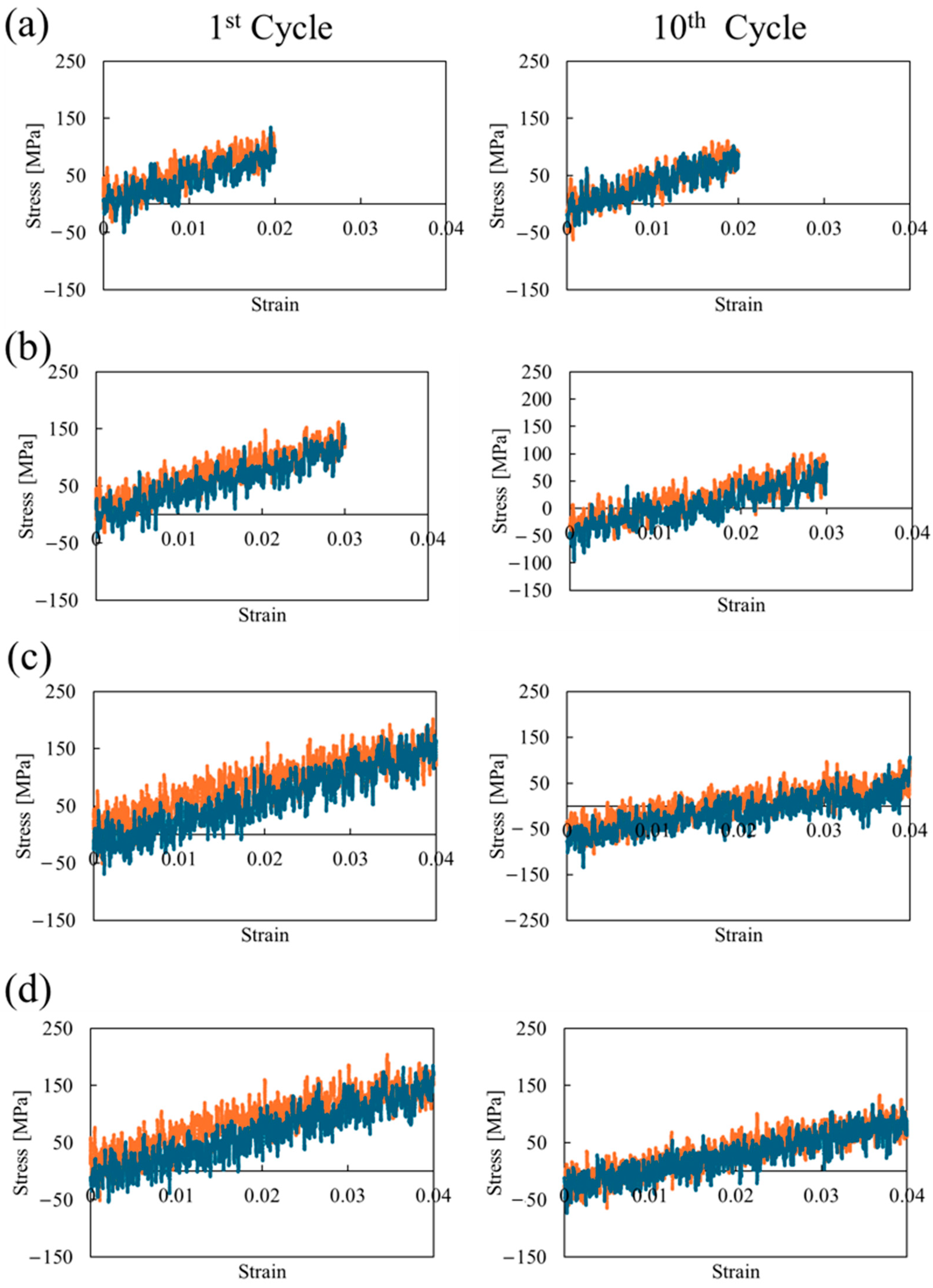
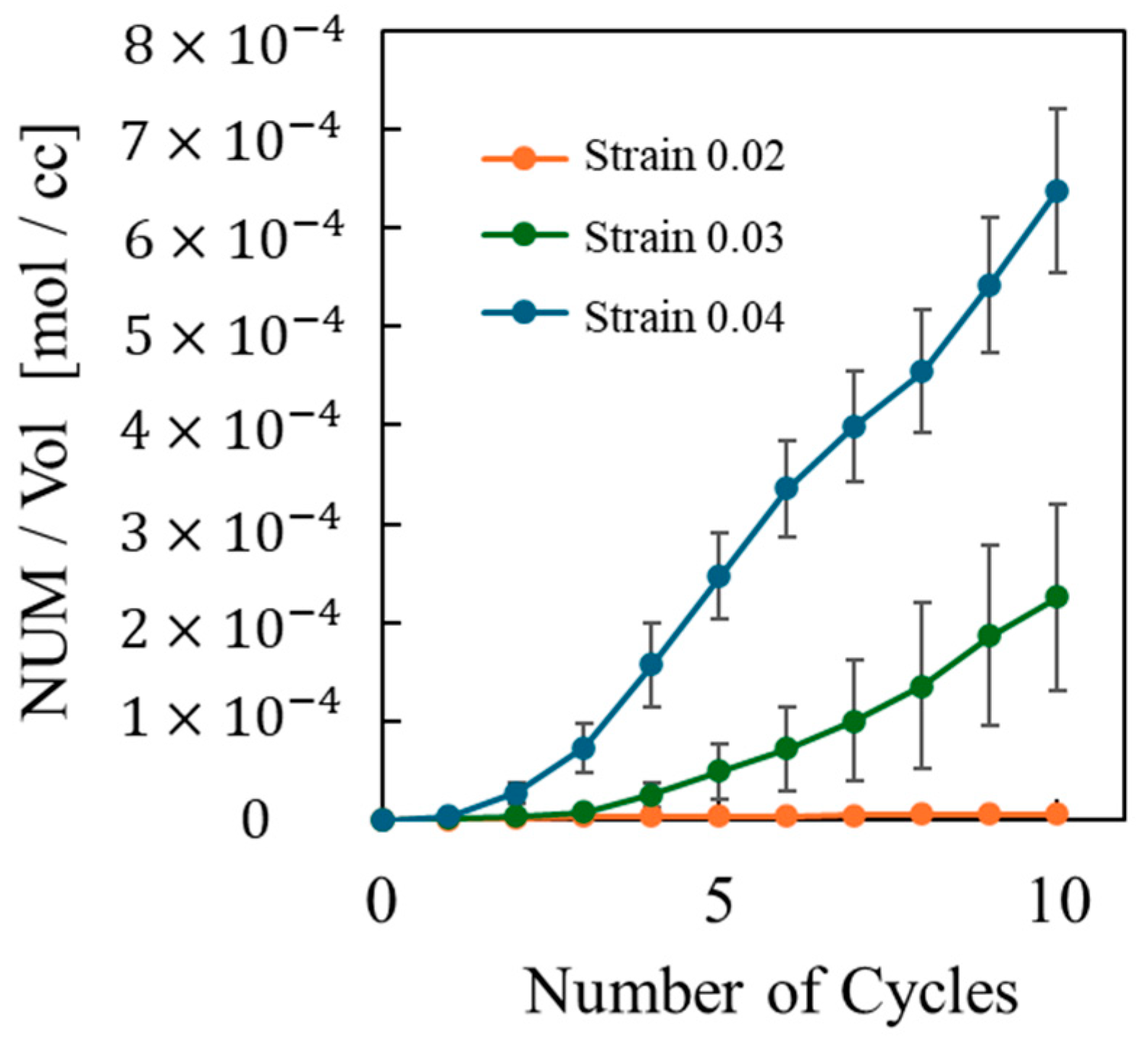
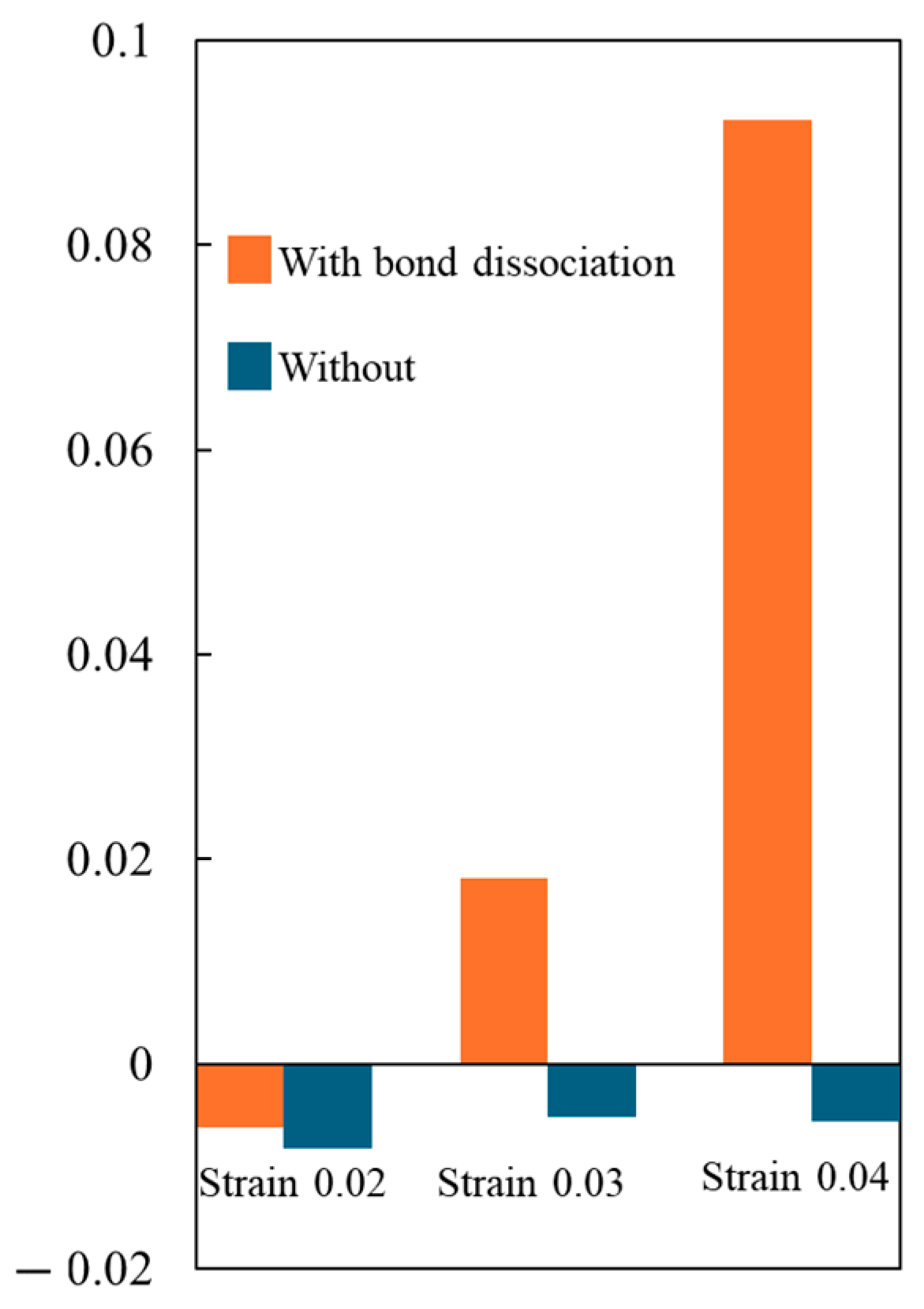
3. Results and Discussions
4. Conclusions
- (1)
- Entropy and void volume increase with both the number of cyclic loadings and their amplitude, resulting in the thermosetting polymer exhibiting inelastic behavior. The accumulated entropy and void volume showed a strong positive correlation with the number of dissociated bonds.
- (2)
- The damage at the nanoscale initiates and propagates through the following process: Initially, under cyclic loading, covalent bonds align with the applied load direction. Subsequently, tensioned covalent bonds break, causing the surrounding bonds to fracture sequentially, resulting in the formation of significant voids. Consequently, stress–strain curves display non-linear and inelastic behavior.
- (3)
- Covalent bond dissociation reduces the system density and mitigates the decrease in dissipation energy per cycle, qualitatively in line with the previous experimental observations.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Lee, M.S.; Seo, H.Y.; Kang, C.G. Comparative study on mechanical properties of CR340/CFRP composites through three point bending test by using theoretical and experimental methods. Int. J. Precis. Eng. Manuf.-Green Technol. 2016, 3, 359–365. [Google Scholar] [CrossRef]
- Alshammari, B.A.; Alsuhybani, M.S.; Almushaikeh, A.M.; Altotaibi, B.M.; Alenad, A.M.; Alqahtani, N.B. Comprehensive review of the properties and modifications of carbon fiber-reinforced thermoplastic composites. Polymers 2021, 13, 2474. [Google Scholar] [CrossRef]
- Müzel, S.D.; Bonhin, E.P.; Guimarães, N.M.; Guidi, E.S. Application of the finite element method in the analysis of composite materials: A review. Polymers 2020, 12, 818. [Google Scholar] [CrossRef]
- Solahuddin, B.A.; Yahaya, F.M. A state-of-the-art review on experimental investigation and finite element analysis on structural behaviour of fibre reinforced polymer reinforced concrete beam. Helion 2023, 9, el4225. [Google Scholar] [CrossRef]
- Wan, L.; Ismail, Y.; Sheng, Y.; Ye, J.; Yang, D. A review on micromechanical modelling of progressive failure in unidirectional fibre-reinforced composites. Compos. Part C Open Access 2023, 10, 100348. [Google Scholar] [CrossRef]
- Ratna, D. Recent Advances and Applications of Thermoset Resins, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2022. [Google Scholar]
- Dhanasekar, S.; Stella, T.J.; Thenmozhi, A.; Bharathi, N.D.; Thiyagarajan, K.; Reddy, Y.S.; Srinivas, G.; Jayakumar, M. Study of polymer matrix composites for electronics applications. J. Nanomater. 2022, 2022, 8605099. [Google Scholar] [CrossRef]
- Karak, N. Overview of Epoxies and Their Thermosets. In Sustainable Epoxy Thermosets and Nanocomposites Napaam; American Chemical Society: Washington, DC, USA, 2021; pp. 1–36. [Google Scholar]
- Koo, B.; Subramanian, N.; Chattopadhyay, A. Molecular dynamics study of brittle fracture in epoxy-based thermoset polymer. Compos. Part B 2016, 95, 433–439. [Google Scholar] [CrossRef]
- Yamada, N.; Oya, Y.; Kato, N.; Mori, K.; Koyanagi, J. A molecular dynamics simulation for thermal activation process in covalent bond dissociation of a crosslinked thermosetting polymer. Molecules 2023, 28, 2736. [Google Scholar] [CrossRef]
- Vassilopoulos, A.P. The history of fiber-reinforced polymer composite laminate fatigue. Int. J. Fatigue 2020, 134, 105512. [Google Scholar] [CrossRef]
- Takase, N.; Koyanagi, J.; Mori, K.; Sakai, T. Molecular dynamics simulation for evaluating fracture entropy of a polymer material under various combined stress states. Materials 2021, 14, 1884. [Google Scholar] [CrossRef]
- Hussain, M.A.; Yamamoto, T.; Adil, S.F.; Yao, S. Preparation and Characterization of High-Density Polyethylene with Alternating Lamellar Stems Using Molecular Dynamics Simulations. Polymers 2024, 16, 304. [Google Scholar] [CrossRef]
- Lian, Q.; Chen, H.; Luo, Y.; Li, Y.; Cheng, Y.; Liu, Y. Toughning mechanism based on the physical entanglement of branched epoxy resin in the non-phase-separated inhomogeneous crosslinking network: An experimental and molecular dynamics simulation study. Polymer 2022, 247, 124754. [Google Scholar] [CrossRef]
- Iwamoto, S.; Oya, Y.; Koyanagi, J. Evaluation of microscopic damage of PEEK polymers under cyclic loading using molecular dynamics simulations. Polymers 2022, 14, 4955. [Google Scholar] [CrossRef]
- Sun, Y.; Tang, X.; Bao, H.; Yang, Z.; Ma, F. The effects of hydroxide and epoxide functional groups on the mechanical properties of graphene oxide and its failure mechanism by molecular dynamics simulations. RSC Adv. 2020, 10, 29610–29617. [Google Scholar] [CrossRef]
- Shirasu, K.; Kitayama, S.; Liu, F.; Yamamoto, G.; Hashida, T. Molecular Dynamics Simulations and theoretical model for engineering tensile properties of single-and multi-walled carbon nanotubes. Nanomaterials 2021, 11, 795. [Google Scholar] [CrossRef]
- Park, C.; Yun, G.J. Characterization of Interfacial Properties of Graphene-Reinforced Polymer Nanocomposites by Molecular Dynamics-Shear Deformation Model. J. Appl. Mech. 2018, 85, 091007. [Google Scholar] [CrossRef]
- Alian, A.R.; Meguid, S.A. Molecular dynamics simulations of the effect of waviness and agglomeration of CNTs on interface strength of thermoset nanocomposites. Phys. Chem. Chem. Phys. 2017, 19, 4426–4434. [Google Scholar] [CrossRef]
- Mahmud, H.A.; Radue, M.S.; Chinkanjanarot, S.; Pisani, W.A.; Gowtham, S.; Odegard, G.M. Multiscale modeling of carbon fiber- graphene nanoplatelet-epoxy hybrid composites using a reactive force field. Compos. Part B Eng. 2019, 172, 628–635. [Google Scholar] [CrossRef]
- Sun, Y.; Chen, L.; Cui, L.; Zhang, Y.; Du, X. Molecular dynamics simulation of cross-linked epoxy resin and its interaction energy with graphene under two typical force fields. Comput. Mater. Sci. 2018, 143, 240–247. [Google Scholar] [CrossRef]
- Salahshoor, H.; Rahbar, N. Nano-scale fracture toughness and behavior of graphene/epoxy interface. J. Appl. Phys. 2012, 112, 023510. [Google Scholar] [CrossRef]
- Oya, Y.; Inuyama, K.; Okabe, T. Analysis of structure characteristics in laminated graphene oxide nanocomposites using molecular dynamics simulation. Adv. Compos. Mater. 2018, 27, 427–438. [Google Scholar] [CrossRef]
- Shen, J.; Li, X.; Zhang, L.; Lin, X.; Li, H.; Shen, X.; Ganesan, V.; Liu, J. Mechanical and Viscoelastic Properties of Polymer-Grafted Nanorod Composites from Molecular Dynamics Simulation. Macromolecules 2018, 51, 2641–2652. [Google Scholar] [CrossRef]
- Yang, M.; Koutsos, V.; Zaiser, M. Interactions between Polymers and Carbon Nanotubes: A Molecular Dynamics Study. J. Phys. Chem. B 2005, 109, 10009–10014. [Google Scholar] [CrossRef]
- Eslami, H.; Behrouz, M. Molecular Dynamics Simulation of a Polyamide-66/Carbon Nanotube Nanocomposite. J. Phys. Chem. C 2014, 118, 9841–9851. [Google Scholar] [CrossRef]
- Lee, S.; Lyulin, A.V.; Frank, C.W.; Yoon, D.Y. Interface characteristics of polystyrene melts in free-standing thin films and on graphite surface from molecular dynamics simulations. Polymer 2017, 116, 540–548. [Google Scholar] [CrossRef]
- Morita, M.; Oya, Y.; Kato, N.; Mori, K.; Koyanagi, J. Effect of electrostatic interactions on the interfacial energy between thermoplastic polymers and graphene oxide: A molecular dynamics study. Polymers 2022, 14, 2579. [Google Scholar] [CrossRef]
- Koyanagi, J.; Itano, N.; Yamamoto, M.; Mori, K.; Ishida, Y.; Bazhirov, T. Evaluation of themechanical properties of carbon fiber/polymer resin interfaces by molecular simulation. Adv. Compos. Mater. 2019, 28, 639–652. [Google Scholar] [CrossRef]
- Kasahara, S.; Koyanagi, J.; Mori, K.; Yabe, M. Evaluation of interface properties of carbon fiber/resin using the full atomistic model considering the electric charge state. Adv. Compos. Mater. 2020, 30, 164–175. [Google Scholar] [CrossRef]
- Odegard, G.M.; Jensen, B.D.; Gowtham, S.; Wu, J.; He, J.; Zhang, Z. Predicting mechanical response of crosslinked epoxy using ReaxFF. Chem. Phys. Lett. 2014, 591, 175–178. [Google Scholar] [CrossRef]
- Jang, C.W.; Mullinax, J.W.; Lawson, J.W. Mechanical properties and failure of aerospace-grade epoxy resins from molecular dynamics simulations with nanoscale defects. ACS Appl. Polym. Mater. 2022, 4, 5269–5274. [Google Scholar] [CrossRef]
- Konrad, J.; Meißner, R.H.; Bitzek, E.; Zahn, D. A molecular simulation approach to bond reorganization in epoxy resins: From curing to deformation and fracture. ACS Polym. Au 2021, 1, 165–174. [Google Scholar] [CrossRef]
- Okabe, T.; Oya, Y.; Tanabe, K.; Kikugawa, G.; Yoshioka, K. Molecular dynamics simulation of crosslinked epoxy resins: Curing and mechanical properties. Eur. Polym. J. 2016, 80, 78. [Google Scholar] [CrossRef]
- Odagiri, N.; Shirasu, K.; Kawagoe, Y.; Kikugawa, G.; Oya, Y.; Kishimoto, N.; Ohuchi, F.S.; Okabe, T. Amine/epoxy stoichiometric ratio dependence of crosslinked structure and ductility in amine-cured epoxy thermosetting resins. J. Appl. Polym. Sci. 2021, 1, 138. [Google Scholar]
- Li, J.; Sakamoto, J.; Waizumi, H.; Oya, Y.; Huang, Y.; Kishimoto, N.; Okabe, T. A multiscale model for the synthesis of thermosetting resins: From the addition reaction to cross-linked network formation. Chem. Phys. Lett. 2019, 720, 64–69. [Google Scholar] [CrossRef]
- Yamamoto, S.; Kuwahara, R.; Aoki, M.; Shundo, A.; Tanaka, K. Molecular events for an epoxy-amine system at a copper interface. ACS Appl. Polym. Mater. 2020, 2, 1474–1481. [Google Scholar] [CrossRef]
- Zhao, Y.; Kikugawa, G.; Kawagoe, Y.; Shirasu, K.; Kishimoto, N.; Xi, Y.; Okabe, T. Uncovering the mechanism of size effect on the thermomechanical properties of highly cross-linked epoxy resins. J. Phys. Chem. B 2022, 126, 2593. [Google Scholar] [CrossRef]
- Zhao, Y.; Kikugawa, G.; Kawagoe, Y.; Shirasu, K.; Okabe, T. Molecular-scale investigation on relationship between thermal conductivity and the structure of crosslinked epoxy resin. Int. J. Heat Mass Transf. 2022, 198, 123429. [Google Scholar] [CrossRef]
- Wu, C.; Xu, W. Atomistic molecular simulations of structure and dynamics of crosslinked epoxy resin. Polymer 2007, 48, 5802–5817. [Google Scholar] [CrossRef]
- Komarov, P.V.; Chiu, Y.T.; Chen, S.M.; Khalatur, P.G.; Reineker, P. Highly cross-linked epoxy resins: An atomistic molecular dynamics simulation combined with a mapping/reverse mapping procedure. Macromolecules 2007, 40, 8104–8113. [Google Scholar] [CrossRef]
- Varshney, V.; Patnail, S.S.; Roy, A.K.; Rarmer, B.L. Amolecular dynamics study of epoxy- based networks: Cross-linking procedure and prediction of molecular and material properties. Macromolecules 2001, 41, 6837–6842. [Google Scholar] [CrossRef]
- Li, C.; Strachan, A. Molecular simulations of crosslinking process of thermosetting polymers. Polymer 2010, 51, 6058–6070. [Google Scholar] [CrossRef]
- Li, C.; Coons, E.; Strachan, A. Material property prediction of thermoset polymers by molecular dynamics simulations. Acta Mech. 2014, 225, 1187–1196. [Google Scholar] [CrossRef]
- Ghosh, S.; Kumar, A.; Sundararaghavan, V.; Waas, A.M. Non-local modeling of epoxy using an atomistically-informed kernel. Inter. J. Solids Struct. 2013, 50, 2837–2845. [Google Scholar] [CrossRef]
- Unger, R.; Braun, U.; Fankhänel, J.; Daum, B.; Arash, B.; Rolfes, R. Molecular modeling of epoxy resin crosslinking experimentally validated by near-infrared spectroscopy. Comput. Mater. Sci. 2019, 161, 223–235. [Google Scholar] [CrossRef]
- Duan, K.; Zhang, J.; Hu, Y.; Zhu, W.; Wang, X. Diamond nanothreads as novel nanofillers for cross-linked epoxy nanocomposites. Compos. Sci. Technol. 2019, 174, 84–93. [Google Scholar] [CrossRef]
- Li, C.; Jaramillo, E.; Strachan, A. Moleucular dyndmics simulatons on cyclic deformation of an epoxy thermoset. Polymer 2013, 54, 881–890. [Google Scholar] [CrossRef]
- Park, H.; Chung, I.; Cho, M. Effect of molecular structure of curing agents on cyclic creep in highly cross-linked epoxy polymers. J. Polym. Sci. 2020, 58, 1617–1631. [Google Scholar] [CrossRef]
- Schichtel, J.J.; Chattopadhyay, A. An atomistic study of damage and localized anisotropic mechanical property evolution in thermoset polymers. Int. J. Mech. Sci. 2020, 174, 105507. [Google Scholar] [CrossRef]
- Sato, M.; Hasegawa, K.; Koyanagi, J.; Higuchi, R.; Ishida, Y. Residual strength prediction for unidirectional CFRP using a nonlinear viscoelastic constitutive equation considering entropy damage. Compos. Part A Appl. Sci. Manuf. 2021, 141, 106178. [Google Scholar] [CrossRef]
- Sakai, T.; Takase, N.; Oya, Y.; Koyanagi, J. A Possibility for Quantitative Detection of Mechanically-Induced Invisible Damage by Thermal Property Measurement via Entropy Generation for a Polymer Material. Materials 2022, 15, 737. [Google Scholar] [CrossRef]
- Huang, J.; Yang, H.; Liu, W.; Zhang, K.; Huang, A. Confidence level and reliability analysis of the fatigue life of CFRP laminates predicted based on fracture fatigue entropy. Int. J. Fatigue 2022, 156, 106659. [Google Scholar] [CrossRef]
- Basaran, C.; Nie, S. An irreversible thermodynamics theory for damage mechanics of solids. Int. J. Damage Mech. 2004, 13, 205–223. [Google Scholar] [CrossRef]
- LAMMPS[soft]. Available online: https://www.lammps.org/#gsc.tab=0 (accessed on 25 April 2024).
- PolyParGen. Available online: http://polypargen.com/ (accessed on 24 April 2024).
- Jorgensen, W.L.; Maxwell, D.S.; Tirado-Rives, J. Development and Testing of the OPLS All-Atom Force Field on Conformational Energetics and Properties of Organic Liquids. J. Am. Chem. Soc. 1996, 118, 11225–11236. [Google Scholar] [CrossRef]
- Cornell, W.D.; Cieplak, P.; Bayly, C.I.; Kollman, P.A. Application of RESP charges to calculate conformational energies, hydrogen bond energies, and free energies of solvation. J. Am. Chem. Soc. 1993, 115, 9620–9631. [Google Scholar] [CrossRef]
- Valiev, M.; Bylaska, E.J.; Govind, N.; Kowalski, K.; Straatsma, T.P.; Van Dam, H.J.; Wang, D.; Nieplocha, J.; Aprà, E.; Windus, T.L.; et al. NWChem: A comprehensive and scalable open-source solution for large scale molecular simulations. Comput. Phys. Commun. 2010, 181, 1477–1489. [Google Scholar] [CrossRef]
- Rycroft, C.H. VORO++: A three-dimensional Voronoi celllibrary in C++. Chaos 2009, 19, 041111. [Google Scholar] [CrossRef]
- Kudo, N.; Fujita, R.; Oya, Y.; Sakai, T.; Nagano, H.; Koyanagi, J. Identification of invisible fatigue damage of thermosetting epoxy resin by non-destructive thermal measurement using entropy generation. Adv. Comp. Mater. 2024, 33, 233–249. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yamada, N.; Morita, M.; Takamura, M.; Murashima, T.; Oya, Y.; Koyanagi, J. Molecular Dynamics Simulation of Cumulative Microscopic Damage in a Thermosetting Polymer under Cyclic Loading. Polymers 2024, 16, 1813. https://doi.org/10.3390/polym16131813
Yamada N, Morita M, Takamura M, Murashima T, Oya Y, Koyanagi J. Molecular Dynamics Simulation of Cumulative Microscopic Damage in a Thermosetting Polymer under Cyclic Loading. Polymers. 2024; 16(13):1813. https://doi.org/10.3390/polym16131813
Chicago/Turabian StyleYamada, Naoki, Mayu Morita, Maruri Takamura, Takahiro Murashima, Yutaka Oya, and Jun Koyanagi. 2024. "Molecular Dynamics Simulation of Cumulative Microscopic Damage in a Thermosetting Polymer under Cyclic Loading" Polymers 16, no. 13: 1813. https://doi.org/10.3390/polym16131813
APA StyleYamada, N., Morita, M., Takamura, M., Murashima, T., Oya, Y., & Koyanagi, J. (2024). Molecular Dynamics Simulation of Cumulative Microscopic Damage in a Thermosetting Polymer under Cyclic Loading. Polymers, 16(13), 1813. https://doi.org/10.3390/polym16131813





