Detailed Analysis of Gamma-Shielding Characteristics of Ternary Composites Using Experimental, Theoretical and Monte Carlo Simulation Methods
Abstract
1. Introduction
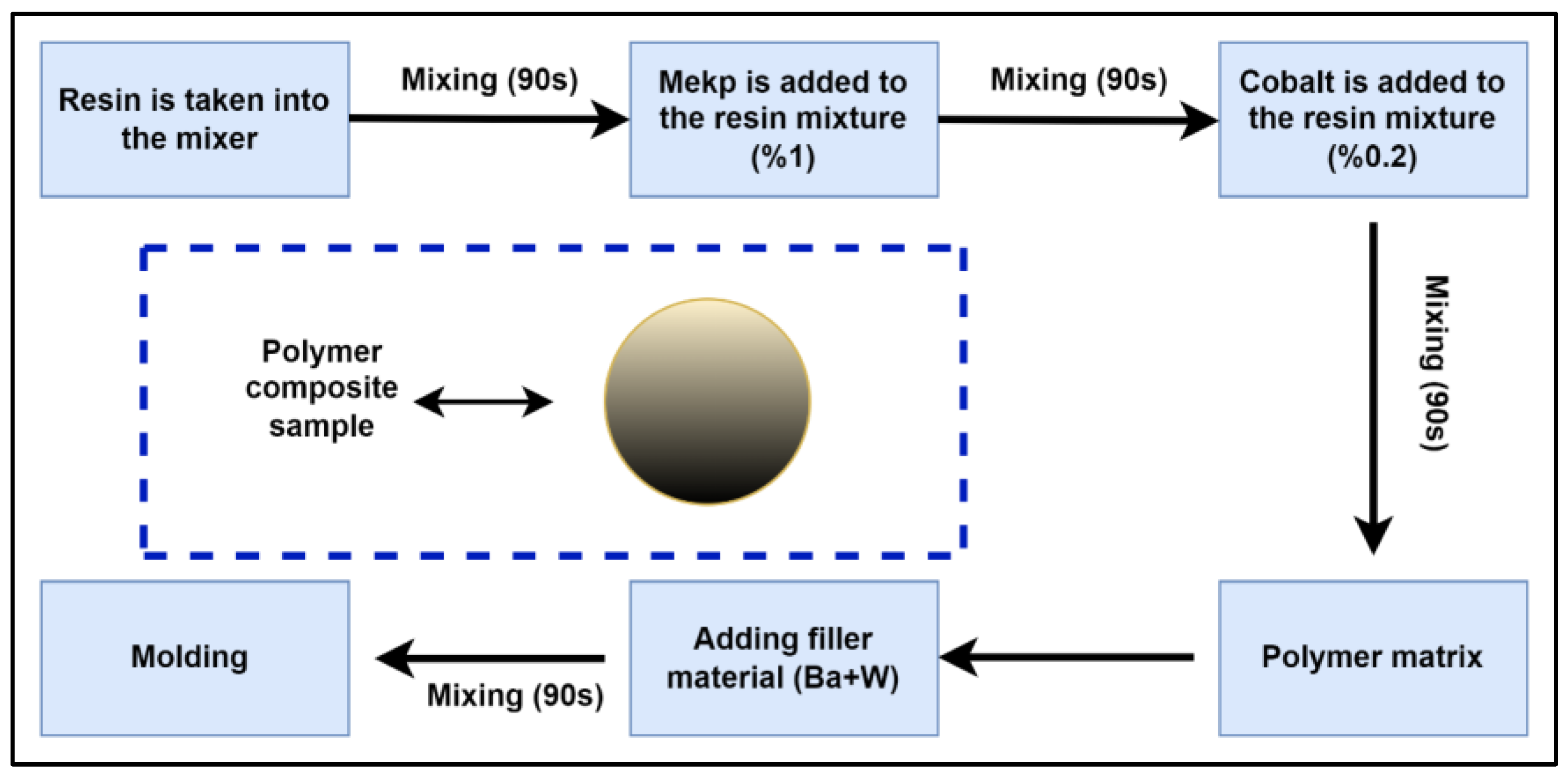
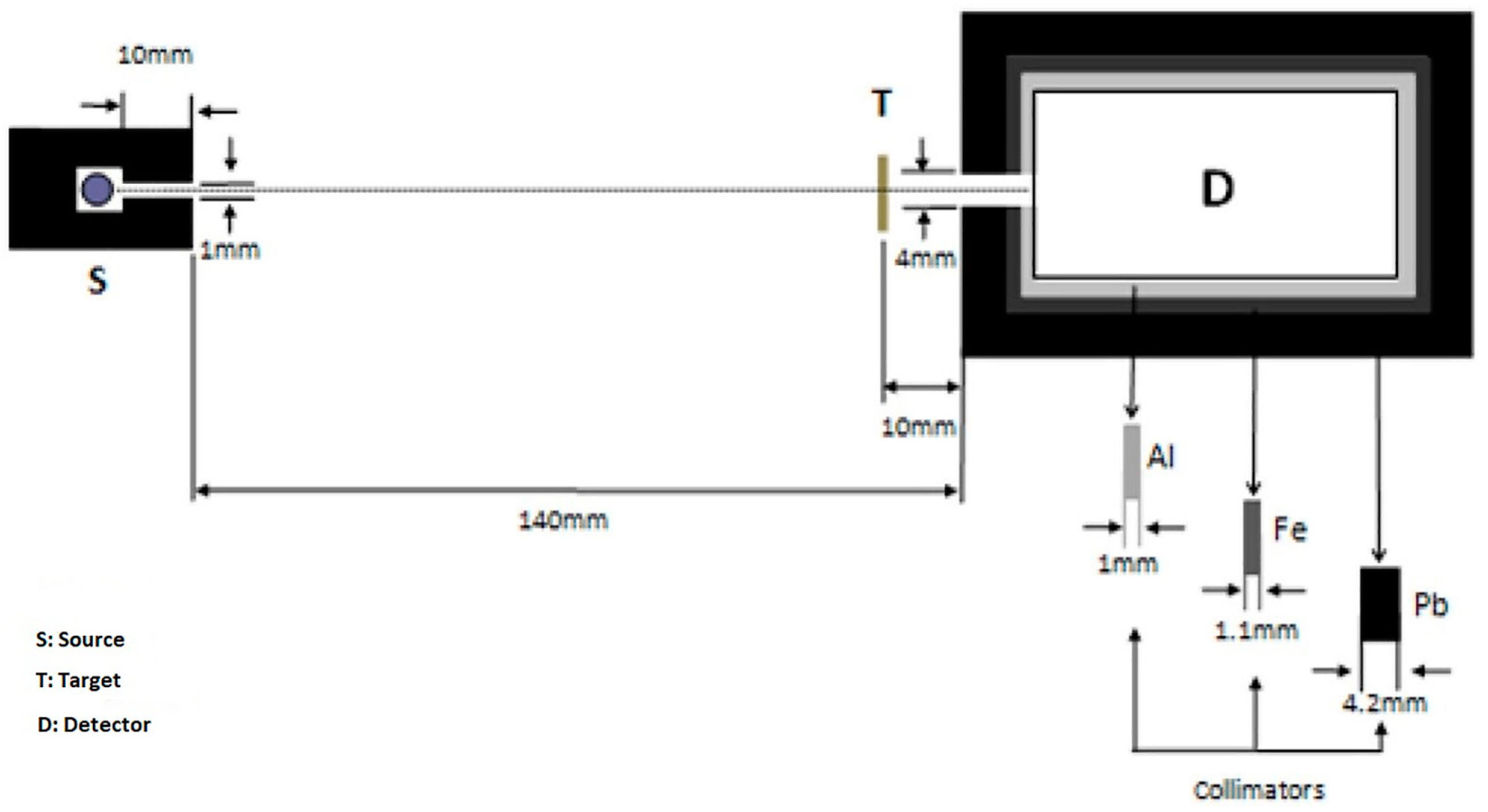
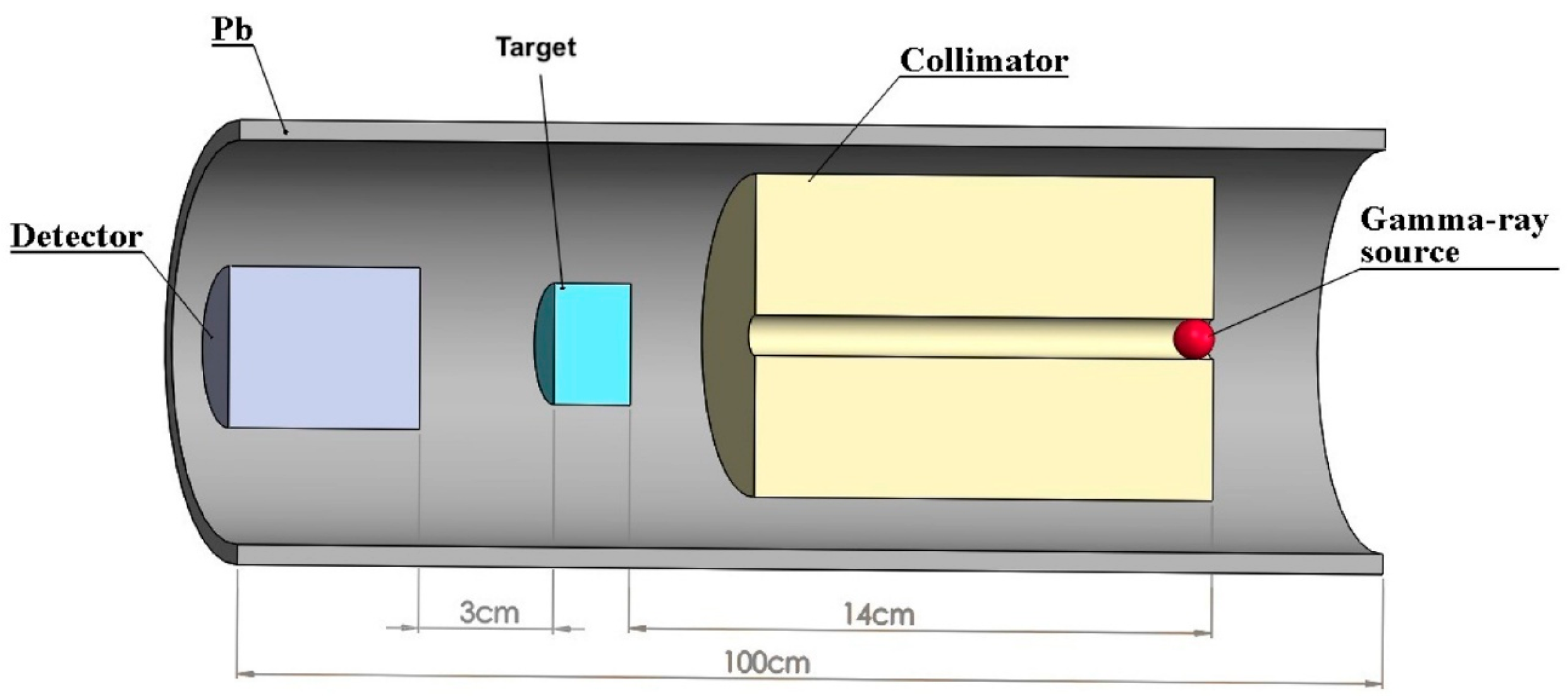
2. Materials and Methods
3. Results
4. Conclusions
- (1)
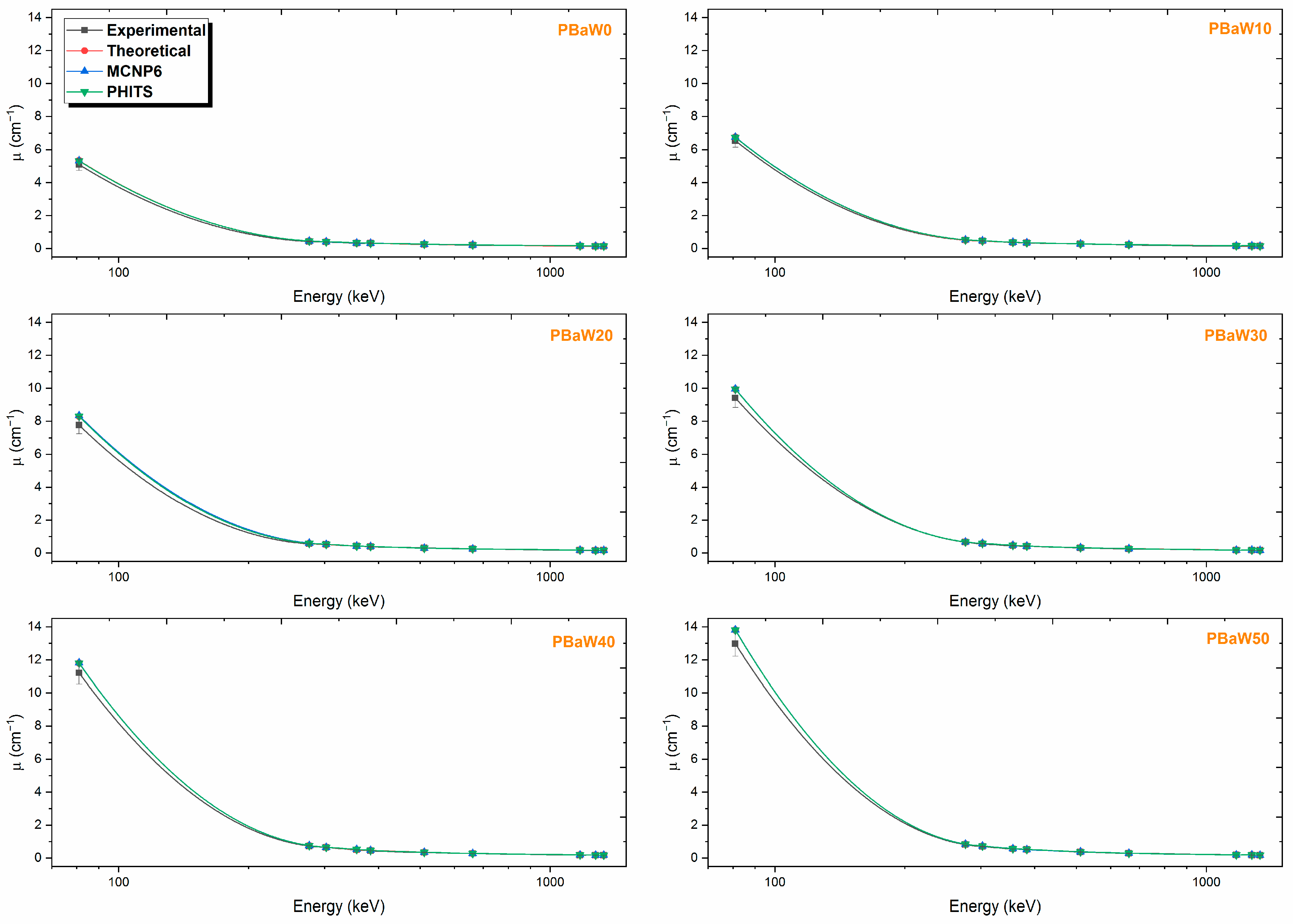
- The experimental findings closely align with both the theoretical and Monte Carlo simulation results. The Monte Carlo simulation and theoretical calculations can be used in the absence of experimental facilities.
- (2)
- The linear attenuation coefficients at 81 keV photon energy were experimentally found to be 5.0840 ± 0.7039 cm−1 for PBaW0, 6.5264 ± 0.7987 cm−1 for PBaW10, 7.7616 ± 0.5224 cm−1 for PBaW20, 9.4154 ± 0.5825 cm−1 for PBaW30, 11.2051 ± 0.6836 cm−1 for PBaW40, and 12.9676 ± 0.7597 cm−1 for PBaW50. It was determined that PBaW50, which has the highest W ratio, has the highest linear attenuation coefficient value.
- (3)
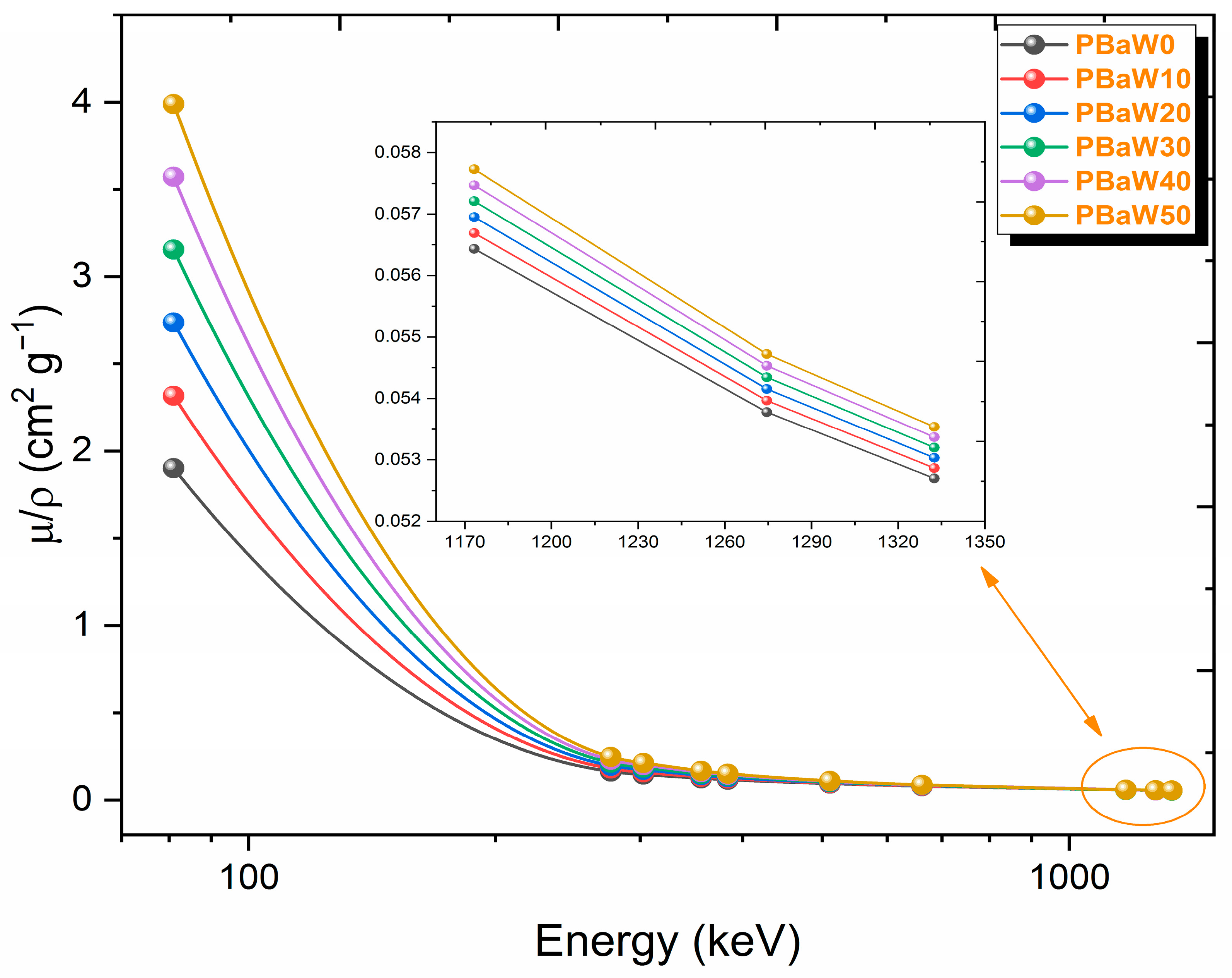
- The mass attenuation coefficients at 81 keV photon energy were experimentally found to be 1.8156 cm2/g for PBaW0, 2.2422 cm2/g for PBaW10, 2.5605 cm2/g for PBaW20, 2.9848 cm2/g for PBaW30, 3.3914 cm2/g for PBaW40, and 3.7498 cm2/g for PBaW50.
- (4)
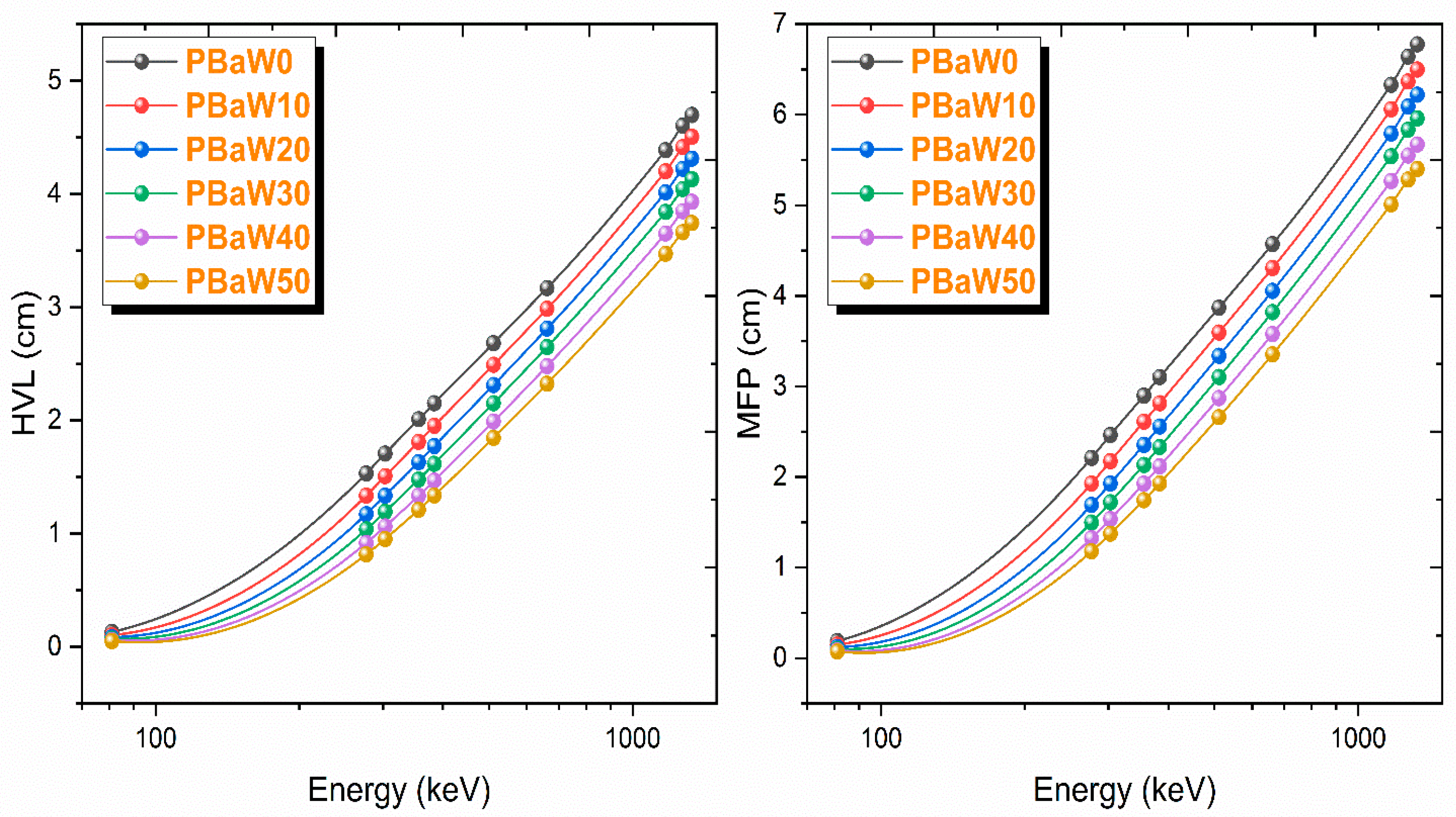
- The HVL results at 81 keV photon energy were experimentally found to be 0.1363 cm for PBaW0, 0.1062 cm for PBaW10, 0.0893 cm for PBaW20, 0.0736 cm for PBaW30, 0.0619 cm for PBaW40, and 0.0535 cm for PBaW50. The TVL results at 81 keV photon energy were experimentally found to be 0.4529 cm for PBaW0, 0.3528 cm for PBaW10, 0.2967 cm for PBaW20, 0.2446 cm for PBaW30, 0.2055 cm for PBaW40, and 0.1776 cm for PBaW50. The polymer with the lowest HVL and TVL values was identified as PBaW50.
- (5)
- The RPE values for 1 cm thickness of the materials were found to be as follows: 95.29% for PBaW0, 98.72% for PBaW10, 99.60% for PBaW20, 99.67% for PBaW30, 99.77% for PBaW40, and 99.88% for PBaW50.
- (6)
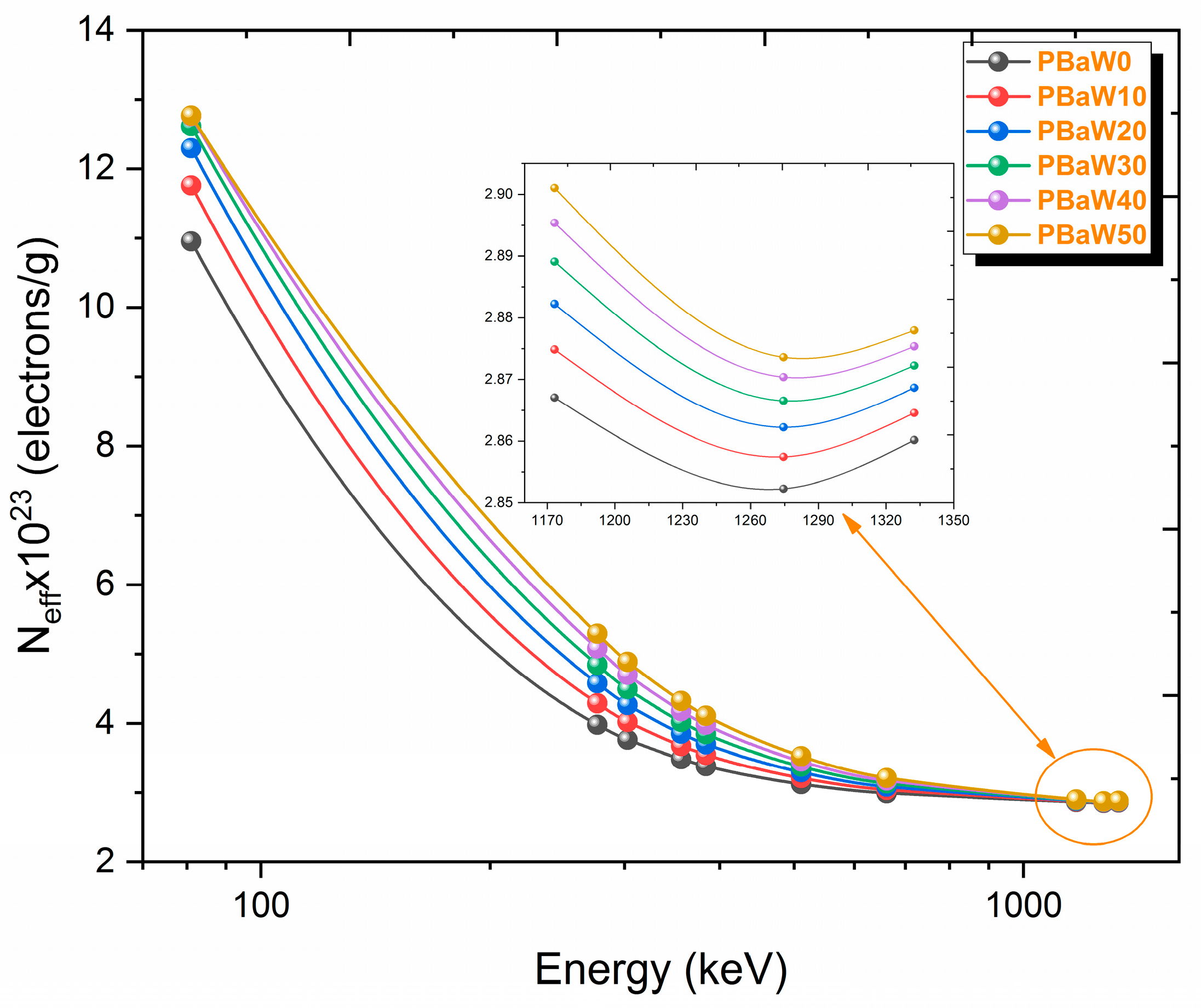
- Considering the LAC, MAC, HVL, TVL, and RPE values, it was concluded that PBaW50, the polymer with the highest W ratio, is the most effective material for radiation shielding among those studied. PBaW50 exhibits the highest LAC, MAC, and RPE values, along with the lowest HVL and TVL values, making it the best choice for radiation shielding. Consequently, the PBaW50 sample demonstrates outstanding attenuation performance and could be considered for applications requiring durable and lightweight materials in sectors such as industry, medicine, and aerospace. By incorporating high-atomic-number elements like tungsten (W) into new materials, more effective radiation shielding can be achieved. Before producing shielding materials, they should be designed according to their intended use and purpose, considering factors such as the weight, importance, and cost.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Özdoğan, H.; Kiliçoğlu Mehmetcik, Ö.; Akman, F.; Ağar, O. Comparison of Monte Carlo simulations and theoretical calculations of nuclear shielding characteristics of various borate glasses including Bi V Fe and Cd. Appl. Radiat. Isot. 2022, 189, 110454. [Google Scholar] [CrossRef] [PubMed]
- Issa, S.A.; Tekin, H.O.; Elsaman, R.; Kilicoglu, O.; Saddeek, Y.B.; Sayyed, M.I. Radiation shielding and mechanical properties of Al2O3-Na2O-B2O3-Bi2O3 glasses using MCNPX Monte Carlo code. Mater. Chem. Phys. 2019, 223, 209–219. [Google Scholar] [CrossRef]
- Mahmoud, I.S.; Issa, S.A.; Saddeek, Y.B.; Tekin, H.O.; Kilicoglu, O.; Alharbi, T.; Elsaman, R. Gamma, neutron shielding and mechanical parameters for lead vanadate glasses. Ceram. Int. 2019, 45, 14058–14072. [Google Scholar] [CrossRef]
- Kilicoglu, O.; Tekin, H.O. Bioactive glasses and direct effect of increased K2O additive for nuclear shielding performance: A comparative investigation. Ceram. Int. 2020, 46, 1323–1333. [Google Scholar] [CrossRef]
- Agar, O. Feasibility of a novel shield of nuclear radiation with W–Ni–Fe–Co and La–Bi alloys alternative to Pb and ordinary concrete absorbers. Prog. Nucl. Energy 2023, 156, 104537. [Google Scholar]
- Tyagi, G.; Singhal, A.; Routroy, S.; Bhunia, D.; Lahoti, M. Radiation shielding concrete with alternate constituents: An approach to address multiple hazards. J. Hazard. Mater. 2021, 404, 124201. [Google Scholar] [CrossRef] [PubMed]
- Çakıroğlu, M.A.; Kaplan, A.N.; Süzen, A.A. Experimental and DBN-Based neural network extraction of radiation attenuation coefficient of dry mixture shotcrete produced using different additives. Radiat. Phys. Chem. 2021, 188, 109636. [Google Scholar] [CrossRef]
- Medhat, M.E.; Singh, V.P. Mass attenuation coefficients of composite materials by Geant4, XCOM and experimental data: Comparative study. Radiat. Eff. Defect. Solid 2014, 169, 800–807. [Google Scholar] [CrossRef]
- Buyuk, B.; Tugrul, A.B.; Cengiz, M.; Yucel, O.; Goller, G.; Sahin, F.C. Radiation Shielding Properties of Spark Plasma Sintered Boron Carbide-Aluminium Composites. Acta Phys. Pol. A 2015, 128, B-132–B-134. [Google Scholar] [CrossRef]
- Singh, M.; Mudahar, G.S. Energy dependence of total photon attenuation coefficients of composite materials. Appl. Radiat. Isot. 1992, 43, 907–911. [Google Scholar] [CrossRef]
- Nagaraja, N.; Manjunatha, H.C.; Seenappa, L.; Sridhar, K.N.; Ramalingam, H.B. Selection of shielding materials for gamma/X-ray and neutron radiations among the commonly used polymers. Int. J. Nucl. Energy Sci. Technol. 2019, 13, 325–339. [Google Scholar] [CrossRef]
- Marashdeh, M.; Abdulkarim, M. Determination of the Attenuation Coefficients of Epoxy Resin with Carbopol Polymer as a Breast Phantom Material at Low Photon Energy Range. Polymers 2023, 15, 2645. [Google Scholar] [CrossRef] [PubMed]
- Mirji, R.; Lobo, B. Computation of the mass attenuation coefficient of polymeric materials at specific gamma photon energies. Radiat. Phys. Chem. 2017, 135, 32–44. [Google Scholar] [CrossRef]
- Erkoyuncu, İ.; Akman, F.; Ogul, H.; Kaçal, M.; Polat, H.; Demirkol, I.; Dilsiz, K.; Ertuğral, B. A detailed investigation of gamma and neutron shielding capabilities of ternary composites doped with polyacrylonitrile and gadolinium (III) sulfate. Appl. Radiat. Isot. 2023, 110789. [Google Scholar] [CrossRef] [PubMed]
- Gürel, H.; Özdemir, M.; Kaçal, M.; Akman, F.; Polat, H.; Agar, O. Investigation of gamma radiation shielding characteristics of bismuth reinforced ternary composites in wide photon energy region. Radiat. Phys. Chem. 2023, 208, 110924. [Google Scholar] [CrossRef]
- Gharieb, M.; Kenawy, S.H.; El-Bassyouni, G.T.; Hamzawy, E.M.A. Gamma ray and fast neutron shielding of ZrSiO4-Al2O3 ceramic refractor. Part. Sci. Technol. 2022, 41, 2088431. [Google Scholar] [CrossRef]
- İrim, G.Ş.; Alchekh, A.; Keskin, W.M.A.; Baykara, O.; Ozkoc, G.; Avcı, A.; Doğru, M.; Karakoc, M. Physical, mechanical and neutron shielding properties of h-BN/Gd2O3/HDPE ternary nanocomposites. Radiat. Phys. Chem. 2018, 146, 25–31. [Google Scholar]
- Kiani, M.A.; Ahmadi, S.J.; Outokesh, M.; Adeli, R.; Kiani, H. Study on physico-mechanical and gamma-ray shielding characteristics of new ternary nanocomposites. Appl. Radiat. Isot. 2019, 148, 53–61. [Google Scholar] [CrossRef] [PubMed]
- Zhang, P.; Jia, C.; Li, J.; Wang, W. Shielding composites for neutron and gamma-radiation with Gd2O3@W core-shell structured particles. Mater. Lett. 2020, 258, 128082. [Google Scholar] [CrossRef]
- Akman, F.; Ozdogan, H.; Kilicoglu, O.; Ogul, H.; Agar, O.K.; Polat, H.; Tursucu, A. Gamma, charged particle and neutron radiation shielding capacities of ternary composites having polyester/barite/tungsten boride. Radiat. Phys. Chem. 2023, 212, 111120. [Google Scholar] [CrossRef]
- Gerward, L.; Guilbert, N.; Jensen, K.B.; Levring, H. WinXCom—A program for calculating X-ray attenuation coefficients. Radiat. Phys. Chem. 2004, 71, 653–654. [Google Scholar] [CrossRef]
- Sato, T.; Niita, K.; Matsuda, N.; Hashimoto, S.; Iwamoto, Y.; Noda, S.; Ogawa, T.; Iwase, H.; Nakashima, H.; Fukahori, T.; et al. Particle and heavy ion transport code system, PHITS, version 2.52. J. Nucl. Sci. Technol. 2013, 50, 913–923. [Google Scholar] [CrossRef]
- Goorley, J.T.; James, M.R.; Booth, T.E.; Brown, F.B.; Bull, J.S.; Cox, L.J.; Durkee, J.W., Jr.; Elson, J.S.; Fensin, M.L.; Forster, R.A., III; et al. Initial MCNP6 Release Overview-MCNP6, version 1.0; Los Alamos National Lab. (LANL): Los Alamos, NM, USA, 2013. [Google Scholar]
- Erkoyuncu, İ.; Demirkol, İ.; Akman, F.; Dilsiz, K.; Kaçal, M.R.; Polat, H. A detailed investigation of gamma and neutron shielding capabilities of concrete doped with bronze and boron carbide. Radiat. Phys. Chem. 2004, 215, 111358. [Google Scholar] [CrossRef]
- Kaçal, M.R.; Polat, H.; Oltulu, M.; Akman, F.; Agar, O.; Tekin, H.O. Gamma shielding and compressive strength analyses of polyester composites reinforced with zinc: An experiment, theoretical, and simulation based study. Appl. Phys. A 2020, 126, 205. [Google Scholar] [CrossRef]
- National Council on Radiation Protection and Measurements. Radiation Protection Design Guidelines for 0.1–100 MeV Particle Accelerator Facilities* (NCRP Report No. 51); NCRP: Bethesda, MD, USA, 1977. [Google Scholar]
- National Council on Radiation Protection and Measurements. Neutron Contamination from Medical Electron Accelerators* (NCRP Report No. 79); NCRP: Bethesda, MD, USA, 1984. [Google Scholar]
- National Council on Radiation Protection and Measurements. Structural Shielding Design and Evaluation for Megavoltage X- and Gamma-ray Radiotherapy Facilities (NCRP Report No. 151); NCRP: Bethesda, MD, USA, 2005. [Google Scholar]
- Akman, F.; Kaçal, M.R.; Polat, H.; Aktas, G.; Gultekin, A.; Agar, O. A comparative study on the nuclear shielding properties of BiBr3 and PbSO4 incorporated composites. J. Phys. Chem. Solids 2021, 152, 109978. [Google Scholar] [CrossRef]
- Niksarlıoğlu, S.; Akman, F.; Pekdemir, M.E.; Kuzu, S.Y.; Kaçal, M.R.; Yılmaz, M. An extensive investigation on gamma shielding properties of PLA/Gd2O3 nanocomposites. Radiat. Phys. Chem. 2003, 208, 110936. [Google Scholar] [CrossRef]
- Bashter, I.I. Calculation of radiation attenuation coefficients for shielding concretes. Ann. Nucl. Energy 1997, 24, 1389–1401. [Google Scholar] [CrossRef]
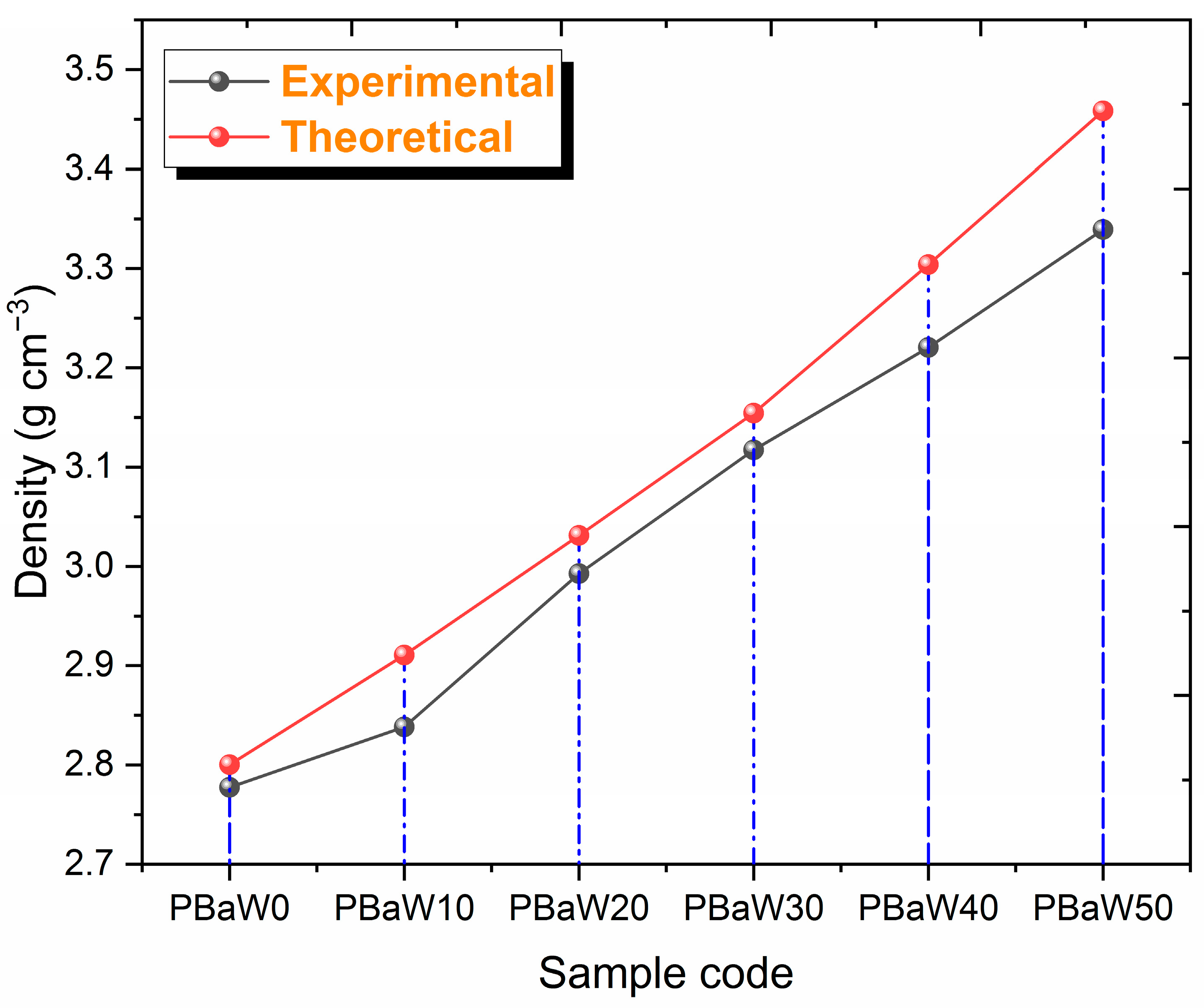



| Sample Code | Chemical Composition (%) | Density (g/cm3) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| H | C | O | S | Co | Ba | W | Exp. | Theo. | |
| PBaW0 | 0.9025 | 12.1200 | 28.9989 | 10.9746 | 0.0024 | 47.0017 | 0.0000 | 2.7775 | 2.8002 |
| PBaW10 | 0.9025 | 12.1200 | 26.8182 | 9.8820 | 0.0024 | 42.3224 | 7.9525 | 2.8383 | 2.9107 |
| PBaW20 | 0.9025 | 12.1200 | 24.6181 | 8.7797 | 0.0024 | 37.6013 | 15.9760 | 2.9927 | 3.0313 |
| PBaW30 | 0.9025 | 12.1200 | 22.4277 | 7.6822 | 0.0024 | 32.9012 | 23.9640 | 3.1174 | 3.1544 |
| PBaW40 | 0.9025 | 12.1200 | 20.2373 | 6.5848 | 0.0024 | 28.2010 | 31.9521 | 3.2206 | 3.3040 |
| PBaW50 | 0.9025 | 12.1200 | 18.0469 | 5.4873 | 0.0024 | 23.5008 | 39.9401 | 3.3392 | 3.4583 |
| Energy (keV) | PBaW0 | PBaW10 | ||||||
| Experimental | Theo. | MCNP6 | PHITS | Experimental | Theo. | MCNP6 | PHITS | |
| 81.0 | 5.0840 ± 0.7039 | 5.3229 | 5.3151 | 5.3173 | 6.5264 ± 0.7987 | 6.7428 | 6.7406 | 6.7340 |
| 276.4 | 0.4315 ± 0.3537 | 0.4528 | 0.4552 | 0.4545 | 0.5156 ± 0.3873 | 0.5192 | 0.5202 | 0.5199 |
| 302.9 | 0.3912 ± 0.0207 | 0.4063 | 0.4074 | 0.4097 | 0.4645 ± 0.0254 | 0.4602 | 0.4629 | 0.4629 |
| 356.0 | 0.3257 ± 0.0115 | 0.3449 | 0.3460 | 0.3475 | 0.3692 ± 0.0143 | 0.3832 | 0.3842 | 0.3862 |
| 383.9 | 0.3241 ± 0.0073 | 0.3221 | 0.3228 | 0.3247 | 0.3446 ± 0.0085 | 0.3551 | 0.3562 | 0.3581 |
| 511.0 | 0.2555 ± 0.0157 | 0.2585 | 0.2597 | 0.2610 | 0.2743 ± 0.0175 | 0.2782 | 0.2793 | 0.2792 |
| 661.7 | 0.2144 ± 0.0065 | 0.2188 | 0.2198 | 0.2201 | 0.2213 ± 0.0071 | 0.2321 | 0.2329 | 0.2337 |
| 1173.2 | 0.1533 ± 0.0047 | 0.1580 | 0.1591 | 0.1588 | 0.1543 ± 0.0048 | 0.1650 | 0.1663 | 0.1663 |
| 1274.5 | 0.1425 ± 0.0036 | 0.1506 | 0.1520 | 0.1520 | 0.1472 ± 0.0036 | 0.1571 | 0.1585 | 0.1588 |
| 1332.5 | 0.1387 ± 0.0037 | 0.1476 | 0.1490 | 0.1489 | 0.1563 ± 0.0037 | 0.1539 | 0.1550 | 0.1550 |
| Energy (keV) | PBaW20 | PBaW30 | ||||||
| Experimental | Theo. | MCNP6 | PHITS | Experimental | Theo. | MCNP6 | PHITS | |
| 81.0 | 7.7616 ± 0.5224 | 8.2937 | 8.3414 | 8.2886 | 9.4154 ± 0.5825 | 9.9479 | 9.9524 | 9.9492 |
| 276.4 | 0.5528 ± 0.0278 | 0.5918 | 0.5956 | 0.5920 | 0.6571 ± 0.0453 | 0.6688 | 0.6691 | 0.6684 |
| 302.9 | 0.5275 ± 0.0169 | 0.5192 | 0.5246 | 0.5215 | 0.5559 ± 0.0175 | 0.5815 | 0.5830 | 0.5831 |
| 356.0 | 0.4208 ± 0.0096 | 0.4251 | 0.4291 | 0.4275 | 0.4435 ± 0.0101 | 0.4693 | 0.4713 | 0.4713 |
| 383.9 | 0.3752 ± 0.0214 | 0.3911 | 0.3937 | 0.3939 | 0.4166 ± 0.0241 | 0.4290 | 0.4307 | 0.4317 |
| 511.0 | 0.3044 ± 0.0080 | 0.2997 | 0.3026 | 0.3023 | 0.3047 ± 0.0077 | 0.3222 | 0.3222 | 0.3240 |
| 661.7 | 0.2494 ± 0.0055 | 0.2466 | 0.2487 | 0.2481 | 0.2469 ± 0.0054 | 0.2618 | 0.2627 | 0.2641 |
| 1173.2 | 0.1676 ± 0.0039 | 0.1726 | 0.1745 | 0.1742 | 0.1775 ± 0.0041 | 0.1805 | 0.1811 | 0.1822 |
| 1274.5 | 0.1574 ± 0.0040 | 0.1642 | 0.1667 | 0.1666 | 0.1641 ± 0.0042 | 0.1714 | 0.1728 | 0.1739 |
| 1332.5 | 0.1657 ± 0.0037 | 0.1608 | 0.1625 | 0.1620 | 0.1593 ± 0.0035 | 0.1678 | 0.1687 | 0.1694 |
| Energy (keV) | PBaW40 | PBaW50 | ||||||
| Experimental | Theo. | MCNP6 | PHITS | Experimental | Theo. | MCNP6 | PHITS | |
| 81.0 | 11.2051 ± 0.6836 | 11.7990 | 11.8124 | 11.8009 | 12.9676 ± 0.7597 | 13.7941 | 13.8048 | 13.7960 |
| 276.4 | 0.7363 ± 0.0371 | 0.7559 | 0.7553 | 0.7553 | 0.8134 ± 0.0466 | 0.8492 | 0.8465 | 0.8484 |
| 302.9 | 0.6357 ± 0.0201 | 0.6524 | 0.6542 | 0.6539 | 0.6937 ± 0.0223 | 0.7281 | 0.7302 | 0.7293 |
| 356.0 | 0.4940 ± 0.0112 | 0.5198 | 0.5208 | 0.5222 | 0.5490 ± 0.0124 | 0.5735 | 0.5746 | 0.5754 |
| 383.9 | 0.4443 ± 0.0255 | 0.4724 | 0.4743 | 0.4743 | 0.5257 ± 0.0305 | 0.5186 | 0.5196 | 0.5207 |
| 511.0 | 0.3394 ± 0.0086 | 0.3482 | 0.3490 | 0.3505 | 0.3692 ± 0.0097 | 0.3758 | 0.3764 | 0.3778 |
| 661.7 | 0.2750 ± 0.0060 | 0.2795 | 0.2805 | 0.2815 | 0.2897 ± 0.0063 | 0.2982 | 0.2984 | 0.3012 |
| 1173.2 | 0.1815 ± 0.0042 | 0.1899 | 0.1907 | 0.1913 | 0.1927 ± 0.0044 | 0.1996 | 0.2002 | 0.2012 |
| 1274.5 | 0.1776 ± 0.0045 | 0.1802 | 0.1817 | 0.1822 | 0.1854 ± 0.0047 | 0.1892 | 0.1907 | 0.1913 |
| 1332.5 | 0.1649 ± 0.0037 | 0.1763 | 0.1770 | 0.1777 | 0.1773 ± 0.0039 | 0.1851 | 0.1859 | 0.1868 |
| Energy (keV) | PBaW0 | PBaW10 | PBaW20 | PBaW30 | PBaW40 | PBaW50 | Pb | Ordinary concrete (OC) | Steel–Magnetite Concrete (SMC) | Ilmenite–Limonite Concrete (ILC) | Hematite–Serpentine Concrete (HSC) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 81.0 | 0.4326 | 0.3415 | 0.2776 | 0.2315 | 0.1952 | 0.1669 | 0.0865 | 4.9501 | 0.9213 | 2.1476 | 2.9432 |
| 276.4 | 5.0855 | 4.4346 | 3.8908 | 3.4431 | 3.0463 | 2.7116 | 0.4234 | 8.9257 | 3.9187 | 7.0256 | 8.1027 |
| 302.9 | 5.6674 | 5.0030 | 4.4352 | 3.9594 | 3.5297 | 3.1625 | 0.5132 | 9.2519 | 4.1217 | 7.3460 | 8.4462 |
| 356.0 | 6.6763 | 6.0083 | 5.4165 | 4.9064 | 4.4302 | 4.0146 | 0.7061 | 9.8669 | 4.4810 | 7.9239 | 9.0736 |
| 383.9 | 7.1477 | 6.4844 | 5.8877 | 5.3672 | 4.8740 | 4.4396 | 0.8117 | 10.1732 | 4.6515 | 8.2025 | 9.3792 |
| 511.0 | 8.9078 | 8.2777 | 7.6840 | 7.1475 | 6.6122 | 6.1270 | 1.2990 | 11.4622 | 5.3326 | 9.3363 | 10.6362 |
| 661.7 | 10.5252 | 9.9212 | 9.3360 | 8.7966 | 8.2378 | 7.7225 | 1.8411 | 12.8426 | 6.0255 | 10.5125 | 11.9547 |
| 1173.2 | 14.5711 | 13.9544 | 13.3378 | 12.7590 | 12.1267 | 11.5336 | 3.2851 | 16.8846 | 7.9890 | 13.8888 | 15.7661 |
| 1274.5 | 15.2909 | 14.6594 | 14.0268 | 13.4324 | 12.7802 | 12.1679 | 3.5038 | 17.6164 | 8.3347 | 14.4900 | 16.4491 |
| 1332.5 | 15.6042 | 14.9646 | 14.3234 | 13.7209 | 13.0588 | 12.4370 | 3.6144 | 18.0227 | 8.5249 | 14.8221 | 16.8272 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Özdoğan, H.; Üncü, Y.A.; Akman, F.; Polat, H.; Kaçal, M.R. Detailed Analysis of Gamma-Shielding Characteristics of Ternary Composites Using Experimental, Theoretical and Monte Carlo Simulation Methods. Polymers 2024, 16, 1778. https://doi.org/10.3390/polym16131778
Özdoğan H, Üncü YA, Akman F, Polat H, Kaçal MR. Detailed Analysis of Gamma-Shielding Characteristics of Ternary Composites Using Experimental, Theoretical and Monte Carlo Simulation Methods. Polymers. 2024; 16(13):1778. https://doi.org/10.3390/polym16131778
Chicago/Turabian StyleÖzdoğan, Hasan, Yiğit Ali Üncü, Ferdi Akman, Hasan Polat, and Mustafa Recep Kaçal. 2024. "Detailed Analysis of Gamma-Shielding Characteristics of Ternary Composites Using Experimental, Theoretical and Monte Carlo Simulation Methods" Polymers 16, no. 13: 1778. https://doi.org/10.3390/polym16131778
APA StyleÖzdoğan, H., Üncü, Y. A., Akman, F., Polat, H., & Kaçal, M. R. (2024). Detailed Analysis of Gamma-Shielding Characteristics of Ternary Composites Using Experimental, Theoretical and Monte Carlo Simulation Methods. Polymers, 16(13), 1778. https://doi.org/10.3390/polym16131778






