Development and Validation of a 1D Dynamic Model of an Injection Moulding Process and Design of a Model-Based Nozzle Pressure Controller
Abstract
1. Introduction
2. Previous Work
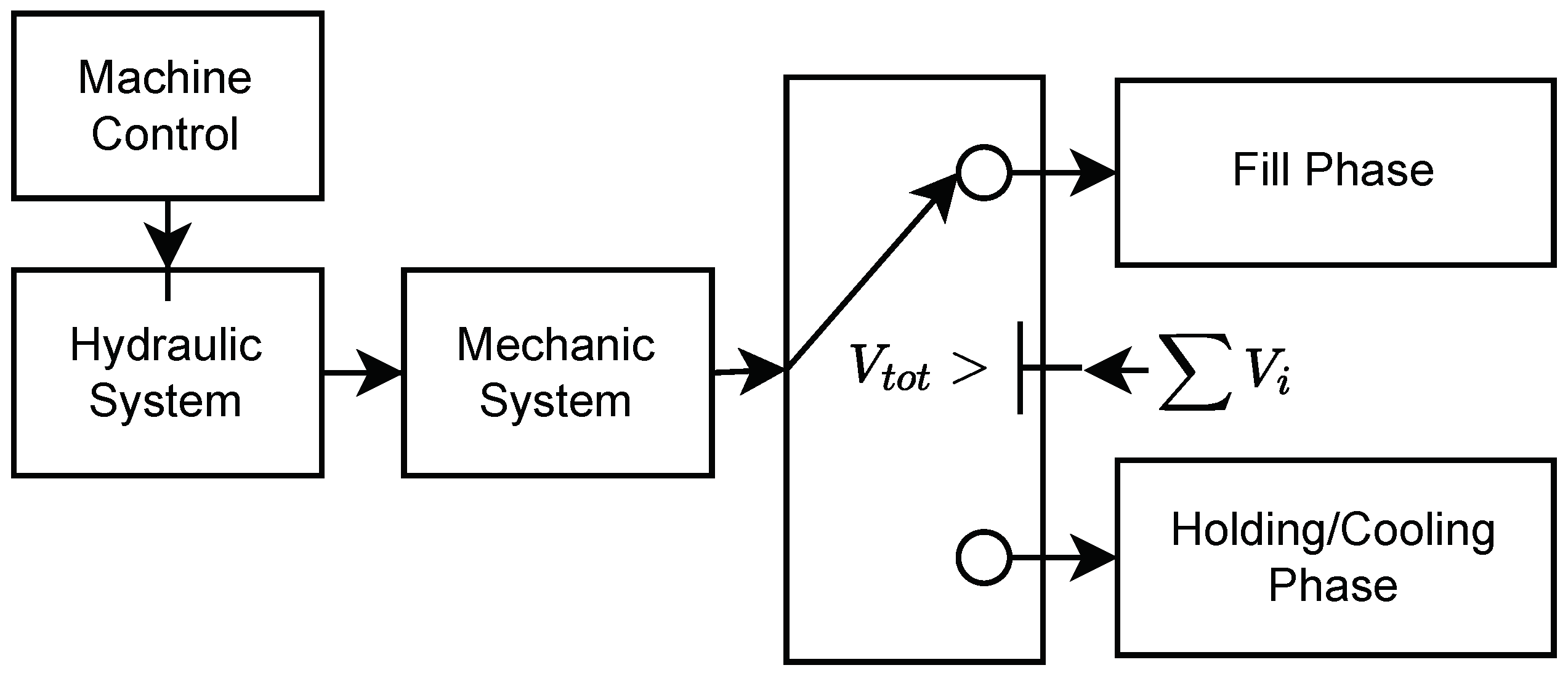
3. Model Structure
4. Hydraulic System
5. Filling Phase
6. Hydraulic Dimensions
Initial Conditions for the Packing Phase
7. Packing Phase
Cooling
- The mould has constant a temperature independent of position;
- The heat flux is perpendicular and is equal in all directions at any given position;
- The heat from shear and inflow of hot material in the packing phase is not considered.
8. Control
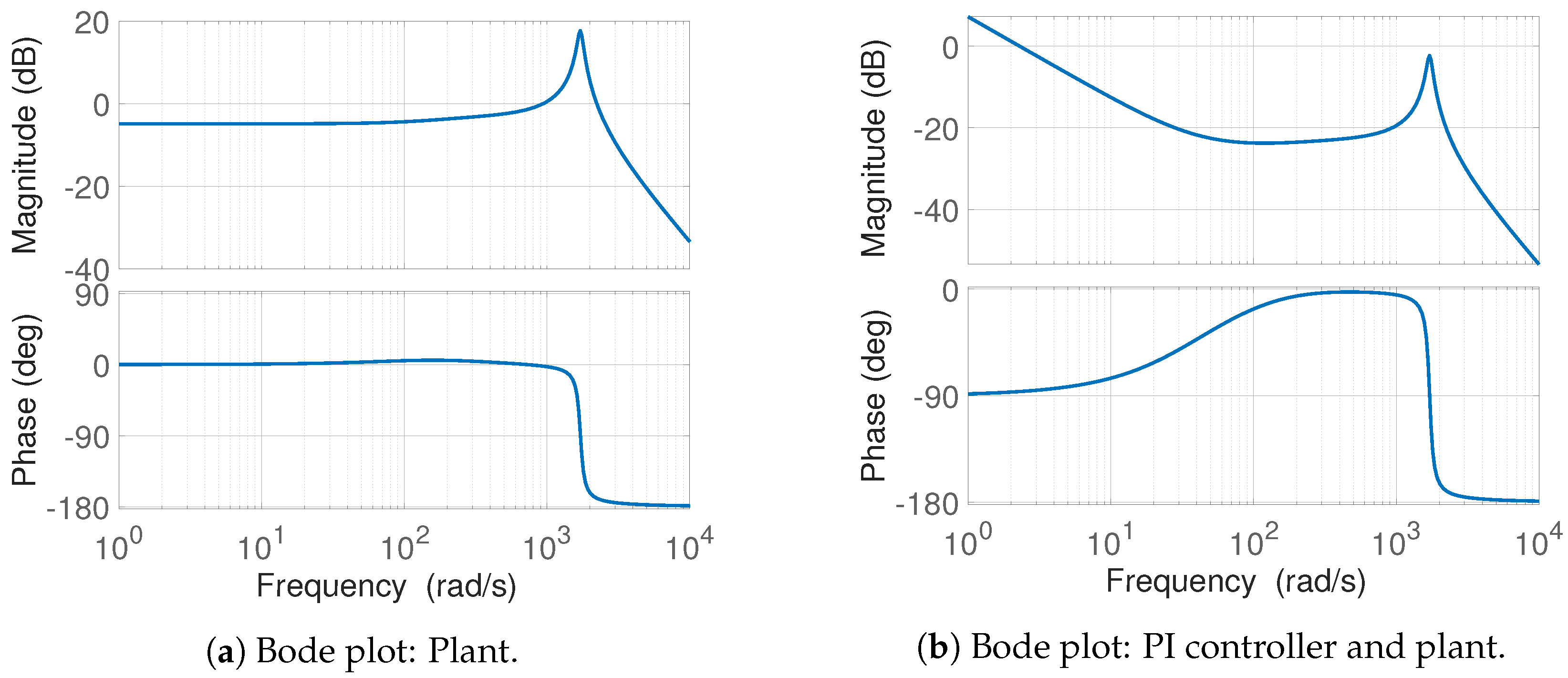
8.1. Model Linearisation
8.1.1. Fill Phase
8.1.2. Holding Phase
8.2. Controller Design
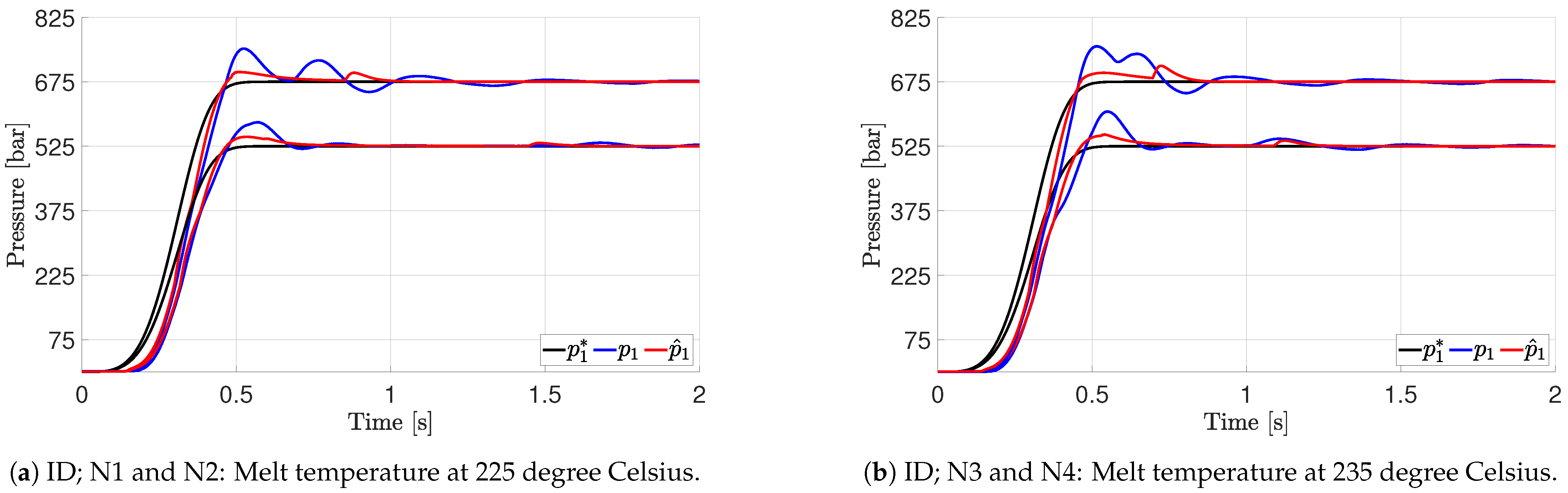
9. Experimental Validation
9.1. Validation: Nonlinear Model
9.2. Validation: Control Performance
10. Discussion
11. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Notation
| Reference | |
| Linearisation point | |
| Initial condition | |
| i refers to a volume in the nozzle, extender, sprue, runner, gate or cavity and can take the value 1–6 | |
| j refers to the sensor position in the given section i and can take the value 1–2 | |
| Hydraulic chamber and can take the value A or B | |
| Double time derivative | |
| Time derivative | |
| Average | |
| Estimated value |
Nomenclature
| Cross-sectional area of the i-th section | |
| Area of cylinder chamber A | |
| Surface area of the i-th section | |
| Viscous friction | |
| Displacement of pump k | |
| Hydraulic diameter of the i-th section | |
| Hydraulic diameter after cooling of the i-th section | |
| Coulomb friction | |
| Resistive shear force of the i-th section | |
| Controller for section i | |
| Hydraulic length of the i-th section | |
| Integral gain of controller i | |
| Proportional gain of controller i | |
| Flow of the i-th section | |
| Flow from pump k | |
| Leakage flow across cylinder | |
| Glass transition temperature | |
| Cooling water temperature | |
| Temperature of the mould | |
| Peak temperature of the polymer | |
| Temperature of the i-th section | |
| Volume of the i-th section | |
| Volume of hydraulic chamber k | |
| Bulk modulus of hydraulic chamber k | |
| Bulk modulus of the i-th section | |
| Shear rate of the i-th section | |
| Zero shear viscosity | |
| Viscosity of the i-th section | |
| Pressure in the i-th section | |
| Adiabatic compressibility of the i-th section | |
| Specific volume of the i-th section | |
| Poisson ratio | |
| Bandwidth of level pressure controller | |
| Bandwidth of load pressure controller | |
| Percentage of frozen layer | |
| Density of the i-th section | |
| Shear stress of the i-th section | |
| b | Two-domain Tait parameters |
| Thermal effusivity of the polymer | |
| Thermal effusivity of the mould | |
| Specific heat of the plastic | |
| k | Thermal conductivity of the polymer |
| m | Mass of injection unit and screw |
| Mass of the i-th section | |
| Hydraulic level pressure | |
| Hydraulic load pressure | |
| Hydraulic pressure in chamber k | |
| Holding pressure | |
| t | Time |
| Decompression distance | |
| Starting point of ram |
Appendix A. Hydraulic Dimensions: Sprue

References
- Ciofu, C.; Mindru, D.T. Injection and Micro Injection of Polymeric Plastics Materials: A Review. Int. J. Mod. Manufact. Technol. 2013, 1, 49–68. [Google Scholar]
- Ageyeva, T.; Horváth, S.; Kovács, J. In-Mold Sensors for Injection Molding: On the Way to Industry 4.0. Sensors 2019, 19, 3551. [Google Scholar] [CrossRef] [PubMed]
- Zhao, P.; Ji, K.; Zhang, J.; Chen, Y.; Dong, Z.; Zheng, J.; Fu, J. In-Situ Ultrasonic Measurement of Molten Polymers during Injection Molding. J. Mater. Process. Technol. 2021, 293, 117081. [Google Scholar] [CrossRef]
- Hertz, R.A.; Christensen, J.K.; Kristiansen, S.; Therkelsen, O.; Schmidt, L. In-Line Process and Material Property Measurement in Injection Moulding—A Theoretical Review. Prod. Manuf. Res. 2022, 10, 938–963. [Google Scholar] [CrossRef]
- Ljung, L. System Identification. In Proceedings of the Uncertainty and Control, Bonn, Germany, 2–4 May 1985; Ackermann, J., Ed.; Lecture Notes in Control and Information Sciences. Springer: Berlin/Heidelberg, Germany, 2005; Volume 5, pp. 48–83. [Google Scholar] [CrossRef]
- Obendrauf, W.; Kukla, C.; Langecker, G. Quick measurement of temperature with IR sensors. Kunststoffe Ger. Plast. 1993, 83, 971–974. [Google Scholar]
- Gordon, G.; Kazmer, D.O.; Tang, X.; Fan, Z.; Gao, R.X. Quality Control Using a Multivariate Injection Molding Sensor. Int. J. Adv. Manuf. Technol. 2015, 78, 1381–1391. [Google Scholar] [CrossRef]
- Chen, Z.; Turng, L.S. A Review of Current Developments in Process and Quality Control for Injection Molding. Adv. Polym. Technol. 2005, 24, 165–182. [Google Scholar] [CrossRef]
- Hopmann, C.; Ressmann, A.; Reiter, M.; Stemmler, S.; Abel, D. A Self-Optimising Injection Moulding Process with Model-Based Control System Parameterisation. Int. J. Comput. Integr. Manuf. 2016, 29, 1190–1199. [Google Scholar] [CrossRef]
- Abu Fara, D. Control of Nozzle and Cavity Pressure during Filling and Packing in Thermoplastics Injection Molding. Ph.D. Thesis, McGill University, Montréal, QC, Canada, 1988. [Google Scholar]
- Isermann, R. Practical Aspects of Process Identification. Automatica 1980, 16, 575–587. [Google Scholar] [CrossRef]
- Shankar, A.; Paul, F.W. A Mathematical Model for the Evaluation of Injection Molding Machine Control. J. Dyn. Syst. Meas. Control 1982, 104, 86–92. [Google Scholar] [CrossRef]
- Chiu, C.P.; Shih, L.C.; Wei, J.H. Dynamic Modeling of the Mold Filling Process in an Injection Molding Machine. Polym. Eng. Sci. 1991, 31, 1417–1425. [Google Scholar] [CrossRef]
- Woll, S.L.B. Quality Monitoring and Control of the Injection Molding Process Using a Pattern-Based Approach. Ph.D. Thesis, The University of Connecticut, Storrs, CT, USA, 1995. [Google Scholar]
- Woll, S.L.B.; Cooper, D.J. A Dynamic Injection-Molding Process Model for Simulating Mold Cavity Pressure Patterns. Polym.-Plast. Technol. Eng. 1997, 36, 809–840. [Google Scholar] [CrossRef]
- Agrawal, A.R.; Pandelidis, I.O.; Pecht, M. Injection-Molding Process Control—A Review. Polym. Eng. Sci. 1987, 27, 1345–1357. [Google Scholar] [CrossRef]
- Froehlich, C.; Kemmetmüller, W.; Kugi, A. Control-Oriented Modeling of Servo-Pump Driven Injection Molding Machines in the Filling and Packing Phase. Math. Comput. Model. Dyn. Syst. 2018, 24, 451–474. [Google Scholar] [CrossRef]
- Spencer, R.S.; Gilmore, G.D. Some Flow Phenomena in the Injection Molding of Polystyrene. J. Colloid Sci. 1951, 6, 118–132. [Google Scholar] [CrossRef]
- McKelvey, J.M. Polymer Processing, 99th ed.; John Wiley & Sons: New York, NY, USA, 1962. [Google Scholar]
- Pearson, J.R.A. Mechanical Principles of Polymer Melt Processing, 1st ed.; Pergamon Press: Oxford, UK, 1966. [Google Scholar]
- Harry, D.H.; Parrott, R.G. Numerical Simulation of Injection Mold Filling. Polym. Eng. Sci. 1970, 10, 209–214. [Google Scholar] [CrossRef]
- Kamal, M.R.; Kenig, S. The Injection Molding of Thermoplastics Part I: Theoretical Model. Polym. Eng. Sci. 1972, 12, 294–301. [Google Scholar] [CrossRef]
- Kamal, M.R.; Kenig, S. The Injection Molding of Thermoplastics Part II: Experimental Test of the Model. Polym. Eng. Sci. 1972, 12, 302–308. [Google Scholar] [CrossRef]
- Nunn, R.E.; Fenner, R.T. Flow and Heat Transfer in the Nozzle of an Injection Molding Machine. Polym. Eng. Sci. 1977, 17, 811–818. [Google Scholar] [CrossRef]
- Huilier, D.G. Modeling of Injection Mold Post-Filling: A Review and Some Critical Problems to Solve. J. Polym. Eng. 1990, 9, 237–302. [Google Scholar] [CrossRef]
- Zheng, R.; Tanner, R.I.; Fan, X.J. Injection Molding: Integration of Theory and Modeling Methods; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar] [CrossRef]
- Kennedy, P.; Zheng, R. Flow Analysis of Injection Molds. In Flow Analysis of Injection Molds; Carl Hanser Verlag GmbH & Co. KG: München, Germany, 2013; pp. I–XXIX. [Google Scholar] [CrossRef]
- Fernandes, C.; Pontes, A.J.; Viana, J.C.; Gaspar-Cunha, A. Modeling and Optimization of the Injection-Molding Process: A Review. Adv. Polym. Technol. 2018, 37, 429–449. [Google Scholar] [CrossRef]
- Qian, C.C.; Deshpande, A.; Jesri, M.; Groves, R.; Reynolds, N.; Kendall, K. A Comprehensive Assessment of Commercial Process Simulation Software for Compression Moulding of Sheet Moulding Compound. 2021. Available online: https://popups.uliege.be/esaform21/index.php?id=2771 (accessed on 17 May 2024).
- Kamal, M.R.; Patterson, W.I.; Fara, D.A.; Haber, A. A Study in Injection Molding Dynamics. Polym. Eng. Sci. 1984, 24, 686–691. [Google Scholar] [CrossRef]
- Fara, D.A.; Kamal, M.R.; Patterson, W.I. Evaluation of Simple Dynamic Models and Controllers for Hydraulic and Nozzle Pressure in Injection Molding. Polym. Eng. Sci. 1985, 25, 714–723. [Google Scholar] [CrossRef]
- Kamal, M.R.; Patterson, W.I.; Conley, N.; Fara, D.A.; Lohfink, G. Dynamics and Control of Pressure in the Injection Molding of Thermoplastics. Polym. Eng. Sci. 1987, 27, 1403–1410. [Google Scholar] [CrossRef]
- Abu-Ayyad, M.; Dubay, R. Development of an Extended Predictive Controller for Injection Speed. In Proceedings of the Society of Plastics Engineers Annual Technical Conference, 2007, Annual Technical Conference—ANTEC, Conference Proceedings, Cincinnati, OH, USA, 6–11 May 2007; pp. 679–683. [Google Scholar]
- Hu, J.; Vogel, J.H. Dynamic Modeling and Control of Packing Pressure in Injection Molding. J. Eng. Mater. Technol. 1994, 116, 244–249. [Google Scholar] [CrossRef]
- Kazmer, D.; Barkan, P. The Process Capability of Multi-Cavity Pressure Control for the Injection Molding Process. Polym. Eng. Sci. 1997, 37, 1880–1895. [Google Scholar] [CrossRef]
- Yiğit, İ.; Ercan, Y.; Saritaş, S. Cavity Pressure Control of Powder Injection Moulding Machines. Trans. Inst. Meas. Control 2004, 26, 393–415. [Google Scholar] [CrossRef]
- Rafizadeh, M.; Patterson, W.I.; Kamal, M.R. Physically-Based Model of Thermoplastics Injection Molding for Control Applications. Int. Polym. Process. 1996, 11, 352–362. [Google Scholar] [CrossRef]
- Rafizadeh, M.; Patterson, W.I.; Kamali, M.R. Physically-Based Adaptive Control of Cavity Pressure in Injection Moulding Process: Packing Phase. Iran. Polym. J. 1999, 8, 99–113. [Google Scholar]
- Wei, J.H.; Chang, C.C.; Chiu, C.P. A Nonlinear Dynamic Model of a Servo-Pump Controlled Injection Molding Machine. Polym. Eng. Sci. 1994, 34, 881–887. [Google Scholar] [CrossRef]
- Lin, Y.W.; Cheng, J.W.J. Model-Based Melt Flow Virtual Sensors for Filling Process of Injection Molding. Polym. Eng. Sci. 2008, 48, 543–555. [Google Scholar] [CrossRef]
- Orzechowski, S.; Paris, A.; Dobbin, C.J. Process Monitoring and Control System for Injection Molding Using Nozzle-Based Pressure and Temperature Sensors. In Proceedings of the Annual Technical Conference—ANTEC, Conference Proceedings, Atlanta, GA, USA, 26–30 April 1998; Volume 1, pp. 424–430. [Google Scholar]
- Yang, Y.; Gao, F. Cycle-to-Cycle and within-Cycle Adaptive Control of Nozzle Pressure during Packing-Holding for Thermoplastic Injection Molding. Polym. Eng. Sci. 1999, 39, 2042–2063. [Google Scholar] [CrossRef]
- Zhao, P.; Zhang, J.; Dong, Z.; Huang, J.; Zhou, H.; Fu, J.; Turng, L.S. Intelligent Injection Molding on Sensing, Optimization, and Control. Adv. Polym. Technol. 2020, 2020, e7023616. [Google Scholar] [CrossRef]
- Hertz, R.A.; Christensen, J.K.; Therkelsen, O.; Kristiansen, S.; Helver, C.E.; Hansson, F.A.; Schmidt, L. A Novel Approach to Control Switchover Between Injection and Holding Phase for a Hydraulic Injection Moulding Machine. In Proceedings of the ANTEC® 2023—Proceedings of the Technical Conference & Exhibition, Denver, CO, USA, 27–30 March 2023. [Google Scholar]
- Hertz, R.A.; Therkelsen, O.; Kristiansen, S.; Christensen, J.K.; Hansson, F.A.; Schmidt, L. Control of Hydraulic Injection Moulding Machine With Electro-Hydraulic Variable-Speed Drive. In Fluid Power Systems Technology; American Society of Mechanical Engineers Digital Collection: New York, NY, USA, 2023. [Google Scholar] [CrossRef]
- Hertz, R.A.; Therkelsen, O.; Kristiansen, S.; Christensen, J.K.; Helver, C.E.; Schmidt, L. Practical Implementation of Secondary Control Principles in an Electro-Hydraulic Speed-Variable Drive Applied to an Injection Moulding Machine. In Fluid Power Systems Technology; American Society of Mechanical Engineers Digital Collection: New York, NY, USA, 2023. [Google Scholar] [CrossRef]
- Schmidt, L.; Hansen, K.V. Electro-Hydraulic Variable-Speed Drive Networks—Idea, Perspectives, and Energy Saving Potentials. Energies 2022, 15, 1228. [Google Scholar] [CrossRef]
- Schmidt, L.; Andersen, T.O. Application of Second Order Sliding Mode Algorithms for Output Feedback Control in Hydraulic Cylinder Drives with Profound Valve Dynamics. e & i Elektrotechnik Informationstechnik 2016, 133, 238–247. [Google Scholar] [CrossRef]
- Schmidt, L.; Andersen, T.O.; Pedersen, H.C. On Application of Second Order Sliding Mode Control to Electro-Hydraulic Systems. In Engineering Systems Design and Analysis; American Society of Mechanical Engineers Digital Collection: New York, NY, USA, 2014. [Google Scholar] [CrossRef]
- Schmidt, L.; Andersen, T.O.; Pedersen, H.C.; Bech, M.M. 2-SMC of Electro-Hydraulic Drives Using the Twisting Algorithm. Appl. Mech. Mater. 2012, 233, 131–134. [Google Scholar] [CrossRef]
- Li, H.; Gong, Z.; Lin, W.; Lippa, T. Motion Profile Planning for Reduced Jerk and Vibration Residuals. Simtech Tech. Rep. 2007, 8, 32–37. [Google Scholar] [CrossRef]
- Lee, A.Y.; Jang, G.; Choi, Y. Infinitely Differentiable and Continuous Trajectory Planning for Mobile Robot Control. In Proceedings of the 2013 10th International Conference on Ubiquitous Robots and Ambient Intelligence (URAI), Jeju, Korea, 30 October–2 November 2013; pp. 357–361. [Google Scholar] [CrossRef]
- Praher, B.; Straka, K.; Usanovic, J.; Steinbichler, G. Ultrasound Based Monitoring of the Injection Moulding Process—Methods, Applications and Limitations. In AIP Conference Proceedings; American Institute of Physics: College Park, MD, USA, 2014; Volume 1593, pp. 159–162. [Google Scholar] [CrossRef]
- Wang, J.; Hopmann, C.; Kahve, C.; Hohlweck, T.; Alms, J. Measurement of Specific Volume of Polymers under Simulated Injection Molding Processes. Mater. Des. 2020, 196, 109136. [Google Scholar] [CrossRef]
- Yi, Y.X.; Zoller, P. An Experimental and Theoretical Study of the PVT Equation of State of Butadiene and Isoprene Elastomers to 200 ∘C and 200 MPa. J. Polym. Sci. Part B Polym. Phys. 1993, 31, 779–788. [Google Scholar] [CrossRef]
- Speranza, V.; Vietri, U.; Pantani, R. Monitoring of Injection Molding of Thermoplastics: Average Solidification Pressure as a Key Parameter for Quality Control. Macromol. Res. 2011, 19, 542–554. [Google Scholar] [CrossRef]
- Mohan, C.R.; Sathya, R.; Nithiananthi, P.; Jayakumar, K. Ultrasonic Velocimetry Studies on Different Salts of Chitosan: Effect of Ion Size. Int. J. Biol. Macromol. 2017, 104, 1596–1603. [Google Scholar] [CrossRef] [PubMed]
- Hopmann, C.; Menges, G.; Michaeli, W.; Mohren, P. SpritzgießWerkzeuge: Auslegung, Bau, Anwendung; Carl Hanser Verlag GmbH Co KG: München, Germany, 2018. [Google Scholar]
- Zheng, L. A Practical Computer-Aided Tuning Technique for Fuzzy Control. In Proceedings of the [Proceedings 1993] Second IEEE International Conference on Fuzzy Systems, San Francisco, CA, USA, 28 March–1 April 1993; Volume 2, pp. 702–707. [Google Scholar] [CrossRef]



| Parameter | Nozzle | Extender | Sprue | Runner | Gate | Cavity | Unit |
|---|---|---|---|---|---|---|---|
| i | 1 | 2 | 3 | 4 | 5 | 6 | - |
| 70.68 | 25.51 | - | 26.29 | 4.5 | 40.39 | mm2 | |
| - | 2148 | - | 3948 | 26.69 | 4032 | mm2 | |
| 30 | 5.7 | - | 5.120 | 2 | 5.086 | mm | |
| - | 120 | 87.3 | 192.2 | 2.966 | 127 | mm | |
| - | 3062 | 2171 | 5054 | 13.34 | 5128 | mm3 |
| ID | Mass Temperature | Injection Velocity | Hydraulic Holding Pressure |
|---|---|---|---|
| [∘C] | [mm/s] | [bar] | |
| 3 | 225 | 40 | 55 |
| 5 | 235 | 30 | 45 |
| ID | Mass Temperature | Nozzle Pressure Target |
|---|---|---|
| [∘C] | [bar] | |
| N1 | 225 | 525 |
| N2 | 225 | 625 |
| N3 | 235 | 525 |
| N4 | 235 | 625 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hertz, R.A.; Therkelsen, O.; Kristiansen, S.; Christensen, J.K.; Hansson, F.A.; Schmidt, L. Development and Validation of a 1D Dynamic Model of an Injection Moulding Process and Design of a Model-Based Nozzle Pressure Controller. Polymers 2024, 16, 1432. https://doi.org/10.3390/polym16101432
Hertz RA, Therkelsen O, Kristiansen S, Christensen JK, Hansson FA, Schmidt L. Development and Validation of a 1D Dynamic Model of an Injection Moulding Process and Design of a Model-Based Nozzle Pressure Controller. Polymers. 2024; 16(10):1432. https://doi.org/10.3390/polym16101432
Chicago/Turabian StyleHertz, Rasmus Aagaard, Ole Therkelsen, Søren Kristiansen, Jesper Kjærsgaard Christensen, Frederik Agervig Hansson, and Lasse Schmidt. 2024. "Development and Validation of a 1D Dynamic Model of an Injection Moulding Process and Design of a Model-Based Nozzle Pressure Controller" Polymers 16, no. 10: 1432. https://doi.org/10.3390/polym16101432
APA StyleHertz, R. A., Therkelsen, O., Kristiansen, S., Christensen, J. K., Hansson, F. A., & Schmidt, L. (2024). Development and Validation of a 1D Dynamic Model of an Injection Moulding Process and Design of a Model-Based Nozzle Pressure Controller. Polymers, 16(10), 1432. https://doi.org/10.3390/polym16101432






