Morphological Study before and after Thermal Treatment of Polymer-Polymer Mixed-Matrix Membranes for Gas Separations
Abstract
1. Introduction
2. Experimental Section
2.1. Materials
2.2. Polymer Characterization
2.3. TGA, DSC, FTIR, WAXS, SEM, CO2 Adsorption Isotherm, and Gas Permeability
- The thermogravimetric analysis (TGA) was performed using a Q500 thermogravimetric analyzer from TA Instruments (New Castle, DE, USA). A heating ramp mode from room temperature up to 800 °C at a rate of 10 °C/min was used with samples of around 5 mg under a 50 cm3/min flow rate of ultra-high-purity nitrogen and a flow rate of 40 cm3/min through the scale chamber.
- The glass transition temperature values were determined with a Differential Scanning Calorimetric (DSC) DSC-25 Analyzer (also from TA Instruments). DSC analyses for TR polymers were carried out at a heating rate of 20 °C /min up to 360 °C. In all cases, the experiments were performed under an ultra-high-purity N2 atmosphere using 6–10 mg of membrane in gas-tight aluminum containers. The Tg was determined in the first heating cycle from the inflection point (Ti,g) of the measured DSC curve in the glass transition region.
- Attenuated Total Reflectance-Fourier Transform Infrared (ATR-FTIR) spectra were performed using a Perkin Elmer Spectrum One FT-IR (Perkin-Elmer, Waltham, MA, USA) coupled with a universal attenuated total reflection (ATR) sampling module with a diamond-tipped probe, following the band’s intensity.
- The membranes were also tested via wide-angle X-ray scattering (WAXS) at room temperature using a Bruker (Bruker, Billerica, MA, USA) D8 discover A25 advanced diffractometer equipped with a Goebel mirror. The LynxEye detector was operated at a speed of 0.5 s with a step scanning mode ranging from 5° to 70° and a 2θ step of 0.020°. A Cu Kα (λ = 1.542 Å) radiation source in a ceramic tube was used.
- The adsorption isotherms were carried out in a volumetric device Autosorb IQ (Quantachrome Instruments, Boynton Beach, FL, USA). The samples were first measured for CO2 at 273.15 K (up to , afterwards with N2 at 77 K (up to ). Samples were degassed at 100 °C for 10 h under vacuum before the sorption measurements to eliminate possible adsorbed gases or water vapor. The adsorption isotherm data were used to obtain the pore size distribution via the non-local density functional theory equilibrium model (NLDFT). Acquisition and calculation were carried out by Quantachrome® ASiQwin software (version 5.21).
- Both permeability and ideal selectivity of the membranes have been determined by using a constant volume-variable pressure apparatus at 35 °C and an upstream pressure of 3 bar. The gas flow through the membrane is determined by measuring the pressure versus time on the low-pressure side when the system reaches steady-state conditions, as described elsewhere [14,27]. All the gases used have purity greater than 99,999.
2.4. Procedures to Study the Integration of PPN Particles within the Polymer Matrix
2.4.1. Description of the Polishing Process and Device
2.4.2. Description of the Partial Dissolution Process
2.4.3. Surface Etching with Argon Plasma Process
2.4.4. Scanning Electron Microscopy (SEM)
2.4.5. Atomic Force Microscopy (AFM)
3. Results and Discussion
3.1. AFM Characterization
3.1.1. Polished Samples
3.1.2. Partial Dissolved Samples with NMP
3.1.3. Plasma-Treated Samples
3.2. Other Characterization Technique
3.2.1. ATR-FTIR and WAXS Measurements
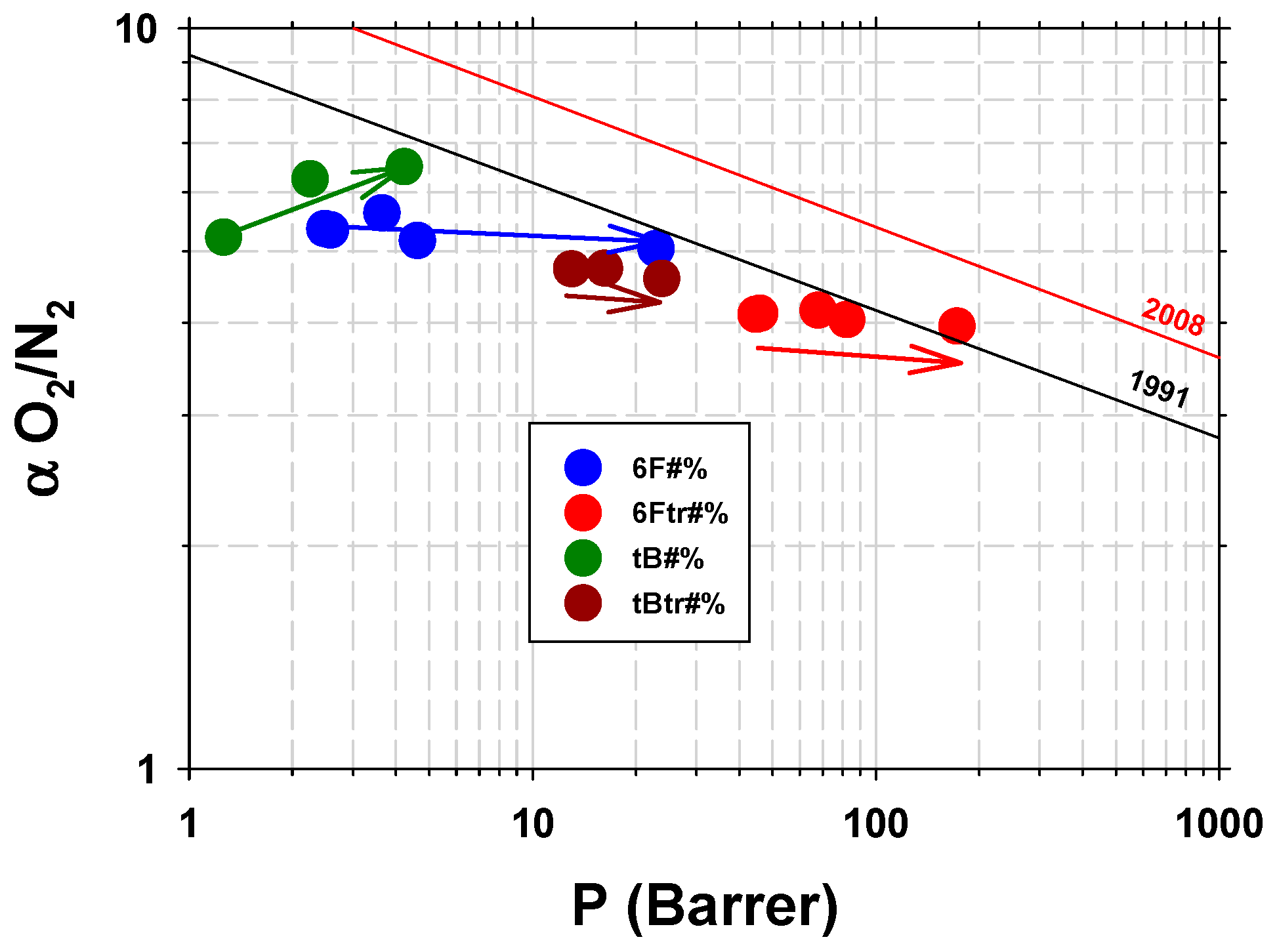
3.2.2. Gas Permeability Characterization
3.2.3. CO2 and N2 Adsorption Measurements
3.3. SEM Characterization
3.4. Interpretation of the Structure
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Baker, R.W. Future Directions of Membrane Gas Separation Technology. Ind. Eng. Chem. Res. 2002, 41, 1393–1411. [Google Scholar] [CrossRef]
- Baker, R.W.; Low, B.T. Gas Separation Membrane Materials: A Perspective. Macromolecules 2014, 47, 6999–7013. [Google Scholar] [CrossRef]
- Xu, S.; Zhao, N.; Wu, L.; Kang, S.; Zhang, Z.; Huo, G.; Dai, Z.; Li, N. Carbon molecular sieve gas separation membranes from crosslinkable bromomethylated 6FDA-DAM polyimide. J. Membr. Sci. 2022, 659, 120781. [Google Scholar] [CrossRef]
- Robeson, L.M. The upper bound revisited. J. Membr. Sci. 2008, 320, 390–400. [Google Scholar] [CrossRef]
- Robeson, L.M. Correlation of separation factor versus permeability for polymeric membranes. J. Membr. Sci. 1991, 62, 165–185. [Google Scholar] [CrossRef]
- Kim, S.; Lee, Y.M. Thermally rearranged (TR) polymer membranes with nanoengineered cavities tuned for CO2 separation. J. Nanoparticle Res. 2012, 14, 949. [Google Scholar] [CrossRef]
- Scholes, C.A.; Freeman, B.D.; Kentish, S.E. Water vapor permeability and competitive sorption in thermally rearranged (TR) membranes. J. Membr. Sci. 2014, 470, 132–137. [Google Scholar] [CrossRef]
- Sanders, D.F.; Guo, R.; Smith, Z.P.; Liu, Q.; Stevens, K.A.; McGrath, J.E.; Paul, D.R.; Freeman, B.D. Influence of polyimide precursor synthesis route and ortho-position functional group on thermally rearranged (TR) polymer properties: Conversion and free volume. Polymer 2014, 55, 1636–1647. [Google Scholar] [CrossRef]
- Vinh-Thang, H.; Kaliaguine, S. Predictive Models for Mixed-Matrix Membrane Performance: A Review. Chem. Rev. 2013, 113, 4980–5028. [Google Scholar] [CrossRef] [PubMed]
- Yampolskii, Y. Polymeric Gas Separation Membranes. Macromolecules 2012, 45, 3298–3311. [Google Scholar] [CrossRef]
- Comesaña-Gándara, B.; Chen, J.; Bezzu, C.G.; Carta, M.; Rose, I.; Ferrari, M.-C.; Esposito, E.; Fuoco, A.; Jansen, J.C.; McKeown, N.B. Redefining the Robeson upper bounds for CO2/CH4 and CO2/N2 separations using a series of ultrapermeable benzotriptycene-based polymers of intrinsic microporosity. Energy Environ. Sci. 2019, 12, 2733–2740. [Google Scholar] [CrossRef]
- Barnett, J.W.; Bilchak, C.R.; Wang, Y.; Benicewicz, B.C.; Murdock, L.A.; Bereau, T.; Kumar, S.K. Designing exceptional gas-separation polymer membranes using machine learning. Sci. Adv. 2020, 6, eaaz4301. [Google Scholar] [CrossRef]
- Tamaddondar, M.; Foster, A.B.; Carta, M.; Gorgojo, P.; McKeown, N.B.; Budd, P.M. Mitigation of Physical Aging with Mixed Matrix Membranes Based on Cross-Linked PIM-1 Fillers and PIM-1. ACS Appl. Mater. Interfaces 2020, 12, 46756–46766. [Google Scholar] [CrossRef]
- Soto, C.; Aguilar Lugo, C.; Rodríguez, S.; Palacio, L.; Lozano, Á.E.; Prádanos, P.; Hernandez, A. Enhancement of CO2/CH4 permselectivity via thermal rearrangement of mixed matrix membranes made from an o-hydroxy polyamide with an optimal load of a porous polymer network. Sep. Purif. Technol. 2020, 247, 116895. [Google Scholar] [CrossRef]
- Gascon, J.; Kapteijn, F.; Zornoza, B.; Sebastián, V.; Casado, C.; Coronas, J. Practical Approach to Zeolitic Membranes and Coatings: State of the Art, Opportunities, Barriers, and Future Perspectives. Chem. Mater. 2012, 24, 2829–2844. [Google Scholar] [CrossRef]
- Dong, G.; Li, H.; Chen, V. Challenges and opportunities for mixed-matrix membranes for gas separation. J. Mater. Chem. A 2013, 1, 4610–4630. [Google Scholar] [CrossRef]
- Singh, A.; Koros, W.J. Significance of Entropic Selectivity for Advanced Gas Separation Membranes. Ind. Eng. Chem. Res. 1996, 35, 1231–1234. [Google Scholar] [CrossRef]
- Sanyal, O.; Zhang, C.; Wenz, G.B.; Fu, S.; Bhuwania, N.; Xu, L.; Rungta, M.; Koros, W.J. Next generation membranes—Using tailored carbon. Carbon 2018, 127, 688–698. [Google Scholar] [CrossRef]
- Smith, S.J.D.; Hou, R.; Lau, C.H.; Konstas, K.; Kitchin, M.; Dong, G.; Lee, J.; Lee, W.H.; Seong, J.G.; Lee, Y.M.; et al. Highly permeable Thermally Rearranged Mixed Matrix Membranes (TR-MMM). J. Membr. Sci. 2019, 585, 260–270. [Google Scholar] [CrossRef]
- Koros, W.J.; Zhang, C. Materials for next-generation molecularly selective synthetic membranes. Nat. Mater. 2017, 16, 289–297. [Google Scholar] [CrossRef]
- Moore, T.T.; Koros, W.J. Non-ideal effects in organic–inorganic materials for gas separation membranes. J. Mol. Struct. 2005, 739, 87–98. [Google Scholar] [CrossRef]
- Jomekian, A.; Bazooyar, B.; Behbahani, R.M.; Mohammadi, T.; Kargari, A. Ionic liquid-modified Pebax® 1657 membrane filled by ZIF-8 particles for separation of CO2 from CH4, N2 and H2. J. Membr. Sci. 2017, 524, 652–662. [Google Scholar] [CrossRef]
- Nunes, S.P.; Culfaz-Emecen, P.Z.; Ramon, G.Z.; Visser, T.; Koops, G.H.; Jin, W.; Ulbricht, M. Thinking the future of membranes: Perspectives for advanced and new membrane materials and manufacturing processes. J. Membr. Sci. 2020, 598, 117761. [Google Scholar] [CrossRef]
- Li, H.; Zhuang, S.; Zhao, B.; Yu, Y.; Liu, Y. Visualization of the gas permeation in core–shell MOF/Polyimide mixed matrix membranes and structural optimization based on finite element equivalent simulation. Sep. Purif. Technol. 2023, 305, 122504. [Google Scholar] [CrossRef]
- Jheng, L.-C.; Park, J.; Wook Yoon, H.; Chang, F.-C. Mixed matrix membranes comprising 6FDA-based polyimide blends and UiO-66 with co-continuous structures for gas separations. Sep. Purif. Technol. 2023, 310, 123126. [Google Scholar] [CrossRef]
- Xu, Z.-L.; Yu, L.-Y.; Han, L.-F. Polymer-nanoinorganic particles composite membranes: A brief overview. Front. Chem. Eng. China 2009, 3, 318–329. [Google Scholar] [CrossRef]
- Soto, C.; Carmona, J.; Freeman, B.D.; Palacio, L.; González-Ortega, A.; Prádanos, P.; Lozano, Á.E.; Hernandez, A. Free Volume and Permeability of Mixed Matrix Membranes Made from a Terbutil-M-terphenyl Polyamide and a Porous Polymer Network. Polymers 2022, 14, 3176. [Google Scholar] [CrossRef]
- Aroon, M.A.; Ismail, A.F.; Matsuura, T.; Montazer-Rahmati, M.M. Performance studies of mixed matrix membranes for gas separation: A review. Sep. Purif. Technol. 2010, 75, 229–242. [Google Scholar] [CrossRef]
- Moore, T.T.; Mahajan, R.; Vu, D.Q.; Koros, W.J. Hybrid membrane materials comprising organic polymers with rigid dispersed phases. AIChE J. 2004, 50, 311–321. [Google Scholar] [CrossRef]
- Silva, V.; Montalvillo, M.; Carmona, F.J.; Palacio, L.; Hernández, A.; Prádanos, P. Prediction of single salt rejection in nanofiltration membranes by independent measurements. Desalination 2016, 382, 1–12. [Google Scholar] [CrossRef]
- Rasband, W. Image J. Image Processing and Analysis in Java; Version 1.52p; National Institutes of Health: Bethesda, MD, USA, 2019.
- Longo, M.; De Santo, M.P.; Esposito, E.; Fuoco, A.; Monteleone, M.; Giorno, L.; Jansen, J.C. Force spectroscopy determination of Young’s modulus in mixed matrix membranes. Polymer 2018, 156, 22–29. [Google Scholar] [CrossRef]
- Soto, C.; Torres-Cuevas, E.S.; González-Ortega, A.; Palacio, L.; Prádanos, P.; Freeman, B.D.; Lozano, Á.E.; Hernandez, A. Hydrogen Recovery by Mixed Matrix Membranes Made from 6FCl-APAF HPA with Different Contents of a Porous Polymer Network and Their Thermal Rearrangement. Polymers 2021, 13, 4343. [Google Scholar] [CrossRef]
- Khulbe, K.C.; Matsuura, T. Characterization of PPO membranes by oxygen plasma etching, gas separation and atomic force microscopy. J. Membr. Sci. 2000, 171, 273–284. [Google Scholar] [CrossRef]
- Fritzsche, A.K.; Cruse, C.A.; Murphy, M.K.; Kesting, R.E. Polyethersulfone and polyphenylsulfone hollow fiber trilayer membranes spun from Lewis acid: Base complexes—Structure determination by SEM, DSC, and oxygen plasma ablation. J. Membr. Sci. 1990, 54, 29–50. [Google Scholar] [CrossRef]
- Kesting, R.E. The four tiers of structure in integrally skinned phase inversion membranes and their relevance to the various separation regimes. J. Appl. Polym. Sci. 1990, 41, 2739–2752. [Google Scholar] [CrossRef]
- Khulbe, K.C.; Matsuura, T.; Lamarche, G.; Kim, H.J. The morphology characterisation and performance of dense PPO membranes for gas separation. J. Membr. Sci. 1997, 135, 211–223. [Google Scholar] [CrossRef]
- Kong, J.; Carmona-Reyes, J.; Creel, J.; Hyde, T.W. Relationship Between the DC Bias and the Debye Length in a Complex Plasma. IEEE Trans. Plasma Sci. 2007, 35, 323–327. [Google Scholar] [CrossRef][Green Version]
- Stuart, B.H. Analytical Techniques in the Sciences: Polymer Analysis; Wiley: Kent, UK, 2002. [Google Scholar]
- Diez, B.; Cuadrado, P.; Marcos-Fernandez, A.; Pradanos, P.; Tena, A.; Palacio, L.; Lozano, A.E.; Hernandez, A. Helium Recovery by Membrane Gas Separation Using Poly(o-acyloxyamide)s. Ind. Eng. Chem. Res. 2014, 53, 12809–12818. [Google Scholar] [CrossRef]
- Fernández, L.; Sánchez, M.; Carmona, F.J.; Palacio, L.; Calvo, J.I.; Hernández, A.; Prádanos, P. Analysis of the Grafting Process of PVP on a Silicon Surface by AFM and Contact Angle. Langmuir 2011, 27, 11636–11649. [Google Scholar] [CrossRef]
- Alvarez-Quintana, S.; Carmona, F.J.; Palacio, L.; Hernandez, A.; Pradanos, P. Water viscosity in confined nanoporous media and flow through nanofiltration membranes. Microporous Mesoporous Mater. 2020, 303, 110289. [Google Scholar] [CrossRef]
- Nakamura, Y.; Nakamae, K. Adhesion Between Plasma-Treated Polypropylene Films and Thin Aluminum Films. J. Adhes. 1996, 59, 75–86. [Google Scholar] [CrossRef]
- HErickson, B.L.; Asthana, H.; Drzal, L.T. Sulfonation of polymer surfaces-I. Improving adhesion of polypropylene and polystyrene to epoxy adhesives via gas phase sulfonation. J. Adhes. Sci. Technol. 1997, 11, 1249–1267. [Google Scholar] [CrossRef]
- Comyn, J.; Mascia, L.; Xiao, G.; Parker, B. Corona-discharge treatment of polyetheretherketone (PEEK) for adhesive bonding. Int. J. Adhes. Adhes. 1996, 16, 301–304. [Google Scholar] [CrossRef]

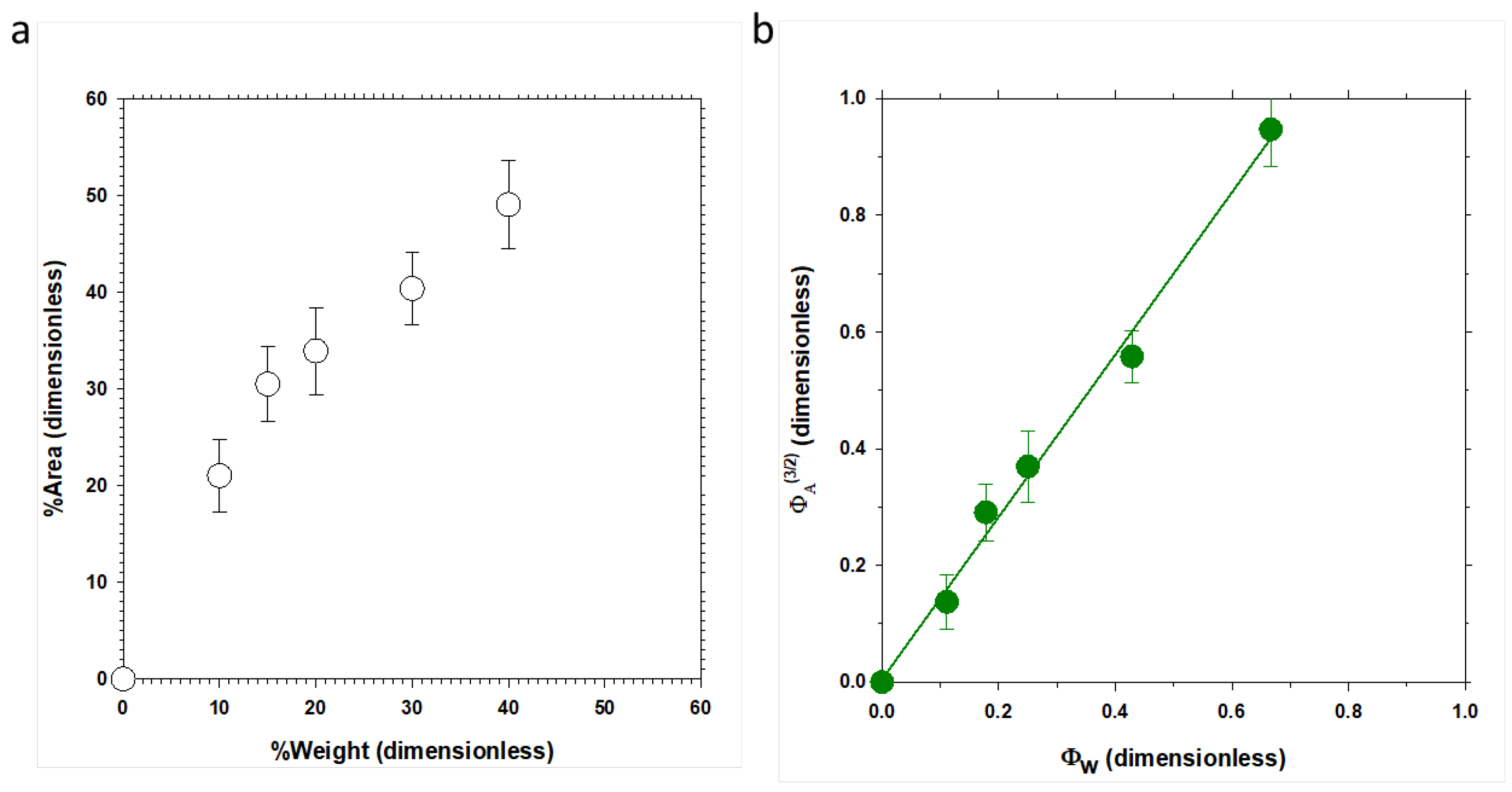
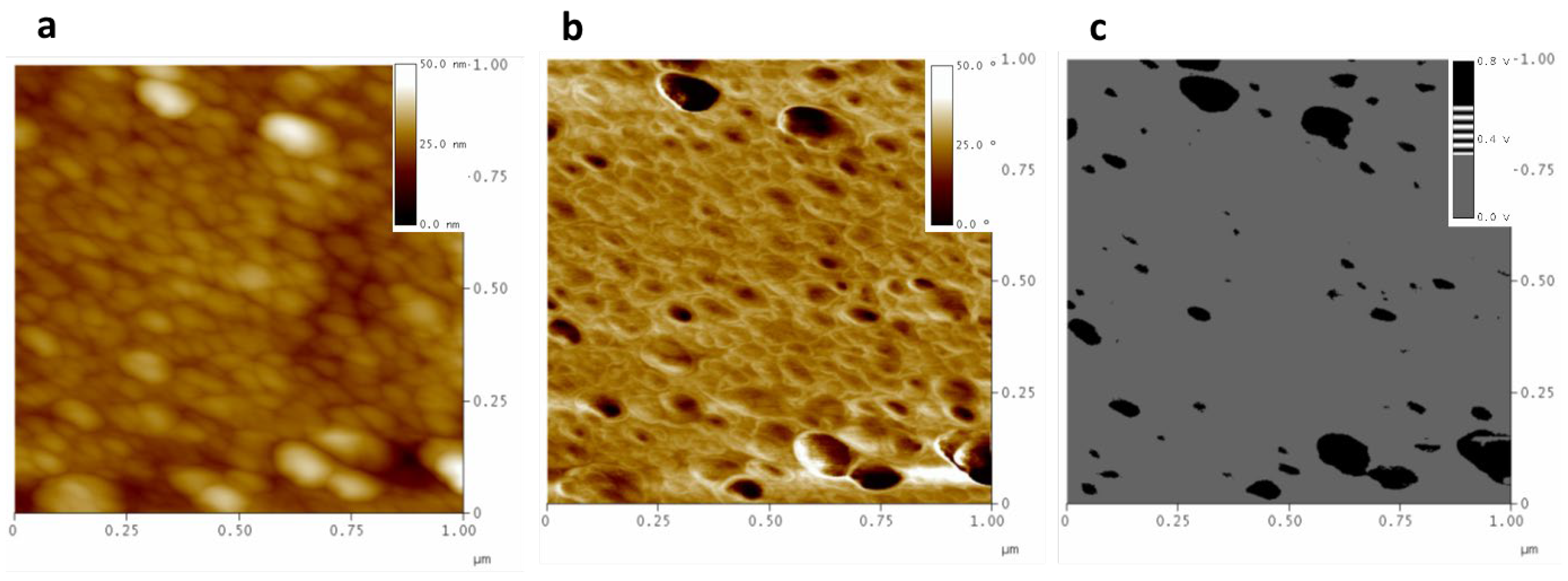





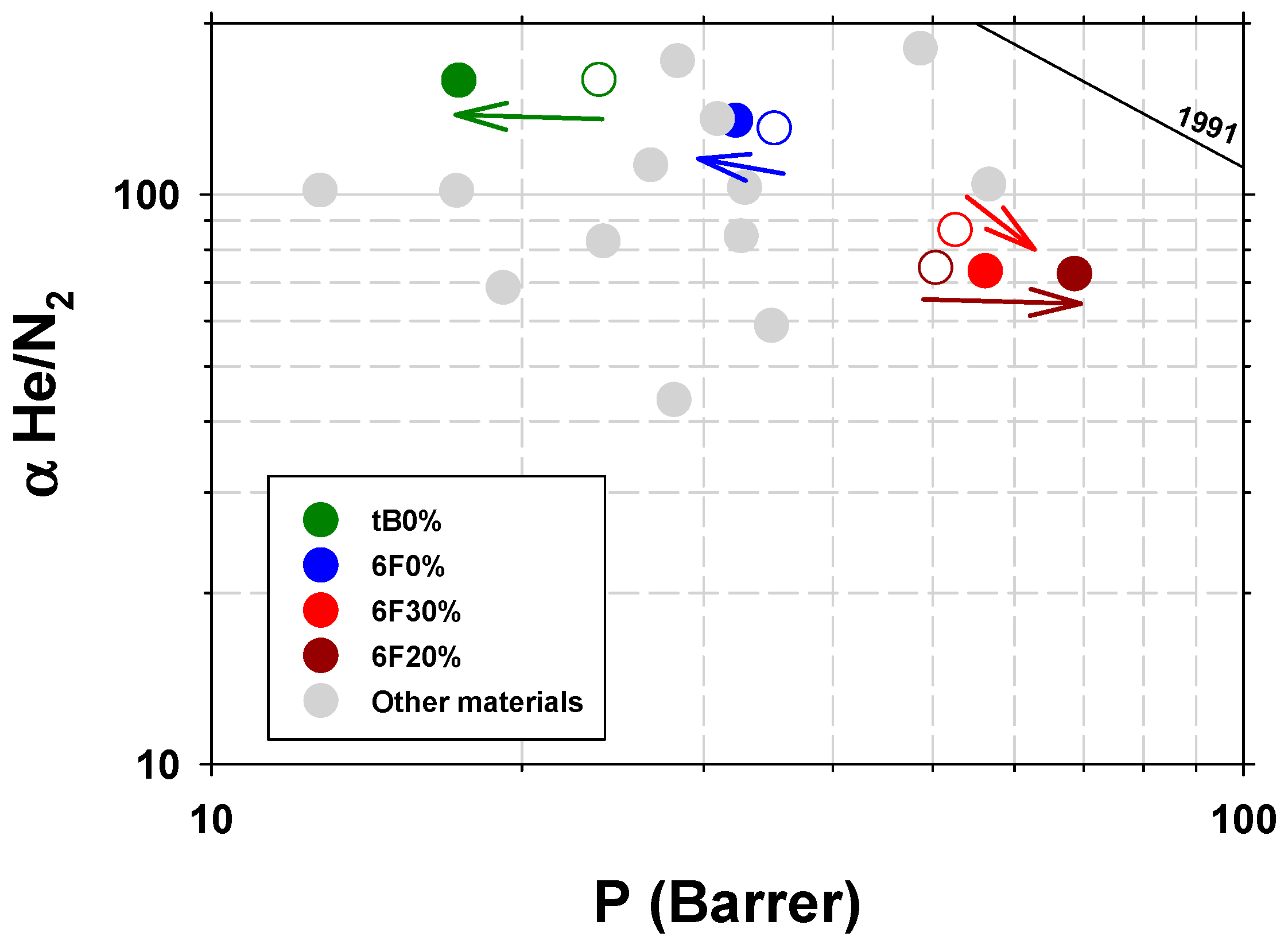






| Sample | Polymer | #% (%wt of PPN2 in the MMM) |
|---|---|---|
| 6F#% | 6FCl-APAF | 0, 10, 15, 20, 30, 40 |
| 6Ftr#% | TR-6FCl-APAF | 0, 10, 15, 20, 30, 40 |
| tB#% | tBTmCl-APAF | 0, 20, 30, 40 |
| tBtr#% | TR-tBTmCl-APAF | 20, 30, 40 |
| MMM | (g/cm3) a | (g/cm3) b | |
|---|---|---|---|
| 6F#% | 1.39 ± 0.06 | 1.38 ± 0.07 | 1.460 ± 0.005 |
| 6Ftr#% | 1.35 ± 0.08 | 1.34 ± 0.08 | 1.435 ± 0.002 |
| tB#% | 1.20 ± 0.09 | 1.19 ± 0.10 | 1.308 ± 0.008 |
| tBtr#% | 1.16 ± 0.06 | 1.15 ± 0.07 | 1.200 ± 0.019 c |
| MMM | μ ± σ (μm) |
|---|---|
| 6F10% | 2.4 ± 1.3 |
| 6F15% | 3.2 ± 1.7 |
| 6Ftr10% | 2.5 ± 1.4 |
| 6Ftr15% | 3.1 ± 1.9 |
| MMM | Force Modulation μ ± σ (μm) |
|---|---|
| 6F#% | 87 ± 42 |
| 6Ftr#% | 76 ± 35 |
| tB#% | 78 ± 39 |
| tBtr#% | 73 ± 41 |
| Case 1 | Case 2 | Figures | |
|---|---|---|---|
| SIMILARITIES | Plasma treatment > 8 h | Plasma treatment~30 min | Figure 5f |
| DIFFERENCES | Polymer 6F | Polymer tB | Figure 6a vs. Figure 6c |
| Not TR | With TR | Figure 6a vs. Figure 6b | |
| Without PPN2 | With PPN2 | Figure 6a vs. Figure 6d |
| Sample | 〈〉 ± σ (nm) | 〈Cell Size〉 ± σ (nm) |
|---|---|---|
| 6F#% and 6Ftr#% | 27 ± 4 | 281 ± 50 |
| tB#% and tBtr#% | 21 ± 3 | 215 ± 29 |
| Sample | Mw (Da) | Mn (Da) | Mw/Mn | Mi (Da) | 〈Ni〉ns | 〈N〉nsd |
|---|---|---|---|---|---|---|
| 6F0% | 161,400 | 105,500 | 1.5 | 722.5 | 12,500 ± 1800 | 86 ± 15 |
| 6Ftr0% | - | 100,300 | - | 686.4 | 13,000 ± 1900 | 89 ± 17 |
| tB0% | 104,800 | 58,900 | 1.8 | 704.9 | 5400 ± 900 | 65 ± 11 |
| tBtr0% | - | 55,900 | - | 668.8 | 5200 ± 900 | 63 ± 11 |
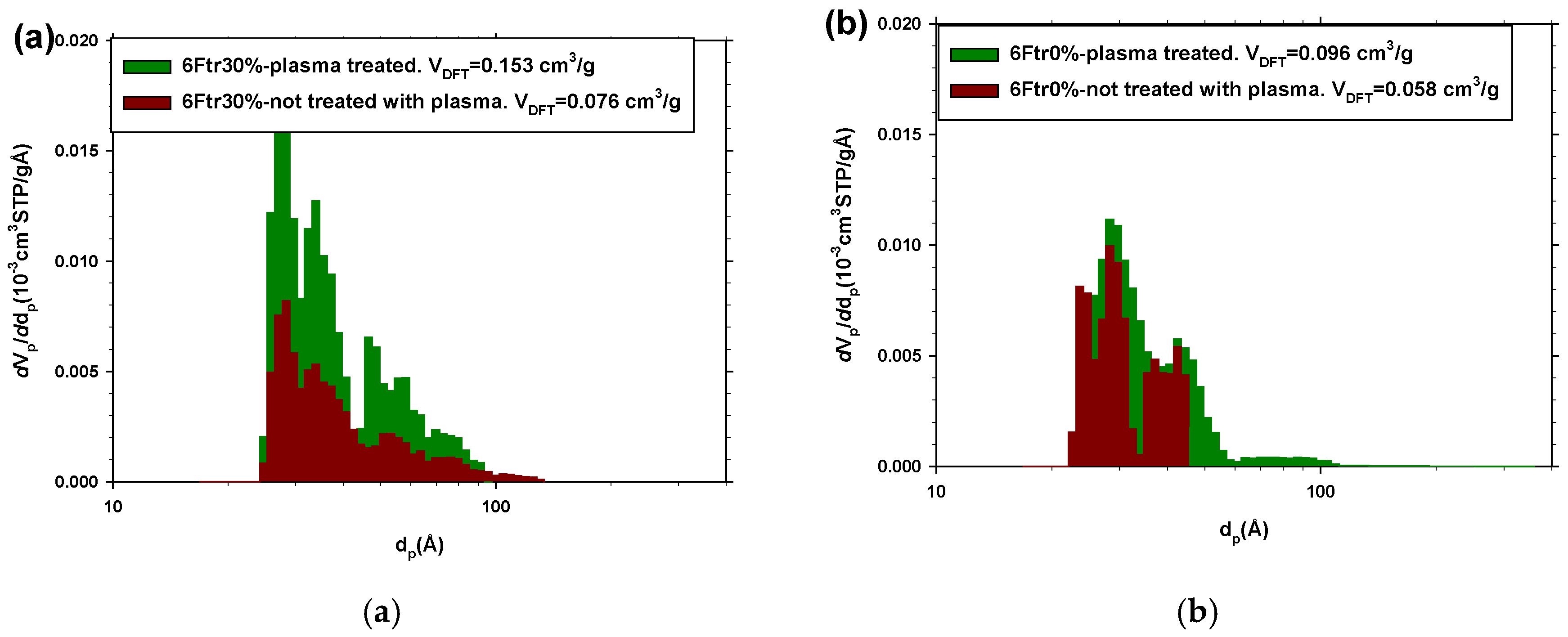
| Sample | 6Ftr30% with Plasma | 6Ftr30% without Plasma | 6Ftr0% with Plasma | 6Ftr0% without Plasma | PPN2 |
|---|---|---|---|---|---|
| SBET (cm3/g) | 152 ± 7 | 101 ± 5 | 115 ± 5 | 64 ± 3 | 650 ± 30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pradanos, P.; Soto, C.; Carmona, F.J.; Lozano, Á.E.; Hernández, A.; Palacio, L. Morphological Study before and after Thermal Treatment of Polymer-Polymer Mixed-Matrix Membranes for Gas Separations. Polymers 2024, 16, 1397. https://doi.org/10.3390/polym16101397
Pradanos P, Soto C, Carmona FJ, Lozano ÁE, Hernández A, Palacio L. Morphological Study before and after Thermal Treatment of Polymer-Polymer Mixed-Matrix Membranes for Gas Separations. Polymers. 2024; 16(10):1397. https://doi.org/10.3390/polym16101397
Chicago/Turabian StylePradanos, Pedro, Cenit Soto, Francisco Javier Carmona, Ángel E. Lozano, Antonio Hernández, and Laura Palacio. 2024. "Morphological Study before and after Thermal Treatment of Polymer-Polymer Mixed-Matrix Membranes for Gas Separations" Polymers 16, no. 10: 1397. https://doi.org/10.3390/polym16101397
APA StylePradanos, P., Soto, C., Carmona, F. J., Lozano, Á. E., Hernández, A., & Palacio, L. (2024). Morphological Study before and after Thermal Treatment of Polymer-Polymer Mixed-Matrix Membranes for Gas Separations. Polymers, 16(10), 1397. https://doi.org/10.3390/polym16101397












