Filled Elastomers: Mechanistic and Physics-Driven Modeling and Applications as Smart Materials
Abstract
1. Introduction
2. Materials
2.1. Polymer Matrix
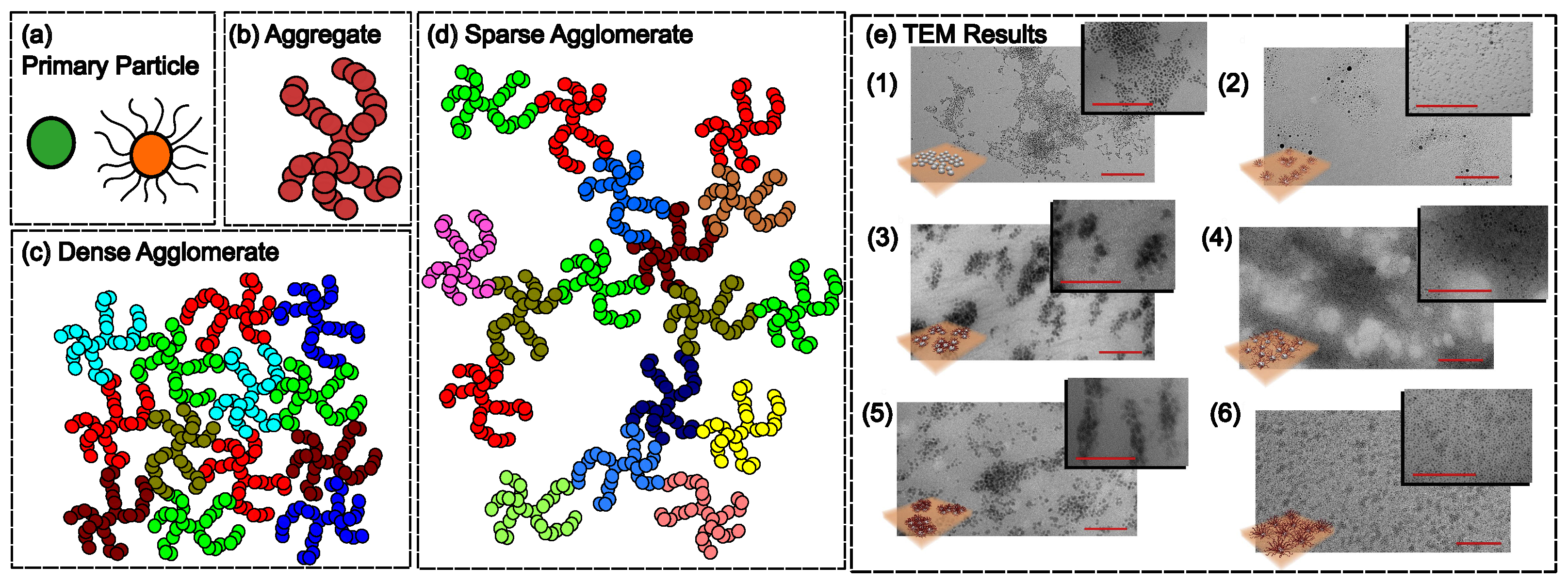
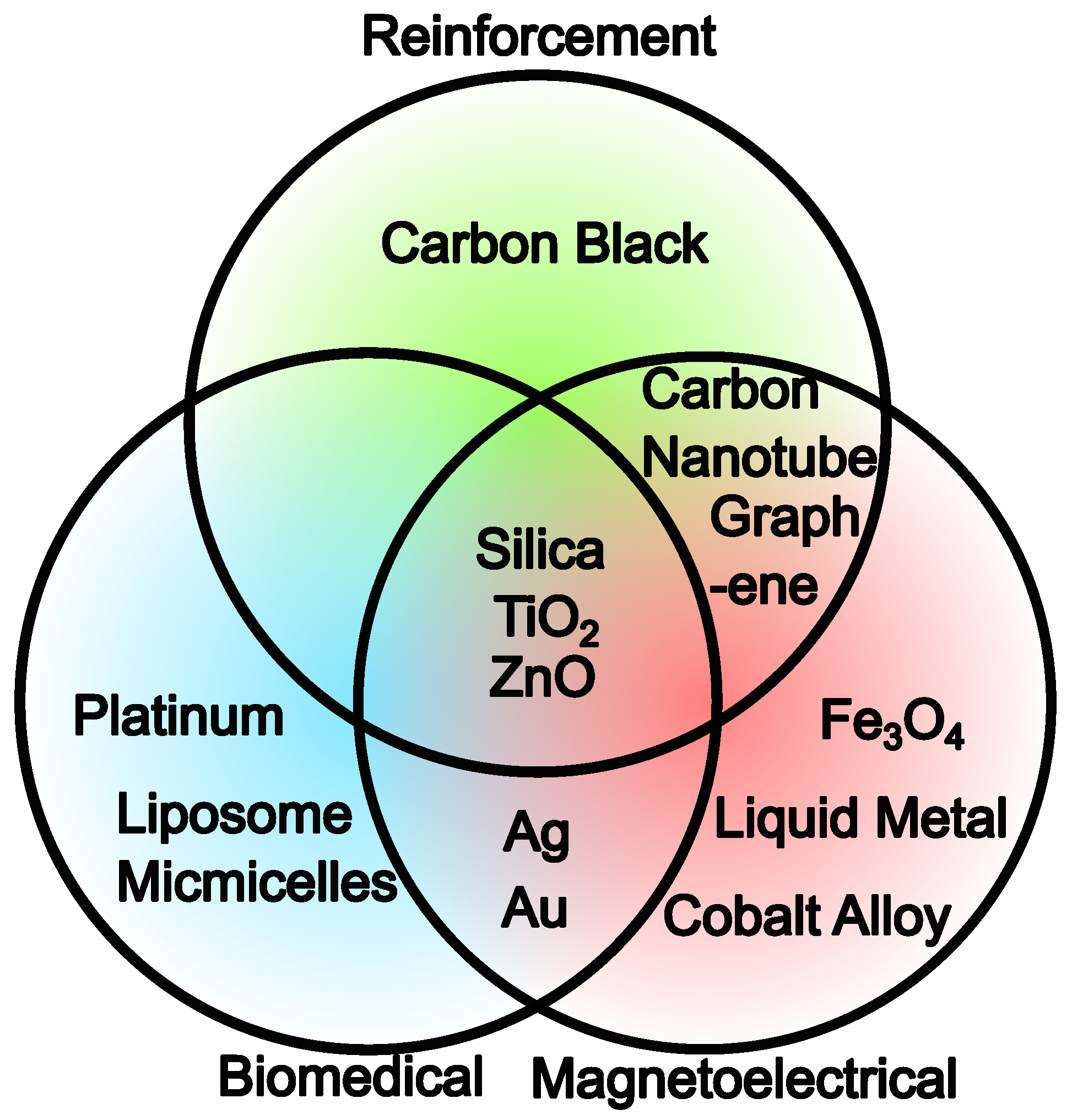
2.2. Filler Particle
3. Constitutive Modeling
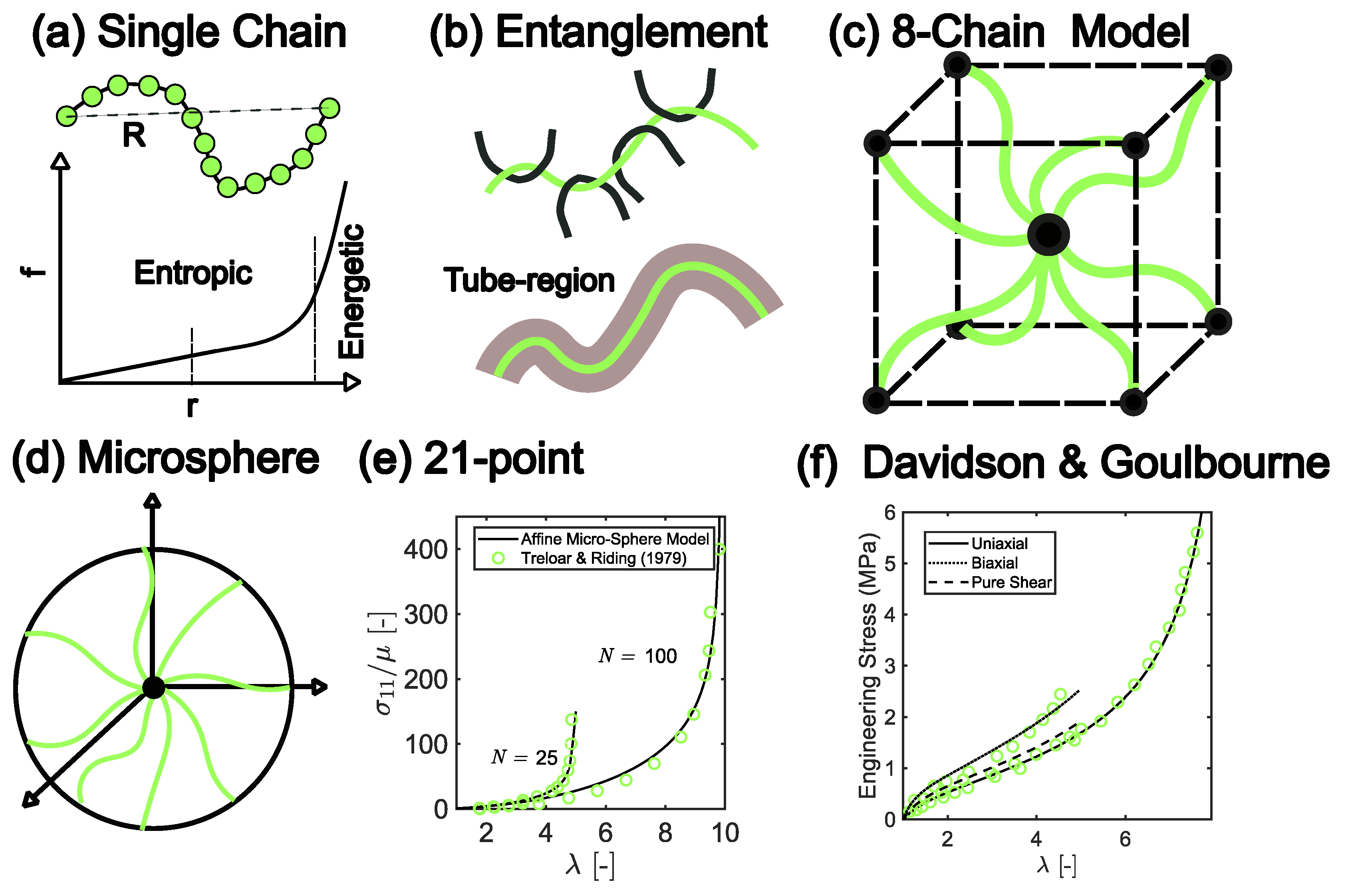
3.1. Hyperelasticity
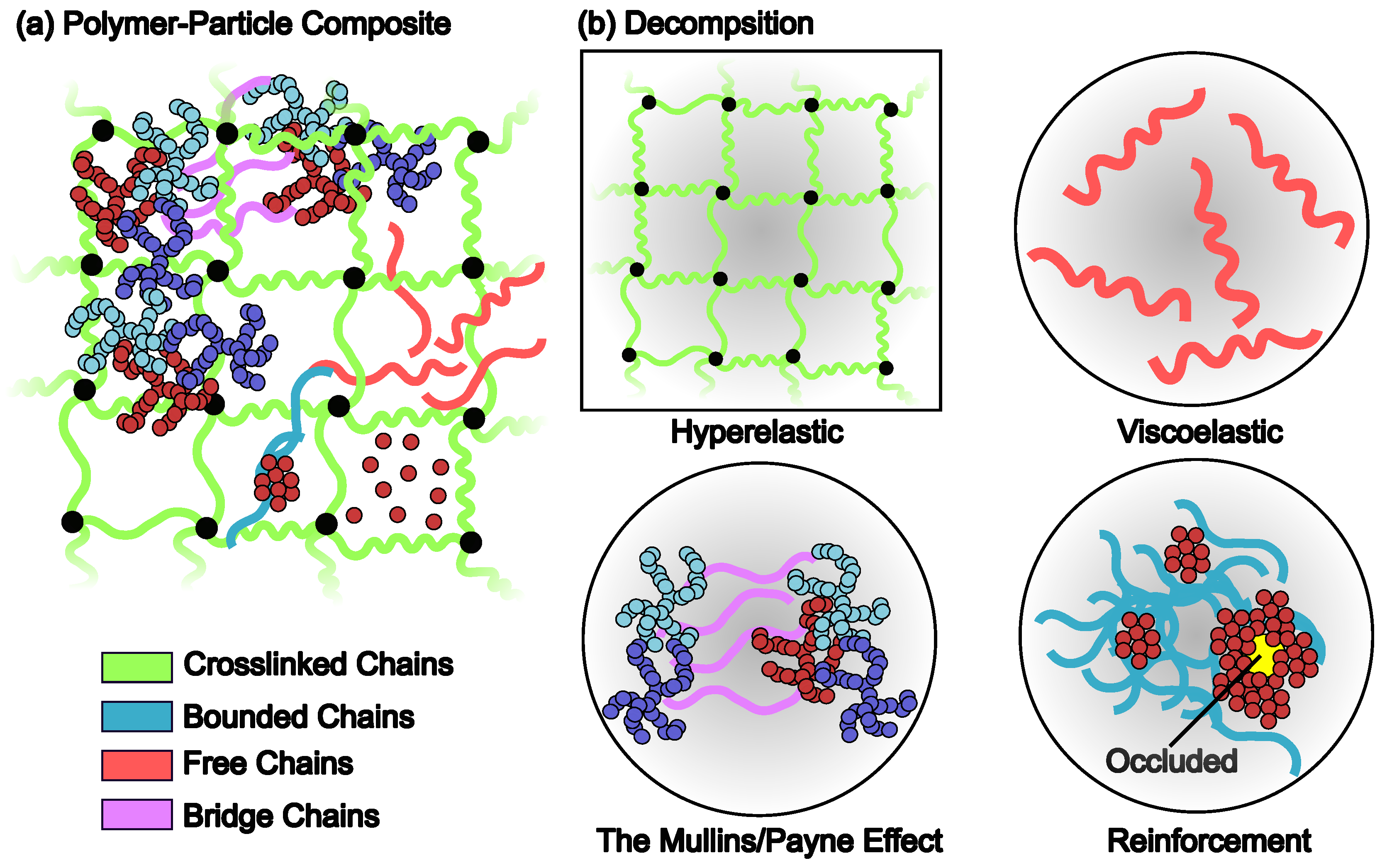
3.2. Reinforcement
3.2.1. Hydrodynamic Effect
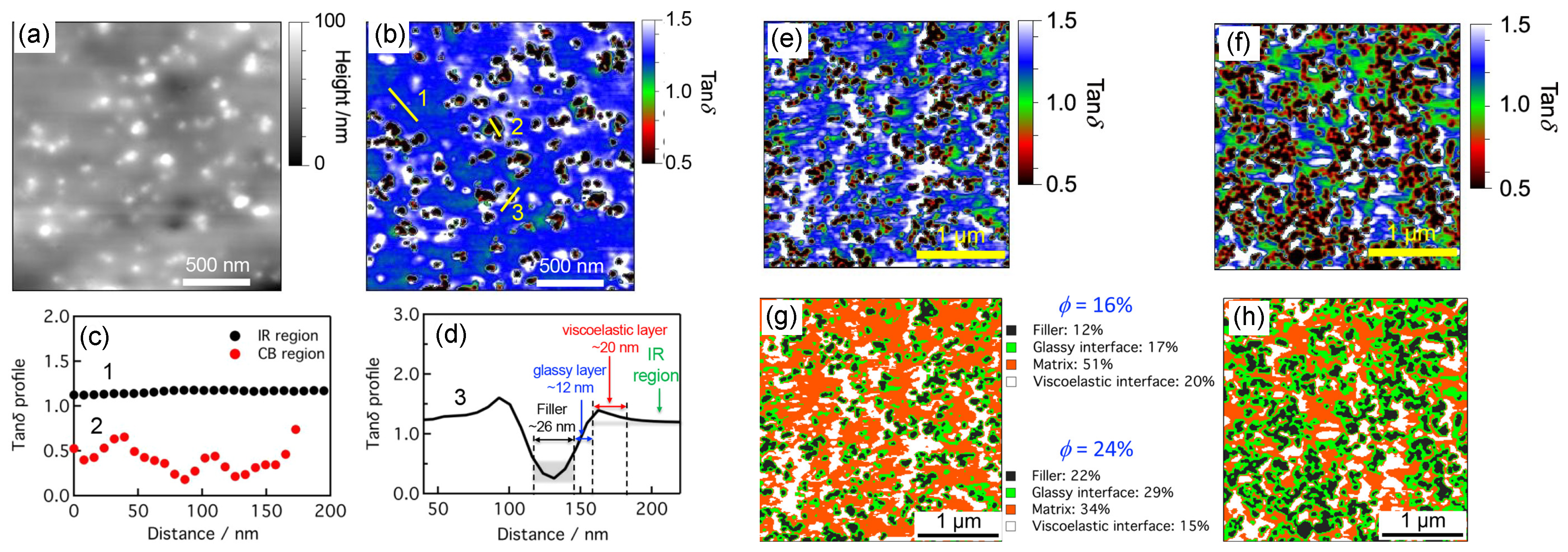
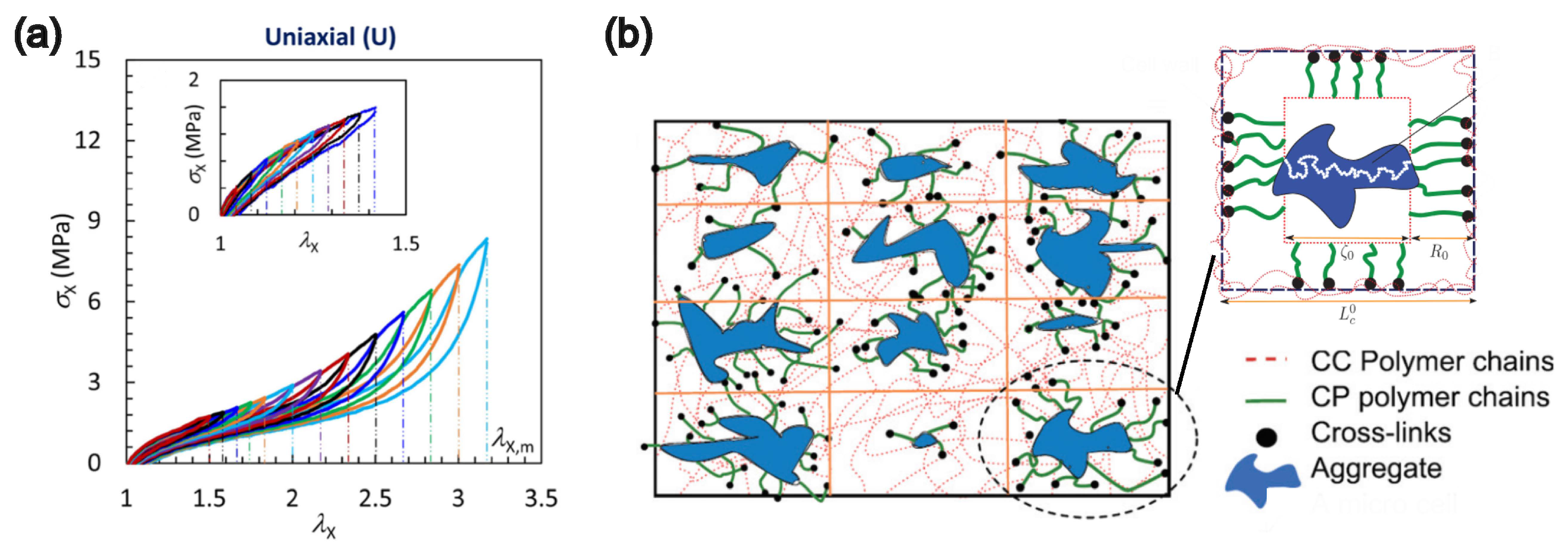
3.2.2. Percolated Network of the Filler Particles
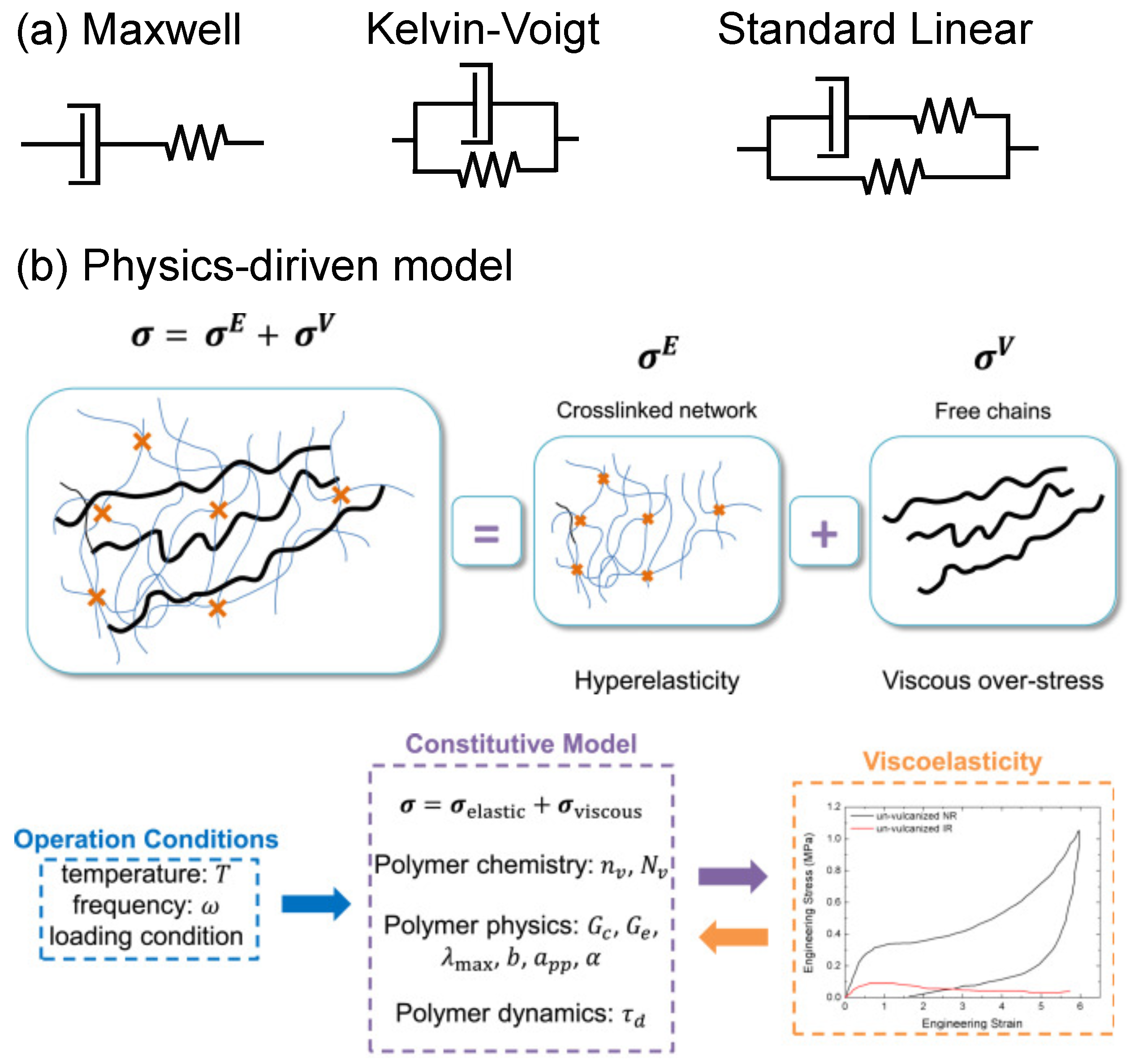
3.3. Viscoelasticity
3.4. The Mullins Effect
3.5. Strain-Induced Anisotropy
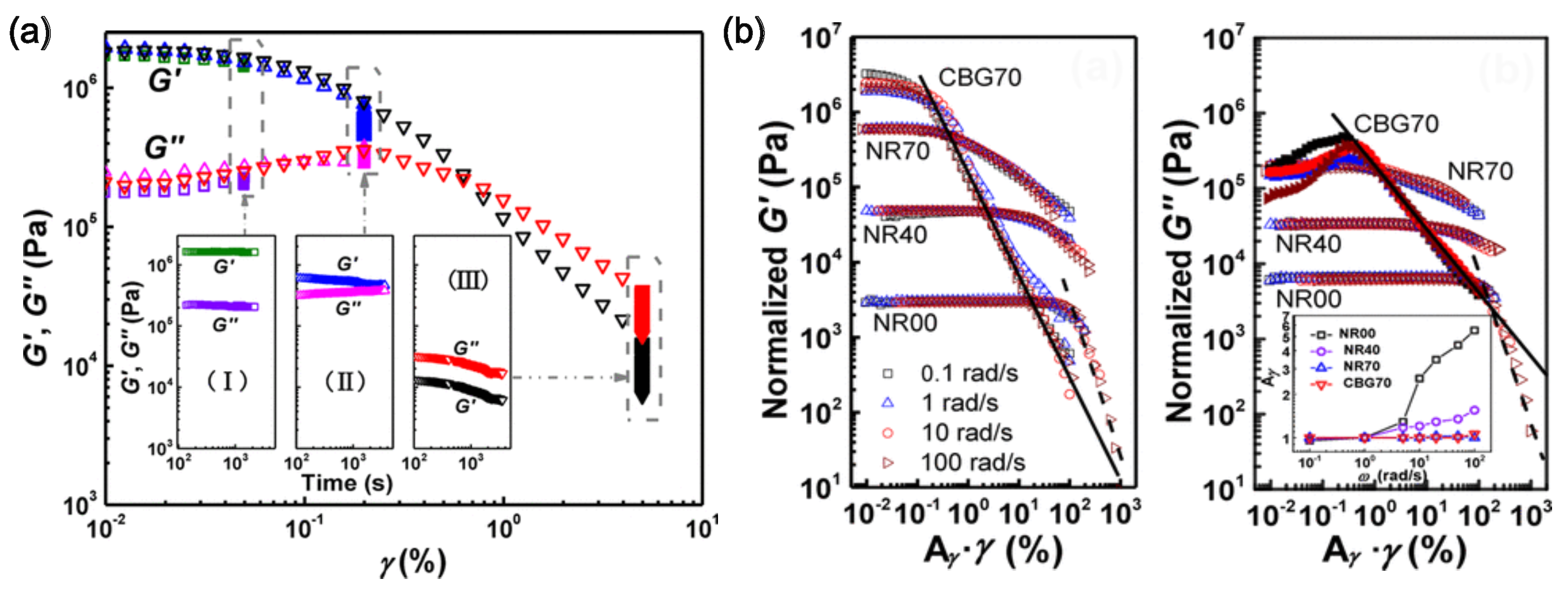
3.6. The Payne Effect
4. Smart Materials
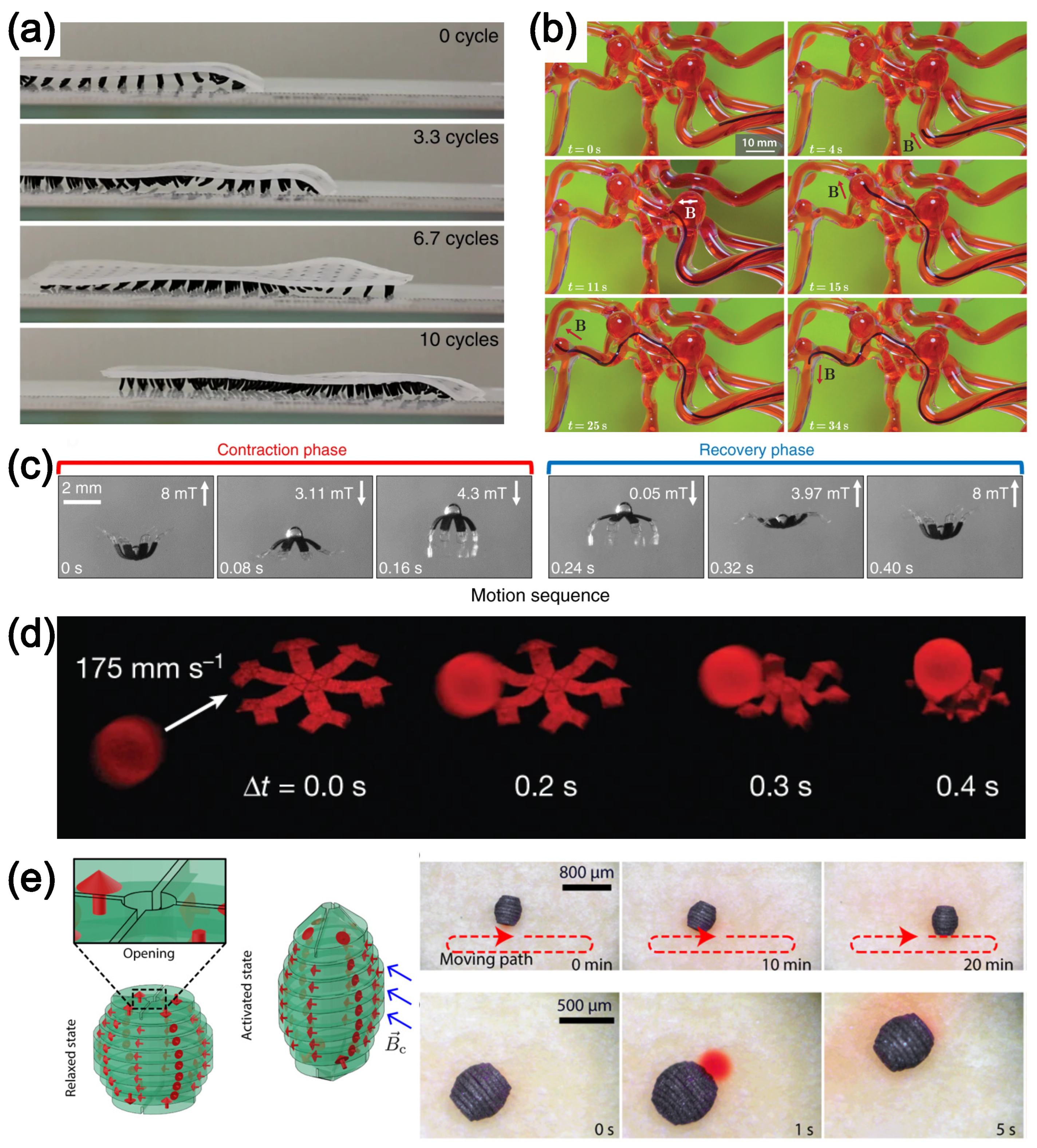
4.1. Magnetoelastic Materials
4.2. Shape-Memory Polymer
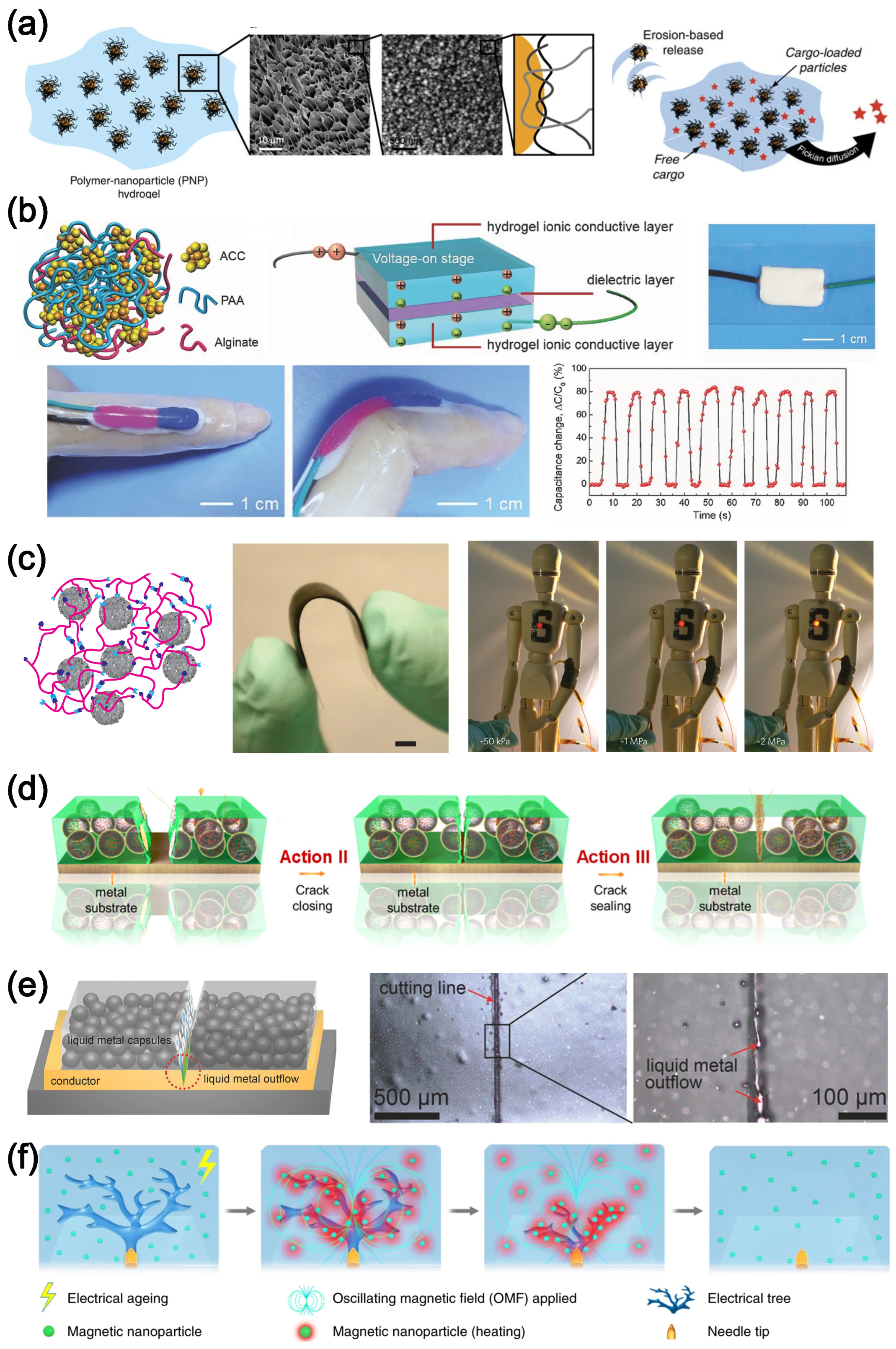
4.3. Self-Healing Polymer
4.4. Constitutive Modeling for Smart Materials
5. Discussion and Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Hancock, T. Personal Narrative of the Origin and Progress of the Caoutchouc or India-Rubber Manufacture in England; Longman, Brown, Green, Longmans, & Roberts: London, UK, 1857. [Google Scholar]
- Guise-Richardson, C. Redefining Vulcanization: Charles Goodyear, patents, and industrial control, 1834–1865. Technol. Cult. 2010, 51, 357–387. [Google Scholar] [CrossRef]
- Staudinger, H. Über Polymerization (On Polymerization). Ber. Dtsch. Chem. Ges 1920, 53, 1073. [Google Scholar] [CrossRef]
- Edwards, D. Polymer-filler interactions in rubber reinforcement. J. Mater. Sci. 1990, 25, 4175–4185. [Google Scholar] [CrossRef]
- Seiffert, S.; Sprakel, J. Physical chemistry of supramolecular polymer networks. Chem. Soc. Rev. 2012, 41, 909–930. [Google Scholar] [CrossRef] [PubMed]
- Jin, F.L.; Li, X.; Park, S.J. Synthesis and application of epoxy resins: A review. J. Ind. Eng. Chem. 2015, 29, 1–11. [Google Scholar] [CrossRef]
- Einstein, A. On the motion of small particles suspended in liquids at rest required by the molecular-kinetic theory of heat. Ann. Phys. 1905, 17, 208. [Google Scholar]
- Guth, E.; Gold, O. On the hydrodynamical theory of the viscosity of suspensions. Phys. Rev. 1938, 53, 322. [Google Scholar]
- Heinrich, G.; Kipscholl, R.; Stoček, R. Degradation of Elastomers in Practice, Experiments and Modeling; Springer: Berlin/Heidelberg, Germany, 2023. [Google Scholar]
- Rahman, T.; Simmons, D.S. Near-Substrate Gradients in Chain Relaxation and Viscosity in a Model Low-Molecular Weight Polymer. Macromolecules 2021, 54, 5935–5949. [Google Scholar] [CrossRef]
- Popov, I.; Carroll, B.; Bocharova, V.; Genix, A.C.; Cheng, S.; Khamzin, A.; Kisliuk, A.; Sokolov, A.P. Strong reduction in amplitude of the interfacial segmental dynamics in polymer nanocomposites. Macromolecules 2020, 53, 4126–4135. [Google Scholar] [CrossRef]
- Fredrickson, G.H. Recent developments in dynamical theories of the liquid-glass transition. Annu. Rev. Phys. Chem. 1988, 39, 149–180. [Google Scholar] [CrossRef]
- Kango, S.; Kalia, S.; Celli, A.; Njuguna, J.; Habibi, Y.; Kumar, R. Surface modification of inorganic nanoparticles for development of organic–inorganic nanocomposites—A review. Prog. Polym. Sci. 2013, 38, 1232–1261. [Google Scholar] [CrossRef]
- Li, Y.; Abberton, B.C.; Kröger, M.; Liu, W.K. Challenges in multiscale modeling of polymer dynamics. Polymers 2013, 5, 751–832. [Google Scholar] [CrossRef]
- Zhai, C.; Li, T.; Shi, H.; Yeo, J. Discovery and design of soft polymeric bio-inspired materials with multiscale simulations and artificial intelligence. J. Mater. Chem. B 2020, 8, 6562–6587. [Google Scholar] [CrossRef] [PubMed]
- Bahl, S.; Nagar, H.; Singh, I.; Sehgal, S. Smart materials types, properties and applications: A review. Mater. Today Proc. 2020, 28, 1302–1306. [Google Scholar] [CrossRef]
- Robertson, C.G.; Hardman, N.J. Nature of carbon black reinforcement of rubber: Perspective on the original polymer nanocomposite. Polymers 2021, 13, 538. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, Y. Structure and biosynthesis mechanism of natural polyisoprene. Prog. Polym. Sci. 1989, 14, 339–371. [Google Scholar] [CrossRef]
- Carothers, W.H.; Williams, I.; Collins, A.M.; Kirby, J.E. Acetylene polymers and their derivatives. II. A new synthetic rubber: Chloroprene and its polymers. J. Am. Chem. Soc. 1931, 53, 4203–4225. [Google Scholar] [CrossRef]
- Dossin, L.M.; Graessley, W.W. Rubber elasticity of well-characterized polybutadiene networks. Macromolecules 1979, 12, 123–130. [Google Scholar] [CrossRef]
- Yoon, D.; Sundararajan, P.; Flory, P. Conformational characteristics of polystyrene. Macromolecules 1975, 8, 776–783. [Google Scholar] [CrossRef]
- Hertz, D., Jr.; Bussem, H.; Ray, T. Nitrile rubber—Past, present and future. Rubber Chem. Technol. 1995, 68, 540–546. [Google Scholar] [CrossRef]
- Polmanteer, K.E. Silicone rubber, its development and technological progress. Rubber Chem. Technol. 1988, 61, 470–502. [Google Scholar] [CrossRef]
- Shit, S.C.; Shah, P. A review on silicone rubber. Natl. Acad. Sci. Lett. 2013, 36, 355–365. [Google Scholar] [CrossRef]
- Zhang, M.; Zhao, X. Alginate hydrogel dressings for advanced wound management. Int. J. Biol. Macromol. 2020, 162, 1414–1428. [Google Scholar] [CrossRef]
- Awasthi, S.; Gaur, J.K.; Bobji, M.; Srivastava, C. Nanoparticle-reinforced polyacrylamide hydrogel composites for clinical applications: A review. J. Mater. Sci. 2022, 57, 8041–8063. [Google Scholar] [CrossRef]
- Shi, L.; Zhang, J.; Zhao, M.; Tang, S.; Cheng, X.; Zhang, W.; Li, W.; Liu, X.; Peng, H.; Wang, Q. Effects of polyethylene glycol on the surface of nanoparticles for targeted drug delivery. Nanoscale 2021, 13, 10748–10764. [Google Scholar] [CrossRef] [PubMed]
- Adelnia, H.; Ensandoost, R.; Moonshi, S.S.; Gavgani, J.N.; Vasafi, E.I.; Ta, H.T. Freeze/thawed polyvinyl alcohol hydrogels: Present, past and future. Eur. Polym. J. 2022, 164, 110974. [Google Scholar] [CrossRef]
- Leblanc, J.L. Rubber–filler interactions and rheological properties in filled compounds. Prog. Polym. Sci. 2002, 27, 627–687. [Google Scholar] [CrossRef]
- Pothen, L.; Chan, C.H.; Thomas, S. Natural Rubber Materials, Volume 2-Composites and Nanocomposites; Royal Society of Chemistry: London, UK, 2013. [Google Scholar]
- Jancar, J.; Douglas, J.; Starr, F.W.; Kumar, S.; Cassagnau, P.; Lesser, A.; Sternstein, S.S.; Buehler, M. Current issues in research on structure–property relationships in polymer nanocomposites. Polymer 2010, 51, 3321–3343. [Google Scholar] [CrossRef]
- Sinha, P.; Datar, A.; Jeong, C.; Deng, X.; Chung, Y.G.; Lin, L.C. Surface area determination of porous materials using the Brunauer–Emmett–Teller (BET) method: Limitations and improvements. J. Phys. Chem. C 2019, 123, 20195–20209. [Google Scholar] [CrossRef]
- Pal, N.; Lee, J.H.; Cho, E.B. Recent trends in morphology-controlled synthesis and application of mesoporous silica nanoparticles. Nanomaterials 2020, 10, 2122. [Google Scholar] [CrossRef]
- Teoh, W.Y.; Amal, R.; Mädler, L. Flame spray pyrolysis: An enabling technology for nanoparticles design and fabrication. Nanoscale 2010, 2, 1324–1347. [Google Scholar] [CrossRef] [PubMed]
- Plueddemann, E.; Clark, H.; Nelson, L.; Hoffmann, K. Silane coupling agents for reinforced plastics. Mod. Plast 1962, 39, 135. [Google Scholar]
- Sidorenko, A.; Minko, S.; Gafijchuk, G.; Voronov, S. Radical polymerization initiated from a solid substrate. 3. Grafting from the surface of an ultrafine powder. Macromolecules 1999, 32, 4539–4543. [Google Scholar] [CrossRef]
- Wang, X.; Song, X.; Lin, M.; Wang, H.; Zhao, Y.; Zhong, W.; Du, Q. Surface initiated graft polymerization from carbon-doped TiO2 nanoparticles under sunlight illumination. Polymer 2007, 48, 5834–5838. [Google Scholar] [CrossRef]
- Abbas, Z.M.; Tawfilas, M.; Khani, M.M.; Golian, K.; Marsh, Z.M.; Jhalaria, M.; Simonutti, R.; Stefik, M.; Kumar, S.K.; Benicewicz, B.C. Reinforcement of polychloroprene by grafted silica nanoparticles. Polymer 2019, 171, 96–105. [Google Scholar] [CrossRef]
- Sang, L.; Zhao, Y.; Burda, C. TiO2 nanoparticles as functional building blocks. Chem. Rev. 2014, 114, 9283–9318. [Google Scholar] [CrossRef] [PubMed]
- Ong, C.B.; Ng, L.Y.; Mohammad, A.W. A review of ZnO nanoparticles as solar photocatalysts: Synthesis, mechanisms and applications. Renew. Sustain. Energy Rev. 2018, 81, 536–551. [Google Scholar] [CrossRef]
- Dykman, L.; Khlebtsov, N. Gold nanoparticles in biomedical applications: Recent advances and perspectives. Chem. Soc. Rev. 2012, 41, 2256–2282. [Google Scholar] [CrossRef]
- Kim, Y.; Zhao, X. Magnetic soft materials and robots. Chem. Rev. 2022, 122, 5317–5364. [Google Scholar] [CrossRef]
- Rahmat, M.; Hubert, P. Carbon nanotube–polymer interactions in nanocomposites: A review. Compos. Sci. Technol. 2011, 72, 72–84. [Google Scholar] [CrossRef]
- Young, R.J.; Kinloch, I.A.; Gong, L.; Novoselov, K.S. The mechanics of graphene nanocomposites: A review. Compos. Sci. Technol. 2012, 72, 1459–1476. [Google Scholar] [CrossRef]
- Li, B.; Zhong, W.H. Review on polymer/graphite nanoplatelet nanocomposites. J. Mater. Sci. 2011, 46, 5595–5614. [Google Scholar] [CrossRef]
- Malakooti, M.H.; Bockstaller, M.R.; Matyjaszewski, K.; Majidi, C. Liquid metal nanocomposites. Nanoscale Adv. 2020, 2, 2668–2677. [Google Scholar] [CrossRef]
- Gurtin, M.E.; Fried, E.; Anand, L. The Mechanics and Thermodynamics of Continua; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Mooney, M. A theory of large elastic deformation. J. Appl. Phys. 1940, 11, 582–592. [Google Scholar] [CrossRef]
- Treloar, L. The elasticity of a network of long-chain molecules—II. Trans. Faraday Soc. 1943, 39, 241–246. [Google Scholar] [CrossRef]
- Rivlin, R.S. Large elastic deformations of isotropic materials IV. Further developments of the general theory. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1948, 241, 379–397. [Google Scholar]
- Arruda, E.M.; Boyce, M.C. A three-dimensional constitutive model for the large stretch behavior of rubber elastic materials. J. Mech. Phys. Solids 1993, 41, 389–412. [Google Scholar] [CrossRef]
- Rubinstein, M.; Panyukov, S. Elasticity of polymer networks. Macromolecules 2002, 35, 6670–6686. [Google Scholar] [CrossRef]
- Davidson, J.D.; Goulbourne, N.C. A nonaffine network model for elastomers undergoing finite deformations. J. Mech. Phys. Solids 2013, 61, 1784–1797. [Google Scholar] [CrossRef]
- Mullins, L.; Tobin, N. Theoretical model for the elastic behavior of filler-reinforced vulcanized rubbers. Rubber Chem. Technol. 1957, 30, 555–571. [Google Scholar] [CrossRef]
- Simo, J.C. On a fully three-dimensional finite-strain viscoelastic damage model: Formulation and computational aspects. Comput. Methods Appl. Mech. Eng. 1987, 60, 153–173. [Google Scholar] [CrossRef]
- Dargazany, R.; Itskov, M. Constitutive modeling of the Mullins effect and cyclic stress softening in filled elastomers. Phys. Rev. E 2013, 88, 012602. [Google Scholar] [CrossRef]
- Payne, A. A note on the existence of a yield point in the dynamic modulus of loaded vulcanizates. J. Appl. Polym. Sci. 1960, 3, 127. [Google Scholar] [CrossRef]
- Kraus, G. Mechanical losses in carbon-black-filled rubbers. J. Appl. Polym. Sci. Appl. Polym. Symp. 1984, 39, 75–92. [Google Scholar]
- Klüppel, M.; Heinrich, G. Fractal structures in carbon black reinforced rubbers. Rubber Chem. Technol. 1995, 68, 623–651. [Google Scholar] [CrossRef]
- Lion, A. A constitutive model for carbon black filled rubber: Experimental investigations and mathematical representation. Contin. Mech. Thermodyn. 1996, 8, 153–169. [Google Scholar] [CrossRef]
- Miehe, C.; Göktepe, S. A micro–macro approach to rubber-like materials. Part II: The micro-sphere model of finite rubber viscoelasticity. J. Mech. Phys. Solids 2005, 53, 2231–2258. [Google Scholar] [CrossRef]
- Li, Y.; Tang, S.; Kröger, M.; Liu, W.K. Molecular simulation guided constitutive modeling on finite strain viscoelasticity of elastomers. J. Mech. Phys. Solids 2016, 88, 204–226. [Google Scholar]
- Guo, J.; Liu, M.; Zehnder, A.T.; Zhao, J.; Narita, T.; Creton, C.; Hui, C.Y. Fracture mechanics of a self-healing hydrogel with covalent and physical crosslinks: A numerical study. J. Mech. Phys. Solids 2018, 120, 79–95. [Google Scholar] [CrossRef]
- Mao, Y.; Chen, F.; Hou, S.; Qi, H.J.; Yu, K. A viscoelastic model for hydrothermally activated malleable covalent network polymer and its application in shape memory analysis. J. Mech. Phys. Solids 2019, 127, 239–265. [Google Scholar] [CrossRef]
- Wang, L.; Kim, Y.; Guo, C.F.; Zhao, X. Hard-magnetic elastica. J. Mech. Phys. Solids 2020, 142, 104045. [Google Scholar] [CrossRef]
- Rubinsten, M.; Colby, R.H. Polymer Physics; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Wang, S.; Panyukov, S.; Craig, S.L.; Rubinstein, M. Contribution of Unbroken Strands to the Fracture of Polymer Networks. Macromolecules 2023, 56, 2309–2318. [Google Scholar] [CrossRef]
- De Gennes, P.G. Reptation of a polymer chain in the presence of fixed obstacles. J. Chem. Phys. 1971, 55, 572–579. [Google Scholar] [CrossRef]
- Doi, M.; Edwards, S. Dynamics of concentrated polymer systems. Part 1.—Brownian motion in the equilibrium state. J. Chem. Soc. Faraday Trans. 2 Mol. Chem. Phys. 1978, 74, 1789–1801. [Google Scholar] [CrossRef]
- Miehe, C.; Göktepe, S.; Lulei, F. A micro-macro approach to rubber-like materials—Part I: The non-affine micro-sphere model of rubber elasticity. J. Mech. Phys. Solids 2004, 52, 2617–2660. [Google Scholar] [CrossRef]
- Treloar, L.; Riding, G. A non-Gaussian theory for rubber in biaxial strain. I. Mechanical properties. Proc. R. Soc. Lond. A Math. Phys. Sci. 1979, 369, 261–280. [Google Scholar]
- Yeoh, O.H. Some forms of the strain energy function for rubber. Rubber Chem. Technol. 1993, 66, 754–771. [Google Scholar] [CrossRef]
- Gent, A.N. A new constitutive relation for rubber. Rubber Chem. Technol. 1996, 69, 59–61. [Google Scholar] [CrossRef]
- Valanis, K.; Landel, R.F. The strain-energy function of a hyperelastic material in terms of the extension ratios. J. Appl. Phys. 1967, 38, 2997–3002. [Google Scholar] [CrossRef]
- Ogden, R.W. Large deformation isotropic elasticity–on the correlation of theory and experiment for incompressible rubberlike solids. Proc. R. Soc. Lond. A Math. Phys. Sci. 1972, 326, 565–584. [Google Scholar] [CrossRef]
- Wang, M.C.; Guth, E. Statistical theory of networks of non-Gaussian flexible chains. J. Chem. Phys. 1952, 20, 1144–1157. [Google Scholar] [CrossRef]
- Flory, P.J.; Rehner, J., Jr. Statistical mechanics of cross-linked polymer networks II. Swelling. J. Chem. Phys. 1943, 11, 521–526. [Google Scholar] [CrossRef]
- Treloar, L. The photoelastic properties of short-chain molecular networks. Trans. Faraday Soc. 1954, 50, 881–896. [Google Scholar] [CrossRef]
- Wu, P.; Van Der Giessen, E. On improved network models for rubber elasticity and their applications to orientation hardening in glassy polymers. J. Mech. Phys. Solids 1993, 41, 427–456. [Google Scholar] [CrossRef]
- Rubinstein, M.; Panyukov, S. Nonaffine deformation and elasticity of polymer networks. Macromolecules 1997, 30, 8036–8044. [Google Scholar] [CrossRef]
- Meissner, B.; Matějka, L. A Langevin-elasticity-theory-based constitutive equation for rubberlike networks and its comparison with biaxial stress–strain data. Part I. Polymer 2003, 44, 4599–4610. [Google Scholar] [CrossRef]
- Kaliske, M.; Heinrich, G. An extended tube-model for rubber elasticity: Statistical-mechanical theory and finite element implementation. Rubber Chem. Technol. 1999, 72, 602–632. [Google Scholar] [CrossRef]
- Deam, R.; Edwards, S.F. The theory of rubber elasticity. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1976, 280, 317–353. [Google Scholar]
- Xiang, Y.; Zhong, D.; Wang, P.; Mao, G.; Yu, H.; Qu, S. A general constitutive model of soft elastomers. J. Mech. Phys. Solids 2018, 117, 110–122. [Google Scholar] [CrossRef]
- Edwards, S. The statistical mechanics of polymerized material. Proc. Phys. Soc. 1967, 92, 9. [Google Scholar] [CrossRef]
- Verron, E.; Gros, A. An equal force theory for network models of soft materials with arbitrary molecular weight distribution. J. Mech. Phys. Solids 2017, 106, 176–190. [Google Scholar] [CrossRef]
- Zhong, M.; Wang, R.; Kawamoto, K.; Olsen, B.D.; Johnson, J.A. Quantifying the impact of molecular defects on polymer network elasticity. Science 2016, 353, 1264–1268. [Google Scholar] [CrossRef] [PubMed]
- Sorichetti, V.; Ninarello, A.; Ruiz-Franco, J.M.; Hugouvieux, V.; Kob, W.; Zaccarelli, E.; Rovigatti, L. Effect of chain polydispersity on the elasticity of disordered polymer networks. Macromolecules 2021, 54, 3769–3779. [Google Scholar] [CrossRef] [PubMed]
- Zhan, L.; Wang, S.; Qu, S.; Steinmann, P.; Xiao, R. A new micro–macro transition for hyperelastic materials. J. Mech. Phys. Solids 2023, 171, 105156. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Gambarova, P.G. Crack shear in concrete: Crack band microflane model. J. Struct. Eng. 1984, 110, 2015–2035. [Google Scholar] [CrossRef]
- Duering, E.R.; Kremer, K.; Grest, G.S. Structure and relaxation of end-linked polymer networks. J. Chem. Phys. 1994, 101, 8169–8192. [Google Scholar] [CrossRef]
- Song, L.; Patil, S.; Song, Y.; Chen, L.; Tian, F.; Chen, L.; Li, X.; Li, L.; Cheng, S. Nanoparticle Clustering and Viscoelastic Properties of Polymer Nanocomposites with Non-Attractive Polymer–Nanoparticle Interactions. Macromolecules 2022, 55, 7626–7636. [Google Scholar] [CrossRef]
- Song, L.; Wang, Z.; Tang, X.; Chen, L.; Chen, P.; Yuan, Q.; Li, L. Visualizing the toughening mechanism of nanofiller with 3D X-ray nano-CT: Stress-induced phase separation of silica nanofiller and silicone polymer double networks. Macromolecules 2017, 50, 7249–7257. [Google Scholar] [CrossRef]
- Kumar, S.K.; Benicewicz, B.C.; Vaia, R.A.; Winey, K.I. 50th anniversary perspective: Are polymer nanocomposites practical for applications? Macromolecules 2017, 50, 714–731. [Google Scholar] [CrossRef]
- Huber, G.; Vilgis, T.A.; Heinrich, G. Universal properties in the dynamical deformation of filled rubbers. J. Phys. Condens. Matter 1996, 8, L409. [Google Scholar] [CrossRef]
- Einstein, A. A new determination of molecular dimensions. Annln. Phys. 1906, 19, 289–306. [Google Scholar] [CrossRef]
- Vilgis, T.A.; Heinrich, G.; Klüppel, M. Reinforcement of Polymer Nano-Composites: Theory, Experiments and Applications; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Guth, E. Theory of filler reinforcement. Rubber Chem. Technol. 1945, 18, 596–604. [Google Scholar] [CrossRef]
- Bergstrom, J.S.; Boyce, M.C. Mechanical behavior of particle filled elastomers. Rubber Chem. Technol. 1999, 72, 633–656. [Google Scholar] [CrossRef]
- Bhattacharya, M.; Bhowmick, A.K. Polymer–filler interaction in nanocomposites: New interface area function to investigate swelling behavior and Young’s modulus. Polymer 2008, 49, 4808–4818. [Google Scholar] [CrossRef]
- Fukahori, Y.; Hon, A.; Jha, V.; Busfield, J. Modified guth–gold equation for carbon black–filled rubbers. Rubber Chem. Technol. 2013, 86, 218–232. [Google Scholar] [CrossRef]
- Kumar, V.; Alam, M.N.; Yewale, M.A.; Park, S.S. Tailoring Triple Filler Systems for Improved Magneto-Mechanical Performance in Silicone Rubber Composites. Polymers 2023, 15, 2287. [Google Scholar] [CrossRef]
- Potts, J.R.; Shankar, O.; Du, L.; Ruoff, R.S. Processing–morphology–property relationships and composite theory analysis of reduced graphene oxide/natural rubber nanocomposites. Macromolecules 2012, 45, 6045–6055. [Google Scholar] [CrossRef]
- Sternstein, S.; Amanuel, S.; Shofner, M.L. Reinforcement mechanisms in nanofilled polymer melts and elastomers. Rubber Chem. Technol. 2010, 83, 181–198. [Google Scholar] [CrossRef]
- Affdl, J.H.; Kardos, J. The Halpin-Tsai equations: A review. Polym. Eng. Sci. 1976, 16, 344–352. [Google Scholar] [CrossRef]
- Cox, H. The elasticity and strength of paper and other fibrous materials. Br. J. Appl. Phys. 1952, 3, 72. [Google Scholar] [CrossRef]
- Ahmed, S.; Jones, F. A review of particulate reinforcement theories for polymer composites. J. Mater. Sci. 1990, 25, 4933–4942. [Google Scholar] [CrossRef]
- Clyne, T.W.; Hull, D. An Introduction to Composite Materials; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Chen, Q.; Gong, S.; Moll, J.; Zhao, D.; Kumar, S.K.; Colby, R.H. Mechanical reinforcement of polymer nanocomposites from percolation of a nanoparticle network. ACS Macro Lett. 2015, 4, 398–402. [Google Scholar] [CrossRef] [PubMed]
- Steck, J.; Kim, J.; Kutsovsky, Y.; Suo, Z. Multiscale stress deconcentration amplifies fatigue resistance of rubber. Nature 2023, 624, 303–308. [Google Scholar] [CrossRef] [PubMed]
- Stauffer, D.; Aharony, A. Introduction to Percolation Theory; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Kantor, Y.; Webman, I. Elastic properties of random percolating systems. Phys. Rev. Lett. 1984, 52, 1891. [Google Scholar] [CrossRef]
- Klüppel, M.; Schuster, R.H.; Heinrich, G. Structure and properties of reinforcing fractal filler networks in elastomers. Rubber Chem. Technol. 1997, 70, 243–255. [Google Scholar] [CrossRef]
- Wang, M.J. Effect of polymer-filler and filler-filler interactions on dynamic properties of filled vulcanizates. Rubber Chem. Technol. 1998, 71, 520–589. [Google Scholar] [CrossRef]
- Colby, R.H.; Gillmor, J.R.; Rubinstein, M. Dynamics of near-critical polymer gels. Phys. Rev. E 1993, 48, 3712. [Google Scholar] [CrossRef] [PubMed]
- Yavitt, B.M.; Salatto, D.; Zhou, Y.; Huang, Z.; Endoh, M.; Wiegart, L.; Bocharova, V.; Ribbe, A.E.; Sokolov, A.P.; Schweizer, K.S.; et al. Collective nanoparticle dynamics associated with bridging network formation in model polymer nanocomposites. ACS Nano 2021, 15, 11501–11513. [Google Scholar] [CrossRef] [PubMed]
- Cui, W.; You, W.; Sun, Z.; Yu, W. Decoupled polymer dynamics in weakly attractive poly (methyl methacrylate)/silica nanocomposites. Macromolecules 2021, 54, 5484–5497. [Google Scholar] [CrossRef]
- Dargazany, R.; Itskov, M. A network evolution model for the anisotropic Mullins effect in carbon black filled rubbers. Int. J. Solids Struct. 2009, 46, 2967–2977. [Google Scholar] [CrossRef]
- Champagne, J.; Cantournet, S.; Colombo, D.; Jamonneau, S.; Le Gorju, K.; Lequeux, F.; Montes, H. Role of glassy bridges on the mechanics of filled rubbers under pressure. Macromolecules 2020, 53, 3728–3737. [Google Scholar] [CrossRef]
- Schneider, H.; Roos, M.; Golitsyn, Y.; Steiner, K.; Saalwächter, K. Dynamic Heterogeneity of Filler-Associated Interphases in Polymer Nanocomposites. Macromol. Rapid Commun. 2021, 42, 2100061. [Google Scholar] [CrossRef]
- Li, S.; Ding, M.; Shi, T. Spatial distribution of entanglements and dynamics in polymer films confined by smooth walls. Polymer 2019, 172, 365–371. [Google Scholar] [CrossRef]
- Schneider, G.; Nusser, K.; Willner, L.; Falus, P.; Richter, D. Dynamics of entangled chains in polymer nanocomposites. Macromolecules 2011, 44, 5857–5860. [Google Scholar] [CrossRef]
- Harton, S.E.; Kumar, S.K.; Yang, H.; Koga, T.; Hicks, K.; Lee, H.; Mijovic, J.; Liu, M.; Vallery, R.S.; Gidley, D.W. Immobilized polymer layers on spherical nanoparticles. Macromolecules 2010, 43, 3415–3421. [Google Scholar] [CrossRef]
- Rittigstein, P.; Priestley, R.D.; Broadbelt, L.J.; Torkelson, J.M. Model polymer nanocomposites provide an understanding of confinement effects in real nanocomposites. Nat. Mater. 2007, 6, 278–282. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, H.K.; Nakajima, K. Evidence of the Transition from a Flexible to Rigid Percolating Network in Polymer Nanocomposites. Macromolecules 2022, 55, 2739–2745. [Google Scholar] [CrossRef]
- Medalia, A. Effective degree of immobilization of rubber occluded within carbon black aggregates. Rubber Chem. Technol. 1972, 45, 1171–1194. [Google Scholar] [CrossRef]
- McLeish, T.C. Tube theory of entangled polymer dynamics. Adv. Phys. 2002, 51, 1379–1527. [Google Scholar] [CrossRef]
- Lakes, R.S. Viscoelastic Materials; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Dal, H.; Gültekin, O.; Açıkgöz, K. An extended eight-chain model for hyperelastic and finite viscoelastic response of rubberlike materials: Theory, experiments and numerical aspects. J. Mech. Phys. Solids 2020, 145, 104159. [Google Scholar] [CrossRef]
- Caffyn, J.; Blair, G.S. Significance of power-law relations in rheology. Nature 1945, 155, 171–172. [Google Scholar] [CrossRef]
- Williams, G.; Watts, D.C. Non-symmetrical dielectric relaxation behaviour arising from a simple empirical decay function. Trans. Faraday Soc. 1970, 66, 80–85. [Google Scholar] [CrossRef]
- Finley, W.; Lai, J.; Onaran, K. Creep and Relaxation of Nonlinear Viscoelastic Material; Elsevier: Amsterdam, The Netherlands, 1976. [Google Scholar]
- Bagley, R.L.; Torvik, P.J. Fractional calculus—A different approach to the analysis of viscoelastically damped structures. AIAA J. 1983, 21, 741–748. [Google Scholar] [CrossRef]
- Adolfsson, K.; Enelund, M.; Olsson, P. On the fractional order model of viscoelasticity. Mech. Time-Depend. Mater. 2005, 9, 15–34. [Google Scholar] [CrossRef]
- Bonfanti, A.; Kaplan, J.L.; Charras, G.; Kabla, A. Fractional viscoelastic models for power-law materials. Soft Matter 2020, 16, 6002–6020. [Google Scholar] [CrossRef] [PubMed]
- Green, A.E.; Rivlin, R.S. The mechanics of non-linear materials with memory. Arch. Ration. Mech. Anal. 1957, 1, 1–21. [Google Scholar] [CrossRef]
- Pipkin, A.; Rogers, T. A non-linear integral representation for viscoelastic behaviour. J. Mech. Phys. Solids 1968, 16, 59–72. [Google Scholar] [CrossRef]
- Rajagopal, K.; Srinivasa, A. A Gibbs-potential-based formulation for obtaining the response functions for a class of viscoelastic materials. Proc. R. Soc. A Math. Phys. Eng. Sci. 2011, 467, 39–58. [Google Scholar] [CrossRef]
- Govindjee, S.; Simo, J.C. Mullins’ effect and the strain amplitude dependence of the storage modulus. Int. J. Solids Struct. 1992, 29, 1737–1751. [Google Scholar] [CrossRef]
- Lubliner, J. A model of rubber viscoelasticity. Mech. Res. Commun. 1985, 12, 93–99. [Google Scholar] [CrossRef]
- Lion, A. On the large deformation behaviour of reinforced rubber at different temperatures. J. Mech. Phys. Solids 1997, 45, 1805–1834. [Google Scholar] [CrossRef]
- Keck, J.; Miehe, C. An Eulerian overstress-type viscoplastic constitutive model in spectral form. Formulation and numerical implementation. Comput. Plast. Fundam. Appl. 1997, 1, 997–1003. [Google Scholar]
- Li, Y.; Tang, S.; Abberton, B.C.; Kröger, M.; Burkhart, C.; Jiang, B.; Papakonstantopoulos, G.J.; Poldneff, M.; Liu, W.K. A predictive multiscale computational framework for viscoelastic properties of linear polymers. Polymer 2012, 53, 5935–5952. [Google Scholar] [CrossRef]
- Bergström, J.S.; Boyce, M.C. Constitutive modeling of the large strain time-dependent behavior of elastomers. J. Mech. Phys. Solids 1998, 46, 931–954. [Google Scholar] [CrossRef]
- Tang, S.; Greene, M.S.; Liu, W.K. Two-scale mechanism-based theory of nonlinear viscoelasticity. J. Mech. Phys. Solids 2012, 60, 199–226. [Google Scholar] [CrossRef]
- Stephanou, P.S.; Baig, C.; Tsolou, G.; Mavrantzas, V.G.; Kröger, M. Quantifying chain reptation in entangled polymer melts: Topological and dynamical mapping of atomistic simulation results onto the tube model. J. Chem. Phys. 2010, 132, 124904. [Google Scholar] [CrossRef] [PubMed]
- Likhtman, A.E.; Ponmurugan, M. Microscopic definition of polymer entanglements. Macromolecules 2014, 47, 1470–1481. [Google Scholar] [CrossRef]
- Yoon, B.; Kim, J.Y.; Hong, U.; Oh, M.K.; Kim, M.; Han, S.B.; Nam, J.D.; Suhr, J. Dynamic viscoelasticity of silica-filled styrene-butadiene rubber/polybutadiene rubber (SBR/BR) elastomer composites. Compos. Part B Eng. 2020, 187, 107865. [Google Scholar] [CrossRef]
- Taniguchi, Y.; Mai, T.T.; Yamaguchi, M.; Tsunoda, K.; Urayama, K. Investigating multiaxial mullins effect of carbon-black-reinforced elastomers using electrical resistivity measurements. ACS Appl. Polym. Mater. 2022, 4, 1139–1149. [Google Scholar] [CrossRef]
- Bouasse, H.; Carrière, Z. Sur les courbes de traction du caoutchouc vulcanisé. Ann. Fac. Sci. Toulouse Math. 1903, 5, 257–283. [Google Scholar] [CrossRef]
- Mullins, L. Effect of stretching on the properties of rubber. Rubber Chem. Technol. 1948, 21, 281–300. [Google Scholar] [CrossRef]
- Mullins, L. Thixotropic behavior of carbon black in rubber. Rubber Chem. Technol. 1950, 23, 733–743. [Google Scholar] [CrossRef]
- Mullins, L. Softening of rubber by deformation. Rubber Chem. Technol. 1969, 42, 339–362. [Google Scholar] [CrossRef]
- Beatty, M.F. The Mullins effect in a pure shear. J. Elast. Phys. Sci. Solids 2000, 59, 369–392. [Google Scholar]
- Ogden, R.W.; Roxburgh, D.G. A pseudo–elastic model for the Mullins effect in filled rubber. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1999, 455, 2861–2877. [Google Scholar] [CrossRef]
- Ragni, L.; Tubaldi, E.; Dall’Asta, A.; Ahmadi, H.; Muhr, A. Biaxial shear behaviour of HDNR with Mullins effect and deformation-induced anisotropy. Eng. Struct. 2018, 154, 78–92. [Google Scholar] [CrossRef]
- Mai, T.T.; Morishita, Y.; Urayama, K. Novel features of the Mullins effect in filled elastomers revealed by stretching measurements in various geometries. Soft Matter 2017, 13, 1966–1977. [Google Scholar] [CrossRef] [PubMed]
- Johnson, M.; Beatty, M. The Mullins effect in uniaxial extension and its influence on the transverse vibration of a rubber string. Contin. Mech. Thermodyn. 1993, 5, 83–115. [Google Scholar] [CrossRef]
- Zhao, X. A theory for large deformation and damage of interpenetrating polymer networks. J. Mech. Phys. Solids 2012, 60, 319–332. [Google Scholar] [CrossRef]
- Maiti, A.; Small, W.; Gee, R.; Weisgraber, T.; Chinn, S.; Wilson, T.; Maxwell, R. Mullins effect in a filled elastomer under uniaxial tension. Phys. Rev. E 2014, 89, 012602. [Google Scholar] [CrossRef]
- Dorfmann, A.; Ogden, R.W. A constitutive model for the Mullins effect with permanent set in particle-reinforced rubber. Int. J. Solids Struct. 2004, 41, 1855–1878. [Google Scholar] [CrossRef]
- Besdo, D.; Ihlemann, J. A phenomenological constitutive model for rubberlike materials and its numerical applications. Int. J. Plast. 2003, 19, 1019–1036. [Google Scholar] [CrossRef]
- Qi, H.; Boyce, M. Constitutive model for stretch-induced softening of the stress–stretch behavior of elastomeric materials. J. Mech. Phys. Solids 2004, 52, 2187–2205. [Google Scholar] [CrossRef]
- Merckel, Y.; Diani, J.; Brieu, M.; Caillard, J. Constitutive modeling of the anisotropic behavior of Mullins softened filled rubbers. Mech. Mater. 2013, 57, 30–41. [Google Scholar] [CrossRef]
- Harwood, J.; Mullins, L.; Payne, A.R. Stress softening in natural rubber vulcanizates. Part II. Stress softening effects in pure gum and filler loaded rubbers. J. Appl. Polym. Sci. 1965, 9, 3011–3021. [Google Scholar] [CrossRef]
- Bueche, F. Molecular basis for the Mullins effect. J. Appl. Polym. Sci. 1960, 4, 107–114. [Google Scholar] [CrossRef]
- Bueche, F. Mullins effect and rubber–filler interaction. J. Appl. Polym. Sci. 1961, 5, 271–281. [Google Scholar] [CrossRef]
- Houwink, R. Slipping of molecules during the deformation of reinforced rubber. Rubber Chem. Technol. 1956, 29, 888–893. [Google Scholar] [CrossRef]
- Kraus, G.; Childers, C.; Rollmann, K. Stress softening in carbon black-reinforced vulcanizates. Strain rate and temperature effects. J. Appl. Polym. Sci. 1966, 10, 229–244. [Google Scholar] [CrossRef]
- Fukahori, Y.; Seki, W. Molecular behaviour of elastomeric materials under large deformation: 2. Rheological model of polymer networks. Polymer 1992, 33, 1058–1068. [Google Scholar] [CrossRef]
- Govindjee, S.; Simo, J. A micro-mechanically based continuum damage model for carbon black-filled rubbers incorporating Mullins’ effect. J. Mech. Phys. Solids 1991, 39, 87–112. [Google Scholar] [CrossRef]
- Diani, J.; Brieu, M.; Vacherand, J. A damage directional constitutive model for Mullins effect with permanent set and induced anisotropy. Eur. J. Mech.-A/Solids 2006, 25, 483–496. [Google Scholar] [CrossRef]
- Sotta, P.; Albouy, P.A. Strain-induced crystallization in natural rubber: Flory’s theory revisited. Macromolecules 2020, 53, 3097–3109. [Google Scholar] [CrossRef]
- Flory, P.J. Thermodynamics of crystallization in high polymers. I. Crystallization induced by stretching. J. Chem. Phys. 1947, 15, 397–408. [Google Scholar] [CrossRef]
- Callister, W.D.; Rethwisch, D.G. Fundamentals of Materials Science and Engineering; Wiley: London, UK, 2000; Volume 471660817. [Google Scholar]
- Regrain, C.; Laiarinandrasana, L.; Toillon, S.; Saï, K. Multi-mechanism models for semi-crystalline polymer: Constitutive relations and finite element implementation. Int. J. Plast. 2009, 25, 1253–1279. [Google Scholar] [CrossRef]
- Ayoub, G.; Zaïri, F.; Naït-Abdelaziz, M.; Gloaguen, J.M. Modelling large deformation behaviour under loading–unloading of semicrystalline polymers: Application to a high density polyethylene. Int. J. Plast. 2010, 26, 329–347. [Google Scholar] [CrossRef]
- Ayoub, G.; Zaïri, F.; Fréderix, C.; Gloaguen, J.M.; Naït-Abdelaziz, M.; Seguela, R.; Lefebvre, J.M. Effects of crystal content on the mechanical behaviour of polyethylene under finite strains: Experiments and constitutive modelling. Int. J. Plast. 2011, 27, 492–511. [Google Scholar] [CrossRef]
- Boyce, M.; Socrate, S.; Llana, P. Constitutive model for the finite deformation stress–strain behavior of poly (ethylene terephthalate) above the glass transition. Polymer 2000, 41, 2183–2201. [Google Scholar] [CrossRef]
- Van Dommelen, J.V.; Parks, D.; Boyce, M.; Brekelmans, W.; Baaijens, F. Micromechanical modeling of the elasto-viscoplastic behavior of semi-crystalline polymers. J. Mech. Phys. Solids 2003, 51, 519–541. [Google Scholar] [CrossRef]
- Popa, C.; Fleischhauer, R.; Schneider, K.; Kaliske, M. Formulation and implementation of a constitutive model for semicrystalline polymers. Int. J. Plast. 2014, 61, 128–156. [Google Scholar] [CrossRef]
- Lee, B.; Parks, D.; Ahzi, S. Micromechanical modeling of large plastic deformation and texture evolution in semi-crystalline polymers. J. Mech. Phys. Solids 1993, 41, 1651–1687. [Google Scholar] [CrossRef]
- Dargazany, R.; Khiêm, V.N.; Itskov, M. A generalized network decomposition model for the quasi-static inelastic behavior of filled elastomers. Int. J. Plast. 2014, 63, 94–109. [Google Scholar] [CrossRef]
- Dargazany, R.; Khiêm, V.N.; Poshtan, E.A.; Itskov, M. Constitutive modeling of strain-induced crystallization in filled rubbers. Phys. Rev. E 2014, 89, 022604. [Google Scholar] [CrossRef]
- Nguyen, T.D. Modeling shape-memory behavior of polymers. Polym. Rev. 2013, 53, 130–152. [Google Scholar] [CrossRef]
- Xin, X.; Liu, L.; Liu, Y.; Leng, J. Mechanical models, structures, and applications of shape-memory polymers and their composites. Acta Mech. Solida Sin. 2019, 32, 535–565. [Google Scholar] [CrossRef]
- Song, K.; Wu, L.F.; Liu, D.; Huang, L.Z.; Miao, X.R.; Wang, Z. Flow-Induced Shish Nucleation in Lightly Crosslinked Polyethylene: Connecting Polymer Properties and Strain to the Final Shish–Kebab Structure. Macromolecules 2022, 55, 6866–6875. [Google Scholar] [CrossRef]
- Hashimoto, K.; Shiwaku, T.; Aoki, H.; Yokoyama, H.; Mayumi, K.; Ito, K. Strain-induced crystallization and phase separation used for fabricating a tough and stiff slide-ring solid polymer electrolyte. Sci. Adv. 2023, 9, eadi8505. [Google Scholar] [CrossRef] [PubMed]
- Hartquist, C.M.; Lin, S.; Zhang, J.H.; Wang, S.; Rubinstein, M.; Zhao, X. An elastomer with ultrahigh strain-induced crystallization. Sci. Adv. 2023, 9, eadj0411. [Google Scholar] [CrossRef]
- Shojaei, A.; Li, G. Viscoplasticity analysis of semicrystalline polymers: A multiscale approach within micromechanics framework. Int. J. Plast. 2013, 42, 31–49. [Google Scholar] [CrossRef]
- Corté, L.; Leibler, L. A model for toughening of semicrystalline polymers. Macromolecules 2007, 40, 5606–5611. [Google Scholar] [CrossRef]
- Altorbaq, A.S.; Krauskopf, A.A.; Wen, X.; Pérez-Camargo, R.A.; Su, Y.; Wang, D.; Müller, A.J.; Kumar, S.K. Crystallization kinetics and nanoparticle ordering in semicrystalline polymer nanocomposites. Prog. Polym. Sci. 2022, 128, 101527. [Google Scholar] [CrossRef]
- Gehman, S.; Woodford, D.; Stambaugh, R. Dynamic properties of rubber. Ind. Eng. Chem. 1941, 33, 1032–1038. [Google Scholar] [CrossRef]
- Waring, J. Dynamic study of reinforcement. Rubber Chem. Technol. 1951, 24, 787–809. [Google Scholar] [CrossRef]
- Fletcher, W.; Gent, A. Nonlinearity in the dynamic properties of vulcanized rubber compounds. Rubber Chem. Technol. 1954, 27, 209–222. [Google Scholar] [CrossRef]
- Gan, S.; Wu, Z.L.; Xu, H.; Song, Y.; Zheng, Q. Viscoelastic behaviors of carbon black gel extracted from highly filled natural rubber compounds: Insights into the Payne effect. Macromolecules 2016, 49, 1454–1463. [Google Scholar] [CrossRef]
- Ulmer, J. Strain dependence of dynamic mechanical properties of carbon black-filled rubber compounds. Rubber Chem. Technol. 1996, 69, 15–47. [Google Scholar] [CrossRef]
- Metzler, R.; Nonnenmacher, T.F. Fractional relaxation processes and fractional rheological models for the description of a class of viscoelastic materials. Int. J. Plast. 2003, 19, 941–959. [Google Scholar] [CrossRef]
- Lion, A.; Kardelky, C.; Haupt, P. On the frequency and amplitude dependence of the Payne effect: Theory and experiments. Rubber Chem. Technol. 2003, 76, 533–547. [Google Scholar] [CrossRef]
- Lion, A.; Kardelky, C. The Payne effect in finite viscoelasticity: Constitutive modelling based on fractional derivatives and intrinsic time scales. Int. J. Plast. 2004, 20, 1313–1345. [Google Scholar] [CrossRef]
- Van de Walle, A.; Tricot, C.; Gerspacher, M. Modeling carbon black reinforcement in rubber compounds. Kautschuk und Gummi Kunststoffe 1996, 49, 172–179. [Google Scholar]
- Lin, C.R.; Lee, Y.D. Strain-dependent dynamic properties of filled rubber network systems, 2: The physical meaning of parameters in the L-N-B model and their applicability. Macromol. Theory Simul. 1997, 6, 339–350. [Google Scholar] [CrossRef]
- Vieweg, S.; Unger, R.; Hempel, E.; Donth, E. Kinetic structure of glass transition in polymer interfaces between filler and SBR matrix. J. Non-Cryst. Solids 1998, 235, 470–475. [Google Scholar] [CrossRef]
- Lockhorn, D.; Klüppel, M. Structure–property relationships of silica/silane formulations in natural rubber, isoprene rubber and styrene–butadiene rubber composites. J. Appl. Polym. Sci. 2020, 137, 48435. [Google Scholar] [CrossRef]
- Wunde, M.; Klüppel, M. Impact of mixing procedure on phase morphology and fracture mechanical properties of carbon black-filled NR/SBR blends. Contin. Mech. Thermodyn. 2017, 29, 1135–1148. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, H.; Mao, J.; Chirarattananon, P.; Helbling, E.F.; Hyun, N.S.P.; Clarke, D.R.; Wood, R.J. Controlled flight of a microrobot powered by soft artificial muscles. Nature 2019, 575, 324–329. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Chen, X.; Zhou, F.; Liang, Y.; Xiao, Y.; Cao, X.; Zhang, Z.; Zhang, M.; Wu, B.; Yin, S.; et al. Self-powered soft robot in the Mariana Trench. Nature 2021, 591, 66–71. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Lau, G.C.; Yuan, H.; Aggarwal, A.; Dominguez, V.L.; Liu, S.; Sai, H.; Palmer, L.C.; Sather, N.A.; Pearson, T.J.; et al. Fast and programmable locomotion of hydrogel-metal hybrids under light and magnetic fields. Sci. Robot. 2020, 5, eabb9822. [Google Scholar] [CrossRef] [PubMed]
- Hu, W.; Lum, G.Z.; Mastrangeli, M.; Sitti, M. Small-scale soft-bodied robot with multimodal locomotion. Nature 2018, 554, 81–85. [Google Scholar] [CrossRef]
- Huang, H.W.; Sakar, M.S.; Petruska, A.J.; Pané, S.; Nelson, B.J. Soft micromachines with programmable motility and morphology. Nat. Commun. 2016, 7, 12263. [Google Scholar] [CrossRef]
- Jiralerspong, T.; Bae, G.; Lee, J.H.; Kim, S.K. Wireless control of two-and three-dimensional actuations of kirigami patterns composed of magnetic-particles–polymer composites. ACS Nano 2020, 14, 17589–17596. [Google Scholar] [CrossRef]
- Lee, Y.; Koehler, F.; Dillon, T.; Loke, G.; Kim, Y.; Marion, J.; Antonini, M.J.; Garwood, I.C.; Sahasrabudhe, A.; Nagao, K.; et al. Magnetically Actuated Fiber-Based Soft Robots. Adv. Mater. 2023, 35, 2301916. [Google Scholar] [CrossRef] [PubMed]
- Xu, T.; Zhang, J.; Salehizadeh, M.; Onaizah, O.; Diller, E. Millimeter-scale flexible robots with programmable three-dimensional magnetization and motions. Sci. Robot. 2019, 4, eaav4494. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.; Parada, G.A.; Liu, S.; Zhao, X. Ferromagnetic soft continuum robots. Sci. Robot. 2019, 4, eaax7329. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.; Genevriere, E.; Harker, P.; Choe, J.; Balicki, M.; Regenhardt, R.W.; Vranic, J.E.; Dmytriw, A.A.; Patel, A.B.; Zhao, X. Telerobotic neurovascular interventions with magnetic manipulation. Sci. Robot. 2022, 7, eabg9907. [Google Scholar] [CrossRef] [PubMed]
- Nelson, B.J.; Pané, S. Delivering drugs with microrobots. Science 2023, 382, 1120–1122. [Google Scholar] [CrossRef] [PubMed]
- Alapan, Y.; Karacakol, A.C.; Guzelhan, S.N.; Isik, I.; Sitti, M. Reprogrammable shape morphing of magnetic soft machines. Sci. Adv. 2020, 6, eabc6414. [Google Scholar] [CrossRef] [PubMed]
- Ma, C.; Wu, S.; Ze, Q.; Kuang, X.; Zhang, R.; Qi, H.J.; Zhao, R. Magnetic multimaterial printing for multimodal shape transformation with tunable properties and shiftable mechanical behaviors. ACS Appl. Mater. Interfaces 2020, 13, 12639–12648. [Google Scholar] [CrossRef] [PubMed]
- Ze, Q.; Kuang, X.; Wu, S.; Wong, J.; Montgomery, S.M.; Zhang, R.; Kovitz, J.M.; Yang, F.; Qi, H.J.; Zhao, R. Magnetic shape memory polymers with integrated multifunctional shape manipulation. Adv. Mater. 2020, 32, 1906657. [Google Scholar] [CrossRef] [PubMed]
- Kuang, X.; Wu, S.; Ze, Q.; Yue, L.; Jin, Y.; Montgomery, S.M.; Yang, F.; Qi, H.J.; Zhao, R. Magnetic dynamic polymers for modular assembling and reconfigurable morphing architectures. Adv. Mater. 2021, 33, 2102113. [Google Scholar] [CrossRef]
- Zhang, J.; Guo, Y.; Hu, W.; Soon, R.H.; Davidson, Z.S.; Sitti, M. Liquid crystal elastomer-based magnetic composite films for reconfigurable shape-morphing soft miniature machines. Adv. Mater. 2021, 33, 2006191. [Google Scholar] [CrossRef]
- Chen, G.; Jin, B.; Shi, Y.; Zhao, Q.; Shen, Y.; Xie, T. Rapidly and repeatedly reprogrammable liquid crystalline elastomer via a shape memory mechanism. Adv. Mater. 2022, 34, 2201679. [Google Scholar] [CrossRef] [PubMed]
- Zhao, W.; Zhang, F.; Leng, J.; Liu, Y. Personalized 4D printing of bioinspired tracheal scaffold concept based on magnetic stimulated shape memory composites. Compos. Sci. Technol. 2019, 184, 107866. [Google Scholar] [CrossRef]
- Lin, C.; Lv, J.; Li, Y.; Zhang, F.; Li, J.; Liu, Y.; Liu, L.; Leng, J. 4D-printed biodegradable and remotely controllable shape memory occlusion devices. Adv. Funct. Mater. 2019, 29, 1906569. [Google Scholar] [CrossRef]
- Roach, D.J.; Sun, X.; Peng, X.; Demoly, F.; Zhou, K.; Qi, H.J. 4D Printed Multifunctional Composites with Cooling-Rate Mediated Tunable Shape Morphing. Adv. Funct. Mater. 2022, 32, 2203236. [Google Scholar] [CrossRef]
- Liu, Y.D.; Fang, F.F.; Choi, H.J. Core–shell-structured silica-coated magnetic carbonyl iron microbead and its magnetorheology with anti-acidic characteristics. Colloid Polym. Sci. 2011, 289, 1295–1298. [Google Scholar] [CrossRef]
- Behrooz, M.; Sutrisno, J.; Zhang, L.; Fuchs, A.; Gordaninejad, F. Behavior of magnetorheological elastomers with coated particles. Smart Mater. Struct. 2015, 24, 035026. [Google Scholar] [CrossRef]
- Gu, H.; Boehler, Q.; Cui, H.; Secchi, E.; Savorana, G.; De Marco, C.; Gervasoni, S.; Peyron, Q.; Huang, T.Y.; Pane, S.; et al. Magnetic cilia carpets with programmable metachronal waves. Nat. Commun. 2020, 11, 2637. [Google Scholar] [CrossRef] [PubMed]
- Ren, Z.; Hu, W.; Dong, X.; Sitti, M. Multi-functional soft-bodied jellyfish-like swimming. Nat. Commun. 2019, 10, 2703. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.; Yuk, H.; Zhao, R.; Chester, S.A.; Zhao, X. Printing ferromagnetic domains for untethered fast-transforming soft materials. Nature 2018, 558, 274–279. [Google Scholar] [CrossRef]
- Zhang, J.; Ren, Z.; Hu, W.; Soon, R.H.; Yasa, I.C.; Liu, Z.; Sitti, M. Voxelated three-dimensional miniature magnetic soft machines via multimaterial heterogeneous assembly. Sci. Robot. 2021, 6, eabf0112. [Google Scholar] [CrossRef]
- Zhao, Y.; Gao, S.; Zhang, X.; Huo, W.; Xu, H.; Chen, C.; Li, J.; Xu, K.; Huang, X. Fully flexible electromagnetic vibration sensors with annular field confinement origami magnetic membranes. Adv. Funct. Mater. 2020, 30, 2001553. [Google Scholar] [CrossRef]
- Kawasetsu, T.; Horii, T.; Ishihara, H.; Asada, M. Mexican-hat-like response in a flexible tactile sensor using a magnetorheological elastomer. Sensors 2018, 18, 587. [Google Scholar] [CrossRef]
- Qi, Z.; Zhou, M.; Li, Y.; Xia, Z.; Huo, W.; Huang, X. Reconfigurable flexible electronics driven by origami magnetic membranes. Adv. Mater. Technol. 2021, 6, 2001124. [Google Scholar] [CrossRef]
- Yakacki, C.M.; Shandas, R.; Lanning, C.; Rech, B.; Eckstein, A.; Gall, K. Unconstrained recovery characterization of shape-memory polymer networks for cardiovascular applications. Biomaterials 2007, 28, 2255–2263. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Du, H.; Liu, L.; Leng, J. Shape memory polymers and their composites in aerospace applications: A review. Smart Mater. Struct. 2014, 23, 023001. [Google Scholar] [CrossRef]
- Lendlein, A.; Jiang, H.; Jünger, O.; Langer, R. Light-induced shape-memory polymers. Nature 2005, 434, 879–882. [Google Scholar] [CrossRef] [PubMed]
- Kumpfer, J.R.; Rowan, S.J. Thermo-, photo-, and chemo-responsive shape-memory properties from photo-cross-linked metallo-supramolecular polymers. J. Am. Chem. Soc. 2011, 133, 12866–12874. [Google Scholar] [CrossRef]
- Aoki, D.; Teramoto, Y.; Nishio, Y. SH-containing cellulose acetate derivatives: Preparation and characterization as a shape memory-recovery material. Biomacromolecules 2007, 8, 3749–3757. [Google Scholar] [CrossRef] [PubMed]
- Lee, K.M.; Wang, D.H.; Koerner, H.; Vaia, R.A.; Tan, L.S.; White, T.J. Enhancement of photogenerated mechanical force in azobenzene-functionalized polyimides. Angew. Chem. 2012, 124, 4193–4197. [Google Scholar] [CrossRef]
- Wang, X.; Guo, X.; Ye, J.; Zheng, N.; Kohli, P.; Choi, D.; Zhang, Y.; Xie, Z.; Zhang, Q.; Luan, H.; et al. Freestanding 3D mesostructures, functional devices, and shape-programmable systems based on mechanically induced assembly with shape memory polymers. Adv. Mater. 2019, 31, 1805615. [Google Scholar] [CrossRef]
- Zhang, Y.F.; Zhang, N.; Hingorani, H.; Ding, N.; Wang, D.; Yuan, C.; Zhang, B.; Gu, G.; Ge, Q. Fast-response, stiffness-tunable soft actuator by hybrid multimaterial 3D printing. Adv. Funct. Mater. 2019, 29, 1806698. [Google Scholar] [CrossRef]
- Chen, T.; Bilal, O.R.; Shea, K.; Daraio, C. Harnessing bistability for directional propulsion of soft, untethered robots. Proc. Natl. Acad. Sci. USA 2018, 115, 5698–5702. [Google Scholar] [CrossRef] [PubMed]
- Yu, K.; Liu, Y.; Leng, J. Shape memory polymer/CNT composites and their microwave induced shape memory behaviors. RSC Adv. 2014, 4, 2961–2968. [Google Scholar] [CrossRef]
- Wei, H.; Zhang, Q.; Yao, Y.; Liu, L.; Liu, Y.; Leng, J. Direct-write fabrication of 4D active shape-changing structures based on a shape memory polymer and its nanocomposite. ACS Appl. Mater. Interfaces 2017, 9, 876–883. [Google Scholar] [CrossRef] [PubMed]
- Xie, Y.; Meng, Y.; Wang, W.; Zhang, E.; Leng, J.; Pei, Q. Bistable and reconfigurable photonic crystals—Electroactive shape memory polymer nanocomposite for ink-free rewritable paper. Adv. Funct. Mater. 2018, 28, 1802430. [Google Scholar] [CrossRef]
- Wang, S.; Urban, M.W. Self-healing polymers. Nat. Rev. Mater. 2020, 5, 562–583. [Google Scholar] [CrossRef]
- Kim, Y.H.; Wool, R.P. A theory of healing at a polymer-polymer interface. Macromolecules 1983, 16, 1115–1120. [Google Scholar] [CrossRef]
- Chen, Y.; Guan, Z. Multivalent hydrogen bonding block copolymers self-assemble into strong and tough self-healing materials. Chem. Commun. 2014, 50, 10868–10870. [Google Scholar] [CrossRef] [PubMed]
- Yanagisawa, Y.; Nan, Y.; Okuro, K.; Aida, T. Mechanically robust, readily repairable polymers via tailored noncovalent cross-linking. Science 2018, 359, 72–76. [Google Scholar] [CrossRef]
- Appel, E.A.; Tibbitt, M.W.; Webber, M.J.; Mattix, B.A.; Veiseh, O.; Langer, R. Self-assembled hydrogels utilizing polymer–nanoparticle interactions. Nat. Commun. 2015, 6, 6295. [Google Scholar] [CrossRef]
- Lei, Z.; Wang, Q.; Sun, S.; Zhu, W.; Wu, P. A bioinspired mineral hydrogel as a self-healable, mechanically adaptable ionic skin for highly sensitive pressure sensing. Adv. Mater. 2017, 29, 1700321. [Google Scholar] [CrossRef] [PubMed]
- Tee, B.C.; Wang, C.; Allen, R.; Bao, Z. An electrically and mechanically self-healing composite with pressure-and flexion-sensitive properties for electronic skin applications. Nat. Nanotechnol. 2012, 7, 825–832. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Deng, L.; Ju, P.; Huang, L.; Qian, H.; Zhang, D.; Li, X.; Terryn, H.A.; Mol, J.M. Triple-action self-healing protective coatings based on shape memory polymers containing dual-function microspheres. ACS Appl. Mater. Interfaces 2018, 10, 23369–23379. [Google Scholar] [CrossRef] [PubMed]
- Chu, K.; Song, B.G.; Yang, H.I.; Kim, D.M.; Lee, C.S.; Park, M.; Chung, C.M. Smart Passivation Materials with a Liquid Metal Microcapsule as Self-Healing Conductors for Sustainable and Flexible Perovskite Solar Cells. Adv. Funct. Mater. 2018, 28, 1800110. [Google Scholar] [CrossRef]
- Yang, Y.; He, J.; Li, Q.; Gao, L.; Hu, J.; Zeng, R.; Qin, J.; Wang, S.X.; Wang, Q. Self-healing of electrical damage in polymers using superparamagnetic nanoparticles. Nat. Nanotechnol. 2019, 14, 151–155. [Google Scholar] [CrossRef] [PubMed]
- Zhao, R.; Kim, Y.; Chester, S.A.; Sharma, P.; Zhao, X. Mechanics of hard-magnetic soft materials. J. Mech. Phys. Solids 2019, 124, 244–263. [Google Scholar] [CrossRef]
- Ye, H.; Li, Y.; Zhang, T. Magttice: A lattice model for hard-magnetic soft materials. Soft Matter 2021, 17, 3560–3568. [Google Scholar] [CrossRef] [PubMed]
- Conti, S.; Lenz, M.; Rumpf, M. Modeling and simulation of magnetic-shape-memory polymer composites. J. Mech. Phys. Solids 2007, 55, 1462–1486. [Google Scholar] [CrossRef]
- Ge, Q.; Luo, X.; Rodriguez, E.D.; Zhang, X.; Mather, P.T.; Dunn, M.L.; Qi, H.J. Thermomechanical behavior of shape memory elastomeric composites. J. Mech. Phys. Solids 2012, 60, 67–83. [Google Scholar] [CrossRef]
- Mao, Y.; Robertson, J.M.; Mu, X.; Mather, P.T.; Qi, H.J. Thermoviscoplastic behaviors of anisotropic shape memory elastomeric composites for cold programmed non-affine shape change. J. Mech. Phys. Solids 2015, 85, 219–244. [Google Scholar] [CrossRef]
- Xiao, R.; Choi, J.; Lakhera, N.; Yakacki, C.M.; Frick, C.P.; Nguyen, T.D. Modeling the glass transition of amorphous networks for shape-memory behavior. J. Mech. Phys. Solids 2013, 61, 1612–1635. [Google Scholar] [CrossRef]
- Mergheim, J.; Steinmann, P. Phenomenological modelling of self-healing polymers based on integrated healing agents. Comput. Mech. 2013, 52, 681–692. [Google Scholar] [CrossRef]
- Hui, C.Y.; Long, R. A constitutive model for the large deformation of a self-healing gel. Soft Matter 2012, 8, 8209–8216. [Google Scholar] [CrossRef]
- Khiêm, V.N.; Mai, T.T.; Urayama, K.; Gong, J.P.; Itskov, M. A multiaxial theory of double network hydrogels. Macromolecules 2019, 52, 5937–5947. [Google Scholar] [CrossRef]
- Ducrot, E.; Chen, Y.; Bulters, M.; Sijbesma, R.P.; Creton, C. Toughening elastomers with sacrificial bonds and watching them break. Science 2014, 344, 186–189. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Zheng, X.; Ouchi, T.; Kouznetsova, T.B.; Beech, H.K.; Av-Ron, S.; Matsuda, T.; Bowser, B.H.; Wang, S.; Johnson, J.A.; et al. Toughening hydrogels through force-triggered chemical reactions that lengthen polymer strands. Science 2021, 374, 193–196. [Google Scholar] [CrossRef]
- Wang, S.; Hu, Y.; Kouznetsova, T.B.; Sapir, L.; Chen, D.; Herzog-Arbeitman, A.; Johnson, J.A.; Rubinstein, M.; Craig, S.L. Facile mechanochemical cycloreversion of polymer cross-linkers enhances tear resistance. Science 2023, 380, 1248–1252. [Google Scholar] [CrossRef] [PubMed]
- Kremer, K.; Grest, G.S. Dynamics of entangled linear polymer melts: A molecular-dynamics simulation. J. Chem. Phys. 1990, 92, 5057–5086. [Google Scholar] [CrossRef]
- Fan, J.; Anastassiou, A.; Macosko, C.W.; Tadmor, E.B. Molecular dynamics predictions of thermomechanical properties of an epoxy thermosetting polymer. Polymer 2020, 196, 122477. [Google Scholar] [CrossRef]
- Xian, W.; He, J.; Maiti, A.; Saab, A.P.; Li, Y. Investigating structure and dynamics of unentangled poly (dimethyl-co-diphenyl) siloxane via molecular dynamics simulation. Soft Matter 2023, 19, 4265–4276. [Google Scholar] [CrossRef]
- Yuan, C.; Levin, A.; Chen, W.; Xing, R.; Zou, Q.; Herling, T.W.; Challa, P.K.; Knowles, T.P.; Yan, X. Nucleation and growth of amino acid and peptide supramolecular polymers through liquid–liquid phase separation. Angew. Chem. Int. Ed. 2019, 58, 18116–18123. [Google Scholar] [CrossRef] [PubMed]
- Wagner, R.J.; Hobbs, E.; Vernerey, F.J. A network model of transient polymers: Exploring the micromechanics of nonlinear viscoelasticity. Soft Matter 2021, 17, 8742–8757. [Google Scholar] [CrossRef] [PubMed]
- Lamont, S.C.; Weishaar, K.; Bruns, C.J.; Vernerey, F.J. Micromechanics and damage in slide-ring networks. Phys. Rev. E 2023, 107, 044501. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Rocklin, D.Z.; Sander, L.M.; Mao, X. Fiber networks below the isostatic point: Fracture without stress concentration. Phys. Rev. Mater. 2017, 1, 052602. [Google Scholar] [CrossRef]
- Shekhawat, A.; Zapperi, S.; Sethna, J.P. From damage percolation to crack nucleation through finite size criticality. Phys. Rev. Lett. 2013, 110, 185505. [Google Scholar] [CrossRef] [PubMed]
- Ramprasad, R.; Batra, R.; Pilania, G.; Mannodi-Kanakkithodi, A.; Kim, C. Machine learning in materials informatics: Recent applications and prospects. npj Comput. Mater. 2017, 3, 54. [Google Scholar] [CrossRef]
- Chen, G.; Shen, Z.; Iyer, A.; Ghumman, U.F.; Tang, S.; Bi, J.; Chen, W.; Li, Y. Machine-learning-assisted de novo design of organic molecules and polymers: Opportunities and challenges. Polymers 2020, 12, 163. [Google Scholar] [CrossRef] [PubMed]
- Gurnani, R.; Kamal, D.; Tran, H.; Sahu, H.; Scharm, K.; Ashraf, U.; Ramprasad, R. PolyG2G: A novel machine learning algorithm applied to the generative design of polymer dielectrics. Chem. Mater. 2021, 33, 7008–7016. [Google Scholar] [CrossRef]
- Nguyen, D.; Tao, L.; Li, Y. Integration of machine learning and coarse-grained molecular simulations for polymer materials: Physical understandings and molecular design. Front. Chem. 2022, 9, 820417. [Google Scholar] [CrossRef]
- Ma, R.; Zhang, H.; Xu, J.; Sun, L.; Hayashi, Y.; Yoshida, R.; Shiomi, J.; Wang, J.X.; Luo, T. Machine learning-assisted exploration of thermally conductive polymers based on high-throughput molecular dynamics simulations. Mater. Today Phys. 2022, 28, 100850. [Google Scholar] [CrossRef]
- Tao, L.; Varshney, V.; Li, Y. Benchmarking machine learning models for polymer informatics: An example of glass transition temperature. J. Chem. Inf. Model. 2021, 61, 5395–5413. [Google Scholar] [CrossRef]
- Kuenneth, C.; Schertzer, W.; Ramprasad, R. Copolymer informatics with multitask deep neural networks. Macromolecules 2021, 54, 5957–5961. [Google Scholar] [CrossRef]
- Karapiperis, K.; Stainier, L.; Ortiz, M.; Andrade, J.E. Data-driven multiscale modeling in mechanics. J. Mech. Phys. Solids 2021, 147, 104239. [Google Scholar] [CrossRef]
- Fetters, L.; Lohse, D.; Richter, D.; Witten, T.; Zirkel, A. Connection between polymer molecular weight, density, chain dimensions, and melt viscoelastic properties. Macromolecules 1994, 27, 4639–4647. [Google Scholar] [CrossRef]
- Xian, W.; Liu, C.H.; Kangarlou, B.; Chang, S.Y.; Wu, C.; Cao, Y.; Sun, L.; Ma, A.W.; Nieh, M.P.; Maiti, A.; et al. Effect of Diphenyl Content on Viscoelasticity of Poly (dimethyl-co-diphenyl) siloxane Melt and Network. ACS Appl. Polym. Mater. 2023, 5, 1915–1925. [Google Scholar] [CrossRef]
- Bock, F.E.; Aydin, R.C.; Cyron, C.J.; Huber, N.; Kalidindi, S.R.; Klusemann, B. A review of the application of machine learning and data mining approaches in continuum materials mechanics. Front. Mater. 2019, 6, 110. [Google Scholar] [CrossRef]
- Ghaboussi, J.; Garrett, J., Jr.; Wu, X. Knowledge-based modeling of material behavior with neural networks. J. Eng. Mech. 1991, 117, 132–153. [Google Scholar] [CrossRef]
- Hashash, Y.; Jung, S.; Ghaboussi, J. Numerical implementation of a neural network based material model in finite element analysis. Int. J. Numer. Methods Eng. 2004, 59, 989–1005. [Google Scholar] [CrossRef]
- Chung, I.; Im, S.; Cho, M. A neural network constitutive model for hyperelasticity based on molecular dynamics simulations. Int. J. Numer. Methods Eng. 2021, 122, 5–24. [Google Scholar] [CrossRef]
- Liang, G.; Chandrashekhara, K. Neural network based constitutive model for elastomeric foams. Eng. Struct. 2008, 30, 2002–2011. [Google Scholar] [CrossRef]
- Yang, H.; Guo, X.; Tang, S.; Liu, W.K. Derivation of heterogeneous material laws via data-driven principal component expansions. Comput. Mech. 2019, 64, 365–379. [Google Scholar] [CrossRef]
- Li, L.; Chen, C. Equilibrium-based convolution neural networks for constitutive modeling of hyperelastic materials. J. Mech. Phys. Solids 2022, 164, 104931. [Google Scholar] [CrossRef]
- Peirlinck, M.; Linka, K.; Hurtado, J.A.; Kuhl, E. On automated model discovery and a universal material subroutine for hyperelastic materials. Comput. Methods Appl. Mech. Eng. 2024, 418, 116534. [Google Scholar] [CrossRef]
- Kim, D.W.; Go, M.S.; Lim, J.H.; Lee, S. Data-driven stress and strain curves of the unidirectional composites by deep neural networks with principal component analysis and selective-data augmentation. Compos. Struct. 2023, 313, 116902. [Google Scholar] [CrossRef]
- Wang, J.; Zhu, B.; Hui, C.Y.; Zehnder, A.T. Determination of material parameters in constitutive models using adaptive neural network machine learning. J. Mech. Phys. Solids 2023, 177, 105324. [Google Scholar] [CrossRef]
- Bhattacharjee, S.; Matouš, K. A nonlinear manifold-based reduced order model for multiscale analysis of heterogeneous hyperelastic materials. J. Comput. Phys. 2016, 313, 635–653. [Google Scholar] [CrossRef]
- Nguyen-Thanh, V.M.; Zhuang, X.; Rabczuk, T. A deep energy method for finite deformation hyperelasticity. Eur. J. Mech.-A/Solids 2020, 80, 103874. [Google Scholar] [CrossRef]
- Abueidda, D.W.; Koric, S.; Al-Rub, R.A.; Parrott, C.M.; James, K.A.; Sobh, N.A. A deep learning energy method for hyperelasticity and viscoelasticity. Eur. J. Mech.-A/Solids 2022, 95, 104639. [Google Scholar] [CrossRef]
- Wang, Z.; Xian, W.; Li, Y.; Xu, H. Embedding physical knowledge in deep neural networks for predicting the phonon dispersion curves of cellular metamaterials. Comput. Mech. 2023, 72, 221–239. [Google Scholar] [CrossRef]
- Linden, L.; Klein, D.K.; Kalina, K.A.; Brummund, J.; Weeger, O.; Kästner, M. Neural networks meet hyperelasticity: A guide to enforcing physics. J. Mech. Phys. Solids 2023, 179, 105363. [Google Scholar] [CrossRef]
- Tang, S.; Zhang, G.; Yang, H.; Li, Y.; Liu, W.K.; Guo, X. MAP123: A data-driven approach to use 1D data for 3D nonlinear elastic materials modeling. Comput. Methods Appl. Mech. Eng. 2019, 357, 112587. [Google Scholar] [CrossRef]
- Tang, S.; Li, Y.; Qiu, H.; Yang, H.; Saha, S.; Mojumder, S.; Liu, W.K.; Guo, X. MAP123-EP: A mechanistic-based data-driven approach for numerical elastoplastic analysis. Comput. Methods Appl. Mech. Eng. 2020, 364, 112955. [Google Scholar] [CrossRef]
- Tang, S.; Yang, H.; Qiu, H.; Fleming, M.; Liu, W.K.; Guo, X. MAP123-EPF: A mechanistic-based data-driven approach for numerical elastoplastic modeling at finite strain. Comput. Methods Appl. Mech. Eng. 2021, 373, 113484. [Google Scholar] [CrossRef]
- Flaschel, M.; Kumar, S.; De Lorenzis, L. Unsupervised discovery of interpretable hyperelastic constitutive laws. Comput. Methods Appl. Mech. Eng. 2021, 381, 113852. [Google Scholar] [CrossRef]
- Molnar, C. Interpretable Machine Learning; Lulu. com, 2020. [Google Scholar]
- Linka, K.; Hillgärtner, M.; Abdolazizi, K.P.; Aydin, R.C.; Itskov, M.; Cyron, C.J. Constitutive artificial neural networks: A fast and general approach to predictive data-driven constitutive modeling by deep learning. J. Comput. Phys. 2021, 429, 110010. [Google Scholar] [CrossRef]
- Linka, K.; Kuhl, E. A new family of Constitutive Artificial Neural Networks towards automated model discovery. Comput. Methods Appl. Mech. Eng. 2023, 403, 115731. [Google Scholar] [CrossRef]
- Taç, V.; Linka, K.; Sahli-Costabal, F.; Kuhl, E.; Tepole, A.B. Benchmarking physics-informed frameworks for data-driven hyperelasticity. Comput. Mech. 2023, 73, 49–65. [Google Scholar] [CrossRef]
- Abdusalamov, R.; Hillgärtner, M.; Itskov, M. Automatic generation of interpretable hyperelastic material models by symbolic regression. Int. J. Numer. Methods Eng. 2023, 124, 2093–2104. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xian, W.; Zhan, Y.-S.; Maiti, A.; Saab, A.P.; Li, Y. Filled Elastomers: Mechanistic and Physics-Driven Modeling and Applications as Smart Materials. Polymers 2024, 16, 1387. https://doi.org/10.3390/polym16101387
Xian W, Zhan Y-S, Maiti A, Saab AP, Li Y. Filled Elastomers: Mechanistic and Physics-Driven Modeling and Applications as Smart Materials. Polymers. 2024; 16(10):1387. https://doi.org/10.3390/polym16101387
Chicago/Turabian StyleXian, Weikang, You-Shu Zhan, Amitesh Maiti, Andrew P. Saab, and Ying Li. 2024. "Filled Elastomers: Mechanistic and Physics-Driven Modeling and Applications as Smart Materials" Polymers 16, no. 10: 1387. https://doi.org/10.3390/polym16101387
APA StyleXian, W., Zhan, Y.-S., Maiti, A., Saab, A. P., & Li, Y. (2024). Filled Elastomers: Mechanistic and Physics-Driven Modeling and Applications as Smart Materials. Polymers, 16(10), 1387. https://doi.org/10.3390/polym16101387







