Utilization of Prepared Nanocellulose as a Biopolymer for Adsorption Kinetics of Cobalt Ions from Wastewater
Abstract
1. Introduction
- The metal diffuses from the solution onto the outer surface of the sorbent particle;
- The metal diffuses through the solution into the pores of the adsorption sites;
- Metal ions bond with sorbent particles in a chemical reaction.
2. Experimental Work
2.1. Nanocellulose Biopolymer as an Adsorbent
2.2. Characterization of Nanocellulose Biopolymer as an Adsorbent
2.2.1. Transmission Electron Microscopy (TEM)
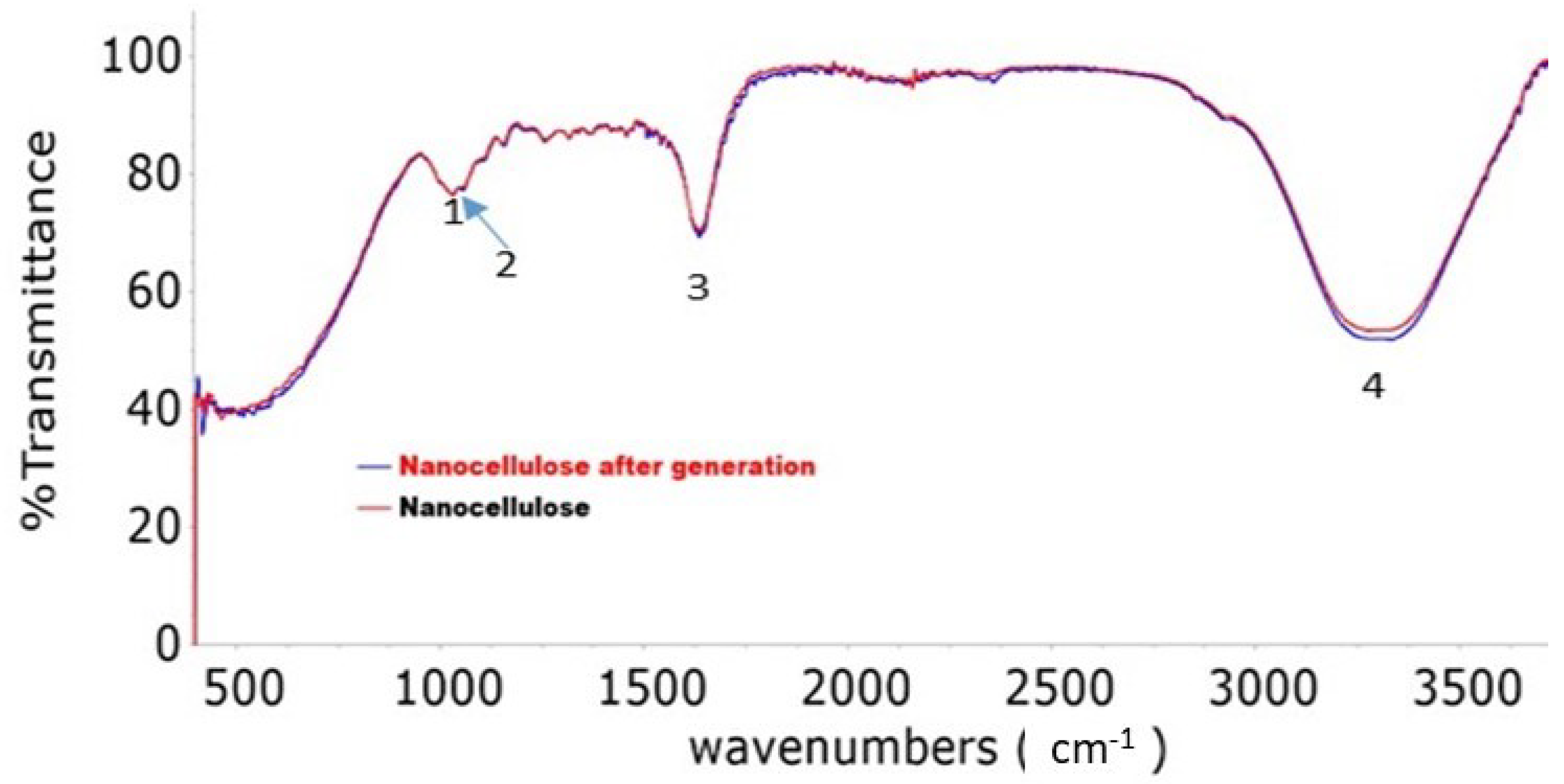
2.2.2. Fourier Transform Infrared Spectroscopy (FT-IRS)
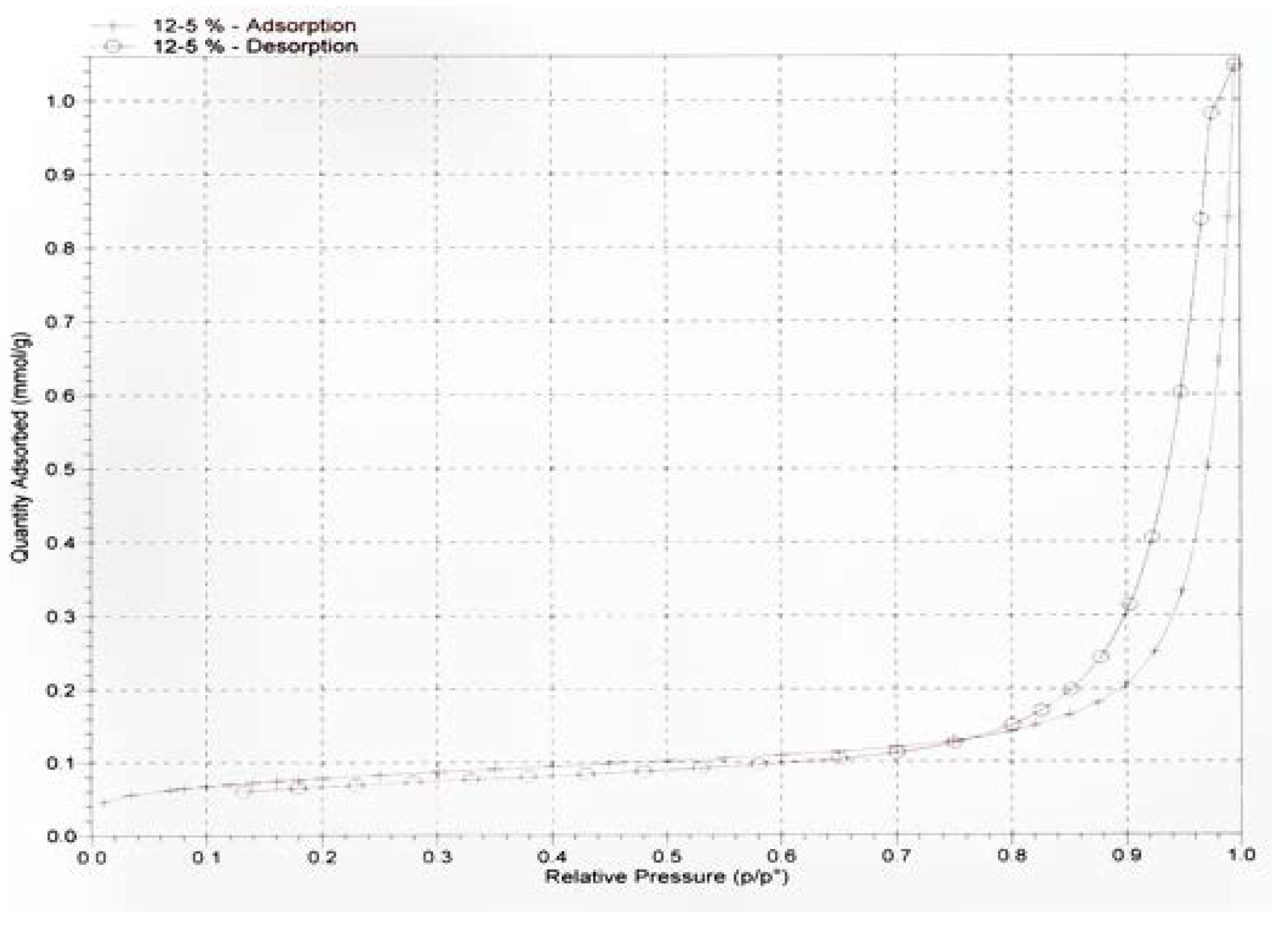
2.2.3. BET Surface Area
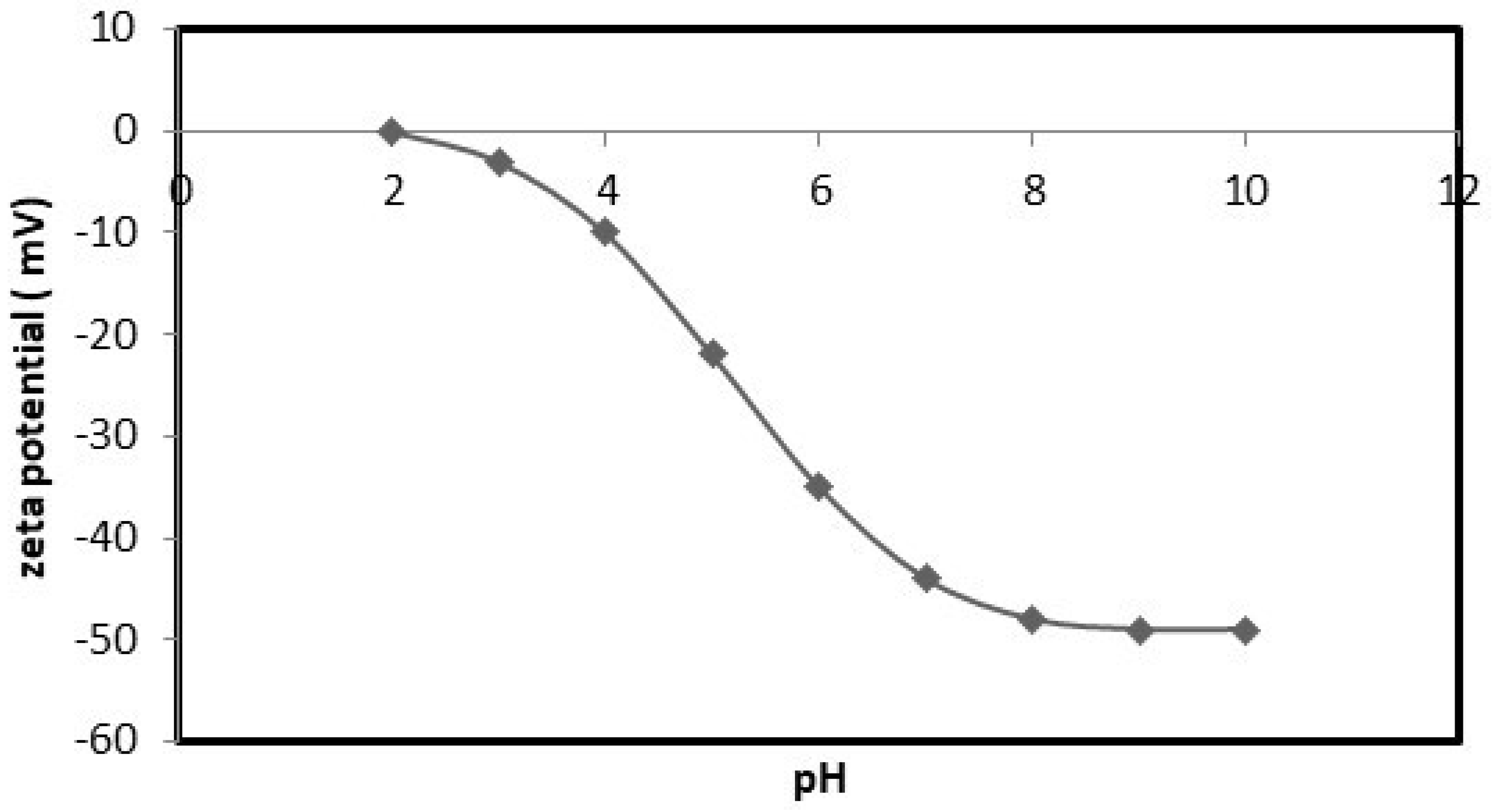
2.2.4. Zeta Potential
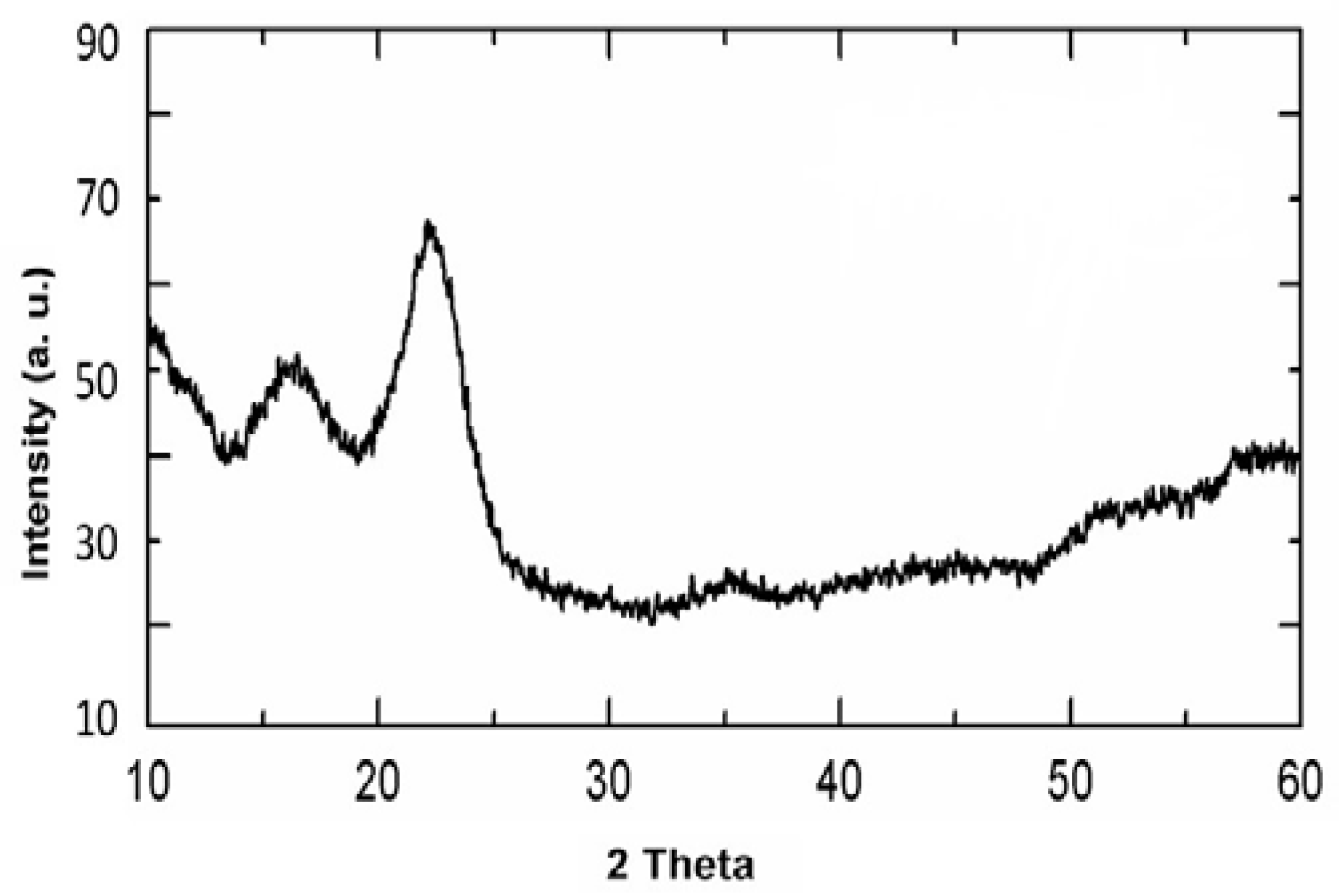
2.2.5. X-ray Diffraction
2.3. Experimental Adsorption Equilibrium Isotherm
2.4. Kinetic Experiments
3. Adsorption Equilibrium Isotherm Models
3.1. Langmuir Isotherm Model
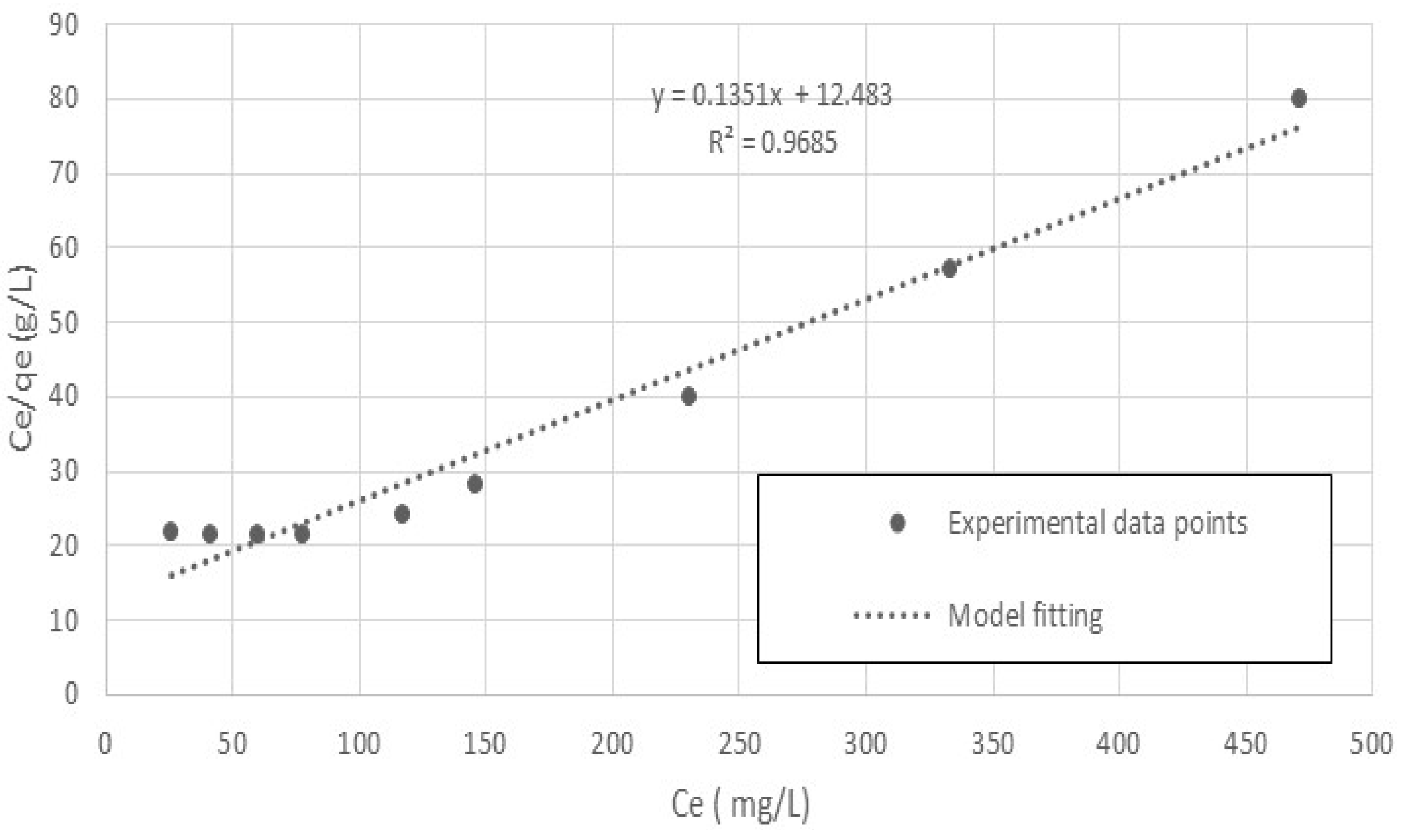
3.2. Freundlich Isotherm Model
4. Kinetic Models
4.1. Describing the Batch Adsorption Process Using Reaction Models
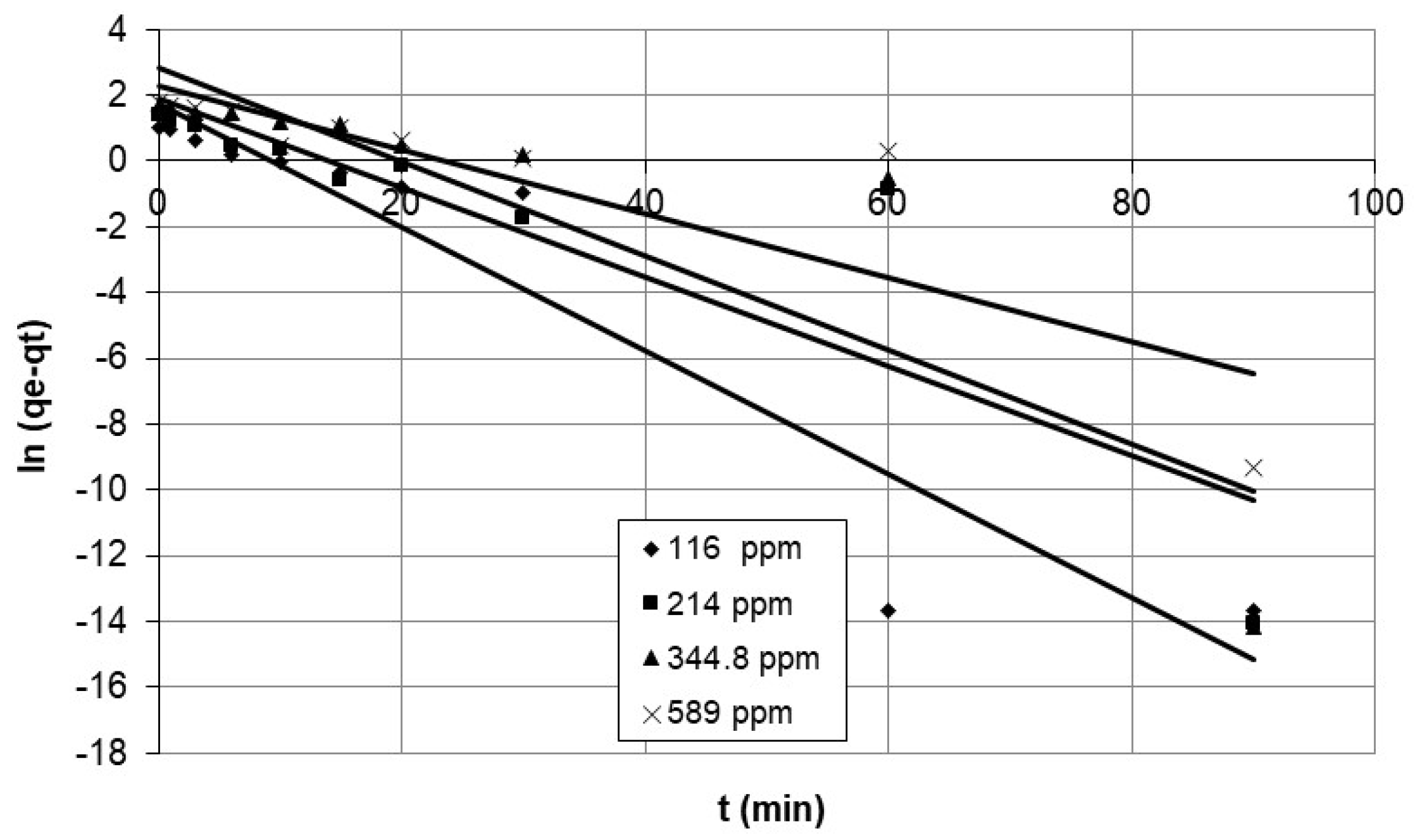
4.1.1. Pseudo-First-Order Model
4.1.2. Pseudo-Second-Order Model
4.1.3. Elovich Model
4.2. Describing the Batch Adsorption Process Using an Intraparticle Diffusion Model
- The initial cobalt concentration is evenly distributed in the total solution. In contrast, the cobalt concentration on the outer surface is zero at the beginning of the adsorption process (t = 0);
- There is a local equilibrium between the cobalt concentration in the adsorbent pores and the cobalt adsorption on the inner pore-surface sites. Therefore, the linear-equilibrium isotherm equation can be applied as an adsorption equilibrium equation;
- Compared to the internal resistance to mass transfer, the external mass-transfer resistance’s effect is negligible;
- Adsorbent particles take the shape of spherical particles;
- The diffusion coefficient is constant and cobalt diffusion occurs only along the radial axis of a spherical particle.
5. Results and Discussions
5.1. Nanocellulose as Biopolymer Characterizations
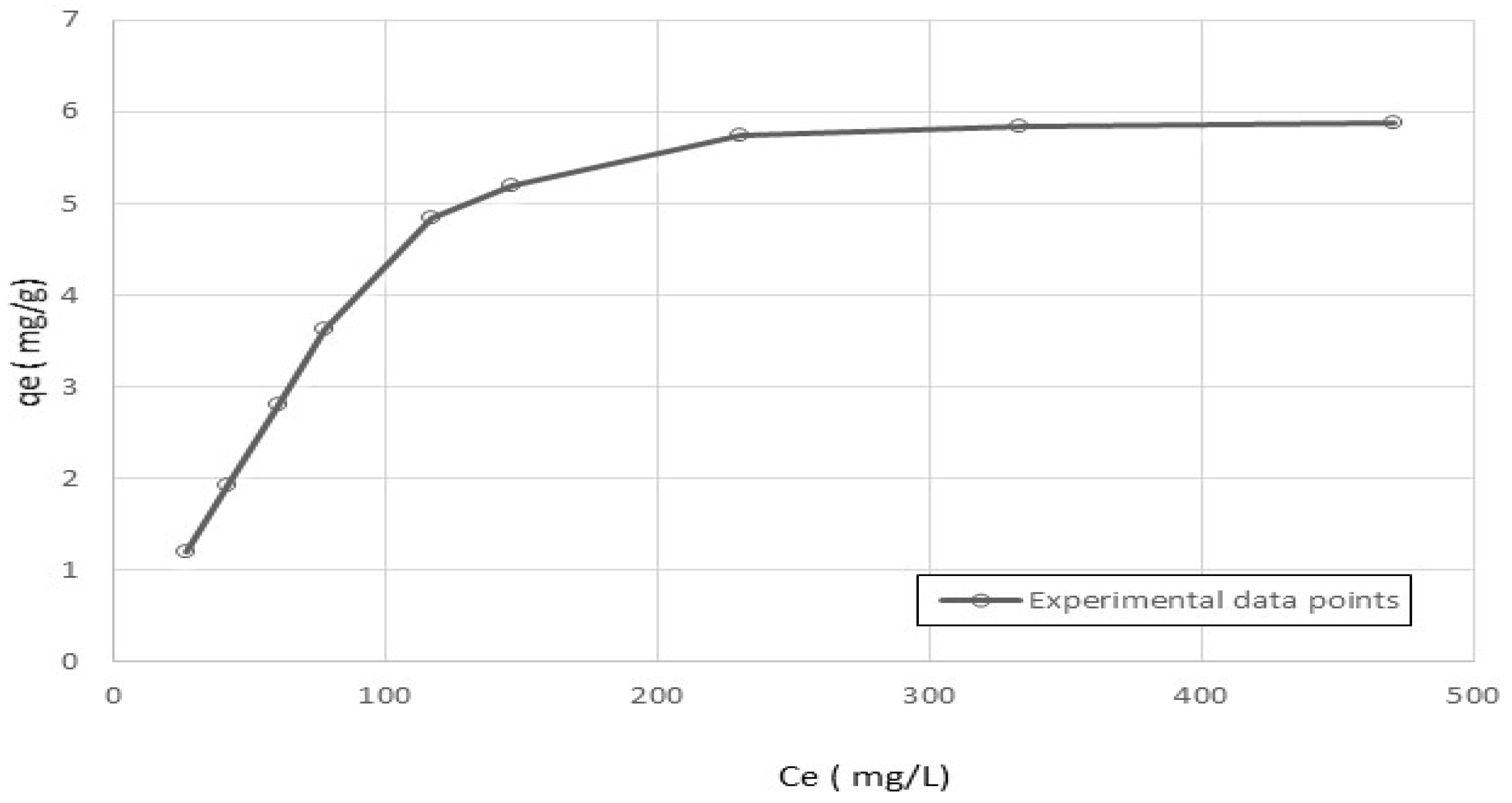
5.2. Adsorption-Equilibrium Isotherm
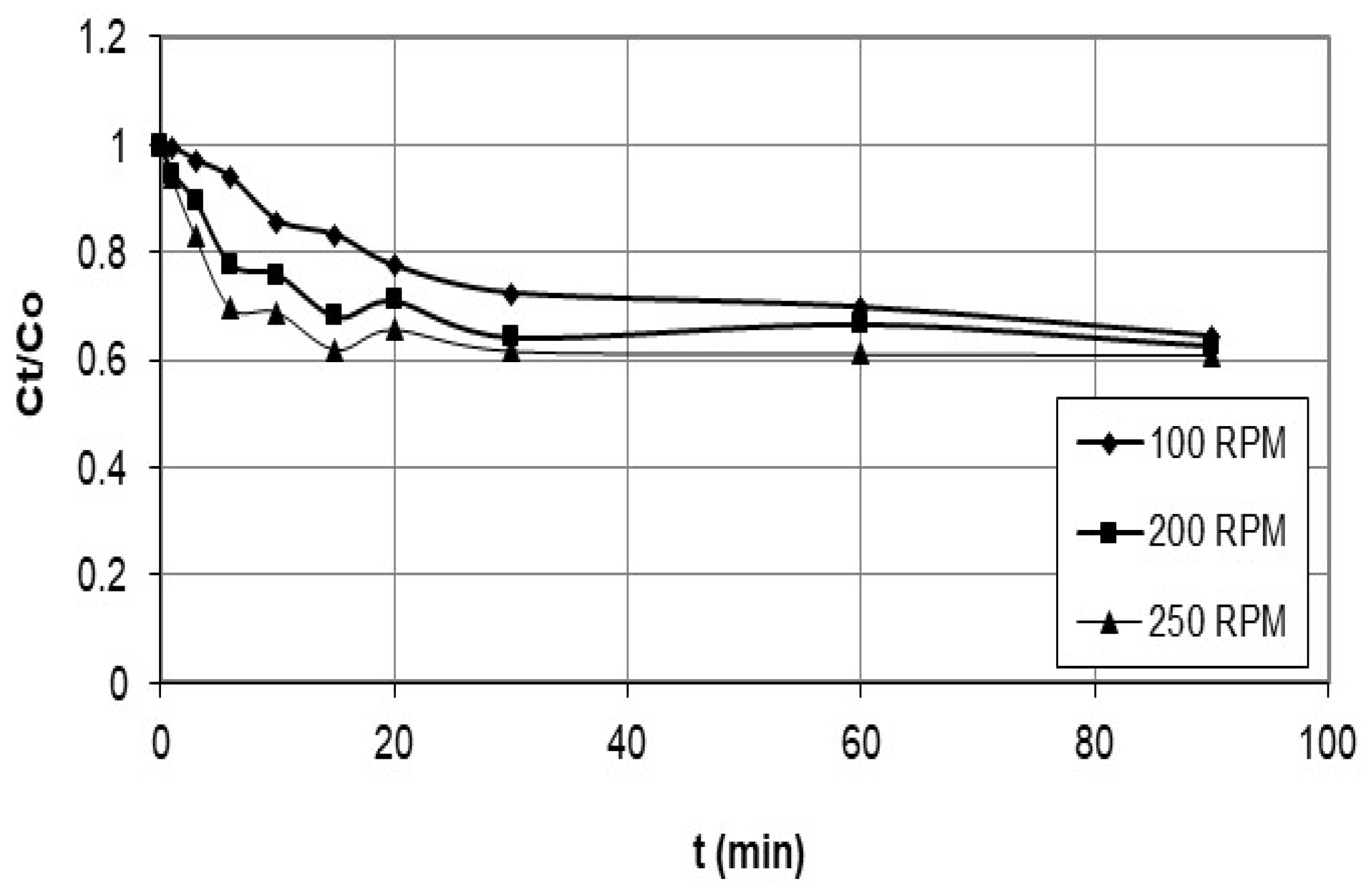
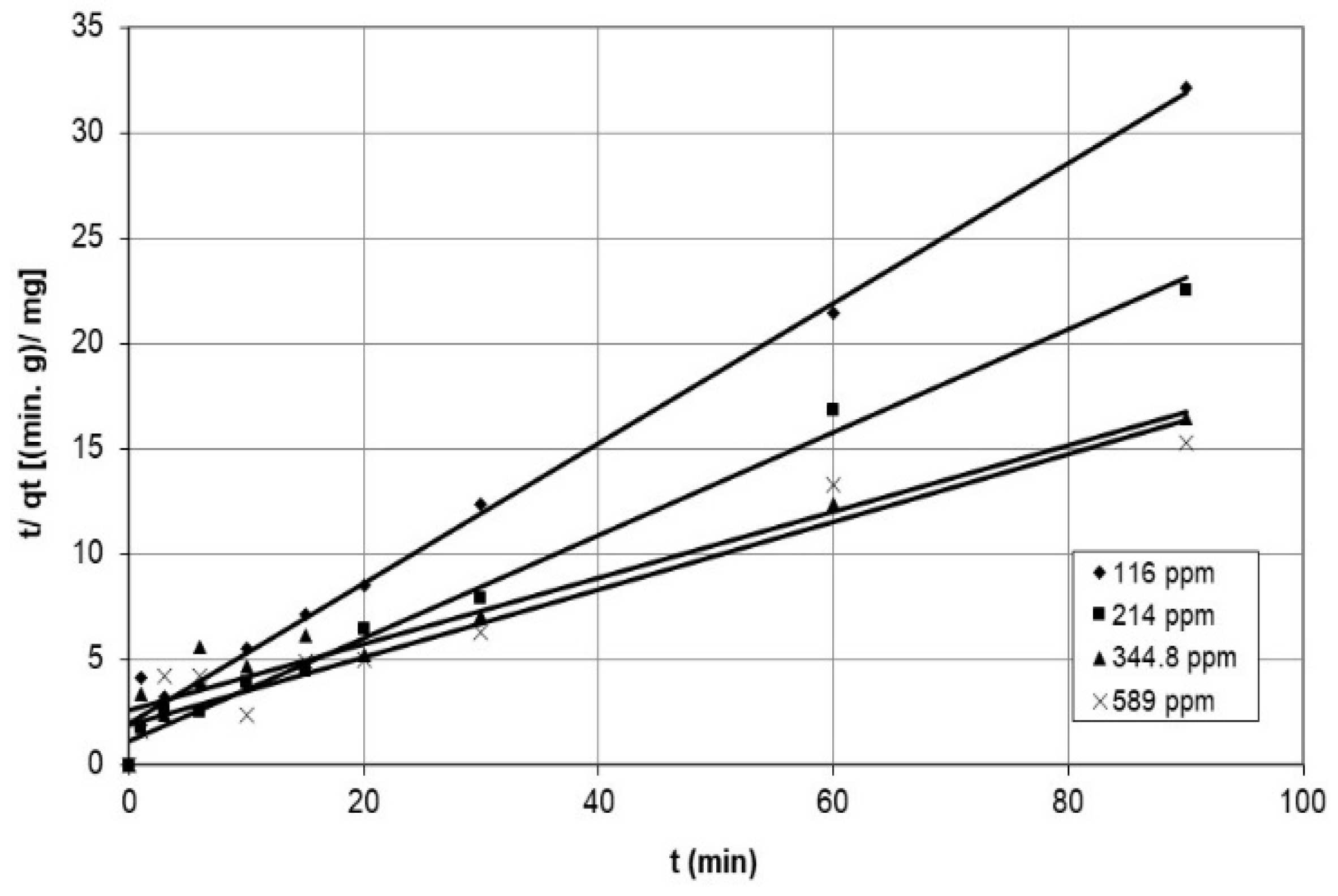
5.3. Kinetic Studies
5.3.1. Investigation of the Mechanism of Adsorption Using Experimental Kinetic Data
Discussion of the Effect of the Chemical Reaction as a Rate Controlling Step Using Reaction Models to Describe the Chemical-Reaction Mechanism
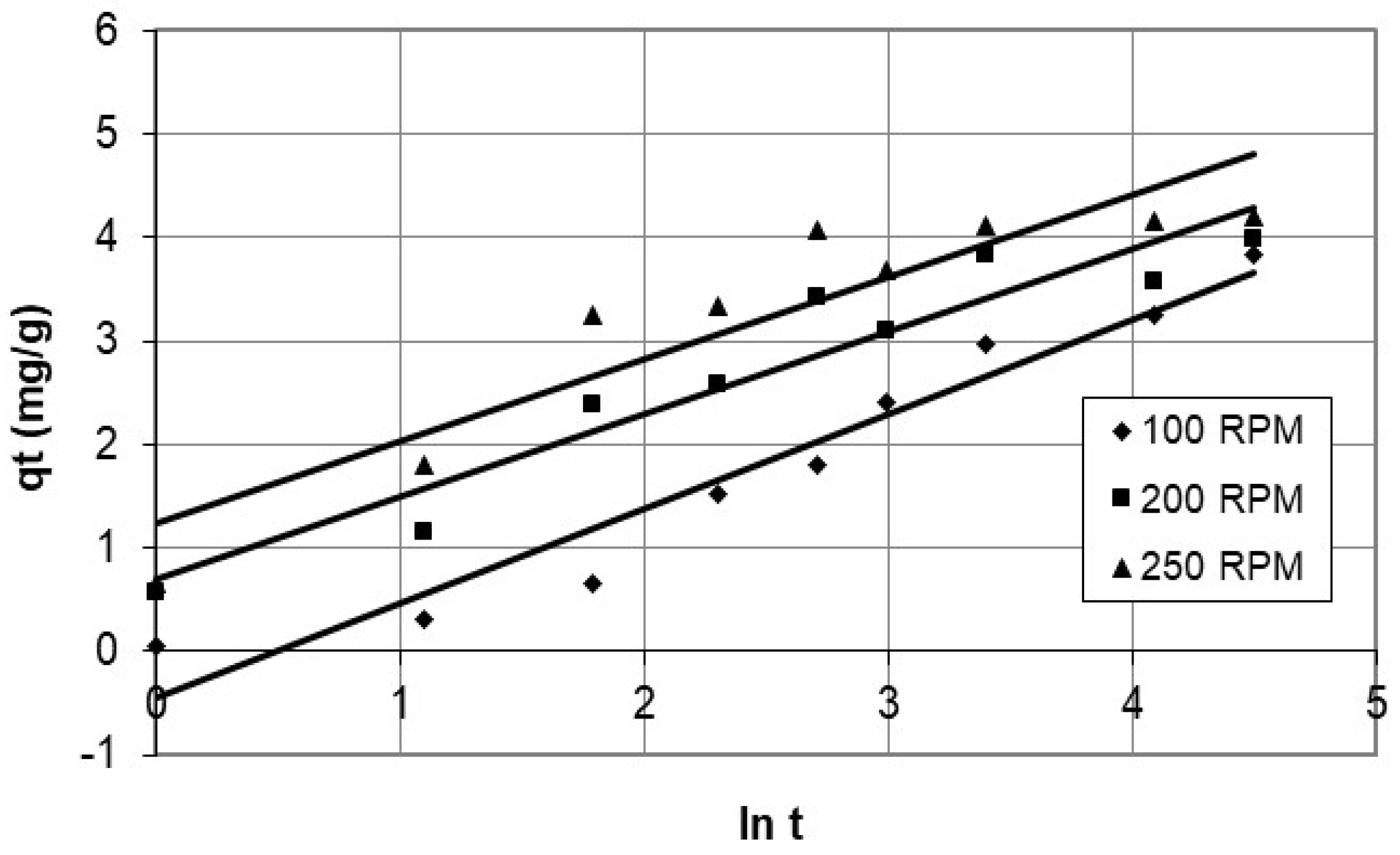
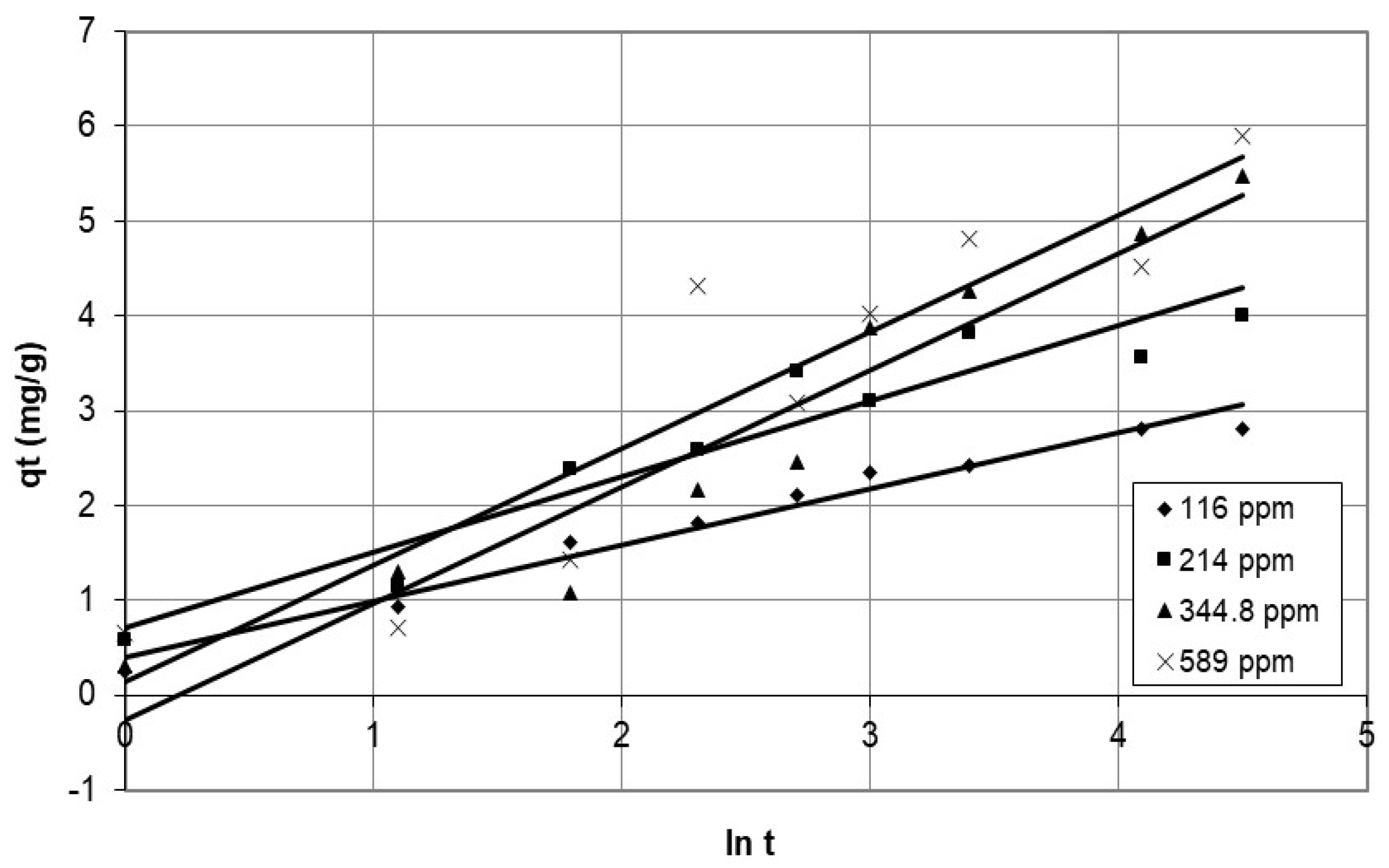
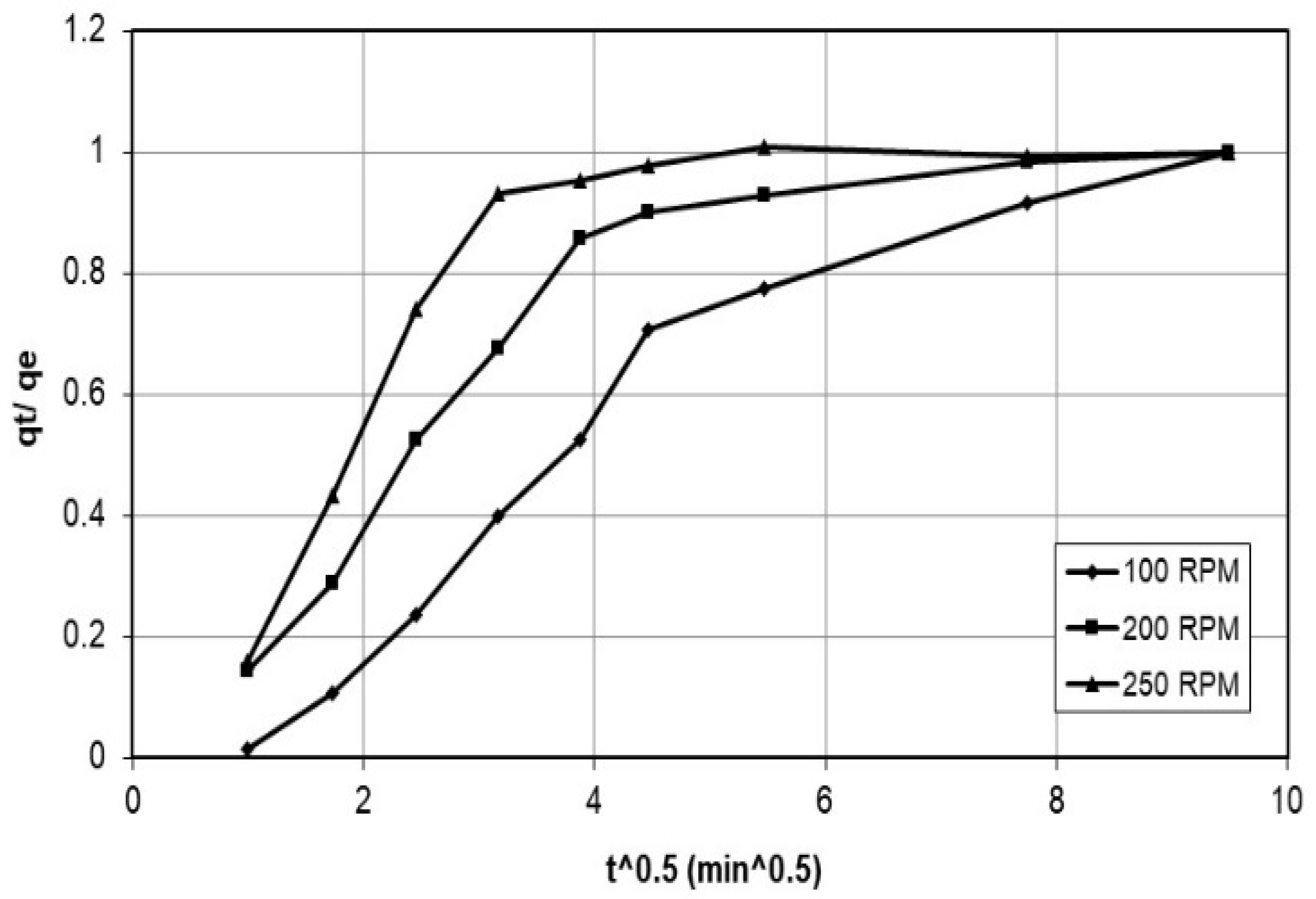
Discussion of the Effect of Mass Transfer as a Rate-Controlling Step Using Intraparticle Diffusion Model to Describe Diffusion Mechanism
Comparison between the Kinetic Models
6. Comparison of Waste Palm Leaves-Derived Nanocellulose as an Adsorbent with Literature-Reported Adsorbents
7. Assessing the Stability of Nanocellulose Composite for Cobalt Ion Removal
8. The Efficiency of Nanocellulose as an Adsorbent for Real Industrial Wastewater Treatment: A Study on Heavy Metal Removal
9. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, R.; Deng, L.; Fan, X.; Li, K.; Lu, H.; Li, W. Removal of heavy metal ion cobalt (II) from wastewater via adsorption method using microcrystalline cellulose–magnesium hydroxide. Int. J. Biol. Macromol. 2021, 189, 607–617. [Google Scholar] [CrossRef]
- Varghese, A.G.; Paul, S.A.; Latha, M.S. Remediation of heavy metals and dyes from wastewater using cellulose-based adsorbents. Environ. Chem. Lett. 2018, 17, 867–877. [Google Scholar] [CrossRef]
- Zhang, W.; Zhao, J.; Ao, C.; Lu, C. Nanocellulose Materials in Water Treatment. Video Proc. Adv. Mater. 2021, 2, 210185. [Google Scholar] [CrossRef]
- Khalilzadeh, M.A.; Hosseini, S.E.; Rad, A.S.; Venditti, R.A. Synthesis of grafted nano-fibrillated cellulose-based hydrogel and study of its thermodynamic, kinetic, and electronic properties. J. Agric. Food Chem. 2020, 68, 8710–8719. [Google Scholar] [CrossRef]
- Ogwang, G.; Olupot, P.; Kasedde, H.; Menya, E.; Storz, H.; Kiros, Y. Experimental evaluation of rice husk ash for applications in geopolymer mortars. J. Bioresour. Bioprod. 2021, 6, 160–167. [Google Scholar] [CrossRef]
- Obey, G.; Adelaide, M.; Ramaraj, R. Biochar derived from non-customized matamba fruit shell as an adsorbent for wastewater treatment. J. Bioresour. Bioprod. 2022, 7, 109–115. [Google Scholar] [CrossRef]
- Hasan, I.; El-Din, S.; AbdElRaady, A. Peppermint-Mediated Green Synthesis of Nano ZrO2 and Its Adsorptive Removal of Cobalt from Water. Inorganics 2022, 10, 257. [Google Scholar] [CrossRef]
- Gad, H.; Omar, H.; Aziz, M.; Hassan, M.; Khalil, M. Treatment of Rice Husk Ash to Improve Adsorption Capacity of Cobalt from Aqueous Solution. Asian J. Chem. 2016, 28, 385–394. [Google Scholar] [CrossRef]
- Swelam, A.; Salem, A.; Ayman, A.; Farghly, A. Kinetic and Thermodynamic Sorption Study of Cobalt Removal from Water Solution with Magnetic Nano-Hydroxyapatite. Al Azhar Bull. Sci. 2018, 29, 45–58. [Google Scholar]
- Essaadaoui, Y.; Lebkiri, A.; Rifi, E.; Kadiri, L.; Ouass, A. Adsorption of cobalt from aqueous solutions onto Bark of Eucalyptus. Mediterr. J. Chem. 2018, 7, 145–155. [Google Scholar] [CrossRef]
- Gomaa, H.; Hussein, M.A.; Motawea, M.M.; Aboraia, A.M.; Cheira, M.F.; Alotaibi, M.T.; El-Bahy, S.M.; Ali, H.M. A hybrid mesoporous CuO@barley straw-derived SiO2 nanocomposite for adsorption and photocatalytic degradation of methylene blue from real wastewater. Colloids Surf. A Physicochem. Eng. Asp. 2022, 644, 128811. [Google Scholar] [CrossRef]
- Gomaa, H.; Sayed, A.; Mahross, M.; Mohamed, A.; Ismail, M.; Othman, A.; Jiansheng, B.; El-Bahy, M. A hybrid spongy-like porous carbon-based on azopyrazole-benzenesulfonamide derivative for highly selective Fe3+-adsorption from real water samples. Microporous Mesoporous Mater. 2022, 330, 111578. [Google Scholar] [CrossRef]
- Gomaa, H.; El-Monaem, E.; Eltaweil, A.; Omer, A. Efcient removal of noxious methylene blue and crystal violet dyes at neutral conditions by reusable montmorillonite/NiFe2O4@amine-functionalized chitosan composite. Sci. Rep. 2022, 12, 15499. [Google Scholar] [CrossRef] [PubMed]
- Kassem, K.; Hussein, M.; Motawea, M.; Alrowaili, Z.; Ezzeldien, M. Design of mesoporous ZnO @ silica fume-derived SiO2 nanocomposite as photocatalyst for efficient crystal violet removal: Effective route to recycle industrial waste. J. Clean. Prod. 2021, 326, 129416. [Google Scholar] [CrossRef]
- Salama, R.; El-Hakam, S.; Samra, S.; El-Dafrawy, S.; Ibrahim, A.; Ahmed, A. Synthesis, characterization of titania supported on mesoporous MCM-41 and its application for the removal of methylene blue. Delta Univ. Sci. J. 2022, 5, 321–339. [Google Scholar] [CrossRef]
- Bakry, A.; Alamier, W.; Salama, R.; El-Shall, M.; Awad, F. Remediation of water containing phosphate using ceria nanoparticles decorated partially reduced graphene oxide (CeO2-PRGO) composite. Surf. Interfaces 2022, 31, 102006. [Google Scholar] [CrossRef]
- Ibrahim, A.; Salama, R.; El-Hakam, S.; Khder, A.; Ahmed, A. Synthesis of 12-tungestophosphoric acid supported on Zr/MCM-41 composite with excellent heterogeneous catalyst and promising adsorbent of methylene blue. Colloids Surf. A Physicochem. Eng. Asp. 2021, 631, 127–753. [Google Scholar] [CrossRef]
- Kyzas, G.Z.; Favvas, E.P.; Kostoglou, M.; Mitropoulos, A.C. Effect of agitation on batch adsorption process facilitated by using nanobubbles. Colloids Surf. A Physicochem. Eng. Asp. 2020, 607, 125440. [Google Scholar] [CrossRef]
- Quiton, K.G.N.; Huang, Y.H.; Lu, M.C. Recovery of cobalt and copper from single and co-contaminated simulated electroplating wastewater via carbonate and hydroxide precipitation. Sustain. Environ. Res. 2022, 32, 31. [Google Scholar] [CrossRef]
- Sparks, L. Soil Physical Chemistry; CRC Press: Boca, FL, USA, 2018; 432p. [Google Scholar]
- Do, D. Adsorption Analysis: Equilibria and Kinetics; Imperial College Press: London, UK, 1998; Part 2. [Google Scholar]
- Mckay, G. The adsorption of dyestuffs from aqueous solutions using activated carbon. III. Intraparticle diffusion processes. J. Chem. Technol. Biotechnol. 1983, 33A, 196. [Google Scholar] [CrossRef]
- Mckay, G.; Otterbun, S.; Sweeney, G. The removal of color from effluents using various adsorbents-III. Silica: Rate process. Water Res. 1980, 14, 15–27. [Google Scholar] [CrossRef]
- Crank, J. The Mathematics of Diffusion; Clarendon Press: Oxford, UK, 1965. [Google Scholar]
- Nazir, M.; Wahjoedi, B.; Yussof, A.; Abdullah, M. Eco-friendly extraction and characterization of cellulose from oil palm empty fruit bunches. BioResources 2013, 8, 2161–2172. [Google Scholar] [CrossRef]
- EL-Geundi, M. Adsorption Equilibria of Basic Dyestuffs onto Maize Cob. Adsorp. Sci. Technol. 1990, 7, 114. [Google Scholar] [CrossRef]
- Suresh, S.; Srivastava, V.; Mishra, I. Study of Catechol and Resorcinol Adsorption Mechanism through Granular Activated Carbon Characterization, pH and Kinetic Study. Sep. Sci. Technol. Sep. Sci. Technol. 2011, 46, 1750–1766. [Google Scholar] [CrossRef]
- Demirbaş, E. Adsorption of cobalt (II) ions from aqueous solution onto activated carbon prepared from hazelnut shells. Adsorpt. Sci. Technol. 2003, 21, 951–963. [Google Scholar] [CrossRef]
- Qasem, A.; Mohammed, H.; Lawal, U. Removal of heavy metal ions from wastewater: A comprehensive and critical review. npj Clean Water 2021, 4, 36. [Google Scholar] [CrossRef]
- Samyuktha, S.; Shreya, k.; Sadamanti, A.; Sreedhar, I.; Kale, S. Heavy metal removal from wastewater using nanomaterials, process and engineering aspects. Process Saf. Environ. Prot. 2021, 150, 323–355. [Google Scholar]
- Mckay, G.; Ho, S. Application of kinetic models to the sorption of copper (II) on to peat. Adsorpt. Sci. Technol. 2002, 20, 797. [Google Scholar]
- Averettet, C.; Leenheer, A.; Mcknight, M.; Thorn, A. Humic Substances in the Suwanne River, Georgia: Interactions, Properties, Proposed Structure; US Government Printing Office: Washington, DC, USA, 1994; Series number 87-557. [Google Scholar]
- Leenheer, A.; Brown, K.; McCarthy, P.; Cabaniss, E. Models of Metal Binding Structures in Fulvic Acid from the Suwannee River, Georgia. Environ. Sci. Technol. 1998, 32, 2410. [Google Scholar] [CrossRef]
- Juang, S.; Tseng, L.; Wu, C.; Lee, H. Adsorption behavior of reactive dyes from aquous solutions on chitosan. J. Chem. Technol. Biotechnol. 1997, 70, 391. [Google Scholar] [CrossRef]
- Yadava, P.; Tyagi, S.; Singh, N. Effect of temperature on the removal of lead(II) by adsorption on China clay and wollastonite. J. Chem. Technol. Biotechnol. 1991, 51, 47. [Google Scholar] [CrossRef]
- Juang, S.; Wu, C.; Lee, H. Liquid-phase adsorption of phenol and its derivatives on activated carbon fibers. Sep. Sci. Technol. 1996, 31, 1915. [Google Scholar] [CrossRef]
- Juang, S.; Swei, L. Effect of dye nature on its adsorption from aqueous solutions onto activated carbon. Sep. Sci. Technol. 1996, 31, 2143. [Google Scholar] [CrossRef]
- Stuart, X.; Camp, T. Solution of the fixed bed physical adsorption problem with two significant rate controlling steps. AIChE Symp. Ser. 1973, 69, 33. [Google Scholar]
- Yalçın Altunkaynak, Y.; Canpolat, M.; Yavuz, Ö. Adsorption of cobalt (II) ions from aqueous solution using orange peel waste: Equilibrium, kinetic and thermodynamic studies. J. Iran. Chem. Soc. 2022, 19, 2437–2448. [Google Scholar] [CrossRef]
- Al-Shahrani, A.; Fadi Alakhras, F.; Al-Mazaideh, G. Sorption of Cobalt (II) Ions from Aqueous Solutions Using Chemically Modified Chitosan. Glob. NEST J. 2018, 20, 182–189. [Google Scholar]
- Bernabé, I.; Gómez, J.; Díez, E.; Sáez, P.; Rodríguez, A. Optimization and Adsorption-Based Recovery of Cobalt Using Activated Disordered Mesoporous Carbons. Adv. Mater. Sci. Eng. 2019, 2019, 3430176. [Google Scholar] [CrossRef]
- Oca-Palma, R.; Solache-Ríos, M.; Jiménez-Reye, M.; García-Sánchez, J.; Almazán-Sánchez, P. Adsorption of cobalt by using inorganic components of sediment samples from water bodies. Int. J. Sediment Res. 2021, 36, 524–531. [Google Scholar] [CrossRef]
- Ramos-Vargas, S.; Huirache-Acuña, R.; Rutiaga-Quiñones, J.; Cortés-Martínez, R. Effective lead removal from aqueous solutions using cellulose nanofibers obtained from water hyacinth. Water Supply 2020, 20, 2715–2736. [Google Scholar] [CrossRef]
- Pescode, M.B. Wastewater Treatment and Use in Agriculture; FAO Irrigation and Drainage Paper 47; Food and Agriculture Organization of the United Nations: Rome, Italy, 1992. [Google Scholar]






| Element | Nanocellulose |
|---|---|
| Average pore width (4 V/A by BET), nm | 11.13 |
| Langmuir Isotherm | Freundlich Isotherm | ||||
|---|---|---|---|---|---|
| K (L/g) | b (L/mg) | R2 | kF (L/g) | n (-) | R2 |
| 0.0801 | 0.0108 | 0.97 | 0.282 | 1.8 | 0.85 |
| Adsorbent Parameters | Pseudo-First-Order | Pseudo-Second-Order | Elovich | ||||
|---|---|---|---|---|---|---|---|
| k1 (min−1) | R2 | k2 (g/mg·min) | R2 | œ (mg/g·min) | ß (g/mg) | R2 | |
| Initial conc. (mg/L) | |||||||
| 116 | 0.1873 | 0.898 | 0.0556 | 0.991 | 3.275 | 0.5925 | 0.970 |
| 214 | 0.1357 | 0.763 | 0.0520 | 0.991 | 3.053 | 0.7963 | 0.913 |
| 344.8 | 0.1427 | 0.757 | 0.0096 | 0.934 | 0.659 | 1.228 | 0.924 |
| 589 | 0.0972 | 0.748 | 0.0134 | 0.931 | 0.906 | 1.233 | 0.851 |
| Agitation speed (rpm) | |||||||
| 100 | 0.1376 | 0.747 | 0.0044 | 0.577 | 0.663 | 0.9141 | 0.946 |
| 200 | 0.1357 | 0.763 | 0.0520 | 0.991 | 3.053 | 0.7963 | 0.913 |
| 250 | 0.1446 | 0.877 | 0.0865 | 0.997 | 6.004 | 0.7928 | 0.849 |
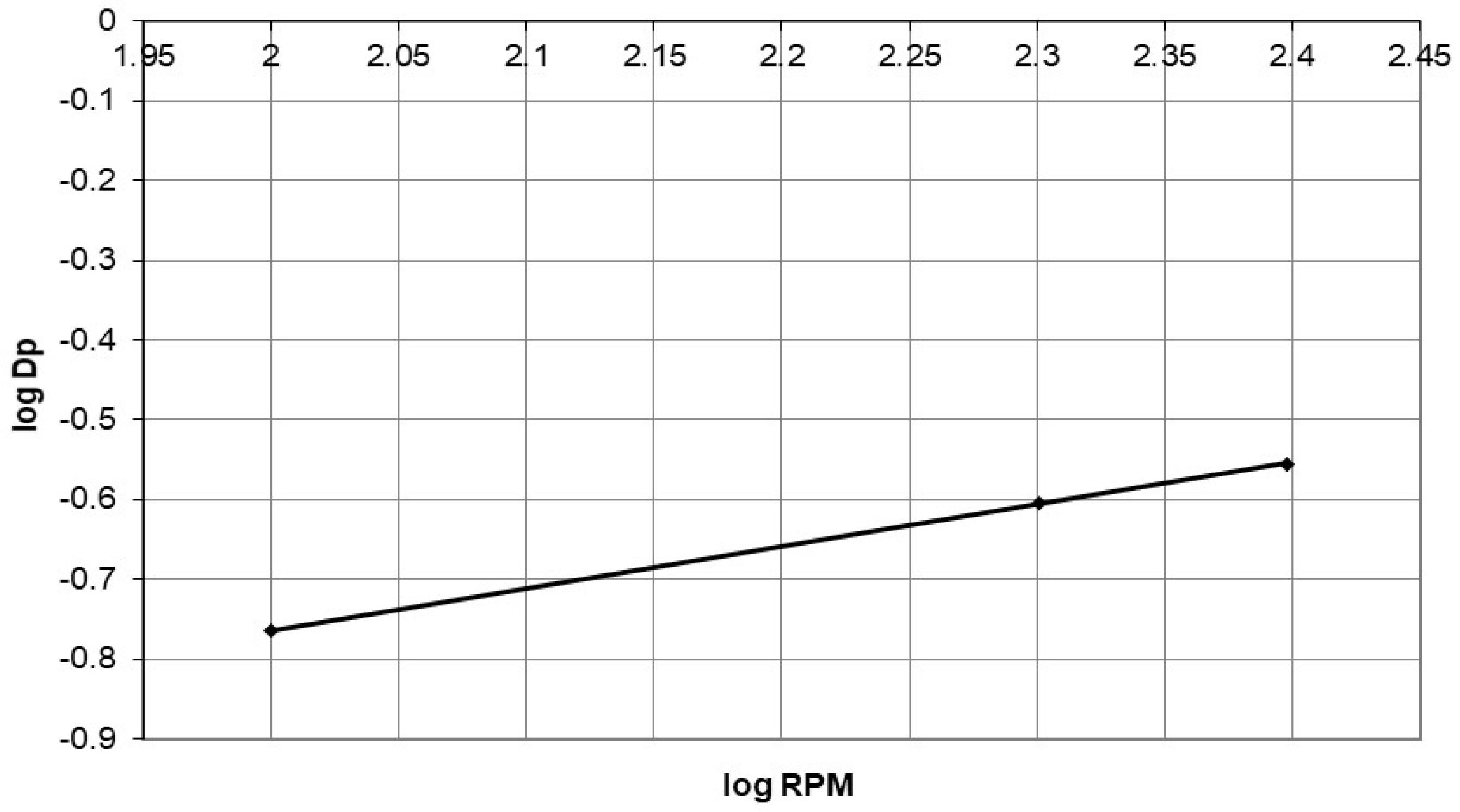
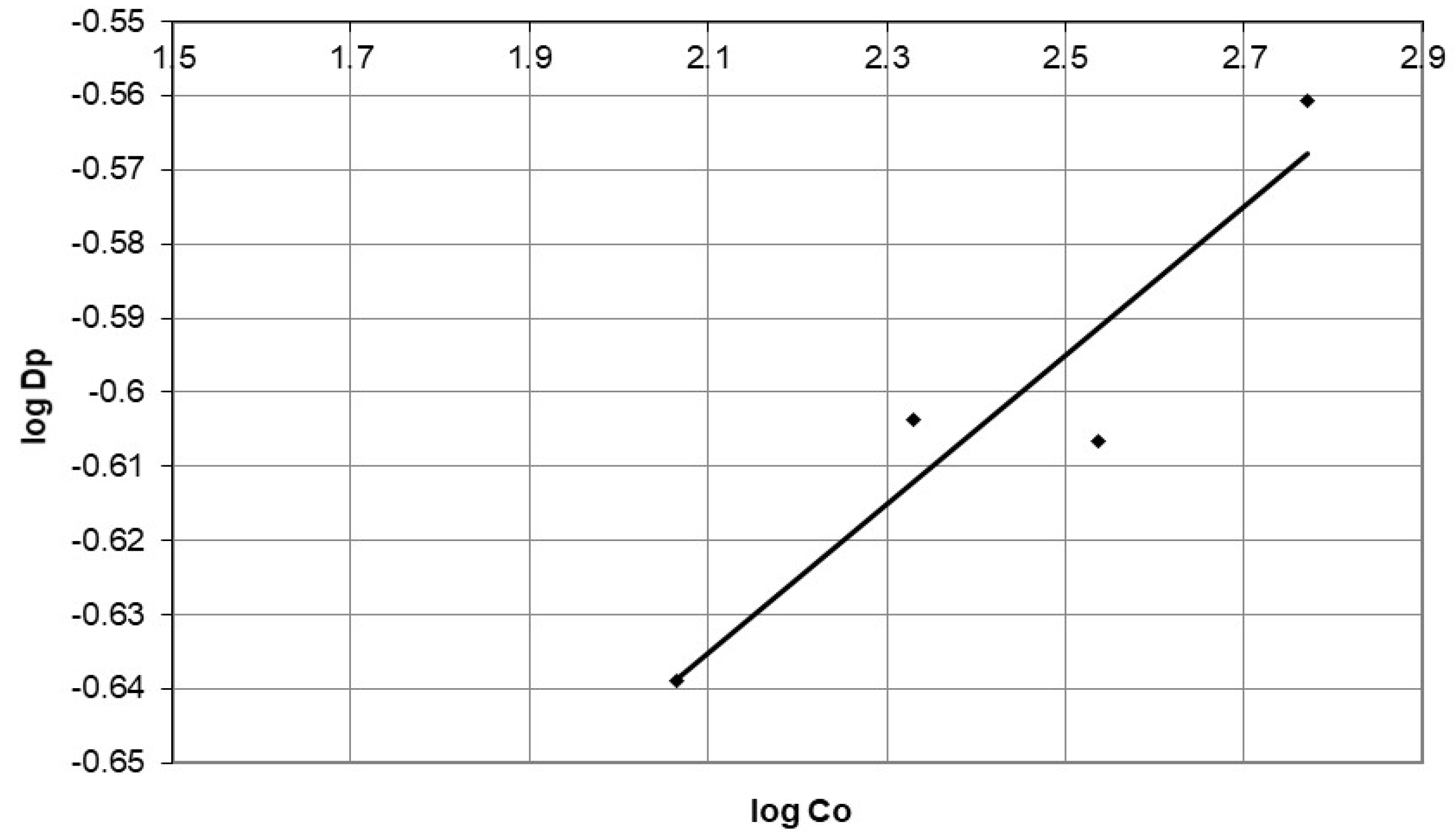
| Initial Concentration (mg/L) | Dp (mg/g·min 0.5) | R2 | |
|---|---|---|---|
| 116 | 0.2297 | 0.946 | |
| 214 | 0.249 | 0.966 | |
| 344.8 | 0.247 | 0.999 | |
| 589 | 0.275 | 0.763 | |
| A | 0.143 | ||
| B | 0.101 | ||
| R2 | 0.86 | ||
| Agitation speed (rpm) | |||
| 100 | 0.172 | 0.955 | |
| 200 | 0.249 | 0.966 | |
| 250 | 0.278 | 0.931 | |
| A | 0.0153 | ||
| B | 0.5263 | ||
| R2 | 0.99 | ||
| Ref | Adsorbent Type | Solution | T (°C) | Capacity (mg/g) |
|---|---|---|---|---|
| [28] | Activated Carbon Prepared from Hazelnut Shells | Cobalt ions | 25 | 3.8 |
| [39] | Orange Peel Waste | Cobalt ions | 25 | 4.25 |
| [40] | Chemically Modified Chitosan | Cobalt ions | 25 | 5.89 |
| [41] | Activated Disordered Mesoporous Carbons | Cobalt ions | 25 | 2 |
| [42] | Sediments From a Dam | Cobalt ions | 25 | 0.93 |
| This work | Nanocellulose | Cobalt ions | 25 | 5.98 |
| Adsorption by Nanocellulose | |||
|---|---|---|---|
| Heavy Metals | Concentration before Treatment (In the Collected Real Wastewater) | Concentration after Treatment | Treatment Efficiency % |
| Co | 3.97 | 0.003 | 99.92 |
| Cu | 3.58 | 0.007 | 99.80 |
| Zn | 0.83 | 0 | 100 |
| Pb | 2.71 | 0.002 | 99.93 |
| As | 3.14 | 0.078 | 97.52 |
| Cd | 2.87 | 0.001 | 99.97 |
| Cr | 1.85 | 0.001 | 99.95 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bin Bandar, K.; Aljlil, S. Utilization of Prepared Nanocellulose as a Biopolymer for Adsorption Kinetics of Cobalt Ions from Wastewater. Polymers 2023, 15, 2143. https://doi.org/10.3390/polym15092143
Bin Bandar K, Aljlil S. Utilization of Prepared Nanocellulose as a Biopolymer for Adsorption Kinetics of Cobalt Ions from Wastewater. Polymers. 2023; 15(9):2143. https://doi.org/10.3390/polym15092143
Chicago/Turabian StyleBin Bandar, Khaled, and Saad Aljlil. 2023. "Utilization of Prepared Nanocellulose as a Biopolymer for Adsorption Kinetics of Cobalt Ions from Wastewater" Polymers 15, no. 9: 2143. https://doi.org/10.3390/polym15092143
APA StyleBin Bandar, K., & Aljlil, S. (2023). Utilization of Prepared Nanocellulose as a Biopolymer for Adsorption Kinetics of Cobalt Ions from Wastewater. Polymers, 15(9), 2143. https://doi.org/10.3390/polym15092143





