Molecular Weight Distribution of Branched Polymers: Comparison between Monte Carlo Simulation and Flory-Stockmayer Theory
Abstract
:1. Introduction
2. The Flory-Stockmayer Theory of Step-Growth Polymers
3. Monte Carlo Model of Polymerization of Branched Polyetherimides (PEIs)
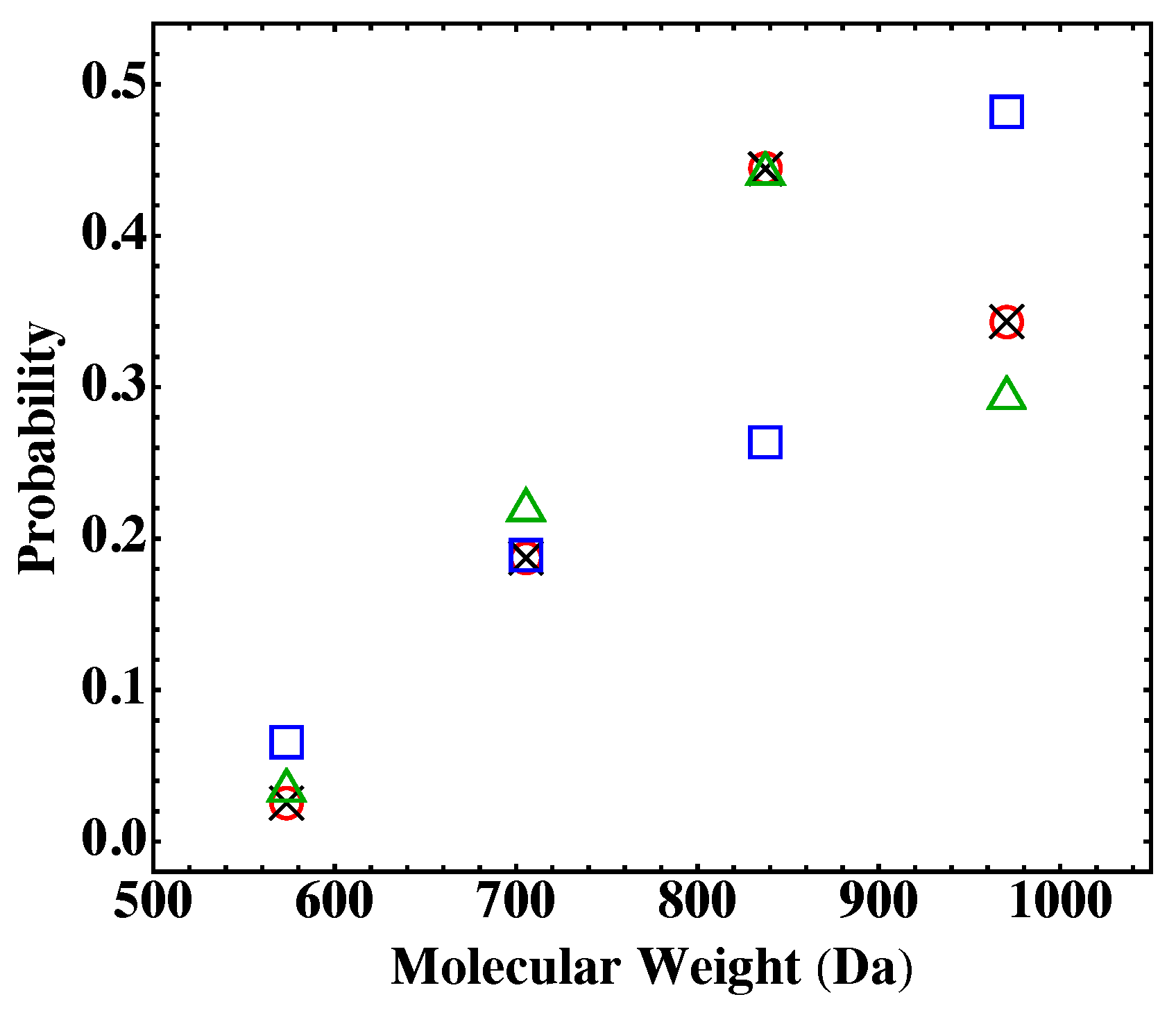
4. Results and Discussion
4.1. Rate Constant k
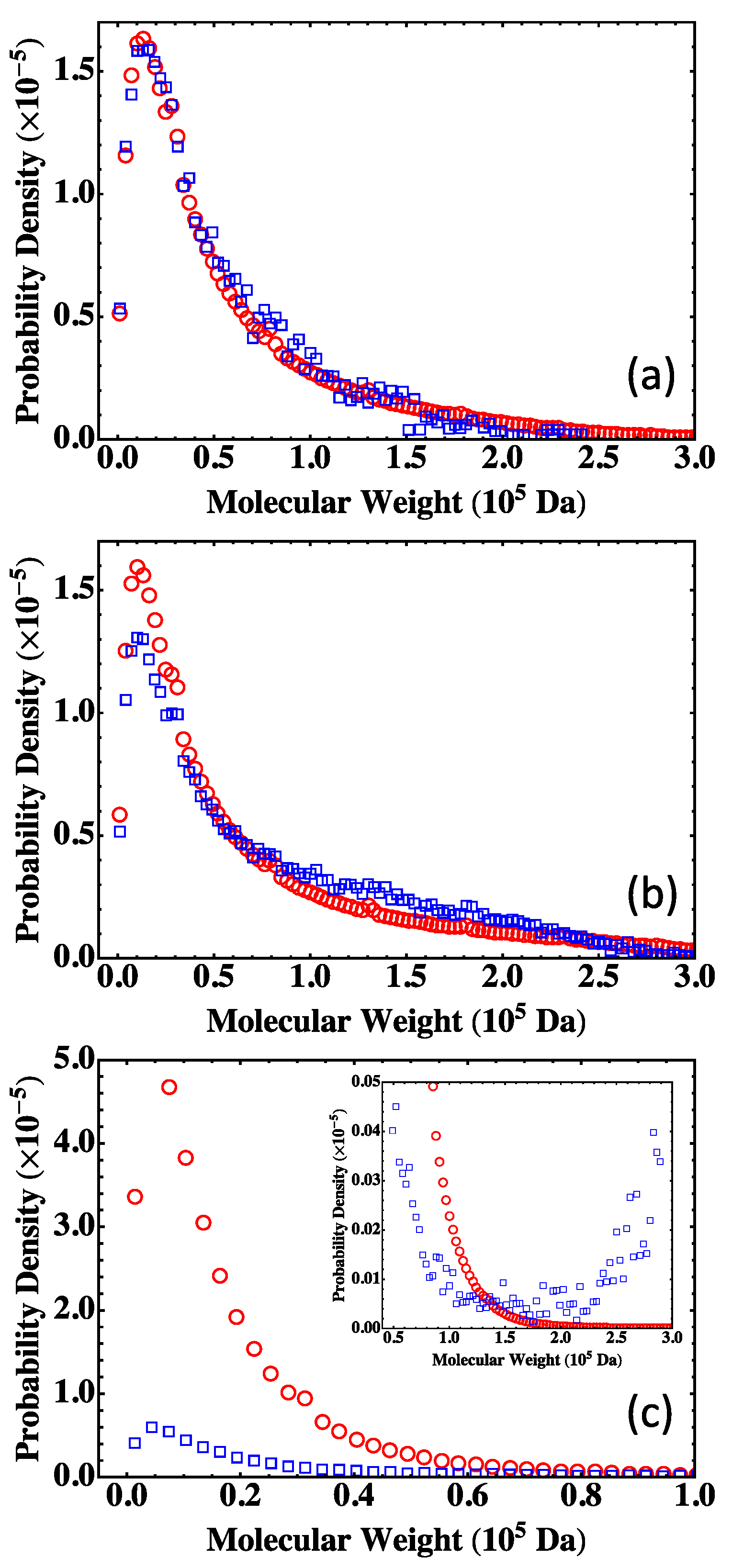
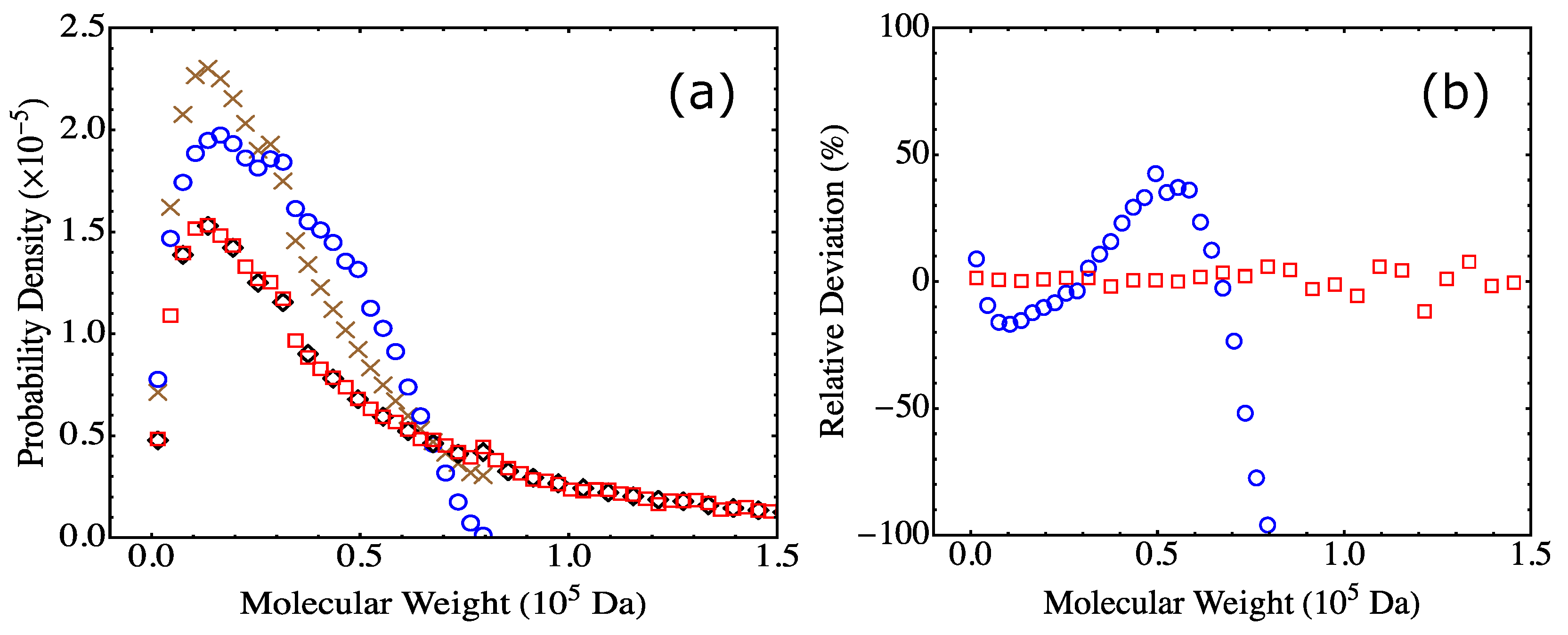
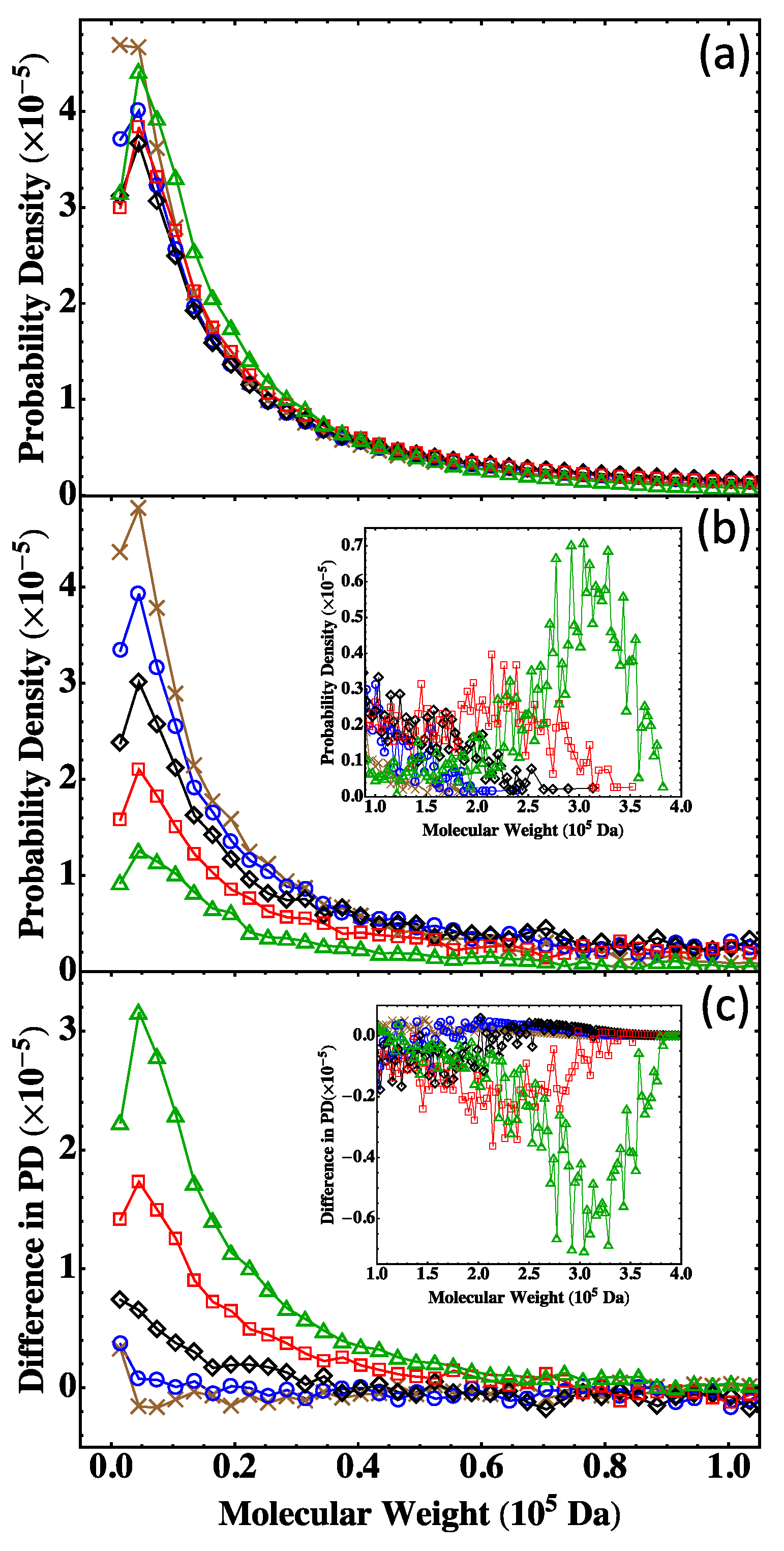
4.2. Fully Reacted Stoichiometric Systems
4.3. Effect of System Size
4.4. Partially Reacted Stoichiometric Systems
4.5. Nonstoichiometric Systems
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MC | Monte Carlo |
| MWD | molecular weight distribution |
| PEI | polyetherimide |
| BPADA | 4,4-bisphenol A dianhydride |
| MPD | m-phenylenediamine |
| PA | phthalic anhydride |
| TAPE | tris[4-(4-aminophenoxy)phenyl] ethane |
| PD | probability density |
| number-average molecular weight | |
| weight-average molecular weight | |
| z-average molecular weight |
References
- Rubinstein, M.; Colby, R.H. Polymer Physics; Oxford University Press: New York, NY, USA, 2003. [Google Scholar]
- Nunes, R.W.; Martin, J.R.; Johnson, J.F. Influence of molecular weight and molecular weight distribution on mechanical properties of polymers. Polym. Eng. Sci. 1982, 22, 205–228. [Google Scholar] [CrossRef]
- Suneel; Buzza, D.M.A.; Groves, D.J.; McLeish, T.C.B.; Parker, D.; Keeney, A.J.; Feast, W.J. Rheology and molecular weight distribution of hyperbranched polymers. Macromolecules 2002, 35, 9605–9612. [Google Scholar] [CrossRef]
- Mead, D.W. Determination of molecular weight distributions of linear flexible polymers from linear viscoelastic material functions. J. Rheol. 1994, 38, 1797. [Google Scholar] [CrossRef]
- Williamson, N.H.; Nydén, M.; Röding, M. The lognormal and gamma distribution models for estimating molecular weight distributions of polymers using PGSE NMR. J. Magn. Reson. 2016, 267, 54–62. [Google Scholar] [CrossRef]
- Nichetti, D.; Manas-Zloczower, I. Viscosity model for polydisperse polymer melts. J. Rheol. 1998, 42, 951–969. [Google Scholar] [CrossRef] [Green Version]
- Read, D.J. From reactor to rheology in industrial polymers. J. Polym. Sci. B Polym. Phys. 2015, 53, 123–141. [Google Scholar] [CrossRef] [Green Version]
- Flory, P.J. Molecular size distribution in three dimensional polymers. I. Gelation. J. Am. Chem. Soc. 1941, 63, 3083–3090. [Google Scholar] [CrossRef]
- Flory, P.J. Molecular size distribution in three dimensional polymers. II. Trifunctional branching units. J. Am. Chem. Soc. 1941, 63, 3091–3096. [Google Scholar] [CrossRef]
- Flory, P.J. Molecular size distribution in three dimensional polymers. III. Tetrafunctional branching units. J. Am. Chem. Soc. 1941, 63, 3096–3100. [Google Scholar] [CrossRef]
- Stockmayer, W.H. Theory of molecular size distribution and gel formation in branched-chain polymers. J. Chem. Phys. 1943, 11, 45–55. [Google Scholar] [CrossRef]
- Stockmayer, W.H. Theory of molecular size distribution and gel formation in branched polymers: II. General cross linking. J. Chem. Phys. 1944, 12, 125–131. [Google Scholar] [CrossRef]
- Stockmayer, W.H. Molecular distribution in condensation polymers. J. Polym. Sci. 1952, IX, 69–71. [Google Scholar] [CrossRef]
- Peebles, L.H. Molecular Weight Distributions in Polymers; Wiley-Interscience: New York, NY, USA, 1971. [Google Scholar]
- Matsumoto, A. Free-radical crosslinking polymerization and copolymerization of multivinyl compounds. In Synthesis and Photosynthesis; Springer: Berlin/Heidelberg, Germany, 1995; pp. 41–80. [Google Scholar] [CrossRef]
- Matsumoto, A.; Kitaguchi, Y.; Sonoda, O. Approach to ideal network formation governed by Flory-Stockmayer gelation theory in free-radical cross-linking copolymerization of styrene with m-divinylbenzene. Macromolecules 1999, 32, 8336–8339. [Google Scholar] [CrossRef]
- Bannister, I.; Billingham, N.C.; Armes, S.P.; Rannard, S.P.; Findlay, P. Development of branching in living radical copolymerization of vinyl and divinyl monomers. Macromolecules 2006, 39, 7483–7492. [Google Scholar] [CrossRef]
- Gao, H.; Min, K.; Matyjaszewski, K. Determination of gel point during atom transfer radical copolymerization with cross-linker. Macromolecules 2007, 40, 7763–7770. [Google Scholar] [CrossRef]
- Schultz, K.M.; Baldwin, A.D.; Kiick, K.L.; Furst, E.M. Gelation of covalently cross-linked PEG-Heparin hydrogels. Macromolecules 2009, 42, 5310–5316. [Google Scholar] [CrossRef] [Green Version]
- Rosselgong, J.; Armes, S.P.; Barton, W.; Price, D. Synthesis of highly branched methacrylic copolymers: Observation of near-ideal behavior using RAFT polymerization. Macromolecules 2009, 42, 5919–5924. [Google Scholar] [CrossRef]
- Schamboeck, V.; Iedema, P.D.; Kryven, I. Dynamic networks that drive the process of irreversible step-growth polymerization. Sci. Rep. 2019, 9, 2276. [Google Scholar] [CrossRef] [Green Version]
- Lyu, J.; Gao, Y.; Zhang, Z.; Greiser, U.; Tai, H.; Wang, W. Can Flory-Stockmayer theory be applied to predict conventional free radical polymerization of multivinyl monomers? A study via Monte Carlo simulations. Sci. China Chem. 2018, 61, 319–327. [Google Scholar] [CrossRef] [Green Version]
- Lyu, J.; Gao, Y.; Zhang, Z.; Greiser, U.; Polanowski, P.; Jeszka, J.K.; Matyjaszewski, K.; Tai, H.; Wang, W. Monte Carlo simulations of atom transfer tadical (homo)polymerization of divinyl monomers: Applicability of Flory-Stockmayer theory. Macromolecules 2018, 51, 6673–6681. [Google Scholar] [CrossRef] [Green Version]
- Issa, A.A.; Luyt, A.S. Kinetics of Alkoxysilanes and Organoalkoxysilanes Polymerization: A Review. Polymers 2019, 11, 537. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lísal, M.; Brennan, J.K.; Smith, W.R. Mesoscale simulation of polymer reaction equilibrium: Combining dissipative particle dynamics with reaction ensemble Monte Carlo. I. Polydispersed polymer systems. J. Chem. Phys. 2006, 125, 164905. [Google Scholar] [CrossRef]
- Lísal, M.; Brennan, J.K.; Smith, W.R. Mesoscale simulation of polymer reaction equilibrium: Combining dissipative particle dynamics with reaction ensemble Monte Carlo. II. Supramolecular diblock copolymers. J. Chem. Phys. 2009, 130, 104902. [Google Scholar] [CrossRef] [PubMed]
- Monteferrante, M.; Succi, S.; Pisignano, D.; Lauricella, M. Simulating Polymerization by Boltzmann Inversion Force Field Approach and Dynamical Nonequilibrium Reactive Molecular Dynamics. Polymers 2022, 14, 4529. [Google Scholar] [CrossRef] [PubMed]
- Mohammadi, Y.; Saeb, M.R.; Penlidis, A.; Jabbari, E.; J. Stadler, F.; Zinck, P.; Matyjaszewski, K. Intelligent Machine Learning: Tailor-Making Macromolecules. Polymers 2019, 11, 579. [Google Scholar] [CrossRef] [Green Version]
- Arraez, F.J.; Van Steenberge, P.H.M.; D’hooge, D.R. The Competition of Termination and Shielding to Evaluate the Success of Surface-Initiated Reversible Deactivation Radical Polymerization. Polymers 2020, 12, 1409. [Google Scholar] [CrossRef] [PubMed]
- Ma, J.; Li, J.; Yang, B.; Liu, S.; Jiang, B.P.; Ji, S.; Shen, X.C. A Simple Stochastic Reaction Model for Heterogeneous Polymerizations. Polymers 2022, 14, 3269. [Google Scholar] [CrossRef] [PubMed]
- Landau, D.; Binder, K. A Guide to Monte Carlo Simulations in Statistical Physics; Cambridge University Press: New York, NY, USA, 2005. [Google Scholar]
- Hsu, H.P.; Grassberger, P. A review of Monte Carlo simulations of polymers with PERM. J. Stat. Phys. 2011, 144, 597. [Google Scholar] [CrossRef]
- Brandão, A.L.T.; Soares, J.B.P.; Pinto, J.C.; Alberton, A.L. When polymer reaction engineers play dice: Applications of Monte Carlo models in PRE. Macromol. React. Eng. 2015, 9, 141–185. [Google Scholar] [CrossRef]
- Ganazzoli, F.; Raffaini, G. Dendrimer dynamics: A review of analytical theories and molecular simulation methods. Polymers 2020, 12, 1387. [Google Scholar] [CrossRef]
- Johnson, A.F.; O’Driscoll, K.F. Monte Carlo simulation of sequence distributions in step growth copolymerization. Eur. Polym. J. 1984, 20, 979–983. [Google Scholar] [CrossRef]
- Tobita, H. Molecular weight distribution in free radical polymerization with long-chain branching. J. Polym. Sci. B Polym. Phys. 1993, 31, 1363–1371. [Google Scholar] [CrossRef]
- Tobita, H.; Hatanaka, K. Long-chain branching in free-radical polymerization due to chain transfer to polymer. J. Polym. Sci. B Polym. Phys. 1995, 33, 841–853. [Google Scholar] [CrossRef]
- Tobita, H.; Mima, T.; Okada, A.; Mori, J.; Tanabe, T. Molecular weight distribution formed during free-radical polymerization in the presence of polyfunctional chain transfer agents. J. Polym. Sci. B Polym. Phys. 1999, 37, 1267–1275. [Google Scholar] [CrossRef]
- Tobita, H.; Uemura, Y. Microgel formation in emulsion copolymerization. I. Polymerization without seed latex. J. Polym. Sci. B Polym. Phys. 1996, 34, 1403–1413. [Google Scholar] [CrossRef]
- Tobita, H.; Yoshihara, Y. Microgel formation in emulsion copolymerization: II. Seeded polymerization. J. Polym. Sci. B Polym. Phys. 1996, 34, 1415–1422. [Google Scholar] [CrossRef]
- Tobita, H. Molecular weight distribution in nonlinear emulsion polymerization. J. Polym. Sci. B Polym. Phys. 1997, 35, 1515–1532. [Google Scholar] [CrossRef]
- Tobita, H. Simultaneous long-chain branching and random scission: I. Monte Carlo simulation. J. Polym. Sci. B Polym. Phys. 2001, 39, 391–403. [Google Scholar] [CrossRef]
- Tobita, H. Dimensions of branched polymers formed in simultaneous long-chain branching and random scission. J. Polym. Sci. B Polym. Phys. 2001, 39, 2960–2968. [Google Scholar] [CrossRef]
- Tobita, H. Molecular weight distribution of living radical polymers 2. Monte Carlo simulation. Macromol. Theo. Simul. 2006, 15, 23–31. [Google Scholar] [CrossRef]
- Tobita, H.; Yanase, F. Monte Carlo simulation of controlled/living radical polymerization in emulsified systems. Macromol. Theo. Simul. 2007, 16, 476–488. [Google Scholar] [CrossRef]
- Hädicke, E.; Stutz, H. Comparison of the structure of step-growth networks obtained by Monte Carlo simulation and branching theory. J. Appl. Polym. Sci. 2002, 85, 929–935. [Google Scholar] [CrossRef]
- He, X.; Liang, H.; Pan, C. Monte Carlo simulation of hyperbranched copolymerizations in the presence of a multifunctional initiator. Macromo. Theor. Simul. 2001, 10, 196–203. [Google Scholar] [CrossRef]
- He, X.; Liang, H.; Pan, C. Self-condensing vinyl polymerization in the presence of multifunctional initiator with unequal rate constants: Monte Carlo simulation. Polymer 2003, 44, 6697–6706. [Google Scholar] [CrossRef]
- Rouault, Y.; Milchev, A. Monte Carlo study of the molecular-weight distribution of living polymers. Phys. Rev. E 1997, 55, 2020–2022. [Google Scholar] [CrossRef]
- He, J.; Zhang, H.; Chen, J.; Yang, Y. Monte Carlo simulation of kinetics and chain length distributions in living free-radical polymerization. Macromolecules 1997, 30, 8010–8018. [Google Scholar] [CrossRef]
- Prescott, S.W. Chain-length dependence in living/controlled free-radical polymerizations: Physical manifestation and Monte Carlo simulation of reversible transfer agents. Macromolecules 2003, 36, 9608–9621. [Google Scholar] [CrossRef]
- Al-Harthi, M.; Soares, J.B.; Simon, L.C. Dynamic Monte Carlo simulation of atom-transfer radical polymerization. Macromol. Mater. Eng. 2006, 291, 993–1003. [Google Scholar] [CrossRef]
- Al-Harthi, M.; Soares, J.B.P.; Simon, L.C. Dynamic Monte Carlo simulation of ATRP with bifunctional initiators. Macromol. React. Eng. 2007, 1, 95–105. [Google Scholar] [CrossRef]
- Al-Harthi, M.A.; Masihullah, J.K.; Abbasi, S.H.; Soares, J.B.P. Dynamic Monte Carlo simulation of ATRP in a batch reactor. Macromol. Theor. Simul. 2009, 18, 307–316. [Google Scholar] [CrossRef]
- Al-Harthi, M.; Khan, M.J.; Abbasi, S.H.; Soares, J.B.P. Gradient copolymers by ATRP in semibatch reactors: Dynamic Monte Carlo simulation. Macromol. React. Eng. 2009, 3, 148–159. [Google Scholar] [CrossRef]
- Polanowski, P.; Jeszka, J.K.; Matyjaszewski, K. Modeling of branching and gelation in living copolymerization of monomer and divinyl cross-linker using dynamic lattice liquid model (DLL) and Flory-Stockmayer model. Polymer 2010, 51, 6084–6092. [Google Scholar] [CrossRef]
- Polanowski, P.; Jeszka, J.K.; Li, W.; Matyjaszewski, K. Effect of dilution on branching and gelation in living copolymerization of monomer and divinyl cross-linker: Modeling using dynamic lattice liquid model (DLL) and Flory-Stockmayer (FS) model. Polymer 2011, 52, 5092–5101. [Google Scholar] [CrossRef]
- Bannister, I.; Billingham, N.C.; Armes, S.P. Monte Carlo modelling of living branching copolymerisation of monovinyl and divinyl monomers: Comparison of simulated and experimental data for ATRP copolymerisation of methacrylic monomers. Soft Matter 2009, 5, 3495–3504. [Google Scholar] [CrossRef]
- Polanowski, P.; Hałagan, K.; Sikorski, A. Star polymers vs. dendrimers: Studies of the synthesis based on computer simulations. Polymers 2022, 14, 2522. [Google Scholar] [CrossRef]
- Gao, H.; Oakley, L.H.; Konstantinov, I.A.; Arturo, S.G.; Broadbelt, L.J. Acceleration of kinetic Monte Carlo method for the simulation of free radical copolymerization through scaling. Ind. Eng. Chem. Res. 2015, 54, 11975–11985. [Google Scholar] [CrossRef]
- Gao, H.; Broadbelt, L.J.; Konstantinov, I.A.; Arturo, S.G. Acceleration of kinetic Monte Carlo simulations of free radical copolymerization: A hybrid approach with scaling. AIChE J. 2017, 63, 4013–4021. [Google Scholar] [CrossRef]
- Meimaroglou, D.; Krallis, A.; Saliakas, V.; Kiparissides, C. Prediction of the bivariate molecular weight - long chain branching distribution in highly branched polymerization systems using Monte Carlo and sectional grid methods. Macromolecules 2007, 40, 2224–2234. [Google Scholar] [CrossRef]
- Meimaroglou, D.; Pladis, P.; Baltsas, A.; Kiparissides, C. Prediction of the molecular and polymer solution properties of LDPE in a high-pressure tubular reactor using a novel Monte Carlo approach. Chem. Eng. Sci. 2011, 66, 1685–1696. [Google Scholar] [CrossRef]
- Meimaroglou, D.; Pladis, P.; Kiparissides, C. Dynamic Monte Carlo simulation of the l,l-Lactide ring-opening polymerization. Macromol. React. Eng. 2017, 11, 1600039. [Google Scholar] [CrossRef] [Green Version]
- Jin, J.; Zheng, R.Q.; Zhou, Y.N.; Luo, Z.H. Network formation kinetics of poly (dimethylsiloxane) based on step-growth polymerization. Macromolecules 2021, 54, 7678–7689. [Google Scholar] [CrossRef]
- Iedema, P.; Remerie, K.; van der Ham, M.; Biemond, E. Development of MWD and branching during peroxide modification of high-density polyethylene by SEC-MALS and Monte Carlo simulation. Polymer 2013, 54, 4093–4104. [Google Scholar] [CrossRef]
- Yaghini, N.; Iedema, P.D. Predicting molecular weight distribution by deterministic modeling and Monte Carlo simulations of radical polymerization with branching and scission allowing for multiradicals and gelation in various reactor configurations. Chem. Eng. Sci. 2015, 130, 310–318. [Google Scholar] [CrossRef]
- De Keer, L.; Van Steenberge, P.H.M.; Reyniers, M.F.; D’hooge, D.R. Going beyond the Carothers, Flory and Stockmayer equation by including cyclization reactions and mobility constraints. Polymers 2021, 13, 2410. [Google Scholar] [CrossRef]
- Carothers, W.H. Polymers and polyfunctionality. Trans. Faraday Soc. 1936, 32, 39–49. [Google Scholar] [CrossRef]
- Flory, P.J. Kinetics of polyesterification: A study of the effects of molecular weight and viscosity on reaction rate. J. Am. Chem. Soc. 1939, 61, 3334–3340. [Google Scholar] [CrossRef]
- Flory, P.J. A comparison of esterification and ester interchange kinetics. J. Am. Chem. Soc. 1940, 62, 2261–2264. [Google Scholar] [CrossRef]
- Milchev, A.; Wittmer, J.P.; Landau, D.P. Dynamical Monte Carlo study of equilibrium polymers: Effects of high density and ring formation. Phys. Rev. E 2000, 61, 2959–2966. [Google Scholar] [CrossRef] [Green Version]
- Gao, Z.; He, J. Monte Carlo modeling of free radical polymerization in microflow reactors. Macromol. React. Eng. 2015, 9, 431–441. [Google Scholar] [CrossRef]
- Maafa, I.M.; Soares, J.B.P.; Elkamel, A. Prediction of chain length distribution of polystyrene made in batch reactors with bifunctional free-radical initiators using dynamic Monte Carlo simulation. Macromol. React. Eng. 2007, 1, 364–383. [Google Scholar] [CrossRef]
- Soares, J.B.P.; Hamielec, A.E. Chain length distributions of polyolefins made with coordination catalysts at very short polymerization times-Analytical solution and Monte Carlo simulation. Macromol. React. Eng. 2007, 1, 53–67. [Google Scholar] [CrossRef]
- Hamzehlou, S.; Reyes, Y.; Leiza, J.R. A new insight into the formation of polymer networks: A kinetic Monte Carlo simulation of the cross-linking polymerization of S/DVB. Macromolecules 2013, 46, 9064–9073. [Google Scholar] [CrossRef]
- Fawcett, A.H.; Mee, R.A.W.; McBride, F.V. A Monte Carlo study of ring formation and molecular configurations during step growth on a lattice in three dimensions. Macromolecules 1995, 28, 1481–1490. [Google Scholar] [CrossRef]
- Tripathi, A.K.; Tsavalas, J.G.; Sundberg, D.C. Monte Carlo simulations of free radical polymerizations with divinyl cross-linker: Pre- and postgel simulations of reaction kinetics and molecular structure. Macromolecules 2015, 48, 184–197. [Google Scholar] [CrossRef]
- Gillespie, D.T. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 1977, 81, 2340–2361. [Google Scholar] [CrossRef]
- Gillespie, D.T. Stochastic simulation of chemical kinetics. Annu. Rev. Phys. Chem. 2007, 58, 35–55. [Google Scholar] [CrossRef]
- Odle, R.R.; Guggenheim, T.L.; Kloppenburg, L.M.; Long, T.E.; Dennis, J.M. Branched Polyimide Compositions, Method of Manufacture, and Uses Thereof. U.S. Patent Application WO2018126141A1, 29 December 2017. [Google Scholar]
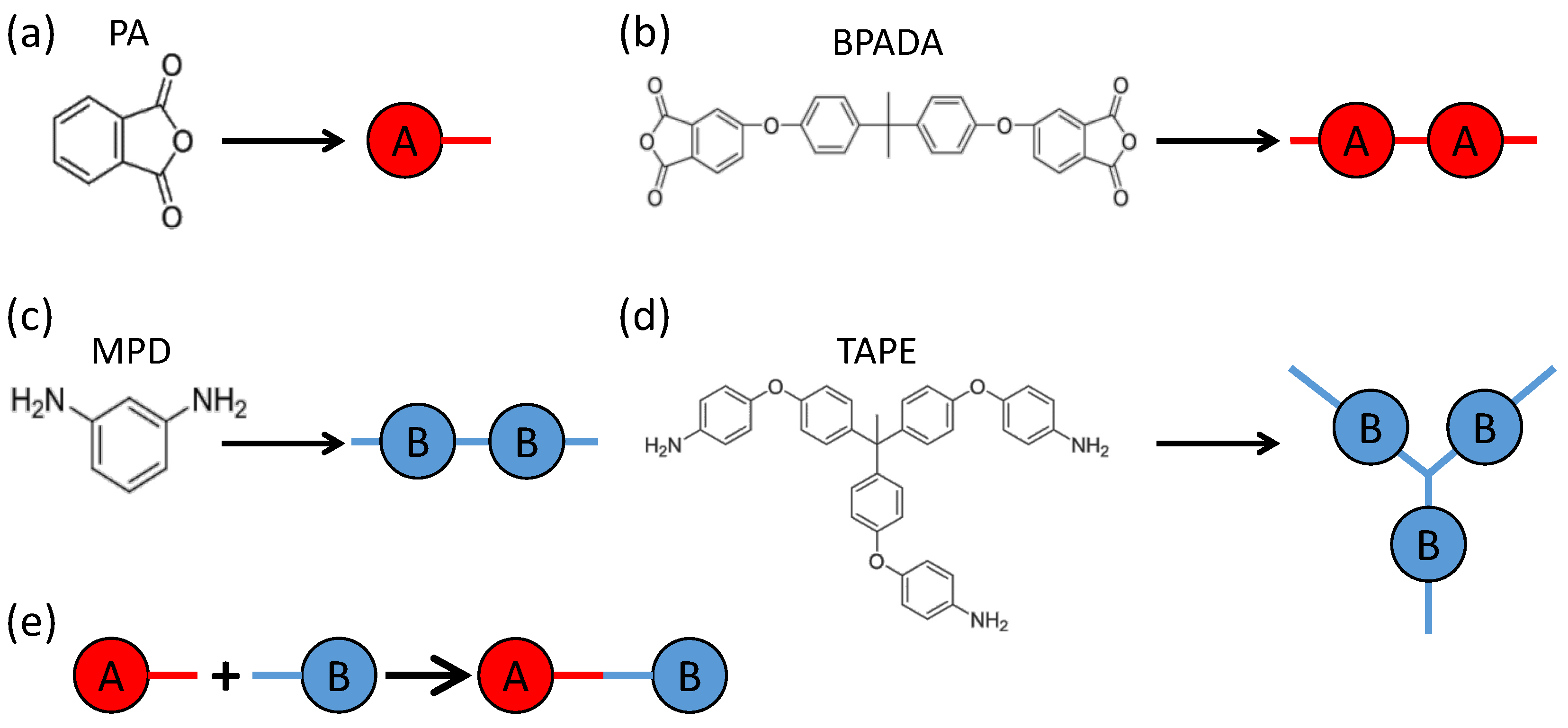
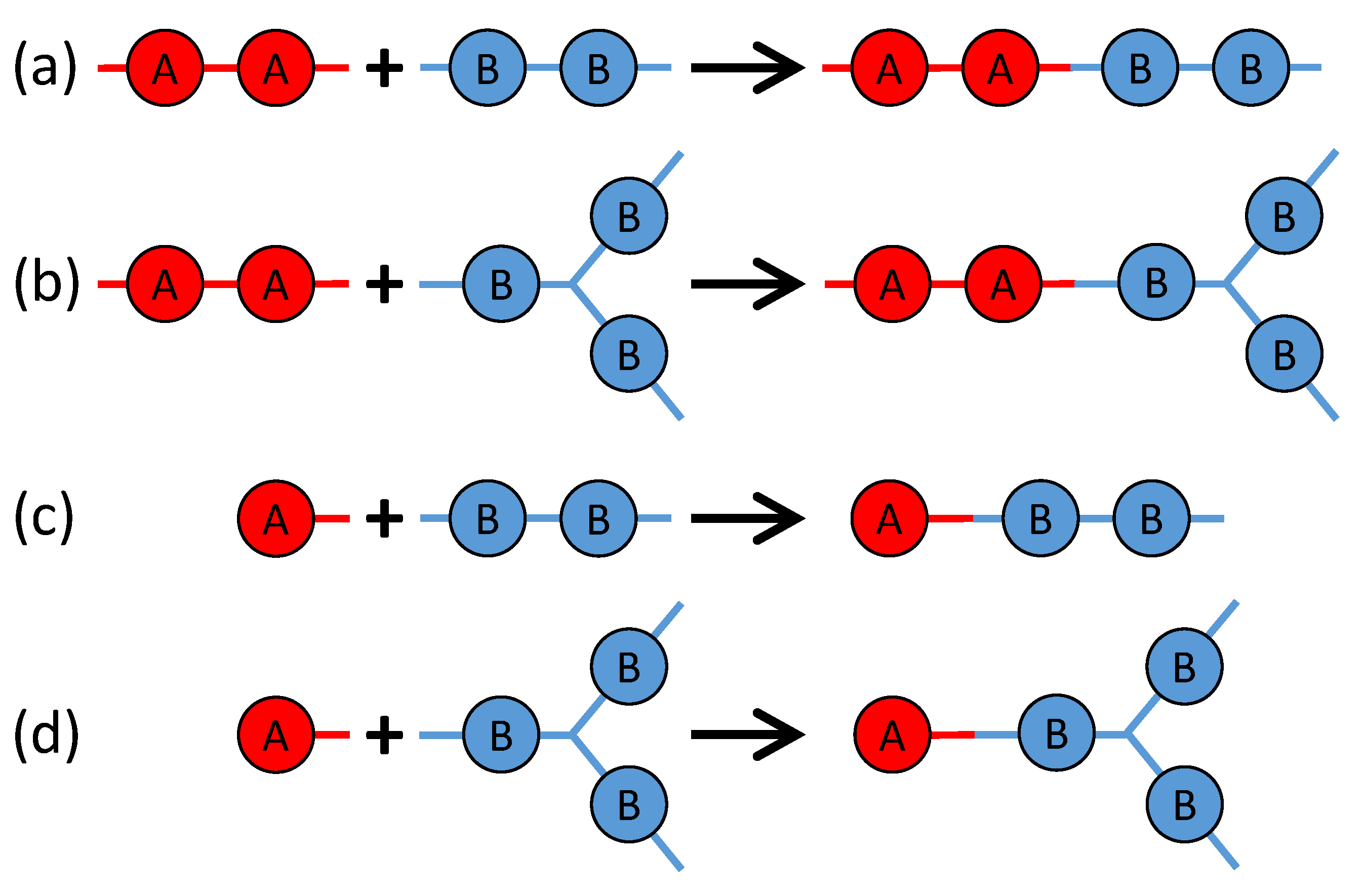
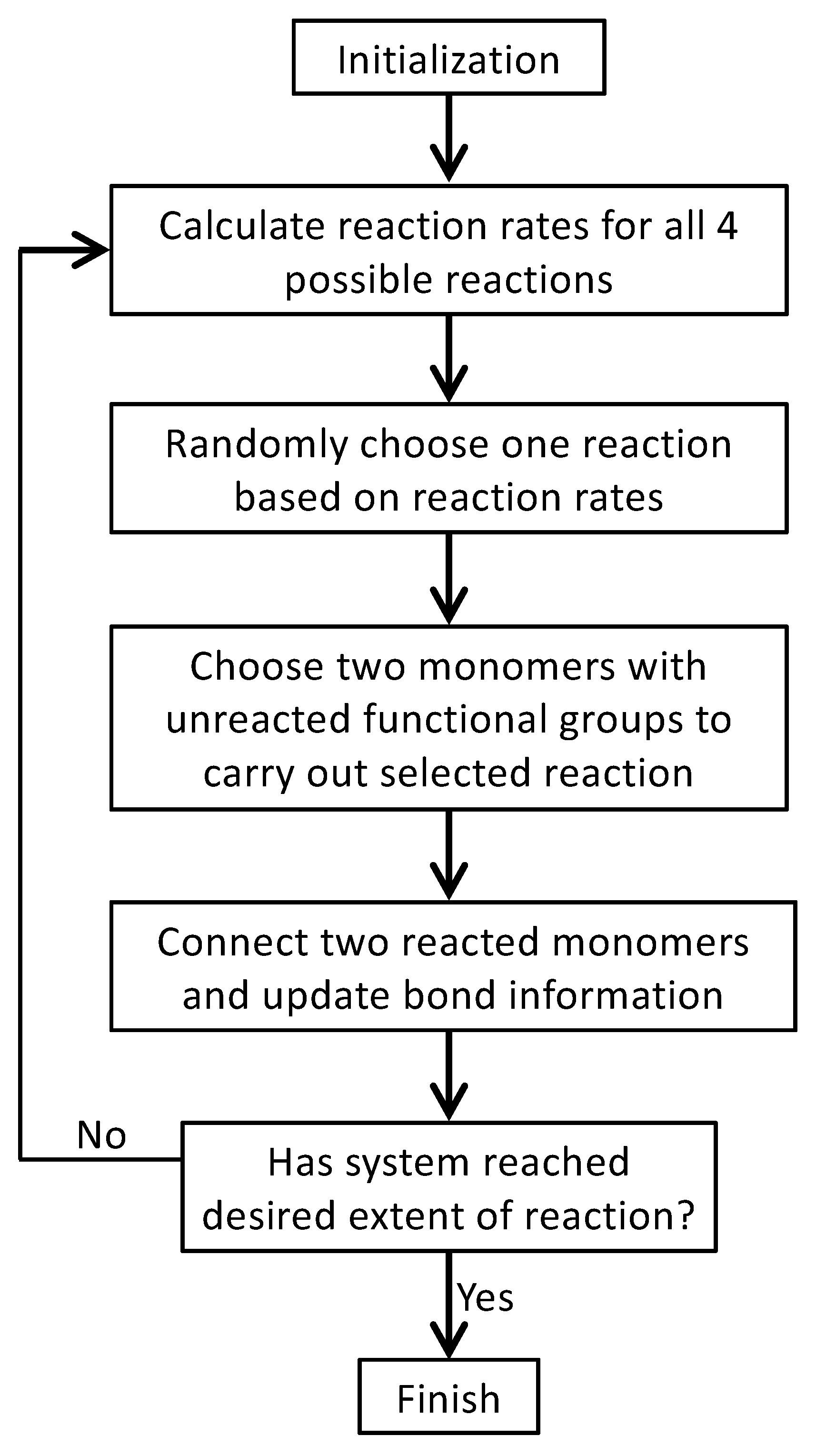


| Monomer | PA | BPADA | MPD | TAPE |
|---|---|---|---|---|
| Number | 2000 | 0 | 0 | 1000 |
| PA | BPADA | MPD | TAPE | (Da) | (Da) | (Da) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 50 | 670 | 680 | 10 | 0.0360 | 0.0216 | 1 | 1 | 0.366 | ||||
| 50 | 670 | 671 | 16 | 0.0360 | 0.0345 | 1 | 1 | 0.481 | ||||
| 50 | 670 | 620 | 50 | 0.0360 | 0.108 | 1 | 1 | 0.743 |
| PA | BPADA | MPD | TAPE | (Da) | (Da) | (Da) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 10 | 134 | 136 | 2 | 0.0360 | 0.0216 | 1 | 1 | 0.366 | ||||
| 100 | 1340 | 1360 | 20 | 0.0360 | 0.0216 | 1 | 1 | 0.366 | ||||
| 500 | 6700 | 6800 | 100 | 0.0360 | 0.0216 | 1 | 1 | 0.366 | ||||
| 800 | 10,720 | 10,880 | 160 | 0.0360 | 0.0216 | 1 | 1 | 0.366 |
| PA | BPADA | MPD | TAPE | (Da) | (Da) | (Da) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 50 | 670 | 620 | 50 | 0.0360 | 0.108 | 0.95 | 0.95 | 0.419 | ||||
| 50 | 670 | 620 | 50 | 0.0360 | 0.108 | 0.96 | 0.96 | 0.462 | ||||
| 50 | 670 | 620 | 50 | 0.0360 | 0.108 | 0.97 | 0.97 | 0.513 | ||||
| 50 | 670 | 620 | 50 | 0.0360 | 0.108 | 0.98 | 0.98 | 0.574 | ||||
| 50 | 670 | 620 | 50 | 0.0360 | 0.108 | 0.99 | 0.99 | 0.649 |
| PA | BPADA | MPD | TAPE | (Da) | (Da) | (Da) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 50 | 670 | 664 | 50 | 0.0360 | 0.101 | 0.99 | 0.93 | 0.445 | ||||
| 50 | 670 | 649 | 50 | 0.0360 | 0.104 | 0.99 | 0.95 | 0.502 | ||||
| 50 | 670 | 634 | 50 | 0.0360 | 0.106 | 0.99 | 0.97 | 0.569 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wen, C.; Odle, R.; Cheng, S. Molecular Weight Distribution of Branched Polymers: Comparison between Monte Carlo Simulation and Flory-Stockmayer Theory. Polymers 2023, 15, 1791. https://doi.org/10.3390/polym15071791
Wen C, Odle R, Cheng S. Molecular Weight Distribution of Branched Polymers: Comparison between Monte Carlo Simulation and Flory-Stockmayer Theory. Polymers. 2023; 15(7):1791. https://doi.org/10.3390/polym15071791
Chicago/Turabian StyleWen, Chengyuan, Roy Odle, and Shengfeng Cheng. 2023. "Molecular Weight Distribution of Branched Polymers: Comparison between Monte Carlo Simulation and Flory-Stockmayer Theory" Polymers 15, no. 7: 1791. https://doi.org/10.3390/polym15071791
APA StyleWen, C., Odle, R., & Cheng, S. (2023). Molecular Weight Distribution of Branched Polymers: Comparison between Monte Carlo Simulation and Flory-Stockmayer Theory. Polymers, 15(7), 1791. https://doi.org/10.3390/polym15071791






