On the Donor: Acceptor Features for Poly(3-hexylthiophene): TiO2 Quantum Dots Hybrid Materials Obtained via Water Vapor Flow Assisted Sol-Gel Growth
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Section
2.2. Characterization of Samples
2.3. Computational Section
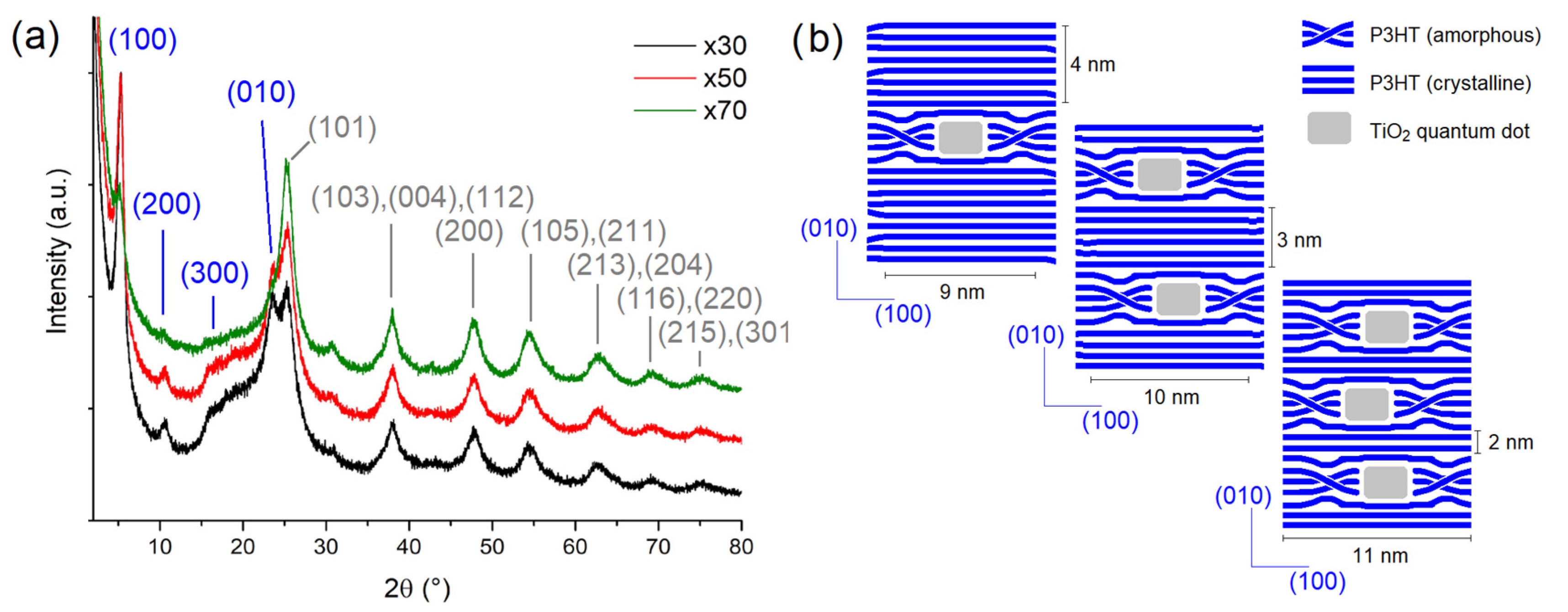
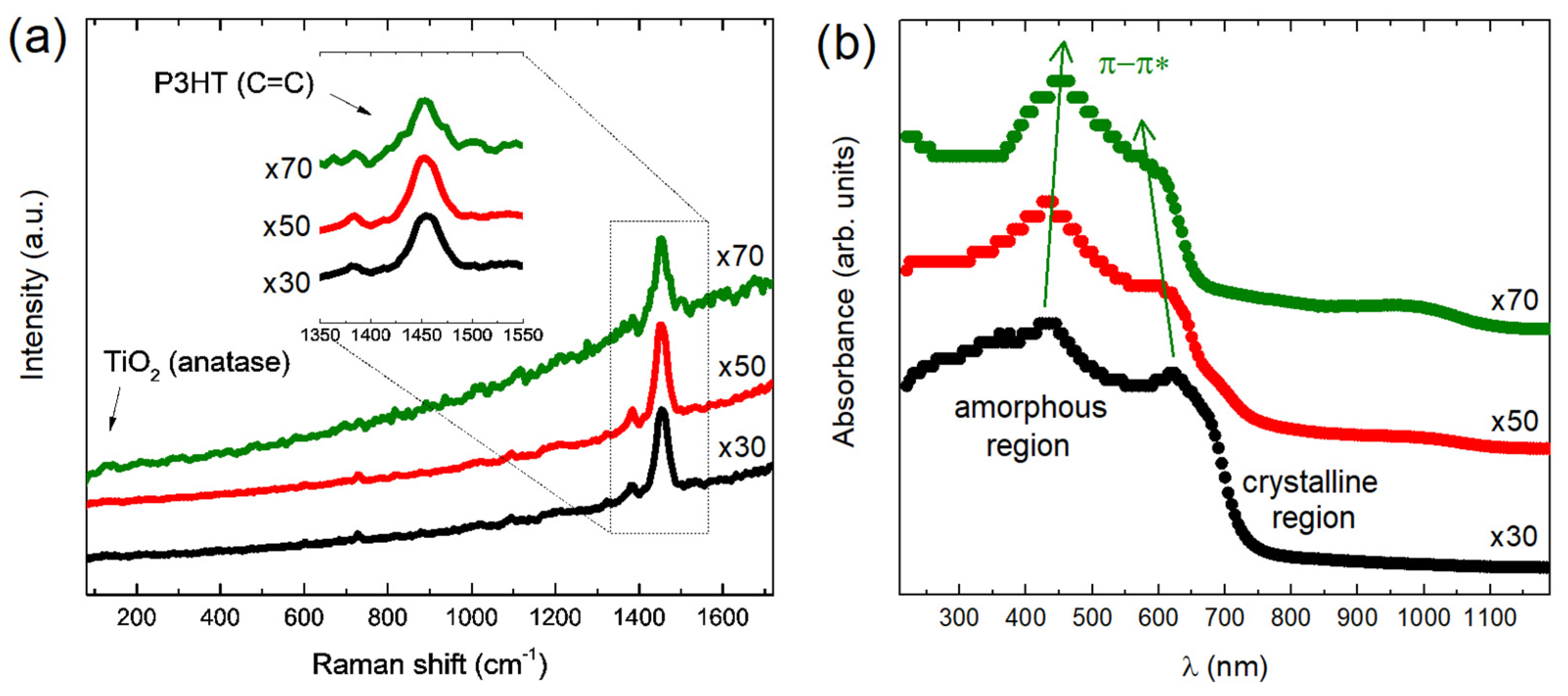
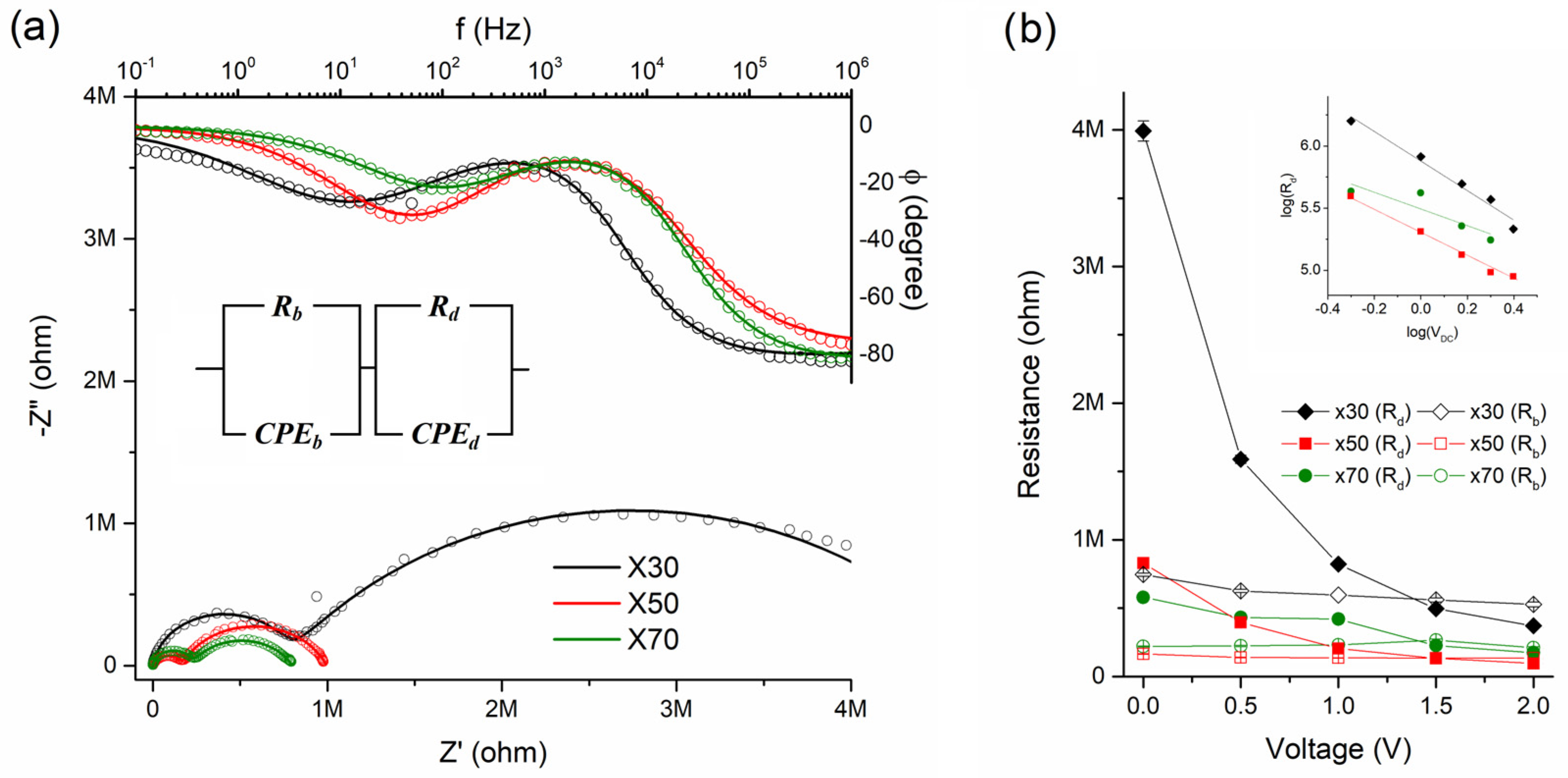
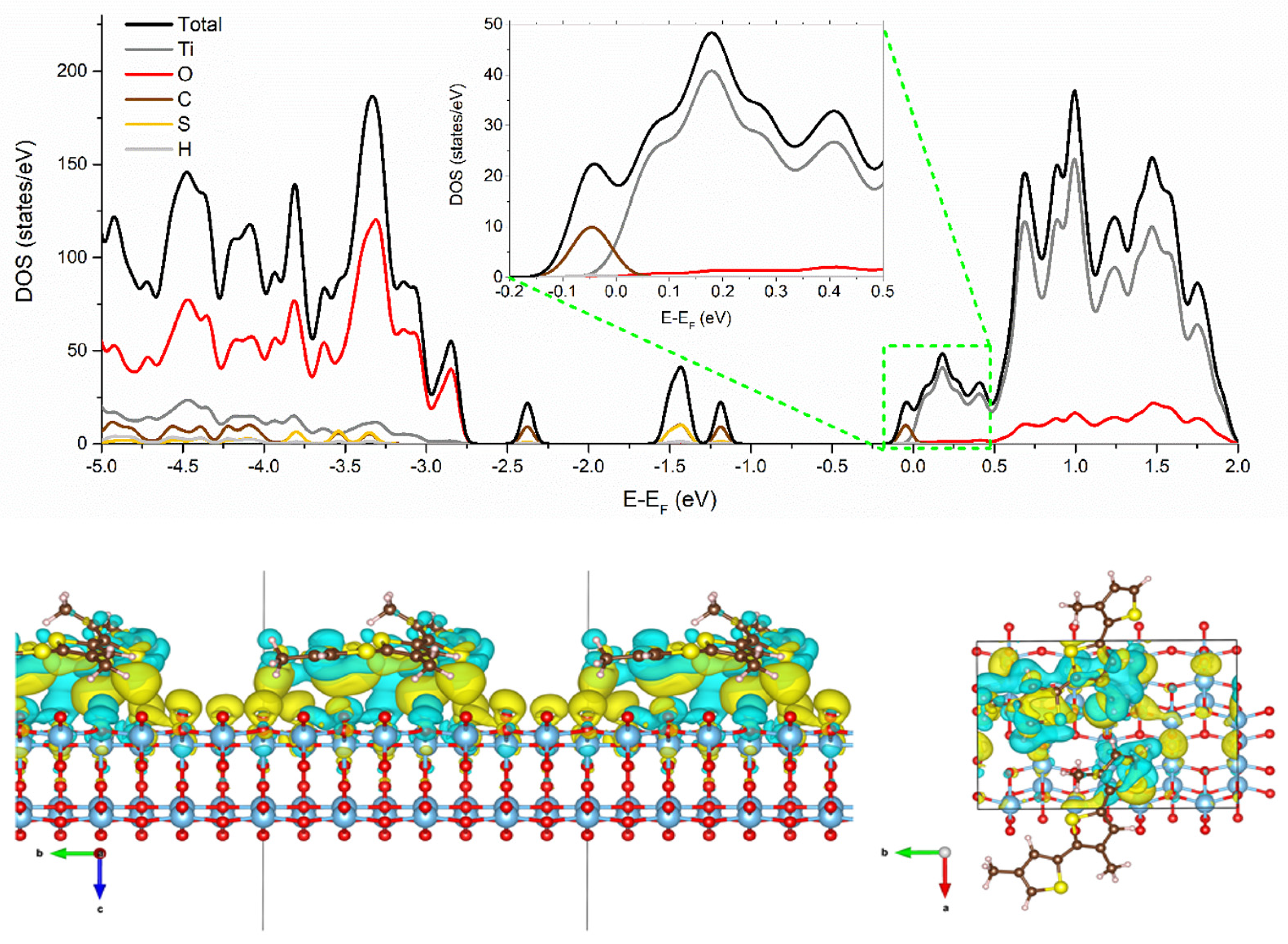
3. Results
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, W.; Li, S.; Huang, J.; Yang, S.; Chen, J.; Zuo, L.; Shi, M.; Zhan, X.; Li, C.-Z.; Chen, H. Nonfullerene Tandem Organic Solar Cells with High Open-Circuit Voltage of 1.97 V. Adv. Mater. 2016, 28, 9729–9734. [Google Scholar] [CrossRef] [PubMed]
- Guo, W.; Zhao, B.; Xin, J.; Liu, H.; Mi, Y.; Zhang, J.; Guo, Z.; Wei, W.; Ma, W.; Gao, C.; et al. Non-Fullerene Small Molecular Acceptors Based on Dithienocyclopentafluorene and Dithienocyclopentacarbazole Cores for Polymer Solar Cells. Dyes Pigm. 2017, 144, 48–57. [Google Scholar] [CrossRef]
- Chakravarthi, N.; Kranthiraja, K.; Gunasekar, K.; Gal, Y.-S.; Cho, Y.-R.; Jin, S.-H. Alkoxyphenyl-Thiophene, -Selenophene and -Furan Substituted Benzodithiophene Based 2d Π-Conjugated Polymers for Polymer Solar Cells and Effect of Chalcogen on Optoelectronic Properties. Synth. Met. 2016, 222, 356–363. [Google Scholar] [CrossRef]
- He, Y.; Li, Y. Fullerene Derivative Acceptors for High Performance Polymer Solar Cells. Phys. Chem. Chem. Phys. 2011, 13, 1970–1983. [Google Scholar] [CrossRef] [PubMed]
- Liu, T.; Troisi, A. What Makes Fullerene Acceptors Special as Electron Acceptors in Organic Solar Cells and How to Replace Them. Adv. Mater. 2013, 25, 1038–1041. [Google Scholar] [CrossRef]
- Anthony, J.E. Small-Molecule, Nonfullerene Acceptors for Polymer Bulk Heterojunction Organic Photovoltaics. Chem. Mater. 2011, 23, 583–590. [Google Scholar] [CrossRef]
- Lin, Y.; Li, Y.; Zhan, X. Small Molecule Semiconductors for High-Efficiency Organic Photovoltaics. Chem. Soc. Rev. 2012, 41, 4245–4272. [Google Scholar] [CrossRef]
- Lin, Y.; Zhan, X. Non-Fullerene Acceptors for Organic Photovoltaics: An Emerging Horizon. Mater. Horiz. 2014, 1, 470–488. [Google Scholar] [CrossRef]
- Nielsen, C.B.; Holliday, S.; Chen, H.-Y.; Cryer, S.J.; McCulloch, I. Non-Fullerene Electron Acceptors for Use in Organic Solar Cells. Acc. Chem. Res. 2015, 48, 2803–2812. [Google Scholar] [CrossRef]
- Lin, Y.; Zhan, X. Oligomer Molecules for Efficient Organic Photovoltaics. Acc. Chem. Res. 2016, 49, 175–183. [Google Scholar] [CrossRef]
- Facchetti, A. Polymer donor–polymer acceptor (all-polymer) solar cells. Mater. Today 2013, 16, 123–132. [Google Scholar] [CrossRef]
- Wright, M.; Uddin, A. Organic-inorganic hybrid solar cells: A comparative review. Sol. Energy Mater. Sol. Cells. 2012, 107, 87–111. [Google Scholar] [CrossRef]
- Wu, M.C.; Chang, C.H.; Lo, H.H.; Lin, Y.S.; Lin, Y.Y.; Yen, W.C.; Su, W.F.; Chen, Y.F.; Chen, C.W. Nanoscale morphology and performance of molecular-weight-dependent poly (3-hexylthiophene)/TiO2 nanorod hybrid solar cells. J. Mater. Chem. 2008, 18, 4097–4102. [Google Scholar] [CrossRef]
- Lin, Y.Y.; Chu, T.H.; Li, S.S.; Chuang, C.H.; Chang, C.H.; Su, W.F.; Chang, C.P.; Chu, M.W.; Chen, C.W. Interfacial nanostructuring on the performance of polymer/TiO2 nanorod bulk heterojunction solar cells. J. Am. Chem. Soc. 2009, 131, 3644–3649. [Google Scholar] [CrossRef]
- Lee, J.; Jho, J.Y. Fabrication of highly ordered and vertically oriented TiO2 nanotube arrays for ordered heterojunction polymer/inorganic hybrid solar cell. Sol. Energy Mater. Sol. Cells. 2011, 95, 3152–3156. [Google Scholar] [CrossRef]
- Abrusci, A.; Ding, I.K.; Al-Hashimi, M.; Segal-Peretz, T.; McGehee, M.D.; Heeney, M.; Frey, G.L.; Snaith, H.J. Facile infiltration of semiconducting polymer into mesoporous electrodes for hybrid solar cells. Energy Environ. Sci. 2011, 4, 3051–3058. [Google Scholar] [CrossRef]
- Weickert, J.; Zimmermann, E.; Reindl, J.B.; Pfadler, T.; Dorman, J.A.; Petrozza, A.; Schmidt-Mende, L. Synergistic effects of interfacial modifiers enhance current and voltage in hybrid solar cells. APL Mater. 2013, 1, 042109. [Google Scholar] [CrossRef]
- Planells, M.; Abate, A.; Snaith, H.J.; Robertson, N. Oligothiophene Interlayer Effect on Photocurrent Generation for Hybrid TiO2/P3HT Solar Cells. ACS Appl. Mater. Interfaces 2014, 6, 17226–17235. [Google Scholar] [CrossRef]
- Phan, H.; Jahnke, J.P.; Chmelka, B.F.; Nguyen, T.Q. Structural and optoelectronic properties of hybrid bulk-heterojunction materials based on conjugated small molecules and mesostructured TiO2. Appl. Phys. Lett. 2014, 104, 233305. [Google Scholar] [CrossRef]
- Leijtens, T.; Lim, J.; Teuscher, J.; Park, T.; Snaith, H.J. Charge Density Dependent Mobility of Organic Hole-Transporters and Mesoporous TiO2 Determined by Transient Mobility Spectroscopy: Implications to Dye-Sensitized and Organic Solar Cells. Adv. Mater. 2013, 25, 3227–3233. [Google Scholar] [CrossRef] [PubMed]
- Frischknecht, A.K.; Yaccuzzi, E.; Plá, J.; Perez, M.D. Anomalous photocurrent response of hybrid TiO2:P3HT solar cells under different incident light wavelengths. Sol. Energy Mater. Sol. Cells 2016, 157, 907–912. [Google Scholar] [CrossRef]
- Cheung, C.H.; Tsung, K.K.; Kwok, K.C.; So, S.K. Using thin film transistors to quantify carrier transport properties of amorphous organic semiconductors. Appl. Phys. Lett. 2008, 93, 083307. [Google Scholar] [CrossRef]
- Tsung, K.K.; So, S.K. Carrier trapping and scattering in amorphous organic hole transporter. Appl. Phys. Lett. 2008, 92, 103315. [Google Scholar] [CrossRef]
- Morfa, A.J.; Nardes, A.M.; Shaheen, S.E.; Kopidakis, N.; van de Lagemaat, J. Time-of-Flight Studies of Electron-Collection Kinetics in Polymer: Fullerene Bulk-Heterojunction Solar Cells. Adv. Funct. Mater. 2011, 21, 2580–2586. [Google Scholar] [CrossRef]
- Liu, S.W.; Lee, C.C.; Su, W.C.; Yuan, C.H.; Lin, C.F.; Chen, K.T.; Shu, Y.S.; Li, Y.Z.; Su, T.H.; Huang, B.Y.; et al. Downscaling the sample thickness to sub-micrometers by employing organic photovoltaic materials as a a charge-generation layer in the time-of-flight measurement. Sci. Rep. 2015, 5, 10384. [Google Scholar] [CrossRef]
- Rohloff, R.; Kotadiya, N.B.; Crăciun, N.I.; Blom, P.W.M.; Wetzelaer, G.A.H. Electron and hole transport in the organic small molecule α-NPD. Appl. Phys. Lett. 2017, 110, 073301. [Google Scholar] [CrossRef]
- Mombrú, D.; Romero, M.; Faccio, R.; Castiglioni, J.; Mombrú, A.W. In situ growth of ceramic quantum dots in polyaniline host via water vapor flow diffusion as potential electrode materials for energy applications. J. Solid State Chem. 2017, 250, 60–67. [Google Scholar] [CrossRef]
- Mombrú, D.; Romero, M.; Faccio, R.; Mombrú, A.W. Raman and Impedance Spectroscopy under Applied Dc Bias Insights on the Electrical Transport for Donor:Acceptor Nanocomposites Based on Poly(vinyl carbazole) and TiO2 Quantum Dots. J. Phys. Chem. C 2017, 121, 23383–23391. [Google Scholar] [CrossRef]
- Mombrú, D.; Romero, M.; Faccio, R.; Tumelero, M.A.; Mombrú, A.W. Extremely Large Magnetic-Field-Effects on the Impedance Response of TiO2 Quantum Dots. Sci. Rep. 2019, 9, 5322. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular-dynamics simulation of the liquid-metalamorphous-semiconductor transition in germanium. Phys. Rev. B 1994, 49, 14251–14269. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868, Erratum in Phys. Rev. Lett. 1997, 78, 1396. [Google Scholar] [CrossRef]
- Fernández-Werner, L.; Faccio, R.; Juan, A.; Pardo, H.; Montenegro, B.; Mombrú, A.W. Ultrathin (001) and (100) TiO2(B) sheets: Surface reactivity and structural properties. Appl. Surf. Sci. 2014, 290, 180–187. [Google Scholar] [CrossRef]
- Mo, R.; Lei, Z.; Sun, K.; Rooney, D. Facile Synthesis of Anatase TiO2 Quantum-Dot/Graphene-Nanosheet Composites with Enhanced Electrochemical Performance for Lithium-Ion Batteries. Adv. Mater. 2013, 26, 2084–2088. [Google Scholar] [CrossRef] [PubMed]
- Chu, C.W.; Yang, H.; Hou, W.J.; Huang, J.; Li, G.; Yang, Y. Control of the nanoscale crystallinity and phase separation in polymer solar cells. Appl. Phys. Lett. 2008, 92, 103306. [Google Scholar] [CrossRef]
- Qu, S.; Yao, Q.; Wang, L.; Chen, Z.; Xu, K.; Zeng, H.; Shi, W.; Zhang, T.; Uher, C.; Chen, L. Highly anisotropic P3HT films with enhanced thermoelectric performance via organic small molecule epitaxy. NPG Asia Mater. 2016, 8, e292. [Google Scholar] [CrossRef]
- Kim, Y.; Cook, S.; Tuladhar, S.M.; Choulis, S.A.; Nelson, J.; Durrant, J.R.; Bradley, D.D.; Giles, M.; McCulloch, I.; Ha, C.S.; et al. A strong regioregularity effect in self-organizing conjugated polymer films and high-efficiency polythiophene:fullerene solar cells. Nat. Mater. 2006, 5, 197–203. [Google Scholar] [CrossRef]
- Brinkmann, M.J. Structure and morphology control in thin films of regioregular poly (3-hexylthiophene). Polym. Sci. Part B Polym. Phys. 2011, 49, 1218–1233. [Google Scholar] [CrossRef]
- Singh, R.K.; Kumar, J.; Singh, R.; Kant, R.; Rastogi, R.C.; Chand, S.; Kumar, V. Structure–conductivity correlation in ferric chloride-doped poly (3-hexylthiophene). New J. Phys. 2006, 8, 112. [Google Scholar] [CrossRef]
- Mombrú, D.; Romero, M.; Faccio, R.; Mombrú, A.W. Roles of amorphous and crystalline regions in determining the optical and electronic properties of donor:acceptor systems comprising poly (3-hexylthiophene) embedded with nitrogen/sulfur-doped graphene quantum dots. Polym. J. 2022, 54, 1465–1476. [Google Scholar] [CrossRef]
- Wang, W.; Chen, C.; Tollan, C.; Yang, F.; Qin, Y.; Knez, M. Efficient and controllable vapor to solid doping of the polythiophene P3HT by low temperature vapor phase infiltration. J. Mater. Chem. C 2017, 5, 2686. [Google Scholar] [CrossRef]
- Tsoi, W.C.; James, D.T.; Kim, J.S.; Nicholson, P.G.; Murphy, C.E.; Bradley, D.D.; Nelson, J.; Kim, J.S. The nature of in-plane skeleton Raman modes of P3HT and their correlation to the degree of molecular order in P3HT: PCBM blend thin films. J. Am. Chem. Soc. 2011, 133, 9834–9843. [Google Scholar] [CrossRef]
- Nightingale, J.; Wade, J.; Moia, D.; Nelson, J.; Kim, J.S. Impact of molecular order on polaron formation in conjugated polymers. J. Phys. Chem. C 2018, 122, 29129–29140. [Google Scholar] [CrossRef]
- Liang, Z.; Reese, M.O.; Gregg, B.A. Chemically treating poly (3-hexylthiophene) defects to improve bulk heterojunction photovoltaics. ACS Appl. Mater. Interfaces 2011, 3, 2042–2050. [Google Scholar] [CrossRef] [PubMed]
- Rahimi, K.; Botiz, I.; Agumba, J.O.; Motamen, S.; Stingelin, N.; Reiter, G. Light absorption of poly (3-hexylthiophene) single crystals. RSC Adv. 2014, 4, 11121. [Google Scholar] [CrossRef]
- Clark, J.; Silva, C.; Friend, R.H.; Spano, F.C. Role of intermolecular coupling in the photophysics of disordered organic semiconductors: Aggregate emission in regioregular polythiophene. Phys. Rev. Lett. 2007, 98, 206406. [Google Scholar] [CrossRef]
- Zhang, Y.; Foster, C.W.; Banks, C.E.; Shao, L.; Hou, H.; Zou, G.; Chen, J.; Huang, Z.; Ji, X. Graphene-Rich Wrapped Petal-Like Rutile TiO2 tuned by Carbon Dots for High-Performance Sodium Storage. Adv. Mater. 2016, 28, 9391–9399. [Google Scholar] [CrossRef]
- Chiguvare, Z.; Parisi, J. Current conduction in poly (3-Hexylthiophene) and in poly (3-hexylthiophene) doped [6,6]-phenyl C61-butyric acid methylester composite thin film devices. Z. Naturforsch. 2012, 67, 589–600. [Google Scholar] [CrossRef]
- Mombrú, D.; Romero, M.; Sandoval, M.G.; Faccio, R.; Mombrú, A.W. Role of surface defects on the adsorption of poly(9-vinylcarbazole) on TiO2 using the monomer as a donor:acceptor model. Appl. Surf. Sci. 2019, 487, 1104–1110. [Google Scholar] [CrossRef]
- Wong, F.; Perez, G.; Bonilla, M.; Colon-Santana, J.A.; Zhang, X.; Sharma, P.; Gruverman, A.; Dowben, P.A.; Rosa, L.G. Changing molecular band offsets in polymer blends of (P3HT/P(VDF–TrFE)) poly (3-hexylthiophene) and poly (vinylidene fluoride with trifluoroethylene) due to ferroelectric poling. RSC Adv. 2014, 4, 3020–3027. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mombrú, D.; Romero, M.; Faccio, R.; Mombrú, A.W. On the Donor: Acceptor Features for Poly(3-hexylthiophene): TiO2 Quantum Dots Hybrid Materials Obtained via Water Vapor Flow Assisted Sol-Gel Growth. Polymers 2023, 15, 1706. https://doi.org/10.3390/polym15071706
Mombrú D, Romero M, Faccio R, Mombrú AW. On the Donor: Acceptor Features for Poly(3-hexylthiophene): TiO2 Quantum Dots Hybrid Materials Obtained via Water Vapor Flow Assisted Sol-Gel Growth. Polymers. 2023; 15(7):1706. https://doi.org/10.3390/polym15071706
Chicago/Turabian StyleMombrú, Dominique, Mariano Romero, Ricardo Faccio, and Alvaro W. Mombrú. 2023. "On the Donor: Acceptor Features for Poly(3-hexylthiophene): TiO2 Quantum Dots Hybrid Materials Obtained via Water Vapor Flow Assisted Sol-Gel Growth" Polymers 15, no. 7: 1706. https://doi.org/10.3390/polym15071706
APA StyleMombrú, D., Romero, M., Faccio, R., & Mombrú, A. W. (2023). On the Donor: Acceptor Features for Poly(3-hexylthiophene): TiO2 Quantum Dots Hybrid Materials Obtained via Water Vapor Flow Assisted Sol-Gel Growth. Polymers, 15(7), 1706. https://doi.org/10.3390/polym15071706








