Near-Surface Nanomechanics of Medical-Grade PEEK Measured by Atomic Force Microscopy
Abstract
1. Introduction
2. Materials and Methods
2.1. Samples, AFM Setup and Calibration
2.2. Indentation Modulus Calculation
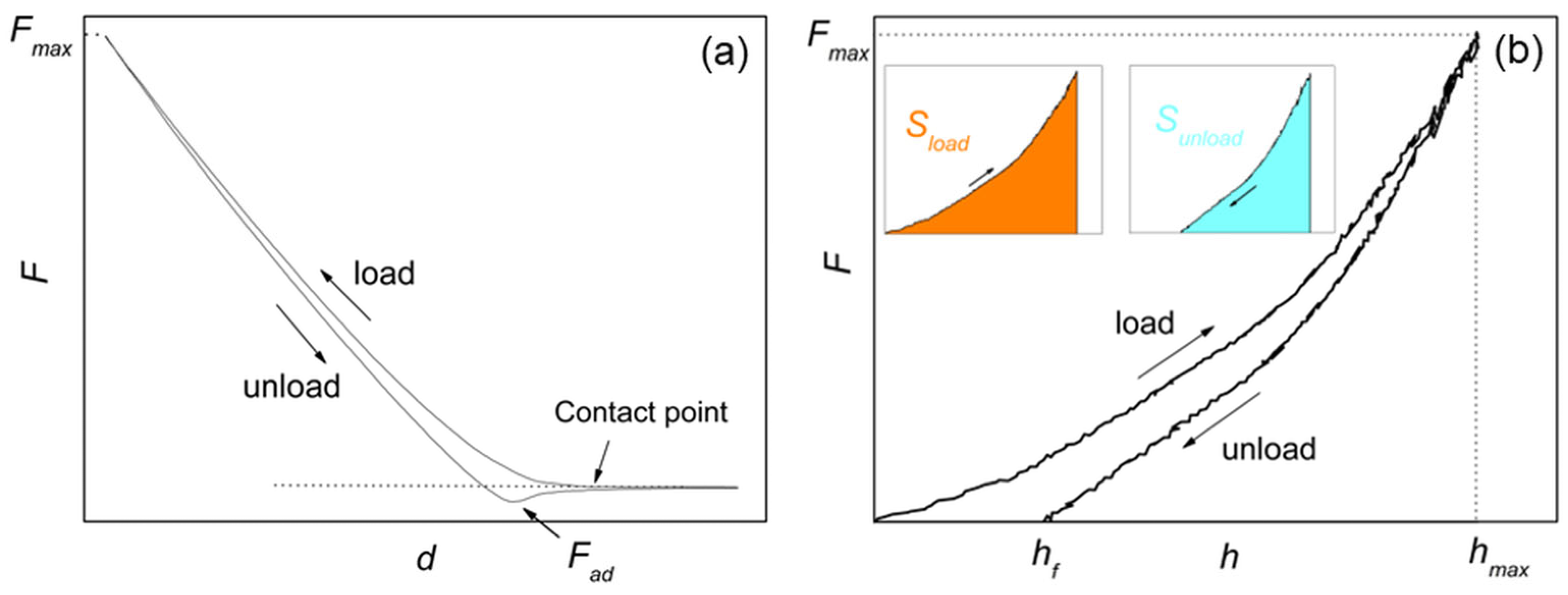
2.3. Data Processing and Analysis
3. Results
3.1. Checking the Elastic Response of the Surface
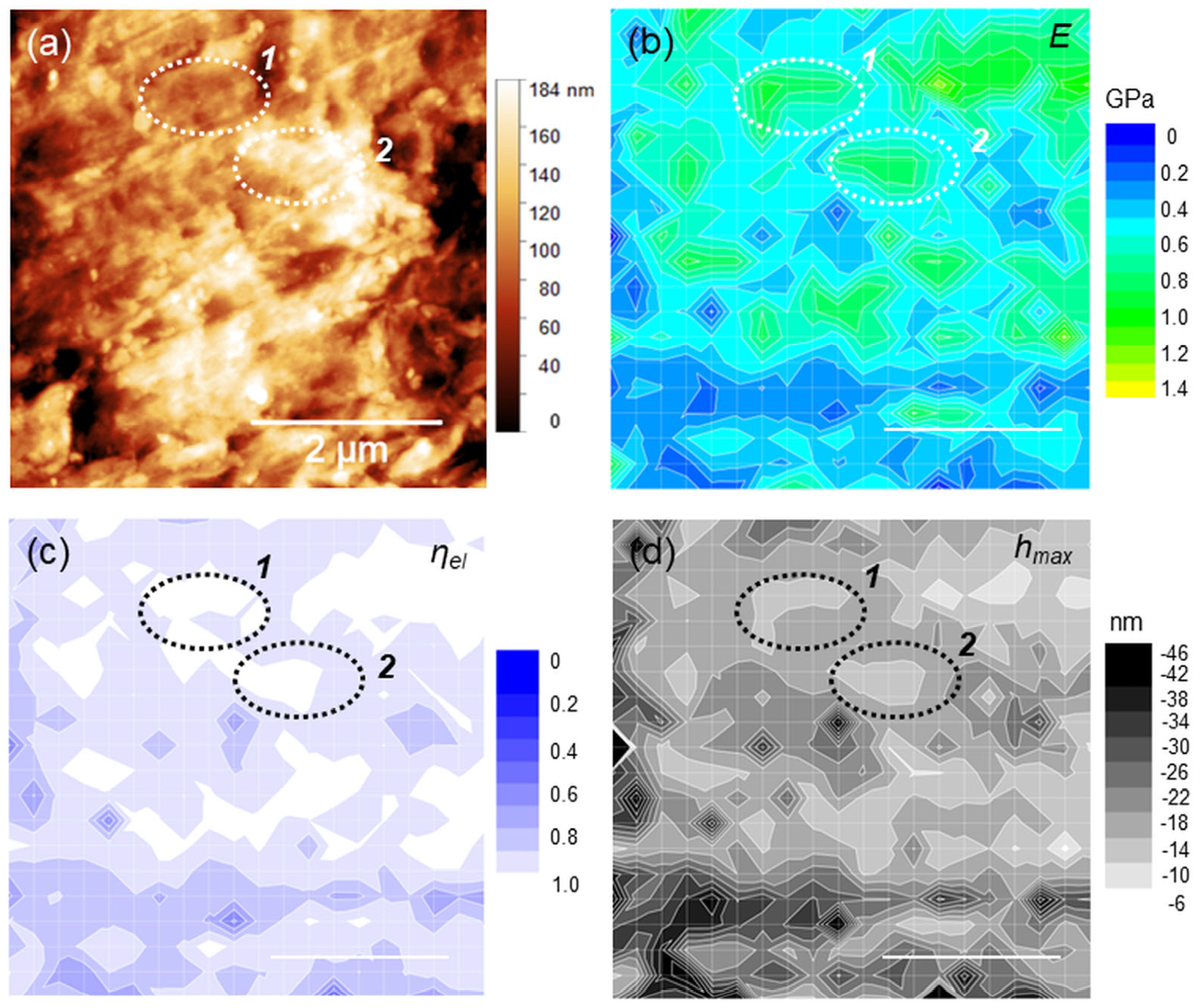
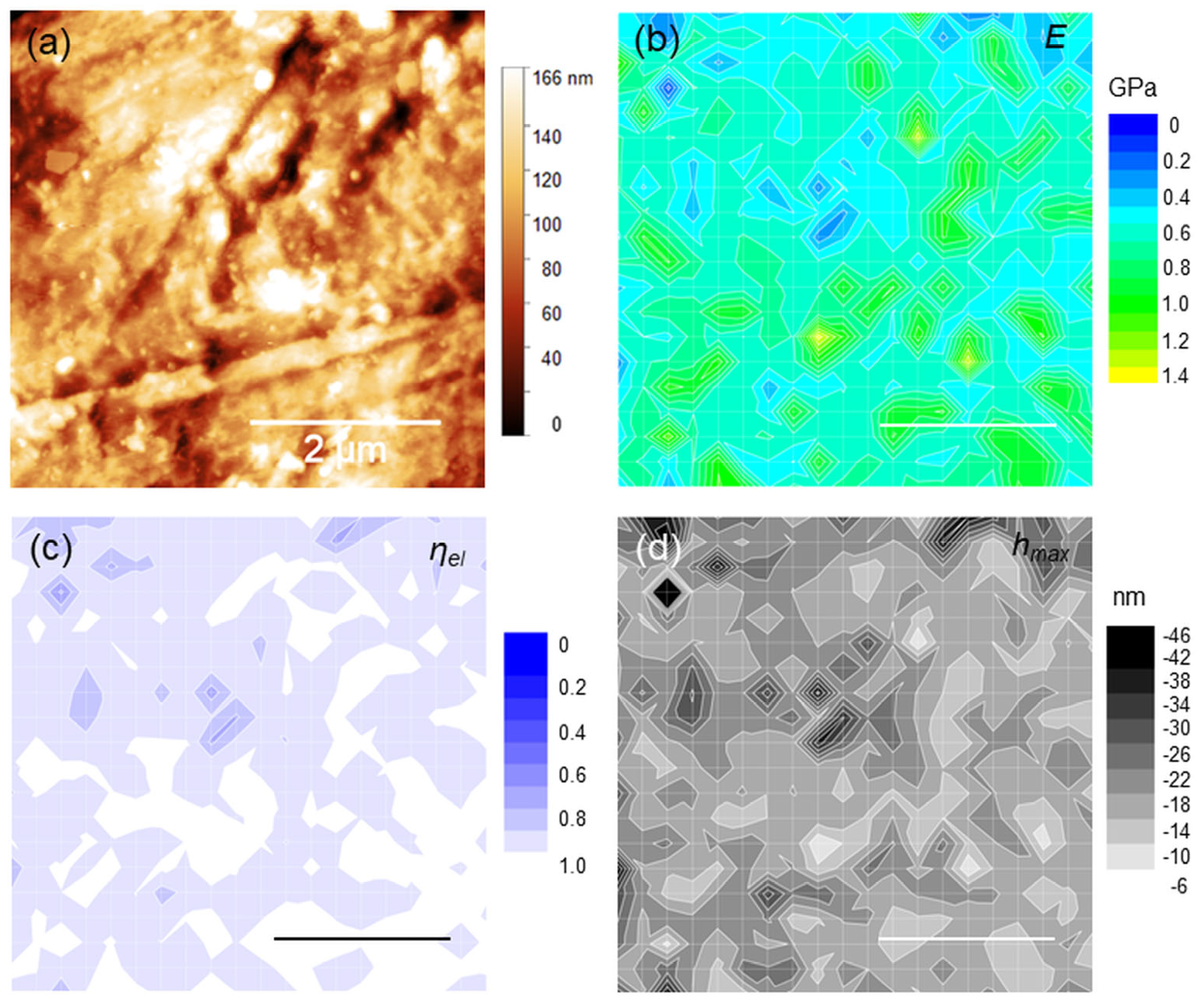
3.2. Force-Mapping Results
4. Discussion
4.1. Some Methodological Remarks: Choise of the Cantilever, Measured Stiffness
4.2. Considerations on the Nanoscale Mechanics of PEEK
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Díez-Pascual, A.M.; Naakh, M.; Marco, C.; Ellis, G.; Gómez-Fatou, M.A. High-performance nanocomposites based on polyetherketones. Prog. Mater. Sci. 2012, 57, 1106–1190. [Google Scholar] [CrossRef]
- Kurtz, S.M.; Devine, J.N. PEEK biomaterials in trauma, orthopedic, and spinal implants. Biomaterials 2007, 28, 4845–4869. [Google Scholar] [CrossRef] [PubMed]
- Massaad, E.; Fatima, N.; Kiapour, A.; Hadzipasic, M.; Shankar, G.M.; Shin, J.H. Polyetheretherketone versus titanium cages for posterior lumbar interbody fusion: Meta-analysis and review of the literature. Neurospine 2020, 17, 125–135. [Google Scholar] [CrossRef] [PubMed]
- Torstrick, F.B.; Klosterho, B.S.; Westerlund, L.E.; Foley, K.T.; Gochuico, J.; Lee, C.S.; Gall, K.; Safranski, D.L. Impaction durability of porous polyether-ether-ketone (PEEK) and titanium-coated PEEK interbody fusion devices. Spine J. 2018, 18, 857–865. [Google Scholar] [CrossRef] [PubMed]
- Mounir, M.; Atef, M.; Abou-Elfetouh, A.; Hakam, M.M. Titanium and polyether ether ketone (PEEK) patient-specific sub-periosteal implants: Two novel approaches for rehabilitation of the severely atrophic anterior maxillary ridge. Int. J. Oral Maxillofac. Surg. 2018, 47, 658–664. [Google Scholar] [CrossRef] [PubMed]
- Alonso-Rodriguez, E.; Cebrian, J.L.; Nieto, M.J.; Del Castillo, J.L.; Hernandez-Godoy, J.; Burgueno, M. Polyetheretherketone custom-made implants for craniofacial defects: Report of 14 cases and review of the literature. J. Craniomaxillofac. Surg. 2015, 43, 1232–1238. [Google Scholar] [CrossRef]
- AL-Rabab’ah, M.; Hamadneh, W.; Alsalem, I.; Khraisat, A.; Karaky, A.A. Use of high performance polymers as dental implant abutments and frameworks: A case series report. J. Prosthodont. 2019, 28, 365–372. [Google Scholar] [CrossRef]
- Rahmitasari, F.; Ishida, Y.; Kurahashi, K.; Matsuda, T.; Watanabe, M.; Ichikawa, T. PEEK with reinforced materials and modifications for dental implant applications. Dent. J. 2017, 5, 35. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, H.; Komasa, S.; Kusumoto, T.; Kuwamoto, S.; Okunishi, T.; Kobayashi, Y.; Hashimoto, Y.; Sekino, T.; Okazaki, J. Immunomodulatory properties and osteogenic activity of polyetheretherketone coated with titanate nanonetwork structures. Int. J. Mol. Sci. 2022, 23, 612. [Google Scholar] [CrossRef]
- Yu, D.; Lei, X.; Zhu, H. Modification of polyetheretherketone (PEEK) physical features to improve osteointegration. J. Zhejiang Univ. Sci. B 2022, 23, 189–203. [Google Scholar] [CrossRef]
- Almasi, D.; Iqbal, N.; Sadeghi, M.; Sudin, I.; Rafiq, M.; Kadir, A.; Kamaru, T. Preparation methods for improving PEEK’s bioactivity for orthopedic and dental application: A review. Int. J. Biomater. 2016, 2016, 8202653. [Google Scholar] [CrossRef]
- Buck, E.; Li, H.; Cerruti, M. Surface modification strategies to improve the osseointegration of poly(etheretherketone) and its composites. Macromol. Biosci. 2020, 20, 1900271. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Yuen, C.Y.; Yeung, K.W.; Tjong, S.C. Sintered hydroxyapatite/polyetheretherketone nanocomposites: Mechanical behavior and biocompatibility aspects. Adv. Eng. Mater. 2012, 14, B155–B165. [Google Scholar] [CrossRef]
- Chan, K.W.; Liao, C.Z.; Wong, H.M.; Yeung, K.W.; Tjong, S.C. Preparation of polyetheretherketone composites with nanohydroxyapatite rods and carbon nanofibers having high strength, good biocompatibility and excellent thermal stability. RSC Adv. 2016, 6, 19417–19429. [Google Scholar] [CrossRef]
- Liu, C.; Chan, K.W.; Shen, J.; Liao, C.Z.; Yeung, K.W.; Tjong, S.C. Polyetheretherketone hybrid composites with bioactive nanohydroxyapatite and multiwalled carbon nanotube fillers. Polymers 2016, 8, 425. [Google Scholar] [CrossRef] [PubMed]
- Han, Z.J.; Rider, A.E.; Ishaq, M.; Kumar, S.; Kondyurin, A.; Bilek, M.M.; Levchenko, I.; Ostrokov, K. Carbon nanostructures for hard tissue engineering. RSC Adv. 2013, 3, 11058–11072. [Google Scholar] [CrossRef]
- Hao, Z.C.; Song, Z.H.; Huang, J.; Hiang, K.; Panetta, A.; Gu, Z.; Wu, J. The scaffold microenvironment for stem cell based bone tissue engineering. Biomater. Sci. 2017, 5, 1382–1392. [Google Scholar] [CrossRef]
- Rangel, A.L.R.; Falentin-Daudré, C.; da Silva Pimentel, B.N.A.; Vergani, C.E.; Migonney, V.; Alves Claro, A.P.R. Nanostructured titanium alloy surfaces for enhanced osteoblast response: A combination of morphology and chemistry. Surf. Coat. Technol. 2020, 383, 125226. [Google Scholar] [CrossRef]
- Dinescu, S.; Ionita, M.; Ignat, S.-R.; Costache, M.; Hermenean, A. Graphene oxide enhances chitosan-based 3D scaffold properties for bone tissue engineering. Int. J. Mol. Sci. 2019, 20, 5077. [Google Scholar] [CrossRef]
- Silva, M.; Alves, N.M.; Paiva, M.C. Graphene-polymer nanocomposites for biomedical applications. Polym. Adv. Technol. 2018, 29, 687–700. [Google Scholar] [CrossRef]
- Ouyang, L.; Chen, M.; Wang, D.; Lu, T.; Wang, H.; Meng, F.; Yang, Y.; Ma, J.; Yeung, K.W.K.; Liu, X. Nano Textured PEEK Surface for Enhanced Osseointegration. ACS Biomater. Sci. Eng. 2019, 5, 1279–1289. [Google Scholar] [CrossRef]
- Fu, Q.; Gabriel, M.; Schmidt, F.; Muller, W.D.; Schwitalla, A.D. The impact of different low-pressure plasma types on the physical, chemical and biological surface properties of PEEK. Dent. Mater. 2021, 37, e15–e22. [Google Scholar] [CrossRef] [PubMed]
- Hickey, D.J.; Lorman, B.; Fedder, I.L. Improved response of osteoprogenitor cells to titanium plasma-sprayed PEEK surfaces. Colloids Surf. B Biointerfaces 2019, 175, 509–516. [Google Scholar] [CrossRef] [PubMed]
- Chaudhuri, O.; Cooper-White, J.; Janmey, P.A.; Mooney, D.J.; Shenoy, V.B. Effects of extracellular matrix viscoelasticity on cellular behaviour. Nature 2020, 584, 535–546. [Google Scholar] [CrossRef] [PubMed]
- Califano, J.P.; Reinhart-King, C.A. Substrate stiffness and cell area predict cellular traction stresses in single cells and cells in contact. Cell. Mol. Bioeng. 2010, 3, 68–75. [Google Scholar] [CrossRef]
- Song, J.; Shi, H.; Liao, Z.; Wang, S.; Liu, Y.; Liu, W.; Peng, Z. Study on the Nanomechanical and Nanotribological Behaviors of PEEK and CFRPEEK for Biomedical Applications. Polymers 2018, 10, 142. [Google Scholar] [CrossRef]
- Liao, C.; Li, Y.; Tjong, S.C. Polyetheretherketone and its composites for bone replacement and regeneration. Polymers 2020, 12, 2858. [Google Scholar] [CrossRef]
- Nobile, S.; Nobile, L. Nanotechnology for biomedical applications: Recent advances in neurosciences and bone tissue engineering. Polym. Eng. Sci. 2017, 57, 644–650. [Google Scholar] [CrossRef]
- Tjong, S.C. Nanocrystalline Materials: Their Synthesis-Structure-Property Relationships and Applications, 2nd ed.; Elsevier: London, UK, 2013; ISBN 9780124077966. [Google Scholar]
- Menezes, B.R.; Rodrigues, K.F.; Fonseca, B.C.; Ribas, R.G.; Montanheiro, T.L.; Thim, G.P. Recent advances in the use of carbon nanotubes as smart biomaterials. J. Mater. Chem. B 2019, 7, 1343–1360. [Google Scholar] [CrossRef]
- Imaninezhad, M.; Schober, J.; Griggs, D.; Ruminski, P.; Kuljanishvili, J.; Zustiak, S.P. Cell attachment and spreading on carbon nanotubes is facilitated by integrin binding. Front. Bioeng. Biotechnol. 2018, 6, 129. [Google Scholar] [CrossRef]
- Molazemhosseini, A.; Tourani, H.; Naimi-Jamal, M.R.; Khavandi, A. Nanoindentation and nanoscratching responses of PEEK based hybrid composites reinforced with short carbon fibers and nano-silica. Polym. Test. 2013, 32, 525–534. [Google Scholar] [CrossRef]
- Collinson, D.W.; Sheridan, R.J.; Palmeri, M.J.; Brinson, L.C. Best practices and recommendations for accurate nanomechanical characterization of heterogeneous polymer systems with atomic force microscopy. Prog. Polym. Sci. 2021, 119, 101420. [Google Scholar] [CrossRef]
- Magonov, S.H.; Reneker, D.H. Characterization of polymer surfaces with atomic force microscopy. Annu. Rev. Mater. Sci. 1997, 27, 175–222. [Google Scholar] [CrossRef]
- Butt, H.J.; Cappella, B.; Kappl, M. Force measurements with the atomic force microscope: Technique, interpretation and applications. Surf. Sci. Rep. 2005, 59, 1–152. [Google Scholar] [CrossRef]
- Olubowale, O.H.; Biswas, S.; Azom, G.; Prather, B.L.; Owoso, S.D.; Rinee, K.C.; Marroquin, K.; Gates, K.A.; Chambers, M.B.; Xu, A.; et al. “May the force be with you!” Force–volume mapping with atomic force microscopy. ACS Omega 2021, 6, 25860–25875. [Google Scholar] [CrossRef] [PubMed]
- Garcìa, R. Nanomechanical mapping of soft materials with the atomic force microscope: Methods, theory and applications. Chem. Soc. Rev. 2020, 49, 5850–5884. [Google Scholar] [CrossRef]
- Tranchida, D.; Kiflie, Z.; Acierno, S.; Piccarolo, S. Nanoscale mechanical characterization of polymers by atomic force microscopy (AFM) nanoindentations: Viscoelastic characterization of a model material. Meas. Sci. Technol. 2009, 20, 095702. [Google Scholar] [CrossRef]
- Yang, Y. Sensitivity of nanoindentation strain rate in poly(ester-ester-ketone) using atomic force microscopy. Polym. Test. 2016, 53, 85–88. [Google Scholar] [CrossRef]
- Qian, W.; Li, W.; Nguyen, C.; Johnson, T.J.; Turner, J.A. Quantitative nanoscale measurements of the thermomechanical properties of poly-ether-etherketone (PEEK). J. Polym. Sci. 2020, 58, 1544–1552. [Google Scholar] [CrossRef]
- Griepentrog, M.; Krämer, G.; Cappella, B. Comparison of nanoindentation and AFM methods for the determination of mechanical properties of polymers. Polym. Test. 2013, 32, 455–460. [Google Scholar] [CrossRef]
- Bontempi, M.; Salamanna, F.; Capozza, R.; Visani, A.; Fini, M.; Gambardella, A. Nanomechanical mapping of hard tissues by atomic force microscopy: An application to cortical bone. Materials 2022, 15, 7512. [Google Scholar] [CrossRef] [PubMed]
- Gambardella, A.; Marchiori, G.; Maglio, M.; Russo, A.; Rossi, C.; Visani, A.; Fini, M. Determination of the spatial anisotropy of the surface microstructures of different implant materials: An atomic force microscopy study. Materials 2021, 14, 4803. [Google Scholar] [CrossRef] [PubMed]
- Kontomaris, S.V.; Malamou, A. Hertz model or Oliver & Pharr analysis? Tutorial regarding AFM nanoindentation experiments on biological samples. Mater. Res. Express 2020, 7, 033001. [Google Scholar] [CrossRef]
- Kontomaris, S.V.; Malamou, A. A novel approximate method to calculate the force applied on an elastic half space by a rigid sphere. Eur. J. Phys. 2021, 42, 025010. [Google Scholar] [CrossRef]
- Van Rossum, G.; Drake, F.L. Python 3 Reference Manual; CreateSpace: Scotts Valley, CA, USA, 2009. [Google Scholar]
- Verma, R.; Marand, H.; Hsiao, B. Morphological changes during secondary crystallization and subsequent melting in Poly(ether ether ketone) as studied by real time small angle x-ray scattering. Macromolecules 1996, 29, 7767–7775. [Google Scholar] [CrossRef]
- Hosoya, R.; Morita, H.; Nakajima, K. Analysis of nanomechanical properties of polyethylene using molecular dynamics simulation. Macromolecules 2020, 53, 6163–6172. [Google Scholar] [CrossRef]
- Doumeng, M.; Makhlouf, L.; Berthet, F.; Marsan, O.; Delbé, K.; Denape, J.; Chabert, F. A comparative study of the crystallinity of polyetheretherketone by using density, DSC, XRD, and Raman spectroscopy techniques. Polym. Test. 2021, 93, 106878. [Google Scholar] [CrossRef]
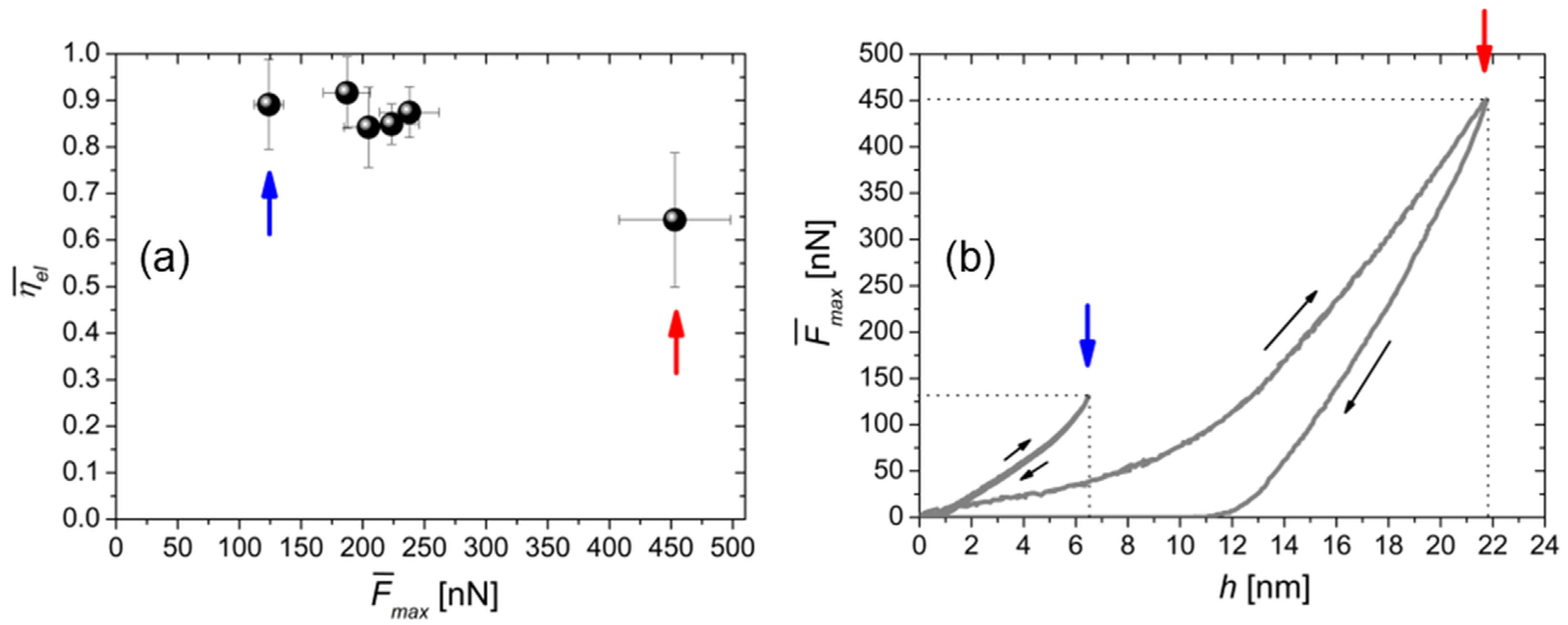
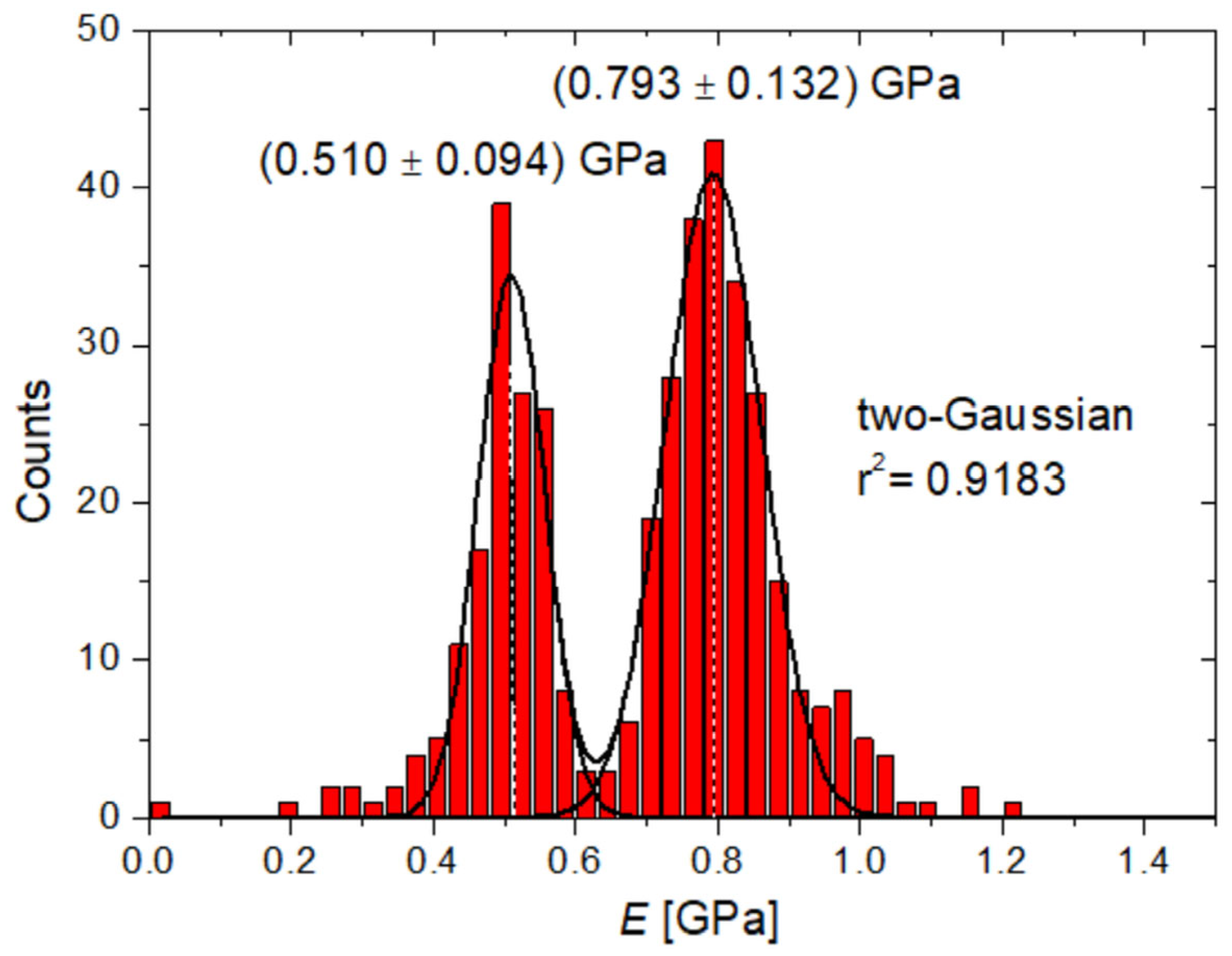
| ± σ [nN] | E1 ± σ1 [GPa] | E2 ± σ2 [GPa] | r2 |
|---|---|---|---|
| 120 ± 11 | - | (1.37 ± 0.85) 1 | (0.8371) 1 |
| 187 ± 19 | 0.510 ± 0.094 | 0.793 ± 0.132 | 0.9183 |
| 205 ± 21 | 0.509 ± 0.210 | 0.828 ± 0.106 | 0.8859 |
| 223 ± 22 | 0.634 ± 0.180 | 0.917 ± 0.142 | 0.9306 |
| 238 ± 25 | 0.626 ± 0.160 | 0.982 ± 0.107 | 0.9031 |
| 453 ± 49 | 1.04 ± 0.374 | 1.98 ± 1.37 | 0.6944 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bontempi, M.; Capozza, R.; Visani, A.; Fini, M.; Giavaresi, G.; Gambardella, A. Near-Surface Nanomechanics of Medical-Grade PEEK Measured by Atomic Force Microscopy. Polymers 2023, 15, 718. https://doi.org/10.3390/polym15030718
Bontempi M, Capozza R, Visani A, Fini M, Giavaresi G, Gambardella A. Near-Surface Nanomechanics of Medical-Grade PEEK Measured by Atomic Force Microscopy. Polymers. 2023; 15(3):718. https://doi.org/10.3390/polym15030718
Chicago/Turabian StyleBontempi, Marco, Rosario Capozza, Andrea Visani, Milena Fini, Gianluca Giavaresi, and Alessandro Gambardella. 2023. "Near-Surface Nanomechanics of Medical-Grade PEEK Measured by Atomic Force Microscopy" Polymers 15, no. 3: 718. https://doi.org/10.3390/polym15030718
APA StyleBontempi, M., Capozza, R., Visani, A., Fini, M., Giavaresi, G., & Gambardella, A. (2023). Near-Surface Nanomechanics of Medical-Grade PEEK Measured by Atomic Force Microscopy. Polymers, 15(3), 718. https://doi.org/10.3390/polym15030718








