Local and Global Order in Dense Packings of Semi-Flexible Polymers of Hard Spheres
Abstract
1. Introduction
2. Model and Methods
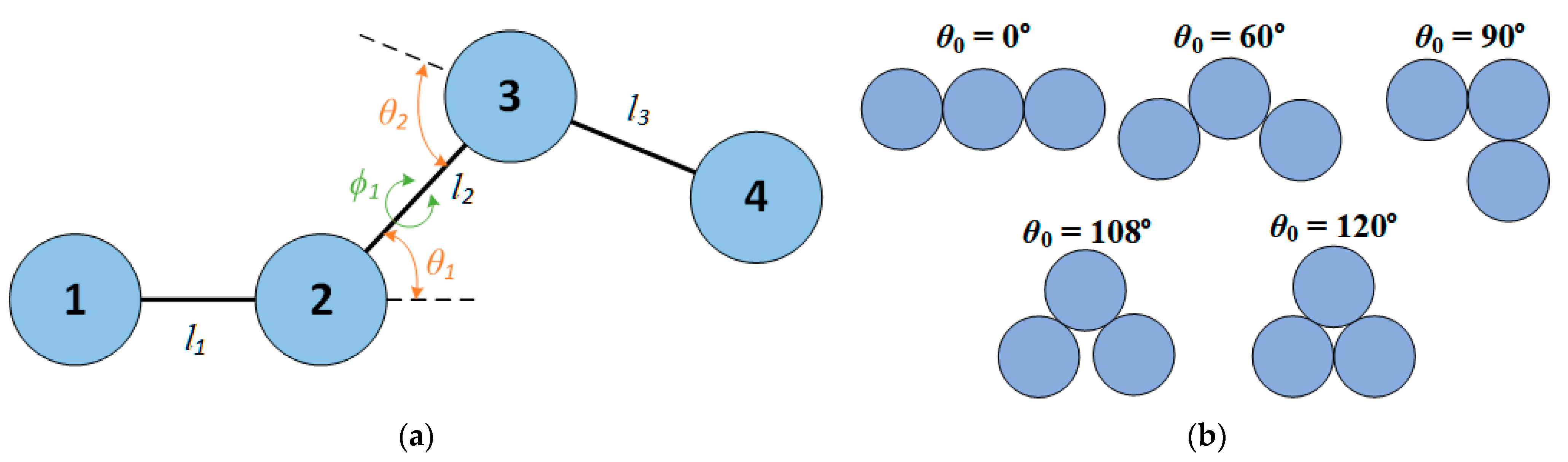
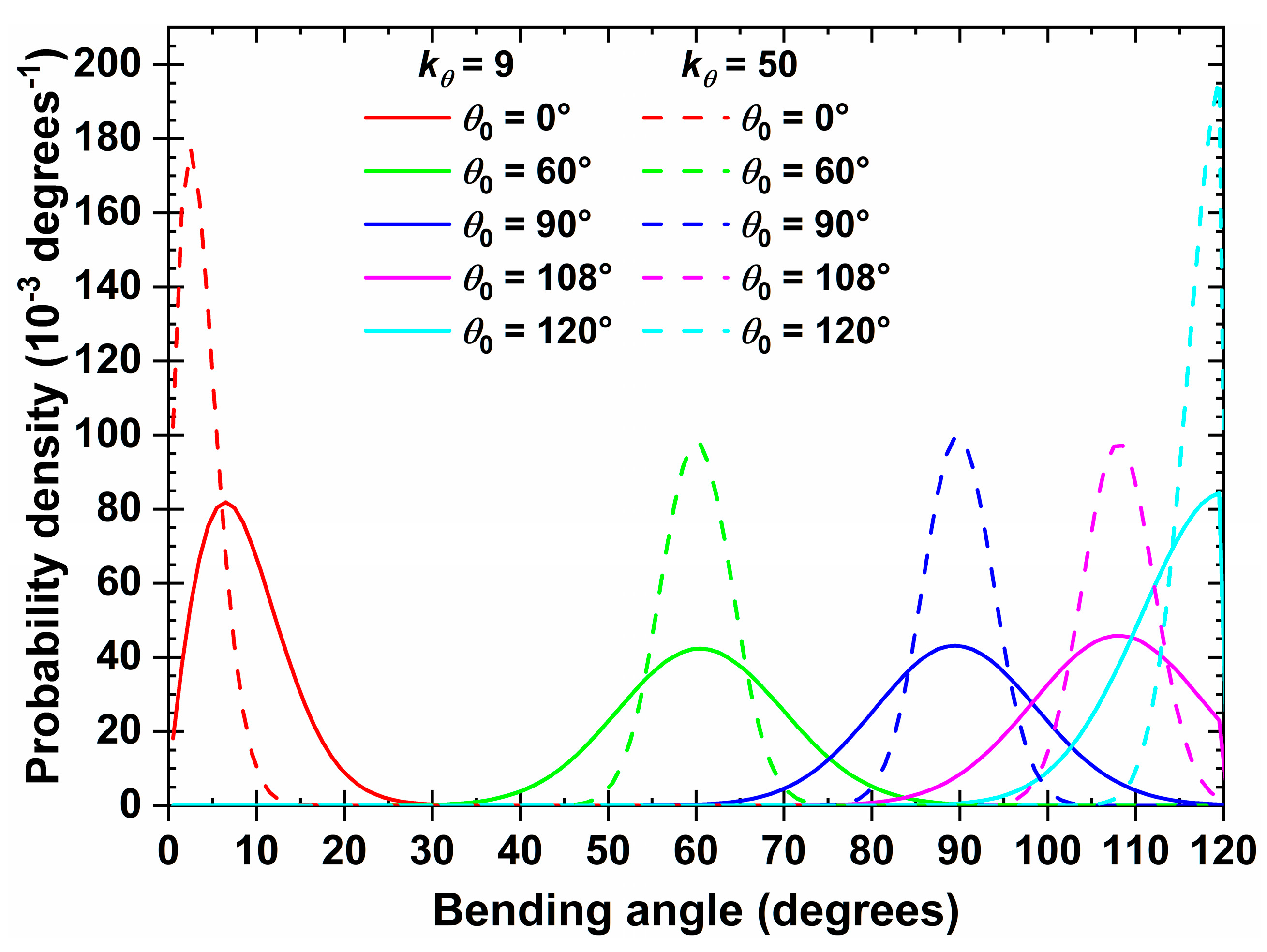
2.1. Molecular Model and Systems studied
2.2. Simulation Algorithm
2.3. Global (Long-Range) Orientational Order
2.4. Local Order: Characteristic Crystallographic Element Norm
3. Results
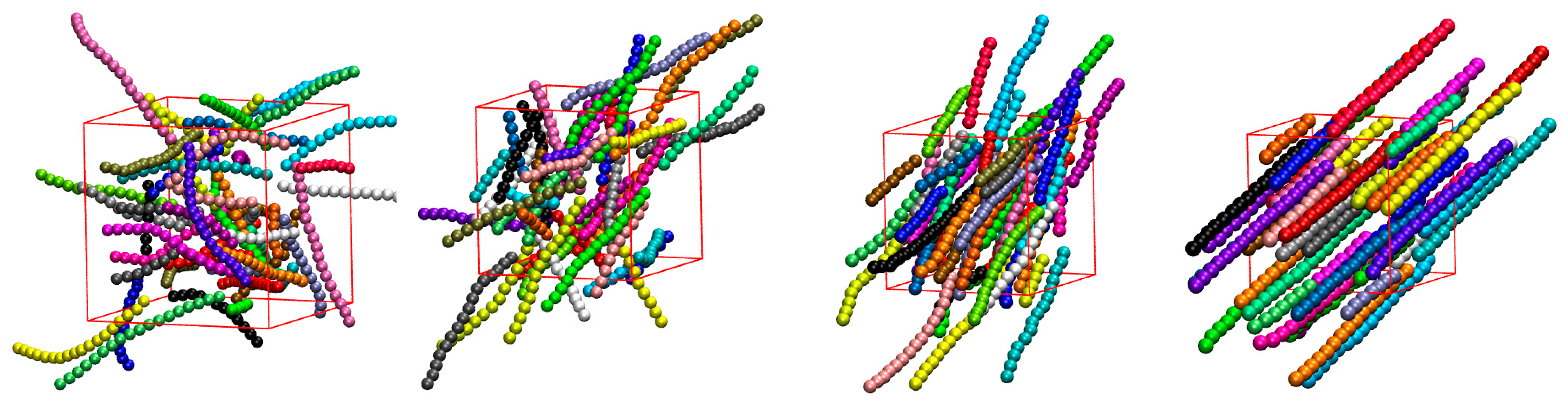
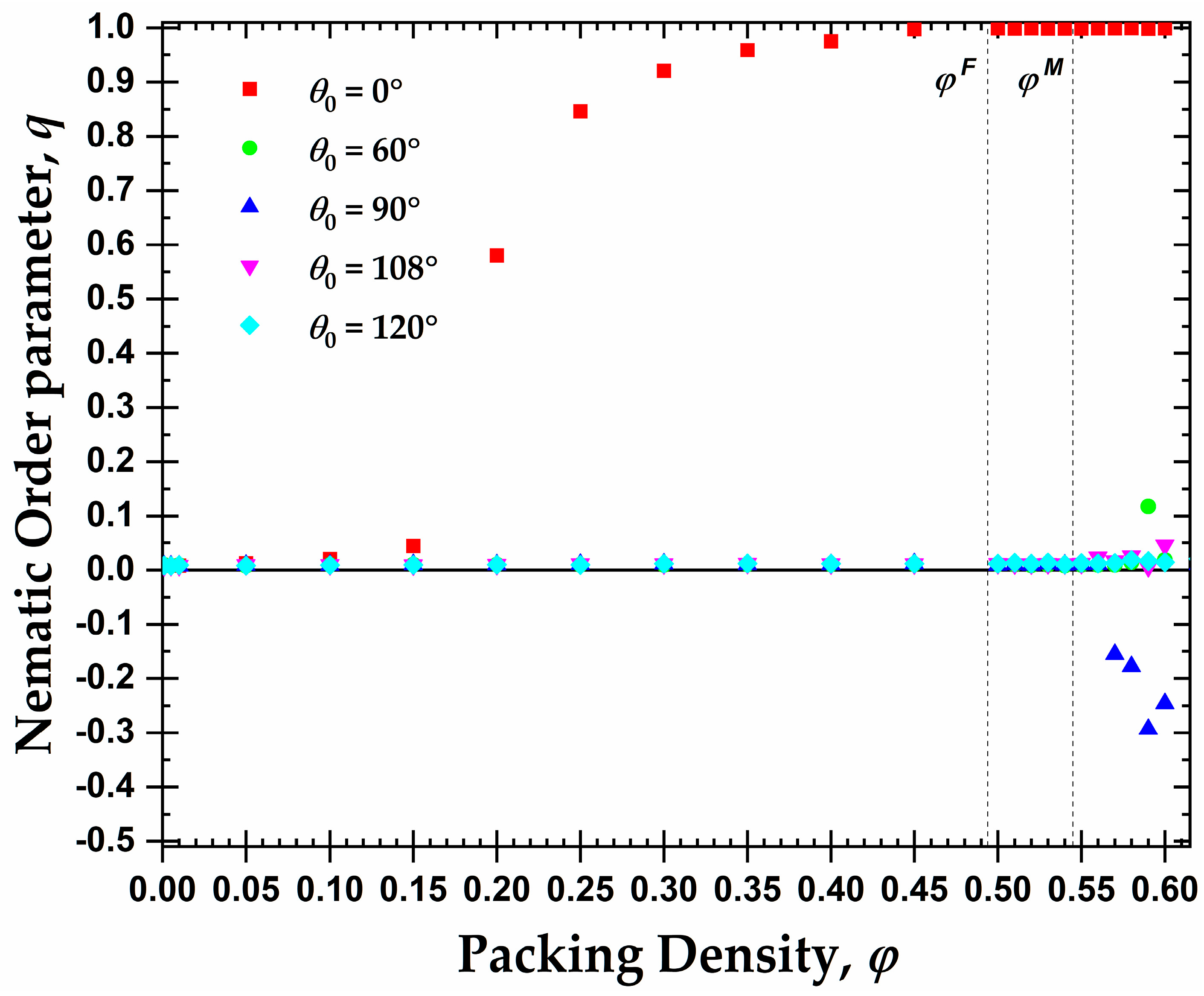
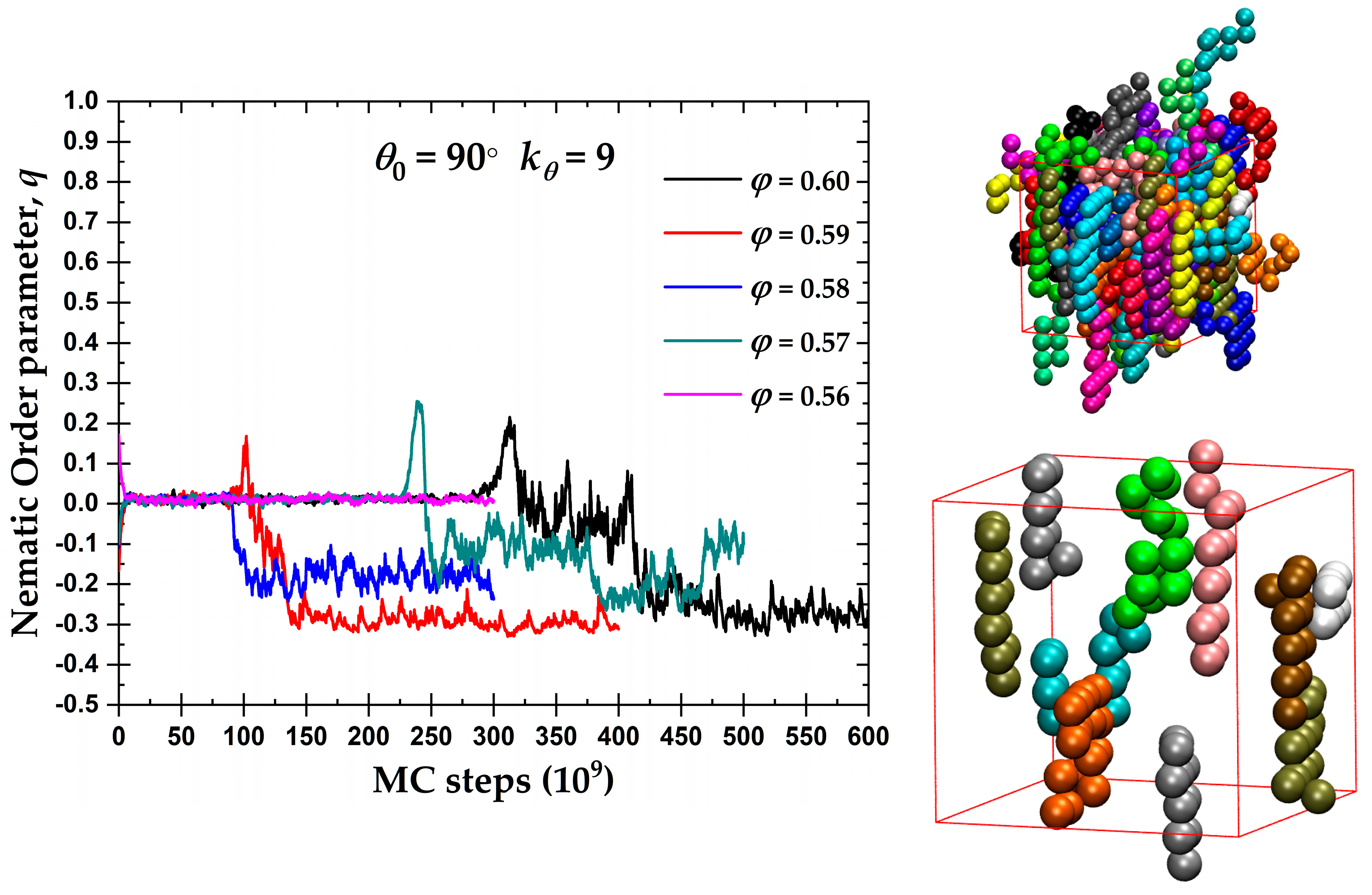
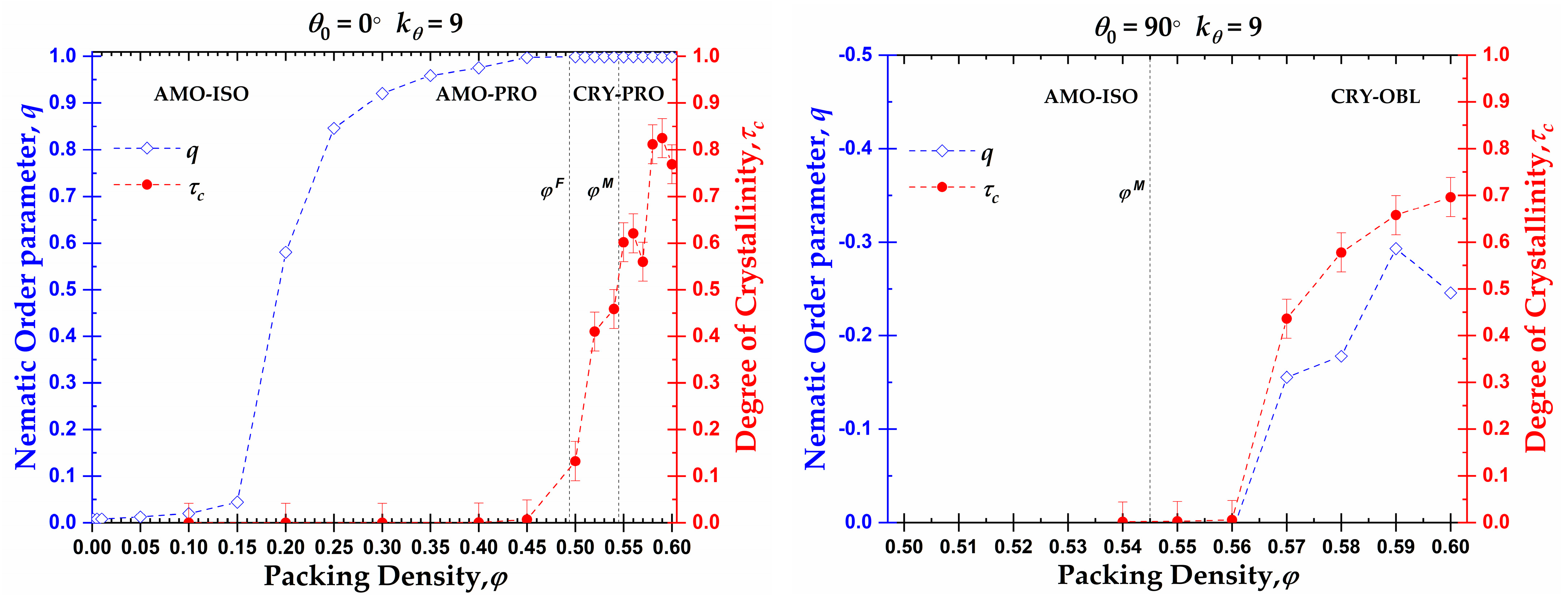
3.1. Global Orientational Order
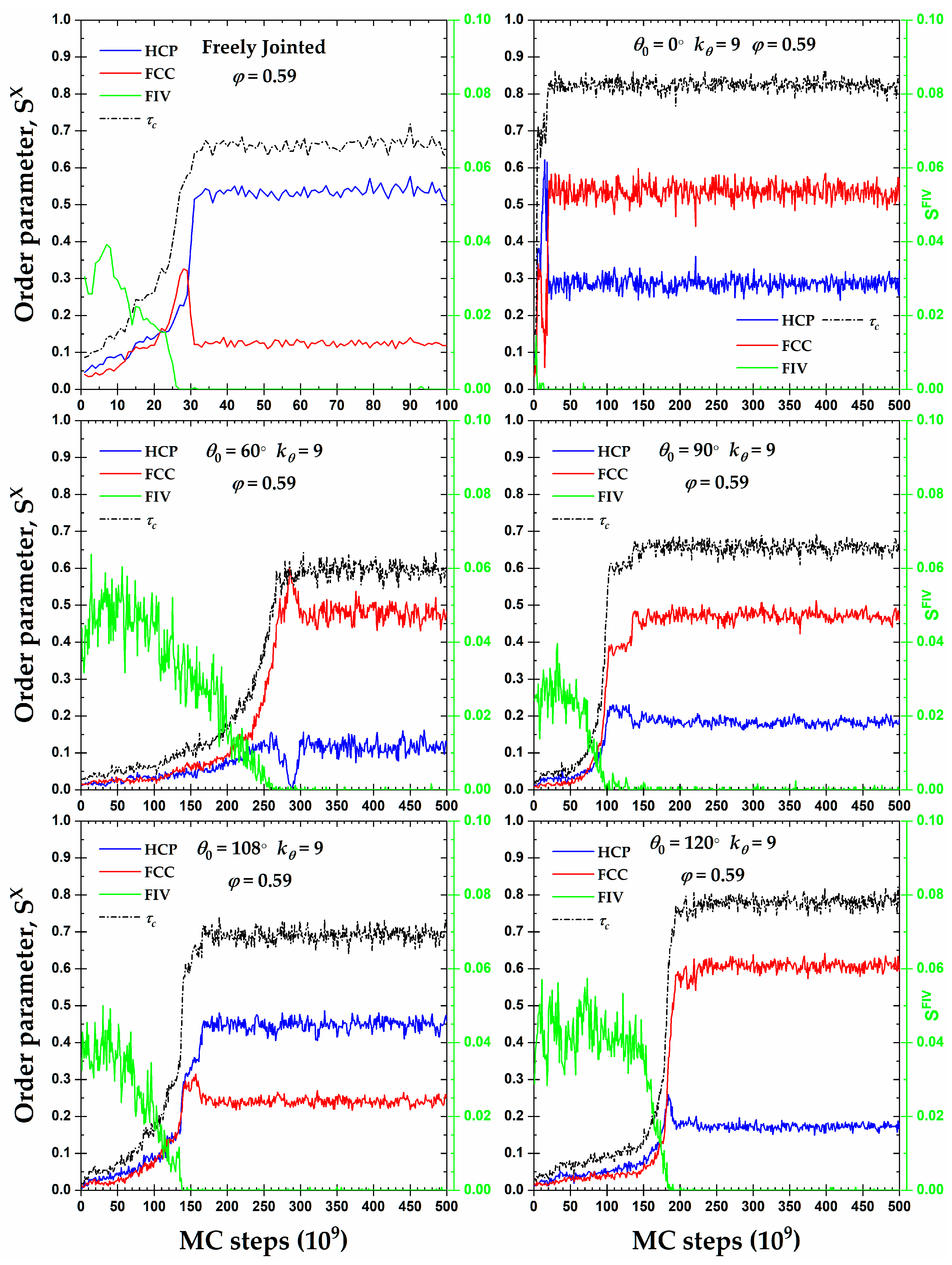
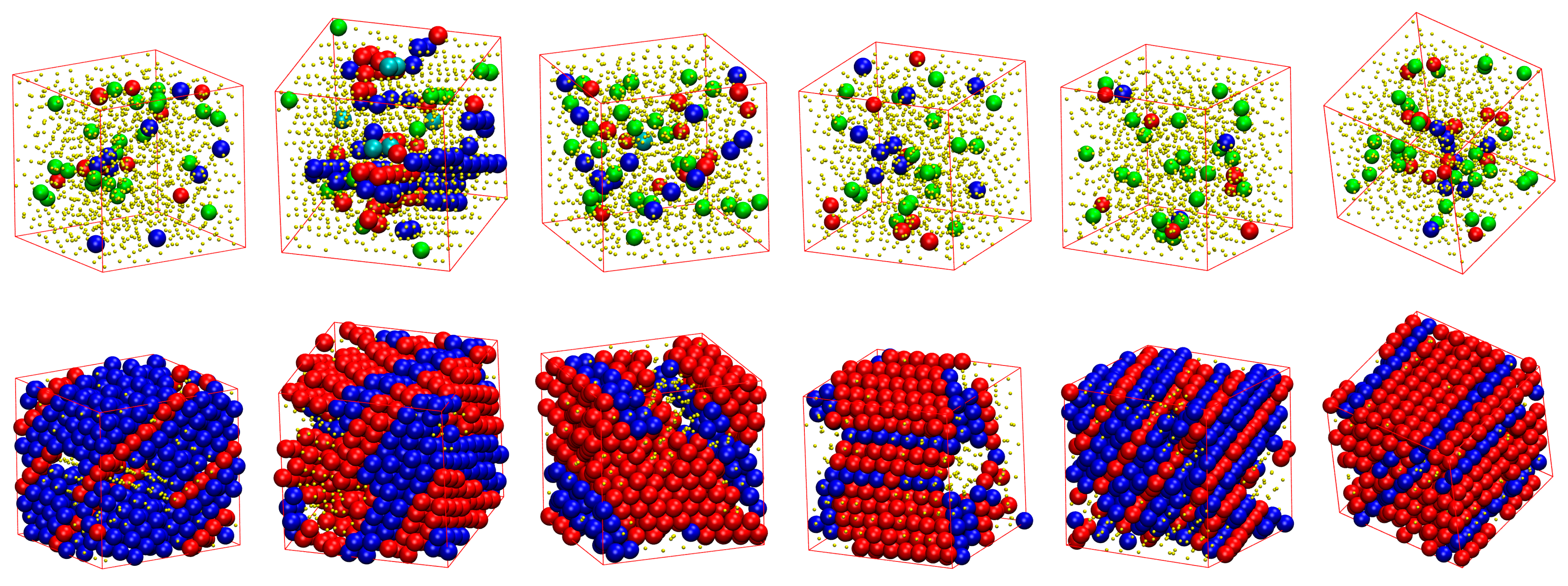
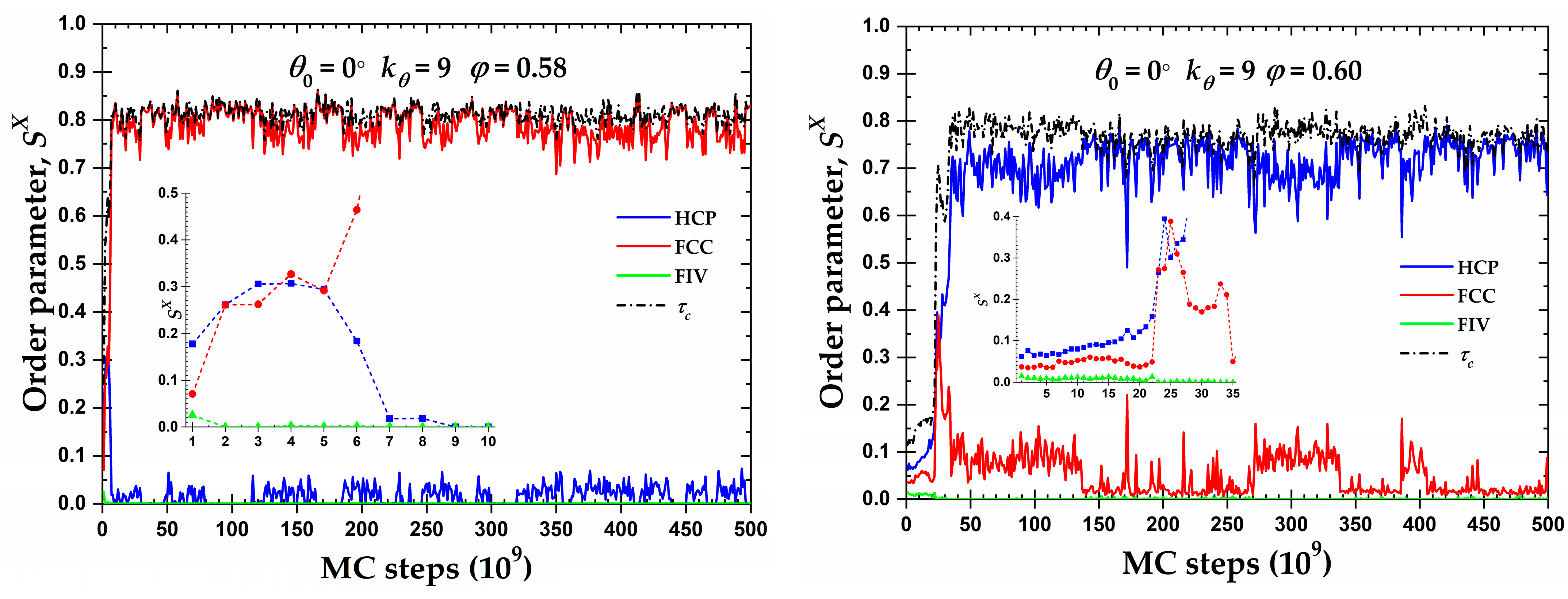
3.2. Local Order: Crystal Nucleation and Growth
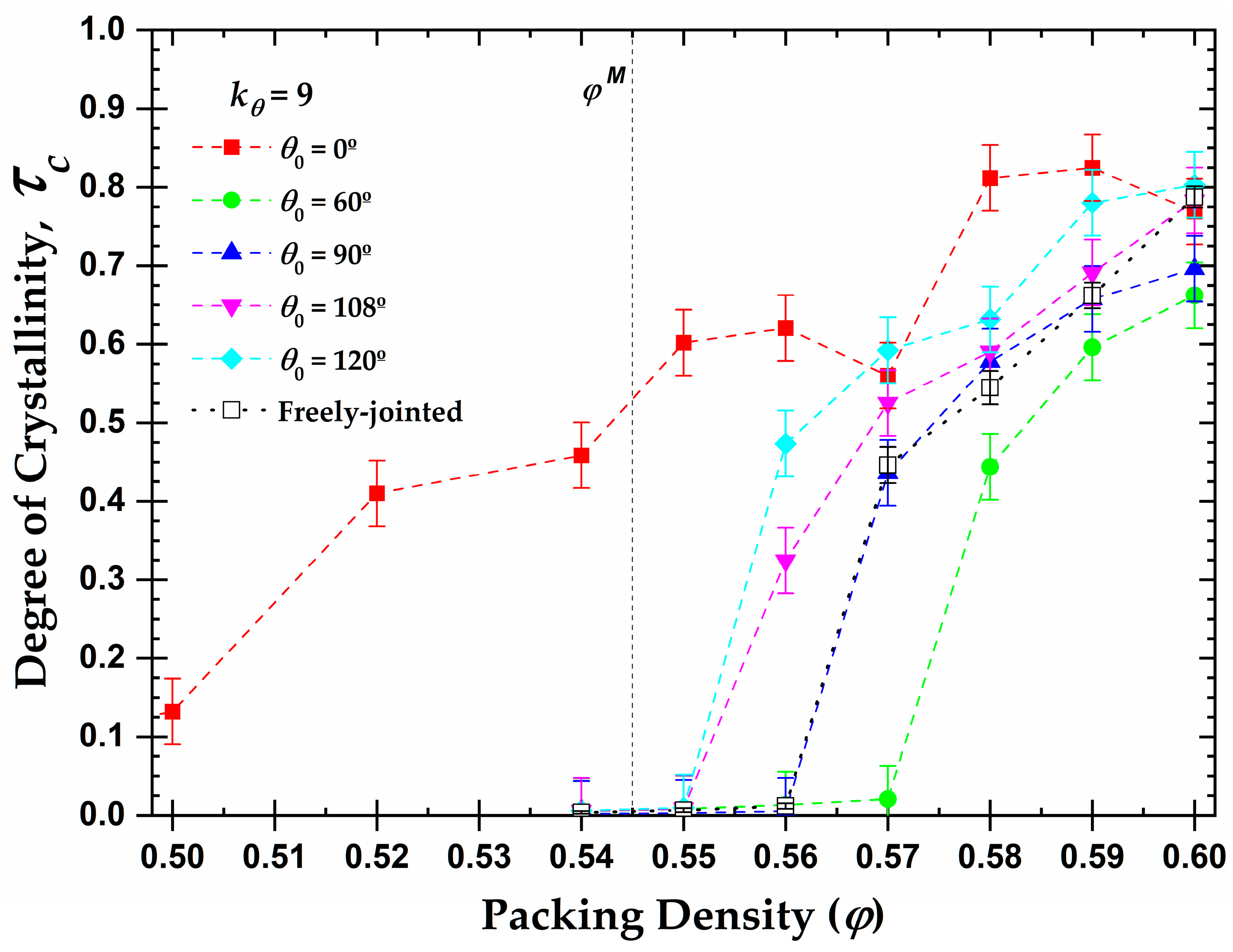
3.3. Local Order: Total Crystallinity
4. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| 2D | Two dimensions |
| 3D | Three dimensions |
| AMO | Amorphous |
| BCC | Body Centered Cubic |
| CB | Configurational Bias |
| CCAM | Chain-Connectivity-Altering Move |
| CCB | End-segment re-arrangement move |
| CCE | Characteristic Crystallographic Element (norm) |
| FCC | Face Centered Cubic |
| FIV | Fivefold |
| FJ | Freely-Jointed |
| HCP | Hexagonal Close Packed |
| HEX | Hexagonal |
| HON | Honeycomb |
| HS | Hard Sphere |
| ISO | Isotropic phase |
| MC | Monte Carlo |
| MD | Molecular Dynamics |
| NCP | Nematic Close Packed |
| NEM | Nematic mesophase |
| OBL | Oblate mesogen, Nematic mesophase |
| PBC | Periodic Boundary Condition |
| PEN | Pentagonal |
| PRO | Prolate mesogen, Nematic mesophase |
| RHCP | Random Hexagonal Close Packing |
| SQU | Square |
| TRI | Triangular |
References
- Flory, P.J. Statistical Mechanics of Chain Molecules; Hanser-Verlag: Munchen, Germany, 1989. [Google Scholar]
- deGennes, P.G. Scaling Concepts in Polymer Physics; Cornell University Press: Ithaca, NY, USA, 1980. [Google Scholar]
- Mullin, J.W. (Ed.) 8—Industrial Techniques and Equipment. In Crystallization, 4th ed.; Butterworth-Heinemann: Oxford, UK, 2001; pp. 315–402. [Google Scholar]
- Reiter, G.; Sommer, J.U. Polymer Crystallization: Obervations, Concepts and Interpretations; Springer: Berlin Heidelberg, 2008. [Google Scholar]
- Zhou, J.H.; Yang, Y.S.; Yang, Y.; Kim, D.S.; Yuan, A.; Tian, X.Z.; Ophus, C.; Sun, F.; Schmid, A.K.; Nathanson, M.; et al. Observing Crystal Nucleation in Four Dimensions Using Atomic Electron Tomography. Nature 2019, 570, 500. [Google Scholar] [CrossRef]
- Hu, Y.C.; Tanaka, H. Physical Origin of Glass Formation from Multicomponent Systems. Sci. Adv. 2020, 6, eabd2928. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.Z.; Park, S.S.; Buru, C.T.; Lin, H.X.; Chen, P.C.; Roth, E.W.; Farha, O.K.; Mirkin, C.A. Colloidal Crystal Engineering with Metal-Organic Framework Nanoparticles and DNA. Nat. Commun. 2020, 11, 2495. [Google Scholar] [CrossRef]
- Dijkstra, M.; Luijten, E. From Predictive Modelling to Machine Learning and Reverse Engineering of Colloidal Self-Assembly. Nat. Mater. 2021, 20, 762–773. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Mazzarello, R.; Wuttig, M.; Ma, E. Designing Crystallization in Phase-Change Materials for Universal Memory and Neuro-Inspired Computing. Nat. Rev. Mater. 2019, 4, 150–168. [Google Scholar] [CrossRef]
- Li, M.M.; Mangalore, D.K.; Zhao, J.B.; Carpenter, J.H.; Yan, H.P.; Ade, H.; Yan, H.; Mullen, K.; Blom, P.W.M.; Pisula, W.; et al. Integrated Circuits Based on Conjugated Polymer Monolayer. Nat. Commun. 2018, 9, 451. [Google Scholar] [CrossRef]
- Xia, X.X.; Lau, T.K.; Guo, X.Y.; Li, Y.H.; Qin, M.C.; Liu, K.; Chen, Z.; Zhan, X.Z.; Xiao, Y.Q.; Chan, P.F.; et al. Uncovering the out-of-Plane Nanomorphology of Organic Photovoltaic Bulk Heterojunction by Gtsaxs. Nat. Commun. 2021, 12, 6226. [Google Scholar] [CrossRef] [PubMed]
- Alder, B.J.; Wainwright, T.E. Phase Transition for a Hard Sphere System. J. Chem. Phys. 1957, 27, 1208–1209. [Google Scholar] [CrossRef]
- Frenkel, D. Entropy-Driven Phase Transitions. Phys. A 1999, 263, 26–38. [Google Scholar] [CrossRef]
- Pusey, P.N.; Vanmegen, W. Phase-Behavior of Concentrated Suspensions of Nearly Hard Colloidal Spheres. Nature 1986, 320, 340–342. [Google Scholar] [CrossRef]
- Miskin, M.Z.; Jaeger, H.M. Adapting Granular Materials through Artificial Evolution. Nat. Mater. 2013, 12, 326–331. [Google Scholar] [CrossRef]
- Athanassiadis, A.G.; Miskin, M.Z.; Kaplan, P.; Rodenberg, N.; Lee, S.H.; Merritt, J.; Brown, E.; Amend, J.; Lipson, H.; Jaeger, H.M. Particle Shape Effects on the Stress Response of Granular Packings. Soft Matter 2014, 10, 48–59. [Google Scholar] [CrossRef] [PubMed]
- Miskin, M.Z.; Jaeger, H.M. Evolving Design Rules for the Inverse Granular Packing Problem. Soft Matter 2014, 10, 3708–3715. [Google Scholar] [CrossRef] [PubMed]
- Zou, L.-N.; Cheng, X.; Rivers, M.L.; Jaeger, H.M.; Nagel, S.R. The Packing of Granular Polymer Chains. Science 2009, 326, 408–410. [Google Scholar] [CrossRef]
- Sacanna, S.; Irvine, W.T.M.; Chaikin, P.M.; Pine, D.J. Lock and Key Colloids. Nature 2010, 464, 575–578. [Google Scholar] [CrossRef] [PubMed]
- Vutukuri, H.R.; Demirors, A.F.; Peng, B.; van Oostrum, P.D.J.; Imhof, A.; van Blaaderen, A. Colloidal Analogues of Charged and Uncharged Polymer Chains with Tunable Stiffness. Angew. Chem. Int. Ed. 2012, 51, 11249–11253. [Google Scholar] [CrossRef]
- Brown, E.; Nasto, A.; Athanassiadis, A.G.; Jaeger, H.M. Strain Stiffening in Random Packings of Entangled Granular Chains. Phys. Rev. Lett. 2012, 108, 108302. [Google Scholar] [CrossRef]
- Feng, L.; Pontani, L.L.; Dreyfus, R.; Chaikin, P.; Brujic, J. Specificity, Flexibility and Valence of DNA Bonds Guide Emulsion Architecture. Soft Matter 2013, 9, 9816–9823. [Google Scholar] [CrossRef]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids, 2nd ed.; Oxford University Press: Oxford, UK, 2017. [Google Scholar]
- Frenkel, D.; Smit, B. Understanding Molecular Simulation: From Algorithms to Applications, 2nd ed.; Academic Press: San Diego, CA, USA, 2002. [Google Scholar]
- Landau, D.P.; Binder, K. A Guide to Monte Carlo Simulations in Statistical Physics, 4th ed.; Cambridge University Press: Cambridge, CA, USA, 2014. [Google Scholar]
- Rapaport, D.C. The Art of Molecular Dynamics Simulation, 2nd ed.; Cambridge University Press: Cambridge, CA, USA, 2004. [Google Scholar]
- Leach, A. Molecular Modelling: Principles and Applications, 2nd ed.; Pearson: London, UK, 2001. [Google Scholar]
- Wood, W.W.; Jacobson, J.D. Preliminary Results from a Recalculation of the Monte Carlo Equation of State of Hard Spheres. J. Chem. Phys. 1957, 27, 1207–1208. [Google Scholar] [CrossRef]
- Hoover, W.G.; Ree, F.H. Melting Transition and Communal Entropy for Hard Spheres. J. Chem. Phys. 1968, 49, 3609–3617. [Google Scholar] [CrossRef]
- Rintoul, M.D.; Torquato, S. Metastability and Crystallization in Hard-Sphere Systems. Phys. Rev. Lett. 1996, 77, 4198–4201. [Google Scholar] [CrossRef]
- Rintoul, M.D.; Torquato, S. Computer Simulations of Dense Hard-Sphere Systems. J. Chem. Phys. 1996, 105, 9258–9265. [Google Scholar] [CrossRef]
- Bolhuis, P.G.; Frenkel, D.; Mau, S.C.; Huse, D.A. Entropy Difference between Crystal Phases. Nature 1997, 388, 235–236. [Google Scholar] [CrossRef]
- Woodcock, L.V. Entropy Difference between the Face-Centred Cubic and Hexagonal Close-Packed Crystal Structures. Nature 1997, 385, 141–143. [Google Scholar] [CrossRef]
- Bruce, A.D.; Wilding, N.B.; Ackland, G.J. Free Energy of Crystalline Solids: A Lattice-Switch Monte Carlo Method. Phys. Rev. Lett. 1997, 79, 3002–3005. [Google Scholar] [CrossRef]
- Pusey, P.N.; Vanmegen, W.; Bartlett, P.; Ackerson, B.J.; Rarity, J.G.; Underwood, S.M. Structure of Crystals of Hard Colloidal Spheres. Phys. Rev. Lett. 1989, 63, 2753–2756. [Google Scholar] [CrossRef]
- Gasser, U.; Weeks, E.R.; Schofield, A.; Pusey, P.N.; Weitz, D.A. Real-Space Imaging of Nucleation and Growth in Colloidal Crystallization. Science 2001, 292, 258–262. [Google Scholar] [CrossRef]
- Zhu, J.X.; Li, M.; Rogers, R.; Meyer, W.; Ottewill, R.H.; Russell, W.B.; Chaikin, P.M. Crystallization of Hard-Sphere Colloids in Microgravity. Nature 1997, 387, 883–885. [Google Scholar] [CrossRef]
- Verhaegh, N.A.M.; Vanduijneveldt, J.S.; Vanblaaderen, A.; Lekkerkerker, H.N.W. Direct Observation of Stacking Disorder in a Colloidal Crystal. J. Chem. Phys. 1995, 102, 1416–1421. [Google Scholar] [CrossRef]
- Petukhov, A.V.; Dolbnya, I.P.; Aarts, D.; Vroege, G.J.; Lekkerkerker, H.N.W. Bragg Rods and Multiple X-Ray Scattering in Random-Stacking Colloidal Crystals. Phys. Rev. Lett. 2003, 90, 028304. [Google Scholar] [CrossRef]
- Vanmegen, W.; Underwood, S.M. Change in Crystallization Mechanism at the Glass-Transition of Colloidal Spheres. Nature 1993, 362, 616–618. [Google Scholar] [CrossRef]
- Medvedev, N.N.; Bezrukov, A.; Shtoyan, D. From Amorphous Solid to Defective Crystal. A Study of Structural Peculiarities in Close Packings of Hard Spheres. J. Struct. Chem. 2004, 45, S23–S30. [Google Scholar] [CrossRef]
- van Meel, J.A.; Frenkel, D.; Charbonneau, P. Geometrical Frustration: A Study of Four-Dimensional Hard Spheres. Phys. Rev. E 2009, 79, 030201. [Google Scholar] [CrossRef]
- O’Malley, B.; Snook, I. Crystal Nucleation in the Hard Sphere System. Phys. Rev. Lett. 2003, 90, 085702. [Google Scholar] [CrossRef] [PubMed]
- Russo, J.; Tanaka, H. Crystal Nucleation as the Ordering of Multiple Order Parameters. J. Chem. Phys. 2016, 145, 211801. [Google Scholar] [CrossRef]
- Lam, M.A.; Khusid, B.; Kondic, L.; Meyer, W.V. Role of Diffusion in Crystallization of Hard-Sphere Colloids. Phys. Rev. E 2021, 104, 054607. [Google Scholar] [CrossRef]
- Auer, S.; Frenkel, D. Prediction of Absolute Crystal-Nucleation Rate in Hard-Sphere Colloids. Nature 2001, 409, 1020–1023. [Google Scholar] [CrossRef]
- Martelozzo, V.C.; Schofield, A.B.; Poon, W.C.K.; Pusey, P.N. Structural Aging of Crystals of Hard-Sphere Colloids. Phys. Rev. E 2002, 66, 021408. [Google Scholar] [CrossRef]
- Kegel, W.K.; Dhont, J.K.G. "Aging" of the Structure of Crystals of Hard Colloidal Spheres. J. Chem. Phys. 2000, 112, 3431–3436. [Google Scholar] [CrossRef]
- Dolbnya, I.P.; Petukhov, A.V.; Aarts, D.; Vroege, G.J.; Lekkerkerker, H.N.W. Coexistence of Rhcp and Fcc Phases in Hard-Sphere Colloidal Crystals. Europhys. Lett. 2005, 72, 962–968. [Google Scholar] [CrossRef]
- Pronk, S.; Frenkel, D. Can Stacking Faults in Hard-Sphere Crystals Anneal out Spontaneously? J. Chem. Phys. 1999, 110, 4589–4592. [Google Scholar] [CrossRef]
- Luchnikov, V.; Gervois, A.; Richard, P.; Oger, L.; Troadec, J.P. Crystallization of Dense Hard Sphere Packings—Competition of Hcp and Fcc Close Order. J. Mol. Liq. 2002, 96–97, 185–194. [Google Scholar] [CrossRef]
- Herranz, M.; Foteinopoulou, K.; Karayiannis, N.C.; Laso, M. Polymorphism and Perfection in Crystallization of Hard Sphere Polymers. Polymers 2022, 14, 4435. [Google Scholar] [CrossRef] [PubMed]
- Espinosa, J.R.; Vega, C.; Valeriani, C.; Frenkel, D.; Sanz, E. Heterogeneous Versus Homogeneous Crystal Nucleation of Hard Spheres. Soft Matter 2019, 15, 9625–9631. [Google Scholar] [CrossRef] [PubMed]
- Vega, C.; McBride, C.; MacDowell, L.G. Liquid Crystal Phase Formation for the Linear Tangent Hard Sphere Model from Monte Carlo Simulations. J. Chem. Phys. 2001, 115, 4203–4211. [Google Scholar] [CrossRef]
- Karayiannis, N.C.; Foteinopoulou, K.; Laso, M. Entropy-Driven Crystallization in Dense Systems of Athermal Chain Molecules. Phys. Rev. Lett. 2009, 103, 045703. [Google Scholar] [CrossRef]
- Karayiannis, N.C.; Foteinopoulou, K.; Abrams, C.F.; Laso, M. Modeling of Crystal Nucleation and Growth in Athermal Polymers: Self-Assembly of Layered Nano-Morphologies. Soft Matter 2010, 6, 2160–2173. [Google Scholar] [CrossRef]
- Karayiannis, N.C.; Foteinopoulou, K.; Laso, M. Spontaneous Crystallization in Athermal Polymer Packings. Int. J. Mol. Sci. 2013, 14, 332–358. [Google Scholar] [CrossRef]
- Karayiannis, N.C.; Foteinopoulou, K.; Laso, M. The Role of Bond Tangency and Bond Gap in Hard Sphere Crystallization of Chains. Soft Matter 2015, 11, 1688–1700. [Google Scholar] [CrossRef]
- Ramos, P.M.; Herranz, M.; Foteinopoulou, K.; Karayiannis, N.C.; Laso, M. Entropy-Driven Heterogeneous Crystallization of Hard-Sphere Chains under Unidimensional Confinement. Polymers 2021, 13, 1352. [Google Scholar] [CrossRef]
- Ramos, P.M.; Herranz, M.; Martinez-Fernandez, D.; Foteinopoulou, K.; Laso, M.; Karayiannis, N.C. Crystallization of Flexible Chains of Tangent Hard Spheres under Full Confinement. J. Phys. Chem. B 2022, 126, 5931–5947. [Google Scholar] [CrossRef]
- Sirota, E.B. Polymer Crystallization: Metastable Mesophases and Morphology. Macromolecules 2007, 40, 1043–1048. [Google Scholar] [CrossRef]
- Sirota, E.B.; Singer, D.M. Phase-Transitions among the Rotator Phases of the Normal-Alkanes. J. Chem. Phys. 1994, 101, 10873–10882. [Google Scholar] [CrossRef]
- Sirota, E.B.; King, H.E.; Singer, D.M.; Shao, H.H. Rotator Phases of the Normal Alkanes—An X-Ray-Scattering Study. J. Chem. Phys. 1993, 98, 5809–5824. [Google Scholar] [CrossRef]
- Bourque, A.; Locker, C.R.; Rutledge, G.C. Molecular Dynamics Simulation of Surface Nucleation During Growth of an Alkane Crystal. Macromolecules 2016, 49, 3619–3629. [Google Scholar] [CrossRef]
- Morthomas, J.; Fusco, C.; Zhai, Z.Q.; Lame, O.; Perez, M. Crystallization of Finite-Extensible Nonlinear Elastic Lennard-Jones Coarse-Grained Polymers. Phys. Rev. E 2017, 96, 052502. [Google Scholar] [CrossRef]
- Luo, C.F.; Kroger, M.; Sommer, J.U. Entanglements and Crystallization of Concentrated Polymer Solutions: Molecular Dynamics Simulations. Macromolecules 2016, 49, 9017–9025. [Google Scholar] [CrossRef]
- Zhang, W.; Zou, L. Molecular Dynamics Simulations of Crystal Nucleation near Interfaces in Incompatible Polymer Blends. Polymers 2021, 13, 347. [Google Scholar] [CrossRef]
- Isobe, M.; Krauth, W. Hard-Sphere Melting and Crystallization with Event-Chain Monte Carlo. J. Chem. Phys. 2015, 143, 084509. [Google Scholar] [CrossRef]
- Zhang, W.; Larson, R.G. Direct All-Atom Molecular Dynamics Simulations of the Effects of Short Chain Branching on Polyethylene Oligomer Crystal Nucleation. Macromolecules 2018, 51, 4762–4769. [Google Scholar] [CrossRef]
- Ramos, J.; Vega, J.F.; Sanmartin, S.; Martinez-Salazar, J. Coarse-Grained Simulations on the Crystallization, Melting and Annealing Processes, of Short Chain Branched Polyolefins. Eur. Polym. J. 2016, 85, 478–488. [Google Scholar] [CrossRef]
- Ramos, J.; Vega, J.F.; Martinez-Salazar, J. Predicting Experimental Results for Polyethylene by Computer Simulation. Eur. Polym. J. 2018, 99, 298–331. [Google Scholar] [CrossRef]
- Fall, W.S.; Baschnagel, J.; Lhost, O.; Meyer, H. Role of Short Chain Branching in Crystalline Model Polyethylenes. Macromolecules 2022, 55, 8438–8450. [Google Scholar] [CrossRef]
- Sanmartin, S.; Ramos, J.; Vega, J.F.; Martinez-Salazar, J. Strong Influence of Branching on the Early Stage of Nucleation and Crystal Formation of Fast Cooled Ultralong N-Alkanes as Revealed by Computer Simulation. Eur. Polym. J. 2014, 50, 190–199. [Google Scholar] [CrossRef]
- Yi, P.; Locker, C.R.; Rutledge, G.C. Molecular Dynamics Simulation of Homogeneous Crystal Nucleation in Polyethylene. Macromolecules 2013, 46, 4723–4733. [Google Scholar] [CrossRef]
- Ramos, J.; Martinez-Salazar, J. Computer Modeling of the Crystallization Process of Single-Chain Ethylene/1-Hexene Copolymers from Dilute Solutions. J. Polym. Sci. Part B-Polym. Phys. 2011, 49, 421–430. [Google Scholar] [CrossRef]
- Yamamoto, T. Chiral Selecting Crystallization of Helical Polymers: A Molecular Dynamics Simulation for the Pom-Like Bare Helix. J. Chem. Phys. 2022, 157, 014901. [Google Scholar] [CrossRef]
- Yi, P.; Rutledge, G.C. Molecular Simulation of Crystal Nucleation in N-Octane Melts. J. Chem. Phys. 2009, 131, 134902. [Google Scholar] [CrossRef]
- Romanos, N.A.; Theodorou, D.N. Crystallization and Melting Simulations of Oligomeric Alpha 1 Isotactic Polypropylene. Macromolecules 2010, 43, 5455–5469. [Google Scholar] [CrossRef]
- Karayiannis, N.C.; Foteinopoulou, K.; Laso, M. The Structure of Random Packings of Freely Jointed Chains of Tangent Hard Spheres. J. Chem. Phys. 2009, 130, 164908. [Google Scholar] [CrossRef]
- Karayiannis, N.C.; Malshe, R.; Kroger, M.; de Pablo, J.J.; Laso, M. Evolution of Fivefold Local Symmetry During Crystal Nucleation and Growth in Dense Hard-Sphere Packings. Soft Matter 2012, 8, 844–858. [Google Scholar] [CrossRef]
- Karayiannis, N.C.; Malshe, R.; de Pablo, J.J.; Laso, M. Fivefold Symmetry as an Inhibitor to Hard-Sphere Crystallization. Phys. Rev. E 2011, 83, 061505. [Google Scholar] [CrossRef] [PubMed]
- Karayiannis, N.C.; Foteinopoulou, K.; Laso, M. Twinning of Polymer Crystals Suppressed by Entropy. Symmetry 2014, 6, 758–780. [Google Scholar] [CrossRef]
- Ni, R.; Dijkstra, M. Effect of Bond Length Fluctuations on Crystal Nucleation of Hard Bead Chains. Soft Matter 2013, 9, 365–369. [Google Scholar] [CrossRef]
- Luo, C.F.; Kroger, M.; Sommer, J.U. Molecular Dynamics Simulations of Polymer Crystallization under Confinement: Entanglement Effect. Polymer 2017, 109, 71–84. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Smith, T.B.; Hoy, R.S.; Karayiannis, N.C. Effect of Chain Stiffness on the Competition between Crystallization and Glass-Formation in Model Unentangled Polymers. J. Chem. Phys. 2015, 143, 144901. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, H.T.; Hoy, R.S. Effect of Chain Stiffness and Temperature on the Dynamics and Microstructure of Crystallizable Bead-Spring Polymer Melts. Phys. Rev. E 2016, 94, 052502. [Google Scholar] [CrossRef] [PubMed]
- Shakirov, T.; Paul, W. Crystallization in Melts of Short, Semiflexible Hard Polymer Chains: An Interplay of Entropies and Dimensions. Phys. Rev. E 2018, 97, 042501. [Google Scholar] [CrossRef]
- Shakirov, T. Crystallisation in Melts of Short, Semi-Flexible Hard-Sphere Polymer Chains: The Role of the Non-Bonded Interaction Range. Entropy 2019, 21, 856. [Google Scholar] [CrossRef]
- Donald, A.M.; Windle, A.H.; Hanna, S. Liquid Crystalline Polymers; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Ciferri, A. Liquid Crystallinity in Polymers; VCH Publishers: Weinheim, Germany, 1991. [Google Scholar]
- Meyer, R.B.; Ciferri, A.; Krigbaum, W.R. Polymer Liquid Crystals; Academic Press Incorporated: San Diego, CA, USA, 1982. [Google Scholar]
- Kato, T.; Uchida, J.; Ichikawa, T.; Soberats, B. Functional Liquid-Crystalline Polymers and Supramolecular Liquid Crystals. Polym. J. 2018, 50, 149–166. [Google Scholar] [CrossRef]
- Li, Y.; Huang, Q.; Shi, T.; An, L. Effects of Chain Flexibility on Polymer Conformation in Dilute Solution Studied by Lattice Monte Carlo Simulation. J. Phys. Chem. B 2006, 110, 23502–23506. [Google Scholar] [CrossRef] [PubMed]
- Lamura, A.; Burkhardt, T.W.; Gompper, G. Semiflexible Polymer in a Uniform Force Field in Two Dimensions. Phys. Rev. E 2001, 64, 061801. [Google Scholar] [CrossRef]
- Hsu, H.-P.; Paul, W.; Binder, K. Polymer Chain Stiffness Vs. Excluded Volume: A Monte Carlo Study of the Crossover Towards the Worm-Like Chain Model. Europhys. Lett. 2010, 92, 28003. [Google Scholar] [CrossRef]
- Cifra, P. Differences and Limits in Estimates of Persistence Length for Semi-Flexible Macromolecules. Polymer 2004, 45, 5995–6002. [Google Scholar] [CrossRef]
- Zierenberg, J.; Marenz, M.; Janke, W. Dilute Semiflexible Polymers with Attraction: Collapse, Folding and Aggregation. Polymers 2016, 8, 333. [Google Scholar] [CrossRef]
- Auhl, R.; Everaers, R.; Grest, G.S.; Kremer, K.; Plimpton, S.J. Equilibration of Long Chain Polymer Melts in Computer Simulations. J. Chem. Phys. 2003, 119, 12718–12728. [Google Scholar] [CrossRef]
- Bulacu, M.; van der Giessen, E. Molecular-Dynamics Simulation Study of the Glass Transition in Amorphous Polymers with Controlled Chain Stiffness. Phys. Rev. E 2007, 76, 011807. [Google Scholar] [CrossRef]
- Plaza-Rivera, C.O.; Nguyen, H.T.; Hoy, R.S. Isostaticity and the Solidification of Semiflexible Polymer Melts. Soft Matter 2017, 13, 7948–7952. [Google Scholar] [CrossRef]
- Onsager, L. The Effects of Shape on the Interaction of Colloidal Particles. Ann. New York Acad. Sci. 1949, 51, 627–659. [Google Scholar] [CrossRef]
- Bolhuis, P.; Frenkel, D. Tracing the Phase Boundaries of Hard Spherocylinders. J. Chem. Phys. 1997, 106, 666–687. [Google Scholar] [CrossRef]
- Khokhlov, A.R.; Semenov, A.N. On the Theory of Liquid-Crystalline Ordering of Polymer-Chains with Limited Flexibility. J. Stat. Phys. 1985, 38, 161–182. [Google Scholar] [CrossRef]
- Khokhlov, A.R.; Semenov, A.N. Liquid-Crystalline Ordering in the Solution of Partially Flexible Macromolecules. Phys. A 1982, 112, 605–614. [Google Scholar] [CrossRef]
- Khokhlov, A.R.; Semenov, A.N. Liquid-Crystalline Ordering in the Solution of Long Persistent Chains. Phys. A 1981, 108, 546–556. [Google Scholar] [CrossRef]
- Yethiraj, A.; Fynewever, H. Isotropic to Nematic Transition in Semiflexible Polymer Melts. Mol. Phys. 1998, 93, 693–701. [Google Scholar] [CrossRef]
- Fynewever, H.; Yethiraj, A. Phase Behavior of Semiflexible Tangent Hard Sphere Chains. J. Chem. Phys. 1998, 108, 1636–1644. [Google Scholar] [CrossRef]
- Jaffer, K.M.; Opps, S.B.; Sullivan, D.E.; Nickel, B.G.; Mederos, L. The Nematic-Isotropic Phase Transition in Semiflexible Fused Hard-Sphere Chain Fluids. J. Chem. Phys. 2001, 114, 3314–3324. [Google Scholar] [CrossRef]
- Ivanov, V.A.; Martemyanova, J.A.; Rodionova, A.S.; Stukan, M.R. Computer Simulation of Stiff-Chain Polymers. Polym. Sci. Ser. C 2013, 55, 4–22. [Google Scholar] [CrossRef]
- Tang, X.L.; Chen, W.; Li, L.B. The Tough Journey of Polymer Crystallization: Battling with Chain Flexibility and Connectivity. Macromolecules 2019, 52, 3575–3591. [Google Scholar] [CrossRef]
- Semenov, A.N.; Subbotin, A.V. Phase Equilibria in Mixtures of Rigid Chain Polymers. Polym. Sci. U.S.S.R. 1989, 31, 2266–2273. [Google Scholar] [CrossRef]
- Egorov, S.A.; Milchev, A.; Virnau, P.; Binder, K. Semiflexible Polymers under Good Solvent Conditions Interacting with Repulsive Walls. J. Chem. Phys. 2016, 144, 174902. [Google Scholar] [CrossRef]
- Egorov, S.A.; Milchev, A.; Binder, K. Semiflexible Polymers in the Bulk and Confined by Planar Walls. Polymers 2016, 8, 296. [Google Scholar] [CrossRef] [PubMed]
- Kos, P.I.; Ivanov, V.A.; Chertovich, A.V. Crystallization of Semiflexible Polymers in Melts and Solutions. Soft Matter 2021, 17, 2392–2403. [Google Scholar] [CrossRef] [PubMed]
- Roy, S.; Chen, Y.L. Rich Phase Transitions in Strongly Confined Polymer-Nanoparticle Mixtures: Nematic Ordering, Crystallization, and Liquid-Liquid Phase Separation. J. Chem. Phys. 2021, 154, 024901. [Google Scholar] [CrossRef] [PubMed]
- Milchev, A.; Egorov, S.A.; Binder, K.; Nikoubashman, A. Nematic Order in Solutions of Semiflexible Polymers: Hairpins, Elastic Constants, and the Nematic-Smectic Transition. J. Chem. Phys. 2018, 149, 174909. [Google Scholar] [CrossRef]
- Milchev, A.; Egorov, S.A.; Midya, J.; Binder, K.; Nikoubashman, A. Blends of Semiflexible Polymers: Interplay of Nematic Order and Phase Separation. Polymers 2021, 13, 2270. [Google Scholar] [CrossRef]
- Purdy, K.R.; Varga, S.; Galindo, A.; Jackson, G.; Fraden, S. Nematic Phase Transitions in Mixtures of Thin and Thick Colloidal Rods. Phys. Rev. Lett. 2005, 94, 057801. [Google Scholar] [CrossRef]
- Russo, P.S.; Cao, T. Phase-Behavior in a Ternary Rod Coil Solvent System—Poly(Gamma-Benzyl-Alpha,L-Glutamate) Nylon-6/M-Cresol. Mol. Cryst. Liq. Cryst. 1988, 157, 501–514. [Google Scholar] [CrossRef]
- Dutta, D.; Fruitwala, H.; Kohli, A.; Weiss, R.A. Polymer Blends Containing Liquid-Crystals—A Review. Polym. Eng. Sci. 1990, 30, 1005–1018. [Google Scholar] [CrossRef]
- Egorov, S.A.; Milchev, A.; Nikoubashman, A.; Binder, K. Phase Separation and Nematic Order in Lyotropic Solutions: Two Types of Polymers with Different Stiffnesses in a Common Solvent. J. Phys. Chem. B 2021, 125, 956–969. [Google Scholar] [CrossRef]
- Midya, J.; Egorov, S.A.; Binder, K.; Nikoubashman, A. Phase Behavior of Flexible and Semiflexible Polymers in Solvents of Varying Quality. J. Chem. Phys. 2019, 151, 034902. [Google Scholar] [CrossRef]
- Dennison, M.; Dijkstra, M.; van Roij, R. The Effects of Shape and Flexibility on Bio-Engineered Fd-Virus Suspensions. J. Chem. Phys. 2011, 135, 144106. [Google Scholar] [CrossRef]
- Dennison, M.; Dijkstra, M.; van Roij, R. Phase Diagram and Effective Shape of Semiflexible Colloidal Rods and Biopolymers. Phys. Rev. Lett. 2011, 106, 208302. [Google Scholar] [CrossRef] [PubMed]
- Dietz, J.D.; Hoy, R.S. Two-Stage Athermal Solidification of Semiflexible Polymers and Fibers. Soft Matter 2020, 16, 6206–6217. [Google Scholar] [CrossRef] [PubMed]
- Hoy, R.S. Jamming of Semiflexible Polymers. Phys. Rev. Lett. 2017, 118, 068002. [Google Scholar] [CrossRef]
- Herranz, M.; Martínez-Fernández, D.; Ramos, P.M.; Foteinopoulou, K.; Karayiannis, N.C.; Laso, M. Simu-D: A Simulator-Descriptor Suite for Polymer-Based Systems under Extreme Conditions. Int. J. Mol. Sci. 2021, 22, 12464. [Google Scholar] [CrossRef]
- Karayiannis, N.C.; Laso, M. Monte Carlo Scheme for Generation and Relaxation of Dense and Nearly Jammed Random Structures of Freely Jointed Hard-Sphere Chains. Macromolecules 2008, 41, 1537–1551. [Google Scholar] [CrossRef]
- Ramos, P.M.; Karayiannis, N.C.; Laso, M. Off-Lattice Simulation Algorithms for Athermal Chain Molecules under Extreme Confinement. J. Comput. Phys. 2018, 375, 918–934. [Google Scholar] [CrossRef]
- Karayiannis, N.C.; Foteinopoulou, K.; Laso, M. Jamming and Crystallization in Athermal Polymer Packings. Philos. Mag. 2013, 93, 4108–4131. [Google Scholar] [CrossRef]
- Foteinopoulou, K.; Karayiannis, N.C.; Laso, M. Monte Carlo Simulations of Densely-Packed Athermal Polymers in the Bulk and under Confinement. Chem. Eng. Sci. 2015, 121, 118–132. [Google Scholar] [CrossRef]
- Karayiannis, N.C.; Foteinopoulou, K.; Laso, M. The Characteristic Crystallographic Element Norm: A Descriptor of Local Structure in Atomistic and Particulate Systems. J. Chem. Phys. 2009, 130, 074704. [Google Scholar] [CrossRef]
- Ramos, P.M.; Herranz, M.; Foteinopoulou, K.; Karayiannis, N.C.; Laso, M. Identification of Local Structure in 2-D and 3-D Atomic Systems through Crystallographic Analysis. Crystals 2020, 10, 1008. [Google Scholar] [CrossRef]
- Siepmann, J.I.; Frenkel, D. Configurational Bias Monte-Carlo—A New Sampling Scheme for Flexible Chains. Mol. Phys. 1992, 75, 59–70. [Google Scholar] [CrossRef]
- Laso, M.; de Pablo, J.J.; Suter, U.W. Simulation of Phase-Equilibria for Chain Molecules. J. Chem. Phys. 1992, 97, 2817–2819. [Google Scholar] [CrossRef]
- Andrienko, D. Introduction to Liquid Crystals. J. Mol. Liq. 2018, 267, 520–541. [Google Scholar] [CrossRef]
- Nye, J.F. Physical Properties of Crystals: Their Representation by Tensors and Matrices; Oxford Science Publications: Oxford, MA, USA, 2010. [Google Scholar]
- Malgrange, C.; Ricolleau, C.; Schlenker, M. Symmetry and Physical Properties of Crystals; Springer: Dordrecht, The Netherlands, 2014. [Google Scholar]
- Giacovazzo, C.; Monaco, H.L.; Artioli, G.; Viterbo, D.; Ferraris, G.; Gilli, G.; Zanotti, G.; Gatti, M. Fundamentals of Crystallography; Oxford Science: Oxford, MA, USA, 2005. [Google Scholar]
- Laso, M.; Jimeno, N. Representation Surfaces for Physical Properties of Materials: A Visual Approach to Understanding Anisotropic Materials; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Humphrey, W.; Dalke, A.; Schulten, K. Vmd: Visual Molecular Dynamics. J. Mol. Graph. Modell. 1996, 14, 33–38. [Google Scholar] [CrossRef] [PubMed]
- Hoy, R.S.; Karayiannis, N.C. Simple Model for Chain Packing and Crystallization of Soft Colloidal Polymers. Phys. Rev. E 2013, 88, 012601. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martínez-Fernández, D.; Herranz, M.; Foteinopoulou, K.; Karayiannis, N.C.; Laso, M. Local and Global Order in Dense Packings of Semi-Flexible Polymers of Hard Spheres. Polymers 2023, 15, 551. https://doi.org/10.3390/polym15030551
Martínez-Fernández D, Herranz M, Foteinopoulou K, Karayiannis NC, Laso M. Local and Global Order in Dense Packings of Semi-Flexible Polymers of Hard Spheres. Polymers. 2023; 15(3):551. https://doi.org/10.3390/polym15030551
Chicago/Turabian StyleMartínez-Fernández, Daniel, Miguel Herranz, Katerina Foteinopoulou, Nikos Ch. Karayiannis, and Manuel Laso. 2023. "Local and Global Order in Dense Packings of Semi-Flexible Polymers of Hard Spheres" Polymers 15, no. 3: 551. https://doi.org/10.3390/polym15030551
APA StyleMartínez-Fernández, D., Herranz, M., Foteinopoulou, K., Karayiannis, N. C., & Laso, M. (2023). Local and Global Order in Dense Packings of Semi-Flexible Polymers of Hard Spheres. Polymers, 15(3), 551. https://doi.org/10.3390/polym15030551








