Simplified Characterization of Anisotropic Yield Criteria for an Injection-Molded Polymer Material
Abstract
:1. Introduction
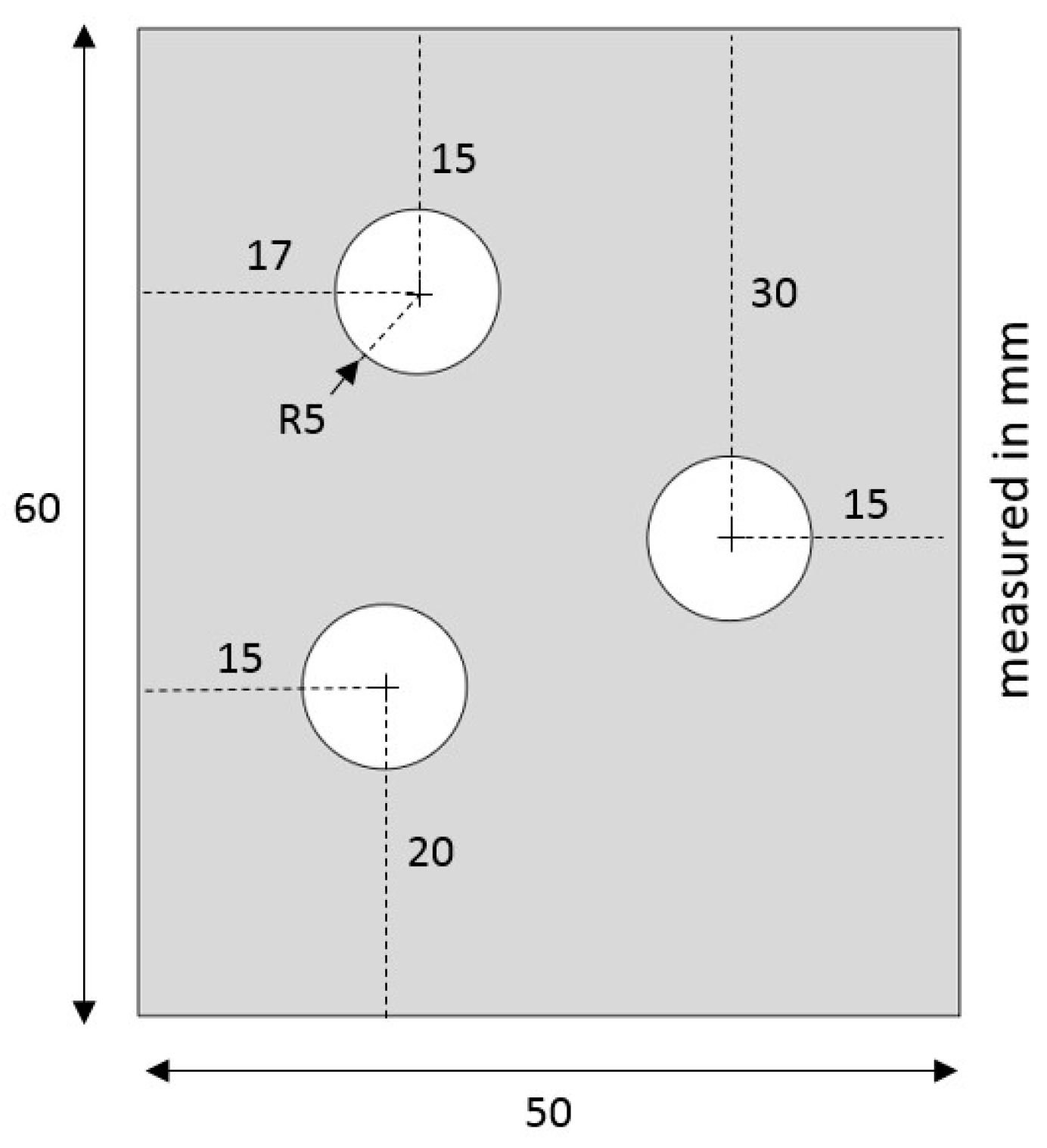
2. Materials and Methods
2.1. LDPE Material
2.2. Experimental Methods
- The uniaxial yield stresses in different material orientations (denoted as σ0, σ45, σ90, etc.);
- The coefficients of uniaxial strain anisotropy (denoted as r0, r45, r90, etc.);
- Hardening stress–strain relation of LDPE in MD.
2.3. Anisotropy Parameters
2.4. Anisotropic Yield Criteria Calibration
2.4.1. von Mises
2.4.2. Hill48
2.4.3. Barlat2004-18P
2.4.4. Barlat Yld91
2.5. Isotropic Hardening
2.6. FE Modeling
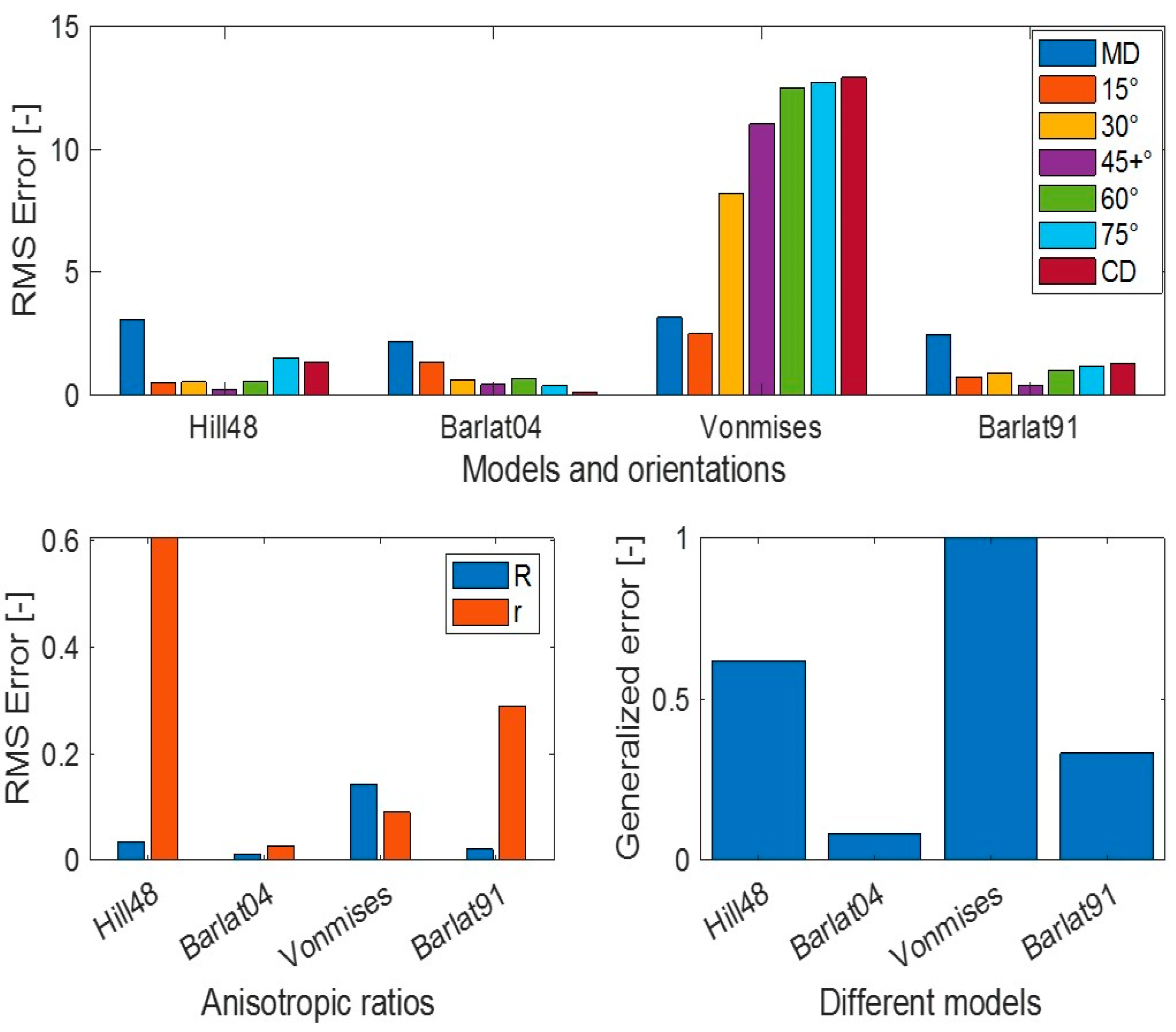
3. Results and Discussion
3.1. Experimental Results
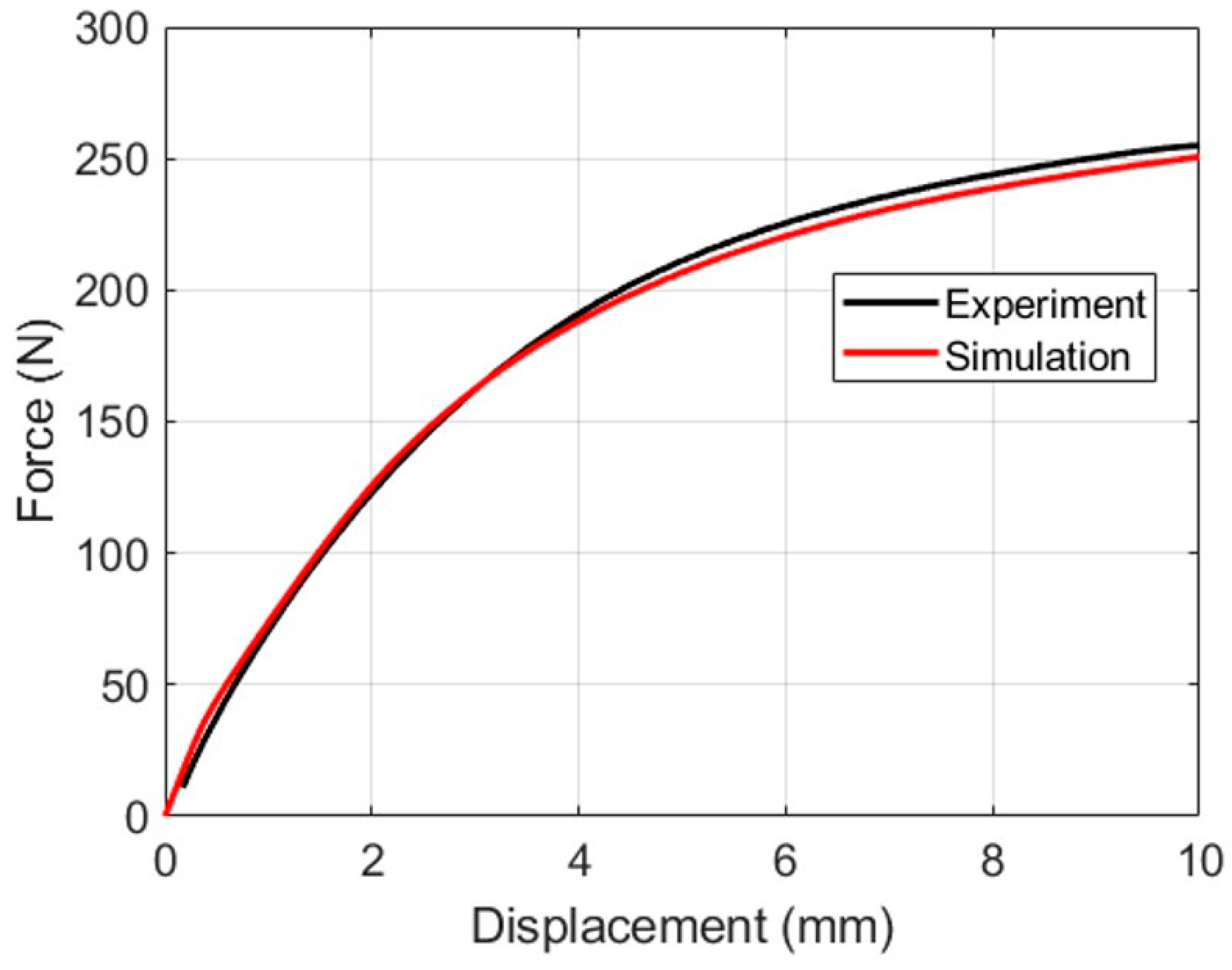
3.2. FE Simulation Results
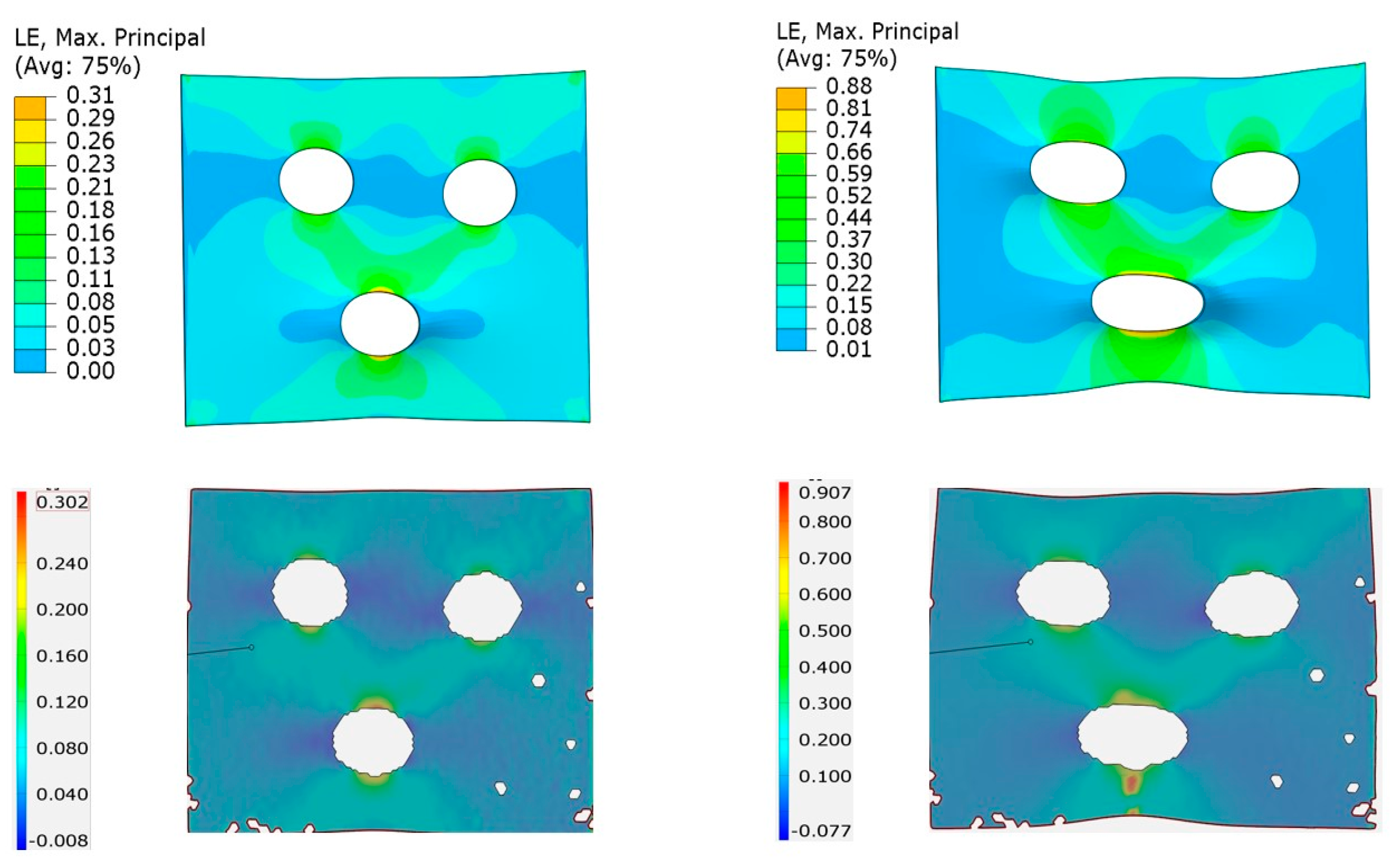
3.3. Validation of Barlat Yld2004-18P in a Nonstandard Tensile Test Model
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kroon, M.; Andreasson, E.; Jutemar, E.P.; Petersson, V.; Persson, L.; Dorn, M.; Olsson, P.A. Anisotropic Elastic-Viscoplastic Properties at Finite Strains of Injection-Moulded Low-Density Polyethylene. Exp. Mech. 2018, 58, 75–86. [Google Scholar] [CrossRef]
- Moy, F.H.; Kamal, M.R. Crystalline and amorphous orientations in injection molded polyethylene. Polym. Eng. Sci. 1980, 20, 957–964. [Google Scholar] [CrossRef]
- Bakerdjian, Z.; Kamal, M.R. Distribution of some physical properties in injection-molded thermoplastic parts. Polym. Eng. Sci. 1977, 17, 96–100. [Google Scholar] [CrossRef]
- Fujiyama, M.; Awaya, H.; Kimura, S. Mechanical anisotropy in injection-moldedpolypropylene. J. Appl. Polym. Sci. 1977, 21, 3291–3309. [Google Scholar] [CrossRef]
- Tan, V.; Kamal, M.R. Morphological zones and orientation in injection-molded polyethylene. J. Appl. Polym. Sci. 1978, 22, 2341–2355. [Google Scholar] [CrossRef]
- Hill, R. A Theory of the Yielding and Plastic Flow of Anisotropic Metals. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1948, 193, 281–297. [Google Scholar]
- Hill, R. Constitutive modelling of orthotropic plasticity in sheet metals. J. Mech. Phys. Solids 1990, 38, 405–417. [Google Scholar] [CrossRef]
- Barlat, F.; Richmond, O. Prediction of tricomponent plane stress yield surfaces and associated flow and failure behavior of strongly textured f.c.c. polycrystalline sheets. Mater. Sci. Eng. 1987, 95, 15–29. [Google Scholar] [CrossRef]
- Barlat, F.; Lege, D.J.; Brem, J.C. A six-component yield function for anisotropic materials. Int. J. Plast. 1991, 7, 693–712. [Google Scholar] [CrossRef]
- Barlat, F.; Aretz, H.; Yoon, J.; Karabin, M.; Brem, J.; Dick, R. Linear transfomation-based anisotropic yield functions. Int. J. Plast. 2005, 21, 1009–1039. [Google Scholar] [CrossRef]
- Comsa, D.S.; Banabic, D. Plane Stress Yield Criterion for Highly Anisotropicsheet Metals; Numisheet: Interlaken, Switzerland, 2008; pp. 43–48. [Google Scholar]
- Mattiasson, K.; Sigvant, M. An evaluation of some recent yield criteria for industrial simulations of sheet forming processes. Int. J. Mech. Sci. 2008, 50, 774–787. [Google Scholar] [CrossRef]
- Banabic, D. Sheet Metal Forming Processes: Constitutive Modelling and Numerical Simulation; Springer Science Business Media: Berlin, Germany, 2010. [Google Scholar]
- Islam, M.S. Fracture and Delamination in Packaging Materials: A Study of Experimental Methods and Simulation Techniques. Ph.D. Thesis, Blekinge Institute of Technology, Karlskrona, Sweden, 2019. [Google Scholar]
- Bazzi, A.; Angelou, A. Simulation of the Anisotropic Material Properties in Polymers Obtained in Thermal Forming Process. Master’s Thesis, Jönköping University, Jönköping, Sweden, 2018. [Google Scholar]
- van Dommelen, J.; Brekelmans, W.; Baaijens, F. Micromechanical modeling of particle-toughening of polymers by locally induced anisotropy. Mech. Mater. 2003, 35, 845–863. [Google Scholar] [CrossRef]
- Erp, T.V. Anisotropic Plasticity in Oriented Semi-Crystalline Polymer Systems. Master’s Thesis, Eindhoven University of Technology, Endhoven, The Netherlands, 2008. [Google Scholar]
- Shahid, S.; Gukhool, W. Experimental Testing and Material Modeling of Anisotropy in Injection Moulded Polymer Materials. Master’s Thesis, Blekinge Institute of Technology, Karlskrona, Sweden, 2020. [Google Scholar]
- Islam, M.S.; Kao-Walter, S.; Yang, G. Study of Ligament Length Effect on Mode Mix of a Modified In-Plane Shear Test Specimen. Mater. Perform. Charact. 2016, 5, 249–259. [Google Scholar] [CrossRef]
- Islam, S.; Khan, A.; Kao-Walter, S.; Jian, L. A Study of Shear Stress Intensity Factor of PP and HDPE by a Modified Experimental Method together with FEM. Int. J. Mech. Aerosp. Ind. Mechatron. Eng. 2013, 7. [Google Scholar] [CrossRef]
- Caro, L.P.; Schill, M.; Haller, K.; Odenberger, E.-L.; Oldenburg, M. Damage and fracture during sheet-metal forming of alloy. Int. J. Mater. Form. 2019, 13, 15–28. [Google Scholar] [CrossRef]
- Vitucci, G. Cruciform specimens biaxial extension performance relationship to constitutive identification. arXiv 2023, arXiv:2308.01260. [Google Scholar]
- Liang, Z.; Li, J.; Zhang, X.; Kan, Q. A viscoelastic-viscoplastic constitutive model and its finite element implementation of amorphous polymers. Polym. Test. 2023, 117. [Google Scholar] [CrossRef]
- Kim, J.S.; Muliana, A.H. A time-integration method for the viscoelastic-viscoplastic analyses of polymers and finite element implementation. Int. J. Numer. Methods Eng. 2009, 79, 550–575. [Google Scholar] [CrossRef]
- Kweon, S.; Benzerga, A.A. Finite element implementation of a macromolecular viscoplastic polymer model. Int. J. Numer. Methods Eng. 2013, 94, 895–919. [Google Scholar] [CrossRef]
- Vanderesse, N.; Lagacé, M.; Bridier, F.; Bocher, P. An Open Source Software for the Measurement of Deformation Fields by Means of Digital Image Correlation. Microsc. Microanal. 2013, 19, 820–821. [Google Scholar] [CrossRef]
- Kumar, S.L.; Aravind, H.; Hossiney, N. Digital image correlation (DIC) for measuring strain in brick masonry specimen using Ncorr open source 2D MATLAB program. Results Eng. 2019, 4, 100061. [Google Scholar] [CrossRef]
- GOM Correlate Release 2018; Carl Zeiss Industrial Metrology, LLC: Maple Grove, MN, USA, 2018; Available online: https://www.gom.com/en/products/metrology-software/gom-correlate-pro (accessed on 18 September 2023).
- ASTM D1238-04; Standard Test Method for Melt Flow Rates of Thermoplastics by Extrusion Plastometer. ASTM: West Conshohocken, PA, USA, 2004.
- ISO 294-5; Plastics-Injection Moulding os Test Specimens of Thermoplastic Materials, Part 5: Preparation of Standard Specimens for Investigating Anisotropy. ISO: Geneva, Switzerland, 2002.
- ISO 527-2; Plastics-Determination of Tensile Properties, Part 2: Test Conditions for Moulding and Extrusion Plastics. ISO: Geneva, Switzerland, 1997.
- Wahlström, I. Fracture Mechanics and Damage Modeling of Injection Molded High Density Polyethylene. Master’s Thesis, Lund University, Lund, Sweden, 2018. [Google Scholar]
- Mises, R.V. Mechanik der plastischen Formänderung von Kristallen. ZAMM-J. Appl. Math. MeChanics/Z. Für Angew. Math. Und Mech. 1928, 8, 161–185. [Google Scholar] [CrossRef]
- Islam, M.S. Shear Fracture and Delamination in Packaging Materials: A Study of Experimental Methods and Simulation Techniques. Ph.D. Thesis, Blekinge Tekniska Högskola, Karlskrona, Sweden, 2016. [Google Scholar]
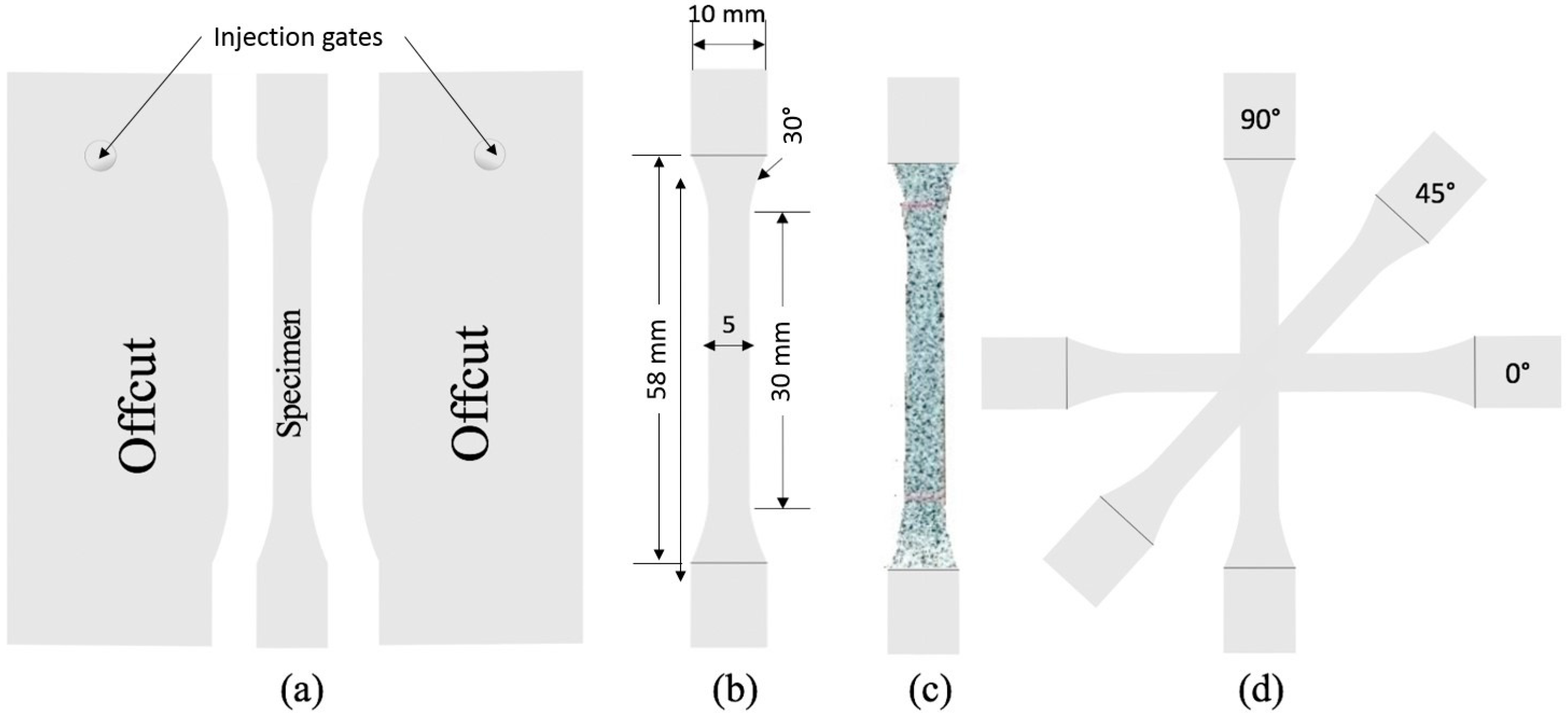
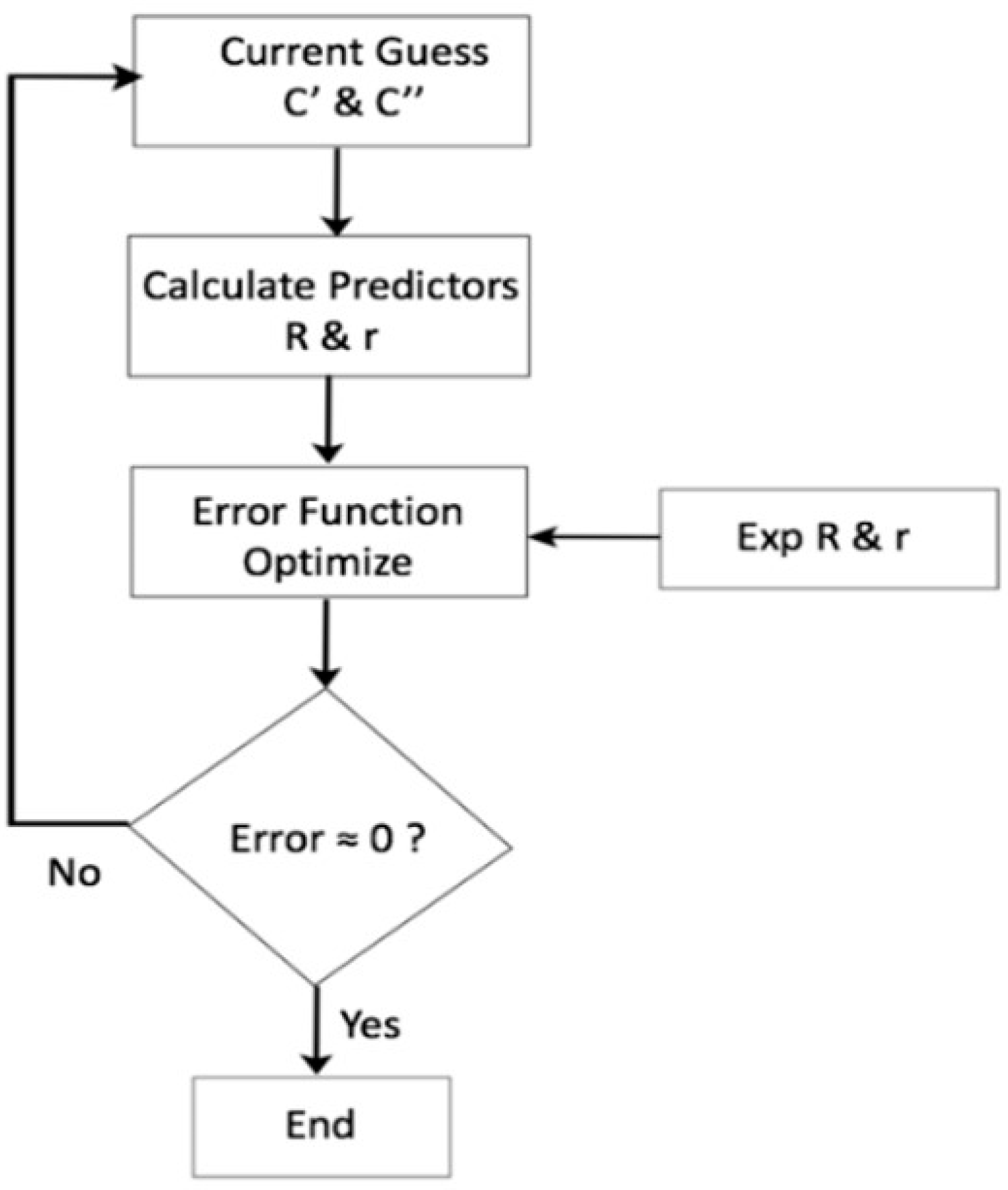
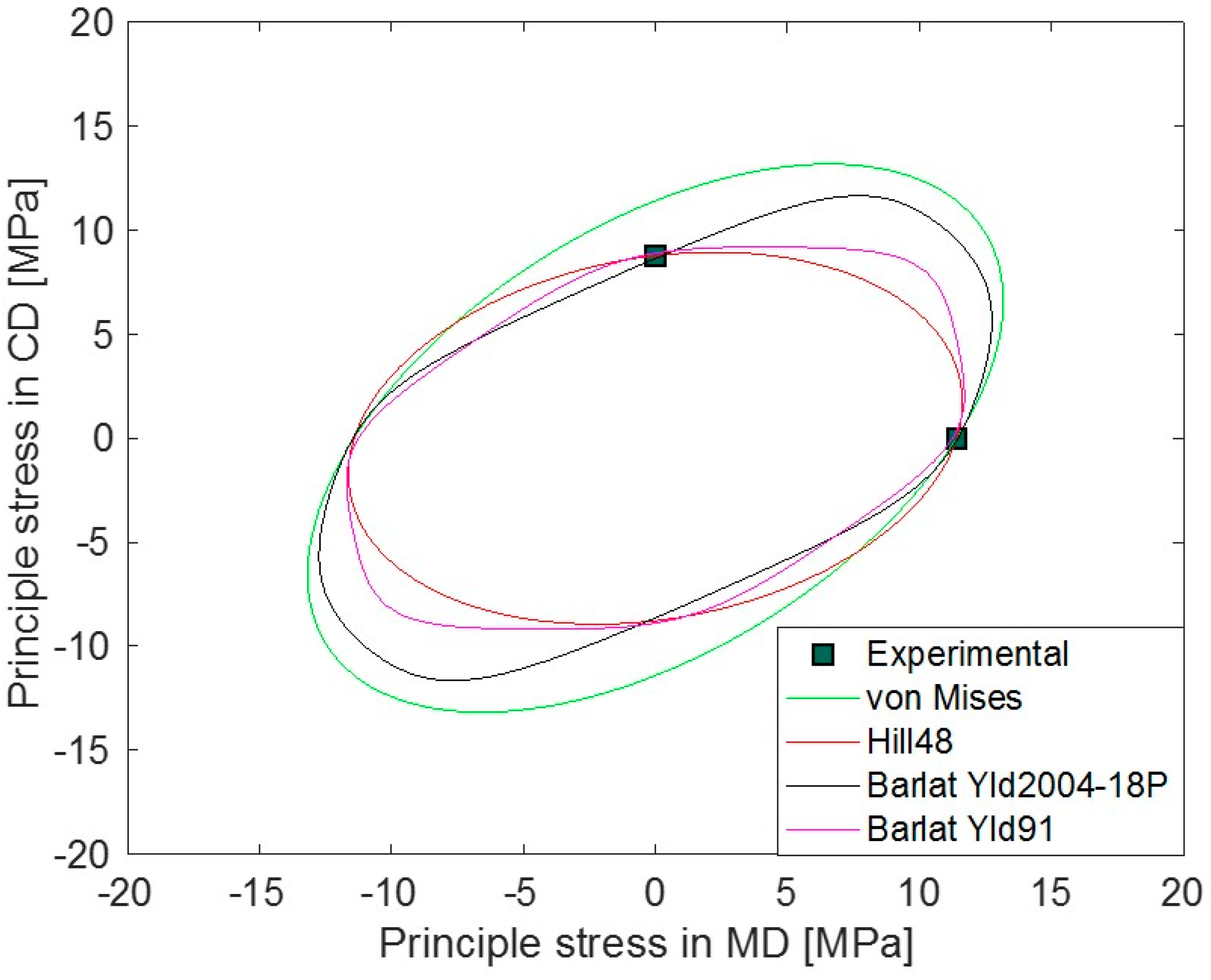

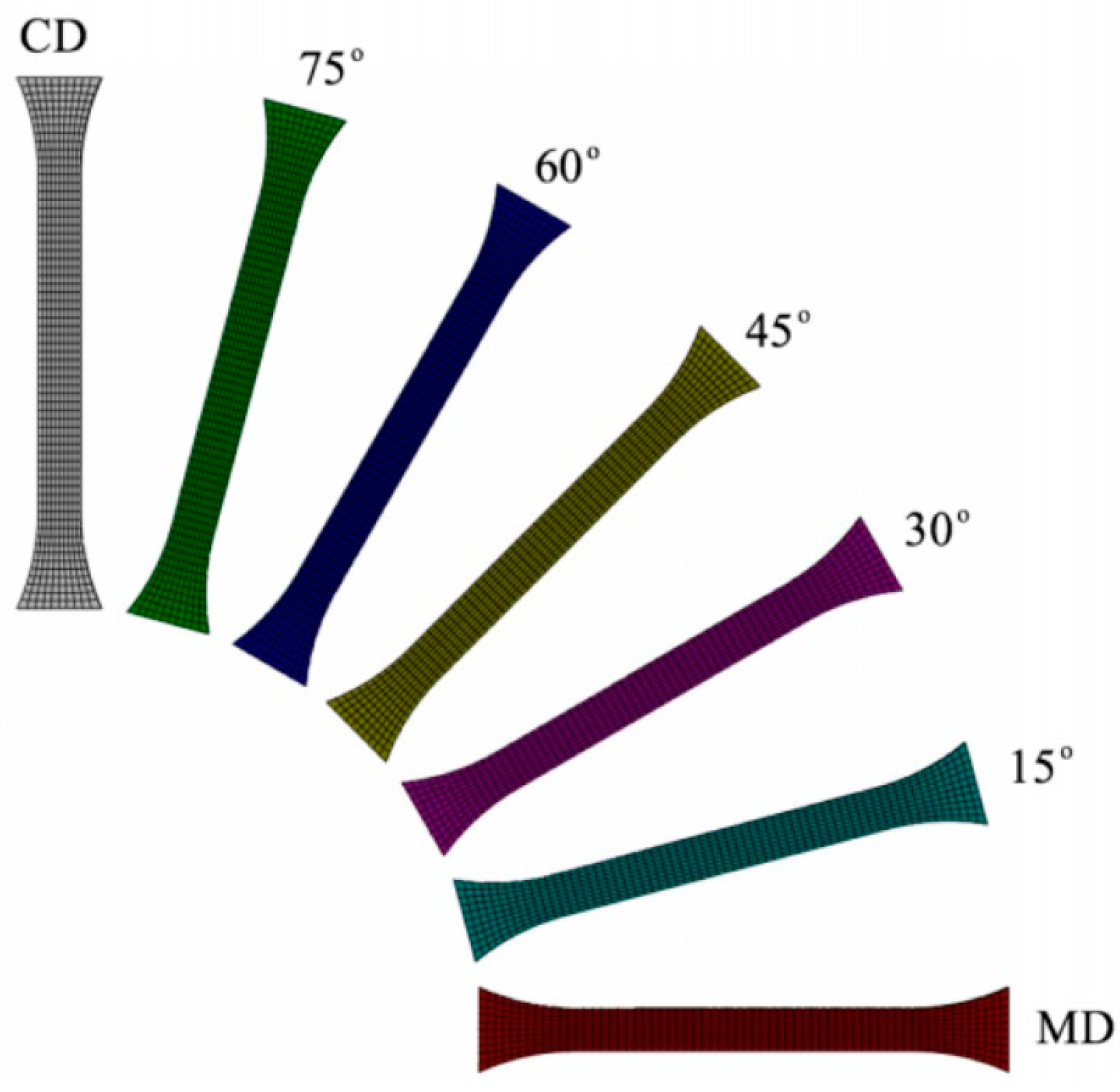
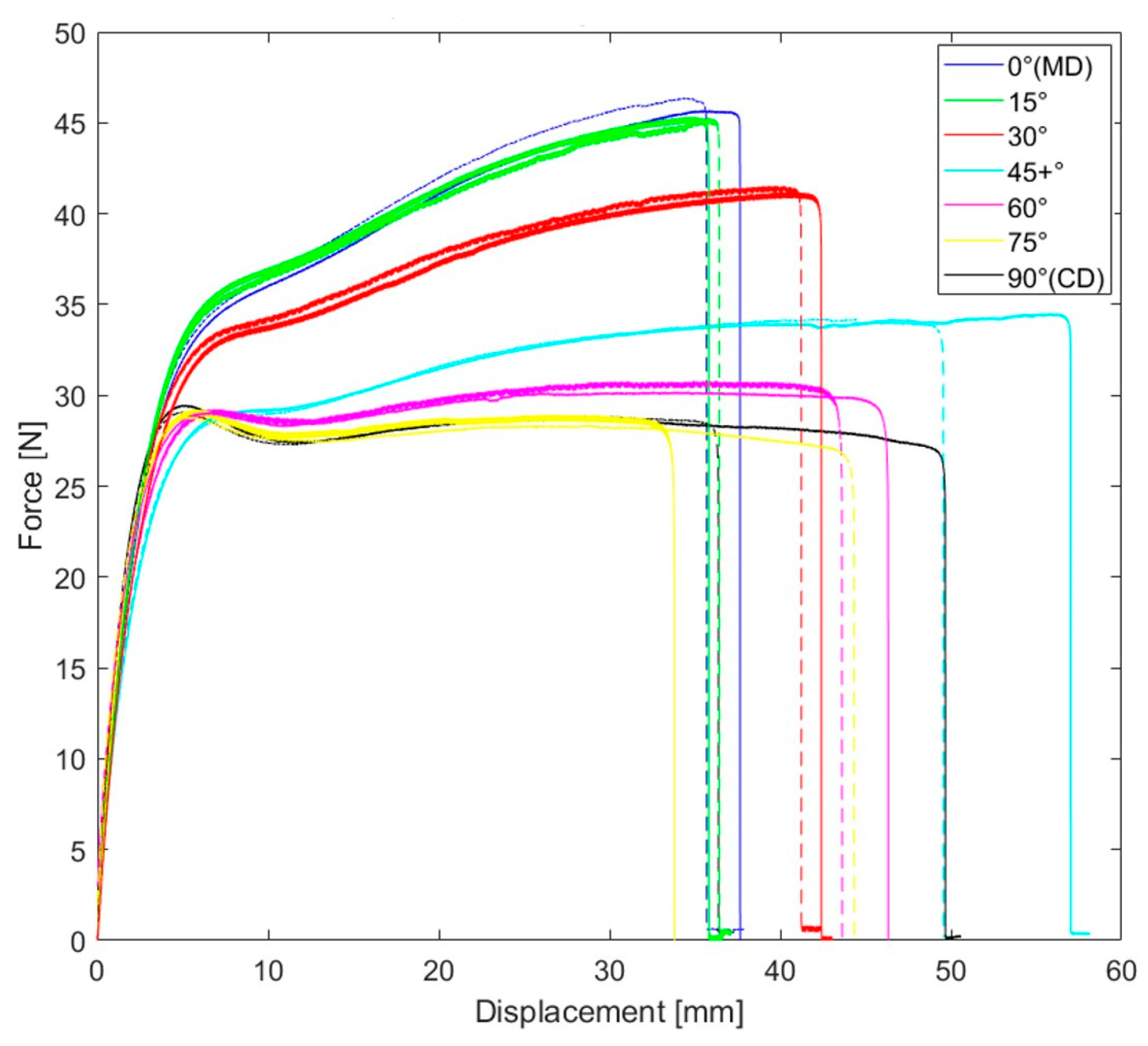

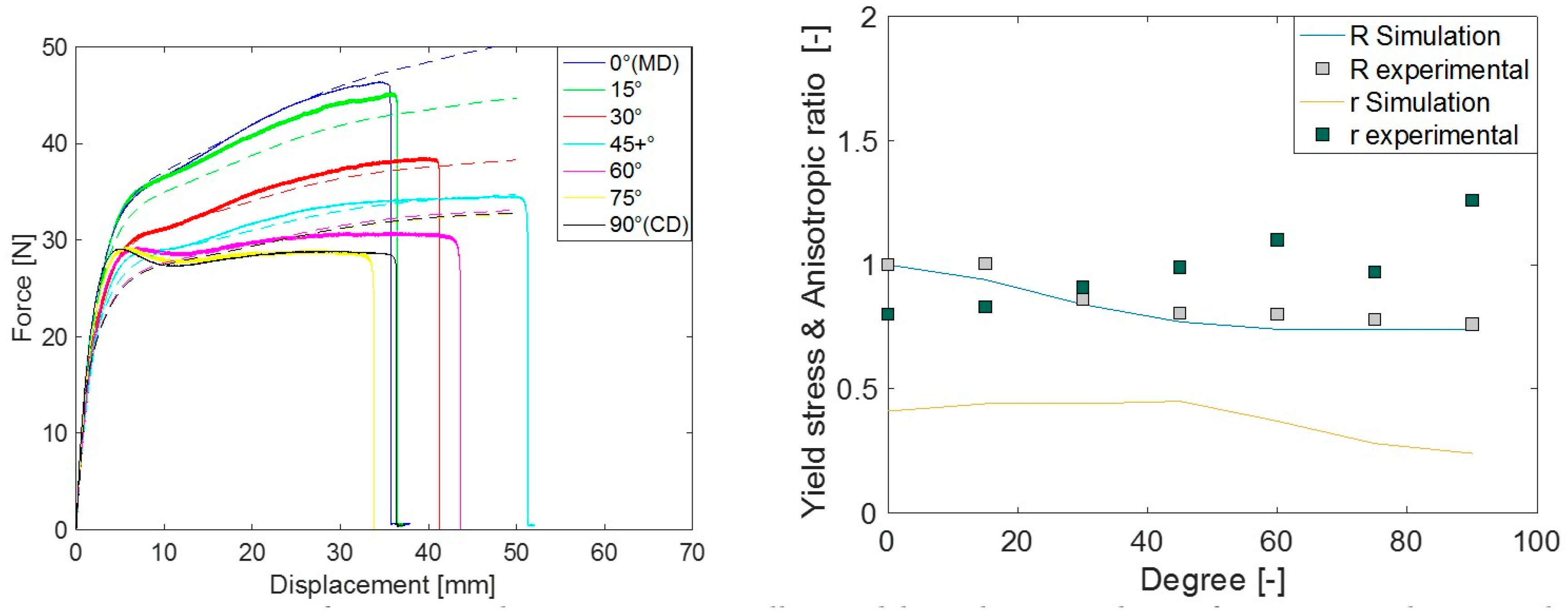


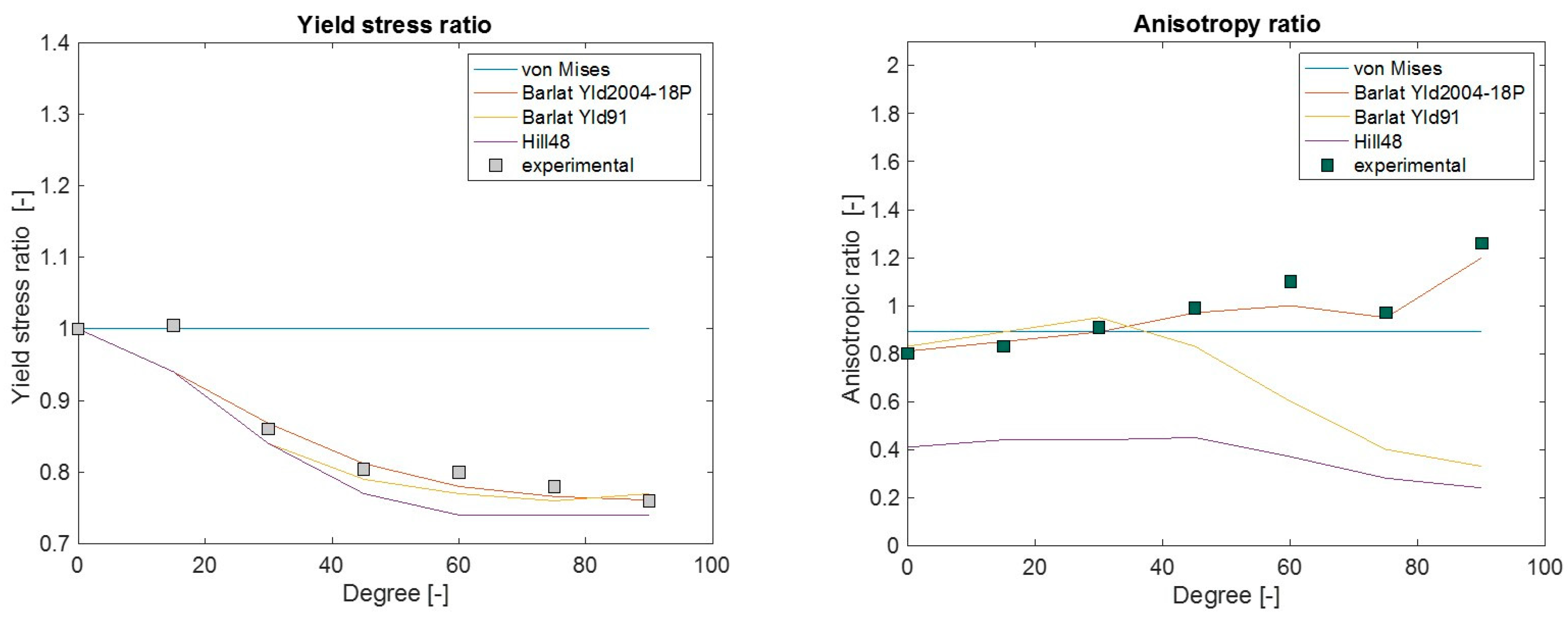
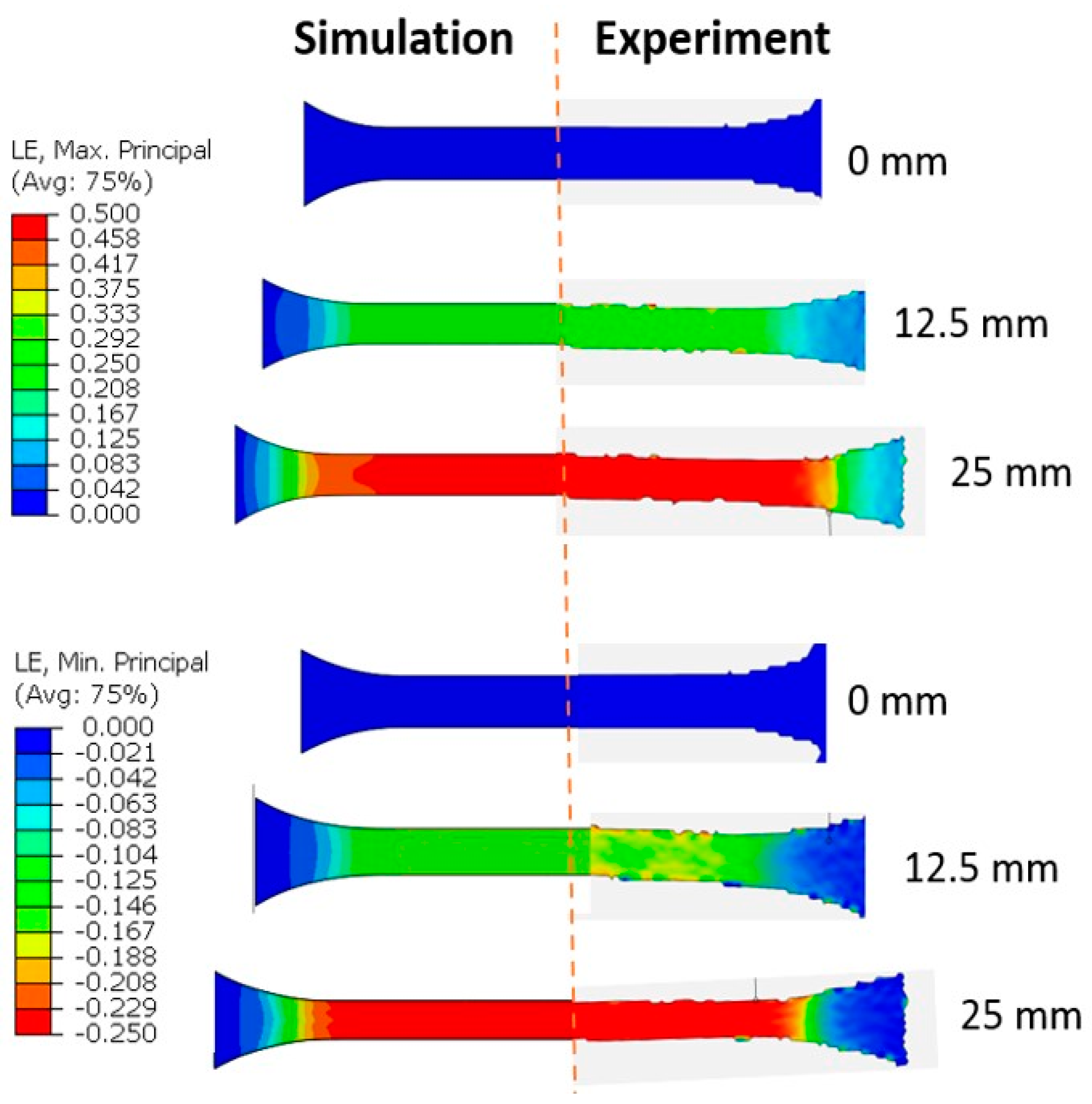
| Orientation (θ) | Yield Stress Ratio (R) | Anisotropic Ratio (r) | Poisson’s Ratio (ν) | Young’s Modulus (MPa) |
|---|---|---|---|---|
| 0° | 1.00 | 0.80 | 0.37 | 240 ± 1 |
| 15° | 1.01 ± 0.01 | 0.83 | 0.39 | 281 ± 2 |
| 30° | 0.86 ± 0.02 | 0.91 | 0.40 | 260 ± 2 |
| 45° | 0.80 ± 0.005 | 0.99 | 0.40 | 203 ± 2 |
| 60° | 0.80 ± 0.01 | 1.10 | 0.46 | 190 ± 2 |
| 75° | 0.78 ± 0.005 | 0.97 | 0.39 | 250 ± 1 |
| 90° | 0.76 ± 0.005 | 1.26 | 0.50 | 232 ± 1 |
| F | G | H | L | M | N |
|---|---|---|---|---|---|
| 1.44 | 0.75 | 0.25 | 1.00 | 1.00 | 1.99 |
| R11 | R22 | R33 | R12 | R13 | R23 |
|---|---|---|---|---|---|
| 1.00 | 0.77 | 0.68 | 0.87 | 1.00 | 1.00 |
| a | b | c | f | g | h |
|---|---|---|---|---|---|
| 1.52 | 1.02 | 1.00 | 0.97 | 0.97 | 1.25 |
| Yield Function | CPU Time (s) | Optimization Time (s) |
|---|---|---|
| von Mises | 55 | NA |
| Hill48 | 82 | 3 |
| Barlat Yld91 | 171 | 392 |
| Barlat Yld2004-18P | 155 | 7200 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shahid, S.; Andreasson, E.; Petersson, V.; Gukhool, W.; Kang, Y.; Kao-Walter, S. Simplified Characterization of Anisotropic Yield Criteria for an Injection-Molded Polymer Material. Polymers 2023, 15, 4520. https://doi.org/10.3390/polym15234520
Shahid S, Andreasson E, Petersson V, Gukhool W, Kang Y, Kao-Walter S. Simplified Characterization of Anisotropic Yield Criteria for an Injection-Molded Polymer Material. Polymers. 2023; 15(23):4520. https://doi.org/10.3390/polym15234520
Chicago/Turabian StyleShahid, Sharlin, Eskil Andreasson, Viktor Petersson, Widaad Gukhool, Yuchi Kang, and Sharon Kao-Walter. 2023. "Simplified Characterization of Anisotropic Yield Criteria for an Injection-Molded Polymer Material" Polymers 15, no. 23: 4520. https://doi.org/10.3390/polym15234520
APA StyleShahid, S., Andreasson, E., Petersson, V., Gukhool, W., Kang, Y., & Kao-Walter, S. (2023). Simplified Characterization of Anisotropic Yield Criteria for an Injection-Molded Polymer Material. Polymers, 15(23), 4520. https://doi.org/10.3390/polym15234520









