Synthesis and Aggregation Behavior of Hexameric Quaternary Ammonium Salt Surfactant Tz-6C12QC
Abstract
:1. Introduction
2. Experimental
2.1. Materials Preparation
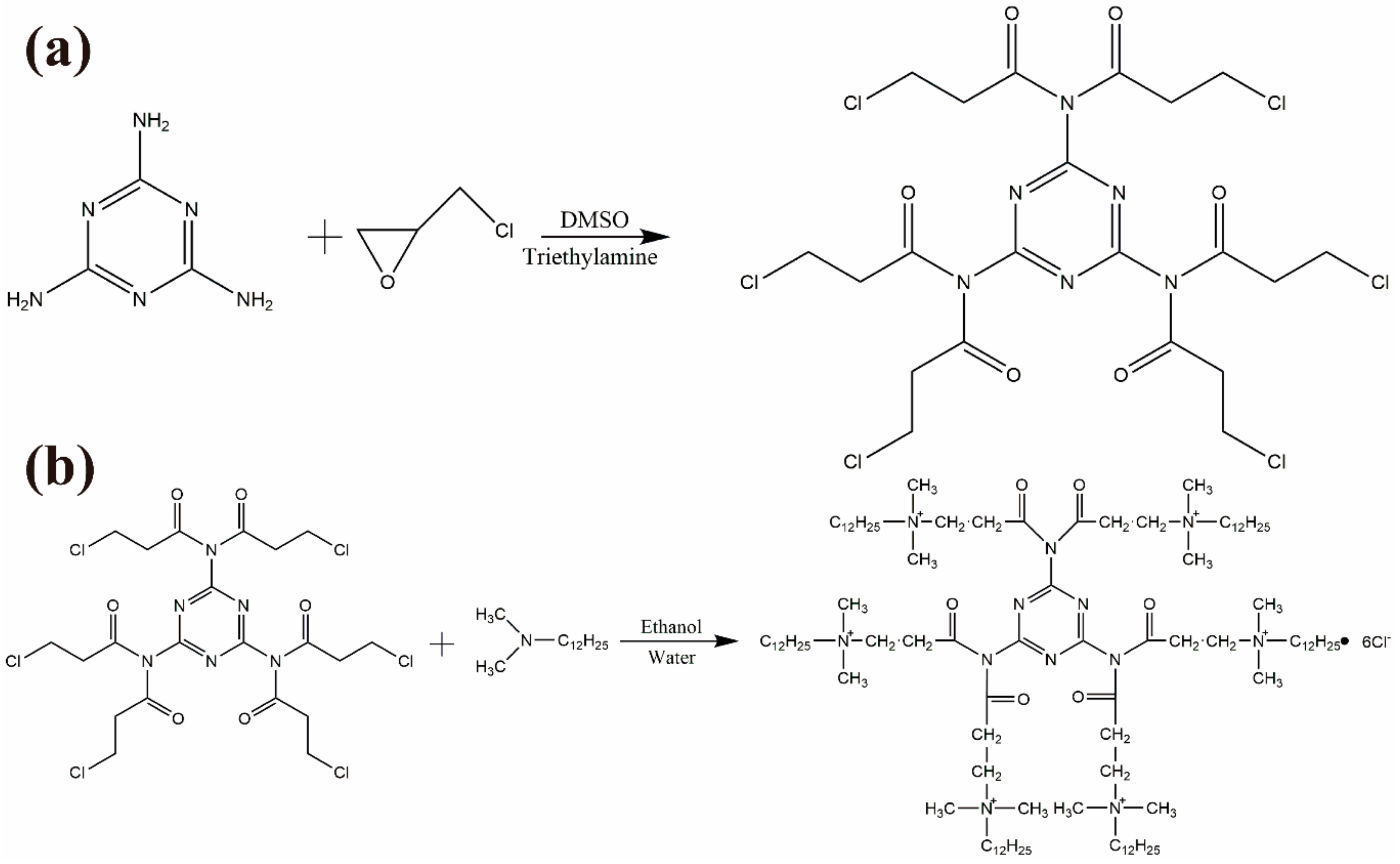
2.2. Synthesis of Tz-6C12QC
2.3. Characterizations
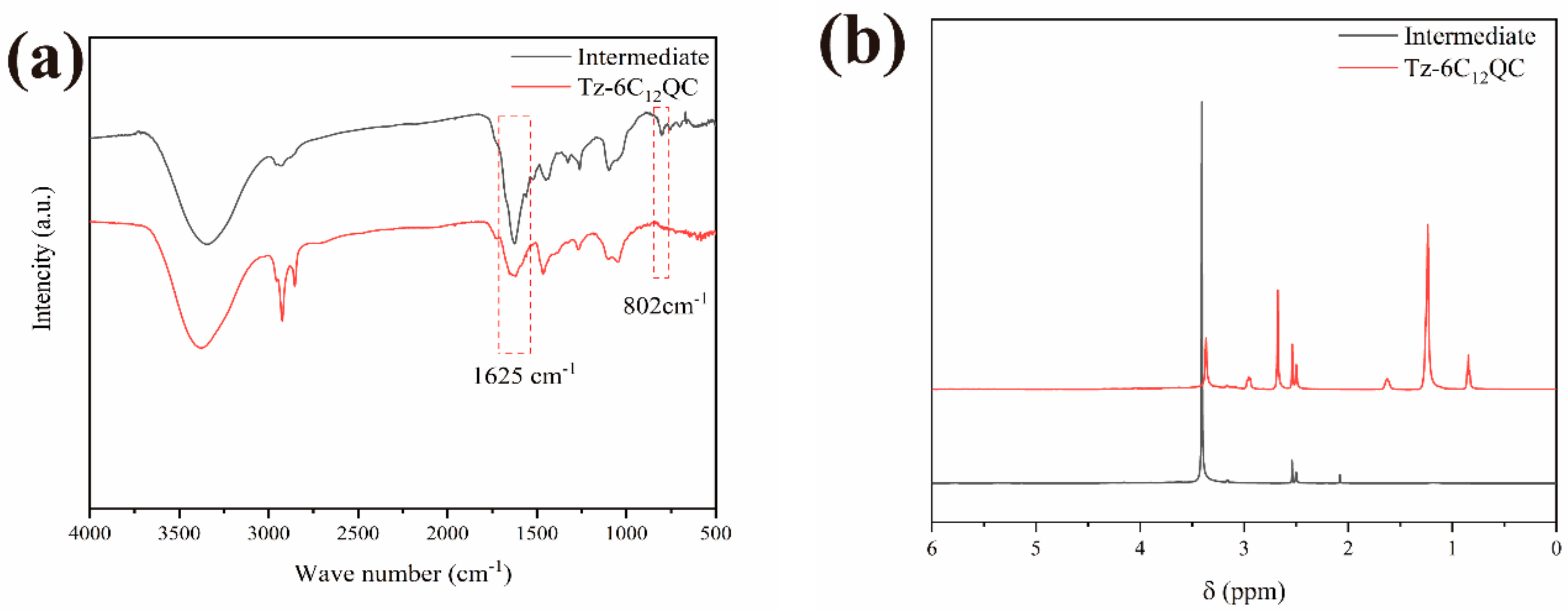
2.3.1. FT-IR Analysis
2.3.2. NMR Analysis
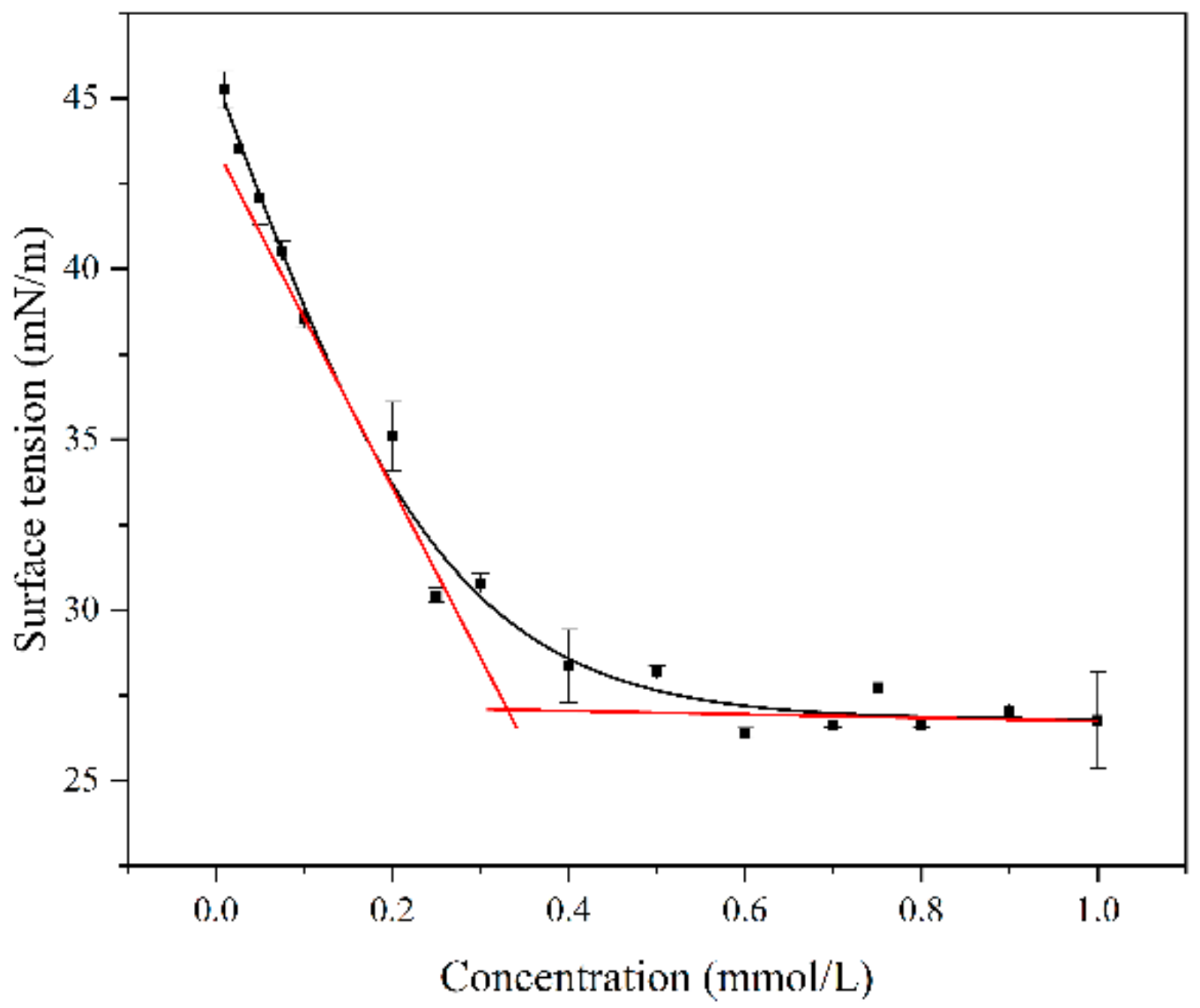
2.3.3. Surface Tension Analysis
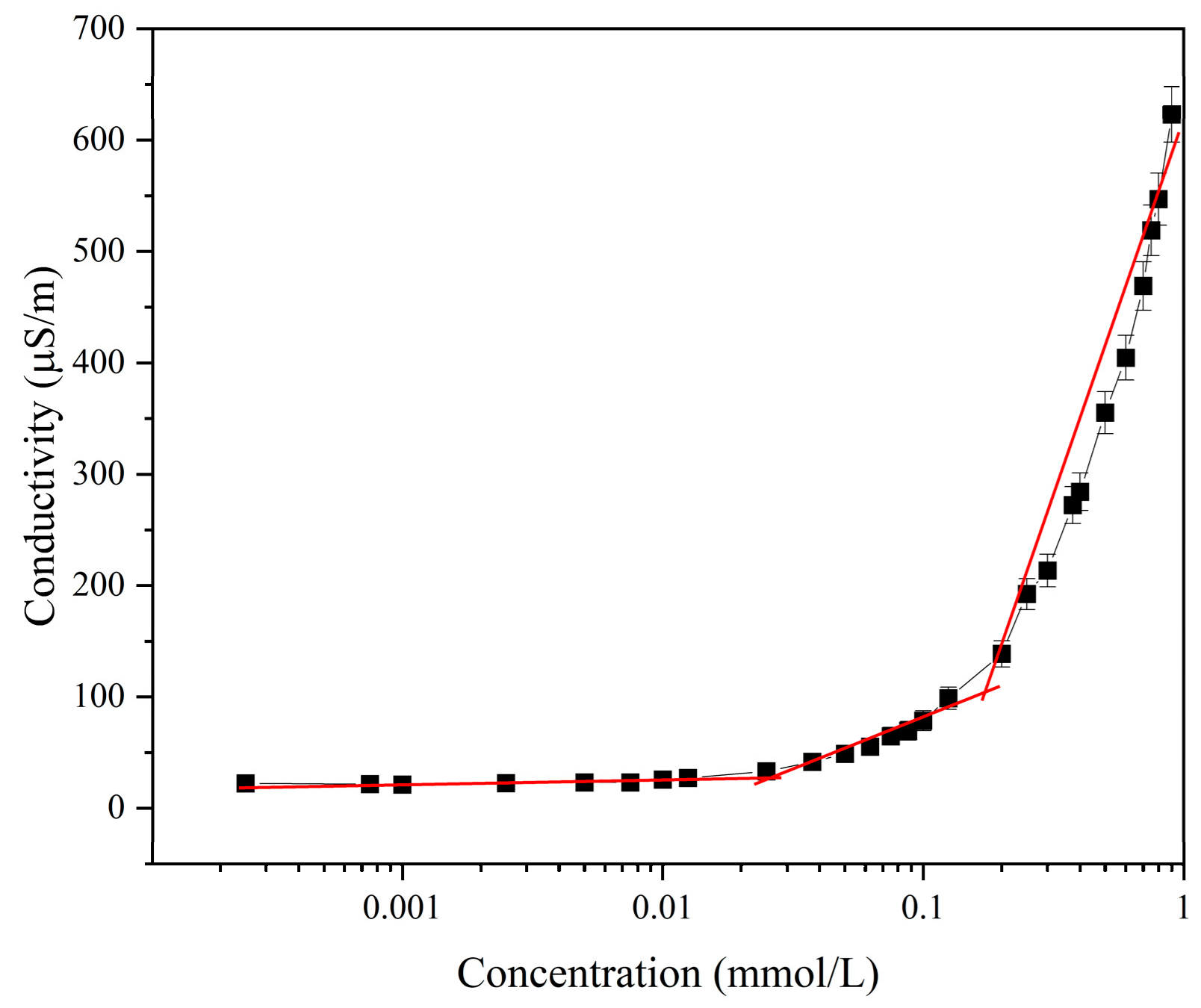
2.3.4. Electrical Conductivity Analysis
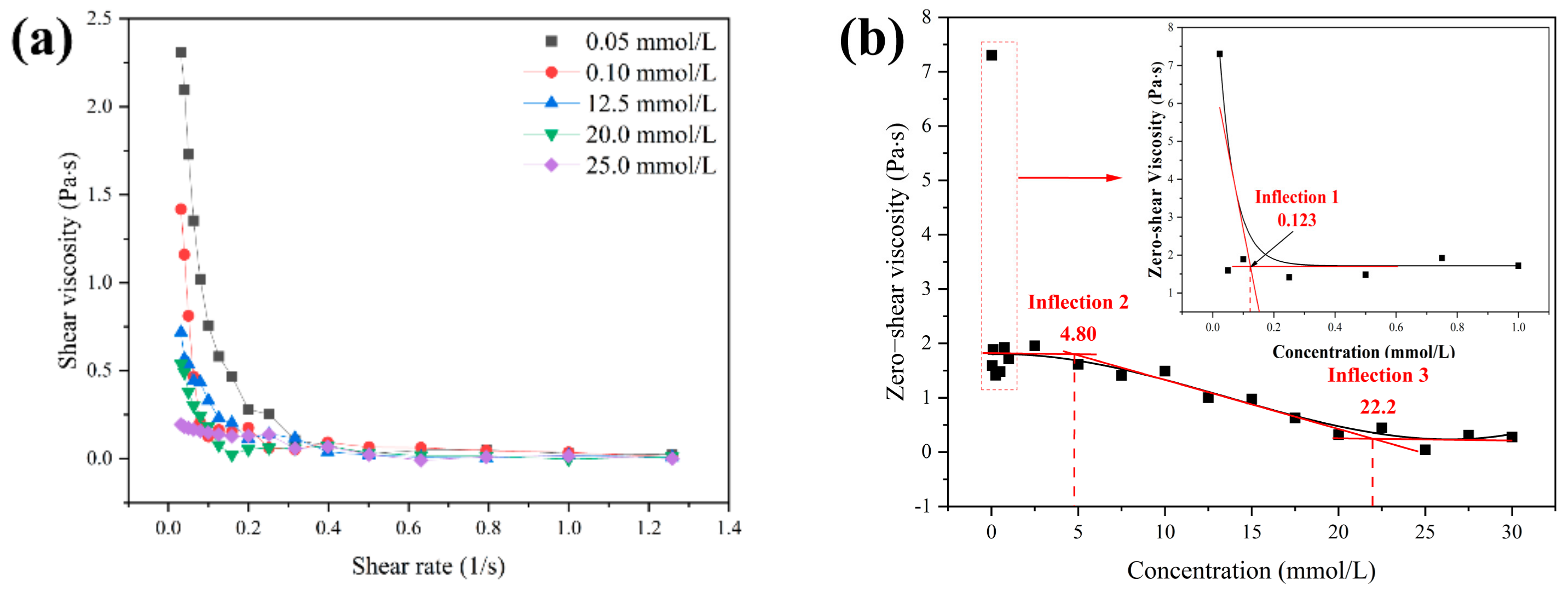
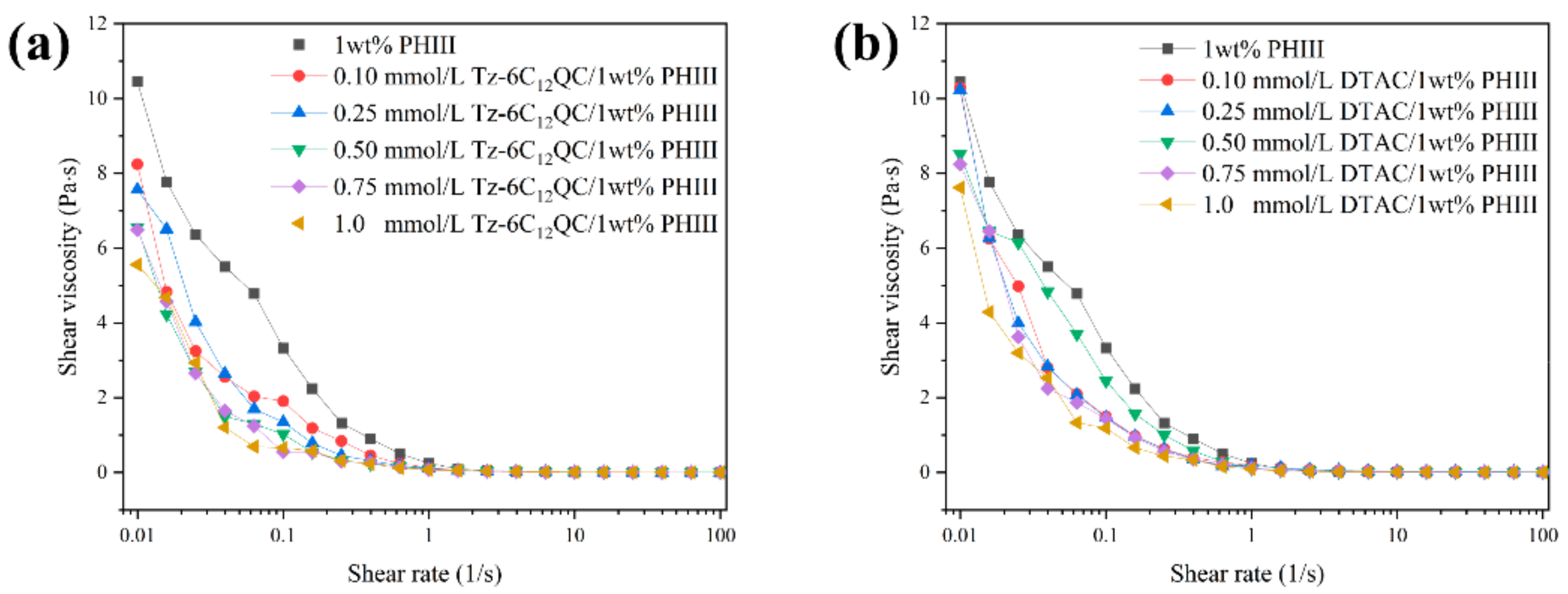
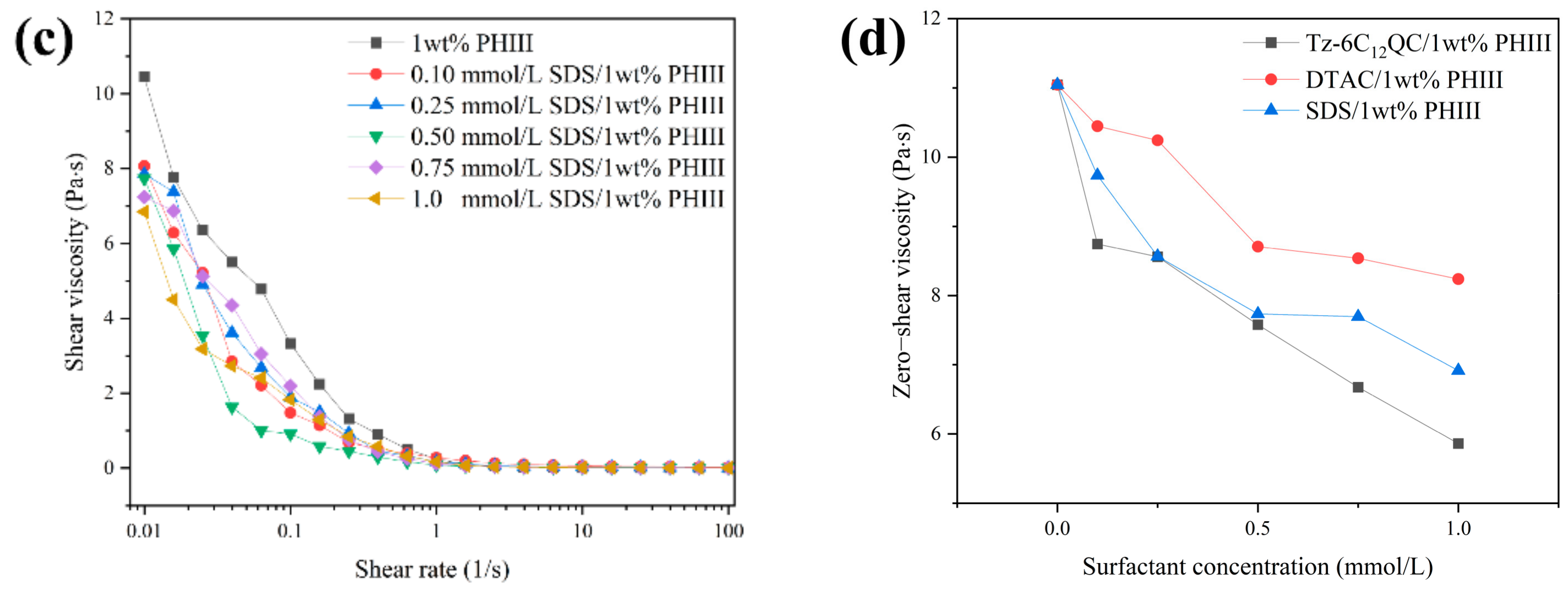
2.3.5. Rheology Analysis
2.3.6. DLS Analysis
2.3.7. TEM Analysis
2.4. Simulation Methods and Models
2.4.1. DPD Simulation Method
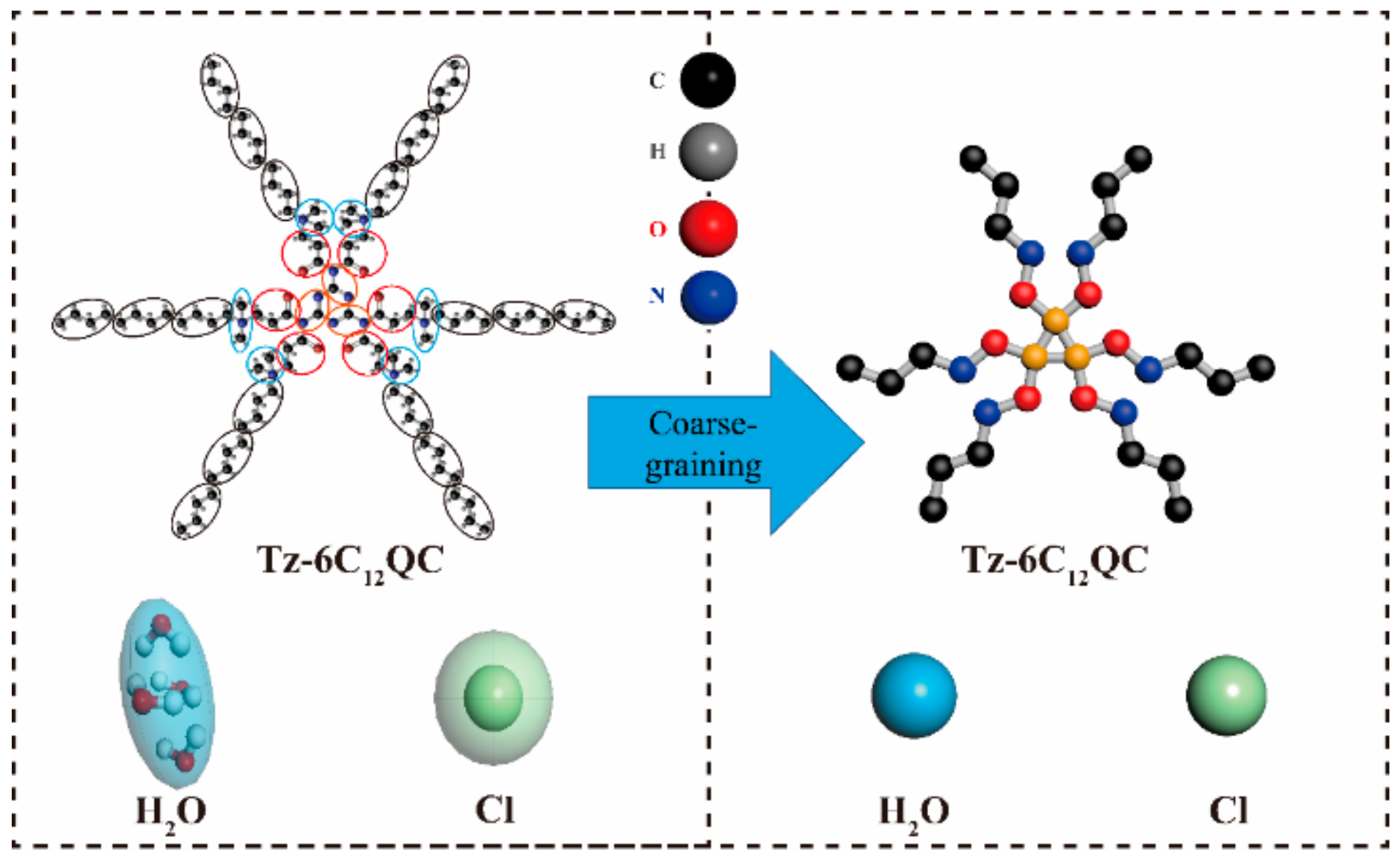
2.4.2. Model and Interaction Parameters
3. Results and Discussion
3.1. Structure of Tz-6C12QC and Its Intermediate
3.2. Surface Activity of Tz-6C12QC
3.3. Thermodynamic Analysis of Micellization
3.4. Shear Rheology Behavior
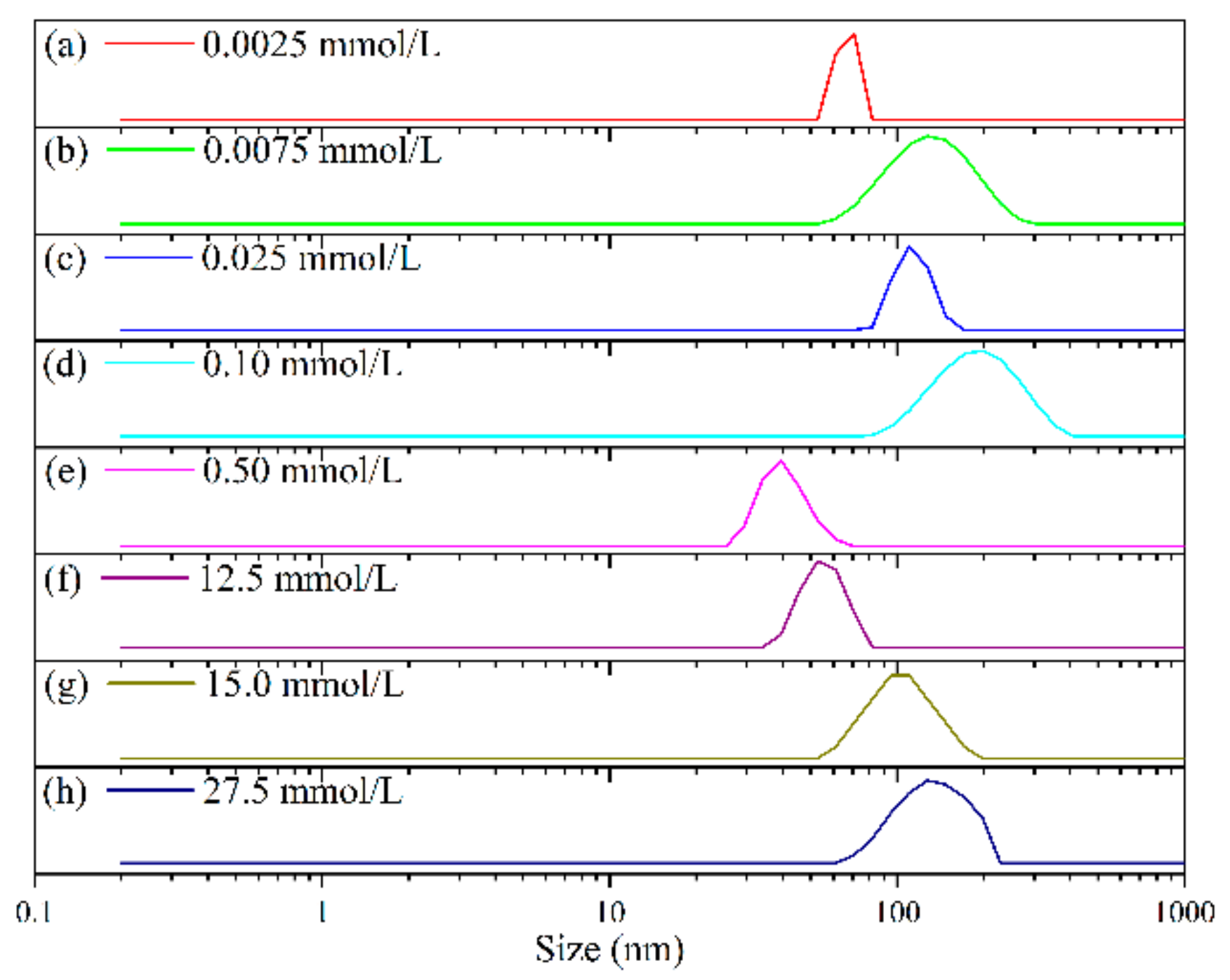
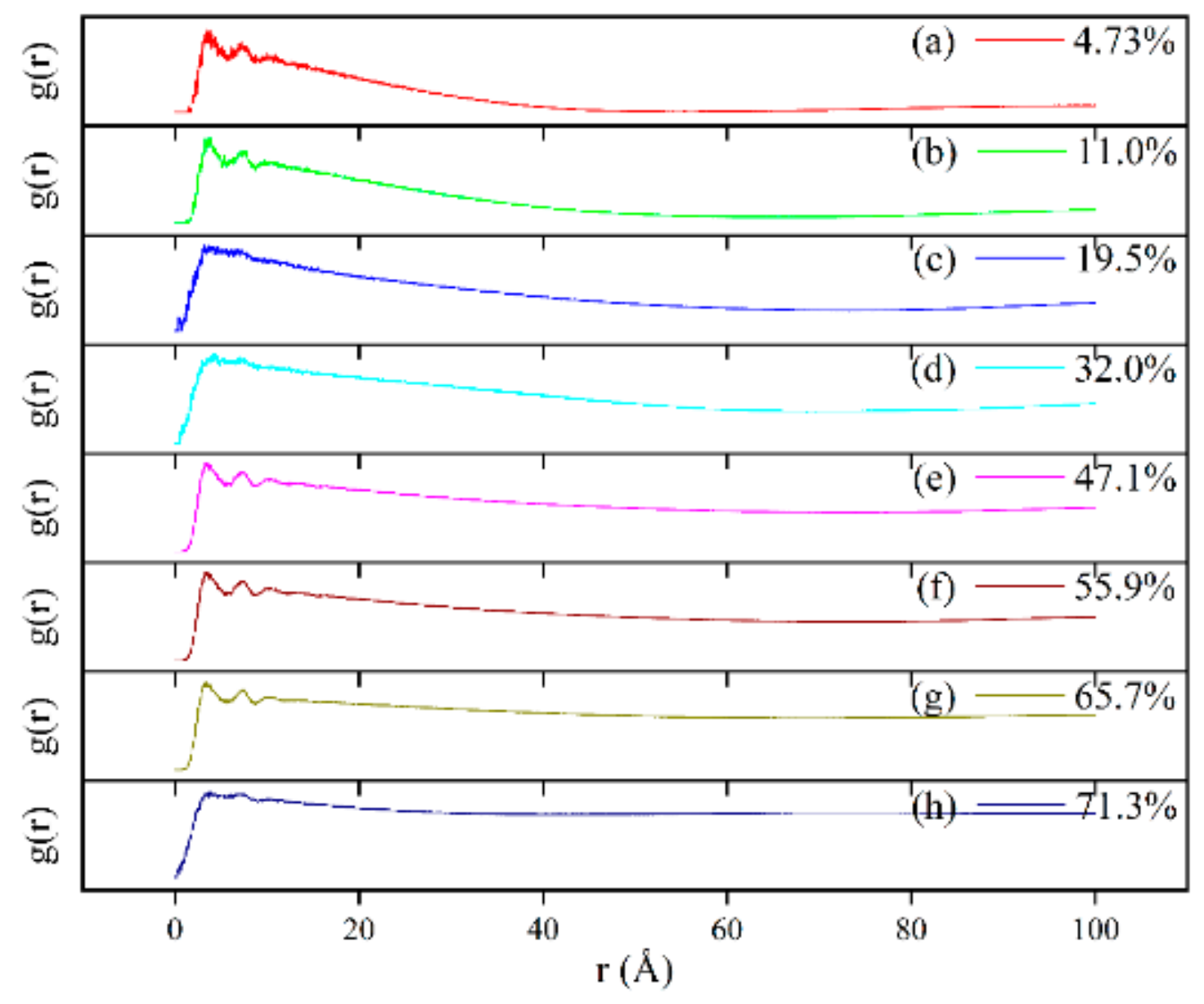
3.5. Size, Distribution, and Morphology Analysis of Tz-6C12QC Aggregates
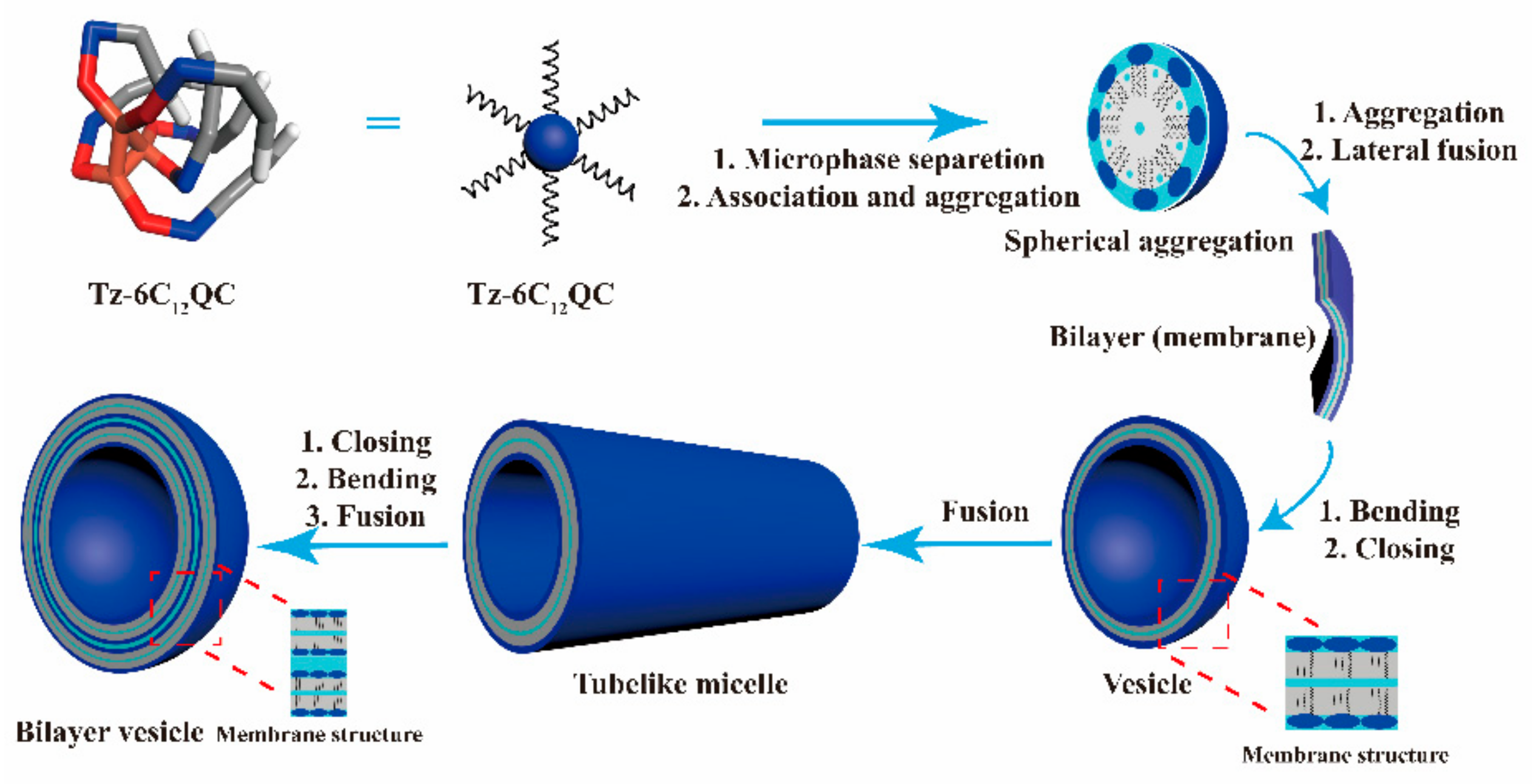
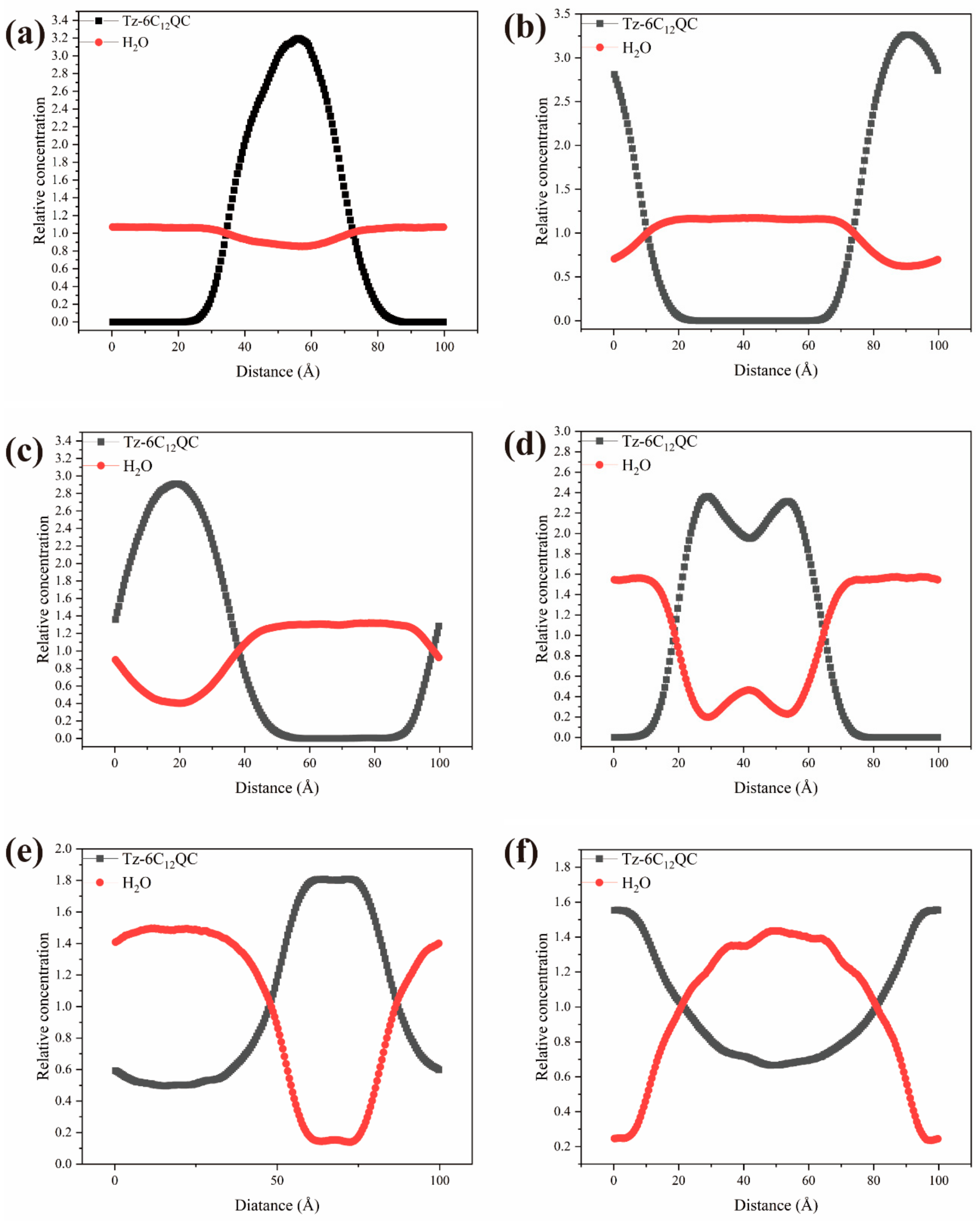
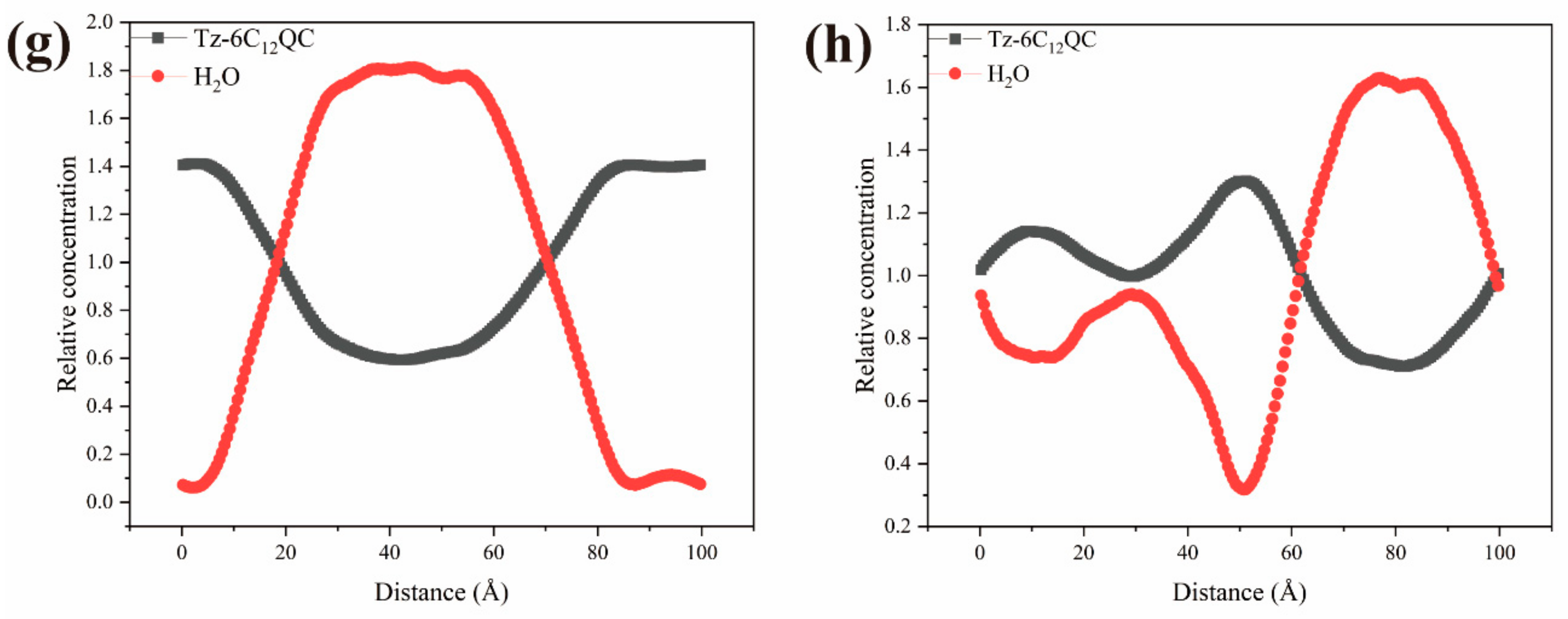
3.6. DPD Simulation of the Self-Assembly Behavior of Tz-6C12QC
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
References
- Kostag, M.; Jedvert, K.; Achtel, C.; Heinze, T.; El Seoud, O. Recent advances in solvents for the dissolution, shaping and derivatization of cellulose: Quaternary ammonium electrolytes and their solutions in water and molecular solvents. Molecules 2018, 23, 511. [Google Scholar] [CrossRef] [PubMed]
- Choi, S.; Kang, B.; Taguchi, S.; Umakoshi, H.; Kim, K.; Kwak, M.K.; Jung, H. A simple method for continuous synthesis of bicelles in microfluidic systems. Langmuir 2021, 37, 12255–12262. [Google Scholar] [CrossRef] [PubMed]
- Cai, B.; Li, S.; Jiang, W.; Zhou, Y. Ph-controlled stereoregular polymerization of poly(methyl methacrylate) in vesicle membranes. Langmuir 2021, 37, 12746–12752. [Google Scholar] [CrossRef] [PubMed]
- Jiang, W.; Zhou, Y.; Yan, D. Hyperbranched polymer vesicles: From self-assembly, characterization, mechanisms, and properties to applications. Chem. Soc. Rev. 2015, 44, 3874–3889. [Google Scholar] [CrossRef]
- Sun, M.; Müllen, K.; Yin, M. Water-soluble perylenediimides: Design concepts and biological applications. Chem. Soc. Rev. 2016, 45, 1513–1528. [Google Scholar] [CrossRef]
- Silva, L.I.M.; Pérez-Gramatges, A.; Larrude, D.G.; Almeida, J.M.S.; Aucélio, R.Q.; Da Silva, A.R. Gold nanoparticles produced using nabh4 in absence and in the presence of one-tail or two-tail cationic surfactants: Characteristics and optical responses induced by aminoglycosides. Colloid Surf. A 2021, 614, 126174. [Google Scholar] [CrossRef]
- Yokota, H.; Kadowaki, M.; Matsuura, T.; Imanaka, H.; Ishida, N.; Imamura, K. The use of a combination of a sugar and surfactant to stabilize au nanoparticle dispersion against aggregation during freeze-drying. Langmuir 2020, 36, 6698–6705. [Google Scholar] [CrossRef]
- Xu, L.; Dong, S.; Hao, J.; Cui, J.; Hoffmann, H. Surfactant-modified ultrafine gold nanoparticles with magnetic responsiveness for reversible convergence and release of biomacromolecules. Langmuir 2017, 33, 3047–3055. [Google Scholar] [CrossRef]
- Khan, S.; Gbadamosi, A.; Norrman, K.; Zhou, X.; Shakil, H.S.M.; Patil, S.; Shakil, S.M. Adsorption study of novel gemini cationic surfactant in carbonate reservoir cores—Influence of critical parameters. Materials 2022, 15, 2527. [Google Scholar] [CrossRef]
- Wu, X.; Zhao, L.; Wang, X.; Wang, J.; Zhang, Y. Synthesis and applications of tri-quaternary ammonium salt gemini surfactant. J. Dispers. Sci. Technol. 2013, 34, 106–110. [Google Scholar] [CrossRef]
- Abd El-Lateef, H.M.; Tantawy, A.H.; Abdelhamid, A.A. Novel quaternary ammonium-based cationic surfactants: Synthesis, surface activity and evaluation as corrosion inhibitors for c1018 carbon steel in acidic chloride solution. J. Surfactants Deterg. 2017, 20, 735–753. [Google Scholar] [CrossRef]
- Qi, F.; Cai, Z.S.; Zhu, X.M.; Shang, S.B.; Pei, L.J. Synthesis, characterization, and performance of a novel polymeric cationic surfactant based on low molecular weight chitosan and 3-chloro-2-hydroxypropyl dimethyl dehydroabietyl ammonium chloride (chpdmdha). J. Surfactants Deterg. 2015, 18, 463–470. [Google Scholar] [CrossRef]
- Kalam, S.; Kamal, M.S.; Patil, S.; Hussain, S.M.S. Impact of spacer nature and counter ions on rheological behavior of novel polymer-cationic gemini surfactant systems at high temperature. Polymers 2020, 5, 1027. [Google Scholar] [CrossRef] [PubMed]
- Ding, Z.; Fang, S. Synthesis, surface and antimicrobial activities of novel cationic gemini surfactants. J. Surfactants Deterg. 2015, 18, 1051–1057. [Google Scholar] [CrossRef]
- Hu, D.; Guo, X.; Jia, L. Synthesis, surface active properties of novel gemini surfactants with amide groups and rigid spacers. J. Surfactants Deterg. 2013, 16, 913–919. [Google Scholar] [CrossRef]
- Lavagnini, E.; Cook, J.L.; Warren, P.B.; Williamson, M.J.; Hunter, C.A. A surface site interaction point method for dissipative particle dynamics parametrization: Application to alkyl ethoxylate surfactant self-assembly. J. Phys. Chem. B 2020, 124, 5047–5055. [Google Scholar] [CrossRef]
- Khedr, A.; Striolo, A. Quantification of ostwald ripening in emulsions via coarse-grained simulations. J. Chem. Theory Comput. 2019, 15, 5058–5068. [Google Scholar] [CrossRef]
- Liu, F.; Zhou, W.; Liu, D.; Chen, F.; Wei, J. Coarse-grained molecular dynamics study on the rheological behaviors of surfactant aqueous solution. J. Mol. Liq. 2018, 265, 572–577. [Google Scholar] [CrossRef]
- Vishnyakov, A.; Lee, M.; Neimark, A.V. Prediction of the critical micelle concentration of nonionic surfactants by dissipative particle dynamics simulations. J. Phys. Chem. Lett. 2013, 4, 797–802. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Pei, S.; Wang, M.; Yan, Y.; Sun, X.; Zhang, J. Coarse-grained molecular dynamics study on the self-assembly of gemini surfactants: The effect of spacer length. Phys. Chem. Chem. Phys. 2017, 19, 4462–4668. [Google Scholar] [CrossRef]
- Zhou, G.; Gao, M.; Deng, X.; Ma, Y.; Mao, C.; Li, G.; Chen, C.; Sun, X.; Khalid, S.; Lu, G. A mesoscopic dpd simulation study on long chain quaternary ammonium gemini surfactant solution. J. Dispers. Sci. Technol. 2020, 42, 58–66. [Google Scholar] [CrossRef]
- Wu, R.; Deng, M.; Kong, B.; Yang, X. Coarse-grained molecular dynamics simulation of ammonium surfactant self-assemblies: Micelles and vesicles. J. Phys. Chem. B 2009, 113, 15010–15016. [Google Scholar] [CrossRef] [PubMed]
- Samanta, S.K.; Bhattacharya, S.; Maiti, P.K. Coarse-grained molecular dynamics simulation of the aggregation properties of multiheaded cationic surfactants in water. J. Phys. Chem. B 2009, 113, 13545–13550. [Google Scholar] [CrossRef]
- Maiti, P.K.; Lansac, Y.; Glaser, M.A.; Clark, N.A.; Rouault, Y. Self-assembly in surfactant oligomers: A coarse-grained description through molecular dynamics simulations. Langmuir 2002, 18, 1908–1918. [Google Scholar] [CrossRef]
- Karaborni, S.; Esselink, K.; Hilbers, P.A.J.; Smit, B.; Karthauser, J.; van Os, N.M.; Zana, R. Simulating the self-assembly of gemini (dimeric) surfactants. Science 1994, 266, 254–256. [Google Scholar] [CrossRef]
- Cheng, L.; Cao, D. Designing a thermo-switchable channel for nanofluidic controllable transportation. ACS Nano 2011, 5, 1102–1108. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Wang, P.; Ma, Y.; Zhang, J.; Dai, C.; Yan, Y.; Liu, B. Tuning the self-assembly of surfactants by the confinement of carbon nanotube arrays: A cornucopia of lamellar phase variants. Nanoscale 2015, 7, 6069–6074. [Google Scholar] [CrossRef]
- Sambasivam, A.; Sangwai, A.V.; Sureshkumar, R. Self-assembly of nanoparticle–surfactant complexes with rodlike micelles: A molecular dynamics study. Langmuir 2016, 32, 1214–1219. [Google Scholar] [CrossRef]
- Wang, P.; Ma, Y.; Liu, Z.; Yan, Y.; Sun, X.; Zhang, J. Vesicle formation of catanionic mixtures of ctac/sds induced by ratio: A coarse-grained molecular dynamic simulation study. RSC Adv. 2016, 6, 13442–13449. [Google Scholar] [CrossRef]
- Urzua, M.D.; Cabrera, W.J.; Ríos, H.E. Surface properties of poly(n-monoalkylmaleamic acid-alt-styrene) sodium salts: Effect of the molecular weight and the side chain length. J. Colloid Interface Sci. 2003, 264, 284–289. [Google Scholar] [CrossRef]
- Samanta, S.; Ghosh, P. Coalescence of bubbles and stability of foams in aqueous solutions of tween surfactants. Chem. Eng. Res. Design 2011, 89, 2344–2355. [Google Scholar] [CrossRef]
- Kundu, P.; Kumar, V.; Mishra, I.M. Study the electro-viscous effect on stability and rheological behavior of surfactant-stabilized emulsions. J. Dispers. Sci. Technol. 2018, 39, 384–394. [Google Scholar] [CrossRef]
- Bhadani, A.; Shrestha, R.G.; Koura, S.; Endo, T.; Sakai, K.; Abe, M.; Sakai, H. Self-aggregation properties of new ester-based gemini surfactants and their rheological behavior in the presence of cosurfactant—Monolaurin. Colloid Surf. A 2014, 461, 258–266. [Google Scholar] [CrossRef]
- Chari, K.; Hsu, R.; Bhargava, P.; Figura, B.; Yang, W.; Park, J.H.; Clifford, T.; Kadir, M. Surfactant-activated microgels: A new pathway to rheology modification. Langmuir 2013, 29, 15521–15528. [Google Scholar] [CrossRef]
- Español, P.; Warren, P. Statistical mechanics of dissipative particle dynamics. Europhys. Lett. 1995, 30, 191–196. [Google Scholar] [CrossRef]
- Groot, R.D.; Warren, P.B. Dissipative particle dynamics: Bridging the gap between atomistic and mesoscopic simulation. J. Chem. Phys. 1997, 107, 4423–4435. [Google Scholar] [CrossRef]
- Mai, Z.; Couallier, E.; Rakib, M.; Rousseau, B. Parameterization of a mesoscopic model for the self-assembly of linear sodium alkyl sulfates. J. Chem. Phys. 2014, 140, 204902. [Google Scholar] [CrossRef]
- Guo, H.; Qiu, X.; Zhou, J. Self-assembled core-shell and janus microphase separated structures of polymer blends in aqueous solution. J. Chem. Phys. 2013, 139, 84907. [Google Scholar] [CrossRef]
- Chang, H.; Lin, Y.; Sheng, Y.; Tsao, H. Multilayered polymersome formed by amphiphilic asymmetric macromolecular brushes. Macromolecules 2012, 45, 4778–4789. [Google Scholar] [CrossRef]
- Shi, K.; Lian, C.; Bai, Z.; Zhao, S.; Liu, H. Dissipative particle dynamics study of the water/benzene/caprolactam system in the absence or presence of non-ionic surfactants. Chem. Eng. Sci. 2015, 122, 185–196. [Google Scholar] [CrossRef]
- Baccile, N.; Seyrig, C.; Poirier, A.; Alonso-De Castro, S.; Roelants, S.L.K.W.; Abel, S. Self-assembly, interfacial properties, interactions with macromolecules and molecular modelling and simulation of microbial bio-based amphiphiles (biosurfactants). A tutorial review. Green Chem. 2021, 23, 3842–3944. [Google Scholar] [CrossRef]
- Yoshimura, T.; Kusano, T.; Iwase, H.; Shibayama, M.; Ogawa, T.; Kurata, H. Star-shaped trimeric quaternary ammonium bromide surfactants: Adsorption and aggregation properties. Langmuir 2012, 28, 9322–9331. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Matayoshi, E. Solubility at the molecular level: Development of a critical aggregation concentration (cac) assay for estimating compound monomer solubility. Pharm. Res. 2012, 29, 1745–1754. [Google Scholar] [CrossRef] [PubMed]
- Chu, K.; Hu, S.; Tsao, H.; Sheng, Y. Strong competition between adsorption and aggregation of surfactant in nanoscale systems. J. Colloid Interface Sci. 2019, 553, 674–681. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.F.; Dong, L.L.; Fang, Y. Synthesis and self-aggregation of a hydroxyl-functionalized imidazolium-based ionic liquid surfactant in aqueous solution. J. Surfactants Deterg. 2011, 14, 203–210. [Google Scholar] [CrossRef]
- Fan, Y.; Hou, Y.; Xiang, J.; Yu, D.; Wu, C.; Tian, M.; Han, Y.; Wang, Y. Synthesis and aggregation behavior of a hexameric quaternary ammonium surfactant. Langmuir 2011, 27, 10570–10579. [Google Scholar] [CrossRef]
- Esumi, K.; Taguma, K.; Koide, Y. Aqueous properties of multichain quaternary cationic surfactants. Langmuir 1996, 12, 4039–4041. [Google Scholar] [CrossRef]
- Menger, F.M.; Keiper, J.S.; Mbadugha, B.N.A.; Caran, K.L.; Romsted, L.S. Interfacial composition of gemini surfactant micelles determined by chemical trapping. Langmuir 2000, 16, 9095–9098. [Google Scholar] [CrossRef]
- Yoshimura, T.; Esumi, K. Physicochemical properties of ring-type trimeric surfactants from cyanuric chloride. Langmuir 2003, 19, 3535–3538. [Google Scholar] [CrossRef]
- In, M.; Bec, V.; Aguerre-Chariol, O.; Zana, R. Quaternary ammonium bromide surfactant oligomers in aqueous solution: Self-association and microstructure. Langmuir 2000, 16, 141–148. [Google Scholar] [CrossRef]
- Menger, F.M.; Migulin, V.A. Synthesis and properties of multiarmed geminis. J. Org. Chem. 1999, 64, 8916–8921. [Google Scholar] [CrossRef]
- Wang, S.; Zhao, K. Dielectric analysis for the spherical and rodlike micelle aggregates formed from a gemini surfactant: Driving forces of micellization and stability of micelles. Langmuir 2016, 32, 7530–7540. [Google Scholar] [CrossRef] [PubMed]
- Geng, F.; Liu, J.; Zheng, L.; Yu, L.; Li, Z.; Li, G.; Tung, C. Micelle formation of long-chain imidazolium ionic liquids in aqueous solution measured by isothermal titration microcalorimetry. J. Chem. Eng. Data 2010, 55, 147–151. [Google Scholar] [CrossRef]
- Pires, P.A.R.; El Seoud, O.A. Benzyl (3-acylaminopropyl) dimethylammonium chloride surfactants: Structure and some properties of the micellar aggregates. Progr. Colloid Polym. Sci. 2006, 133, 131–141. [Google Scholar]
- Vlachy, N.; Drechsler, M.; Verbavatz, J.; Touraud, D.; Kunz, W. Role of the surfactant headgroup on the counterion specificity in the micelle-to-vesicle transition through salt addition. J. Colloid Interface Sci. 2008, 319, 542–548. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Zhang, Y.; Chu, Z.; Feng, Y. Wormlike micelles formed by ultra-long-chain nonionic surfactant. Colloid Polym. Sci. 2021, 299, 1295–1304. [Google Scholar] [CrossRef]
- Jiao, W.; Wang, Z.; Liu, T.; Li, X.; Dong, J. Ph and light dual stimuli-responsive wormlike micelles with a novel gemini surfactant. Colloids Surf. A 2021, 618, 126505. [Google Scholar] [CrossRef]
- Wang, R.; Yan, H.; Hu, W.; Li, Y.; Mei, Z. Micellization of anionic sulfonate gemini surfactants and their interactions with anionic polyacrylamide. J. Surfactants Deterg. 2018, 21, 81–90. [Google Scholar] [CrossRef]
- Zhang, J.; Ping, A.; Liu, Y.; Li, L.; Li, Q.; Wei, X. Structural changes in a cationic surfactant-water mixtures. Phys. Chem. Liq. 2015, 53, 706–716. [Google Scholar] [CrossRef]
- Soltero, J.F.A.; Alvarez-Ramírez, J.G.; Fernández, V.V.A.; Tepale, N.; Bautista, F.; Macías, E.R.; Pérez-López, J.H.; Schulz, P.C.; Manero, O.; Solans, C.; et al. Phase and rheological behavior of the polymerizable surfactant ctavb and water. J. Colloid Interface Sci. 2007, 312, 130–138. [Google Scholar] [CrossRef]
- Benhur, A.M.; Diaz, J.; Amin, S. Impact of polyelectrolyte-surfactant interactions on the rheology and wet lubrication performance of conditioning shampoo. Int. J. Cosmet. Sci. 2021, 43, 246–253. [Google Scholar] [CrossRef] [PubMed]
- Nishimura, T.; Toh, W.; Akiyoshi, K. Synthesis and characterization of shell-cross-linked glycopolymer bilayer vesicles. Macromol. Rapid Commun. 2018, 39, 1800384. [Google Scholar] [CrossRef] [PubMed]
- Falvey, P.; Lim, C.W.; Darcy, R.; Revermann, T.; Karst, U.; Giesbers, M.; Marcelis, A.T.M.; Lazar, A.; Coleman, A.W.; Reinhoudt, D.N.; et al. Bilayer vesicles of amphiphilic cyclodextrins: Host membranes that recognize guest molecules. Chem. Eur. J. 2005, 11, 1171–1180. [Google Scholar] [CrossRef] [PubMed]

| Bead Type | Fragment | Repulsive Parameters aij | ||||||
|---|---|---|---|---|---|---|---|---|
| CN2 | CO(CH2)2 | N+(CH3)2 | (CH2)4 | (CH2)3CH3 | Cl− | (H2O)4 | ||
| A | CN2 | 105.00 | ||||||
| B | CO(CH2)2 | 106.89 | 105.00 | |||||
| C | N+(CH3)2 | 107.33 | 105.30 | 105.00 | ||||
| D | (CH2)4 | 109.11 | 105.38 | 105.28 | 105.00 | |||
| E | (CH2)3CH3 | 109.05 | 105.48 | 105.34 | 105.01 | 105.00 | ||
| F | Cl− | 106.89 | 106.58 | 107.18 | 108.86 | 109.05 | 105.00 | |
| G | (H2O)4 | 104.82 | 105.38 | 105.36 | 106.81 | 107.12 | 103.47 | 105.00 |
| Surfactant | CMC [mmol/L] | γmax [mN/m] | 106Γ [mol/m2] | A [nm2/Molecule] |
|---|---|---|---|---|
| DTAB [42] | 14 | 38.6, 38.9 | 3.42 | 0.49 |
| 2RenQ [47] | 0.90 | 21.4 | 2.31 | 0.72 |
| 12-2-12 [48] | 0.97 | 32.4 | - | 0.1 |
| 3C4NAc-Tz [49] | 0.19 | 32.9 | 3.54 | 0.47 |
| 12-3-12-4-12-3-12 [50] | 0.06 | - | 1.30 | 0.64 |
| AD-6 [51] | 6 | - | - | - |
| Tz-6C12QC | 0.34 | 28.27 | 4.67 | 0.356 |
| T [°C] | α | β | CMC [mmol/L] | [J/mol] | [J/mol] | [J/mol∙K] | [J/mol] |
|---|---|---|---|---|---|---|---|
| 25 | 0.997 | 0.003 | 0.172 | −31,623.19 | −252.79 | 105.22 | −31,370.40 |
| 50 | 1.06 | −0.06 | 0.173 | −30,201.48 | −259.76 | 92.66 | −29,941.71 |
| 75 | 1.11 | −0.11 | 0.175 | −29,042.51 | −267.25 | 82.65 | −28,775.26 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiao, J.; Ma, C.; Zhang, L.; Li, F.; Gao, T.; Wang, L.; Sin, L.T. Synthesis and Aggregation Behavior of Hexameric Quaternary Ammonium Salt Surfactant Tz-6C12QC. Polymers 2023, 15, 4396. https://doi.org/10.3390/polym15224396
Jiao J, Ma C, Zhang L, Li F, Gao T, Wang L, Sin LT. Synthesis and Aggregation Behavior of Hexameric Quaternary Ammonium Salt Surfactant Tz-6C12QC. Polymers. 2023; 15(22):4396. https://doi.org/10.3390/polym15224396
Chicago/Turabian StyleJiao, Jianjian, Chi Ma, Linlin Zhang, Fan Li, Tianxu Gao, Lei Wang, and Lee Tin Sin. 2023. "Synthesis and Aggregation Behavior of Hexameric Quaternary Ammonium Salt Surfactant Tz-6C12QC" Polymers 15, no. 22: 4396. https://doi.org/10.3390/polym15224396
APA StyleJiao, J., Ma, C., Zhang, L., Li, F., Gao, T., Wang, L., & Sin, L. T. (2023). Synthesis and Aggregation Behavior of Hexameric Quaternary Ammonium Salt Surfactant Tz-6C12QC. Polymers, 15(22), 4396. https://doi.org/10.3390/polym15224396







