A Study on Damage of T800 Carbon Fiber/Epoxy Composites under In-Plane Shear Using Acoustic Emission and Digital Image Correlation
Abstract
:1. Introduction
2. Experimental Details
3. Results and Discussion
3.1. Tangential Shear Modulus Calculation and Parameter Analysis of AE Signals
3.2. DIC Analysis
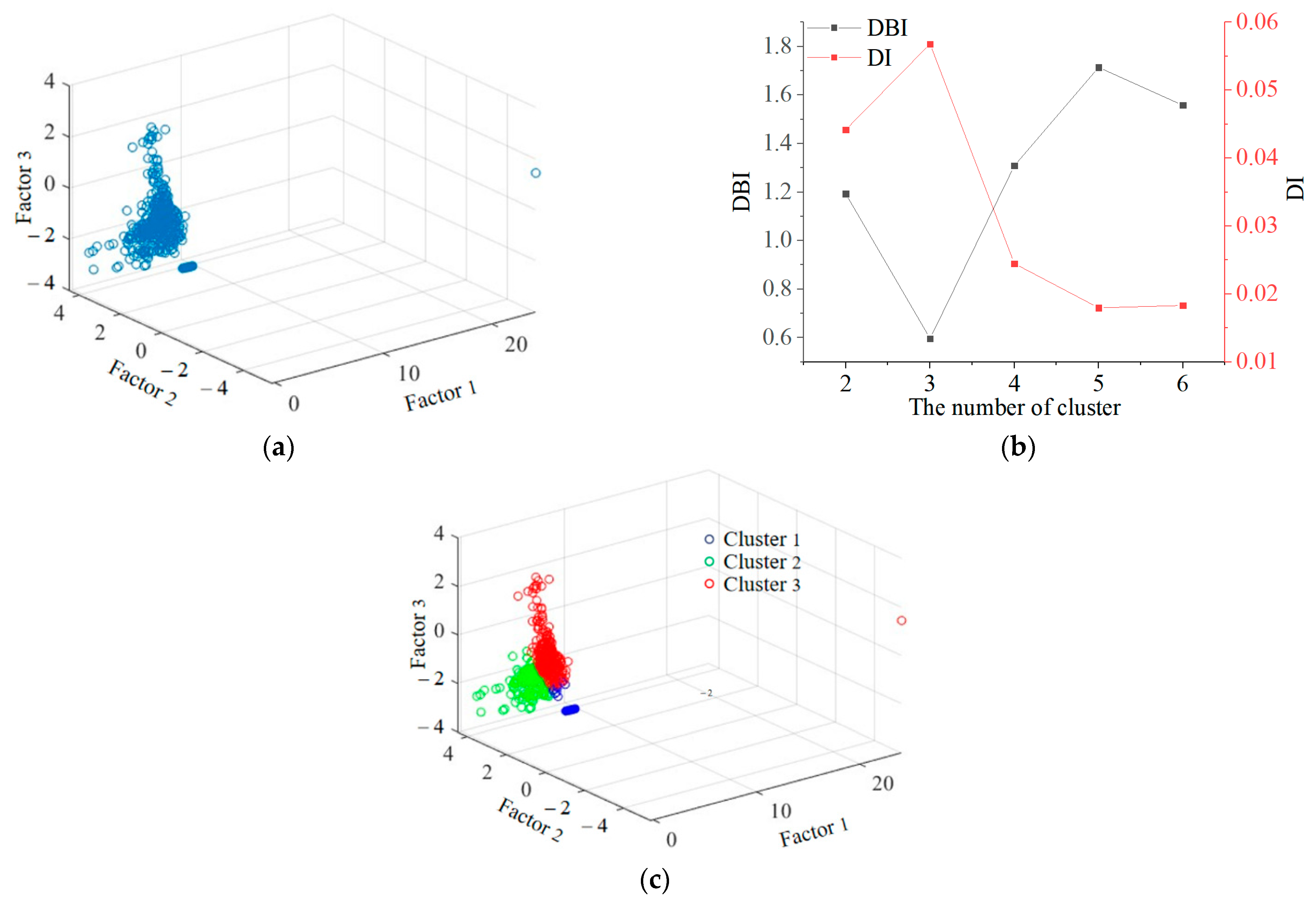
3.3. Factor Analysis
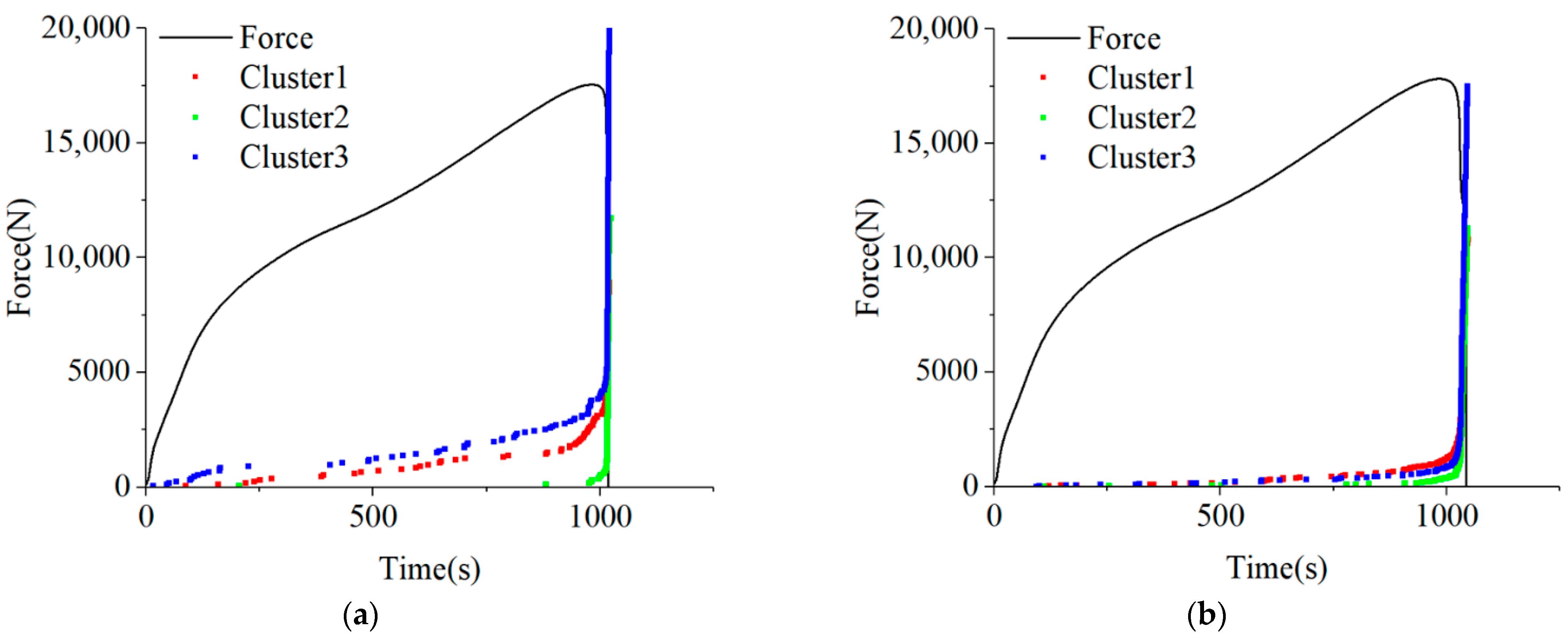
3.4. Fuzzy C-Means
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Golzar, M.; Sinke, J.; Abouhamzeh, M. Novel thermomechanical characterization for shrinkage evolution of unidirectional semi-crystalline thermoplastic prepregs (PPS/CF) in melt, rubbery and glassy states. Compos. Part A Appl. Sci. Manuf. 2022, 156, 106879. [Google Scholar] [CrossRef]
- Tang, S.; Hu, C. Design, Preparation and Properties of Carbon Fiber Reinforced Ultra-High Temperature Ceramic Composites for Aerospace Applications: A Review. J. Mater. Sci. Technol. 2017, 33, 117–130. [Google Scholar] [CrossRef]
- Wysmulski, P. The effect of load eccentricity on the compressed CFRP Z-shaped columns in the weak post-critical state. Compos. Struct. 2022, 301, 116184. [Google Scholar] [CrossRef]
- Rozylo, P.; Debski, H. Failure study of compressed thin-walled composite columns with top-hat cross-section. Thin-Walled Struct. 2022, 180, 109869. [Google Scholar] [CrossRef]
- Muflikhun, M.A.; Higuchi, R.; Yokozeki, T.; Aoki, T. Failure mode analysis of CFRP-SPCC hybrid thin laminates under axial loading for structural applications: Experimental research on strain performance. Compos. Part B Eng. 2019, 172, 262–270. [Google Scholar] [CrossRef]
- Panchal, M.; Kaushik, L.; Ravi, K.R.; Khatirkar, R.; Choi, S.-H.; Singh, J. Recent advances in the in-plane shear testing of Mg alloy sheets. J. Magnes. Alloy. 2023, 11, 405–424. [Google Scholar] [CrossRef]
- Mandegarian, S.; Samareh-Mousavi, S.S.; Taheri-Behrooz, F. Experimental investigation on in-plane shear fatigue failure criteria of ± 45° angle-ply carbon epoxy composite. Int. J. Fatigue 2022, 160, 106873. [Google Scholar] [CrossRef]
- Yu, G.; Xie, C.; Du, J.; Ni, Z.; Chang, L.; Gao, X.; Song, Y. In-plane shear experimental method and mechanical behavior of ceramic matrix mini-composites. J. Mater. Res. Technol. 2023, 24, 5541–5551. [Google Scholar] [CrossRef]
- Harizi, W.; Chaki, S.; Bourse, G.; Ourak, M. Mechanical damage assessment of Polymer–Matrix Composites using active infrared thermography. Compos. Part B Eng. 2014, 66, 204–209. [Google Scholar] [CrossRef]
- Marani, R.; Palumbo, D.; Renò, V.; Galietti, U.; Stella, E.; D’Orazio, T. Modeling and classification of defects in CFRP laminates by thermal non-destructive testing. Compos. Part B Eng. 2018, 135, 129–141. [Google Scholar] [CrossRef]
- Zeng, Z.; Tian, Q.; Wang, H.; Jiao, S.; Li, J. Testing of delamination in multidirectional carbon fiber reinforced polymer laminates using the vertical eddy current method. Compos. Struct. 2019, 208, 314–321. [Google Scholar] [CrossRef]
- Qu, J.; Xu, C.; Meng, S. Experimental investigation on interlaminar and in-plane shear damage evolution of 2D C/SiC composites using acoustic emission and X-ray computed microtomography. Ceram. Int. 2023, 49, 11711–11717. [Google Scholar] [CrossRef]
- Rubio-González, C.; del Pilar de Urquijo-Ventura, M.; Rodríguez-González, J.A. Damage progression monitoring using self-sensing capability and acoustic emission on glass fiber/epoxy composites and damage classification through principal component analysis. Compos. Part B 2023, 254, 110608. [Google Scholar] [CrossRef]
- Liu, J.; Kanwal, H.; Tang, C.; Hao, W. Study on flexural properties of 3D printed lattice-reinforced concrete structures using acoustic emission and digital image correlation. Constr. Build. Mater. 2022, 333, 127418. [Google Scholar] [CrossRef]
- Seyyednourani, M.; Akgun, S.; Ulus, H.; Yildiz, M.; Sas, H.S. Experimental investigation on Compression-After-Impact (CAI) response of aerospace grade thermoset composites under low-temperature conditions assisted with acoustic emission moni-toring. Compos. Struct. 2023, 321, 117260. [Google Scholar] [CrossRef]
- Wang, M.; He, M.; Liang, Z.; Wu, D.; Wang, Y.; Qing, X.; Wang, Y. Fatigue damage monitoring of composite laminates based on acoustic emission and digital image correlation techniques. Compos. Struct. 2023, 321, 117239. [Google Scholar] [CrossRef]
- Ferreira Motta, R., Jr.; Alderliesten, R.; Shiino, M.Y.; Cioffi, M.O.H.; Voorwald, H.J.C. Scrutinizing interlaminar fatigue loading cycle in composites using acoustic emission technique: Stress ratio influence on damage formation. Compos. Part A: Appl. Sci. Manuf. 2020, 138, 106065. [Google Scholar] [CrossRef]
- Mi, Y.; Zhu, C.; Li, X.; Wu, D. Acoustic emission study of effect of fiber weaving on properties of fiber-resin composite materials. Compos. Struct. 2020, 237, 111906. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, L.; Li, Z.; Chen, Z.; Huang, K.; Guo, L. Investigation on damage evolution of open-hole plain woven composites under tensile load by acoustic emission signal analysis. Compos. Struct. 2023, 305, 116481. [Google Scholar] [CrossRef]
- Azadi, M.; Sayar, H.; Ghasemi-Ghalebahman, A.; Jafari, S.M. Tensile loading rate effect on mechanical properties and failure mechanisms in open-hole carbon fiber reinforced polymer composites by acoustic emission approach. Compos. Part B Eng. 2019, 158, 448–458. [Google Scholar] [CrossRef]
- Özaslan, E.; Yetgin, A.; Acar, B.; Güler, M. Damage mode identification of open hole composite laminates based on acoustic emission and digital image correlation methods. Compos. Struct. 2021, 274, 114299. [Google Scholar] [CrossRef]
- Barile, C.; Casavola, C.; Pappalettera, G.; Kannan, V.P. Laplacian score and K-means data clustering for damage characterization of adhesively bonded CFRP composites by means of acoustic emission technique. Appl. Acoust. 2022, 185, 108425. [Google Scholar] [CrossRef]
- Andraju, L.B.; Raju, G. Damage characterization of CFRP laminates using acoustic emission and digital image correlation: Clustering, damage identification and classification. Eng. Fract. Mech. 2023, 277, 108993. [Google Scholar] [CrossRef]
- Sawan, H.A.; Walter, M.E.; Marquette, B. Unsupervised learning for classification of acoustic emission events from tensile and bending experiments with open-hole carbon fiber composite samples. Compos. Sci. Technol. 2015, 107, 89–97. [Google Scholar] [CrossRef]
- Xu, D.; Liu, P.F.; Li, J.G.; Chen, Z.P. Damage mode identification of adhesive composite joints under hygrothermal environment using acoustic emission and machine learning. Compos. Struct. 2019, 211, 351–363. [Google Scholar] [CrossRef]
- Chen, C.; Chen, X.; Ning, Y. Identification of fracture damage characteristics in ultra-high performance cement-based composite using digital image correlation and acoustic emission techniques. Compos. Struct. 2022, 291, 115612. [Google Scholar] [CrossRef]
- Saeedifar, M.; Zarouchas, D. Damage characterization of laminated composites using acoustic emission: A review. Compos. Part B Eng. 2020, 195, 108039. [Google Scholar] [CrossRef]
- Lima, R.; Drobiazko, M.; Bernasconi, A.; Carboni, M. On crack tip localisation in quasi-statically loaded, adhesively bonded double cantilever beam specimens by acoustic emission. Theor. Appl. Fract. Mech. 2022, 118, 103286. [Google Scholar] [CrossRef]
- Yan, L.; Han, B.; Zhang, J.; Li, W.; Xie, H.; Gao, C.; Chen, L.; Yu, J.; Song, Z.; Zuo, B. Experimental study on fatigue damage of continuous steel–concrete composite beam by acoustic emission. Structures 2023, 57, 105185. [Google Scholar] [CrossRef]
- Zhou, W.; Zhao, W.-Z.; Zhang, Y.-N.; Ding, Z.-J. Cluster analysis of acoustic emission signals and deformation measurement for delaminated glass fiber epoxy composites. Compos. Struct. 2018, 195, 349–358. [Google Scholar] [CrossRef]
- Kalteremidou, K.; Murray, B.; Carrella-Payan, D.; Cernescu, A.; Van Hemelrijck, D.; Pyl, L. Failure analysis of CF/epoxy hollow beam components using digital image correlation and acoustic emission analyses. Compos. Struct. 2021, 275, 114481. [Google Scholar] [CrossRef]
- Murray, B.; Kalteremidou, K.; Carrella-Payan, D.; Cernescu, A.; Van Hemelrijck, D.; Pyl, L. Failure characterisation of CF/epoxy V-shape components using digital image correlation and acoustic emission analyses. Compos. Struct. 2020, 236, 111797. [Google Scholar] [CrossRef]
- Kalteremidou, K.-A.; Aggelis, D.G.; Van Hemelrijck, D.; Pyl, L. On the use of acoustic emission to identify the dominant stress/strain component in carbon/epoxy composite materials. Mech. Res. Commun. 2021, 111, 103663. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Z.; Wang, X.; Wang, H.; Li, B.; Niu, Y. Thermal effect on the fracture behavior of granite using acoustic emission and digital image correlation: An experimental investigation. Theor. Appl. Fract. Mech. 2022, 121, 103540. [Google Scholar] [CrossRef]







| Number of specimens | 1 | 2 | 3 | 4 | 5 |
| Value (GPa) | 5.31 | 5.23 | 5.69 | 5.35 | 5.48 |
| Amplitude | Duration | Rise Time | Ring Counts | Rise Counts | Energy | Center Frequency | Peak Frequency | |
|---|---|---|---|---|---|---|---|---|
| Amplitude | 1 | 0.051 | 0.243 ** | 0.064 | 0.618 ** | 0.053 | 0.105 ** | 0.065 |
| Duration | 1 | 0.119 ** | 0.994 ** | 0.087 * | 0.993 ** | 0.005 | 0.038 | |
| Rise time | 1 | 0.106 ** | 0.529 ** | 0.099 * | 0.091 * | −0.015 | ||
| Ring counts | 1 | 0.101 * | 0.999 ** | −0.002 | 0.022 | |||
| Rise counts | 1 | 0.091 * | 0.110 ** | 0.048 | ||||
| Energy | 1 | −0.006 | 0.016 | |||||
| Center frequency | 1 | 0.683 ** | ||||||
| Peak frequency | 1 |
| Factor 1 | Factor 2 | Factor 3 | |
|---|---|---|---|
| Amplitude | 0.192 | 0.694 | −0.300 |
| Duration | 0.980 | −0.178 | 0.059 |
| Rise time | 0.246 | 0.580 | −0.340 |
| Ring counts | 0.982 | −0.178 | 0.045 |
| Rise counts | 0.259 | 0.783 | −0.384 |
| Energy | 0.979 | −0.189 | 0.045 |
| Center frequency | 0.055 | 0.514 | 0.756 |
| Peak frequency | 0.065 | 0.423 | 0.815 |
| Factor 1 | Factor 2 | Factor 3 | |
|---|---|---|---|
| Amplitude | 0.063 | 0.352 | −0.188 |
| Duration | 0.321 | −0.090 | 0.037 |
| Rise time | 0.080 | 0.294 | −0.213 |
| Ring counts | 0.321 | −0.090 | 0.028 |
| Rise counts | 0.085 | 0.397 | −0.241 |
| Energy | 0.321 | −0.096 | 0.028 |
| Center frequency | 0.018 | 0.261 | 0.473 |
| Peak frequency | 0.021 | 0.214 | 0.510 |
| Factor 1 | Factor 2 | Factor 3 | |
|---|---|---|---|
| Cluster 1 | −0.333, 0.079 | −1.544, −0.260 | −1.122, −0.040 |
| Cluster 2 | −0.076, 1.542 | −0.086, 4.516 | −3.230, 0.514 |
| Cluster 3 | −0.245, 24.061 | −5.403, 1.739 | −0.384, 3.794 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, Z.; Shi, C.; Huang, X.; Tang, C.; Yuan, Y. A Study on Damage of T800 Carbon Fiber/Epoxy Composites under In-Plane Shear Using Acoustic Emission and Digital Image Correlation. Polymers 2023, 15, 4319. https://doi.org/10.3390/polym15214319
Lin Z, Shi C, Huang X, Tang C, Yuan Y. A Study on Damage of T800 Carbon Fiber/Epoxy Composites under In-Plane Shear Using Acoustic Emission and Digital Image Correlation. Polymers. 2023; 15(21):4319. https://doi.org/10.3390/polym15214319
Chicago/Turabian StyleLin, Zikai, Changheng Shi, Xiaochu Huang, Can Tang, and Ye Yuan. 2023. "A Study on Damage of T800 Carbon Fiber/Epoxy Composites under In-Plane Shear Using Acoustic Emission and Digital Image Correlation" Polymers 15, no. 21: 4319. https://doi.org/10.3390/polym15214319
APA StyleLin, Z., Shi, C., Huang, X., Tang, C., & Yuan, Y. (2023). A Study on Damage of T800 Carbon Fiber/Epoxy Composites under In-Plane Shear Using Acoustic Emission and Digital Image Correlation. Polymers, 15(21), 4319. https://doi.org/10.3390/polym15214319





