Prediction of Tribological Properties of UHMWPE/SiC Polymer Composites Using Machine Learning Techniques
Abstract
:1. Introduction
2. Experimental Procedure
2.1. Methodology
- -
- Nine data points from the suggested study [16] were collected. To train the models, the SiC loading size, consolidation pressure, and holding time were used as features to determine the coefficient of friction (COF) and specific wear rate (SWR) of the resulting polymer composite combination.
- -
- Using the Mathematica language, two interpolation functions that best represented the correlation between the experimental independent and dependent variables were developed for the SWR and COF from the data points of [16], as shown in Equations (1) and (2), where the variables x, y, and z represent SiC loading, consolidation pressure, and holding time, respectively:
- -
- The interpolation functions were then used to generate a larger dataset consisting of 1499 data points within the bounds of the original nine points.
- -
- The five appropriate machine learning techniques selected were decision trees, random forests, k-nearest neighbors, support vector machine, and artificial neural network.
- -
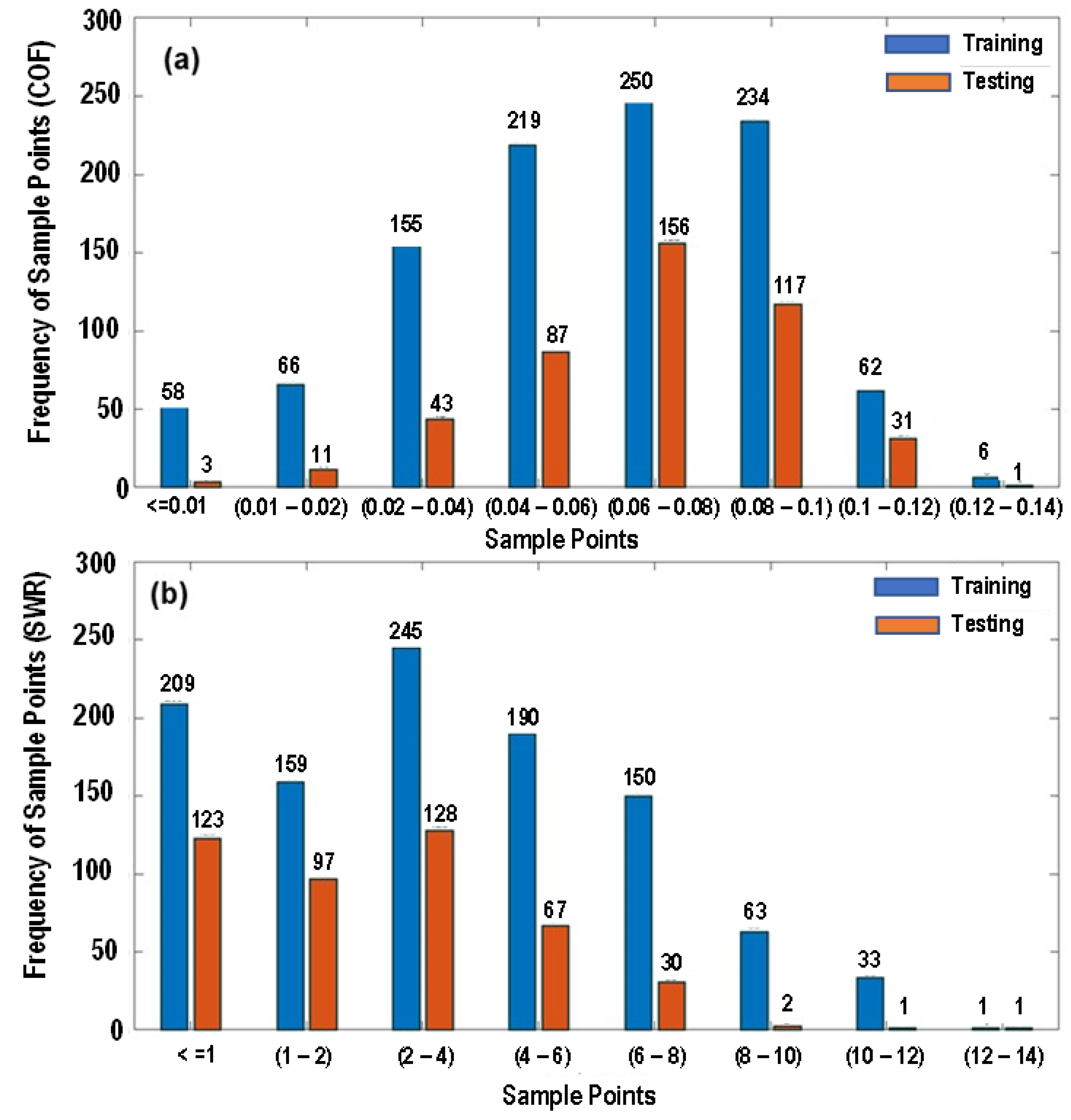
- The dataset was partitioned into 2 components as 70% of the samples were used to train the models, while the remaining 30% were used as an unseen test set for models to predict values. Figure 1a and Figure 1b show the frequency of the training and the testing dataset for the COF and SWR, respectively.
- -
- Using Python, each technique was subjected to a grid search, or the repeated training of the algorithm on a set of data while varying the hyperparameters for each iteration, in order to find the optimal settings that produced the least error rates for each target variable (CoF and SWR). The data points were also rescaled depending on the method.
- -
- The model performances were then compared with each other through regression and error analyses. In order to observe the best performance, the primary metrics used for the comparison consisted of the following:
- (a)
- Root mean squared error (RMSE): a measure of how far off the predictions are from the true values of the test data points. A lower RMSE closer to 0 was indicative of a better performance. The distance measure is calculated as shown in Equation (1), where is the predicted value and x is the true value of each sample.
- (b)
- Mean absolute error (MAE): similar to the RMSE, the MAE is also used as a metric to observe the gap in errors between the predictions and true values of the samples. The value is calculated according to Equation (2), where is the predicted value and x is the true value of each sample.
- (c)
- Coefficient of determination (R2-score): also known as the R-squared value, it is a measure of the correlation between the dependent and independent variables. Ranging from 0 to 1.0 (or 0 to 100%), a higher value is indicative of a better regression fit. The coefficient of determination is calculated, as shown in Equation (3), where is the predicted value of the sample, is the mean of all sample points, and is the true value.
2.2. An Overview of Machine Learning
2.3. Machine Learning Techniques Implemented in the Current Study
3. Results and Analysis
3.1. Performance Analysis
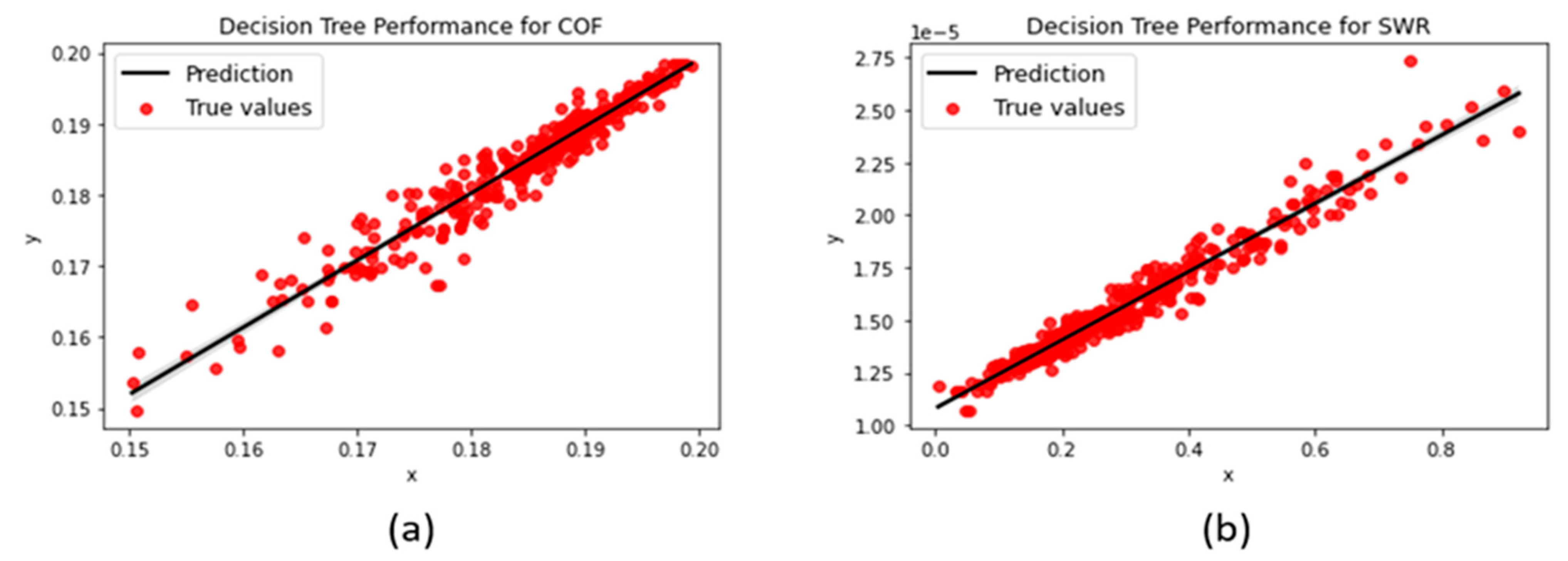
3.1.1. Decision Tree
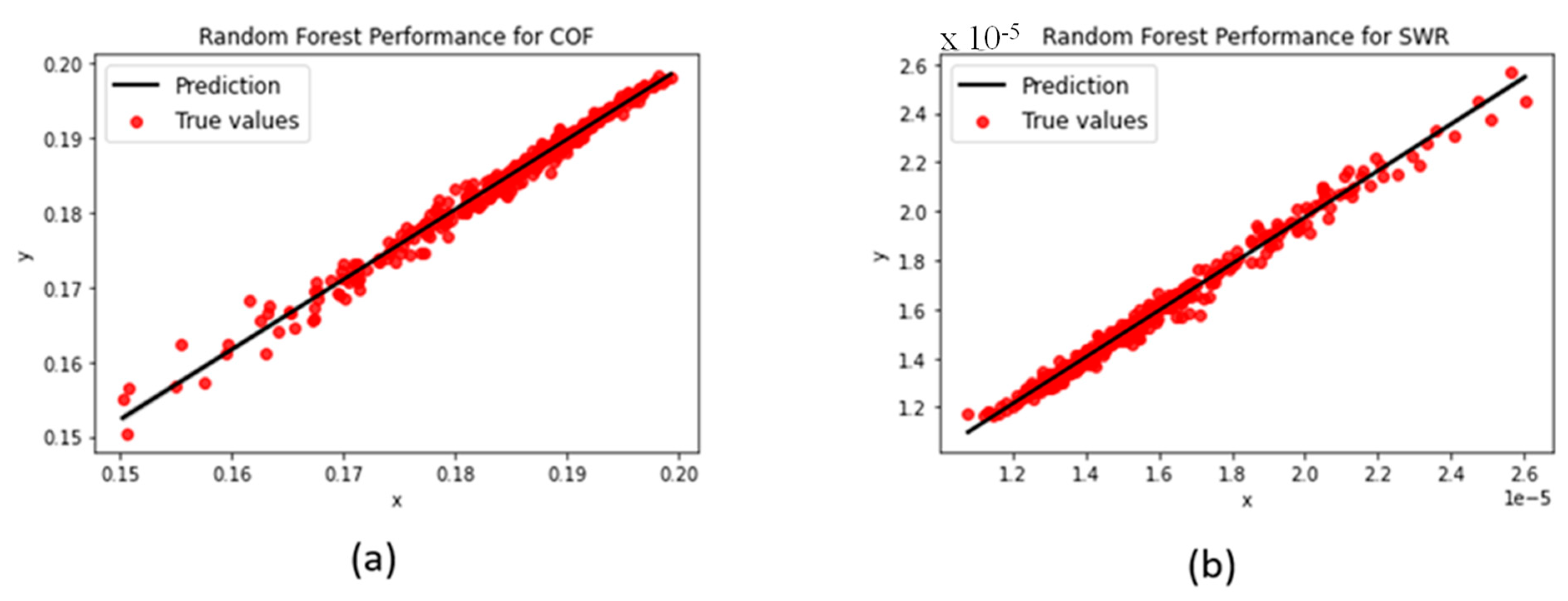
3.1.2. Random Forest
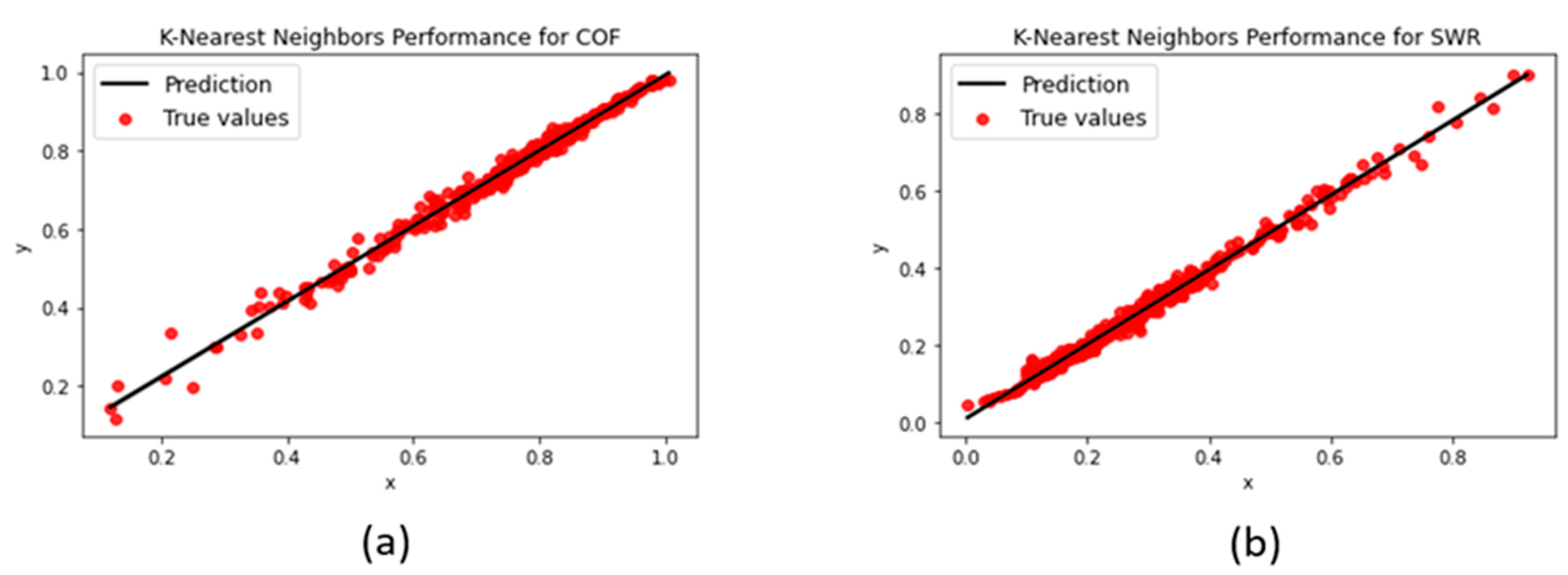
3.1.3. K-Nearest Neighbors
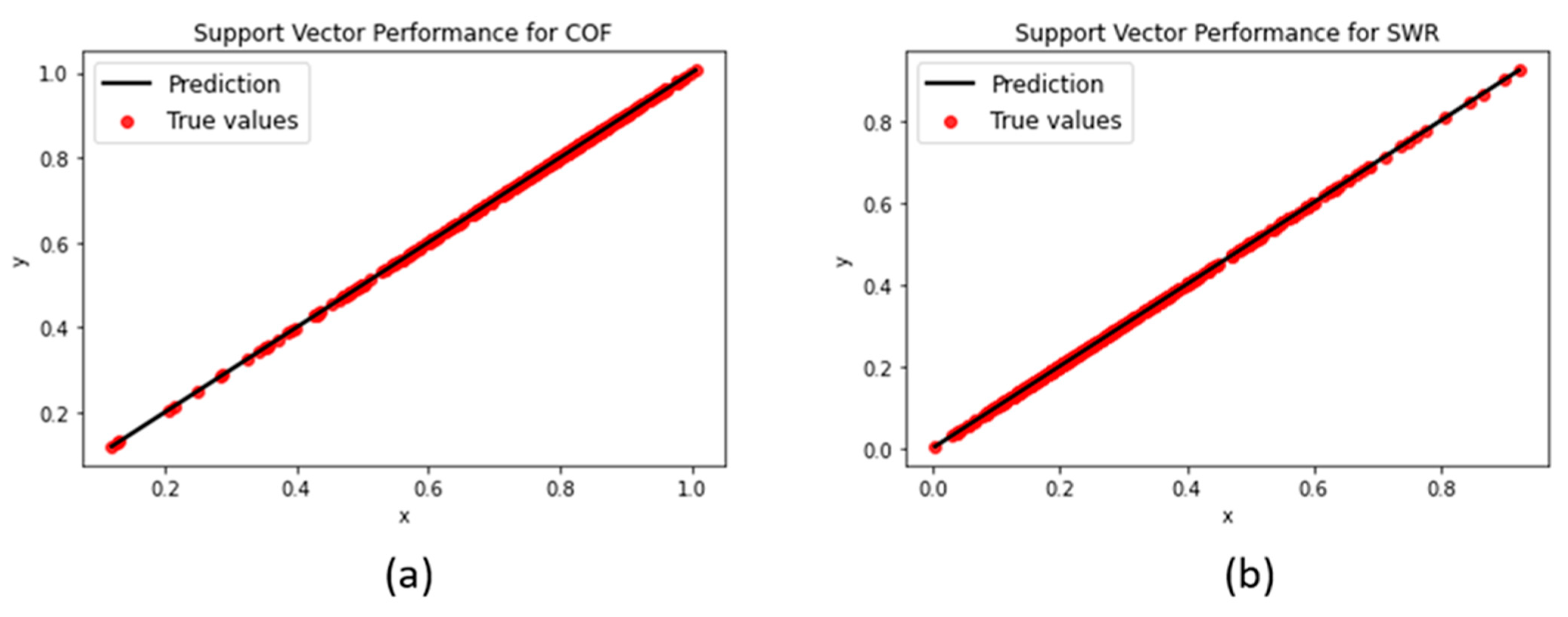
3.1.4. Support Vector Machine
3.1.5. Artificial Neural Network
4. Future Extension
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Kulikova, A.V.; Diaz, D.J.; Chen, T.; Cole, T.J.; Ellington, A.D.; Wilke, C.O. Two sequence- and two structure-based ML models have learned different aspects of protein biochemistry. Sci. Rep. 2023, 13, 13280. [Google Scholar] [CrossRef] [PubMed]
- Shahab, M.; Zheng, G.; Khan, A.; Wei, D.; Novikov, A.S. Machine Learning-Based Virtual Screening and Molecular Simulation Approaches Identified Novel Potential Inhibitors for Cancer Therapy. Biomedicines 2023, 11, 2251. [Google Scholar] [CrossRef] [PubMed]
- Senior, A.W.; Evans, R.; Jumper, J.; Kirkpatrick, J.; Sifre, L.; Green, T.; Qin, C.; Žídek, A.; Nelson, A.W.R.; Bridgland, A.; et al. Improved protein structure prediction using potentials from deep learning. Nature 2020, 577, 706–710. [Google Scholar] [CrossRef]
- Chen, C.; Gu, G. Machine learning for composite materials. MRS Commun. 2019, 9, 556–566. [Google Scholar] [CrossRef]
- Butler, K.T.; Davies, D.W.; Cartwright, H.; Isayev, O.; Walsh, A. Machine learning for molecular and materials science. Nature 2018, 559, 547–555. [Google Scholar] [CrossRef]
- Khanam, P.N.; AlMaadeed, M.A.; AlMaadeed, S.; Kunhoth, S.; Ouederni, M.; Sun, D.; Hamilton, A.; Jones, E.H.; Mayoral, B. Optimization and Prediction of Mechanical and Thermal Properties of Graphene/LLDPE Nanocomposites by Using Artificial Neural Networks. Int. J. Polym. Sci. 2016, 2016, 5340252. [Google Scholar] [CrossRef]
- Vinoth, A.; Dey, S.; Datta, S. Designing UHMWPE hybrid composites using machine learning and metaheuristic algorithms. Compos. Struct. 2021, 267, 113898. [Google Scholar] [CrossRef]
- Kiakojouri, A.; Lu, Z.; Mirring, P.; Powrie, H.; Wang, L. A generalised machine learning model based on multinomial logistic regression and frequency features for rolling bearing fault classification, Insight-Non-Destructive Test. Cond. Monit. 2022, 64, 447–452. [Google Scholar]
- Nazari, A.; Sanjayan, J.G. Modelling of compressive strength of geopolymer paste, mortar and concrete by optimized support vector machine. Ceram. Int. 2015, 41, 12164–12177. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Y. Evaluating the bond strength of FRP-to-concrete composite joints using metaheuristic-optimized least-squares support vector regression. Neural Comput. Appl. 2021, 33, 3621–3635. [Google Scholar] [CrossRef]
- Hasan, M.S.; Kordijazi, A.; Rohatgi, P.K.; Nosonovsky, M. Triboinformatics Approach for Friction and Wear Prediction of Al-Graphite Composites Using Machine Learning Methods. J. Tribol. 2022, 144, 011701. [Google Scholar] [CrossRef]
- Hasan, M.S.; Nosonovsky, M. Triboinformatics: Machine learning algorithms and data topology methods for tribology. Surf. Innov. 2022, 10, 229–242. [Google Scholar] [CrossRef]
- Singh, K.S.K.; Kumar, S.; Singh, K.K. Computational data-driven based optimization of tribological performance of graphene filled glass fiber reinforced polymer composite using machine learning approach. Mater. Today Proc. 2022, 66, 3838–3846. [Google Scholar] [CrossRef]
- Mohammed, A.S.; Dodla, S.; Katiyar, J.K.; Samad, M.A. Prediction of friction coefficient of su-8 and its composite coatings using machine learning techniques. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2022, 237, 943–953. [Google Scholar] [CrossRef]
- Borjali, A.; Monson, K.; Raeymaekers, B. Predicting the polyethylene wear rate in pin-on-disc experiments in the context of prosthetic hip implants: Deriving a data-driven model using machine learning methods. Tribol. Int. 2019, 133, 101–110. [Google Scholar] [CrossRef] [PubMed]
- Aliyu, I.K.; Azam, M.U.; Lawal, D.U.; Samad, M.A. Optimization of SiC concentration and process parameters for a wear-resistant UHMWPE nancocomposite. Arab. J. Sci. Eng. 2020, 45, 849–860. [Google Scholar] [CrossRef]
- Agarwal, M.; Singh, M.K.; Srivastava, R.; Gautam, R.K. Microstructural measurement and artificial neural network analysis for adhesion of tribolayer during sliding wear of powder-chip reinforcement based composites. Measurement 2021, 168, 108417. [Google Scholar] [CrossRef]
- Argatov, I.I.; Chai, Y.S. An artificial neural network supported regression model for wear rate. Tribol. Int. 2019, 138, 211–214. [Google Scholar] [CrossRef]
- Bhaumik, S.; Kamaraj, M. Artificial neural network and multi-criterion decision making approach of designing a blend of biodegradable lubricants and investigating its tribological properties. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2021, 235, 1575–1589. [Google Scholar] [CrossRef]
- Hasan, M.S.; Kordijazi, A.; Rohatgi, P.K.; Nosonovsky, M. Machine learning models of the transition from solid to liquid lubricated friction and wear in aluminum-graphite composites. Tribol. Int. 2022, 165, 107326. [Google Scholar] [CrossRef]
- Kumar, D.S.; Rajmohan, M. Optimizing Wear Behavior of Epoxy Composites Using Response Surface Methodology and Artificial Neural Networks. Polym. Compos. 2019, 40, 2812–2818. [Google Scholar] [CrossRef]
- Liu, X.; Liu, T.; Feng, P. Long-term performance prediction framework based on XGBoost decision tree for pultruded FRP composites exposed to water, humidity and alkaline solution. Compos. Struct. 2022, 284, 115184. [Google Scholar] [CrossRef]
- Costa, V.G.; Pedreira, C.E. Recent advances in decision trees: An updated survey. Artif. Intell. Rev. 2023, 56, 4765–4800. [Google Scholar] [CrossRef]
- Hu, X.; Rudin, C.; Seltzer, M. Optimal sparse decision trees. Adv. Neural Inf. Process. Syst. 2019, 32, 7267–7275. [Google Scholar]
- Amanoul, S.V.; Abdulazeez, A.M.; Zeebare, D.Q.; Ahmed, F.Y.H. Intrusion Detection Systems Based on Machine Learning Algorithms. In Proceedings of the 2021 IEEE International Conference on Automatic Control & Intelligent Systems (I2CACIS), Shah Alam, Malaysia, 26 June 2021; pp. 282–287. [Google Scholar]
- Borup, D.; Christensen, B.J.; Mühlbach, N.S.; Nielsen, M.S. Targeting predictors in random forest regression. Int. J. Forecast. 2023, 39, 841–868. [Google Scholar] [CrossRef]
- Chen, G.H.; Shah, D. Explaining the success of nearest neighbor methods in prediction. Found. Trends® Mach. Learn. 2018, 10, 337–588. [Google Scholar] [CrossRef]
- Borah, P.; Gupta, D. Robust twin bounded support vector machines for outliers and imbalanced data. Appl. Intell. 2021, 51, 5314–5343. [Google Scholar] [CrossRef]
- Awad, M.; Khanna, R. Support vector regression. In Efficient Learning Machines; Springer: Berlin/Heidelberg, Germany, 2015; pp. 67–80. [Google Scholar]
- Kalita, D.J.; Singh, V.P.; Kumar, V. A novel adaptive optimization framework for SVM hyper-parameters tuning in non-stationary environment: A case study on intrusion detection system. Expert. Syst. Appl. 2023, 213, 119189. [Google Scholar] [CrossRef]
- Manoj, I.V.; Soni, H.; Narendranath, S.; Mashinini, P.M.; Kara, F. Examination of machining parameters and prediction of cutting velocity and surface roughness using RSM and ANN using WEDM of Altemp HX. Adv. Mater. Sci. Eng. 2022, 2022, 5192981. [Google Scholar] [CrossRef]
- Li, S.; Shao, M.; Duan, C.; Yan, Y.; Wang, Q.; Wang, T. Tribological behavior prediction of friction materials for ultrasonic motors using Monte Carlo-based artificial neural network. J. Appl. Polym. Sci. 2019, 136, 47157. [Google Scholar] [CrossRef]





| Trial No. | SiC Loading (wt%) | Consolidation Pressure (MPa) | Holding Time (min) | COF |
|---|---|---|---|---|
| 1 | 1 | 10 | 10 | 0.172 |
| 2 | 1 | 16 | 15 | 0.173 |
| 3 | 1 | 22 | 20 | 0.181 |
| 4 | 4 | 10 | 15 | 0.177 |
| 5 | 4 | 16 | 20 | 0.186 |
| 6 | 4 | 22 | 10 | 0.189 |
| 7 | 7 | 10 | 20 | 0.184 |
| 8 | 7 | 16 | 10 | 0.185 |
| 9 | 7 | 22 | 15 | 0.187 |
| Trial No. | SiC Loading (wt%) | Consolidation Pressure (MPa) | Holding Time (min) | SWR × 10−5 (mm3/Nm) |
|---|---|---|---|---|
| 1 | 1 | 10 | 10 | 1.65 |
| 2 | 1 | 16 | 15 | 1.89 |
| 3 | 1 | 22 | 20 | 1.55 |
| 4 | 4 | 10 | 15 | 1.68 |
| 5 | 4 | 16 | 20 | 1.69 |
| 6 | 4 | 22 | 10 | 1.35 |
| 7 | 7 | 10 | 20 | 1.29 |
| 8 | 7 | 16 | 10 | 1.40 |
| 9 | 7 | 22 | 15 | 1.26 |
| Model | Optimal Hyperparameters | RMSE (Test Set) | MAE (Test Set) | R2 Score (Test Set) | |||
|---|---|---|---|---|---|---|---|
| COF | SWR | COF | SWR | COF | SWR | ||
| DT | Max. Depth: 50 | 0.00214 | 5.4 × 10−7 | 0.0014 | 3.7 × 10−7 | 0.9367 | 0.9579 |
| RF | Min. Split: 3 | 0.00111 | 3.1 × 10−7 | 0.0007 | 2.1 × 10−7 | 0.9827 | 0.9861 |
| Min. Leaf Samples: 1 | |||||||
| Impurity Decrease Threshold: None | |||||||
| SVM | Gamma: 0.25 | 0.000209 | 0.0002 | 0.0002 | 0.00016 | 0.9999 | 0.9998 |
| Kernel: Radial Basis Function | |||||||
| C Parameter: 100 | |||||||
| Epsilon: 0.00001 | |||||||
| KNN | No. of Neighbours: 8 | 0.016215 | 0.01511 | 0.0105 | 0.0105 | 0.98891 | 0.99098 |
| Weights based on distance | |||||||
| Distance Computation: Euclidean | |||||||
| ANN | Epochs: 100 | 0.022596 | 0.03349 | 0.0184 | 0.02676 | 0.978471 | 0.95569 |
| Optimizer: “Adam” | |||||||
| Validation amount: 20% | |||||||
| Learning Rate: 0.001 | |||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohammed, A.J.; Mohammed, A.S.; Mohammed, A.S. Prediction of Tribological Properties of UHMWPE/SiC Polymer Composites Using Machine Learning Techniques. Polymers 2023, 15, 4057. https://doi.org/10.3390/polym15204057
Mohammed AJ, Mohammed AS, Mohammed AS. Prediction of Tribological Properties of UHMWPE/SiC Polymer Composites Using Machine Learning Techniques. Polymers. 2023; 15(20):4057. https://doi.org/10.3390/polym15204057
Chicago/Turabian StyleMohammed, Abdul Jawad, Anwaruddin Siddiqui Mohammed, and Abdul Samad Mohammed. 2023. "Prediction of Tribological Properties of UHMWPE/SiC Polymer Composites Using Machine Learning Techniques" Polymers 15, no. 20: 4057. https://doi.org/10.3390/polym15204057
APA StyleMohammed, A. J., Mohammed, A. S., & Mohammed, A. S. (2023). Prediction of Tribological Properties of UHMWPE/SiC Polymer Composites Using Machine Learning Techniques. Polymers, 15(20), 4057. https://doi.org/10.3390/polym15204057






