Investigation of Hole-Transfer Dynamics through Simple EL De-Convolution in Non-Fullerene Organic Solar Cells
Abstract
:1. Introduction
2. Materials and Methods
2.1. Device Fabrication
2.2. Device Characterization
3. Result and Discussion
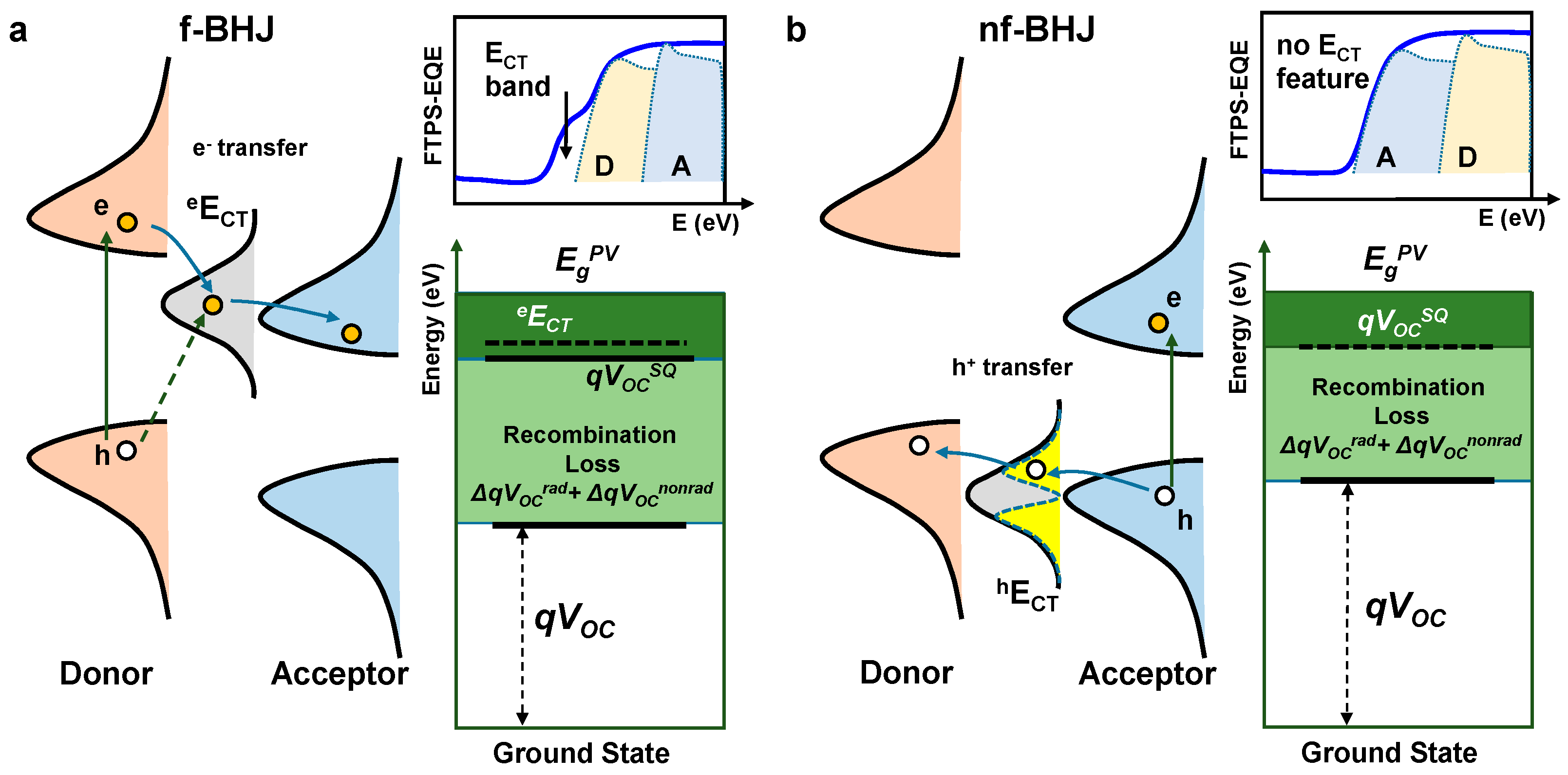
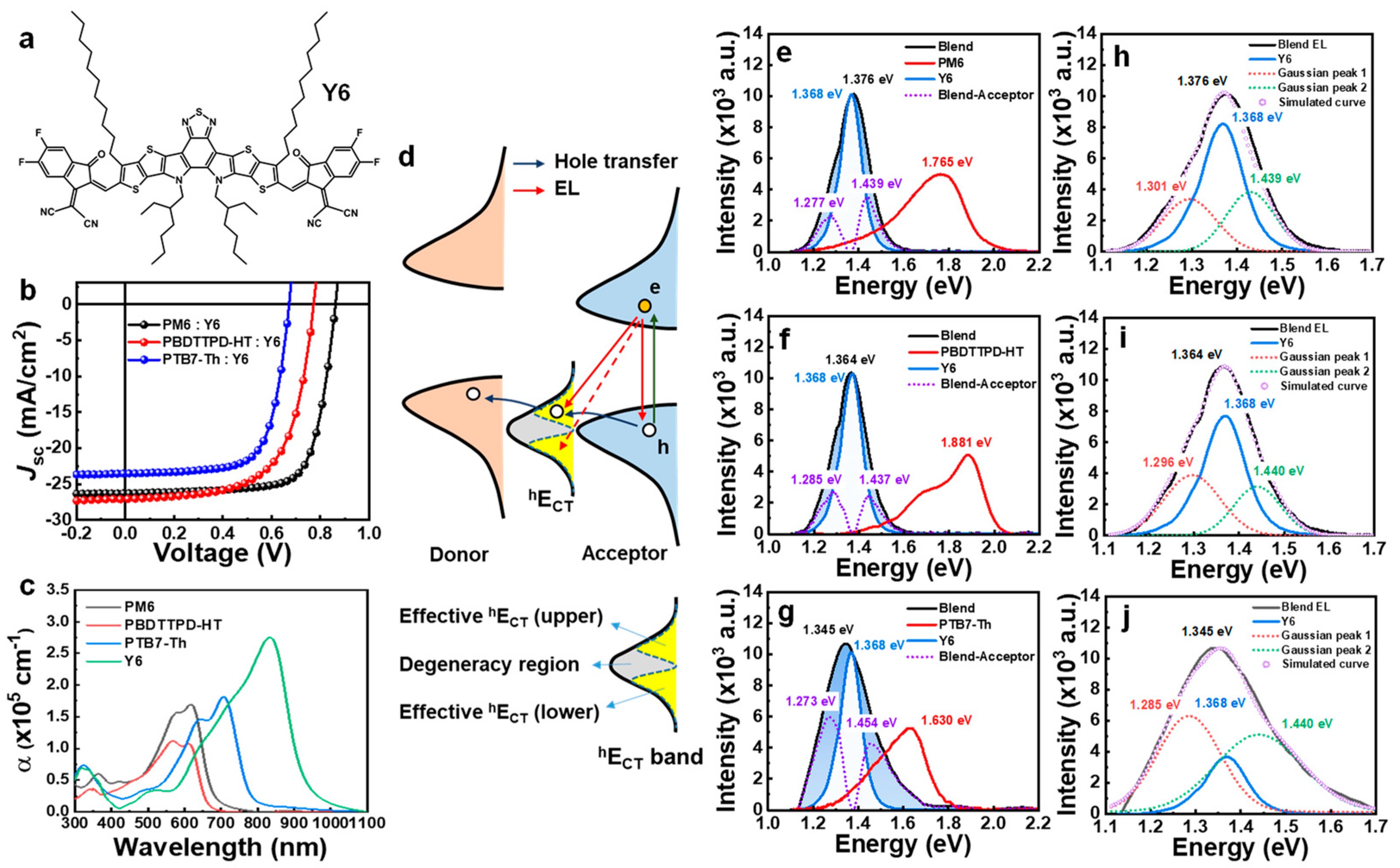
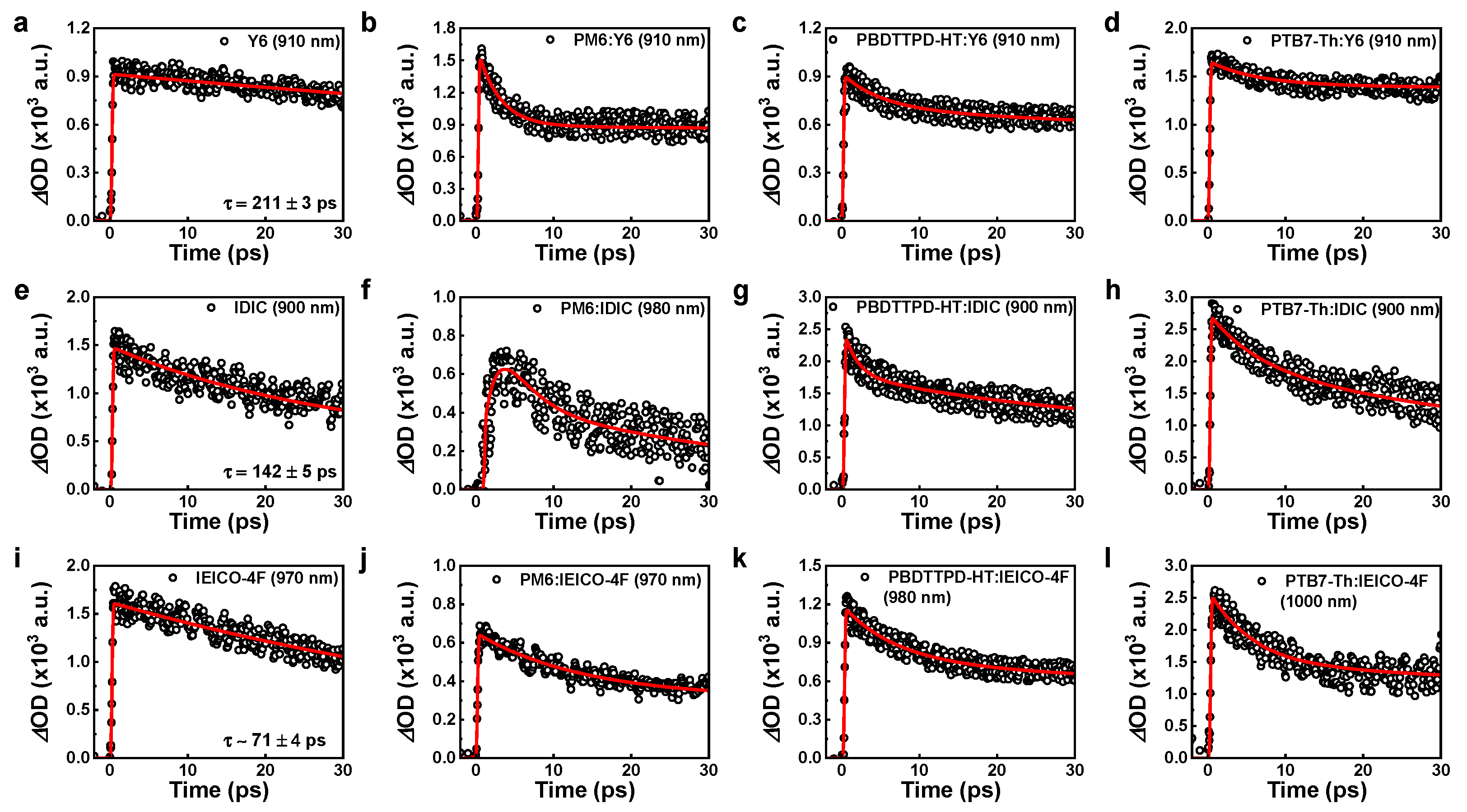
3.1. Y6 Acceptor Based nf-BHJ Systems
3.1.1. Background of hECT Determination
3.1.2. EL Deconvolution
3.1.3. Marcus Theory and Energy Loss Model
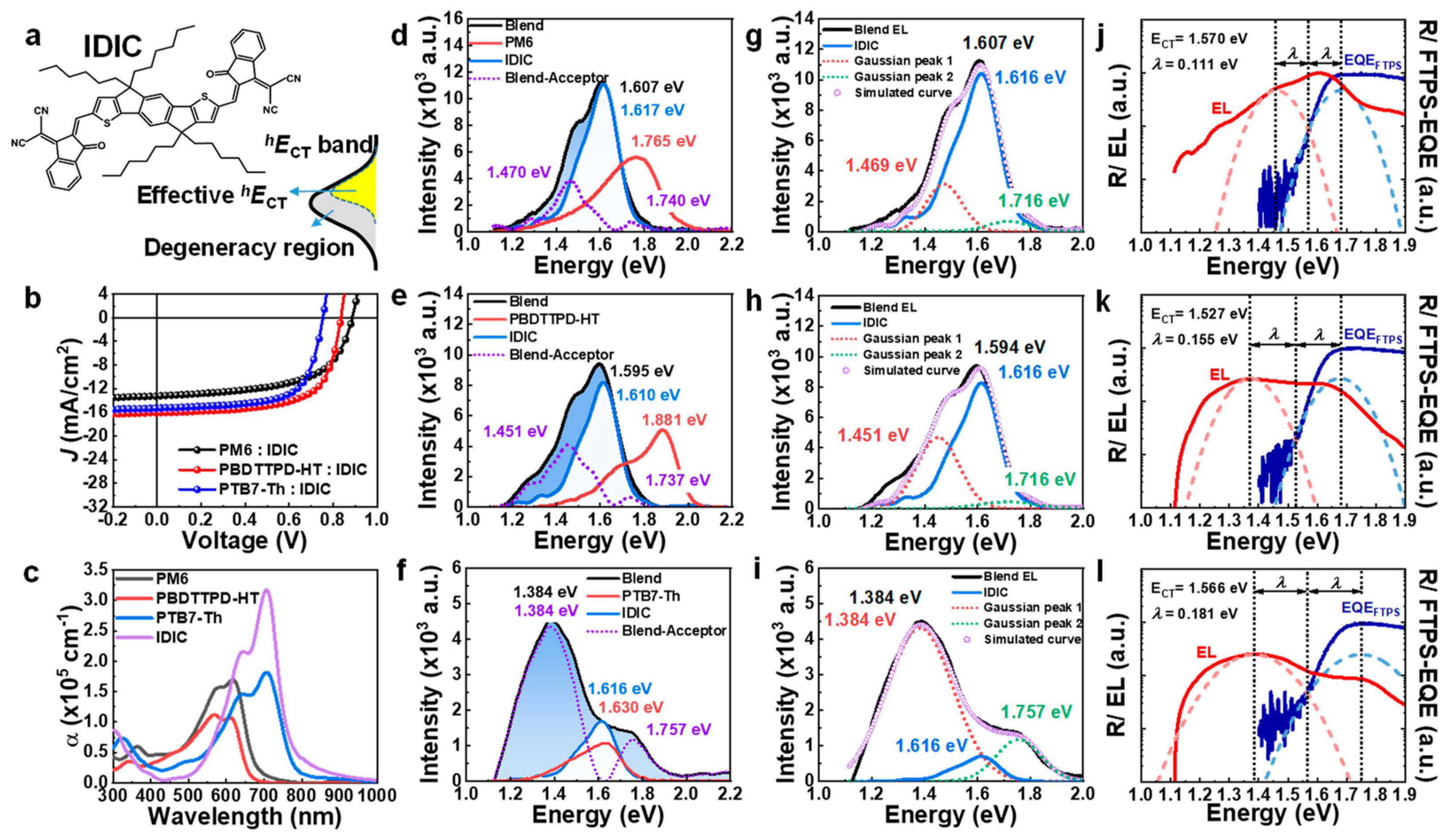
3.2. IDIC-Acceptor-Based nf-BHJ Systems (Larger HOMO Offset)
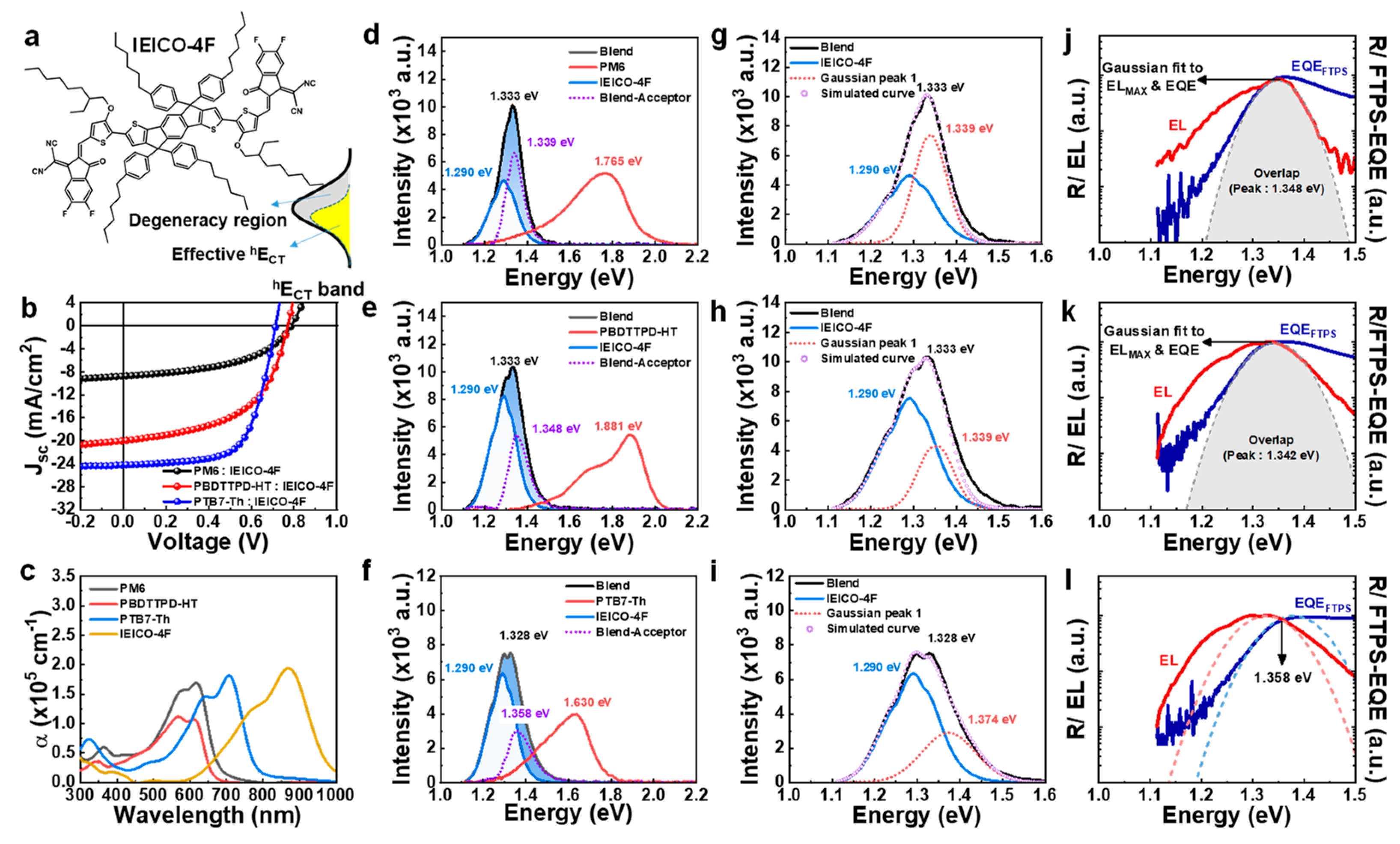
3.3. IEICO-4F-Acceptor-Based BHJ Systems (Smaller HOMO Offset)
3.4. Hole Decay and Transfer Time at hECT
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Marcus Theory
Appendix B
Appendix B.1. Energy Loss Model
Radiative Limit Open-Circuit Voltage
References
- Brabec, C.J.; Gowrisanker, S.; Halls, J.J.M.; Laird, D.; Jia, S.; Williams, S.P. Polymer–Fullerene Bulk-Heterojunction Solar Cells. Adv. Mater. 2010, 22, 3839–3856. [Google Scholar] [CrossRef]
- Park, S.H.; Roy, A.; Beaupré, S.; Cho, S.; Coates, N.; Moon, J.S.; Moses, D.; Leclerc, M.; Lee, K.; Heeger, A.J. Bulk heterojunction solar cells with internal quantum efficiency approaching 100%. Nat. Photonics 2009, 3, 297–302. [Google Scholar] [CrossRef]
- Lu, L.; Zheng, T.; Wu, Q.; Schneider, A.M.; Zhao, D.; Yu, L. Recent Advances in Bulk Heterojunction Polymer Solar Cells. Chem. Rev. 2015, 115, 12666–12731. [Google Scholar] [CrossRef]
- Kaltenbrunner, M.; White, M.S.; Głowacki, E.D.; Sekitani, T.; Someya, T.; Sariciftci, N.S.; Bauer, S. Ultrathin and lightweight organic solar cells with high flexibility. Nat. Commun. 2012, 3, 770. [Google Scholar] [CrossRef] [PubMed]
- Sun, C.; Pan, F.; Bin, H.; Zhang, J.; Xue, L.; Qiu, B.; Wei, Z.; Zhang, Z.-G.; Li, Y. A low cost and high performance polymer donor material for polymer solar cells. Nat. Commun. 2018, 9, 743. [Google Scholar] [CrossRef] [PubMed]
- Yuan, J.; Zhang, Y.; Zhou, L.; Zhang, G.; Yip, H.-L.; Lau, T.-K.; Lu, X.; Zhu, C.; Peng, H.; Johnson, P.A.; et al. Single-Junction Organic Solar Cell with over 15% Efficiency Using Fused-Ring Acceptor with Electron-Deficient Core. Joule 2019, 3, 1140–1151. [Google Scholar] [CrossRef]
- Liu, Q.; Jiang, Y.; Jin, K.; Qin, J.; Xu, J.; Li, W.; Xiong, J.; Liu, J.; Xiao, Z.; Sun, K.; et al. 18% Efficiency organic solar cells. Sci. Bull. 2020, 65, 272–275. [Google Scholar] [CrossRef]
- Ma, R.; Jiang, X.; Fu, J.; Zhu, T.; Yan, C.; Wu, K.; Müller-Buschbaum, P.; Li, G. Revealing the underlying solvent effect on film morphology in high-efficiency organic solar cells through combined ex situ and in situ observations. Energy Environ. Sci. 2023, 16, 2316–2326. [Google Scholar] [CrossRef]
- Zhu, L.; Zhang, M.; Zhou, G.; Hao, T.; Xu, J.; Wang, J.; Qiu, C.; Prine, N.; Ali, J.; Feng, W.; et al. Efficient Organic Solar Cell with 16.88% Efficiency Enabled by Refined Acceptor Crystallization and Morphology with Improved Charge Transfer and Transport Properties. Adv. Energy Mater. 2020, 10, 1904234. [Google Scholar] [CrossRef]
- Yuan, J.; Huang, T.; Cheng, P.; Zou, Y.; Zhang, H.; Yang, J.L.; Chang, S.-Y.; Zhang, Z.; Huang, W.; Wang, R.; et al. Enabling low voltage losses and high photocurrent in fullerene-free organic photovoltaics. Nat. Commun. 2019, 10, 570. [Google Scholar] [CrossRef]
- Vandewal, K.; Tvingstedt, K.; Gadisa, A.; Inganäs, O.; Manca, J.V. Relating the open-circuit voltage to interface molecular properties of donor:acceptor bulk heterojunction solar cells. Phys. Rev. B 2010, 81, 125204. [Google Scholar] [CrossRef]
- Marcus, R.A. Electron transfer reactions in chemistry theory and experiment. J. Electroanal. Chem. 1997, 438, 251–259. [Google Scholar] [CrossRef]
- Liu, S.; Yuan, J.; Deng, W.; Luo, M.; Xie, Y.; Liang, Q.; Zou, Y.; He, Z.; Wu, H.; Cao, Y. High-efficiency organic solar cells with low non-radiative recombination loss and low energetic disorder. Nat. Photonics 2020, 14, 300–305. [Google Scholar] [CrossRef]
- Zhou, Z.; Xu, S.; Song, J.; Jin, Y.; Yue, Q.; Qian, Y.; Liu, F.; Zhang, F.; Zhu, X. High-efficiency small-molecule ternary solar cells with a hierarchical morphology enabled by synergizing fullerene and non-fullerene acceptors. Nat. Energy 2018, 3, 952–959. [Google Scholar] [CrossRef]
- Perdigón-Toro, L.; Zhang, H.; Markina, A.; Yuan, J.; Hosseini, S.M.; Wolff, C.M.; Zuo, G.; Stolterfoht, M.; Zou, Y.; Gao, F.; et al. Barrierless Free Charge Generation in the High-Performance PM6:Y6 Bulk Heterojunction Non-Fullerene Solar Cell. Adv. Mater. 2020, 32, 1906763. [Google Scholar] [CrossRef] [PubMed]
- Karuthedath, S.; Gorenflot, J.; Firdaus, Y.; Chaturvedi, N.; Castro, C.S.P.D.; Harrison, G.T.; Khan, J.I.; Markina, A.; Balawi, A.H.; Peña, T.A.D.; et al. Intrinsic efficiency limits in low-bandgap non-fullerene acceptor oragnic solar cells. Nat. Mater. 2021, 20, 378–384. [Google Scholar] [CrossRef]
- Chen, Z.; Chen, X.; Jia, Z.; Zhou, G.; Xu, J.; Wu, Y.; Xia, X.; Li, X.; Zhang, X.; Deng, C.; et al. Triplet exciton formation for non-radiative voltage in high-efficiency nonfullerene oragnic solar cells. Joule 2021, 5, 1832–1844. [Google Scholar] [CrossRef]
- Liu, Y.; Zuo, L.; Shi, X.; Jen, A.K.-Y.; Ginger, D.S. Unexpectedly Slow Yet Efficient Picosecond to Nanosecond Photoinduced Hole-Transfer Occurs in a Polymer/Nonfullerene Acceptor Organic Photovoltaic Blend. ACS Energy Lett. 2018, 3, 2396–2403. [Google Scholar] [CrossRef]
- Jasiūnas, R.; Zhang, H.; Devižis, A.; Franckevičius, M.; Gao, F.; Gulbinas, V. Thermally Activated Reverse Electron Transfer Limits Carrier Generation Efficiency in PM6:Y6 Non-Fullerene Organic Solar Cells. Sol. RRL 2022, 6, 2100963. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, W.; Zhou, G.; Yi, Y.; Xu, S.; Liu, F.; Zhu, H.; Zhu, X. Accurate Determination of the Minimum HOMO Offset for Efficient Charge Generation using Organic Semiconducting Alloys. Adv. Energy Mater. 2020, 10, 1903298. [Google Scholar] [CrossRef]
- Xie, Y.; Wang, W.; Huang, W.; Lin, F.; Li, T.; Liu, S.; Zhan, X.; Liang, Y.; Gao, C.; Wu, H.; et al. Assessing the energy offset at the electron donor/ acceptor interface in organic solar cells through radiative efficiency measurements. Energy Environ. Sci. 2019, 12, 3556–3566. [Google Scholar] [CrossRef]
- Wu, J.; Lee, J.; Chin, Y.-C.; Yao, H.; Cha, H.; Luke, J.; Hou, J.; Kim, J.-S.; Durrant, J.R. Exceptionally low charge trapping enables highly efficient organic bulk heterojunction solar cells. Energy Environ. Sci. 2020, 13, 2422–2430. [Google Scholar] [CrossRef]
- Hadmojo, W.T.; Wibowo, F.T.A.; Ryu, D.Y.; Jung, I.W.; Jang, S.-Y. Fullerene-Free Organic Solar Cells with an Efficiency of 10.2% and an Energy Loss of 0.59 eV Based on a Thieno[3,4-c]Pyrrole-4,6-dione-Containing Wide Band Gap Polymer Donor. ACS Appl. Mater. Interfaces 2017, 9, 32939–32945. [Google Scholar] [CrossRef] [PubMed]
- Park, S.J.; Wibowo, F.T.A.; Krishna, N.V.; Ryu, J.; Lee, H.; Lee, J.H.; Yoon, Y.J.; Kim, J.Y.; Seo, J.H.; Oh, S.-H.; et al. Importance of interface engineering between the hole transport layer and the indium-tin-oxide electrode for highly efficient polymer solar cells. J. Mater. Chem. A 2021, 9, 15394–15403. [Google Scholar] [CrossRef]
- Rau, U.; Blank, B.; Müller, T.C.M.; Kirchartz, T. Efficiency Potential of Photovoltaic Materials and Devices Unveiled by Detailed-Balance Analysis. Phys. Rev. Appl. 2017, 7, 044016. [Google Scholar] [CrossRef]
- Fu, H.; Wang, Y.; Meng, D.; Ma, Z.; Li, Y.; Gao, F.; Wang, Z.; Sun, Y. Suppression of Recombination Energy Losses by Decreasing the Energetic Offsets in Perylene Diimide-Based Nonfullerene Organic Solar Cells. ACS Energy Lett. 2018, 3, 2729–2735. [Google Scholar] [CrossRef]
- Hofinger, J.; Putz, C.; Mayr, F.; Gugujonovic, K.; Wielend, D.; Scharber, M.C. Understanding the low voltage losses in high-performace non-fullerene acceptor-based organic solar cells. Mater. Adv. 2021, 2, 4291. [Google Scholar] [CrossRef]
- Liu, Y.; Li, M.; Yang, J.; Xue, W.; Feng, S.; Song, J.; Tang, Z.; Ma, W.; Bo, Z. High-Efficiency As-Cast Organic Solar Cells Based on Acceptors with Steric Hindrance Induced Planar Terminal Group. Adv. Energy Mater. 2019, 9, 1901280. [Google Scholar] [CrossRef]
- Shockley, W.; Queisser, H.J. Detailed Balance Limit of Efficiency of p-n Junction Solar Cells. J. Appl. Phys. 1961, 32, 510. [Google Scholar] [CrossRef]
- Kirchartz, T.; Rau, U. Electroluminescence analysis of high efficiency Cu(In,Ga)Se2 solar cells. J. Appl. Phys. 2007, 102, 104510. [Google Scholar] [CrossRef]
- Menke, S.M.; Ran, N.A.; Bazan, G.C.; Friend, R.H. Organic Solar Cells: Toward a New Efficiency Regime. Joule 2018, 2, 25–35. [Google Scholar] [CrossRef]
- Marcus, R.A. Relation between Charge Transfer Absorption and Fluorescence Spectra and the Inverted Region. J. Phys. Chem. 1989, 93, 3078–3086. [Google Scholar] [CrossRef]
- Kirchartz, T.; Rau, U. Detailed balance and reciprocity in solar cells. Phys. Stat. Sol. (A) 2008, 205, 2737–2751. [Google Scholar] [CrossRef]

| BHJ | Eg | hECT | ΔhECT |
|---|---|---|---|
| PM6: Y6 | 1.418 | 1.388 | 0.030 |
| PBDTTPD-HT: Y6 | 1.431 | 1.373 | 0.058 |
| PTB7-Th: Y6 | 1.401 | 1.357 | 0.044 |
| PM6: IDIC | 1.601 | 1.570 | 0.031 |
| PBDTTPD-HT: IDIC | 1.573 | 1.527 | 0.046 |
| PTB7-Th: IDIC | 1.611 | 1.566 | 0.045 |
| PM6: IEICO-4F | 1.323 | n/a | n/a |
| PBDTTPD-HT: IEICO-4F | 1.333 | n/a | n/a |
| PTB7-Th: IEICO-4F | 1.330 | 1.358 | n/a (−0.028) |
| Blend | Hole-Transfer Time (ps) | * (%) |
|---|---|---|
| PM6:Y6 | 2.8 ± 0.3 | 93 |
| PBDTTPD-HT:Y6 | 5.1 ± 0.5 | 81 |
| PTB7-Th:Y6 | 7.0 ± 0.4 | 78 |
| PM6:IDIC | 2.4 ± 0.7 | 75 |
| PBDTTPD-HT:IDIC | 1.8 ± 0.4 | 81 |
| PTB7-Th:IDIC | 6.0 ± 0.4 | 54 |
| PM6:IEICO-4F | 13.0 ± 1.7 | 72 |
| PBDTTPD-HT:IEICO-4F | 7.8 ± 0.7 | 83 |
| PTB7-Th:IEICO-4F | 5.2 ± 0.8 | 96 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, D.; Kim, D.H.; Oh, C.-M.; Park, S.; Krishna, N.V.; Wibowo, F.T.A.; Hwang, I.-W.; Jang, S.-Y.; Cho, S. Investigation of Hole-Transfer Dynamics through Simple EL De-Convolution in Non-Fullerene Organic Solar Cells. Polymers 2023, 15, 4042. https://doi.org/10.3390/polym15204042
Lee D, Kim DH, Oh C-M, Park S, Krishna NV, Wibowo FTA, Hwang I-W, Jang S-Y, Cho S. Investigation of Hole-Transfer Dynamics through Simple EL De-Convolution in Non-Fullerene Organic Solar Cells. Polymers. 2023; 15(20):4042. https://doi.org/10.3390/polym15204042
Chicago/Turabian StyleLee, Dongchan, Do Hui Kim, Chang-Mok Oh, Sujung Park, Narra Vamsi Krishna, Febrian Tri Adhi Wibowo, In-Wook Hwang, Sung-Yeon Jang, and Shinuk Cho. 2023. "Investigation of Hole-Transfer Dynamics through Simple EL De-Convolution in Non-Fullerene Organic Solar Cells" Polymers 15, no. 20: 4042. https://doi.org/10.3390/polym15204042
APA StyleLee, D., Kim, D. H., Oh, C.-M., Park, S., Krishna, N. V., Wibowo, F. T. A., Hwang, I.-W., Jang, S.-Y., & Cho, S. (2023). Investigation of Hole-Transfer Dynamics through Simple EL De-Convolution in Non-Fullerene Organic Solar Cells. Polymers, 15(20), 4042. https://doi.org/10.3390/polym15204042







