A High-Generalizability Machine Learning Framework for Analyzing the Homogenized Properties of Short Fiber-Reinforced Polymer Composites
Abstract
:1. Introduction
2. Material and Method
2.1. Two-Step Homogenization Procedure
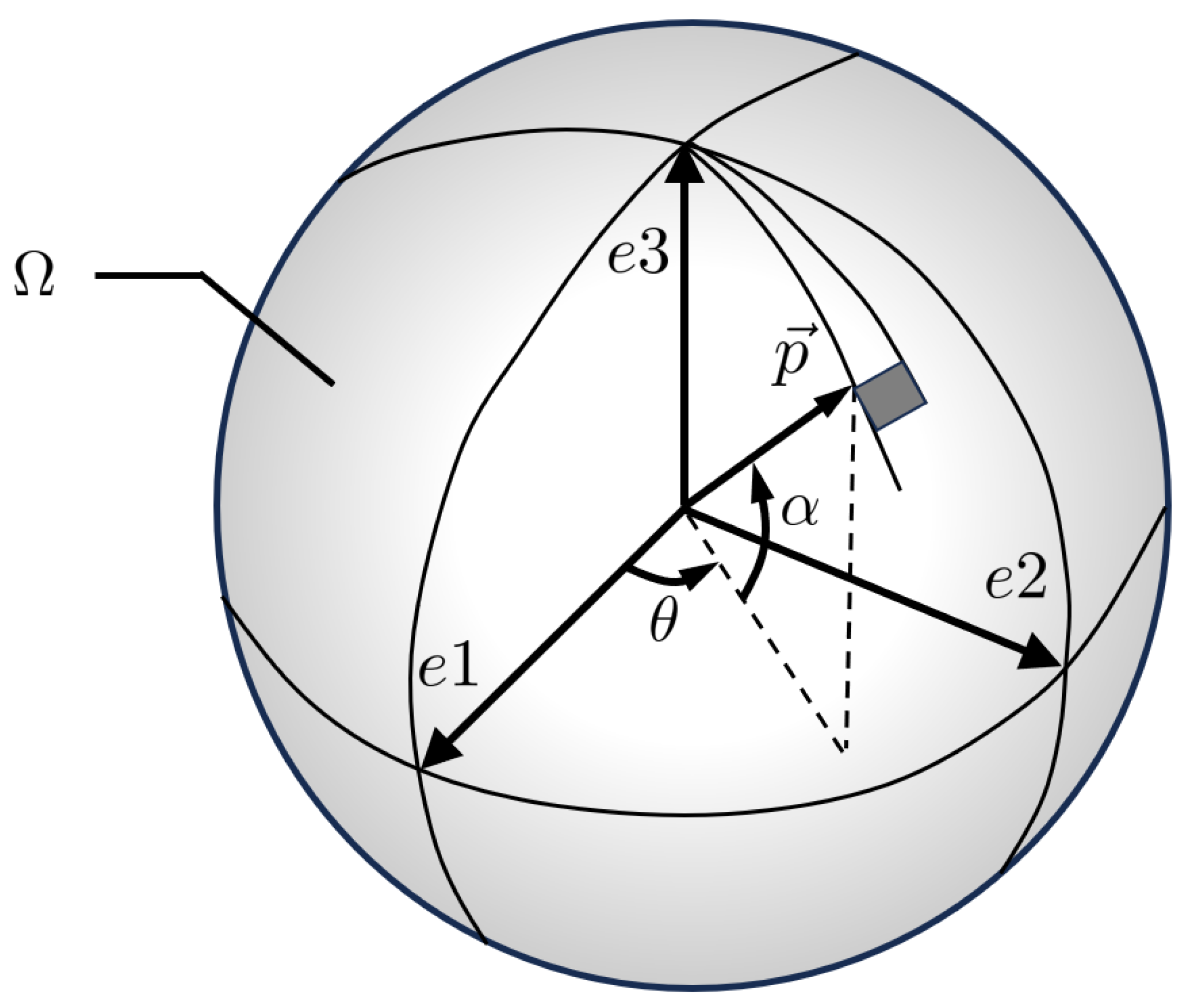
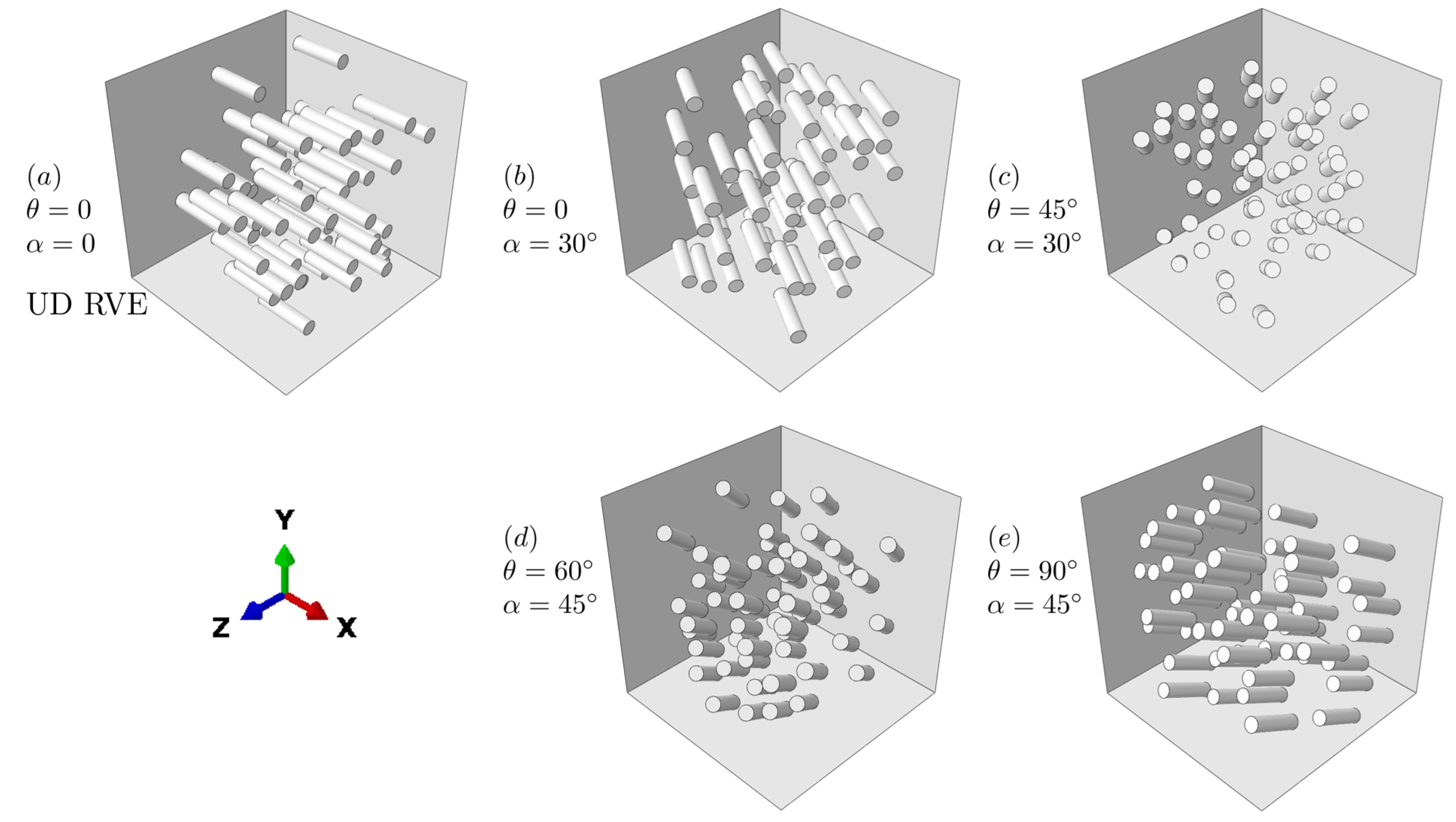
2.1.1. Orientation Tensor for Describing Fiber Distribution
2.1.2. The Two-Step Homogenization Method
2.2. Feature Selection and Data Preparation
2.2.1. Feature Selection
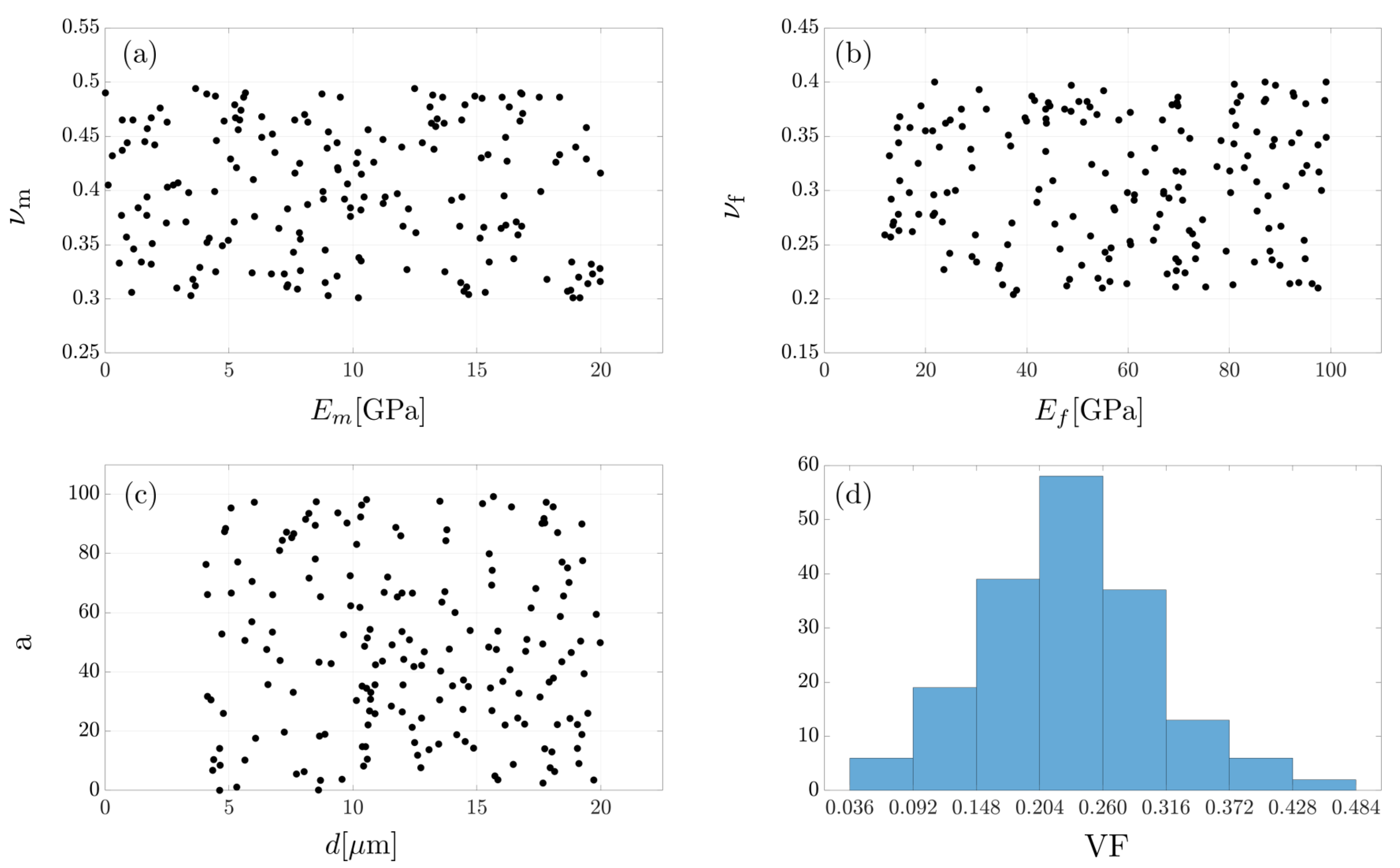
2.2.2. Data Preparation
2.2.3. Data Analysis
2.3. Ensemble Machine Learning
2.3.1. Base Learners
2.3.2. Stacking Mode
2.4. The SHAP-Based Interpretation Analysis
2.5. Hyperparameter Optimization and Model Training
3. Results and Discussion
3.1. Validation of Dataset Based on the Two-Step Homogenization Method
3.2. Model Evaluation on Prediction Accuracy
3.2.1. Evaluation Metrics
3.2.2. Accuracy Comparison between the EML and Base Learners
3.2.3. Model Performance of the EML Model on a Testing Sample
3.3. Model Interpretation via SHAP Analysis
3.3.1. Global Interpretation
3.3.2. Local Interpretation
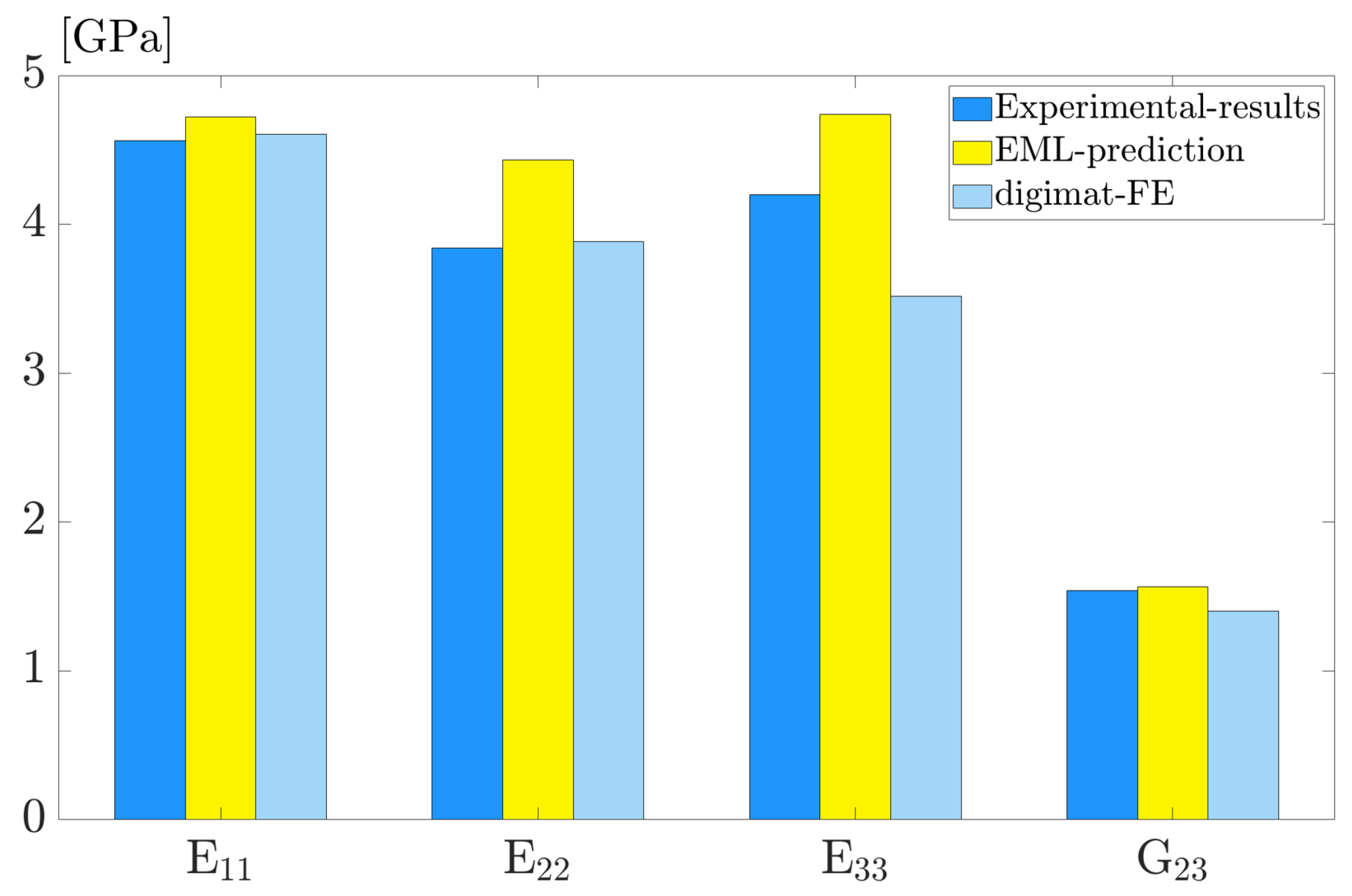
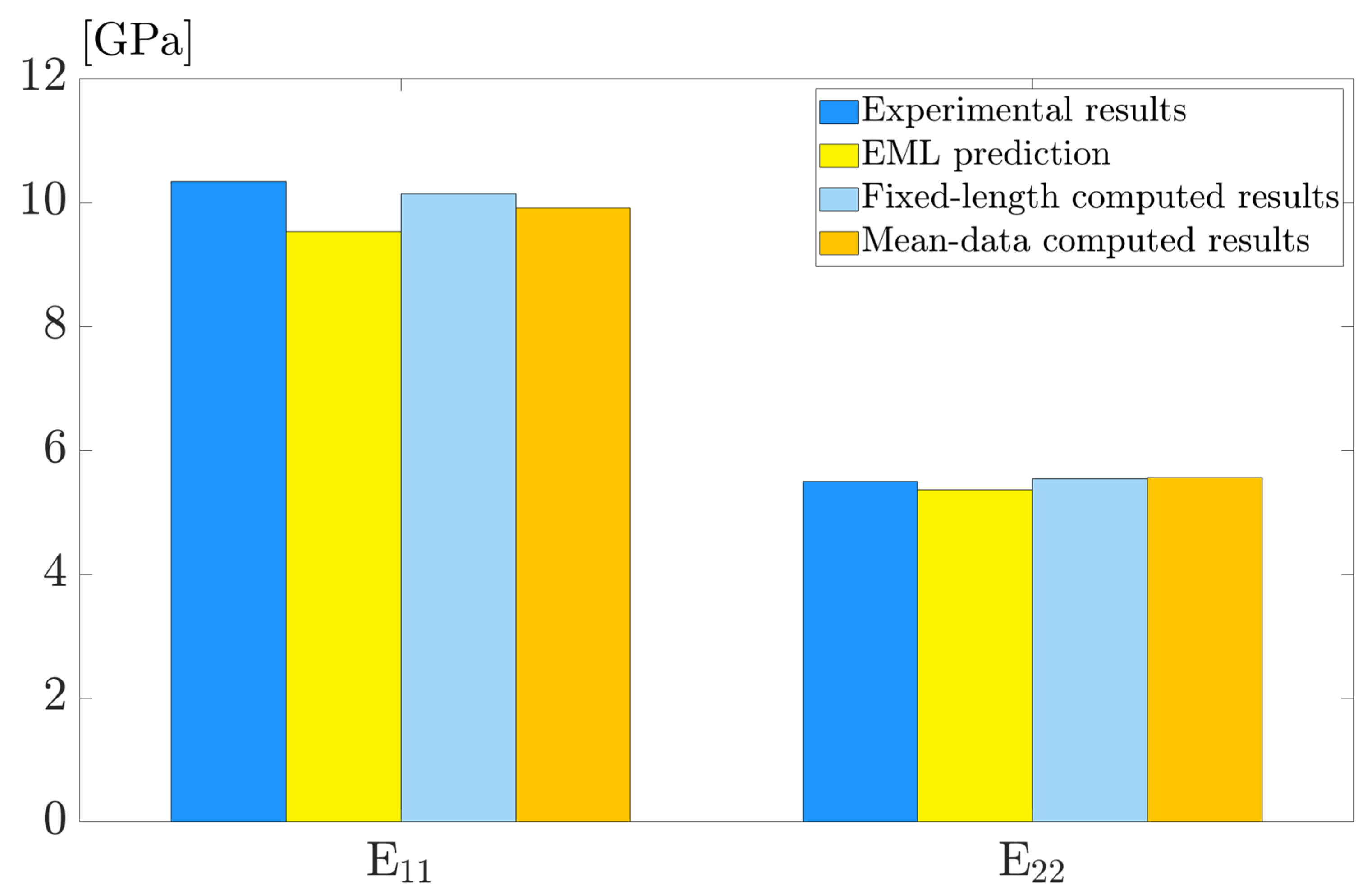
3.4. Model Generalization on Experimental Data
4. Conclusions and Outlook
- (1)
- The two-step homogenization algorithm is validated as an effective approach with which to consider different fiber orientations, which favors the creation of a trustworthy dataset with a variety of the chosen features.
- (2)
- The EML model outperforms the base members of ET, XGBoost, and LBGM on prediction accuracy, achieving values of 0.988 and 0.952 on the train and test datasets, respectively.
- (3)
- According to the SHAP global analysis, the homogenized elastic properties are significantly influenced by , , and , whereas the anisotropy is predominantly determined by , , and . The SHAP local interpretation distinguishes the key modulating mechanism between the key features for individual predictions.
- (4)
- The EML algorithm showcases a highly generalized machine learning model on experimental data, and it is more efficient than high-fidelity computational models by drastically reducing computational expenses and preserving high accuracy.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Input Feature Distribution and Correlation Analysis
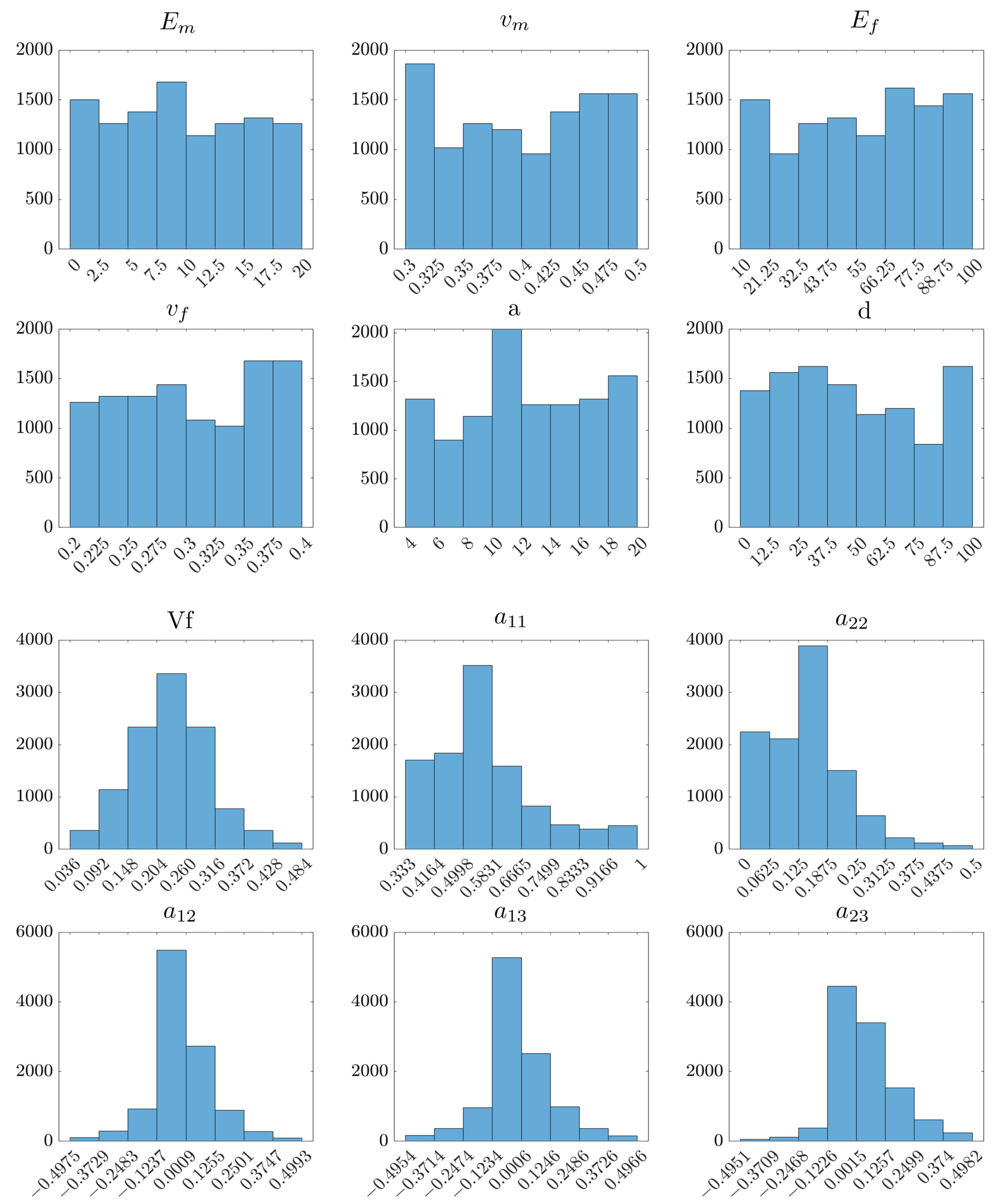
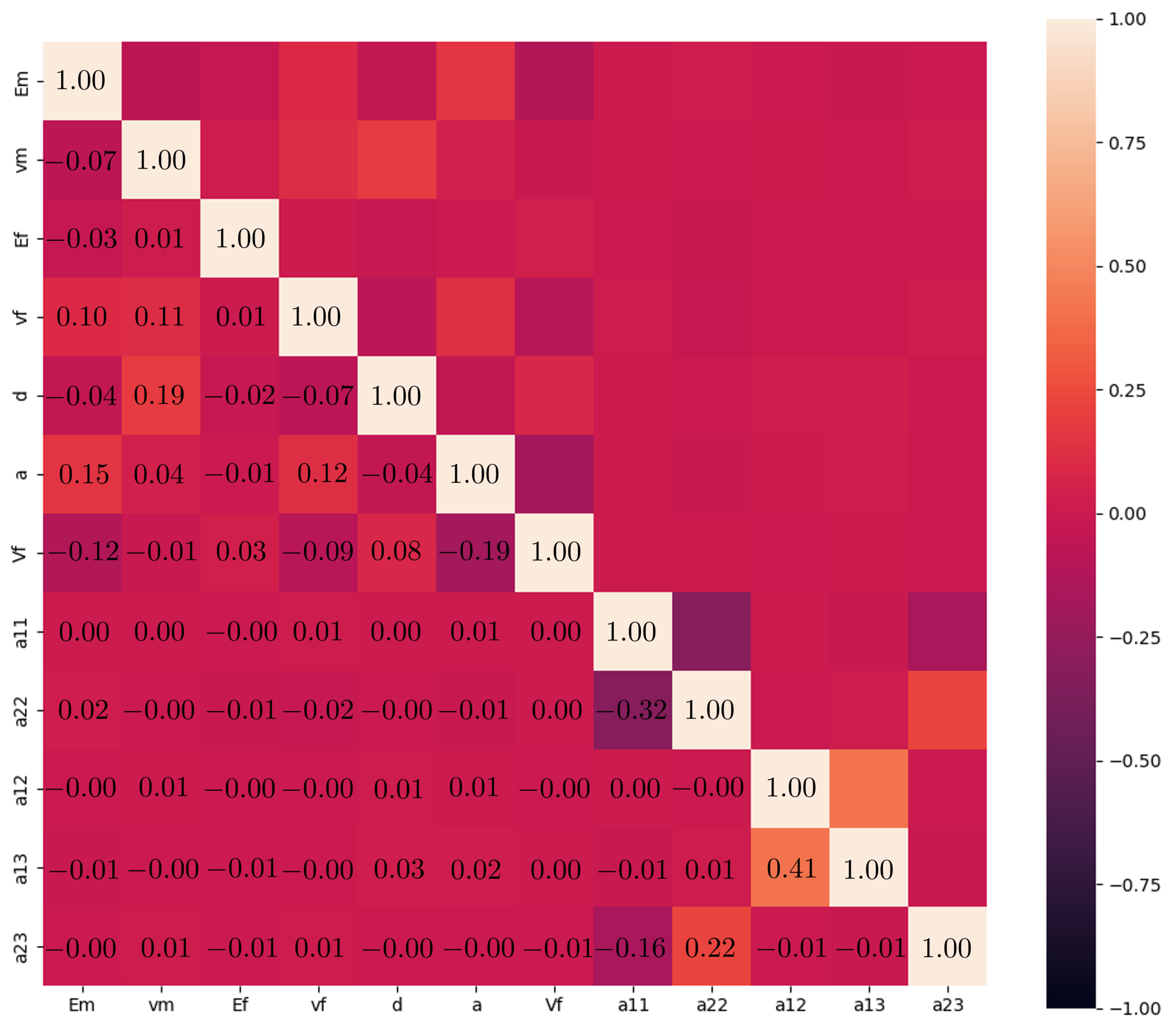
Appendix B. Preliminaries on ML Models Used in This Study
Appendix B.1. ET
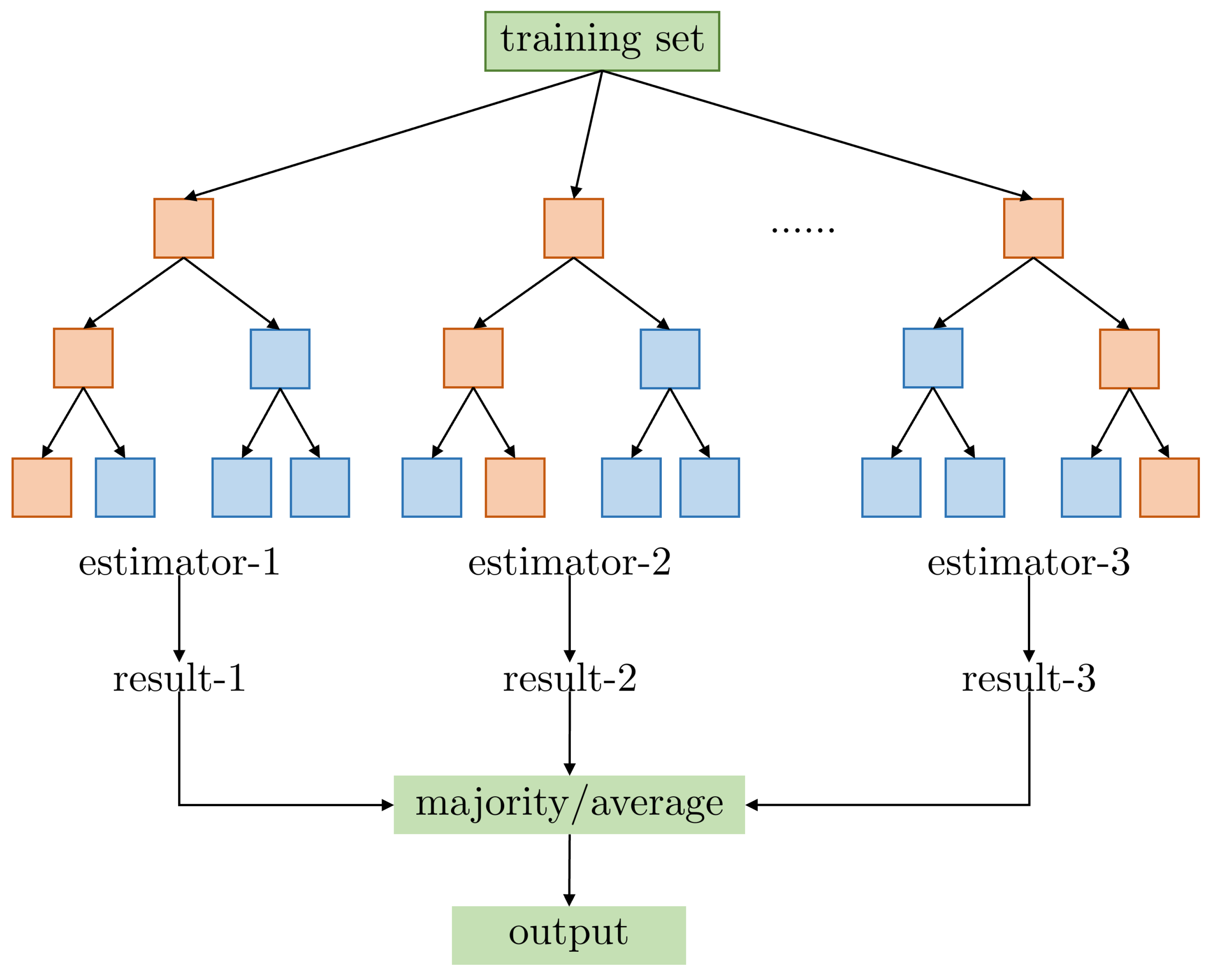
Appendix B.2. XGBoost
Appendix B.3. LGBM
Appendix C. Hyperparameter Optimization
Appendix C.1. Grid search
Appendix C.2. K-Fold Cross-Validation
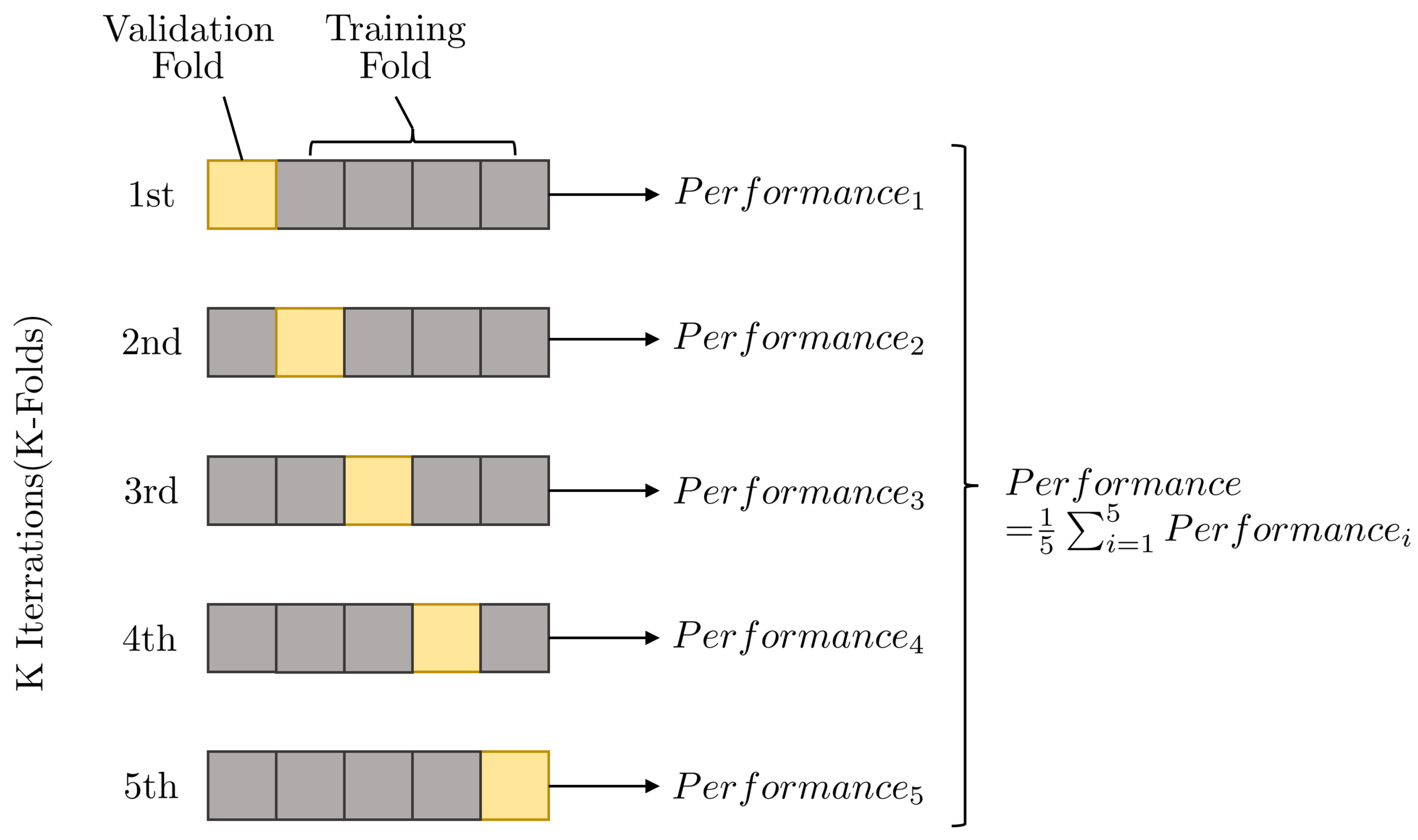
Appendix C.3. Hyperparameters for the Base Learners
- n_estimators is the number of decision trees.
- max_depth is the max depth of trees.
- min_samples_split is the least quantity of samples required for leaf splitting
- min_samples_leaf is the minimum number of sample numbers after child node splitting
- max_features is the number of features considered for a split.
- n_estimators controls the number of trees in the model. Increasing this value generally improves model performance, but can also lead to overfitting.
- max_depth is used to limit the tree depth explicitly.
- learning_rate determines the step size at each iteration while moving toward a minimum of a loss function.
- gamma is the minimum loss reduction to create a new tree-split.
- min_child_weight is the minimum sum of instance weight needed in a child node.
- subsample denotes the proportion of random sampling for each tree.
- colsample_bytree is the subsample ratio of columns when constructing each tree.
- num_leaves is the maximum number of leaves, the main parameter to control the complexity of the tree model.
- min_data_in_leaf very important parameter to prevent over-fitting in a leaf-wise tree.
- max_depth is used to limit the tree depth explicitly.
- n_estimators is the number of boosted trees to fit.
- learning_rate controls the step size at which the algorithm makes updates to the model weights.
- colsample_bytree is the subsample ratio of columns when constructing each tree.
- subsample dictates the proportion of random sampling for each tree.
References
- Hsissou, R.; Seghiri, R.; Benzekri, Z.; Hilali, M.; Rafik, M.; Elharfi, A. Polymer composite materials: A comprehensive review. Compos. Struct. 2021, 262, 113640. [Google Scholar] [CrossRef]
- Tucker, C.L., III; Liang, E. Stiffness predictions for unidirectional short-fiber composites: Review and evaluation. Compos. Sci. Technol. 1999, 59, 655–671. [Google Scholar] [CrossRef]
- Mirkhalaf, S.; Eggels, E.; Van Beurden, T.; Larsson, F.; Fagerström, M. A finite element based orientation averaging method for predicting elastic properties of short fiber-reinforced composites. Compos. Part B Eng. 2020, 202, 108388. [Google Scholar] [CrossRef]
- Chen, H.; Zhu, W.; Tang, H.; Yan, W. Oriented structure of short fiber-reinforced polymer composites processed by selective laser sintering: The role of powder-spreading process. Int. J. Mach. Tools Manuf. 2021, 163, 103703. [Google Scholar] [CrossRef]
- Lionetto, F.; Montagna, F.; Natali, D.; De Pascalis, F.; Nacucchi, M.; Caretto, F.; Maffezzoli, A. Correlation between elastic properties and morphology in short fiber composites by X-ray computed micro-tomography. Compos. Part A Appl. Sci. Manuf. 2021, 140, 106169. [Google Scholar] [CrossRef]
- Bloy, L.; Verma, R. On Computing the Underlying Fiber Directions from the Diffusion Orientation Distribution Function. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2008, New York, NY, USA, 6–10 September 2008; Metaxas, D., Axel, L., Fichtinger, G., Székely, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 1–8. [Google Scholar]
- Sun, P.Y.C.G.H. Modeling the effective elastic and viscoelastic properties of randomly distributed short fiber-reinforced composites. Compos. Commun. 2022, 35, 101341. [Google Scholar]
- Zhao, Y.; Siri, S.; Feng, B.; Pierce, D.M. The macro-and micro-mechanics of the colon and rectum II: Theoretical and computational methods. Bioengineering 2020, 7, 152. [Google Scholar] [CrossRef]
- Tian, W.; Qi, L.; Su, C.; Liang, J.; Zhou, J. Numerical evaluation on mechanical properties of short-fiber-reinforced metal matrix composites: Two-step mean-field homogenization procedure. Compos. Struct. 2016, 139, 96–103. [Google Scholar] [CrossRef]
- Stommel, K.B. RVE modelling of short fiber-reinforced thermoplastics with discrete fiber orientation and fiber length distribution. SN Appl. Sci. 2020, 3, 2523–3963. [Google Scholar]
- Cai, H.; Ye, J.; Wang, Y.; Saafi, M.; Huang, B.; Yang, D.; Ye, J. An effective microscale approach for determining the anisotropy of polymer composites reinforced with randomly distributed short fibers. Compos. Struct. 2020, 240, 112087. [Google Scholar] [CrossRef]
- Maharana, S.K.; Soni, G.; Mitra, M. A machine learning based prediction of elasto-plastic response of a short fiber-reinforced polymer (SFRP) composite. Model. Simul. Mater. Sci. Eng. 2023, 31, 075001. [Google Scholar] [CrossRef]
- Advani, S.G.; Tucker, C.L. The Use of Tensors to Describe and Predict Fiber Orientation in Short Fiber Composites. J. Rheol. 1987, 31, 751–784. [Google Scholar] [CrossRef]
- Mentges, N.; Dashtbozorg, B.; Mirkhalaf, S. A micromechanics-based artificial neural networks model for elastic properties of short fiber composites. Compos. Part B Eng. 2021, 213, 108736. [Google Scholar] [CrossRef]
- Shahab, M.; Zheng, G.; Khan, A.; Wei, D.; Novikov, A.S. Machine Learning-Based Virtual Screening and Molecular Simulation Approaches Identified Novel Potential Inhibitors for Cancer Therapy. Biomedicines 2023, 11, 2251. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.T.; Gu, G.X. Machine learning for composite materials. MRs Commun. 2019, 9, 556–566. [Google Scholar] [CrossRef]
- Ivanov, A.S.; Nikolaev, K.G.; Novikov, A.S.; Yurchenko, S.O.; Novoselov, K.S.; Andreeva, D.V.; Skorb, E.V. Programmable soft-matter electronics. J. Phys. Chem. Lett. 2021, 12, 2017–2022. [Google Scholar] [CrossRef]
- Zhao, J.; Chen, Z.; Tu, J.; Zhao, Y.; Dong, Y. Application of LSTM Approach for Predicting the Fission Swelling Behavior within a CERCER Composite Fuel. Energies 2022, 15, 9053. [Google Scholar] [CrossRef]
- Zhao, Y.; Chen, Z.; Dong, Y.; Tu, J. An interpretable LSTM deep learning model predicts the time-dependent swelling behavior in CERCER composite fuels. Mater. Today Commun. 2023, 37, 106998. [Google Scholar] [CrossRef]
- Zhao, J.; Chen, Z.; Zhao, Y. Toward Elucidating the Influence of Hydrostatic Pressure Dependent Swelling Behavior in the CERCER Composite. Materials 2023, 16, 2644. [Google Scholar] [CrossRef]
- Alber, M.; Buganza Tepole, A.; Cannon, W.R.; De, S.; Dura-Bernal, S.; Garikipati, K.; Karniadakis, G.; Lytton, W.W.; Perdikaris, P.; Petzold, L.; et al. Integrating machine learning and multiscale modeling—perspectives, challenges, and opportunities in the biological, biomedical, and behavioral sciences. NPJ Digit. Med. 2019, 2, 1–11. [Google Scholar] [CrossRef]
- Baek, K.; Hwang, T.; Lee, W.; Chung, H.; Cho, M. Deep learning aided evaluation for electromechanical properties of complexly structured polymer nanocomposites. Compos. Sci. Technol. 2022, 228, 109661. [Google Scholar] [CrossRef]
- Liu, B.; Vu-Bac, N.; Rabczuk, T. A stochastic multiscale method for the prediction of the thermal conductivity of Polymer nanocomposites through hybrid machine learning algorithms. Compos. Struct. 2021, 273, 114269. [Google Scholar] [CrossRef]
- Qi, Z.; Zhang, N.; Liu, Y.; Chen, W. Prediction of mechanical properties of carbon fiber based on cross-scale FEM and machine learning. Compos. Struct. 2019, 212, 199–206. [Google Scholar] [CrossRef]
- Miao, K.; Pan, Z.; Chen, A.; Wei, Y.; Zhang, Y. Machine learning-based model for the ultimate strength of circular concrete-filled fiber-reinforced polymer–steel composite tube columns. Constr. Build. Mater. 2023, 394, 132134. [Google Scholar] [CrossRef]
- Ye, S.; Huang, W.Z.; Li, M.; Feng, X.Q. Deep learning method for determining the surface elastic moduli of microstructured solids. Extrem. Mech. Lett. 2021, 44, 101226. [Google Scholar] [CrossRef]
- Ye, S.; Li, B.; Li, Q.; Zhao, H.P.; Feng, X.Q. Deep neural network method for predicting the mechanical properties of composites. Appl. Phys. Lett. 2019, 115. [Google Scholar] [CrossRef]
- Messner, M.C. Convolutional neural network surrogate models for the mechanical properties of periodic structures. J. Mech. Des. 2020, 142, 024503. [Google Scholar] [CrossRef]
- Korshunova, N.; Jomo, J.; Lékó, G.; Reznik, D.; Balázs, P.; Kollmannsberger, S. Image-based material characterization of complex microarchitectured additively manufactured structures. Comput. Math. Appl. 2020, 80, 2462–2480. [Google Scholar] [CrossRef]
- Gupta, S.; Mukhopadhyay, T.; Kushvaha, V. Microstructural image based convolutional neural networks for efficient prediction of full-field stress maps in short fiber polymer composites. Def. Technol. 2023, 24, 58–82. [Google Scholar] [CrossRef]
- Lipton, Z.C. The mythos of model interpretability: In machine learning, the concept of interpretability is both important and slippery. Queue 2018, 16, 31–57. [Google Scholar] [CrossRef]
- Gustafsson, S. Interpretable Serious Event Forecasting Using Machine Learning and SHAP. 2021. Available online: https://www.diva-portal.org/smash/get/diva2:1561201/FULLTEXT01.pdf (accessed on 6 June 2021).
- Park, D.; Jung, J.; Gu, G.X.; Ryu, S. A generalizable and interpretable deep learning model to improve the prediction accuracy of strain fields in grid composites. Mater. Des. 2022, 223, 111192. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhao, H.; Ai, J.; Dong, Y. Robust data-driven fault detection: An application to aircraft air data sensors. Int. J. Aerosp. Eng. 2022, 2022, 2918458. [Google Scholar] [CrossRef]
- Dong, Y.; Tao, J.; Zhang, Y.; Lin, W.; Ai, J. Deep learning in aircraft design, dynamics, and control: Review and prospects. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 2346–2368. [Google Scholar] [CrossRef]
- Zhou, Z.H. Ensemble Learning. In Machine Learning; Springer: Singapore, 2021; pp. 181–210. [Google Scholar]
- Wang, W.; Zhao, Y.; Li, Y. Ensemble Machine Learning for Predicting the Homogenized Elastic Properties of Unidirectional Composites: A SHAP-based Interpretability Analysis. Acta Mech. Sin. 2023, 40, 423301. [Google Scholar] [CrossRef]
- Liang, M.; Chang, Z.; Wan, Z.; Gan, Y.; Schlangen, E.; Šavija, B. Interpretable Ensemble-Machine-Learning models for predicting creep behavior of concrete. Cem. Concr. Compos. 2022, 125, 104295. [Google Scholar] [CrossRef]
- Milad, A.; Hussein, S.H.; Khekan, A.R.; Rashid, M.; Al-Msari, H.; Tran, T.H. Development of ensemble machine learning approaches for designing fiber-reinforced polymer composite strain prediction model. Eng. Comput. 2022, 38, 3625–3637. [Google Scholar] [CrossRef]
- Shi, M.; Feng, C.P.; Li, J.; Guo, S.Y. Machine learning to optimize nanocomposite materials for electromagnetic interference shielding. Compos. Sci. Technol. 2022, 223, 109414. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.I. A unified approach to interpreting model predictions. Adv. Neural Inf. Process. Syst. 2017, 30, 4768–4777. [Google Scholar]
- Bakouregui, A.S.; Mohamed, H.M.; Yahia, A.; Benmokrane, B. Explainable extreme gradient boosting tree-based prediction of load-carrying capacity of FRP-RC columns. Eng. Struct. 2021, 245, 112836. [Google Scholar] [CrossRef]
- Yan, F.; Song, K.; Liu, Y.; Chen, S.; Chen, J. Predictions and mechanism analyses of the fatigue strength of steel based on machine learning. J. Mater. Sci. 2020, 55, 15334–15349. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, Y.; Ai, J.; Zhao, Y.; Yu, Y.; Dong, Y. A Lightweight and Explainable Data-driven Scheme for Fault Detection of Aerospace Sensors. IEEE Trans. Aerosp. Electron. Syst. 2023, 1–20. [Google Scholar] [CrossRef]
- Zhou, K.; Enos, R.; Zhang, D.; Tang, J. Uncertainty analysis of curing-induced dimensional variability of composite structures utilizing physics-guided Gaussian process meta-modeling. Compos. Struct. 2022, 280, 114816. [Google Scholar] [CrossRef]
- Holmström, P.H.; Hopperstad, O.S.; Clausen, A.H. Anisotropic tensile behaviour of short glass-fibre reinforced polyamide-6. Compos. Part C Open Access 2020, 2, 100019. [Google Scholar] [CrossRef]
- Mehta, A.; Schneider, M. A sequential addition and migration method for generating microstructures of short fibers with prescribed length distribution. Comput. Mech. 2022, 70, 829–851. [Google Scholar] [CrossRef]
- Zhao, Y.; Siri, S.; Feng, B.; Pierce, D. Computational modeling of mouse colorectum capturing longitudinal and through-thickness biomechanical heterogeneity. J. Mech. Behav. Biomed. Mater. 2021, 113, 104127. [Google Scholar] [CrossRef] [PubMed]
- Benesty, J.; Chen, J.; Huang, Y.; Cohen, I. Pearson Correlation Coefficient. In Noise Reduction in Speech Processing; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–4. [Google Scholar]
- Mallick, P.K. Fiber-Reinforced Composites: Materials, Manufacturing, and Design; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Wang, Z.; Mu, L.; Miao, H.; Shang, Y.; Yin, H.; Dong, M. An innovative application of machine learning in prediction of the syngas properties of biomass chemical looping gasification based on extra trees regression algorithm. Energy 2023, 275, 127438. [Google Scholar] [CrossRef]
- Guo, P.; Meng, W.; Xu, M.; Li, V.C.; Bao, Y. Predicting mechanical properties of high-performance fiber-reinforced cementitious composites by integrating micromechanics and machine learning. Materials 2021, 14, 3143. [Google Scholar] [CrossRef]
- Marani, A.; Jamali, A.; Nehdi, M.L. Predicting ultra-high-performance concrete compressive strength using tabular generative adversarial networks. Materials 2020, 13, 4757. [Google Scholar] [CrossRef]
- Ahmad, M.W.; Reynolds, J.; Rezgui, Y. Predictive modeling for solar thermal energy systems: A comparison of support vector regression, random forest, extra trees and regression trees. J. Clean. Prod. 2018, 203, 810–821. [Google Scholar] [CrossRef]
- Konstantinov, A.V.; Utkin, L.V. Interpretable machine learning with an ensemble of gradient boosting machines. Knowl.-Based Syst. 2021, 222, 106993. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Strobl, C.; Boulesteix, A.L.; Kneib, T.; Augustin, T.; Zeileis, A. Conditional variable importance for random forests. BMC Bioinform. 2008, 9, 307. [Google Scholar] [CrossRef] [PubMed]
- Chung, H.; Ko, H.; Kang, W.S.; Kim, K.W.; Lee, H.; Park, C.; Song, H.O.; Choi, T.Y.; Seo, J.H.; Lee, J. Prediction and feature importance analysis for severity of COVID-19 in South Korea using artificial intelligence: Model development and validation. J. Med. Internet Res. 2021, 23, e27060. [Google Scholar] [CrossRef] [PubMed]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. Pytorch: An imperative style, high-performance deep learning library. Adv. Neural Inf. Process. Syst. 2019, 32, 8026–8037. [Google Scholar]
- Probst, P.; Boulesteix, A.L.; Bischl, B. Tunability: Importance of hyperparameters of machine learning algorithms. J. Mach. Learn. Res. 2019, 20, 1934–1965. [Google Scholar]
- Bergstra, J.; Bardenet, R.; Bengio, Y.; Kégl, B. Algorithms for hyper-parameter optimization. Adv. Neural Inf. Process. Syst. 2011, 24, 2546–2554. [Google Scholar]
- Zhang, Y.; Zhao, H.; Ma, J.; Zhao, Y.; Dong, Y.; Ai, J. A deep neural network-based fault detection scheme for aircraft IMU sensors. Int. J. Aerosp. Eng. 2021, 2021, 3936826. [Google Scholar] [CrossRef]
- Zhao, Y.; Feng, B.; Pierce, D.M. Predicting the micromechanics of embedded nerve fibers using a novel three-layered model of mouse distal colon and rectum. J. Mech. Behav. Biomed. Mater. 2022, 127, 105083. [Google Scholar] [CrossRef]
- Dong, W.; Huang, Y.; Lehane, B.; Ma, G. XGBoost algorithm-based prediction of concrete electrical resistivity for structural health monitoring. Autom. Constr. 2020, 114, 103155. [Google Scholar] [CrossRef]
- Haque, M.A.; Chen, B.; Kashem, A.; Qureshi, T.; Ahmed, A.A.M. Hybrid intelligence models for compressive strength prediction of MPC composites and parametric analysis with SHAP algorithm. Mater. Today Commun. 2023, 35, 105547. [Google Scholar] [CrossRef]
- Le, T.T. Practical machine learning-based prediction model for axial capacity of square CFST columns. Mech. Adv. Mater. Struct. 2022, 29, 1782–1797. [Google Scholar] [CrossRef]
- Ralph, B.J.; Hartl, K.; Sorger, M.; Schwarz-Gsaxner, A.; Stockinger, M. Machine learning driven prediction of residual stresses for the shot peening process using a finite element based grey-box model approach. J. Manuf. Mater. Process. 2021, 5, 39. [Google Scholar] [CrossRef]
- Kallel, H.; Joulain, K. Design and thermal conductivity of 3D artificial cross-linked random fiber networks. Mater. Des. 2022, 220, 110800. [Google Scholar] [CrossRef]
- Bapanapalli, S.; Nguyen, B.N. Prediction of elastic properties for curved fiber polymer composites. Polym. Compos. 2008, 29, 544–550. [Google Scholar] [CrossRef]
- Swolfs, Y.; Gorbatikh, L.; Verpoest, I. Fibre hybridisation in polymer composites: A review. Compos. Part A Appl. Sci. Manuf. 2014, 67, 181–200. [Google Scholar] [CrossRef]
- Li, M.; Zhang, H.; Li, S.; Zhu, W.; Ke, Y. Machine learning and materials informatics approaches for predicting transverse mechanical properties of unidirectional CFRP composites with microvoids. Mater. Des. 2022, 224, 111340. [Google Scholar] [CrossRef]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomized trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef]
- Chen, Z.T.; Liu, Y.K.; Chao, N.; Ernest, M.M.; Guo, X.L. Gamma-rays buildup factor calculation using regression and Extra-Trees. Radiat. Phys. Chem. 2023, 209, 110997. [Google Scholar] [CrossRef]
- Khan, I.U.; Aslam, N.; AlShedayed, R.; AlFrayan, D.; AlEssa, R.; AlShuail, N.A.; Al Safwan, A. A proactive attack detection for heating, ventilation, and air conditioning (HVAC) system using explainable extreme gradient boosting model (XGBoost). Sensors 2022, 22, 9235. [Google Scholar] [CrossRef]
- Meng, Q.; Ke, G.; Wang, T.; Chen, W.; Ye, Q.; Ma, Z.M.; Liu, T.Y. A communication-efficient parallel algorithm for decision tree. Adv. Neural Inf. Process. Syst. 2016, 29, 1279–1287. [Google Scholar]
- Yang, L.; Shami, A. On hyperparameter optimization of machine learning algorithms: Theory and practice. Neurocomputing 2020, 415, 295–316. [Google Scholar] [CrossRef]
- Liashchynskyi, P.; Liashchynskyi, P. Grid search, random search, genetic algorithm: A big comparison for NAS. arXiv 2019, arXiv:1912.06059. [Google Scholar]
- Amin, M.N.; Salami, B.A.; Zahid, M.; Iqbal, M.; Khan, K.; Abu-Arab, A.M.; Alabdullah, A.A.; Jalal, F.E. Investigating the bond strength of FRP laminates with concrete using LIGHT GBM and SHAPASH analysis. Polymers 2022, 14, 4717. [Google Scholar] [CrossRef] [PubMed]
- Neelam, R.; Kulkarni, S.A.; Bharath, H.; Powar, S.; Doddamani, M. Mechanical response of additively manufactured foam: A machine learning approach. Results Eng. 2022, 16, 100801. [Google Scholar] [CrossRef]
- Alabdullah, A.A.; Iqbal, M.; Zahid, M.; Khan, K.; Amin, M.N.; Jalal, F.E. Prediction of rapid chloride penetration resistance of metakaolin based high strength concrete using light GBM and XGBoost models by incorporating SHAP analysis. Constr. Build. Mater. 2022, 345, 128296. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]






| Base Learner Model | Hyperparameters | Optimal Values |
|---|---|---|
| ET | n_estimators | 160 |
| max_depth | 21 | |
| min_samples_split | 2 | |
| min_samples_leaf | 1 | |
| max_features | 11 | |
| XGBoost | n_estimators | 200 |
| learning_rate | 0.15 | |
| max_depth | 6 | |
| min_child_weight | 2 | |
| colsample_bytree | 1 | |
| subsample | 1 | |
| gamma | 0 | |
| LGBM | n_estimators | 360 |
| learning_rate | 0.22 | |
| max_depth | −1 | |
| min_child_weight | 3 | |
| colsample_bytree | 1 | |
| subsample | 0.7 | |
| gamma | 0 | |
| num_leaves | 31 |
| Parameter | [GPa] | [GPa] | Fiber Diameter [μm] | Fiber Length [μm] | |||
|---|---|---|---|---|---|---|---|
| Magnitude | 1.6 | 0.4 | 69 | 0.15 | 2 | 8 | 5% |
| Mechanical Properteis | [GPa] | [GPa] | [GPa] | |||
|---|---|---|---|---|---|---|
| Magnitude | 2.187 | 1.827 | 1.830 | 0.393 | 0.392 | 0.328 |
| Mechanical Properteis | [GPa] | [GPa] | [GPa] | |||
| Magnitude | 0.629 | 0.637 | 0.637 | 0.441 | 0.328 | 0.441 |
| [GPa] | [GPa] | [GPa] | ||||
|---|---|---|---|---|---|---|
| FEA | 2.009 | 1.871 | 1.806 | 0.369 | 0.427 | 0.344 |
| Two-step | 1.929 | 1.827 | 1.776 | 0.376 | 0.421 | 0.356 |
| Relative error | 3.95% | 2.31% | 1.69% | 1.84% | 1.46% | 3.57% |
| [GPa] | [GPa] | [GPa] | ||||
| FEA | 0.415 | 0.384 | 0.400 | 0.643 | 0.719 | 0.645 |
| Two-step | 0.413 | 0.387 | 0.401 | 0.634 | 0.706 | 0.636 |
| Relative error | 0.45% | 0.85% | 0.18% | 1.36% | 1.74% | 1.32% |
| [GPa] | [GPa] | [GPa] | ||||
| FEA | 1.786 | 1.786 | 1.777 | 0.398 | 0.396 | 0.398 |
| Two-step | 1.780 | 1.780 | 1.775 | 0.398 | 0.395 | 0.398 |
| Relative error | 0.30% | 0.35% | 0.09% | 0.05% | 0.19% | 0.01% |
| [GPa] | [GPa] | [GPa] | ||||
| FEA | 0.396 | 0.394 | 0.394 | 0.666 | 0.666 | 0.682 |
| Two-step | 0.395 | 0.395 | 0.395 | 0.668 | 0.668 | 0.686 |
| Relative error | 0.14% | 0.16% | 0.28% | 0.32% | 0.36% | 0.59% |
| [GPa] | [GPa] | [GPa] | ||||
| FEA | 1.789 | 1.784 | 1.814 | 0.394 | 0.385 | 0.393 |
| Two-step | 1.786 | 1.764 | 1.797 | 0.394 | 0.386 | 0.391 |
| Relative error | 0.19% | 1.11% | 0.92% | 0.08% | 0.23% | 0.53% |
| [GPa] | [GPa] | [GPa] | ||||
| FEA | 0.401 | 0.390 | 0.407 | 0.697 | 0.656 | 0.650 |
| Two-step | 0.403 | 0.387 | 0.414 | 0.708 | 0.657 | 0.652 |
| Relative error | 0.65% | 0.91% | 1.65% | 1.52% | 0.24% | 0.28% |
| [GPa] | [GPa] | [GPa] | ||||
| FEA | 1.823 | 1.777 | 1.938 | 0.414 | 0.355 | 0.404 |
| Two-step | 1.832 | 1.776E | 1.950 | 0.414 | 0.353 | 0.404 |
| Relative error | 0.46% | 0.06% | 0.62% | 0.00% | 0.43% | 0.07% |
| [GPa] | [GPa] | [GPa] | ||||
| FEA | 0.385 | 0.377 | 0.419 | 0.694 | 0.635 | 0.633 |
| Prediction | 0.383 | 0.373 | 0.424 | 0.714 | 0.636 | 0.634 |
| Relative error | 0.40% | 1.03% | 1.18% | 2.83% | 0.12% | 0.25% |
| Model | ET | XGBoost | LGBM | EML | ||||
|---|---|---|---|---|---|---|---|---|
| Train | Test | Train | Test | Train | Test | Train | Test | |
| 0.981 | 0.932 | 0.983 | 0.943 | 0.984 | 0.946 | 0.988 | 0.952 | |
| MSE | 5.089 | 2.360 | 7.629 | 2.050 | 3.538 | 1.450 | 2.545 | 1.260 |
| MAPE | 0.831% | 1.010% | 0.716% | 1.243% | 0.971% | 1.264% | 0.567% | 0.906% |
| Metrics | |||||||
|---|---|---|---|---|---|---|---|
| 0.99998 | 0.99999 | 0.99999 | 0.91273 | 0.95564 | 0.91864 | 0.99998 | |
| MSE | 1.99 | 1.36 | 1.09 | 8.8 | 2.57 | 9.94 | 2.38 |
| MAPE | 0.336% | 0.533% | 0.708% | 0.671% | 0.773% | 1.063% | 0.347% |
| 0.99999 | 0.92600 | 0.92918 | 0.94278 | 0.99996 | 0.94169 | 0.91682 | |
| MSE | 1.04 | 6.36 | 7.65 | 3.74 | 5.64 | 3.65 | 1.30 |
| MAPE | 0.587% | 0.939% | 0.809% | 1.005% | 0.812% | 1.218% | 1.010% |
| 0.91887 | 0.99929 | 0.90912 | 0.92698 | 0.99920 | 0.92795 | 0.99923 | |
| MSE | 1.18 | 4.46 | 1.8 | 1.5 | 5.04 | 2.31 | 4.82 |
| MAPE | 1.114% | 0.917% | 1.215% | 1.981% | 0.924% | 1.179% | 0.881% |
| Polymer Composite | d | a | a11 | a22 | a33 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| PA15 from [46] | 2.8 | 0.4 | 7.0 | 0.2 | 13.5 | 31.85 | 0.064 | 0.507 | 0.473 | 0.020 |
| PA6GF35 from [47] | 3.0 | 0.4 | 7.2 | 0.22 | 10 | 25 | 0.193 | 0.786 | 0.196 | 0.018 |
| Method | Setting | Computation Cost |
|---|---|---|
| Digimat-FE Simulaiton | 19,937 elements | 2911 s |
| EML prediction | training 378 s (10,800 samples) | <1 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Chen, Z.; Jian, X. A High-Generalizability Machine Learning Framework for Analyzing the Homogenized Properties of Short Fiber-Reinforced Polymer Composites. Polymers 2023, 15, 3962. https://doi.org/10.3390/polym15193962
Zhao Y, Chen Z, Jian X. A High-Generalizability Machine Learning Framework for Analyzing the Homogenized Properties of Short Fiber-Reinforced Polymer Composites. Polymers. 2023; 15(19):3962. https://doi.org/10.3390/polym15193962
Chicago/Turabian StyleZhao, Yunmei, Zhenyue Chen, and Xiaobin Jian. 2023. "A High-Generalizability Machine Learning Framework for Analyzing the Homogenized Properties of Short Fiber-Reinforced Polymer Composites" Polymers 15, no. 19: 3962. https://doi.org/10.3390/polym15193962
APA StyleZhao, Y., Chen, Z., & Jian, X. (2023). A High-Generalizability Machine Learning Framework for Analyzing the Homogenized Properties of Short Fiber-Reinforced Polymer Composites. Polymers, 15(19), 3962. https://doi.org/10.3390/polym15193962







