Review of Additively Manufactured Polymeric Metamaterials: Design, Fabrication, Testing and Modeling
Abstract
:1. Introduction
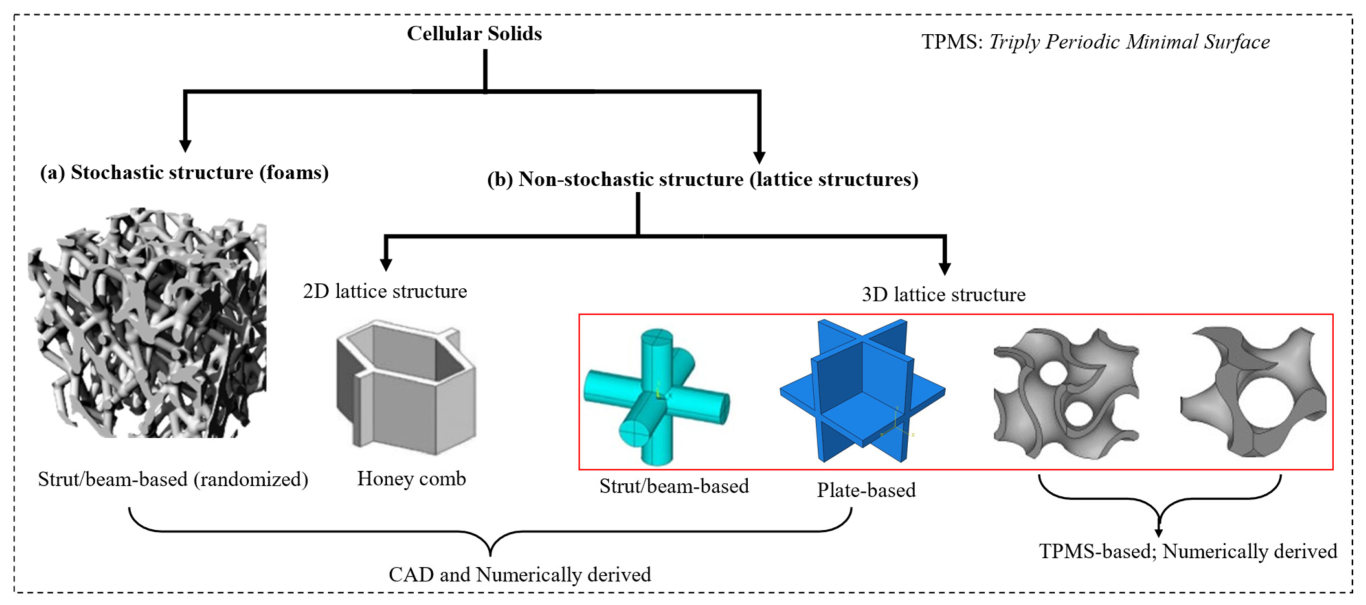
2. Design of Polymeric Metamaterials
2.1. Comb-Based Metamaterials
2.2. Strut-Based Metamaterials
2.3. Plate-Based Metamaterials
2.4. TPMS Metamaterials
2.4.1. Categories of TPMS-Based Lattices and Design Strategies
2.4.2. Design Strategies for Grading TPMS-Lattice Topologies
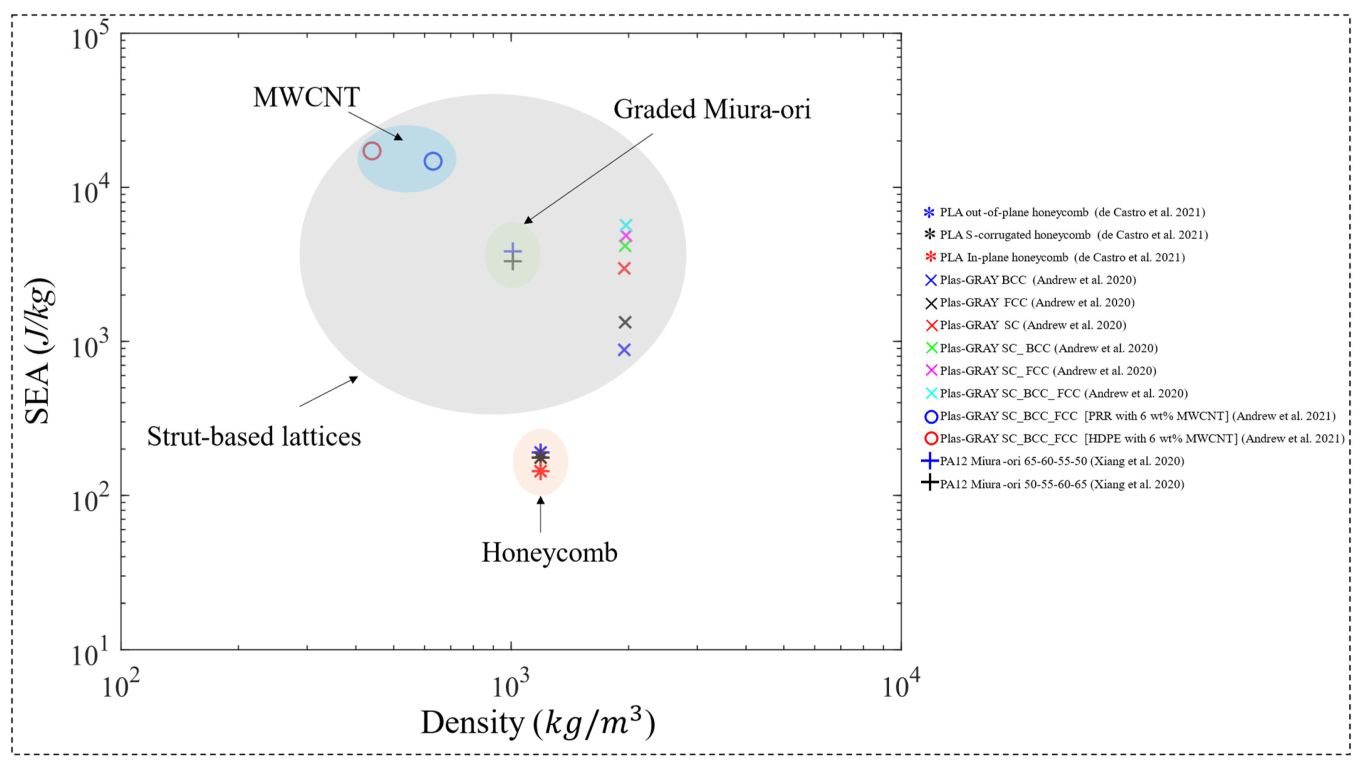
2.5. Stochastic-Based Metamaterials
2.6. Limitations
3. Fabrication of Polymeric Metamaterials
3.1. Optimizing the Fabrication Procedure of Polymeric Metamaterials
3.2. Polymeric Composite Materials
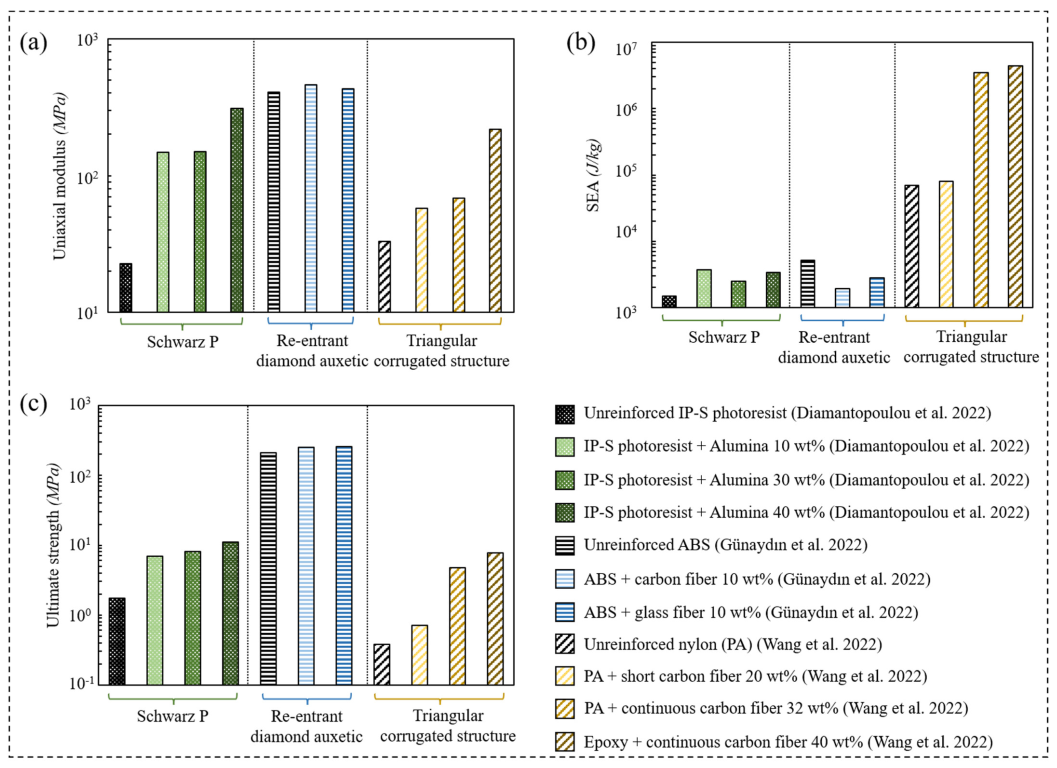
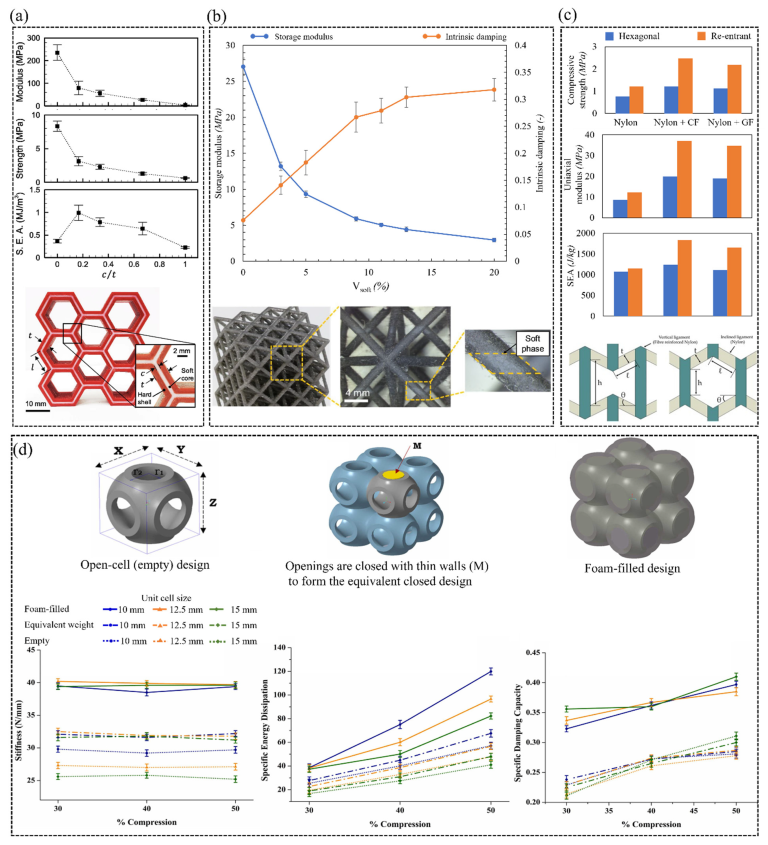
3.2.1. Fiber Reinforced Composites
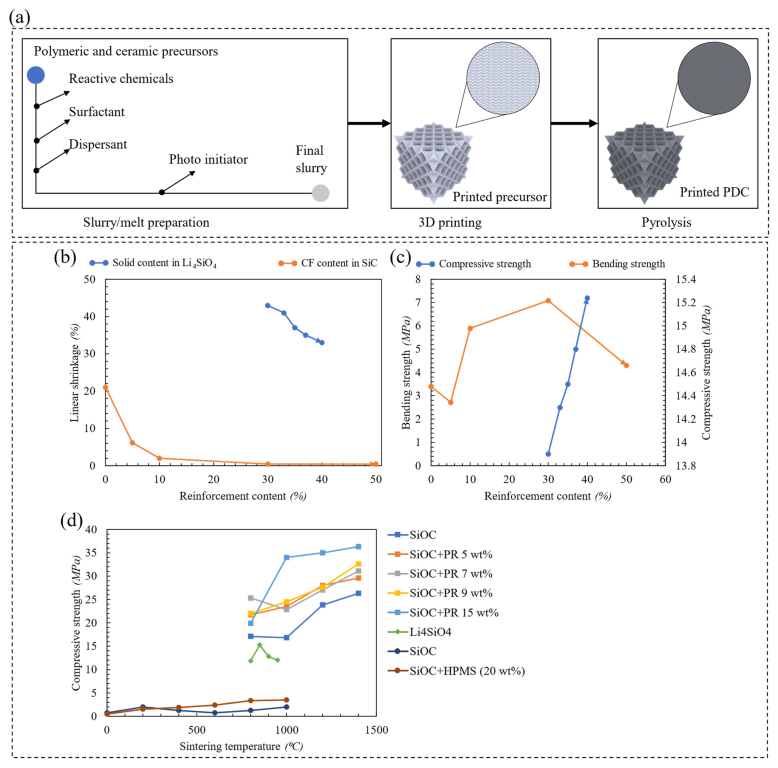
3.2.2. Polymeric-Derived Ceramic Composite
3.2.3. Cementitious Composite
3.3. Multi-Material Additive Manufacturing
3.4. Polymeric Metamaterials’ Fabrication Challenges
4. Mechanical Characterization of Polymeric Metamaterials
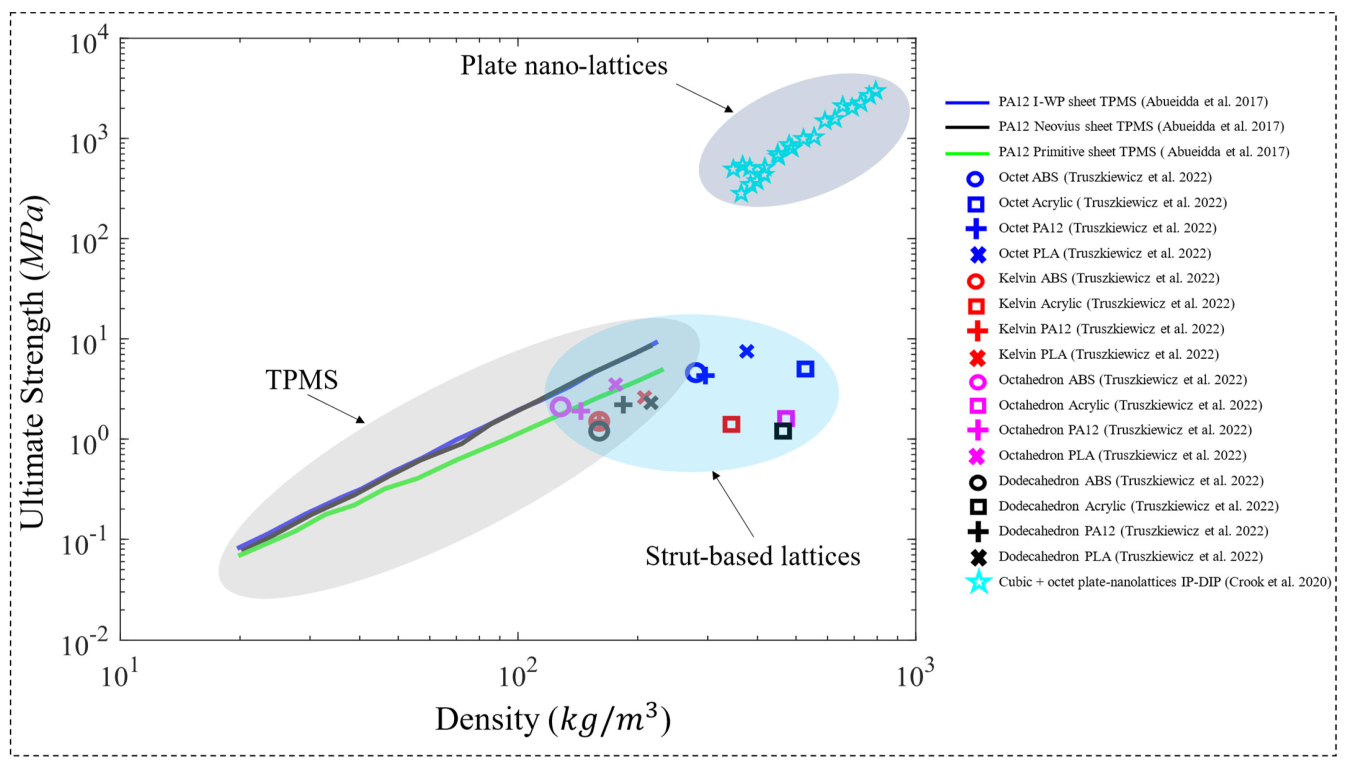
4.1. Uniaxial Compression Tests

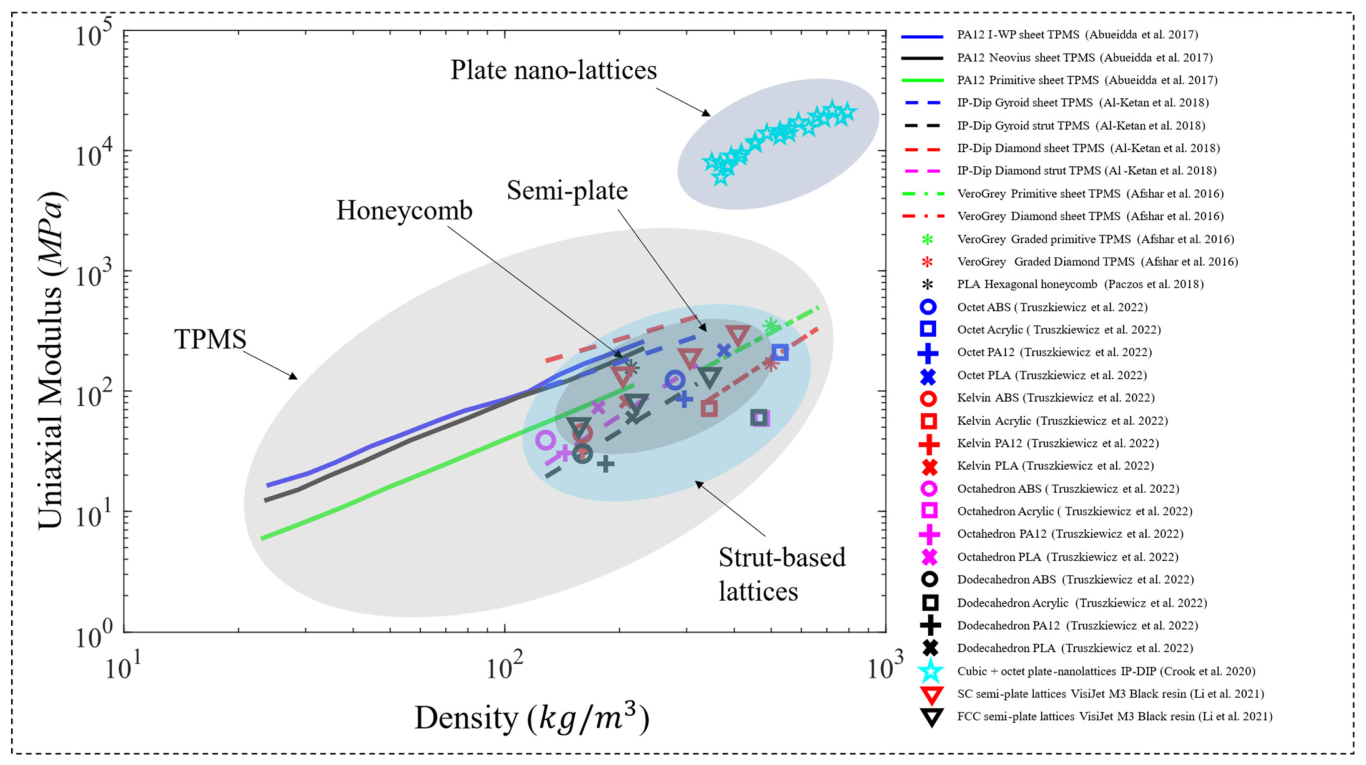

4.2. Bending Tests
4.3. Impact Tests
4.4. Other Tests of Polymeric Metamaterials
5. Conclusions and Future Outlook
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fan, K.; Padilla, W.J. Dynamic electromagnetic metamaterials. Mater. Today 2015, 18, 39–50. [Google Scholar] [CrossRef]
- Cai, W.; Shalaev, V. Optical Metamaterials: Fundamentals and Applications. Phys. Today 2010, 63, 57–58. [Google Scholar] [CrossRef]
- Cummer, S.A.; Christensen, J.; Alù, A. Controlling sound with acoustic metamaterials. Nat. Rev. Mater. 2016, 1, 16001. [Google Scholar] [CrossRef]
- Li, Y.; Li, W.; Han, T.; Zheng, X.; Li, J.; Li, B.; Fan, S.; Qiu, C.W. Transforming heat transfer with thermal metamaterials and devices. Nat. Rev. Mater. 2021, 6, 488–507. [Google Scholar] [CrossRef]
- Bertoldi, K.; Vitelli, V.; Christensen, J.; Van Hecke, M. Flexible mechanical metamaterials. Nat. Rev. Mater. 2017, 2, 17066. [Google Scholar] [CrossRef]
- Surjadi, J.U.; Gao, L.; Du, H.; Li, X.; Xiong, X.; Fang, N.X.; Lu, Y. Mechanical Metamaterials and Their Engineering Applications. Adv. Eng. Mater. 2019, 21, 1800864. [Google Scholar] [CrossRef]
- Papetti, V.; Eggenschwiler, P.D.; Della Torre, A.; Lucci, F.; Ortona, A.; Montenegro, G. Additive Manufactured open cell polyhedral structures as substrates for automotive catalysts. Int. J. Heat Mass Transf. 2018, 126, 1035–1047. [Google Scholar] [CrossRef]
- Yin, S.; Chen, H.; Wu, Y.; Li, Y.; Xu, J. Introducing composite lattice core sandwich structure as an alternative proposal for engine hood. Compos. Struct. 2018, 201, 131–140. [Google Scholar] [CrossRef]
- Hudecki, A.; Kiryczyński, G.; Łos, M.J. Biomaterials, Definition, Overview. In Stem Cells and Biomaterials for Regenerative Medicine; Łos, M.J., Hudecki, A., Wiecheć, E., Eds.; Academic Press: Cambridge, MA, USA, 2019; pp. 85–98. ISBN 9780128122587. [Google Scholar]
- Oladapo, B.I.; Ismail, S.O.; Ikumapayi, O.M.; Karagiannidis, P.G. Impact of rGO-coated PEEK and lattice on bone implant. Colloids Surf. B Biointerfaces 2022, 216, 112583. [Google Scholar] [CrossRef]
- Reyes, R.L.; Ghim, M.S.; Kang, N.U.; Park, J.W.; Gwak, S.J.; Cho, Y.S. Development and assessment of modified-honeycomb-structure scaffold for bone tissue engineering. Addit. Manuf. 2022, 54, 102740. [Google Scholar] [CrossRef]
- Xiong, Y.; Wang, W.; Gao, R.; Zhang, H.; Dong, L.; Qin, J.; Wang, B.; Jia, W.; Li, X. Fatigue behavior and osseointegration of porous Ti-6Al-4V scaffolds with dense core for dental application. Mater. Des. 2020, 195, 108994. [Google Scholar] [CrossRef]
- Li, X.; Xiong, J.; Ma, L.; Wu, L.; Yan, X. Effect of vacuum thermal cycling on the compression and shear performance of composite sandwich structures containing pyramidal truss cores. Compos. Sci. Technol. 2018, 158, 67–78. [Google Scholar] [CrossRef]
- Modi, K.; Kachhadiya, P.; Rathod, J.M.; Panchal, P.H.; Parikh, K. Low-Cost Metamaterial Loaded Microstrip Antenna for Defense Applications. Open J. Antennas Propag. 2021, 9, 1–10. [Google Scholar] [CrossRef]
- Singh, R.K.; Gupta, A. Theoretical and experimental study of angle independent conformal tri-band metamaterial absorber design for industrial and defense applications. Int. J. RF Microw. Comput. Eng. 2022, 32, e23402. [Google Scholar] [CrossRef]
- Cosma, C.; Kessler, J.; Gebhardt, A.; Campbell, I.; Balc, N. Improving the mechanical strength of dental applications and lattice structures SLM processed. Materials 2020, 13, 905. [Google Scholar] [CrossRef]
- Oladapo, B.I.; Kayode, J.F.; Karagiannidis, P.; Naveed, N.; Mehrabi, H.; Ogundipe, K.O. Polymeric composites of cubic-octahedron and gyroid lattice for biomimetic dental implants. Mater. Chem. Phys. 2022, 289, 126454. [Google Scholar] [CrossRef]
- Pendry, J.B.; Schurig, D.; Smith, D.R. Controlling Electromagnetic Fields. Science 2006, 312, 1780–1782. [Google Scholar] [CrossRef]
- Leonhardt, U. Optical Conformal Mapping. Science 2006, 312, 1777–1780. [Google Scholar] [CrossRef]
- Veerabagu, U.; Palza, H.; Quero, F. Review: Auxetic Polymer-Based Mechanical Metamaterials for Biomedical Applications. ACS Biomater. Sci. Eng. 2022, 8, 2798–2824. [Google Scholar] [CrossRef]
- Fan, J.; Zhang, L.; Wei, S.; Zhang, Z.; Choi, S.-K.; Song, B.; Shi, Y. A review of additive manufacturing of metamaterials and developing trends. Mater. Today 2021, 50, 303–328. [Google Scholar] [CrossRef]
- Almesmari, A.; Alagha, A.N.; Naji, M.M.; Sheikh-Ahmad, J.; Jarrar, F. Recent advancements in design optimization of lattice structured materials. Adv. Eng. Mater. 2023, 25, 2201780. [Google Scholar] [CrossRef]
- Al-Ketan, O.; Abu Al-Rub, R.K. Multifunctional Mechanical Metamaterials Based on Triply Periodic Minimal Surface Lattices. Adv. Eng. Mater. 2019, 21, 1900524. [Google Scholar] [CrossRef]
- Al-Ketan, O.; Lee, D.W.; Abu Al-Rub, R.K. Mechanical properties of additively-manufactured sheet-based gyroidal stochastic cellular materials. Addit. Manuf. 2021, 48, 102418. [Google Scholar] [CrossRef]
- Al-Ketan, O.; Lee, D.W.; Rowshan, R.; Abu Al-Rub, R.K. Functionally graded and multi-morphology sheet TPMS lattices: Design, manufacturing, and mechanical properties. J. Mech. Behav. Biomed. Mater. 2020, 102, 103520. [Google Scholar] [CrossRef] [PubMed]
- Ejeh, C.J.; Barsoum, I.; Abu Al-Rub, R.K. Flexural properties of functionally graded additively manufactured AlSi10Mg TPMS latticed-beams. Int. J. Mech. Sci. 2022, 223, 107293. [Google Scholar] [CrossRef]
- Bertoldi, K.; Reis, P.M.; Willshaw, S.; Mullin, T. Negative poisson’s ratio behavior induced by an elastic instability. Adv. Mater. 2010, 22, 361–366. [Google Scholar] [CrossRef]
- Xu, J.; Wu, Y.; Wang, L.; Li, J.; Yang, Y.; Tian, Y.; Gong, Z.; Zhang, P.; Nutt, S.; Yin, S. Compressive properties of hollow lattice truss reinforced honeycombs (Honeytubes) by additive manufacturing: Patterning and tube alignment effects. Mater. Des. 2018, 156, 446–457. [Google Scholar] [CrossRef]
- Zhang, Q.; Yang, X.; Li, P.; Huang, G.; Feng, S.; Shen, C.; Han, B.; Zhang, X.; Jin, F.; Xu, F.; et al. Bioinspired engineering of honeycomb structure—Using nature to inspire human innovation. Prog. Mater. Sci. 2015, 74, 332–400. [Google Scholar] [CrossRef]
- Hanzl, P.; Zetková, I.; Daňa, M. A comparison of lattice structures in metal additive manufacturing. In Proceedings of the 28th DAAAM International Symposium on Intelligent Manufacturing and Automation, Zadar, Croatia, 8–11 November 2017; pp. 481–485. [Google Scholar]
- Altamimi, S.; Lee, D.W.; Barsoum, I.; Rowshan, R.; Jasiuk, I.M.; Abu Al-Rub, R.K. On Stiffness, Strength, Anisotropy, and Buckling of 30 Strut-Based Lattices with Cubic Crystal Structures. Adv. Eng. Mater. 2022, 24, 2101379. [Google Scholar] [CrossRef]
- Syam, W.P.; Jianwei, W.; Zhao, B.; Maskery, I.; Elmadih, W.; Leach, R. Design and analysis of strut-based lattice structures for vibration isolation. Precis. Eng. 2018, 52, 494–506. [Google Scholar] [CrossRef]
- Libonati, F.; Graziosi, S.; Ballo, F.; Mognato, M.; Sala, G. 3D-Printed Architected Materials Inspired by Cubic Bravais Lattices. ACS Biomater. Sci. Eng. 2021, 9, 3935–3944. [Google Scholar] [CrossRef]
- Di Caprio, F.; Franchitti, S.; Borrelli, R.; Bellini, C.; Di Cocco, V.; Sorrentino, L. Ti-6Al-4V Octet-Truss Lattice Structures under Bending Load Conditions: Numerical and Experimental Results. Metals 2022, 12, 410. [Google Scholar] [CrossRef]
- Alwattar, T.A.; Mian, A. Developing an equivalent solid material model for bcc lattice cell structures involving vertical and horizontal struts. J. Compos. Sci. 2020, 4, 74. [Google Scholar] [CrossRef]
- Riva, L.; Ginestra, P.S.; Ceretti, E. Mechanical characterization and properties of laser-based powder bed–fused lattice structures: A review. Int. J. Adv. Manuf. Technol. 2021, 113, 649–671. [Google Scholar] [CrossRef]
- Refai, K.; Montemurro, M.; Brugger, C.; Saintier, N. Determination of the effective elastic properties of titanium lattice structures. Mech. Adv. Mater. Struct. 2020, 27, 1966–1982. [Google Scholar] [CrossRef]
- Tancogne-Dejean, T.; Diamantopoulou, M.; Gorji, M.B.; Bonatti, C.; Mohr, D. 3D Plate-Lattices: An Emerging Class of Low-Density Metamaterial Exhibiting Optimal Isotropic Stiffness. Adv. Mater. 2018, 30, e1803334. [Google Scholar] [CrossRef] [PubMed]
- Tancogne-Dejean, T.; Li, X.; Diamantopoulou, M.; Roth, C.C.; Mohr, D. High Strain Rate Response of Additively-Manufactured Plate-Lattices: Experiments and Modeling. J. Dyn. Behav. Mater. 2019, 5, 361–375. [Google Scholar] [CrossRef]
- Andrew, J.J.; Verma, P.; Kumar, S. Impact behavior of nanoengineered, 3D printed plate-lattices. Mater. Des. 2021, 202, 109516. [Google Scholar] [CrossRef]
- Heidenreich, J.N.; Gorji, M.B.; Tancogne-Dejean, T.; Mohr, D. Design of isotropic porous plates for use in hierarchical plate-lattices. Mater. Des. 2021, 212, 110218. [Google Scholar] [CrossRef]
- Viswanath, A.; Khan, K.A.; Barsoum, I. Design of novel isosurface strut-based lattice structures: Effective stiffness, strength, anisotropy and fatigue properties. Mater. Des. 2022, 224, 111293. [Google Scholar] [CrossRef]
- Song, K.; Wang, Z.; Lan, J.; Ma, S. Porous structure design and mechanical behavior analysis based on TPMS for customized root analogue implant. J. Mech. Behav. Biomed. Mater. 2021, 115, 104222. [Google Scholar] [CrossRef] [PubMed]
- Modrek, M.; Viswanath, A.; Khan, K.A.; Ali, M.I.H.; Abu Al-Rub, R.K. An optimization case study to design additively manufacturable porous heat sinks based on triply periodic minimal surface (TPMS) lattices. Case Stud. Therm. Eng. 2022, 36, 102161. [Google Scholar] [CrossRef]
- Baobaid, N.; Ali, M.I.; Khan, K.A.; Abu Al-Rub, R.K. Fluid flow and heat transfer of porous TPMS architected heat sinks in free convection environment. Case Stud. Therm. Eng. 2022, 33, 101944. [Google Scholar] [CrossRef]
- Yoo, D.J.; Kim, K.H. An advanced multi-morphology porous scaffold design method using volumetric distance field and beta growth function. Int. J. Precis. Eng. Manuf. 2015, 16, 2021–2032. [Google Scholar] [CrossRef]
- Groth, J.H.; Anderson, C.; Magnini, M.; Tuck, C.; Clare, A. Five simple tools for stochastic lattice creation. Addit. Manuf. 2022, 49, 102488. [Google Scholar] [CrossRef]
- Yang, N.; Tian, Y.; Zhang, D. Novel real function based method to construct heterogeneous porous scaffolds and additive manufacturing for use in medical engineering. Med. Eng. Phys. 2015, 37, 1037–1046. [Google Scholar] [CrossRef] [PubMed]
- Tan, L.J.; Zhu, W.; Zhou, K. Recent Progress on Polymer Materials for Additive Manufacturing. Adv. Funct. Mater. 2020, 30, 2003062. [Google Scholar] [CrossRef]
- Wang, X.; Jiang, M.; Zhou, Z.; Gou, J.; Hui, D. 3D printing of polymer matrix composites: A review and prospective. Compos. Part B Eng. 2017, 110, 442–458. [Google Scholar] [CrossRef]
- Huang, J.; Qin, Q.; Wang, J. A review of stereolithography: Processes and systems. Processes 2020, 8, 1138. [Google Scholar] [CrossRef]
- Melchels, F.P.W.; Feijen, J.; Grijpma, D.W. A review on stereolithography and its applications in biomedical engineering. Biomaterials 2010, 31, 6121–6130. [Google Scholar] [CrossRef]
- Saha, S.K.; Wang, D.; Nguyen, V.H.; Chang, Y.; Oakdale, J.S.; Chen, S.C. Scalable submicrometer additive manufacturing. Science 2019, 366, 105–109. [Google Scholar] [CrossRef] [PubMed]
- Carroll, B.E.; Palmer, T.A.; Beese, A.M. Anisotropic tensile behavior of Ti-6Al-4V components fabricated with directed energy deposition additive manufacturing. Acta Mater. 2015, 87, 309–320. [Google Scholar] [CrossRef]
- Lee, J.; Kim, H.C.; Choi, J.W.; Lee, I.H. A review on 3D printed smart devices for 4D printing. Int. J. Precis. Eng. Manuf. Green Technol. 2017, 4, 373–383. [Google Scholar] [CrossRef]
- Gibson, I.; Rosen, D.; Stucker, B.; Khorasani, M. Photopolymerization Processes. In Additive Manufacturing Technologies; Springer: Boston, MA, USA, 2021; pp. 78–119. ISBN 978-1-4419-1120-9. [Google Scholar]
- Yang, T.C. Effect of extrusion temperature on the physico-mechanical properties of unidirectional wood fiber-reinforced polylactic acid composite (WFRPC) components using fused depositionmodeling. Polymers 2018, 10, 976. [Google Scholar] [CrossRef]
- Singh, S.; Ramakrishna, S.; Singh, R. Material issues in additive manufacturing: A review. J. Manuf. Process. 2017, 25, 185–200. [Google Scholar] [CrossRef]
- Ziaee, M.; Crane, N.B. Binder jetting: A review of process, materials, and methods. Addit. Manuf. 2019, 28, 781–801. [Google Scholar] [CrossRef]
- Ahmed, N.; Barsoum, I.; Al-Rub, R.K.A. Numerical investigation of residual stresses in thin-walled additively manufactured structures from selective laser melting. Heliyon 2023, 9, e19385. [Google Scholar] [CrossRef]
- Ahmed, N.; Barsoum, I.; Abu Al-Rub, R.K. Numerical Investigation on the Effect of Residual Stresses on the Effective Mechanical Properties of 3D-Printed TPMS Lattices. Metals 2022, 12, 1344. [Google Scholar] [CrossRef]
- Dallago, M.; Winiarski, B.; Zanini, F.; Carmignato, S.; Benedetti, M. On the effect of geometrical imperfections and defects on the fatigue strength of cellular lattice structures additively manufactured via Selective Laser Melting. Int. J. Fatigue 2019, 124, 348–360. [Google Scholar] [CrossRef]
- Holmes, D.W.; Singh, D.; Lamont, R.; Daley, R.; Forrestal, D.P.; Slattery, P.; Pickering, E.; Paxton, N.C.; Powell, S.K.; Woodruff, M.A. Mechanical behaviour of flexible 3D printed gyroid structures as a tuneable replacement for soft padding foam. Addit. Manuf. 2022, 50, 102555. [Google Scholar] [CrossRef]
- Sala, R.; Regondi, S.; Graziosi, S.; Pugliese, R. Insights into the printing parameters and characterization of thermoplastic polyurethane soft triply periodic minimal surface and honeycomb lattices for broadening material extrusion applicability. Addit. Manuf. 2022, 58, 102976. [Google Scholar] [CrossRef]
- Myers, D.; Abdel-Wahab, A.; Hafeez, F.; Kovacev, N.; Essa, K. Optimisation of the additive manufacturing parameters of polylactic acid (PLA) cellular structures for biomedical applications. J. Mech. Behav. Biomed. Mater. 2022, 136, 3967. [Google Scholar] [CrossRef] [PubMed]
- Aziz, A.R.; Zhou, J.; Thorne, D.; Cantwell, W.J. Geometrical scaling effects in the mechanical properties of 3d-printed body-centered cubic (BCC) lattice structures. Polymers 2021, 13, 3967. [Google Scholar] [CrossRef] [PubMed]
- Poddar, P.; Olles, M.; Cormier, D. Mechanical Response of Carbon Composite Octet Truss Structures Produced via Axial Lattice Extrusion. Polymers 2022, 14, 3553. [Google Scholar] [CrossRef]
- Wong, K.V.; Hernandez, A. A Review of Additive Manufacturing. ISRN Mech. Eng. 2012, 2012, 208760. [Google Scholar] [CrossRef]
- Ngo, T.D.; Kashani, A.; Imbalzano, G.; Nguyen, K.T.Q.; Hui, D. Additive manufacturing (3D printing): A review of materials, methods, applications and challenges. Compos. Part B Eng. 2018, 143, 172–196. [Google Scholar] [CrossRef]
- Gao, X.; Qi, S.; Kuang, X.; Su, Y.; Li, J.; Wang, D. Fused filament fabrication of polymer materials: A review of interlayer bond. Addit. Manuf. 2021, 37, 101658. [Google Scholar] [CrossRef]
- Ding, J.; Qu, S.; Zhang, L.; Wang, M.Y.; Song, X. Geometric deviation and compensation for thin-walled shell lattice structures fabricated by high precision laser powder bed fusion. Addit. Manuf. 2022, 58, 116367. [Google Scholar] [CrossRef]
- Yang, L.; Ferrucci, M.; Mertens, R.; Dewulf, W.; Yan, C.; Shi, Y.; Yang, S. An investigation into the effect of gradients on the manufacturing fidelity of triply periodic minimal surface structures with graded density fabricated by selective laser melting. J. Mater. Process. Technol. 2020, 275, 116367. [Google Scholar] [CrossRef]
- Abou-Ali, A.M.; Al-Ketan, O.; Rowshan, R.; Abu Al-Rub, R. Mechanical Response of 3D Printed Bending-Dominated Ligament-Based Triply Periodic Cellular Polymeric Solids. J. Mater. Eng. Perform. 2019, 28, 2316–2326. [Google Scholar] [CrossRef]
- Yang, X.; Yang, Q.; Shi, Y.; Yang, L.; Wu, S.; Yan, C.; Shi, Y. Effect of volume fraction and unit cell size on manufacturability and compressive behaviors of Ni-Ti triply periodic minimal surface lattices. Addit. Manuf. 2022, 54, 102737. [Google Scholar] [CrossRef]
- Huang, D.; Tao, J.; Cheng, M.; Deng, R.; Chen, S.; Yin, L.; Li, R. Comparative evaluation of printability and compression properties of poly-ether-ether-ketone triply periodic minimal surface scaffolds fabricated by laser powder bed fusion. Addit. Manuf. 2022, 57, 102961. [Google Scholar] [CrossRef]
- Li, T.; Jarrar, F.; Abu Al-Rub, R.; Cantwell, W. Additive manufactured semi-plate lattice materials with high stiffness, strength and toughness. Int. J. Solids Struct. 2021, 230–231, 111153. [Google Scholar] [CrossRef]
- Crook, C.; Bauer, J.; Izard, A.G.; de Oliveira, C.S.; de Souza e Silva, J.M.; Berger, J.B.; Valdevit, L. Plate-nanolattices at the theoretical limit of stiffness and strength. Nat. Commun. 2020, 11, 1579. [Google Scholar] [CrossRef] [PubMed]
- Almesmari, A.; Sheikh-ahmad, J.; Jarrar, F.; Bojanampati, S. Optimizing the specific mechanical properties of lattice structures fabricated by material extrusion additive manufacturing. J. Mater. Res. Technol. 2022, 22, 1821–1838. [Google Scholar] [CrossRef]
- Andrew, J.J.; Schneider, J.; Ubaid, J.; Velmurugan, R.; Gupta, N.K.; Kumar, S. Energy absorption characteristics of additively manufactured plate-lattices under low- velocity impact loading. Int. J. Impact Eng. 2021, 149, 103768. [Google Scholar] [CrossRef]
- Ubaid, J.; Schneider, J.; Deshpande, V.S.; Wardle, B.L.; Kumar, S. Multifunctionality of Nanoengineered Self-Sensing Lattices Enabled by Additive Manufacturing. Adv. Eng. Mater. 2022, 24, 2200194. [Google Scholar] [CrossRef]
- Jiang, D.; Ning, F. Physical-mechanical behaviors of stainless steel plate-lattice built by material extrusion additive manufacturing. J. Mater. Process. Technol. 2022, 309, 117739. [Google Scholar] [CrossRef]
- Zhou, B.; Tian, T. A path planning method of lattice structural components for additive manufacturing. Int. J. Adv. Manuf. Technol. 2021, 116, 1467–1490. [Google Scholar] [CrossRef]
- Abdulla, H.; Maalouf, M.; Barsoum, I.; An, H. Truncated Newton Kernel Ridge Regression for Prediction of Porosity in Additive Manufactured SS316L. Appl. Sci. 2022, 12, 4252. [Google Scholar] [CrossRef]
- Hsissou, R.; Seghiri, R.; Benzekri, Z.; Hilali, M.; Ra, M.; Elhar, A. Polymer composite materials: A comprehensive review. Compos. Struct. 2021, 262, 113640. [Google Scholar] [CrossRef]
- Prashanth, S.; Subbaya, K.M.; Nithin, K.; Sachhidananda, S. Fiber Reinforced Composites—A Review. J. Mater. Sci. Eng. 2017, 6, 1000341. [Google Scholar] [CrossRef]
- Günaydın, K.; Rea, C.; Kazancı, Z. Energy absorption enhancement of additively manufactured hexagonal and re-entrant (auxetic) lattice structures by using multi-material reinforcements. Addit. Manuf. 2022, 59, 103076. [Google Scholar] [CrossRef]
- Wang, B.; Ming, Y.; Zhou, J.; Xiao, H.; Wang, F.; Duan, Y.; Kazancı, Z. Fabrication of triangular corrugated structure using 3D printed continuous carbon fiber-reinforced thermosetting epoxy composites. Polym. Test. 2022, 106, 107469. [Google Scholar] [CrossRef]
- Chikkanna, N.; Logakannan, K.P.; Krishnapillai, S.; Ramachandran, V. Quasi-static compression performance of material extrusion enabled re-entrant diamond auxetic metamaterial: Fabrication, tuning the geometrical parameters and fibre reinforcements. Thin-Walled Struct. 2022, 179, 109550. [Google Scholar] [CrossRef]
- Diamantopoulou, M.; Roth, C.C.; Tancogne-Dejean, T.; Lauener, C.M.; Mohr, D. Ceramic/polymer microlattices: Increasing specific energy absorption through sandwich construction. Extrem. Mech. Lett. 2022, 53, 101708. [Google Scholar] [CrossRef]
- Vakifahmetoglu, C.; Zeydanli, D.; Colombo, P. Porous polymer derived ceramics. Mater. Sci. Eng. R Rep. 2016, 106, 1–30. [Google Scholar] [CrossRef]
- Liu, H.; Mei, D.; Yu, S.; Qian, S.; Wang, Y. Direct ink writing of chopped carbon fibers reinforced polymer-derived SiC composites with low shrinkage and high strength. J. Eur. Ceram. Soc. 2023, 43, 235–244. [Google Scholar] [CrossRef]
- Zhao, L.; Wang, X.; Xiong, H.; Zhou, K.; Zhang, D. Optimized preceramic polymer for 3D structured ceramics via fused deposition modeling. J. Eur. Ceram. Soc. 2021, 41, 5066–5074. [Google Scholar] [CrossRef]
- He, J.; Song, M.; Chen, K.; Kan, D.; Zhu, M. Polymer-Derived Ceramics Technology: Characteristics, Procedure, Product Structures, and Properties, and Development of the Technology in High-Entropy Ceramics. Crystals 2022, 12, 1292. [Google Scholar] [CrossRef]
- Chen, I.; Wang, X. Sintering dense nanocrystalline ceramics without final-stage grain growth. Nature 2000, 404, 168–171. [Google Scholar] [CrossRef]
- Chaudhary, R.P.; Parameswaran, C.; Idrees, M.; Rasaki, A.S.; Liu, C.; Chen, Z.; Colombo, P. Additive manufacturing of polymer-derived ceramics: Materials, technologies, properties and potential applications. Prog. Mater. Sci. 2022, 128, 100969. [Google Scholar] [CrossRef]
- Clarkson, C.M.; Wyckoff, C.; Parvulescu, M.J.S.; Rueschhoff, L.M.; Dickerson, M.B. UV-assisted direct ink writing of Si3N4/SiC preceramic polymer suspensions. J. Eur. Ceram. Soc. 2022, 42, 3374–3382. [Google Scholar] [CrossRef]
- Ryan, E.; Yin, S. Compressive strength of β-TCP scaffolds fabricated via lithography-based manufacturing for bone tissue engineering. Ceram. Int. 2022, 48, 15516–15524. [Google Scholar] [CrossRef]
- Su, F.; Su, Z.; Liu, Y.; Lin, X.; Cao, J.; Liu, Z.; Wang, P.; Liu, C.; Chen, Z. Generative shaping and material-forming (GSM) enables structure engineering of complex-shaped Li4SiO4 ceramics based on 3D printing of ceramic/polymer precursors. Addit. Manuf. 2022, 57, 102963. [Google Scholar] [CrossRef]
- Xiong, S.; Liu, J.; Cao, J.; Li, Z.; Idrees, M.; Lin, X.; Long, Z.; Liu, Z.; Wang, P.; Liu, C.; et al. 3D printing of crack-free dense polymer-derived ceramic monoliths and lattice skeletons with improved thickness and mechanical performance. Addit. Manuf. 2022, 57, 102964. [Google Scholar] [CrossRef]
- He, C.; Ma, C.; Li, X.; Yan, L.; Hou, F.; Liu, J.; Guo, A. Polymer-derived SiOC ceramic lattice with thick struts prepared by digital light processing. Addit. Manuf. 2020, 35, 101366. [Google Scholar] [CrossRef]
- Skoratko, A.; Szatkiewicz, T.; Katzer, J.; Jagoda, M. Mechanical properties of mortar beams reinforced by gyroid 3D printed plastic spatial elements. Cem. Concr. Compos. 2022, 134, 14809. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, H.; Gan, Y.; Šavija, B. Cementitious composites reinforced with 3D printed functionally graded polymeric lattice structures: Experiments and modelling. Addit. Manuf. 2021, 39, 101887. [Google Scholar] [CrossRef]
- Salazar, B.; Aghdasi, P.; Williams, I.D.; Ostertag, C.P.; Taylor, H.K. Polymer lattice-reinforcement for enhancing ductility of concrete. Mater. Des. 2020, 196, 109184. [Google Scholar] [CrossRef]
- Qin, S.; Cao, S.; Yilmaz, E.; Li, J. Influence of types and shapes of 3D printed polymeric lattice on ductility performance of cementitious backfill composites. Constr. Build. Mater. 2021, 307, 124973. [Google Scholar] [CrossRef]
- Hao, W.; Liu, J.; Kanwal, H. Compressive properties of cementitious composites reinforced by 3D printed PA 6 lattice. Polym. Test. 2023, 117, 107811. [Google Scholar] [CrossRef]
- Xu, Z.; Ha, C.S.; Kadam, R.; Lindahl, J.; Kim, S.; Wu, H.F.; Kunc, V.; Zheng, X. Additive manufacturing of two-phase lightweight, stiff and high damping carbon fiber reinforced polymer microlattices. Addit. Manuf. 2020, 32, 101106. [Google Scholar] [CrossRef]
- Cui, H.; Hensleigh, R.; Yao, D.; Maurya, D.; Kumar, P.; Kang, M.G.; Priya, S.; Zheng, X.R. Three-dimensional printing of piezoelectric materials with designed anisotropy and directional response. Nat. Mater. 2019, 18, 234–241. [Google Scholar] [CrossRef] [PubMed]
- Luo, W.; Yan, S.; Zhou, J. Ceramic-based dielectric metamaterials. Interdiscip. Mater. 2022, 1, 11–27. [Google Scholar] [CrossRef]
- Yavas, D.; Liu, Q.; Zhang, Z.; Wu, D. Design and fabrication of architected multi-material lattices with tunable stiffness, strength, and energy absorption. Mater. Des. 2022, 217, 110613. [Google Scholar] [CrossRef]
- Prajapati, M.J.; Kumar, A.; Lin, S.C.; Jeng, J.Y. Multi-material additive manufacturing with lightweight closed-cell foam-filled lattice structures for enhanced mechanical and functional properties. Addit. Manuf. 2022, 54, 102766. [Google Scholar] [CrossRef]
- Chen, D.; Zheng, X. Multi-material Additive Manufacturing of Metamaterials with Giant, Tailorable Negative Poisson’s Ratios. Sci. Rep. 2018, 8, 9139. [Google Scholar] [CrossRef]
- Mauldin, T.C.; Kessler, M.R. Self-healing polymers and composites. Int. Mater. Rev. 2010, 55, 317–346. [Google Scholar] [CrossRef]
- Huang, W.; Zhang, J.; Singh, V.; Xu, L.; Kabi, P.; Bele, E.; Tiwari, M.K. Digital light 3D printing of a polymer composite featuring robustness, self-healing, recyclability and tailorable mechanical properties. Addit. Manuf. 2023, 61, 103343. [Google Scholar] [CrossRef]
- Callens, S.J.P.; Arns, C.H.; Kuliesh, A.; Zadpoor, A.A. Decoupling Minimal Surface Metamaterial Properties Through Multi-Material Hyperbolic Tilings. Adv. Funct. Mater. 2021, 31, 2101373. [Google Scholar] [CrossRef]
- Essmeister, J.; Altun, A.A.; Staudacher, M.; Lube, T.; Schwentenwein, M.; Konegger, T. Stereolithography-based additive manufacturing of polymer-derived SiOC/SiC ceramic composites. J. Eur. Ceram. Soc. 2022, 42, 5343–5354. [Google Scholar] [CrossRef]
- Verma, S.; Kuma, A.; Lin, S.-C.; Jeng, J.-Y. CFD and Strength Analysis of Novel Biomimetic Lattice Structure Designed for Additive Manufacturing and Post-processing. Mater. Des. 2022, 224, 111375. [Google Scholar] [CrossRef]
- Afshar, M.; Anaraki, A.P.; Montazerian, H.; Kadkhodapour, J. Additive manufacturing and mechanical characterization of graded porosity scaffolds designed based on triply periodic minimal surface architectures. J. Mech. Behav. Biomed. Mater. 2016, 62, 481–494. [Google Scholar] [CrossRef]
- Dalaq, A.S.; Abueidda, D.W.; Al-Rub, R.K.A. Mechanical properties of 3D printed interpenetrating phase composites with novel architectured 3D solid-sheet reinforcements. Compos. Part A Appl. Sci. Manuf. 2016, 84, 266–280. [Google Scholar] [CrossRef]
- Abueidda, D.W.; Bakir, M.; Al-Rub, R.K.A.; Bergström, J.S.; Sobh, N.A.; Jasiuk, I. Mechanical properties of 3D printed polymeric cellular materials with triply periodic minimal surface architectures. Mater. Des. 2017, 122, 255–267. [Google Scholar] [CrossRef]
- Al-Ketan, O.; Rezgui, R.; Rowshan, R.; Du, H.; Fang, N.X.; Al-Rub, R.K.A. Microarchitected Stretching-Dominated Mechanical Metamaterials with Minimal Surface Topologies. Adv. Eng. Mater. 2018, 20, 1800029. [Google Scholar] [CrossRef]
- Abueidda, D.W.; Elhebeary, M.; Shiang, C.S.A.; Pang, S.; Abu Al-Rub, R.K.; Jasiuk, I.M. Mechanical properties of 3D printed polymeric Gyroid cellular structures: Experimental and finite element study. Mater. Des. 2019, 165, 107597. [Google Scholar] [CrossRef]
- Zhang, C.; Jiang, Z.; Zhao, L.; Guo, W.; Jiang, Z.; Li, X.; Chen, G. Mechanical characteristics and deformation mechanism of functionally graded triply periodic minimal surface structures fabricated using stereolithography. Int. J. Mech. Sci. 2021, 208, 106679. [Google Scholar] [CrossRef]
- Fu, J.; Taher, S.E.; Al-Rub, R.K.A.; Zhang, T.; Chan, V.; Liao, K. Engineering 3D-Architected Gyroid MXene Scaffolds for Ultrasensitive Micromechanical Sensing. Adv. Eng. Mater. 2022, 24, 2101388. [Google Scholar] [CrossRef]
- Arruda, E.M.; Boyce, M.C.; Jayachandran, R. Effects of strain rate, temperature and thermomechanical coupling on the finite strain deformation of glassy polymers. Mech. Mater. 1995, 19, 193–212. [Google Scholar] [CrossRef]
- Arruda, E.M.; Boyce, M.C. Evolution of plastic anisotropy in amorphous polymers during finite straining. Int. J. Plast. 1993, 9, 697–720. [Google Scholar] [CrossRef]
- Bergström, J. PolyUMod User’s Manual. Veryst Eng. LLC 2009, 1, 7. [Google Scholar]
- Almomani, A.; Deveci, S.; Mourad, A.H.I.; Barsoum, I. Constitutive model calibration for the thermal viscoelastic-viscoplastic behavior of high density polyethylene under monotonic and cyclic loading. Polym. Test. 2023, 118, 107911. [Google Scholar] [CrossRef]
- Shahin, A.; Barsoum, I.; Islam, M.D. Constitutive model calibration of the time and temperature-dependent behavior of high density polyethylene. Polym. Test. 2020, 91, 106800. [Google Scholar] [CrossRef]
- Stratasys PolyJet Materials 2023. Available online: https://www.stratasys.com/en/materials/materials-catalog/polyjet-materials/?filter=MT_PolyJet (accessed on 31 January 2023).
- Paczos, P.; Wichniarek, R.; Magnucki, K. Three-point bending of sandwich beam with special structure of the core. Compos. Struct. 2018, 201, 676–682. [Google Scholar] [CrossRef]
- Truszkiewicz, E.; Thalhamer, A.; Rossegger, M.; Vetter, M.; Meier, G.; Rossegger, E.; Fuchs, P.; Schlögl, S.; Berer, M. Mechanical behavior of 3D-printed polymeric metamaterials for lightweight applications. J. Appl. Polym. Sci. 2022, 139, 51618. [Google Scholar] [CrossRef]
- Kochumalayil, J.J.; Berglund, L.A. “Brick-and-Mortar” Composites of Platelet-Reinforced Polymers. In Encyclopedia of Polymeric Nanomaterials; Kobayashi, S., Müllen, K., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 1–8. ISBN 978-3-642-36199-9. [Google Scholar]
- Han, J.; Zhao, D.; Li, D.; Wang, X.; Jin, Z.; Zhao, K. Polymer-based nanomaterials and applications for vaccines and drugs. Polymers 2018, 10, 31. [Google Scholar] [CrossRef]
- Sahu, A.; Dosi, R.; Kwiatkowski, C.; Schmal, S.; Poler, J.C. Advanced Polymeric Nanocomposite Membranes for Water and Wastewater Treatment: A Comprehensive Review. Polymers 2023, 15, 540. [Google Scholar] [CrossRef]
- Díez-Pascual, A.M.; Cruz, D.L.; Redondo, A.L. Advanced Carbon-Based Polymeric Nanocomposites for Forensic Analysis. Polymers 2022, 14, 3598. [Google Scholar] [CrossRef] [PubMed]
- Díaz-Puertas, R.; Álvarez-Martínez, F.J.; Falco, A.; Barrajón-Catalán, E.; Mallavia, R. Phytochemical-Based Nanomaterials against Antibiotic-Resistant Bacteria: An Updated Review. Polymers 2023, 15, 1392. [Google Scholar] [CrossRef]
- de Castro, B.D.; de Castro Magalhães, F.; Panzera, T.H.; Rubio, J.C.C. An Assessment of Fully Integrated Polymer Sandwich Structures Designed by Additive Manufacturing. J. Mater. Eng. Perform. 2021, 30, 5031–5038. [Google Scholar] [CrossRef]
- Li, T.; Wang, L. Bending behavior of sandwich composite structures with tunable 3D-printed core materials. Compos. Struct. 2017, 175, 46–57. [Google Scholar] [CrossRef]
- Silva, C.; Pais, A.I.; Caldas, G.; Gouveia, B.P.P.A.; Alves, J.L.; Belinha, J. Study on 3D printing of gyroid-based structures for superior structural behaviour. Prog. Addit. Manuf. 2021, 6, 689–703. [Google Scholar] [CrossRef]
- Xiang, X.; Qiang, W.; Hou, B.; Tran, P.; Lu, G. Quasi-static and dynamic mechanical properties of Miura-ori metamaterials. Thin-Walled Struct. 2020, 157, 106993. [Google Scholar] [CrossRef]
- Baghous, N.; Barsoum, I.; Abu Al-Rub, R.K. The effect of Lode parameter on the yield surface of Schoen’s IWP triply periodic minimal surface lattice. Mech. Mater. 2022, 175, 104473. [Google Scholar] [CrossRef]
- Baghous, N.; Barsoum, I.; Abu Al-Rub, R.K. Generalized yield surface for sheet-based triply periodic minimal surface lattices. Int. J. Mech. Sci. 2023, 252, 108370. [Google Scholar] [CrossRef]

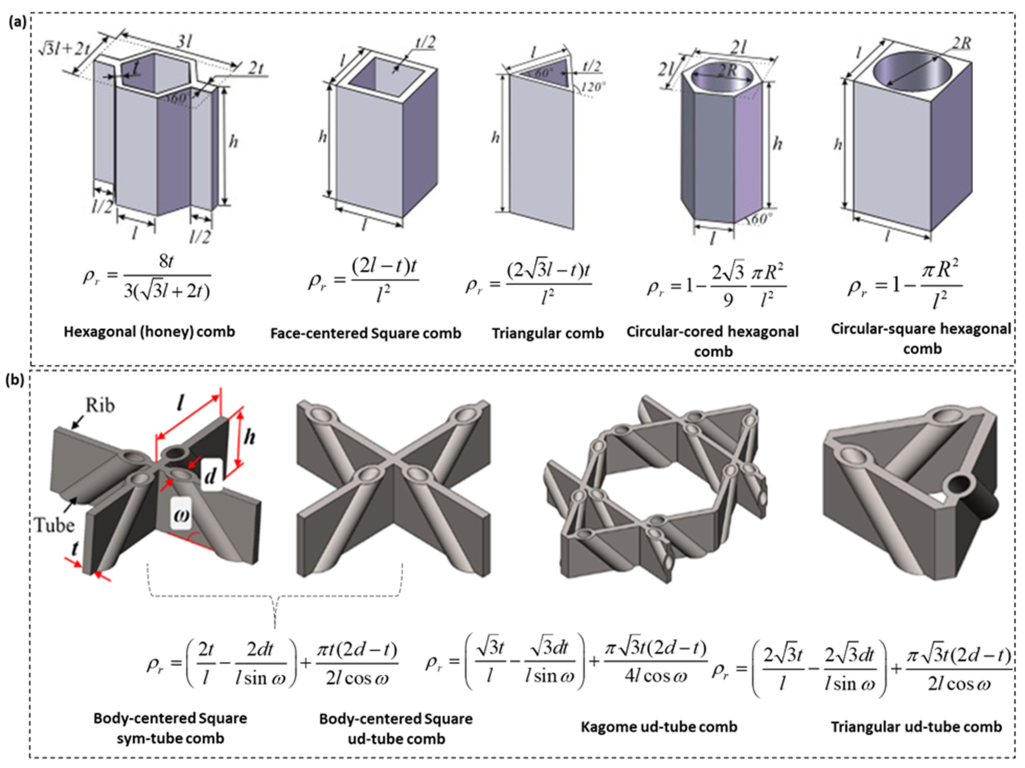


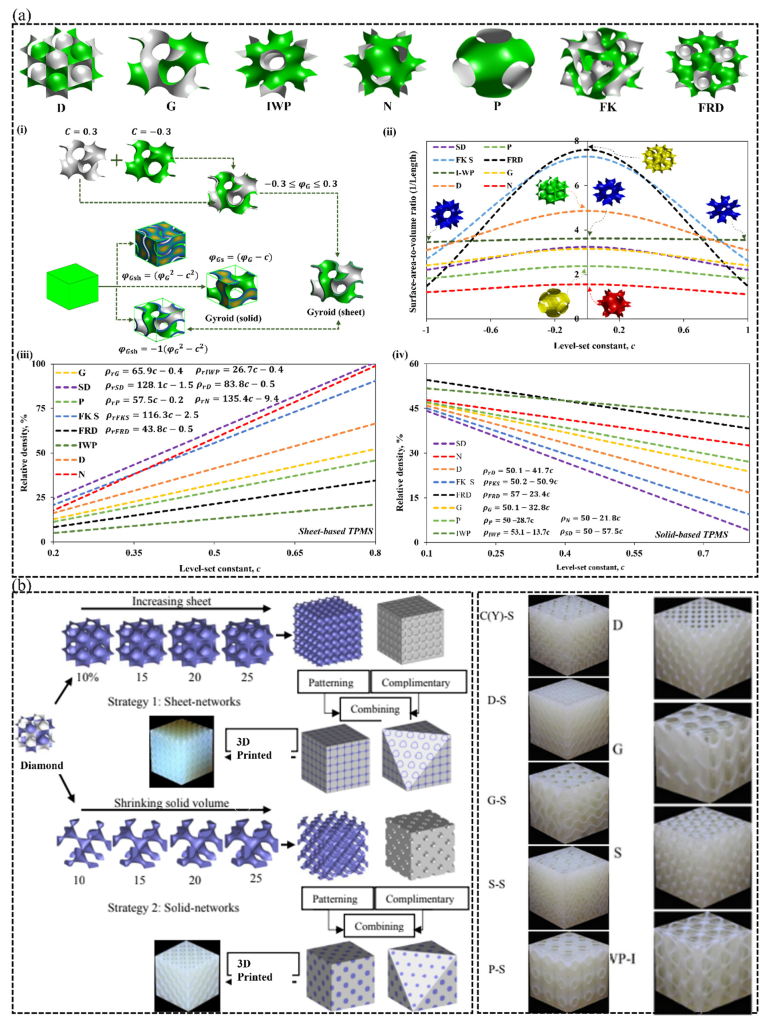

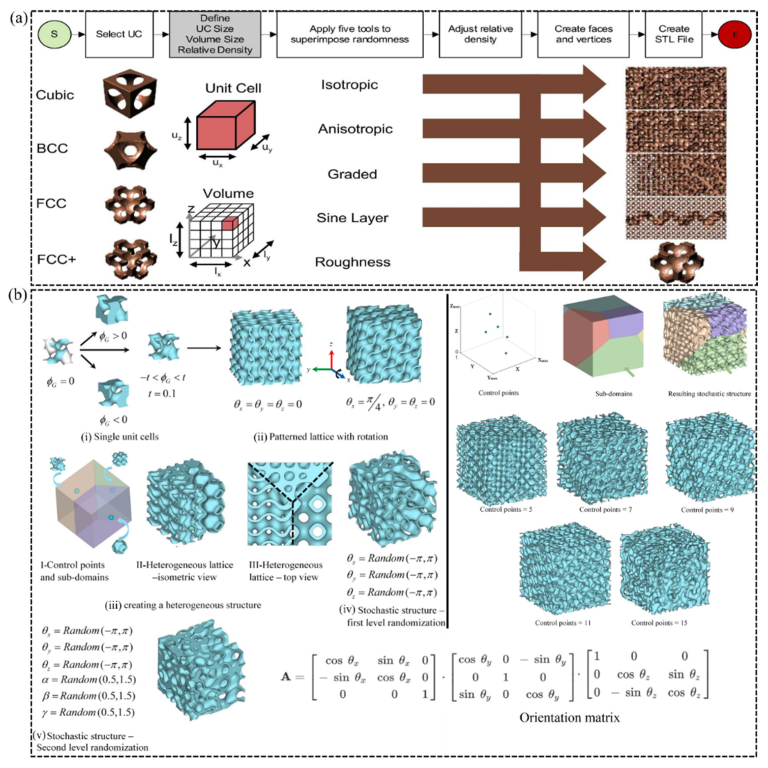
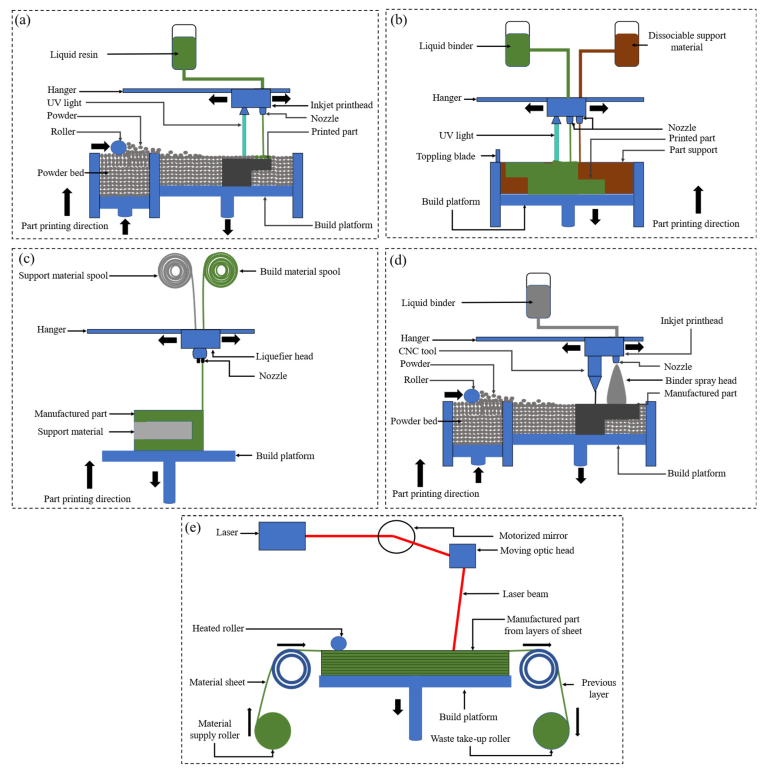

| Study | Application | Lattice Material Topology | Base Material | Physical Property |
|---|---|---|---|---|
| Papetti et al. [7] | Automotive | Kelvin, cubic, octet lattices | Ceramic (Al2O3) | Mass transfer properties |
| Yin et al. [8] | Pyramidal structure | Fiber reinforced composites | Impact mitigation | |
| Xiong et al. [12] | Dentistry | Porous scaffold | Ti-6Al-4V alloy | Fatigue behavior and osteointegration |
| Cosma et al. [16] | Body-centered cubic and circle intersections | 316L stainless steel | Mechanical strength | |
| Oladapo et al. [17] | Cubic-octahedron and Gyroid | Polyether ether ketone (PEEK) and calcium hydroxyapatite composite (cHAP) | Elastic moduli | |
| Oladapo et al. [10] | Bone implant | Cubic-octahedron and Gyroid | PEEK-cHAP, PEEK-reduced graphene oxide | Biocompatibility |
| Reyes et al. [11] | Modified honeycomb | Polycaprolactone | Mechanical strength and stiffness | |
| Li et al. [13] | Spacecraft systems | Pyramidal truss | Carbon fiber-reinforced polymer | Thermal expansion, compression and shear behavior |
| Study | AM Technique | Fabrication Challenge | Fabrication Solution |
|---|---|---|---|
| He et al. [100] | DLP | Strut deformation of polymer-derived ceramic metamaterials during the pyrolysis process | Introduction of 20 wt.% hydroxyl silicone oil prevented the deformation of struts with 0.5 mm thickness |
| Zhao et al. [92] | FDM | Polymeric metamaterials with high ceramic yield are so brittle to be fabricated using FDM | Improving the formability and printability of polycarbosilane using ≤5 wt.% of polypropylene |
| Chen et al. [111] | Micro-SLA | Cross-contamination between two different feedstocks during multi-material additive manufacturing | Integrating a self-cleansing robotic dispenser into the 3D printer for cleaning residue monomer at each layer before a new feedstock is perfused |
| Wang et al. [87] | FDM | Bond and joint failure between a corrugated core and face sheet panels in corrugated structures | Fabricating the structures using single-stroke integrated manufacturing for strengthening the connection between the core and the face sheet panels |
| Shape retention problem during post curing procedure | Utilization of liquid deposition modeling to deposit silicon rubber between the gaps of the unit cells | ||
| Clarkson et al. [96] | DIW | Limited number of commercial printing inks with certain viscosity constrains and shear-thinning requirement | Modifying the conventional DIW procedure to expand the range of printable materials through including UV-assisted reactants in the slurry |
| Essmeister et al. [115] | SLA | Cracks appearing when printing millimeter scale lattice structures made of SiOC PDC | Incorporating SiC particulates within SiOC matrix to produce crack-free millimeter scale features |
| Verma et al. [116] | MJF | Powder entrapment zones in plate/shell-based lattice metamaterials | Introducing a honeycomb shaped structure with ventilated holes to eliminate power entrapment |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almesmari, A.; Baghous, N.; Ejeh, C.J.; Barsoum, I.; Abu Al-Rub, R.K. Review of Additively Manufactured Polymeric Metamaterials: Design, Fabrication, Testing and Modeling. Polymers 2023, 15, 3858. https://doi.org/10.3390/polym15193858
Almesmari A, Baghous N, Ejeh CJ, Barsoum I, Abu Al-Rub RK. Review of Additively Manufactured Polymeric Metamaterials: Design, Fabrication, Testing and Modeling. Polymers. 2023; 15(19):3858. https://doi.org/10.3390/polym15193858
Chicago/Turabian StyleAlmesmari, Abdulla, Nareg Baghous, Chukwugozie J. Ejeh, Imad Barsoum, and Rashid K. Abu Al-Rub. 2023. "Review of Additively Manufactured Polymeric Metamaterials: Design, Fabrication, Testing and Modeling" Polymers 15, no. 19: 3858. https://doi.org/10.3390/polym15193858
APA StyleAlmesmari, A., Baghous, N., Ejeh, C. J., Barsoum, I., & Abu Al-Rub, R. K. (2023). Review of Additively Manufactured Polymeric Metamaterials: Design, Fabrication, Testing and Modeling. Polymers, 15(19), 3858. https://doi.org/10.3390/polym15193858