Polyelectrolyte Cylindrical Brushes in Hairy Gels
Abstract
:1. Introduction
2. Results and Discussion
2.1. Model of the PE Cylindrical Brush
2.2. PE Cylindrical Brush with Uncharged Backbone in Salt-Free Solution
2.3. PE Cylindrical Brush with Uncharged Backbone in Salt-Added Solution
2.4. Globular State of the Cylindrical PE Brush
2.5. Effect of the Backbone Charge Density
2.6. Comparison to Experiments
3. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Sheiko, S.S.; Sumerlin, B.S.; Matyjaszewski, K. Cylindrical molecular brushes: Synthesis, characterization and properties. Prog. Polym. Sci. 2008, 33, 759–785. [Google Scholar] [CrossRef]
- Verduzco, R.; Li, X.; Pesek, S.L.; Stein, G.E. Structure, function, self-assembly of bottlebrush copolymers. Chem. Soc. Rev. 2015, 44, 2405–2420. [Google Scholar] [CrossRef] [Green Version]
- Rzayev, J. Molecular Bottlebrushes: New Opportunities in Nanomaterials Fabrication. ACS Macro Lett. 2012, 1, 1146–1149. [Google Scholar] [CrossRef]
- Liang, H.; Sheiko, S.S.; Dobrynin, A.V. Supersoft Polymer Networks with Brushlike Strands. Macromolecules 2018, 51, 638–645. [Google Scholar] [CrossRef]
- Nian, S.; Lian, H.; Gong, Z.; Zhernenkov, M.; Qin, J.; Cai, L.-H. Molecular Architecture Directs Linear-Bottlebrush-Linear Triblock Copolymers to Self-Assemble to Soft Reprocessable Elastomers. ACS Macro Lett. 2019, 8, 1528–1534. [Google Scholar] [CrossRef] [PubMed]
- Yuan, J.; Müller, A.H.E.; Matyjaszewski, K.; Sheiko, S. Polymer Science: A Comprehensive Reference; Matyjaszewski, K., Möller, M., Eds.; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Xie, G.; Martinez, M.R.; Olszewski, M.; Sheiko, S.S.; Matyjaszewski, K. Molecular Bottlebrushes as Novel Materials. Biomacromolecules 2019, 20, 27–54. [Google Scholar] [CrossRef] [PubMed]
- Vatankhah-Varnosfaderani, M.; Keith, A.N.; Cong, Y.; Liang, H.; Rosenthal, M.; Sztucki, M.; Clair, C.; Magonov, S.; Ivanov, D.A.; Dobrynin, A.V.; et al. Chameleon-like elastomers with molecularly encoded strain-adaptive stiffening and coloration. Science 2018, 359, 1509–1513. [Google Scholar] [CrossRef] [Green Version]
- Sheiko, S.S.; Dobrynin, A.V. Architectural Code for Rubber Elasticity: From Supersoft to Superfirm Materials. Macromolecules 2019, 52, 7531–7546. [Google Scholar] [CrossRef] [Green Version]
- Liberman-Martin, A.L.; Chu, C.K.; Grubbs, R.H. Application of Bottlebrush Block Copolymers as Photonic Crystals. Macromol. Rapid. Comm. 2017, 38, 1700058. [Google Scholar] [CrossRef] [Green Version]
- Song, D.P.; Zhao, T.H.; Guidetti, G.; Vignolini, S.; Parker, R.M. Hierarchical Photonic Pigments via the Confined Self-Assembly of Bottlebrush Block Copolymers. ACS Nano 2019, 13, 1764–1771. [Google Scholar] [CrossRef] [Green Version]
- Zhulina, E.B.; Sheiko, S.S.; Borisov, O.V. Solution and Melts of Barbwire Bottlebrushes: Hierarchical Structure and Scale-Dependent Elasticity. Macromolecules 2019, 52, 1671–1684. [Google Scholar] [CrossRef]
- Feuz, L.; Leermakers, F.A.M.; Textor, M.; Borisov, O. Bending rigidity and induced persistence length of molecular bottle brushes: A self-consistent-field theory. Macromolecules 2005, 38, 8891–8901. [Google Scholar] [CrossRef]
- Ma, X.; Yang, Y.Z.; Zhu, L.; Zhao, B.; Tang, P.; Qiu, F. Binary mixed homopolymer brushes grafted on nanorod particles: A self-consistent field theory study. J. Chem. Phys. 2013, 139, 214902. [Google Scholar] [CrossRef] [PubMed]
- Saariaho, M.; Ikkala, O.; Szleifer, I.; Erukhimovich, I.; ten Brinke, G. On lyotropic behavior of molecular bottle-brushes: A Monte Carlo computer simulation study. J. Chem. Phys. 1997, 107, 3267–3276. [Google Scholar] [CrossRef]
- Saariaho, M.; Szleifer, I.; Ikkala, O.; ten Brinke, G. Extended conformations of isolated molecular bottle-brushes: Influence of side-chain topology. Macromol. Theor. Simul. 1998, 7, 211–216. [Google Scholar] [CrossRef]
- Subbotin, A.; Saariaho, M.; Ikkala, O.; ten Brinke, G. Elasticity of comb copolymer cylindrical brushes. Macromolecules 2000, 33, 3447–3452. [Google Scholar] [CrossRef] [Green Version]
- Elli, S.; Ganazzoli, F.; Timoshenko, E.G.; Kuznetsov, Y.A.; Connolly, R. Size and persistence length of molecular bottle-brushes by Monte Carlo simulations. J. Chem. Phys. 2004, 120, 6257–6267. [Google Scholar] [CrossRef]
- Theodorakis, P.E.; Hsu, H.-P.; Paul, W.; Binder, K. Computer simulation of bottle-brush polymers with flexible backbone: Good solvent versus theta solvent conditions. J. Chem. Phys. 2011, 135, 164903. [Google Scholar] [CrossRef] [Green Version]
- Cao, Z.; Carrillo, J.-M.Y.; Sheiko, S.S.; Dobrynin, A.V. Computer Simulations of Bottle Brushes: From Melts to Soft Networks. Macromolecules 2015, 48, 5006–5015. [Google Scholar] [CrossRef]
- Hsu, H.-P.; Paul, W.; Rathgeber, S.; Binder, K. Characteristic Length Scales and Radial Monomer Density Profiles of Molecular Bottle-Brushes: Simulation and Experiment. Macromolecules 2010, 43, 1592–1601. [Google Scholar] [CrossRef]
- Hsu, H.-P.; Paul, W.; Binder, K. Standard Definitions of Persistence Length Do Not Describe the Local“Intrinsic” Stiffness of Real Polymer Chains. Macromolecules 2010, 43, 3094–3102. [Google Scholar] [CrossRef]
- Zhulina, E.B.; Sheiko, S.S.; Borisov, O.V. Polymer Networks Formed by Molecular Brushes: Scaling Theory. Polym. Sci. A 2019, 61, 799–804. [Google Scholar] [CrossRef]
- Zhulina, E.B.; Borisov, O.V. Bottlebrush polymer gels: Architectural control over swelling and osmotic bulk modulus. Soft Matter 2022, 18, 1239–1246. [Google Scholar] [CrossRef] [PubMed]
- Vashahi, F.; Martinez, M.R.; Dashtimoghadam, E.; Fahimpour, F.; Keith, A.N.; Bersenev, E.A.; Ivanov, D.A.; Zhulina, E.B.; Matyjaszewski, K.; Vatankhah-Varnosfaderani, M.; et al. Injectable hydrogels with tissue-adaptive gelation and mechanical properties. Sci. Adv. 2022, 8, eabm2469. [Google Scholar] [CrossRef] [PubMed]
- Uhlik, F.; Rud, O.V.; Borisov, O.V.; Zhulina, E.B. Hairy gels: A computational study. Gels 2022, 8, 793. [Google Scholar] [CrossRef]
- Mohammadi, E.; Joshi, S.Y.; Deshmukh, S.A. A review of computational studies of bottlebrush polymers. Comput. Mater. Sci. 2021, 199, 110720. [Google Scholar] [CrossRef]
- Qu, L.J.; Jin, X.G.; Liao, Q. Numerical self-consistent field theory of cylindrical polyelectrolyte brushes. Macromol. Theor. Simul. 2009, 18, 162–170. [Google Scholar] [CrossRef]
- Hao, Q.-H.; Chen, Q.; Zheng, Z.; Liu, L.-Y.; Liu, T.-J.; Niu, X.-H.; Song, Q.-G.; Tan, H.-G. Molecular dynamics simulations of cylindrical polyelectrolyte brushes in monovalent and multivalent salt solutions. J. Theor. Comput. Chem. 2016, 15, 1650026. [Google Scholar] [CrossRef]
- Prokacheva, V.M.; Rud, O.V.; Uhlık, F.; Borisov, O.V. Intramolecular micellization and nanopatterning in pH- and thermo-responsive molecular brushes. Soft Matter 2019, 16, 208–218. [Google Scholar] [CrossRef]
- Yan, L.T.; Guo, R.H. Effects of multivalent counterions on the morphology and interactions of carbon nanotubes grafted with polyelectrolyte chains. Soft Matter 2012, 8, 660–666. [Google Scholar] [CrossRef]
- Mehra, N.K.; Mishra, V.; Jain, N.K. A review of ligand tethered surface engineered carbon nanotubes. Biomaterials 2014, 35, 1267–1283. [Google Scholar] [CrossRef]
- Majoinen, J.; Walther, A.; McKee, J.R.; Kontturi, E.; Aseyev, V.; Malho, J.M.; Ruokolainen, J.; Ikkala, O. Polyelectrolyte Brushes Grafted from Cellulose Nanocrystals Using Cu-Mediated Surface-Initiated Controlled Radical Polymerization. Biomacromolecules 2011, 12, 2997–3006. [Google Scholar] [CrossRef]
- Lettow, J.H.; Kaplan, R.Y.; Nealey, P.F.; Rowan, S.J. Enhanced Ion Conductivity through Hydrated, Polyelectrolyte-Grafted Cellulose Nanocrystal Films. Macromolecules 2021, 54, 6925–6936. [Google Scholar] [CrossRef]
- Tao, H.; Chen, L.; Galati, E.; Manion, J.G.; Seferos, D.S.; Zhulina, E.B.; Kumacheva, E. Helicoidal patterning of gold nanorods by phase separation in mixed polymer brushes. Langmuir 2019, 35, 15872–15879. [Google Scholar] [CrossRef]
- Galati, E.; Tao, H.; Tebbe, M.; Ansari, R.; Rubinstein, M.; Zhulina, E.B.; Kumacheva, E. Helicoidal Patterning of Nanorods with Polymer Ligands. Angew. Chem. Int. Ed. 2019, 58, 3123–3127. [Google Scholar] [CrossRef]
- Pincus, P.A. Colloid stabilization with grafted polyelectrolytes. Macromolecules 1991, 24, 2912–2919. [Google Scholar] [CrossRef]
- Ross, R.; Pincus, P.A. The polyelectrolyte brush: Poor solvent. Macromolecules 1992, 25, 2177–2183. [Google Scholar] [CrossRef]
- Borisov, O.V.; Birshtein, T.M.; Zhulina, E.B. Collapse of Grafted Polyelectrolyte Layer. J. Phys. II 1991, 1, 521–526. [Google Scholar] [CrossRef]
- Borisov, O.V.; Zhulina, E.B.; Birshtein, T.M. Diagram of States of Grafted Polyelectrolyte Layer. Macromolecules 1994, 27, 4795–4803. [Google Scholar] [CrossRef]
- Zhulina, E.B.; Borisov, O.V. Polyelectrolytes Grafted to Curved Surfaces. Macromolecules 1996, 29, 2618–2626. [Google Scholar] [CrossRef]
- Guenoun, P. Polyelectrolyte Brushes: Twenty Years after. In Functional Polymer Films; Knoll, W., Advincula, R.C., Eds.; Wiley: Hoboken, NJ, USA, 2012; Chapter 6; pp. 219–237. [Google Scholar]
- Bohinc, K.; Bossa, G.V.; May, S. Incorporation of ion and solvent structure into mean-field modeling of the electric double layer. Adv. Colloid Interface Sci. 2017, 249, 220–233. [Google Scholar] [CrossRef]
- Misra, S.; Mattice, W.L.; Napper, D.H. Structure of Polyelectrolyte Stars and Convex Polyelectrolyte Brushes. Macromolecules 1994, 27, 7090–7098. [Google Scholar] [CrossRef]
- Csajka, F.S.; Netz, R.R.; Seidel, C.; Joanny, J.F. Collapse of polyelectrolyte brushes: Scaling theory and simulations. Eur. Phys. J. E 2001, 4, 505–513. [Google Scholar] [CrossRef]
- Dobrynin, A.V.; Rubinstein, M. Theory of polyelectrolytes in solutions and at surfaces. Prog. Polym. Sci. 2005, 30, 1049–1118. [Google Scholar] [CrossRef]
- Zhulina, E.B.; Rubinstein, M. Ionic Strength Dependence of Polyelectrolyte Brush Thickness. Soft Matter 2012, 8, 9376–9383. [Google Scholar] [CrossRef] [Green Version]
- Miklavic, S.J.; Marcelia, S. Interaction of surfaces carrying grafted polyelectrolytes. J. Phys. Chem. 1988, 92, 6718–6722. [Google Scholar] [CrossRef]
- Misra, S.; Varanasi, S.; Varanasi, P.P. A polyelectrolyte brush theory. Macromolecules 1989, 22, 4173–4179. [Google Scholar] [CrossRef]
- Zhulina, E.B.; Borisov, O.V. Structure and interaction of weakly charged polyelectrolyte brushes: Self-consistent field theory. J. Chem. Phys. 1997, 107, 5952–5967. [Google Scholar] [CrossRef]
- Israels, R.; Leermakers, F.A.M.; Fleer, G.J. On the Theory of Grafted Weak Polyacids. Macromolecules 1994, 27, 3087–3093. [Google Scholar] [CrossRef]
- Seki, H.; Suzuki, Y.Y.; Orland, H. Self-Consistent Field Study of Polyelectrolyte Brushes. J. Phys. Soc. Jpn. 2007, 76, 104601. [Google Scholar] [CrossRef] [Green Version]
- Csajka, F.S.; Seidel, C. Strongly Charged Polyelectrolyte Brushes: A Molecular Dynamics Study. Macromolecules 2000, 33, 2728–2739. [Google Scholar] [CrossRef]
- Sandberg, D.J.; Carrillo, J.-M.Y.; Dobrynin, A.V. Molecular Dynamics Simulations of Polyelectrolyte Brushes: From Single Chains to Bundles of Chains. Langmuir 2007, 23, 12716–12728. [Google Scholar] [CrossRef] [PubMed]
- Yan, L.-T.; Xu, Y.; Ballauff, M.; Müller, A.H.E.; Böker, A. Influence of Counterion Valency on the Conformational Behavior of Cylindrical Polyelectrolyte Brushes. J. Phys. B 2009, 113, 5104–5110. [Google Scholar] [CrossRef]
- Yan, L.-T.; Zhang, X. Dissipative Particle Dynamics Simulations of Complexes Comprised of Cylindrical Polyelectrolyte Brushes and Oppositely Charged Linear Polyelectrolytes. Langmuir 2009, 25, 3808–3813. [Google Scholar] [CrossRef] [PubMed]
- Hao, Q.H.; Liu, L.X.; Xia, G.; Liu, L.Y.; Miao, B. The effects of grafting density and charge fraction on the properties of ring polyelectrolyte brushes: A molecular dynamics simulation study. Colloid Polym. Sci. 2020, 298, 21–33. [Google Scholar] [CrossRef]
- Borisov, O.V.; Zhulina, E.B. Conformations of polyelectrolyte molecular brushes: A mean-filed theory. J. Chem. Phys. 2018, 149, 184904. [Google Scholar] [CrossRef]
- Tang, Q.; Rubinstein, M. Where in the world are condensed counterions? Soft Matter 2022, 18, 1154–1173. [Google Scholar] [CrossRef]
- Borisov, O.V.; Zhulina, E.B. Structure of Weakly Charged Polyelectrolyte Brushes: Monomer Density Profiles. J. Phys. II 1997, 7, 449–458. [Google Scholar] [CrossRef] [Green Version]
- Williams, D.R.M. Grafted polymers in bad solvents: Octopus surface micelles. J. Phys. II 1993, 3, 1313–1318. [Google Scholar] [CrossRef] [Green Version]
- Sheiko, S.S.; Borisov, O.V.; Prokhorova, S.A.; Moller, M. Cylindrical molecular brushes under poor solvent conditions: Microscopic observation and scaling analysis. Eur. Phys. J. E 2004, 13, 125–131. [Google Scholar] [CrossRef]
- Risteen, B.; Delepierre, G.; Srinivasarao, M.; Weder, C.; Russo, P.; Reichmanis, E.; Zoppe, J. Thermoresponsive Liquid Crystals: Thermally Switchable Liquid Crystals Based on Cellulose Nanocrystals with Patchy Polymer Grafts. Small 2018, 14, 1870218. [Google Scholar] [CrossRef]
- Zhulina, E.B.; Borisov, O.V. Absorption of a Polyelectrolyte Brush into an Oppositely Charged Layer. Macromolecules 1998, 31, 7413–7422. [Google Scholar] [CrossRef]
- Rubinstein, M.; Liao, Q.; Panyukov, S. Structure of Liquid Coacervates Formed by Oppositely Charged Polyelectrolytes. Macromolecules 2018, 51, 9572–9588. [Google Scholar] [CrossRef]
- Zhang, Z.; Sèbe, G.; Hou, Y.; Wang, J.; Huang, J.; Zhou, G. Grafting polymers from cellulose nanocrystals via surface-initiated atom transfer radical polymerization. J. Appl. Polym. Sci. 2021, 138, e51458. [Google Scholar] [CrossRef]
- Hemraz, U.D.; Lu, A.; Sunasee, R.; Boluk, Y. Structure of poly(N-isopropylacrylamide) brushes and steric stability of their grafted cellulose nanocrystal dispersions. J. Coll. Int. Sci. 2014, 430, 157–165. [Google Scholar] [CrossRef]
- Akhlaghi, N.G.S.P.; Yao, Z.; Berry, R.; Tam, K.C. Cellulose nanocrystal-poly(oligo(ethylene glycol) methacrylate)brushes with tunable LCSTs. Carbohydr. Polym. 2016, 144, 215–222. [Google Scholar]
- Zhang, X.; Zhang, J.; Dong, L.; Ren, S.; Wu, Q.; Lei, T. Thermoresponsive poly(poly(ethylene glycol) methylacrylate)s grafted cellulose nanocrystals through SI-ATRP polymerization. Cellulose 2017, 24, 4189–4203. [Google Scholar] [CrossRef]
- Kan, K.H.M.; Li, J.; Wijesekera, K.; Cranston, E.D. Polymer-Grafted Cellulose Nanocrystals as pH-Responsive Reversible Flocculants. Biomacromolecules 2013, 14, 3130–3139. [Google Scholar] [CrossRef]
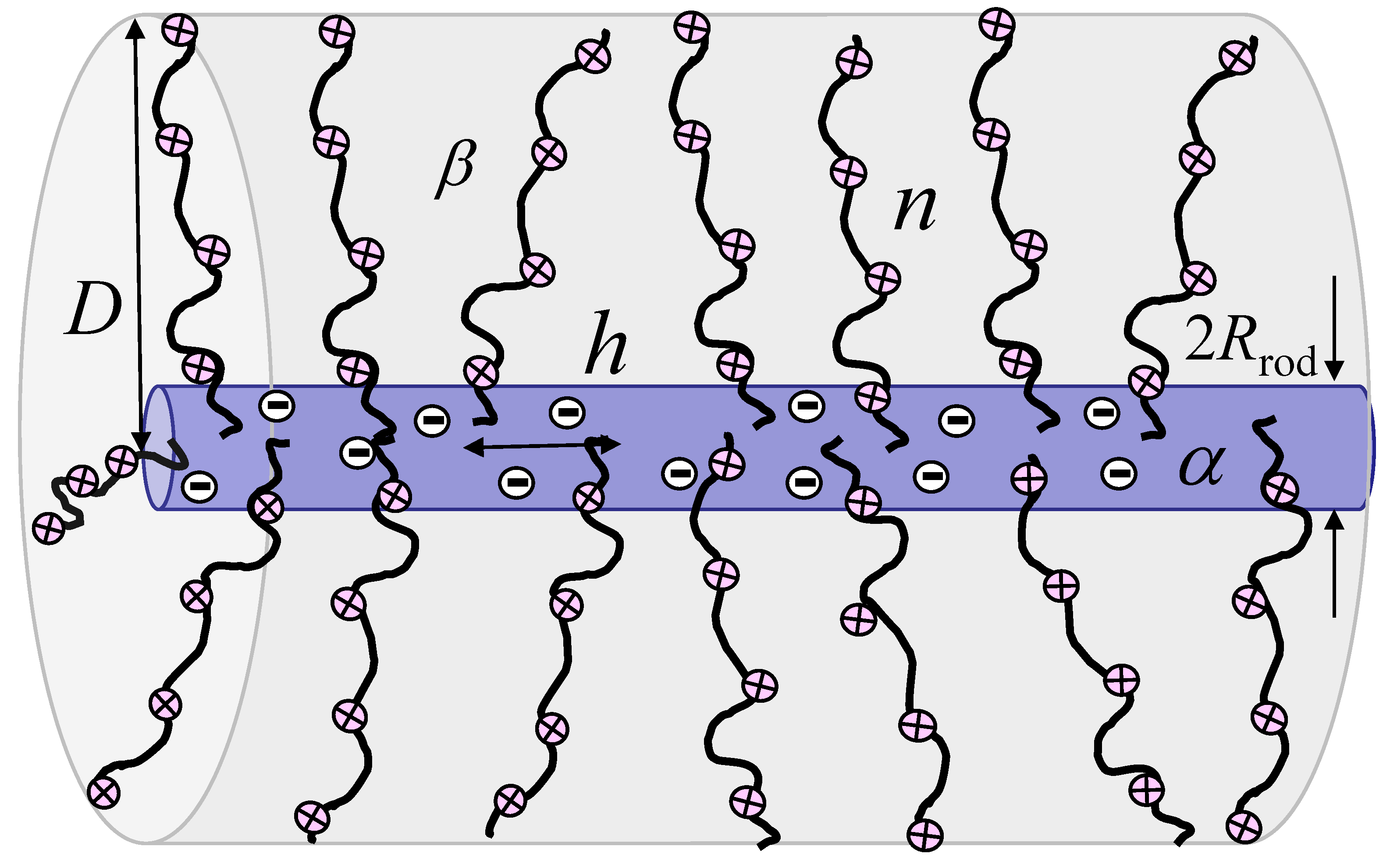
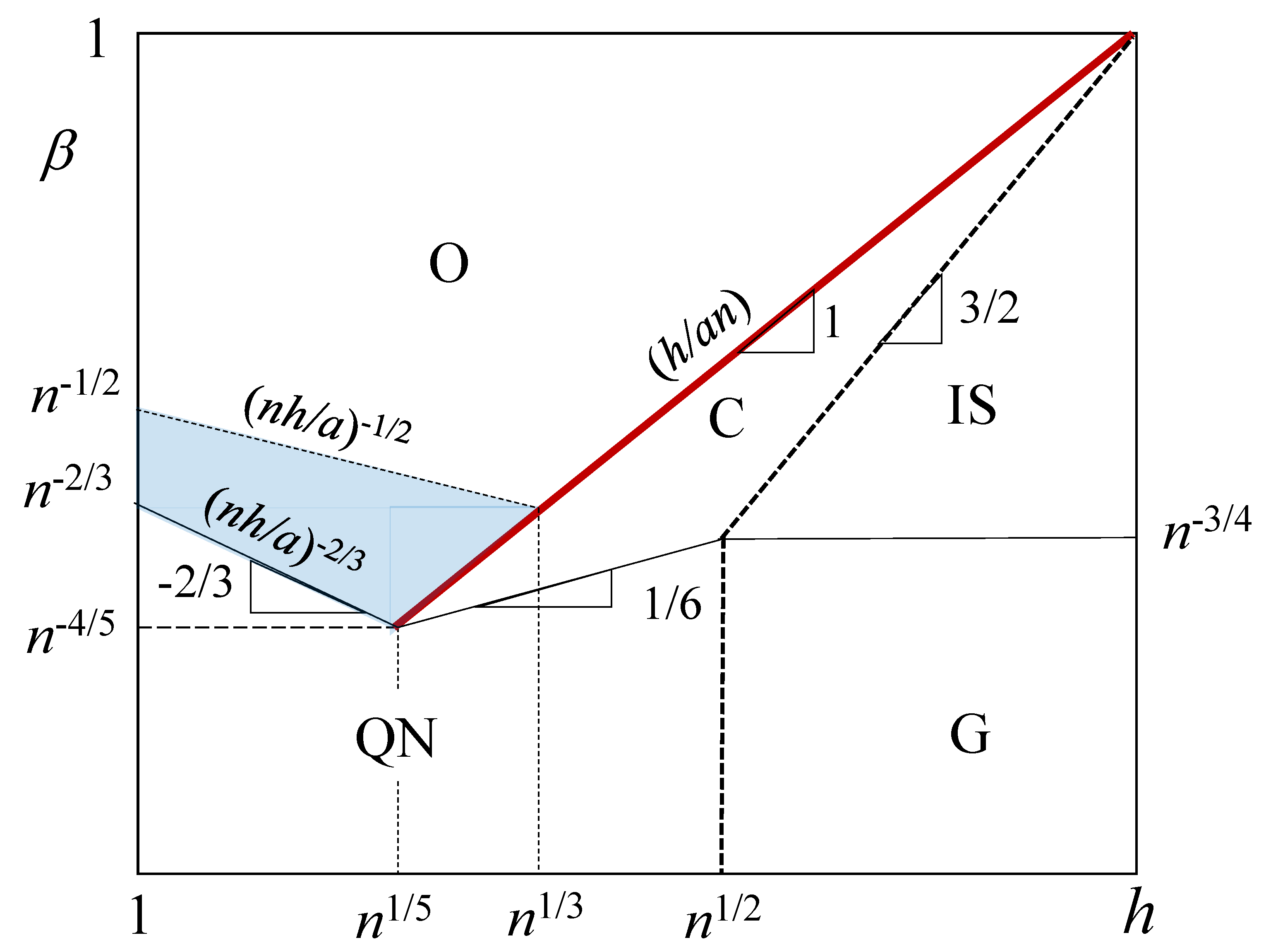


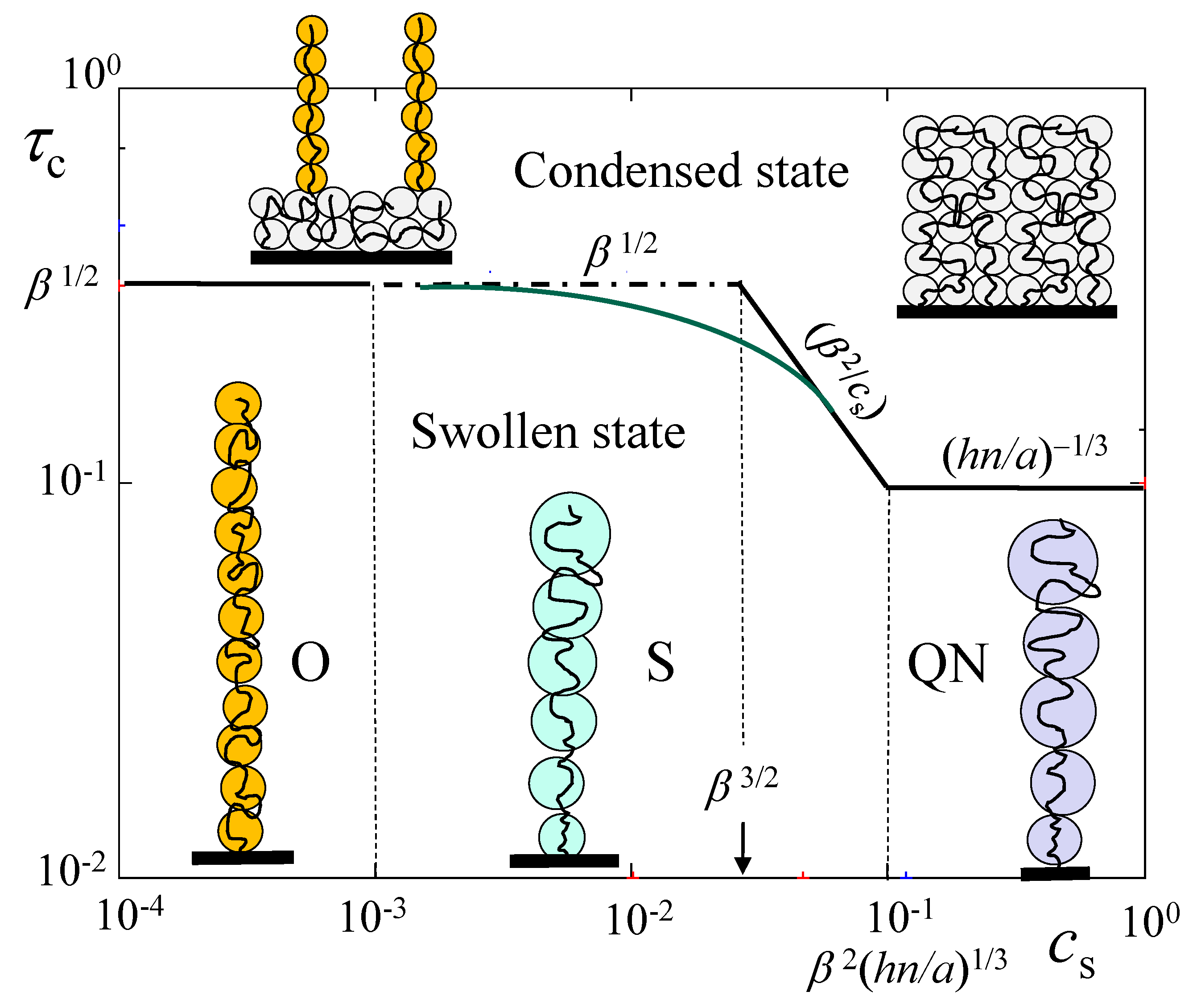
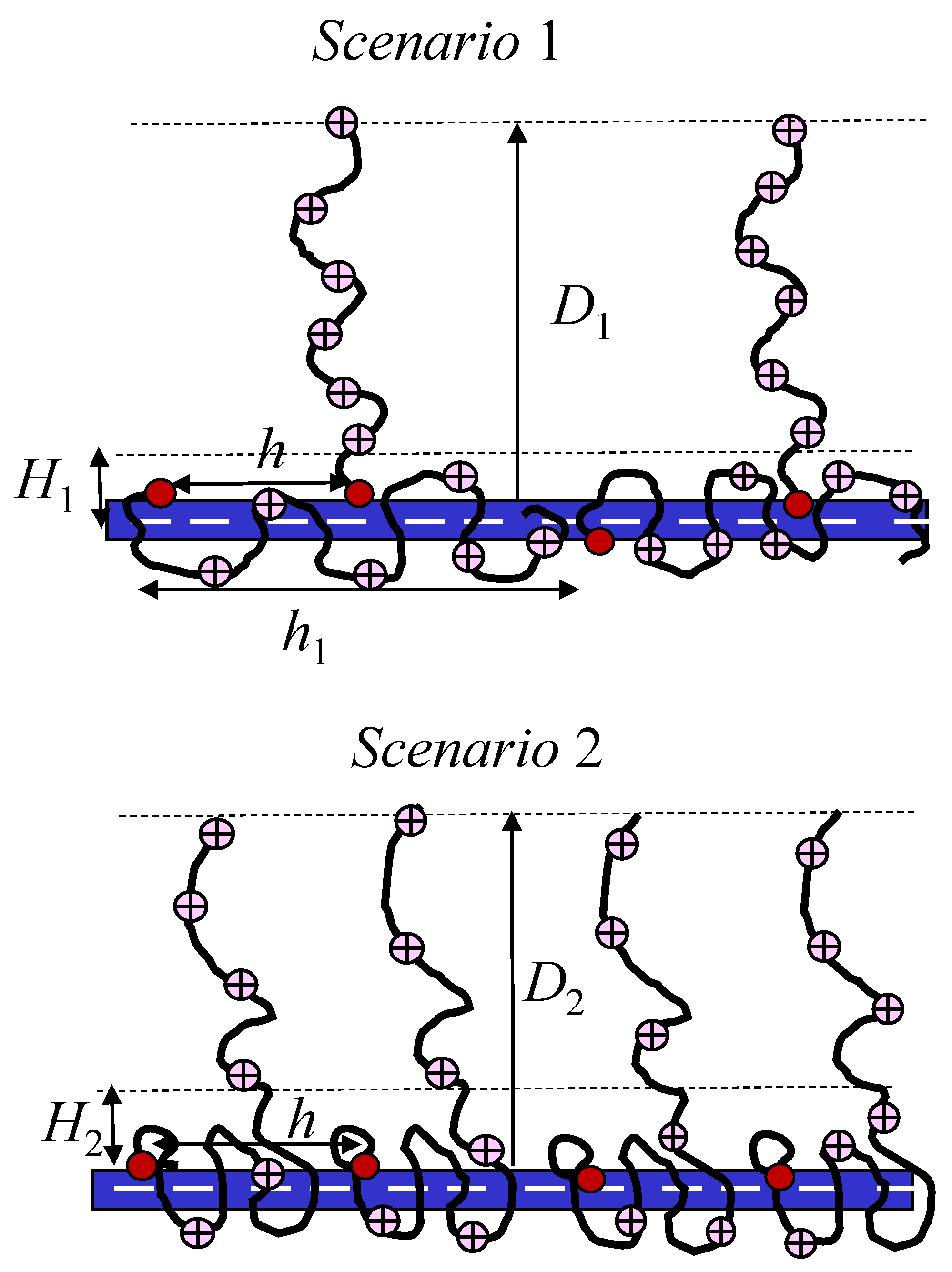
| Regimes | ||
|---|---|---|
| charged (C) | − | |
| osmotic (O) | ||
| quasi-neutral (QN) | ||
| isolated stretched (IS) | ||
| Gaussian (G) |
| Regime O | Regime S | Regime QN | |
|---|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhulina, E.B.; Borisov, O.V. Polyelectrolyte Cylindrical Brushes in Hairy Gels. Polymers 2023, 15, 3261. https://doi.org/10.3390/polym15153261
Zhulina EB, Borisov OV. Polyelectrolyte Cylindrical Brushes in Hairy Gels. Polymers. 2023; 15(15):3261. https://doi.org/10.3390/polym15153261
Chicago/Turabian StyleZhulina, Ekaterina B., and Oleg V. Borisov. 2023. "Polyelectrolyte Cylindrical Brushes in Hairy Gels" Polymers 15, no. 15: 3261. https://doi.org/10.3390/polym15153261
APA StyleZhulina, E. B., & Borisov, O. V. (2023). Polyelectrolyte Cylindrical Brushes in Hairy Gels. Polymers, 15(15), 3261. https://doi.org/10.3390/polym15153261






