Dynamically Adjusting Borophene-Based Plasmon-Induced Transparency in a Polymer-Separated Hybrid System for Broadband-Tunable Sensing
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
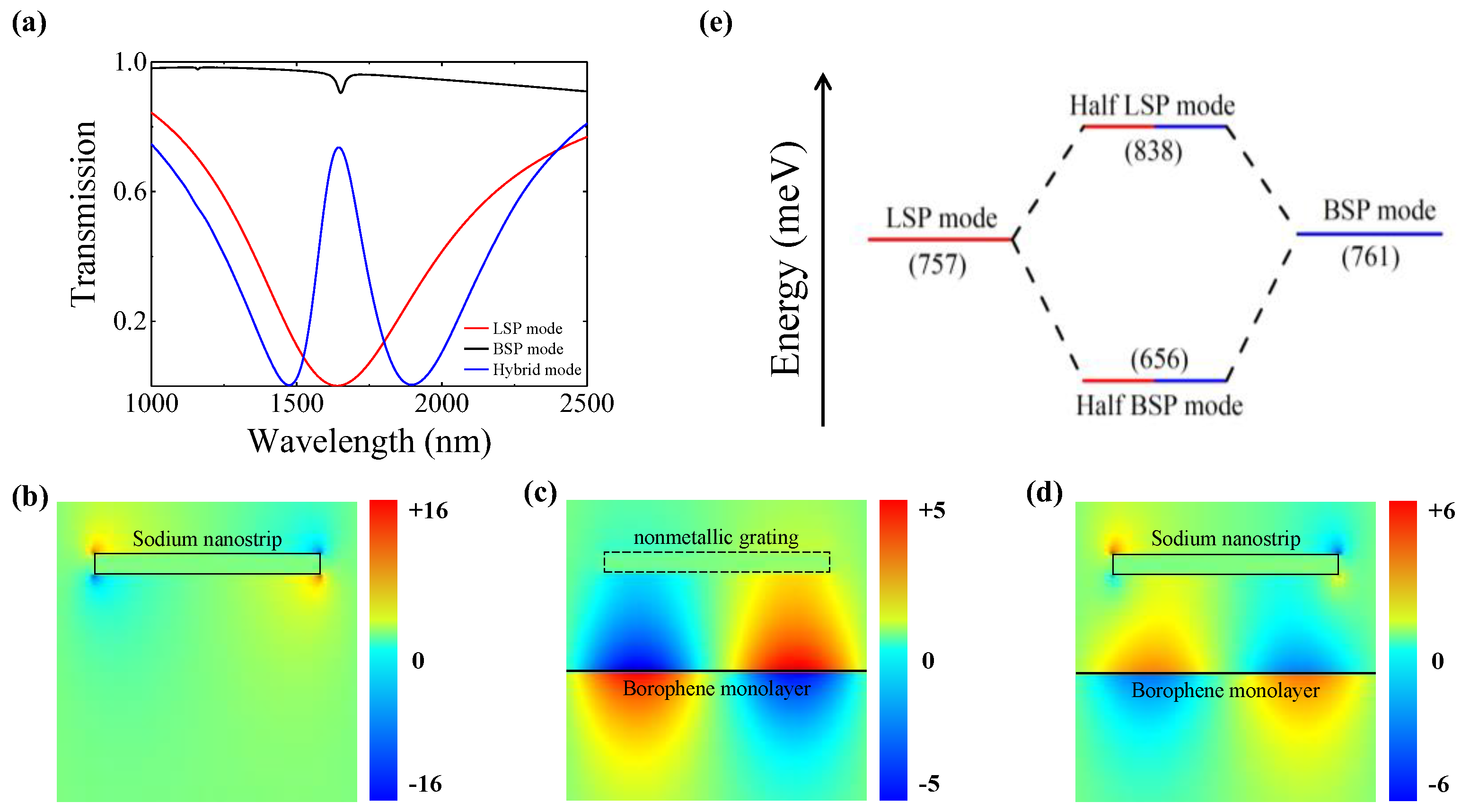
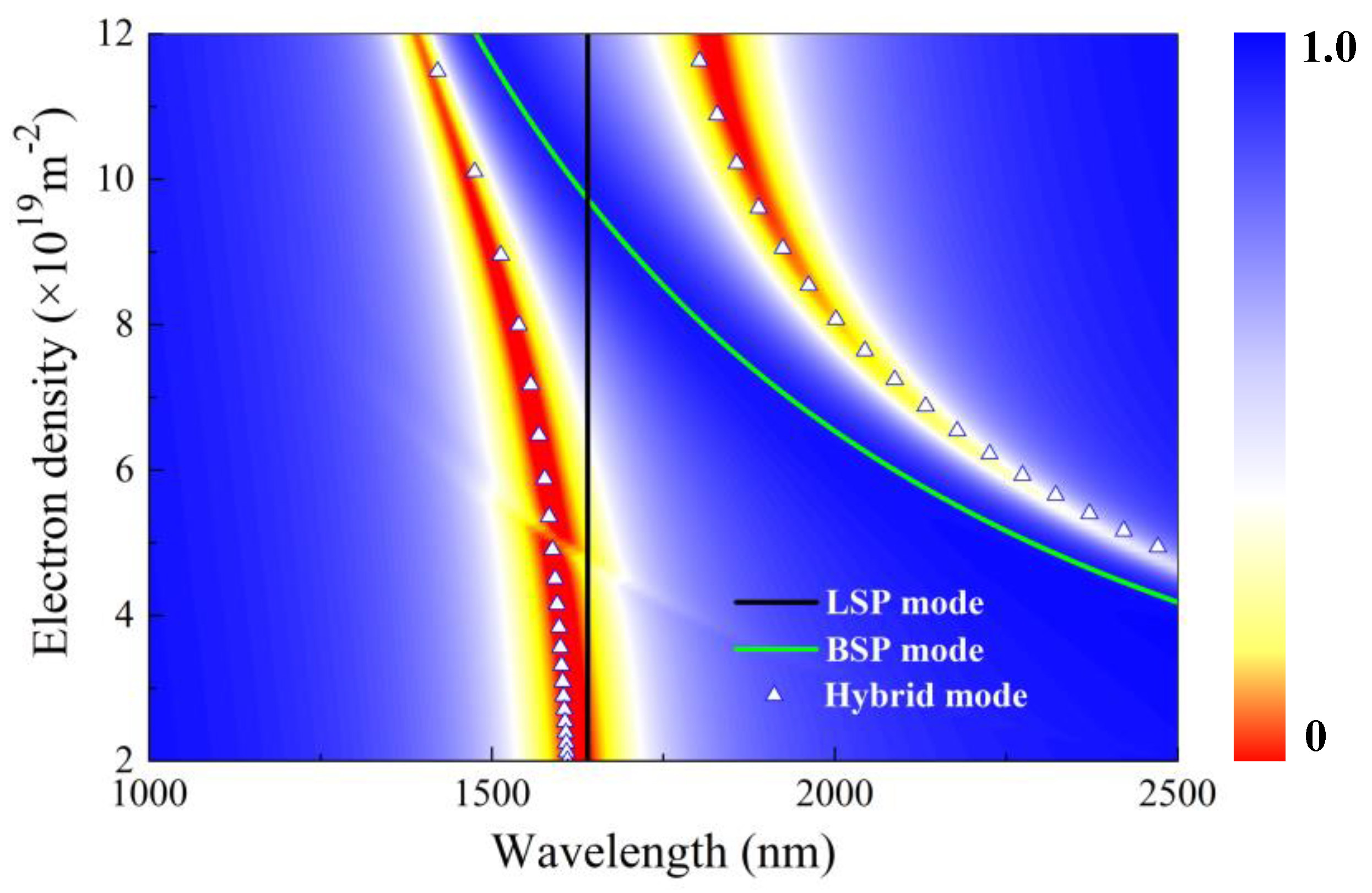
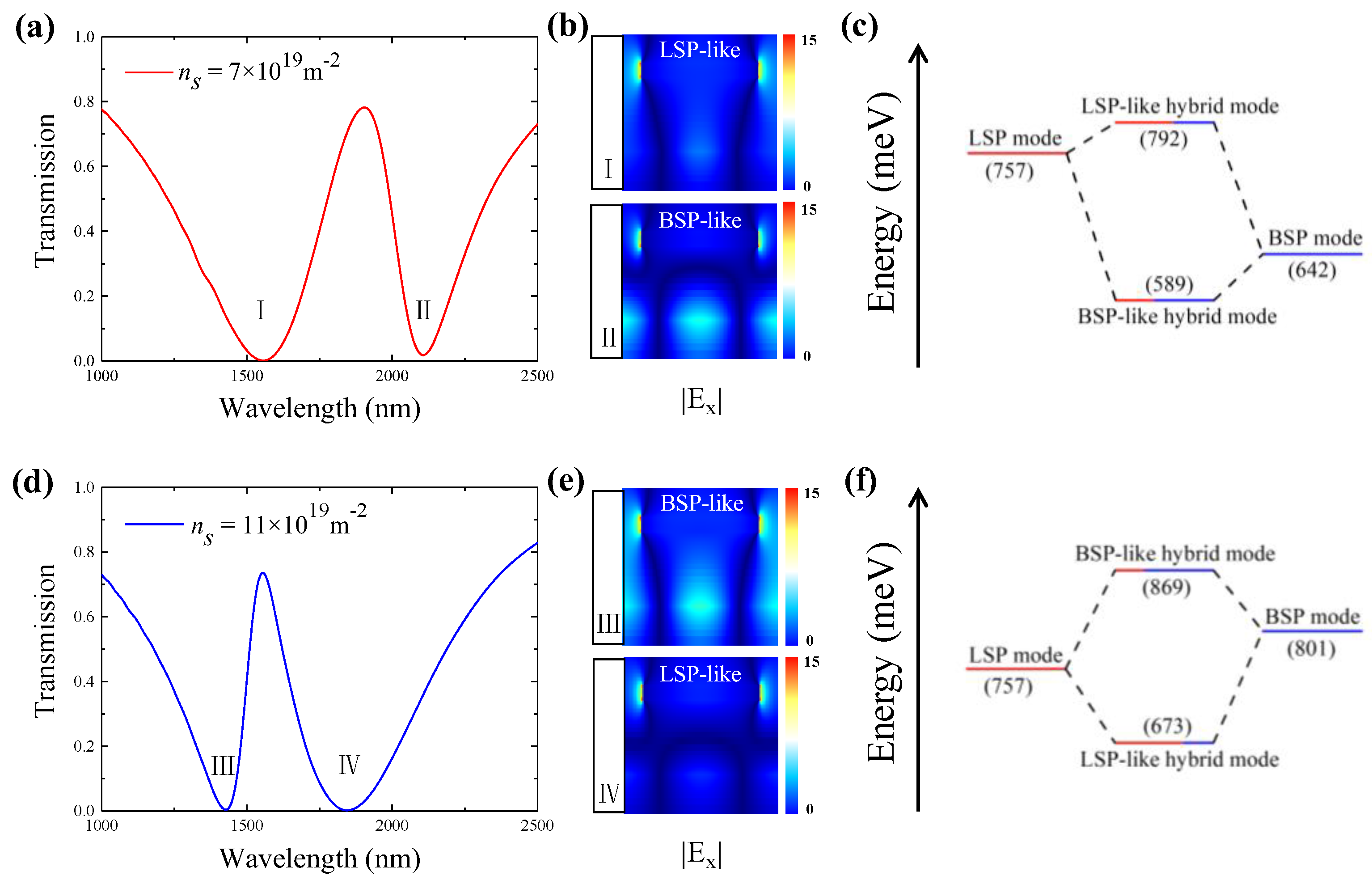
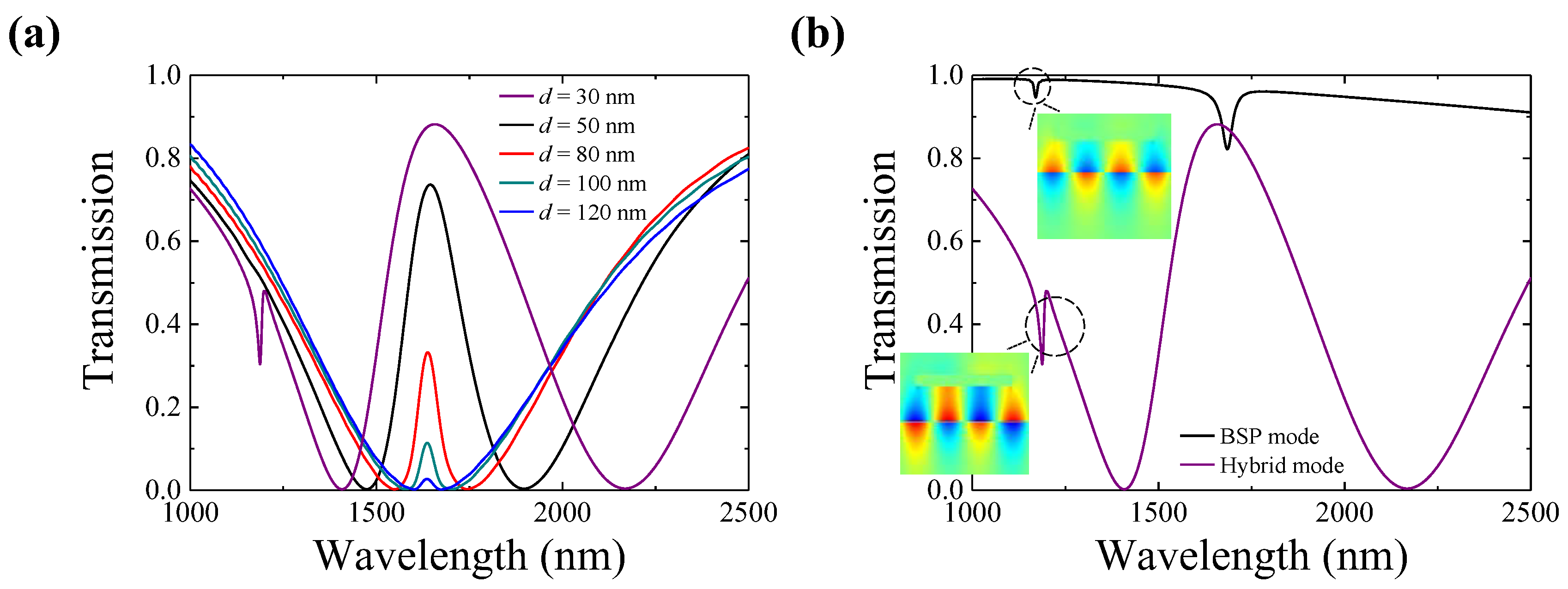
3.1. Controllable Coupling Mechanism
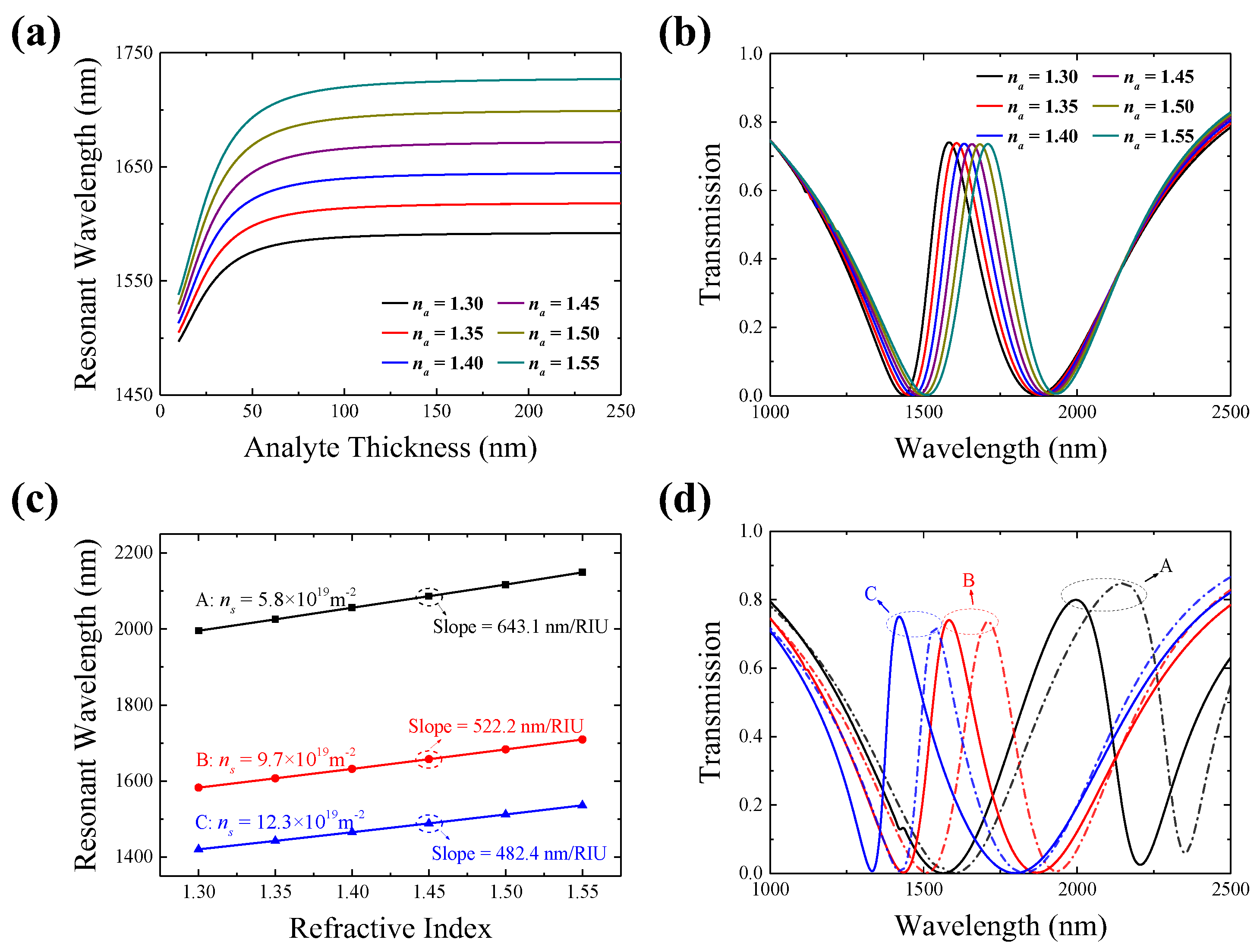
3.2. Broadband Tunable Sensitivity Characteristics
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Barnes, W.L.; Dereux, A.; Ebbesen, T.W. Surface plasmon subwavelength optics. Nature 2003, 424, 824–830. [Google Scholar] [CrossRef]
- Schuller, J.A.; Barnard, E.S.; Cai, W.; Jun, Y.C.; White, J.S.; Brongersma, M.L. Plasmonics for extreme light concentration and manipulation. Nat. Mater. 2010, 9, 193–204. [Google Scholar] [CrossRef] [PubMed]
- Naik, G.V.; Shalaev, V.M.; Boltasseva, A. Alternative Plasmonic Materials: Beyond Gold and Silver. Adv. Mater. 2013, 25, 3264–3294. [Google Scholar] [CrossRef]
- Koppens, F.H.L.; Chang, D.E.; de Abajo, F.J.G. Graphene Plasmonics: A Platform for Strong Light-Matter Interactions. Nano Lett. 2011, 11, 3370–3377. [Google Scholar] [CrossRef]
- Low, T.; Avouris, P. Graphene Plasmonics for Terahertz to Mid-Infrared Applications. ACS Nano 2014, 8, 1086–1101. [Google Scholar] [CrossRef] [PubMed]
- Low, T.; Roldán, R.; Wang, H.; Xia, F.; Avouris, P.; Moreno, L.M.; Guinea, F. Plasmons and screening in monolayer and multilayer black phosphorus. Phys. Rev. Lett. 2014, 113, 106802. [Google Scholar] [CrossRef] [PubMed]
- Lian, C.; Hu, S.Q.; Zhang, J.; Cheng, C.; Yuan, Z.; Gao, S.; Meng, S. Integrated Plasmonics: Broadband Dirac Plasmons in Borophene. Phys. Rev. Lett. 2020, 125, 116802. [Google Scholar] [CrossRef] [PubMed]
- Ranjan, P.; Sahu, T.K.; Bhushan, R.; Yamijala, S.S.; Late, D.J.; Kumar, P.; Vinu, A. Freestanding Borophene and Its Hybrids. Adv. Mater. 2019, 31, 1900353. [Google Scholar] [CrossRef]
- Kiraly, B.; Liu, X.; Wang, L.; Zhang, Z.; Mannix, A.J.; Fisher, B.L.; Yakobson, B.I.; Hersam, M.C.; Guisinger, N.P. Guisinger. Borophene Synthesis on Au(111). ACS Nano 2019, 13, 3816–3822. [Google Scholar] [CrossRef]
- Mannix, A.J.; Zhou, X.-F.; Kiraly, B.; Wood, J.D.; Alducin, D.; Myers, B.D.; Liu, X.; Fisher, B.L.; Santiago, U.; Guest, J.R.; et al. Synthesis of borophenes: Anisotropic, two-dimensional boron polymorphs. Science 2015, 350, 1513–1516. [Google Scholar] [CrossRef]
- Chen, C.; Lv, H.; Zhang, P.; Zhuo, Z.; Wang, Y.; Ma, C.; Li, W.; Wang, X.; Feng, B.; Cheng, P.; et al. Synthesis of bilayer borophene. Nat. Chem. 2022, 14, 25–31. [Google Scholar] [CrossRef] [PubMed]
- Ruan, Q.; Wang, L.; Bets, K.V.; Yakobson, B.I. Step-Edge Epitaxy for Borophene Growth on Insulators. ACS Nano 2021, 15, 18347–18353. [Google Scholar] [CrossRef] [PubMed]
- Rubab, A.; Baig, N.; Sher, M.; Sohail, M. Advances in ultrathin borophene materials. Chem. Eng. J. 2020, 401, 126109. [Google Scholar] [CrossRef]
- Shukla, V.; Wärnå, J.; Jena, N.K.; Grigoriev, A.; Ahuja, R. Toward the Realization of 2D Borophene Based Gas Sensor. J. Phys. Chem. C 2017, 121, 26869–26876. [Google Scholar] [CrossRef]
- Dereshgi, S.A.; Liu, Z.; Aydin, K. Anisotropic localized surface plasmons in borophene. Opt. Express 2020, 28, 16725–16739. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Zhang, Z.; Song, X.; Zhang, H.; Yang, J. Infrared Plasmonic Sensing with Anisotropic Two-Dimensional Material Borophene. Nanomaterials 2021, 11, 1165. [Google Scholar] [CrossRef]
- Nong, J.; Feng, F.; Gan, J.; Min, C.; Yuan, X.; Somekh, M. Active Modulation of Graphene Near-Infrared Electroabsorption Employing Borophene Plasmons in a Wide Waveband. Adv. Opt. Mater. 2022, 10, 2102131. [Google Scholar] [CrossRef]
- Liu, T.; Zhou, C.; Xiao, S. Tailoring anisotropic absorption in a borophene-based structure via critical coupling. Opt. Express 2021, 29, 8941–8950. [Google Scholar] [CrossRef] [PubMed]
- Nong, J.; Feng, F.; Min, C.; Yuan, X.; Somekh, M. Controllable hybridization between localized and delocalized anisotropic borophene plasmons in the near-infrared region. Opt. Lett. 2021, 46, 725–728. [Google Scholar] [CrossRef]
- Zhang, J.; Nong, J.; Feng, F.; Min, C.; Yuan, X.; Somekh, M. Magnetic polaritons assisted effective excitation of multi-order anisotropic borophene surface plasmons in the infrared region. Results Phys. 2021, 29, 104780. [Google Scholar] [CrossRef]
- Nong, J.; Xiao, X.; Feng, F.; Zhao, B.; Min, C.; Yuan, X.; Somekh, M. Active tuning of longitudinal strong coupling between anisotropic borophene plasmons and Bloch surface waves. Opt. Express 2021, 29, 27750–27759. [Google Scholar] [CrossRef] [PubMed]
- Nong, J.; Feng, F.; Min, C.; Yuan, X.; Somekh, M. Effective Transmission Modulation at Telecommunication Wavelengths through Continuous Metal Films Using Coupling between Borophene Plasmons and Magnetic Polaritons. Adv. Opt. Mater. 2021, 9, 2001809. [Google Scholar] [CrossRef]
- Zhang, X.; Qiu, J.; Li, X.; Zhao, J.; Liu, L.H. Complex refractive indices measurements of polymers in visible and near-infrared bands. Appl. Optics 2020, 59, 2337–2344. [Google Scholar] [CrossRef] [PubMed]
- Bhattacharyya, S.; Algieri, C.; Davoli, M.; Calabrò, V.; Chakraborty, S. Polymer-based TiO2 membranes: An efficient route for recalcitrant dye degradation. Chem. Eng. Res. Des. 2023, 193, 641–648. [Google Scholar] [CrossRef]
- Borin Barin, G.; Song, Y.; de Fátima Gimenez, I.; Souza Filho, A.G.; Barreto, L.S.; Kong, J. Optimized graphene transfer: Influence of polymethylmethacrylate (PMMA) layer concentration and baking time on graphene final performance. Carbon 2015, 84, 82–90. [Google Scholar] [CrossRef]
- Feng, B.; Zhang, J.; Liu, R.-Y.; Iimori, T.; Lian, C.; Li, H.; Chen, L.; Wu, K.; Meng, S.; Komori, F.; et al. Direct evidence of metallic bands in a monolayer boron sheet. Phys. Rev. B 2016, 94, 041408(R). [Google Scholar] [CrossRef]
- Huang, Y.; Shirodkar, S.N.; Yakobson, B.I. Two-Dimensional Boron Polymorphs for Visible Range Plasmonics: A First-Principles Exploration. J. Am. Chem. Soc. 2017, 139, 17181–17185. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, J.; Mao, Y.-F.; Chen, J.; Wang, S.; Chen, H.-Z.; Zhang, Y.; Wang, S.-Y.; Chen, X.; Li, T.; et al. Stable, high-performance sodium-based plasmonic devices in the near infrared. Nature 2020, 581, 401–405. [Google Scholar] [CrossRef]
- Ye, H.-Y.; Chen, C.-B.; Zhou, J.-Y.; Meng, Z.-M. Sodium-Based Surface Plasmon Resonances for High-Performance Optical Sensing in the Near Infrared. IEEE J. Sel. Top. Quantum Electron. 2021, 27, 1–8. [Google Scholar] [CrossRef]
- Zhang, S.; Genov, D.A.; Wang, Y.; Liu, M.; Zhang, X. Plasmon-Induced Transparency in Metamaterials. Phys. Rev. Lett. 2008, 101, 047401. [Google Scholar] [CrossRef] [PubMed]
- Manjappa, M.; Turaga, S.P.; Srivastava, Y.K.; Bettiol, A.A.; Singh, R. Magnetic annihilation of the dark mode in a strongly coupled bright-dark terahertz metamaterial. Opt. Lett. 2017, 42, 2106–2109. [Google Scholar] [CrossRef]
- Jin, X.-R.; Park, J.; Zheng, H.; Lee, S.; Lee, Y.; Rhee, J.Y.; Kim, K.W.; Cheong, H.S.; Jang, W.H. Highly-dispersive transparency at optical frequencies in planar metamaterials based on two-bright-mode coupling. Opt. Express 2011, 19, 21652–21657. [Google Scholar] [CrossRef] [PubMed]
- Gao, W.; Shu, J.; Qiu, C.; Xu, Q. Excitation of Plasmonic Waves in Graphene by Guided-Mode Resonances. ACS Nano 2012, 6, 7806–7813. [Google Scholar] [CrossRef]
- Zhao, B.; Zhang, Z.M. Strong Plasmonic Coupling between Graphene Ribbon Array and Metal Gratings. ACS Photonics 2015, 2, 1611–1618. [Google Scholar] [CrossRef]
- Coles, D.M.; Somaschi, N.; Michetti, P.; Clark, C.; Lagoudakis, P.; Savvidis, P.; Lidzey, D. Polariton-mediated energy transfer between organic dyes in a strongly coupled optical microcavity. Nat. Mater. 2014, 13, 712–719. [Google Scholar] [CrossRef] [PubMed]
- Nong, J.; Wei, W.; Wang, W.; Lan, G.; Shang, Z.; Yi, J.; Tang, L. Strong coherent coupling between graphene surface plasmons and anisotropic black phosphorus localized surface plasmons. Opt. Express 2018, 26, 1633–1644. [Google Scholar] [CrossRef] [PubMed]
- Xu, R.; Luo, J.; Sha, J.; Zhong, J.; Xu, Z.; Tong, Y.; Lin, Y.-S. Stretchable IR metamaterial with ultra-narrowband perfect absorption. Appl. Phys. Lett. 2018, 113, 101907. [Google Scholar] [CrossRef]
- Wang, X.; Lin, J.; Yan, Z.; Yi, Z.; Yu, J.; Zhang, W.; Qin, F.; Wu, X.; Zhang, J.; Wu, P. Tunable high-sensitivity sensing detector based on Bulk Dirac semimetal. RSC Adv. 2022, 12, 32583–32591. [Google Scholar] [CrossRef]
- Brockman, J.M.; Nelson, B.P.; Corn, R.M. Surface plasmon resonance imaging measurements of ultrathin organic films. Annu. Rev. Phys. Chem. 2000, 51, 41–63. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, K.; Li, J.; Zhang, H.; Jiang, H.; Zhao, W. Dynamically Adjusting Borophene-Based Plasmon-Induced Transparency in a Polymer-Separated Hybrid System for Broadband-Tunable Sensing. Polymers 2023, 15, 3060. https://doi.org/10.3390/polym15143060
Xiao K, Li J, Zhang H, Jiang H, Zhao W. Dynamically Adjusting Borophene-Based Plasmon-Induced Transparency in a Polymer-Separated Hybrid System for Broadband-Tunable Sensing. Polymers. 2023; 15(14):3060. https://doi.org/10.3390/polym15143060
Chicago/Turabian StyleXiao, Kunpeng, Junming Li, Hui Zhang, Huan Jiang, and Weiren Zhao. 2023. "Dynamically Adjusting Borophene-Based Plasmon-Induced Transparency in a Polymer-Separated Hybrid System for Broadband-Tunable Sensing" Polymers 15, no. 14: 3060. https://doi.org/10.3390/polym15143060
APA StyleXiao, K., Li, J., Zhang, H., Jiang, H., & Zhao, W. (2023). Dynamically Adjusting Borophene-Based Plasmon-Induced Transparency in a Polymer-Separated Hybrid System for Broadband-Tunable Sensing. Polymers, 15(14), 3060. https://doi.org/10.3390/polym15143060





