A Coupled Electro-Mechanical Homogenization-Based Model for PVDF-Based Piezo-Composites Considering α → β Phase Transition and Interfacial Damage
Abstract
1. Introduction
2. Constitutive Equations
2.1. Piezoelectric Multiphase Composites
2.2. Micromechanical Deformation Processes
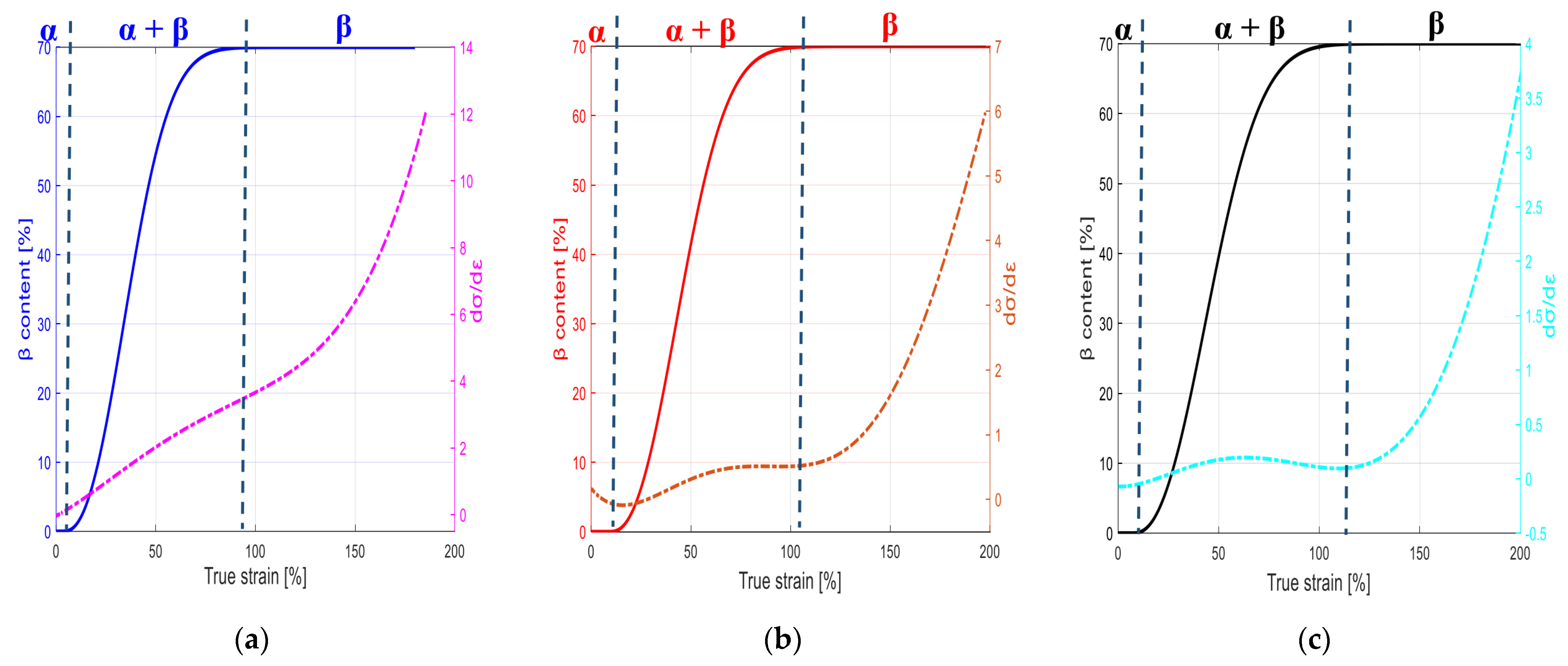
2.2.1. Strain-Induced α → β Phase Transition
2.2.2. Interfacial Debonding
2.3. Piezoelectric Activity
3. Model Application
3.1. Model Constants
3.1.1. Piezoelastic Constants
3.1.2. Phase Transition Constants
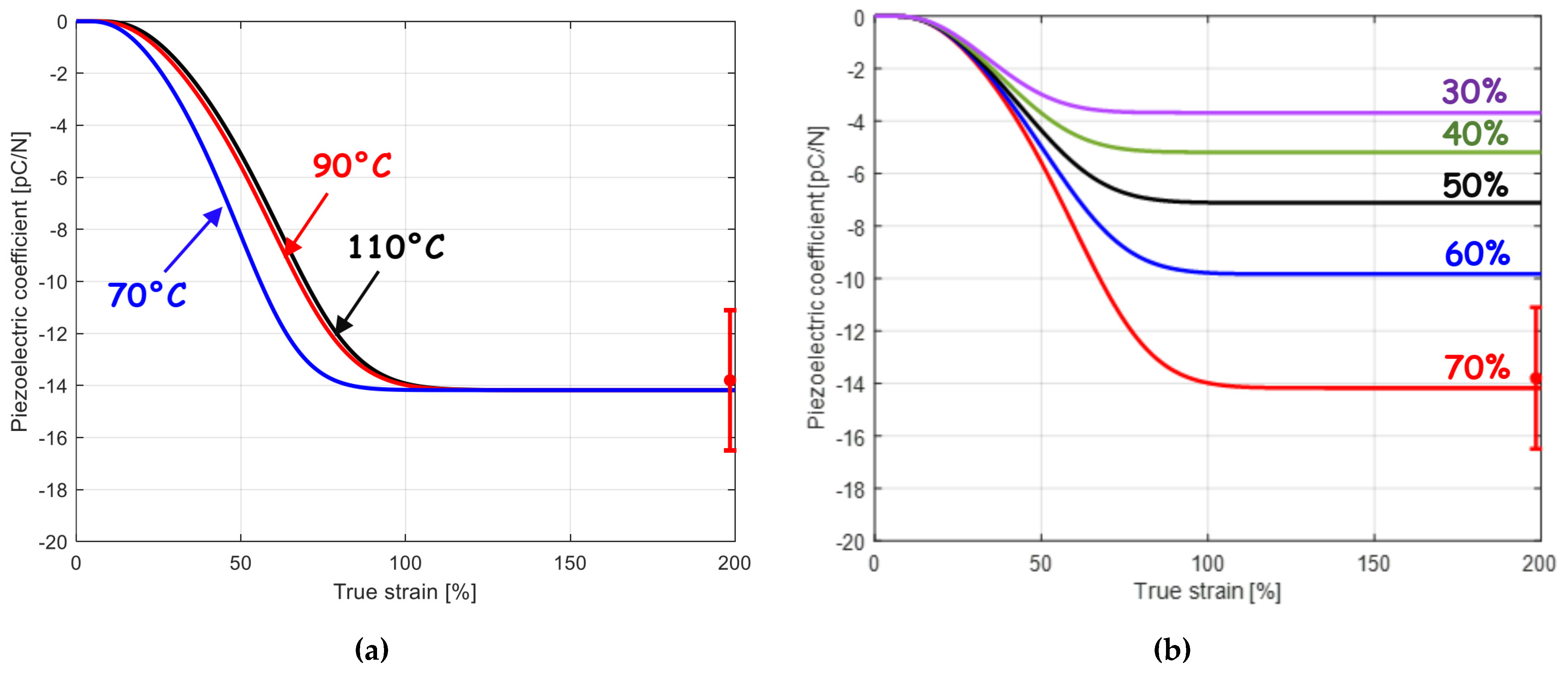
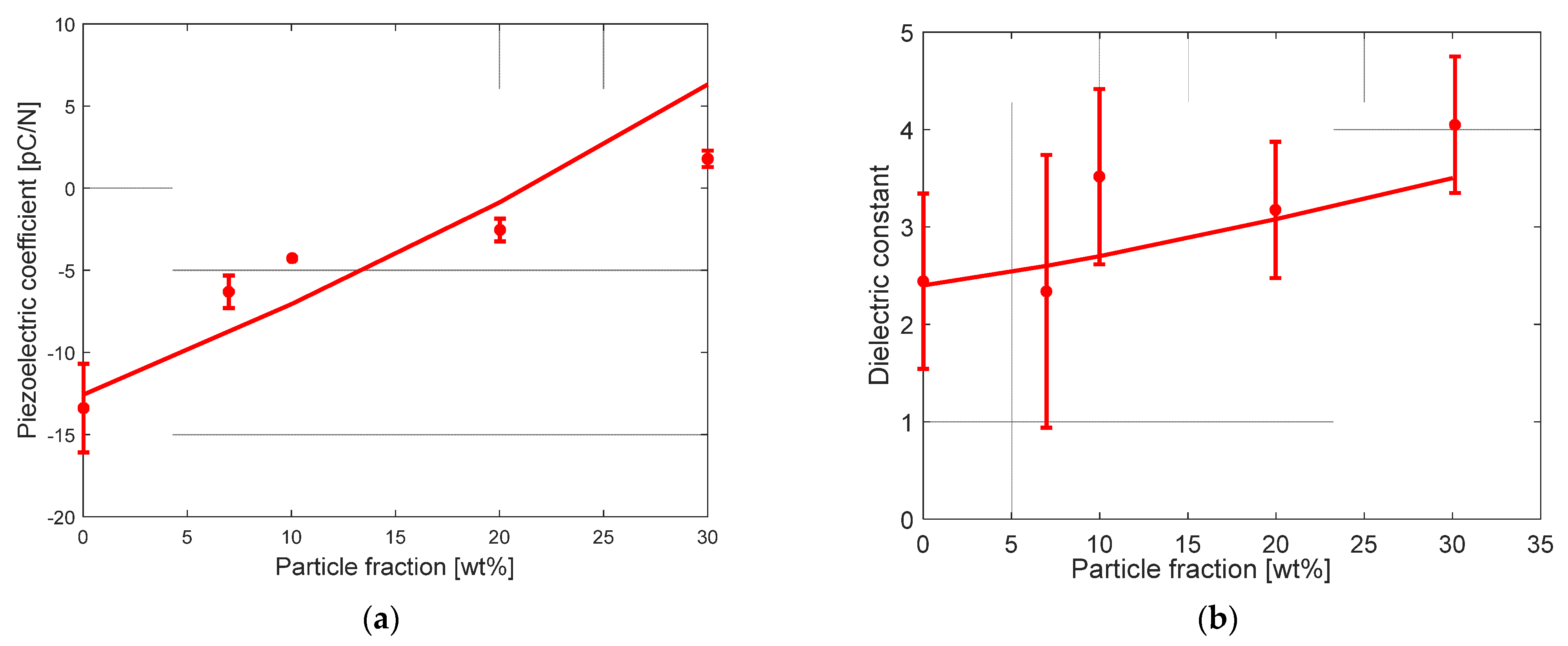
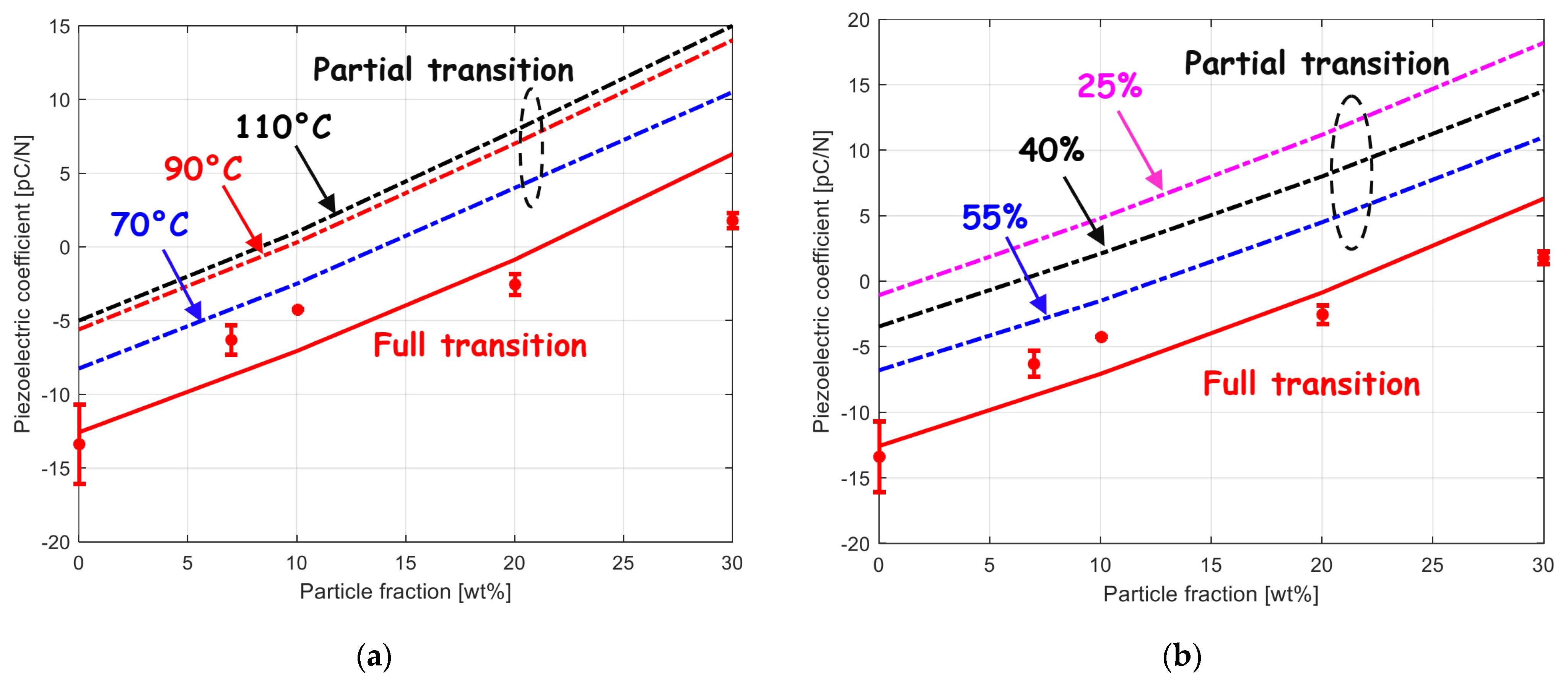
3.2. Piezoelectric Properties
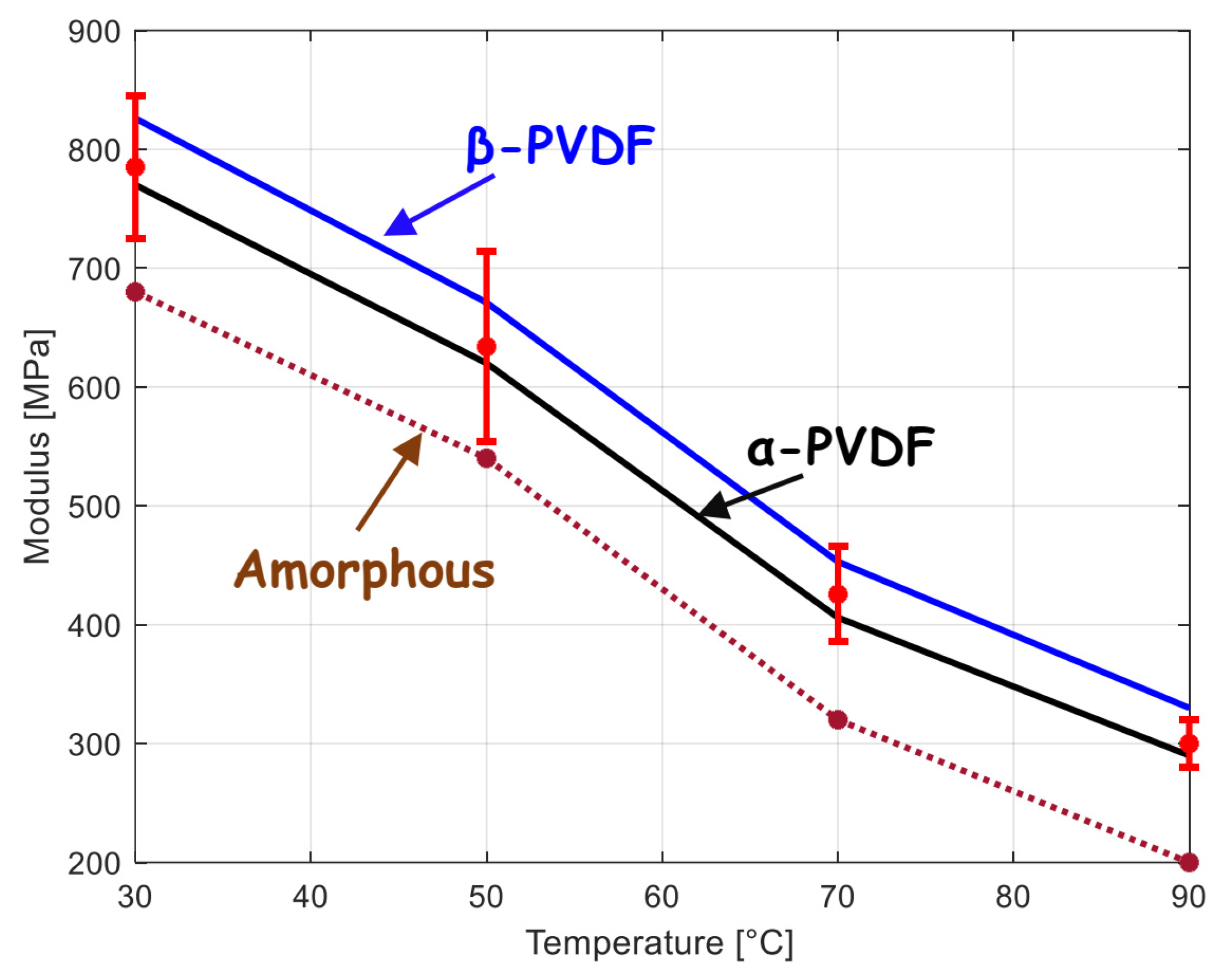
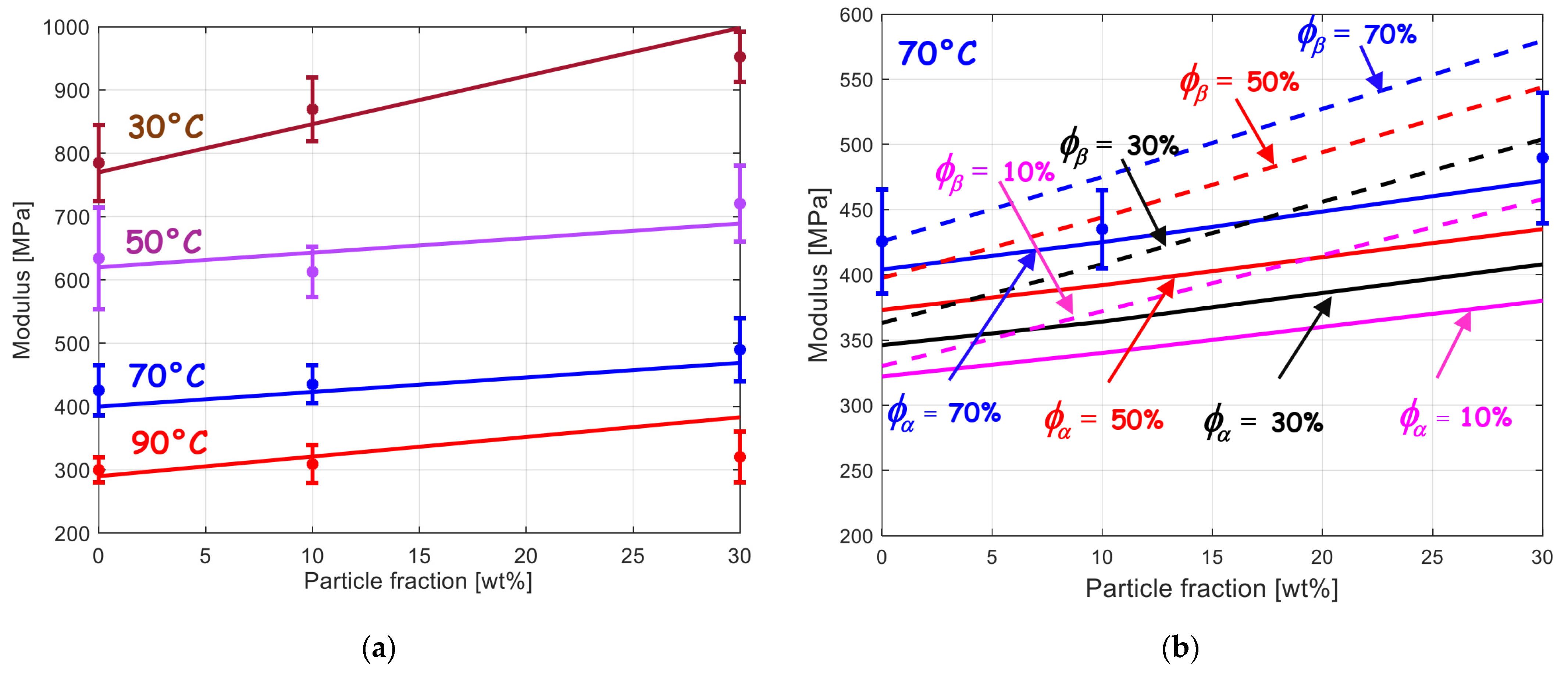
3.3. Mechanical Response
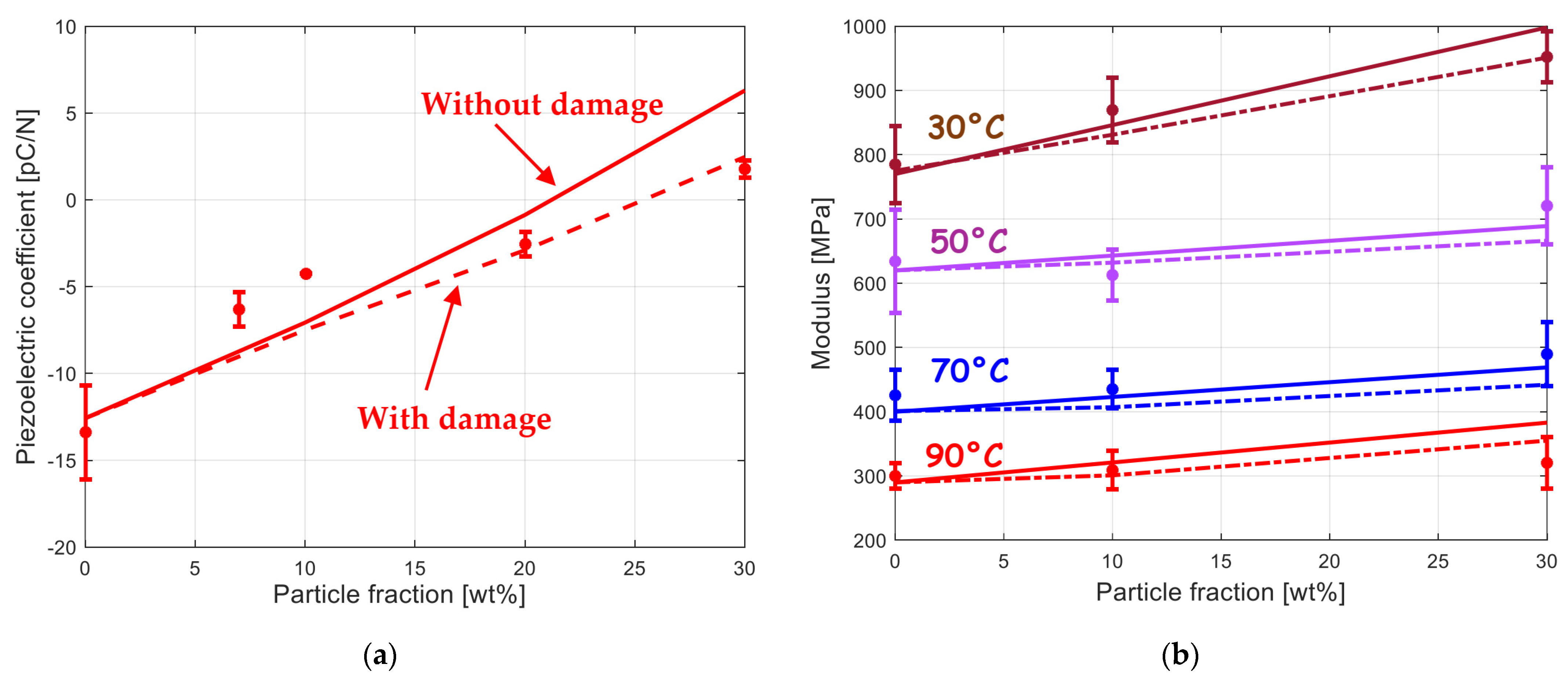
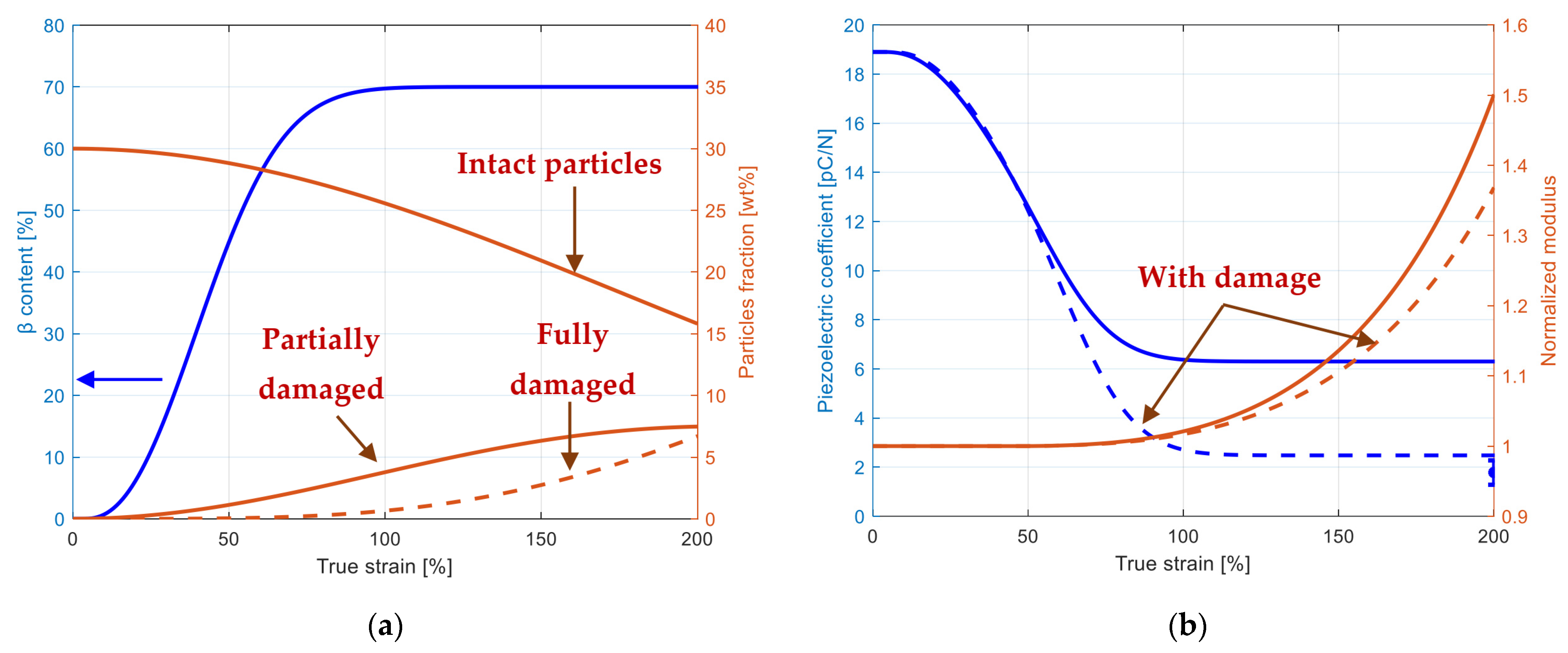
3.4. Interfacial Debonding
4. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chang, J.; Dommer, M.; Chang, C.; Lin, L. Piezoelectric nanofibers for energy scavenging applications. Nano Energy 2012, 1, 356–371. [Google Scholar] [CrossRef]
- Varun, S.; George, N.M.; Chandran, A.M.; Varghese, L.A.; Mural, P.K.S. Multifaceted PVDF nanofibers in energy, water and sensors: A contemporary review (2018 to 2022) and future perspective. J. Fluor. Chem. 2023, 265, 110064. [Google Scholar] [CrossRef]
- Vinogradov, A.; Holloway, F. Electro-mechanical properties of the piezoelectric polymer PVDF. Ferroelectrics 1999, 226, 169–181. [Google Scholar] [CrossRef]
- Martins, P.; Lopes, A.C.; Lanceros-Mendez, S. Electroactive phases of poly(vinylidene fluoride): Determination, processing and applications. Prog. Polym. Sci. 2014, 39, 683–706. [Google Scholar] [CrossRef]
- Nalwa, H.S. Ferroelectric Polymers: Chemistry, Physics and Applications; Marcel Dekker: New York, NY, USA, 1995. [Google Scholar]
- Gomes, J.; Nunes, S.J.; Sencadas, V.; Lanceros-Mendez, S. Influence of the β-phase content and degree of crystallinity on the piezo- and ferroelectric properties of poly(vinylidene fluoride). Smart Mater. Struct. 2010, 19, 065010. [Google Scholar] [CrossRef]
- Wu, L.; Jin, Z.; Liu, Y.; Ning, H.; Liu, X.; Alamusi; Hu, N. Recent advances in the preparation of PVDF-based piezoelectric materials. Nanotechnol. Rev. 2022, 11, 1386–1407. [Google Scholar] [CrossRef]
- Li, L.; Zhang, M.; Rong, M.; Ruan, W. Studies on the transformation process of PVDF from α to β phase by stretching. RSC Adv. 2014, 4, 3938–3943. [Google Scholar] [CrossRef]
- Defebvin, J. Étude des Relations Structure-Propriétés de Matériaux Hybrides Piézoélectriques à Base PVDF. Ph.D. Thesis, Lille University, Lille, France, 2015. [Google Scholar]
- Defebvin, J.; Barrau, S.; Stoclet, G.; Rochas, C.; Lefebvre, J.M. In situ SAXS/WAXS investigation of the structural evolution of poly(vinylidene fluoride) upon uniaxial stretching. Polymer 2016, 84, 148–157. [Google Scholar] [CrossRef]
- Ye, H.J.; Yang, L.; Shao, W.Z.; Sun, S.B.; Zhen, L. Effect of electroactive phase transformation on electron structure and dielectric properties of uniaxial stretching poly(vinylidene fluoride) films. RSC Adv. 2013, 3, 23730–23736. [Google Scholar] [CrossRef]
- Sharma, M.; Madras, G.; Bose, S. Process induced electroactive β-polymorph in PVDF: Effect on dielectric and ferroelectric properties. Phys. Chem. Chem. Phys. 2014, 16, 14792–14799. [Google Scholar] [CrossRef]
- Tang, C.W.; Li, B.; Sun, L.; Lively, B.; Zhong, W.H. The effects of nanofillers, stretching and recrystallization on microstructure, phase transformation and dielectric properties in PVDF nanocomposites. Eur. Polym. J. 2012, 48, 1062–1072. [Google Scholar] [CrossRef]
- Khan, F.; Kowalchik, T.; Roundy, S.; Warren, R. Stretching-induced phase transitions in barium titanate-poly(vinylidene fluoride) flexible composite piezoelectric films. Scr. Mater. 2021, 193, 64–70. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, X.; Chen, X.; Xia, X.; Weng, G.J. Piezoelectricity enhancement in graphene/polyvinylidene fluoride composites due to graphene-induced α → β crystal phase transition. Energy Convers. Manag. 2022, 269, 116121. [Google Scholar] [CrossRef]
- Yan, Z.; Zaïri, F.; Zaoui, F. Multiscale modeling of the strain-induced α → β phase transition and piezoelectric activity in semi-crystalline poly(vinylidene fluoride) over a large-strain range. Mech. Mater. 2023, 182, 104666. [Google Scholar] [CrossRef]
- Dunn, M.L. Electroelastic Green’s functions for transversely isotropic piezoelectric media and their application to the solution of inclusion and inhomogeneity problems. Int. J. Eng. Sci. 1994, 32, 119–131. [Google Scholar] [CrossRef]
- Mikata, Y. Determination of piezoelectric Eshelby tensor in transversely isotropic piezoelectric solids. Int. J. Eng. Sci. 2000, 38, 605–641. [Google Scholar] [CrossRef]
- Mikata, Y. Explicit determination of piezoelectric Eshelby tensors for a spheroidal inclusion. Int. J. Solids Struct. 2001, 38, 7045–7063. [Google Scholar] [CrossRef]
- Wang, B. Three-dimensional analysis of an ellipsoidal inclusion in a piezoelectric material. Int. J. Solids Struct. 1992, 29, 293–308. [Google Scholar]
- Fakri, N.; Azrar, L.; El Bakkali, L. Electroelastic behavior modeling of piezoelectric composite materials containing spatially oriented reinforcements. Int. J. Solids Struct. 2003, 40, 361–384. [Google Scholar] [CrossRef]
- Fakri, N.; Azrar, L. Thermal and electroelastic behavior of piezocomposites and inhomogeneous piezoelectric materials with voids. J. Intell. Mater. Syst. Struct. 2010, 21, 61–174. [Google Scholar] [CrossRef]
- Elouafi, J.; Azrar, L.; Aljinaidi, A.A. Closed-form expressions for the effective moduli of heterogeneous piezoelectric materials. Int. J. Solids Struct. 2015, 52, 19–32. [Google Scholar] [CrossRef]
- Odegard, G.M. Constitutive modeling of piezoelectric polymer composites. Acta Mater. 2004, 52, 5315–5330. [Google Scholar] [CrossRef]
- Wang, Z.; Zhu, J.; Jin, X.Y.; Chen, W.Q.; Zhang, C.H. Effective moduli of ellipsoidal particle reinforced piezoelectric composites with imperfect interfaces. J. Mech. Phys. Solids 2014, 65, 138–156. [Google Scholar] [CrossRef]
- Malakooti, M.H.; Sodano, H.A. Multi-inclusion modeling of multiphase piezoelectric composite. Compos. Part B 2013, 47, 181–189. [Google Scholar] [CrossRef]
- Eynbeygi, M.; Aghdam, M.M. A micromechanical study on the electro-elastic behavior of piezoelectric fiber-reinforced composites using the element-free Galerkin method. Acta Mech. 2015, 226, 3177–3194. [Google Scholar] [CrossRef]
- Eynbeygui, M.; Aghdam, M.M. On the micro-mechanical study of 1-3 type piezoelectric composites with semi-coupled thermo-electro-elastic effects. Meccanica 2017, 52, 3693–3711. [Google Scholar] [CrossRef]
- Mahmoodi, M.J.; Rajabi, Y.; Khodaiepour, B. Electro-thermo-mechanical responses of laminated smart nanocomposite moderately thick plates containing carbon nanotube—A multi-scale modeling. Mech. Mater. 2020, 141, 103247. [Google Scholar] [CrossRef]
- Bédoui, F.; Diani, J.; Régnier, G.; Seiler, W. Micromechanical modelling of isotropic elastic behaviour of semicrystalline polymers. Acta Mater. 2006, 54, 1513–1523. [Google Scholar] [CrossRef]
- Gueguen, O.; Ahzi, S.; Makradi, A.; Belouetta, S. A new three-phase model to estimate the effective elastic properties of semi-crystalline polymers: Application to PET. Mech. Mater. 2010, 42, 1–10. [Google Scholar] [CrossRef]
- Anoukou, K.; Zaïri, F.; Naït-Abdelaziz, M.; Zaoui, A.; Qu, Z.; Gloaguen, J.M.; Lefebvre, J.M. A micromechanical model taking into account the contribution of α- and γ-crystalline phases in the stiffening of polyamide 6-clay nanocomposites: A closed-formulation including the crystal symmetry. Compos. Part B 2014, 64, 84–96. [Google Scholar] [CrossRef]
- Hachour, K.; Zaïri, F.; Naït-Abdelaziz, M.; Gloaguen, J.M.; Aberkane, M.; Lefebvre, J.M. Experiments and modeling of high-crystalline polyethylene yielding under different stress states. Int. J. Plast. 2014, 54, 1–18. [Google Scholar] [CrossRef]
- Mamache, F.E.; Mesbah, A.; Bian, H.; Zaïri, F. Micromechanical modeling of the biaxial deformation-induced phase transformation in polyethylene terephthalate. Polymers 2022, 14, 3028. [Google Scholar] [CrossRef] [PubMed]
- Ju, J.W.; Sun, L.Z. Effective elastoplastic behavior of metal matrix composites containing randomly located aligned spheroidal inhomogeneities. Part I: Micromechanics-based formulation. Int. J. Solids Struct. 2001, 38, 183–201. [Google Scholar] [CrossRef]
- Doufas, A.K.; McHugh, A.J.; Miller, C. Simulation of melt spinning including flow-induced crystallization: Part I. Model development and predictions. J. Non-Newton. Fluid Mech. 2000, 92, 27–66. [Google Scholar] [CrossRef]
- Guo, Q.; Zaïri, F. A physically-based thermo-mechanical model for stretch-induced crystallizable rubbers: Crystallization thermodynamics and chain-network crystallization anisotropy. Int. J. Plast. 2020, 131, 102724. [Google Scholar] [CrossRef]
- Ahzi, S.; Makradi, A.; Gregory, R.V.; Edie, D.D. Modeling of deformation behavior and strain-induced crystallization in poly(ethylene terephthalate) above the glass transition temperature. Mech. Mater. 2003, 35, 1139–1148. [Google Scholar] [CrossRef]
- Makradi, A.; Ahzi, S.; Gregory, R.V.; Edie, D.D. A two-phase self-consistent model for the deformation and phase transformation behavior of polymers above the glass transition temperature: Application to PET. Int. J. Plast. 2005, 21, 741–758. [Google Scholar] [CrossRef]
- Mahjoubi, H.; Zaïri, F.; Vozniak, I.; Tourki, Z.; Zaïri, F. Modeling strain-induced dual-phase transformation in semicrystalline polylactide. Mech. Time-Depend. Mater. 2023, in press. [Google Scholar] [CrossRef]
- Castagnet, S.; Girault, S.; Gacougnolle, J.L.; Dang, P. Cavitation in strained polyvinylidene fluoride: Mechanical and X-ray experimental studies. Polymer 2000, 41, 7523–7530. [Google Scholar] [CrossRef]
- Sun, L.Z.; Ju, J.W.; Liu, H.T. Elastoplastic modeling of metal matrix composites with evolutionary particle debonding. Mech. Mater. 2003, 35, 559–569. [Google Scholar] [CrossRef]
- Mesbah, A.; Zaïri, F.; Naït-Abdelaziz, M.; Gloaguen, J.M.; Anoukou, K.; Zaoui, A.; Qu, Z.; Boukharouba, T.; Lefebvre, J.M. Micromechanics-based constitutive modeling of plastic yielding and damage mechanisms in polymer–clay nanocomposites: Application to polyamide-6 and polypropylene-based nanocomposites. Compos. Sci. Technol. 2014, 101, 71–78. [Google Scholar] [CrossRef]
- Defebvin, J.; Barrau, S.; Lyskawa, J.; Woisel, P.; Lefebvre, J.M. Influence of nitrodopamine-functionalized barium titanate content on the piezoelectric response of poly(vinylidene fluoride) based polymer-ceramic composites. Compos. Sci. Technol. 2017, 147, 16–21. [Google Scholar] [CrossRef]
- McCarthy, G.J.; Roy, R. Gel route to homogeneous glass preparation. II. Gelling and desiccation. J. Am. Ceram. Soc. 1971, 54, 639–640. [Google Scholar] [CrossRef]
- Hasegawa, R.; Takahashi, Y.; Chatani, Y.; Tadokoro, H. Crystal structures of three crystalline forms of poly(vinylidene fluoride). Polym. J. 1972, 3, 600–610. [Google Scholar] [CrossRef]
- Ameduri, B. From vinylidene fluoride (VDF) to the applications of VDF-containing polymers and copolymers: Recent developments and future trends. Chem. Rev. 2009, 109, 6632–6686. [Google Scholar] [CrossRef]
- Pei, Y.; Zeng, X.C. Elastic properties of poly(vinyldene fluoride) (PVDF) crystals: A density functional theory study. J. Appl. Phys. 2011, 109, 093514. [Google Scholar] [CrossRef]
- Venkatragavaraj, E.; Satish, B.; Vinod, P.R.; Vijaya, M.S. Piezoelectric properties of ferroelectric PZT–polymer composites. J. Phys. D Appl. Phys. 2001, 34, 487–492. [Google Scholar] [CrossRef]
- Dupaix, R.B.; Boyce, M.C. Constitutive modeling of the finite strain behavior of amorphous polymers in and above the glass transition. Mech. Mater. 2007, 39, 39–52. [Google Scholar] [CrossRef]
- Laiarinandrasana, L.; Besson, J.; Lafarge, M.; Hochstetter, G. Temperature dependent mechanical behaviour of PVDF: Experiments and numerical modelling. Int. J. Plast. 2009, 25, 1301–1324. [Google Scholar] [CrossRef]
- Tashiro, K.; Kobayashi, M.; Tadokoro, H.; Fukada, E. Calculation of elastic and piezoelectric constants of polymer crystals by a point charge model: Application to poly(vinylidene fluoride) form I. Macromolecules 1980, 13, 691–698. [Google Scholar] [CrossRef]
- Nix, E.L.; Ward, I.M. The measurement of the shear piezoelectric coefficients of polyvinylidene fluoride. Ferroelectrics 1986, 67, 137–141. [Google Scholar] [CrossRef]
| α-PVDF [48] | 16.10 | 15.70 | 148.1 | 0.5 | 3.9 | 6.5 | 6.2 | 8 | 0.8 |
| β-PVDF [48] | 19.83 | 24.50 | 287.33 | 1.17 | 0.33 | 1.67 | 4.33 | 0.83 | 3.33 |
| BaTiO3 particles [21] | 166 | 166 | 162 | 43 | 43 | 43 | 77 | 78 | 78 |
| Parameter | Significance | Value | |
|---|---|---|---|
| Amorphous Phase | Glassy modulus | 3500 MPa | |
| Rubbery modulus | 1500 MPa | ||
| Glass transition temperature | −40.6 °C | ||
| Glass transition interval | 20 °C | ||
| Slope outside glass transition | −10 MPa/°C | ||
| Rubbery Poisson’s ratio | 0.4 | ||
| Phase transition | Reference strain-rate | 0.001/s | |
| Avrami exponent | 2.2 | ||
| Number density of nuclei | 3.88 × 109 (cm−3) | ||
| Interfacial debonding | Weibull parameter | 2 | |
| Weibull parameter | 25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mamache, F.E.; Mesbah, A.; Zaïri, F.; Vozniak, I. A Coupled Electro-Mechanical Homogenization-Based Model for PVDF-Based Piezo-Composites Considering α → β Phase Transition and Interfacial Damage. Polymers 2023, 15, 2994. https://doi.org/10.3390/polym15142994
Mamache FE, Mesbah A, Zaïri F, Vozniak I. A Coupled Electro-Mechanical Homogenization-Based Model for PVDF-Based Piezo-Composites Considering α → β Phase Transition and Interfacial Damage. Polymers. 2023; 15(14):2994. https://doi.org/10.3390/polym15142994
Chicago/Turabian StyleMamache, Fateh Enouar, Amar Mesbah, Fahmi Zaïri, and Iurii Vozniak. 2023. "A Coupled Electro-Mechanical Homogenization-Based Model for PVDF-Based Piezo-Composites Considering α → β Phase Transition and Interfacial Damage" Polymers 15, no. 14: 2994. https://doi.org/10.3390/polym15142994
APA StyleMamache, F. E., Mesbah, A., Zaïri, F., & Vozniak, I. (2023). A Coupled Electro-Mechanical Homogenization-Based Model for PVDF-Based Piezo-Composites Considering α → β Phase Transition and Interfacial Damage. Polymers, 15(14), 2994. https://doi.org/10.3390/polym15142994








