Finite Element Modeling of Debonding Failures in FRP-Strengthened Concrete Beams Using Cohesive Zone Model
Abstract
:1. Introduction
2. Development of FE Model
2.1. Material Properties and Constitutive Models
2.1.1. Concrete
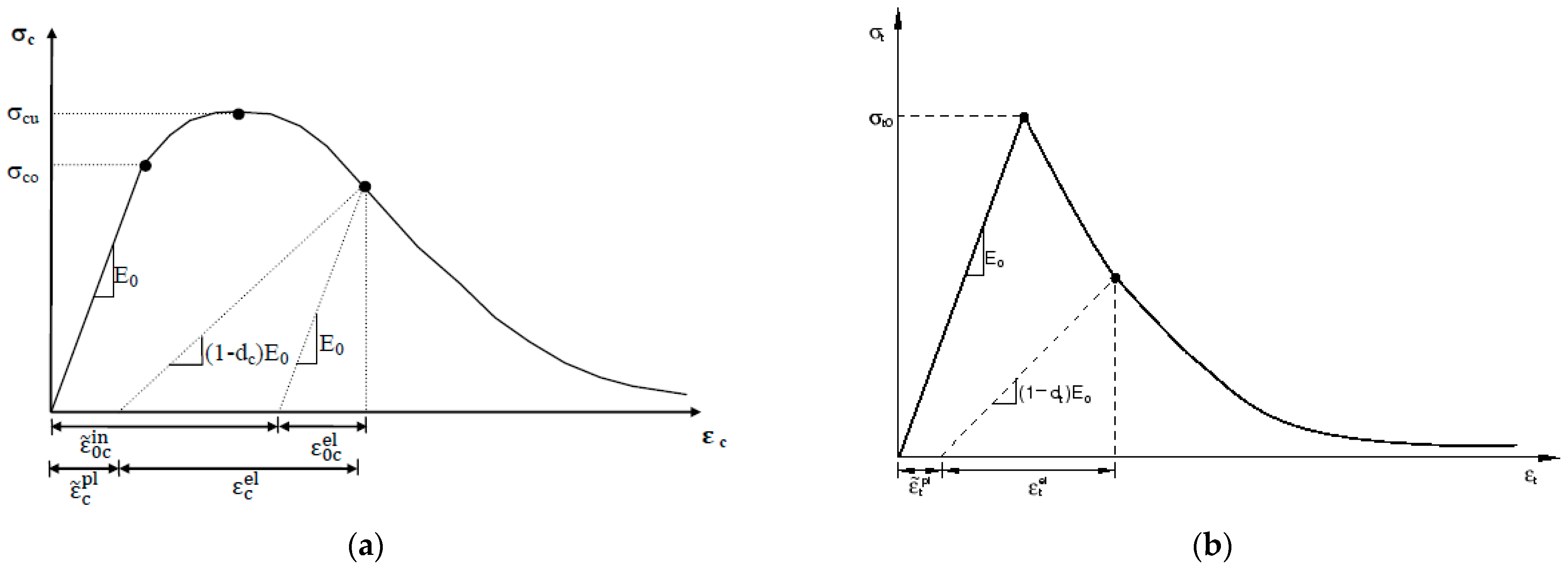
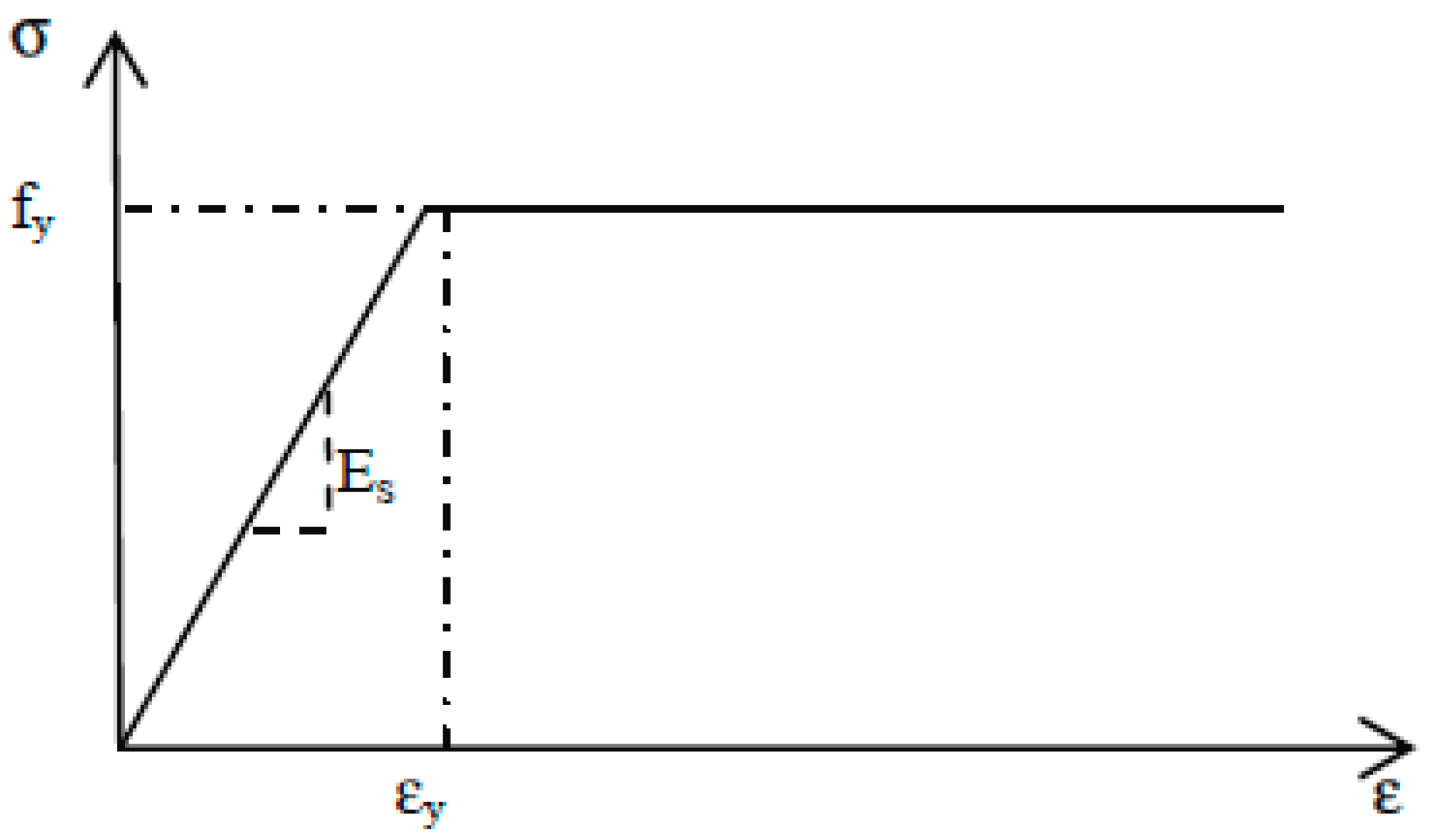
2.1.2. Steel Reinforcement
2.1.3. FRP Reinforcement
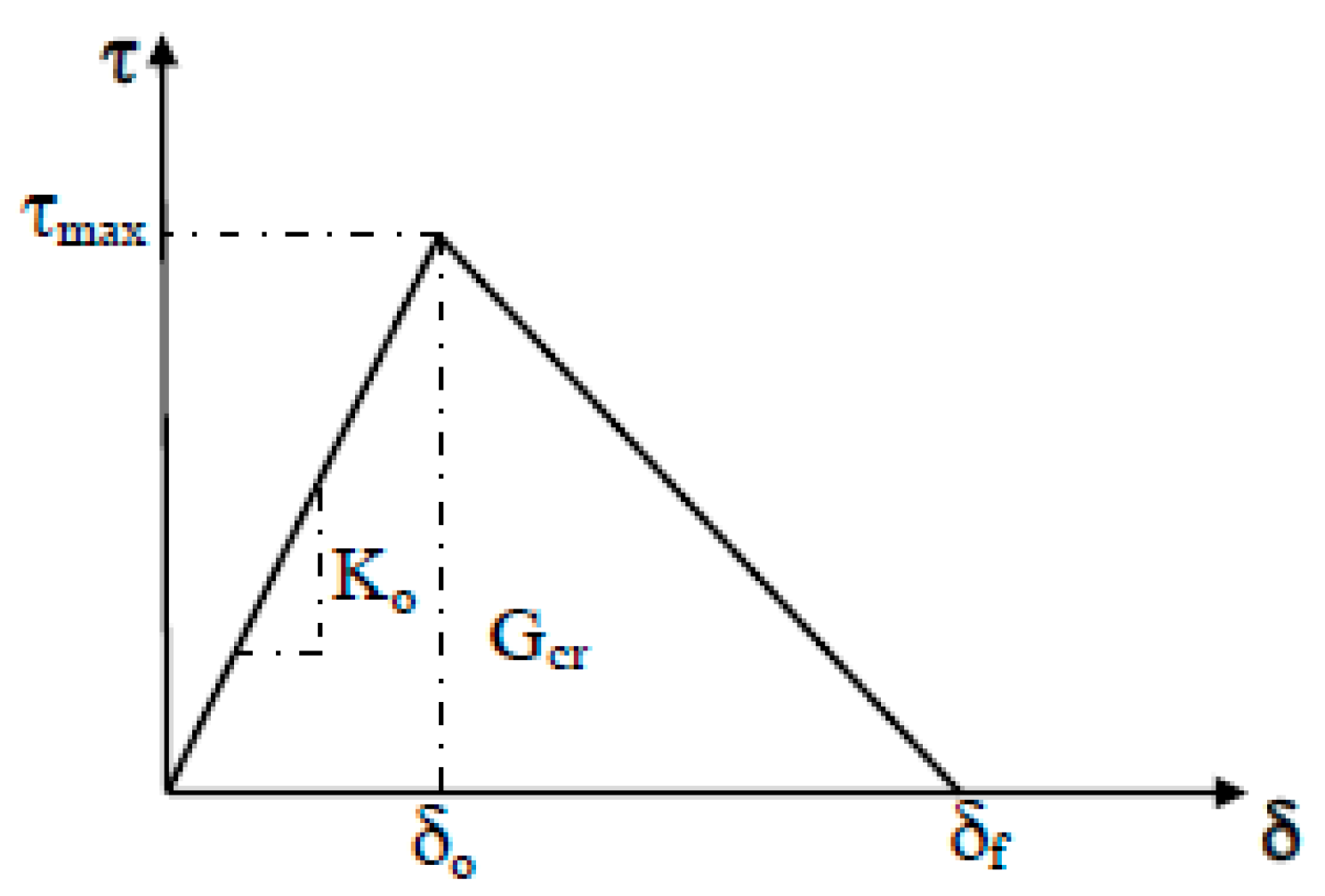
2.2. Modeling of Debonding Failures
2.2.1. Modeling of IC Debonding
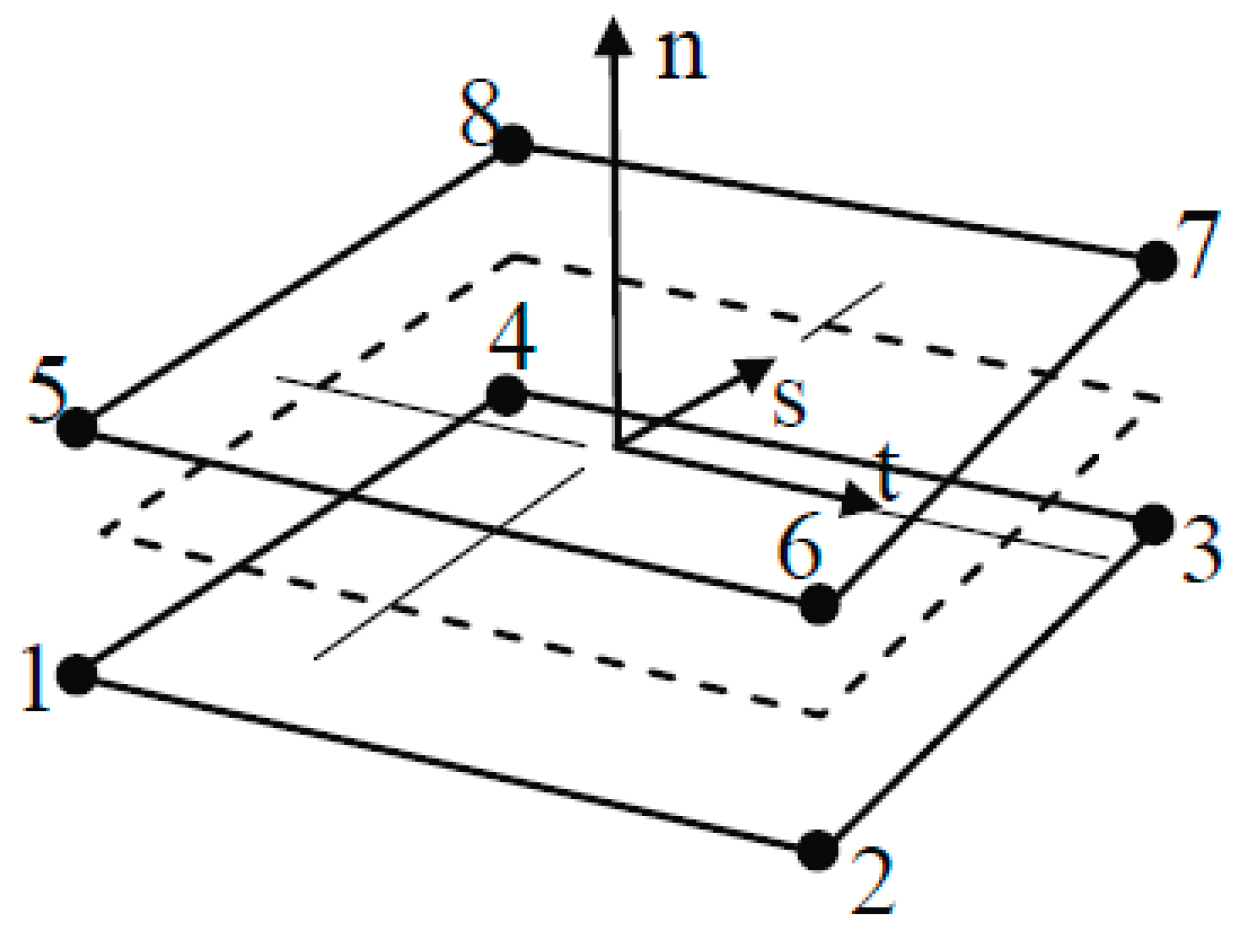
2.2.2. Modeling of CCS Debonding
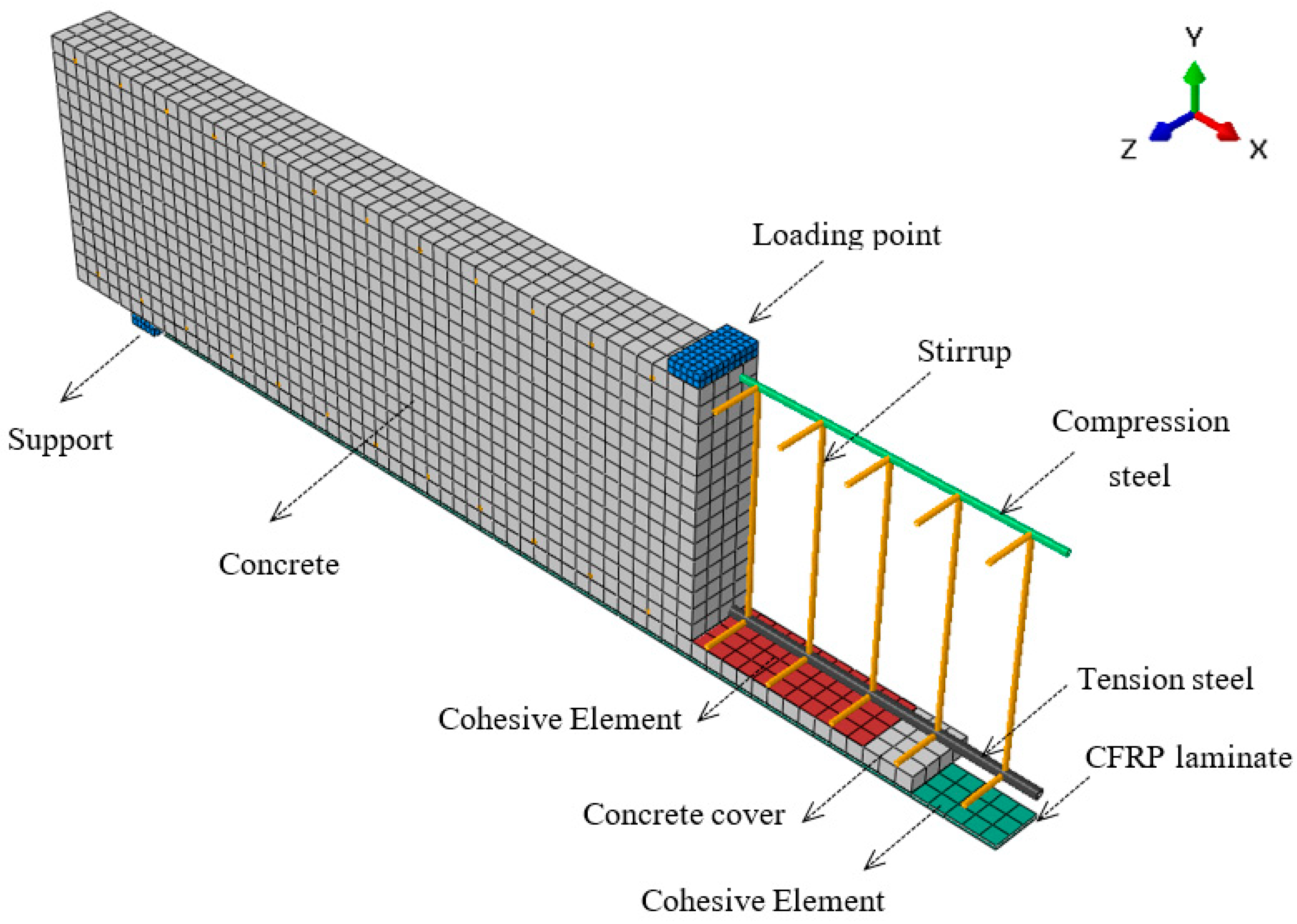
2.3. Model Geometry and Element Types
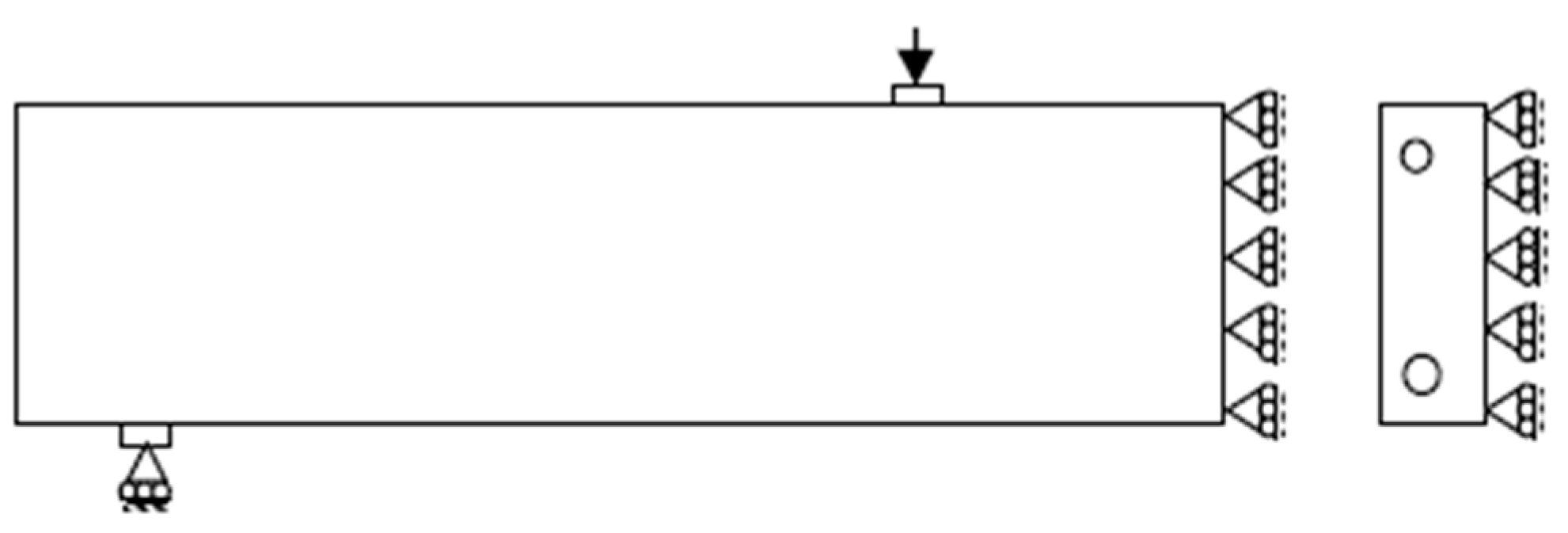
2.4. Mesh Size and Boundary Conditions
3. Model Calibration and Validation

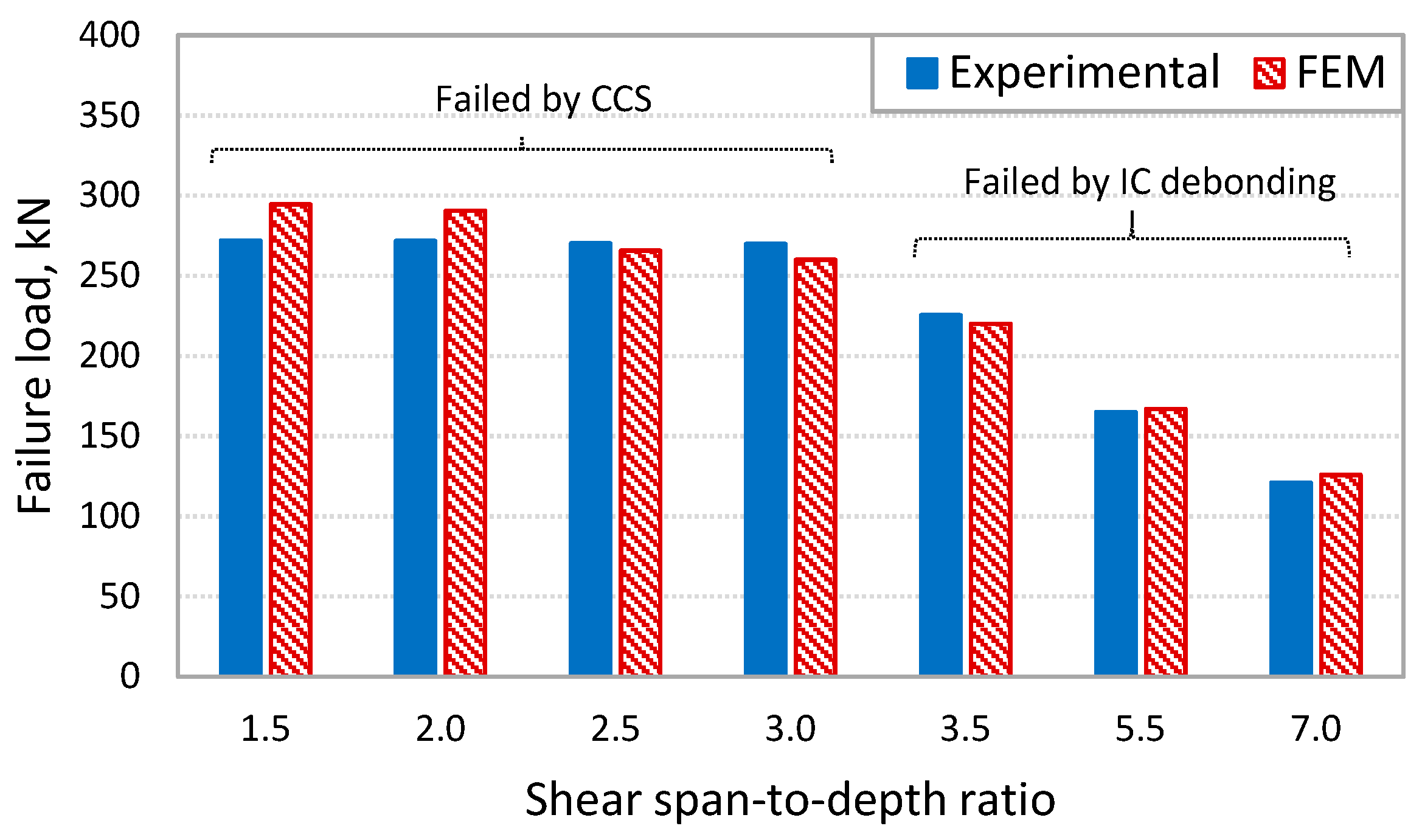
3.1. Ultimate Capacity and Mode of Failure
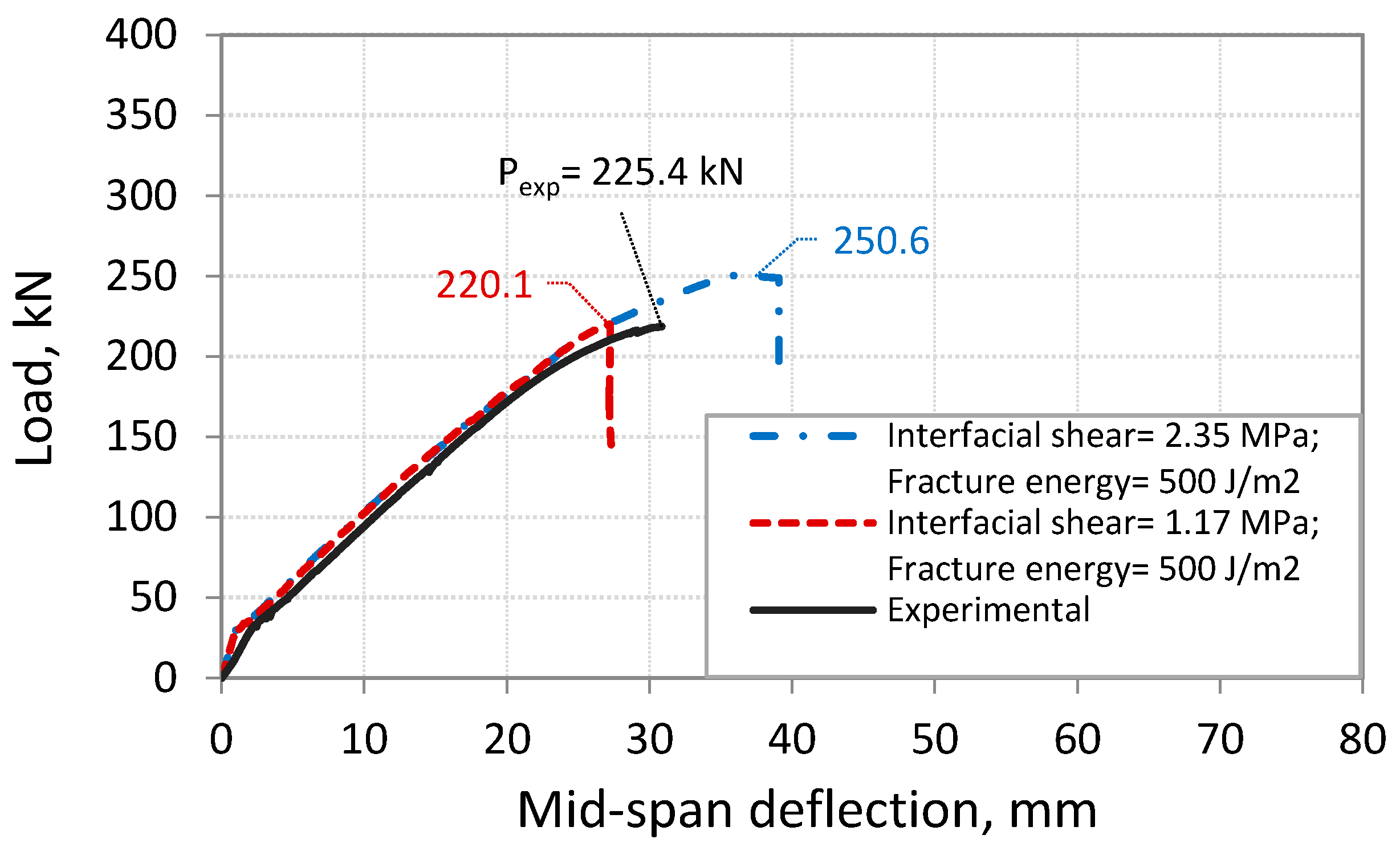
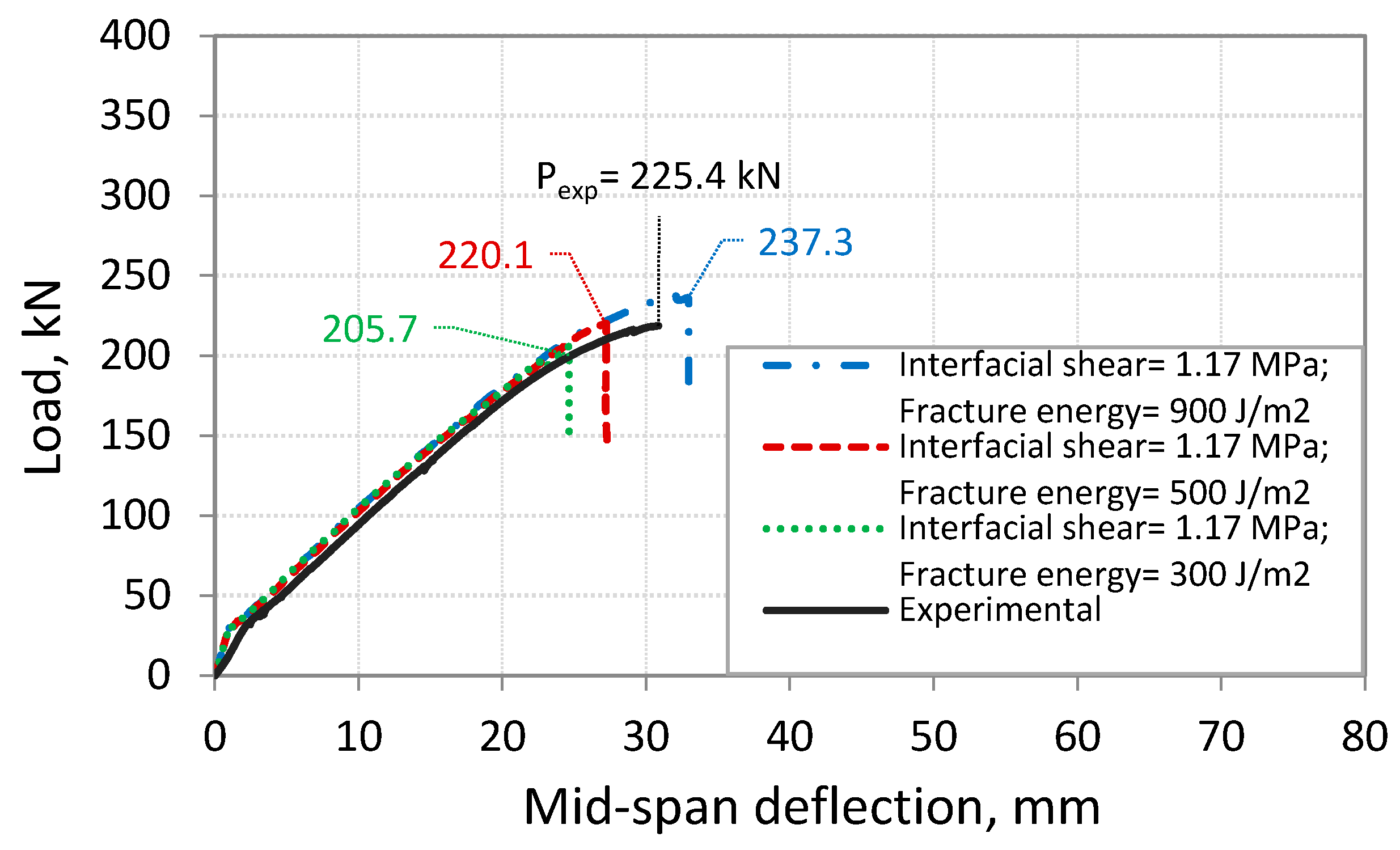
3.2. Load-Deflection Curves
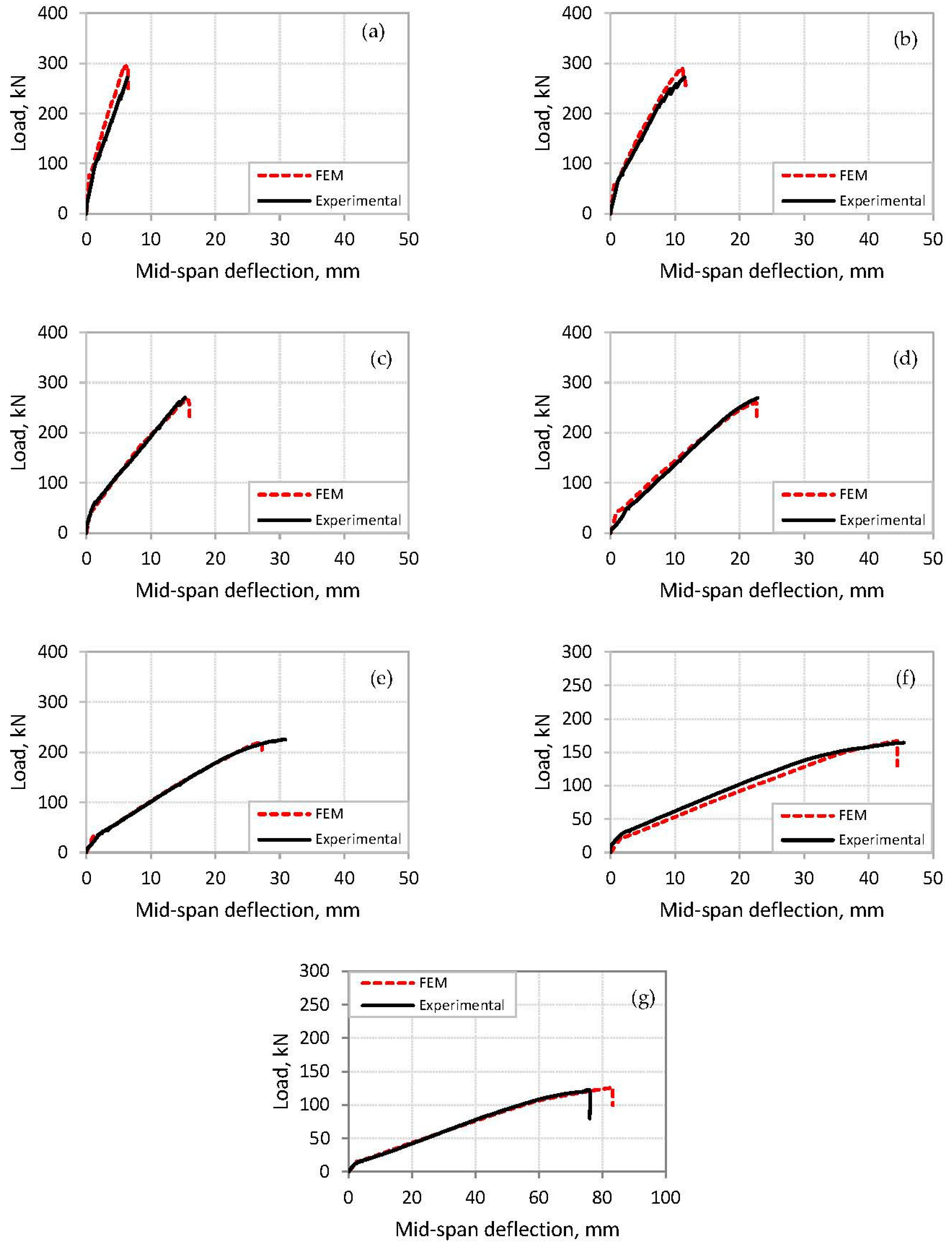
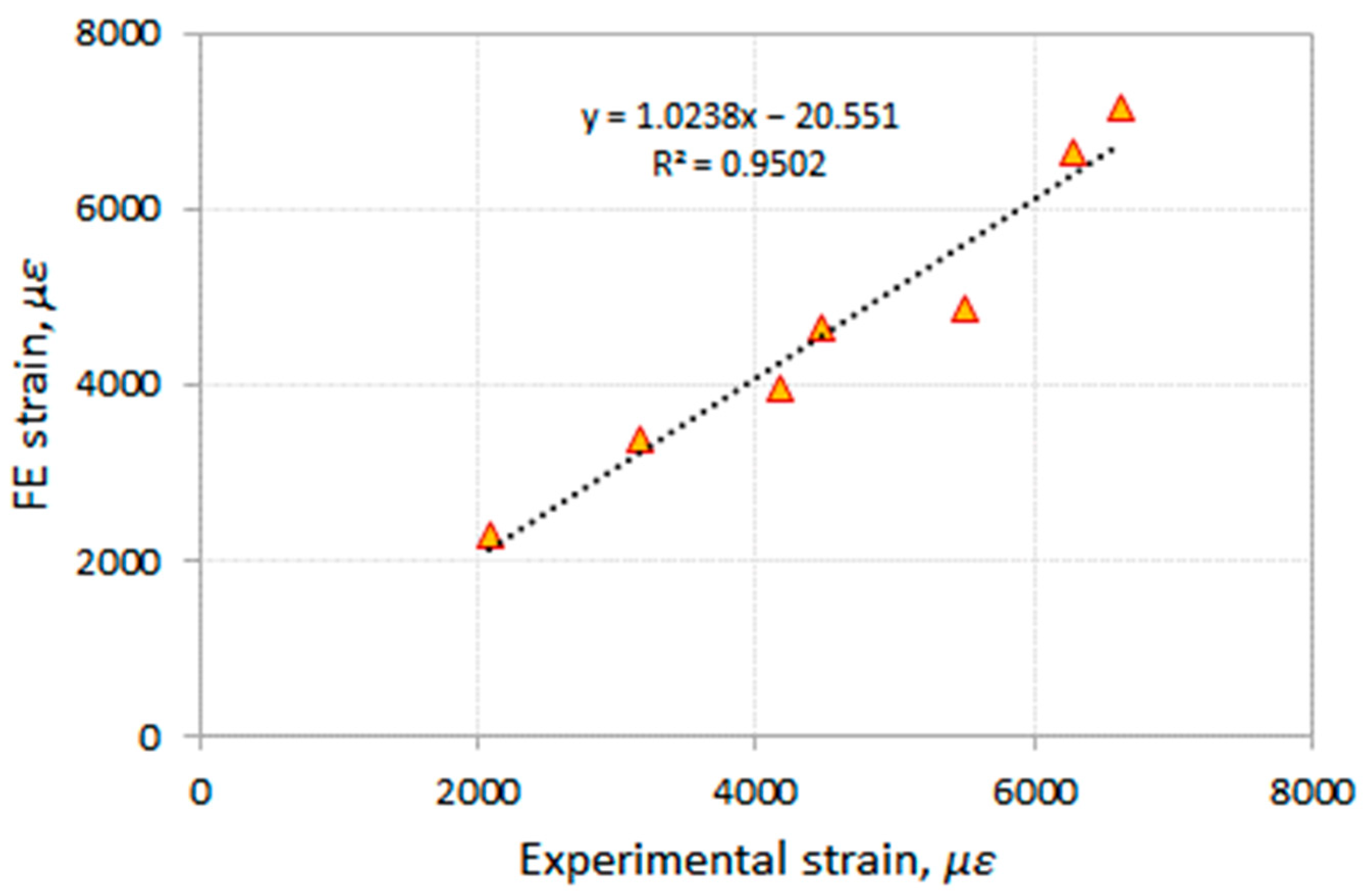
3.3. Strains in CFRP Reinforcement
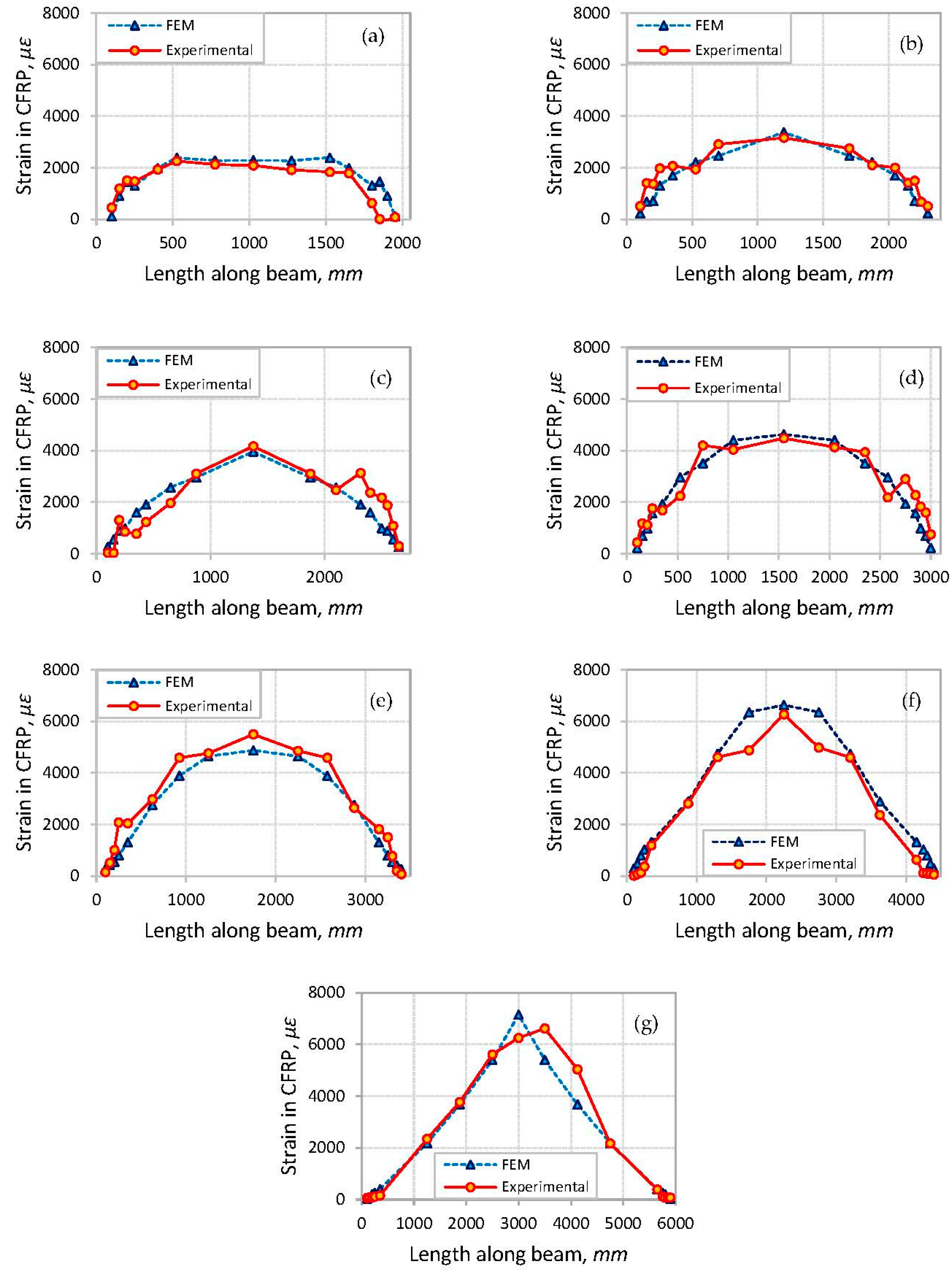
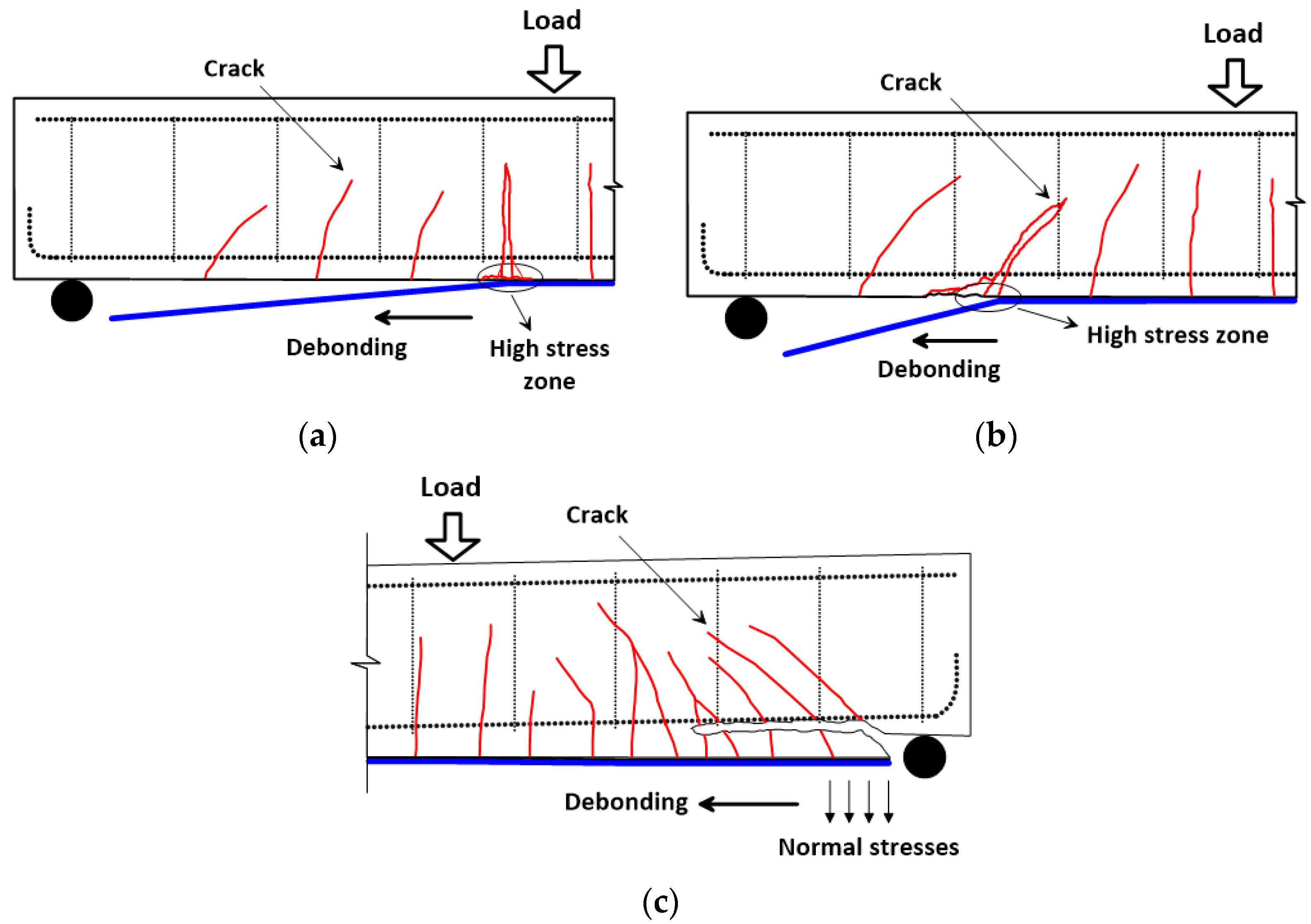
3.4. Crack Patterns

4. Parametric Study
4.1. Effect of Shear Span-to-Depth Ratio on Debonding Failure
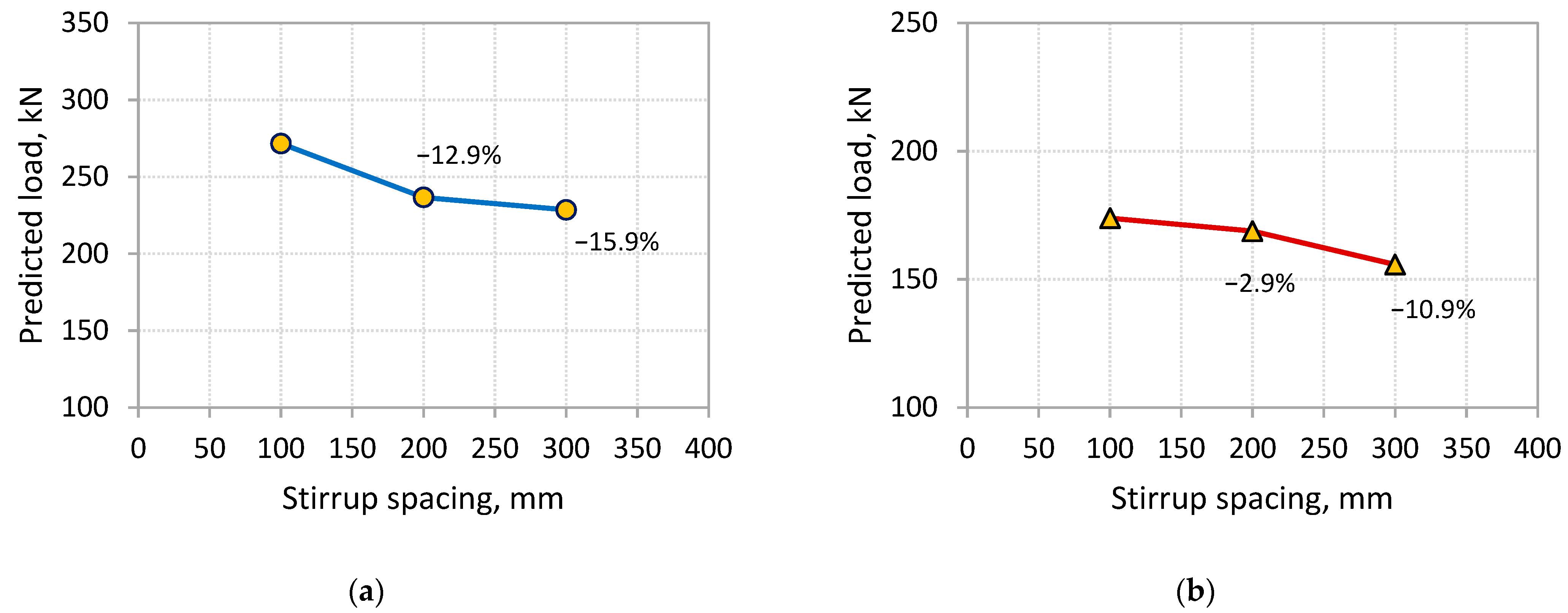
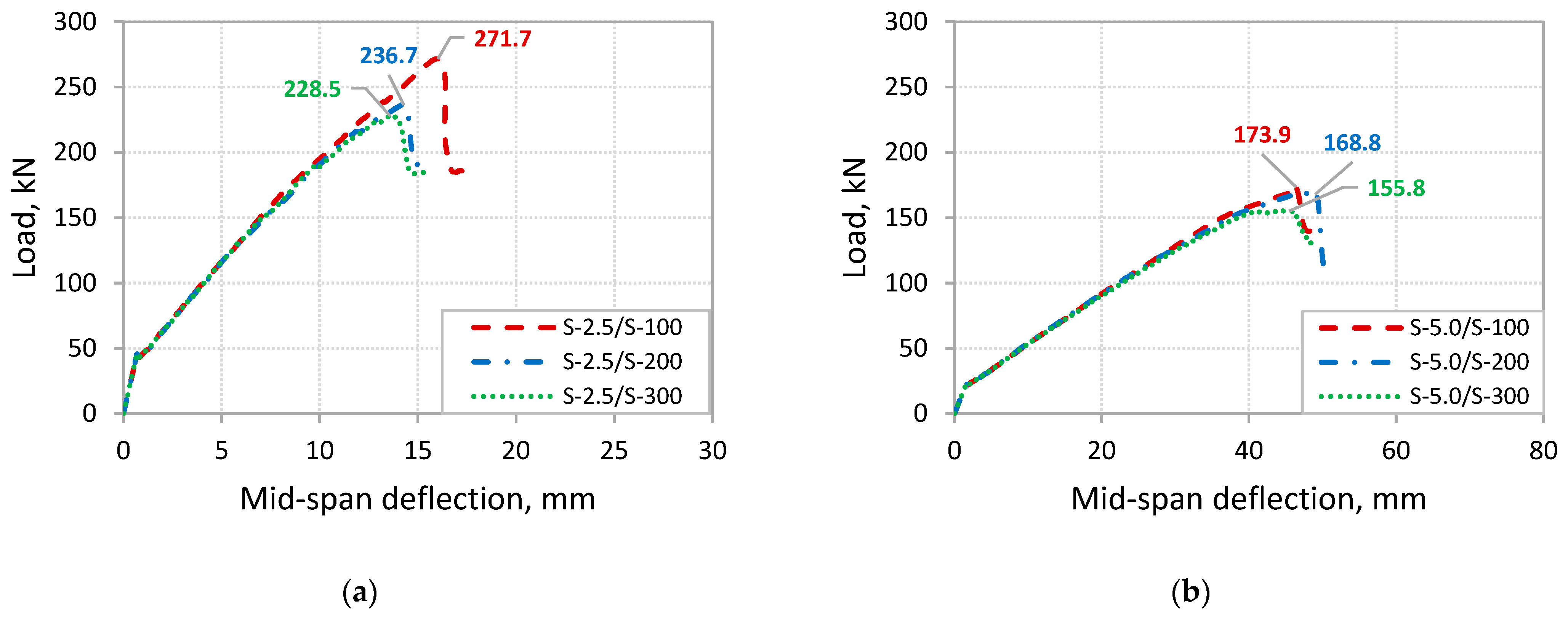
4.2. Effect of Steel Stirrups on Debonding Failure
5. Conclusions
- The developed FE model in this study simulates the flexural behavior and predicts the critical type of debonding failure (IC debonding and CCS failure) and the corresponding capacity at failure for the FRP-strengthened beam.
- The FE results were validated by comparisons with the experimental results for FRP-strengthened beams having a wide range of shear span-to-depth ratios. The comparisons have confirmed the capability of the developed FE model to distinguish between the two critical debonding failure modes in FRP-strengthened beams and to predict the failure loads in close agreement with the experimental values.
- A parametric study was conducted using the developed FE model in order to investigate the effect of shear span-to-depth ratio and the spacing of steel stirrups on the debonding failures in FRP-strengthened beams. The FE analysis showed the effect of shear span-to-depth ratio on the type of debonding failure for RC beams strengthened with CFRP laminates covering the entire span to the supports.
- The results of the FE analysis showed that increasing the spacing of stirrups causes a reduction in the load-carrying capacity at CCS failure. In contrast, a marginal reduction in the load-carrying capacity in the case of the beams that fail by IC debonding was found if the allowable spacing of stirrups specified by design codes is not exceeded. However, increasing the stirrup spacing beyond the codes’ limit causes a change in the location of the IC debonding from the middle of the beam (induced by flexural cracks) to the shear span initiated by flexural-shear cracks at a reduced load-carrying capacity.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xian, G.; Guo, R.; Li, C. Combined effects of sustained bending loading, water immersion and fiber hybrid mode on the mechanical properties of carbon/glass fiber reinforced polymer composite. Compos. Struct. 2022, 281, 115060. [Google Scholar] [CrossRef]
- Teng, J.G.; Smith, S.T.; Yao, J.; Chen, J.F. Intermediate crack-induced debonding in RC beams and slabs. Constr. Build. Mater. 2003, 17, 447–462. [Google Scholar] [CrossRef]
- Al-Negheimish, A.I.; El-Sayed, A.K.; Al-Zaid, R.A.; Shuraim, A.B.; Alhozaimy, A.M. Behavior of wide shallow RC beams strengthened with CFRP reinforcement. J. Compos. Constr. 2012, 16, 418–429. [Google Scholar] [CrossRef]
- Al-Zaid, R.Z.; Al-Negheimish, A.I.; Al-Saawani, M.A.; El-Sayed, A.K. Analytical study on RC beams strengthened for flexure with externally bonded FRP reinforcement. Compos. Part B 2012, 43, 129–141. [Google Scholar] [CrossRef]
- Al-Saawani, M.A.; El-Sayed, A.K.; Al-Negheimish, A.I. Effect of basic design parameters on IC debonding of CFRP-strengthened shallow RC beams. J. Reinf. Plast. Compos. 2015, 34, 1526–1539. [Google Scholar] [CrossRef]
- Al-Saawani, M.A.; El-Sayed, A.K.; Al-Negheimish, A.I. Effect of shear-span/depth ratio on debonding failures of FRP-strengthened RC beams. J. Build. Eng. 2020, 32, 101771. [Google Scholar] [CrossRef]
- Al-Zaid, R.A.; El-Sayed, A.K.; Al-Negheimish, A.I.; Shuraim, A.B. Strengthening of structurally damaged wide shallow RC beams using externally bonded CFRP plates. Lat. Am. J. Solids Struct. 2014, 11, 946–965. [Google Scholar] [CrossRef] [Green Version]
- Al-Negheimish, A.I.; El-Sayed, A.K.; Al-Saawani, M.A.; Alhozaimy, A.M. Effect of Stirrups on Plate End Debonding in Reinforced Concrete Beams Strengthened with Fiber Reinforced Polymers. Polymers 2021, 13, 3322. [Google Scholar] [CrossRef]
- Smith, S.T.; Teng, J.G. Shear-bending interaction in debonding failures of FRP-plated RC beams. Adv. Struct. Eng. 2003, 6, 183–199. [Google Scholar] [CrossRef]
- Teng, J.G.; Yao, J. Plate end debonding in FRP-plated RC beams I: Experiments. Eng. Struct. 2007, 29, 2457–2471. [Google Scholar] [CrossRef]
- El-Sayed, A.K.; Al-Saawani, M.A.; Al-Negheimish, A.I. Empirical shear based model for predicting plate end debonding in FRP strengthened RC beams. J. Civ. Eng. Manag. 2021, 27, 117–138. [Google Scholar] [CrossRef]
- Nour, A.; Massicotte, B.; Yildiz, E.; Koval, V. Finite element modelling of concrete structures reinforced with internal and external fibre-reinforced polymers. Can. J. Civ. Eng. 2007, 34, 340–354. [Google Scholar] [CrossRef]
- Elsanadedy, H.M.; Al-Salloum, Y.A.; Almusallam, T.H.; Alshenawy, A.O.; Abbas, H. Experimental and numerical study on FRP-upgraded RC beams with large rectangular web openings in shear zones. Constr. Build. Mater. 2019, 194, 322–343. [Google Scholar] [CrossRef]
- Barour, S.; Zergua, A. Finite element analysis of CFRP-externally strengthened reinforced concrete beams subjected to three-point bending. World J. Eng. 2019, 17, 183–202. [Google Scholar] [CrossRef]
- Yang, H.; Wu, Z.S.; Yoshizawa, H. Theoretical solutions on interfacial stress transfer of externally bonded steel/composite laminates. J. Struct. Mech. Earthq. Eng. 2001, 18, 27–39. [Google Scholar]
- Ebead, U.A.; Neale, K.W.; Bizindavyi, L. On the interfacial mechanics of FRP-strengthened concrete structures. FRP Compos. Can. J. Civ. Eng. 2004, 34, 367–377. [Google Scholar] [CrossRef]
- Sand, B.; Remlo, H. RC beams with externally bonded CFRP: Finite element modelling of delamination failure. In Doc. No. NTAS F2001-32; Interreg Nordkaotten Institute: Luleå, Sweden, 2001. [Google Scholar]
- Wong, R.S.Y.; Vecchio, F.J. Toward modeling of reinforced concrete members with externally bonded fibre-reinforced polymer composites. ACI Struct. J. 2003, 100, 47–55. [Google Scholar]
- Abdel Baky, H.M.; Ebead, U.A.; Masmoudi, R.; Neale, K.W. Analysis of the flexural response of FRP-strengthened concrete beams. In Advanced Composite Materials in Bridges and Structures; Canadian Society for Civil Engineering: Calgary, AL, Canada, 2004. [Google Scholar]
- Lu, X.Z.; Teng, J.G.; Ye, L.P.; Jiang, J.J. Bond-Slip models for FRP sheets/plates bonded to concrete. Eng. Struct. 2005, 27, 920–937. [Google Scholar] [CrossRef]
- Neale, K.W.; Ebead, U.A.; Baky, H.M.A.; Elsayed, W.E.; Godat, A. Analysis of the load-deformation behaviour and debonding for FRP-strengthened concrete structures. Adv. Struct. Eng. 2006, 9, 751–763. [Google Scholar] [CrossRef]
- Lu, X.Z.; Teng, J.G.; Ye, L.P.; Jiang, J.J. Intermediate crack debonding in FRP-strengthened RC beams: FE analysis and strength model. J. Compos. Constr. 2007, 11, 161–174. [Google Scholar] [CrossRef]
- Baky, H.A.; Ebead, U.A.; Neale, K.W. Flexural and interfacial behaviour of FRP-strengthened reinforced concrete beams. J. Compos. Constr. 2007, 11, 629–639. [Google Scholar] [CrossRef]
- Kotynia, R.; Baky, H.A.; Neale, K.W.; Ebead, U.A. Flexural strengthening of RC beams with externally bonded CFRP systems: Test results and 3D nonlinear FE analysis. J. Compos. Constr. 2008, 12, 190–201. [Google Scholar] [CrossRef]
- Pham, H.B.; Al-Mahaidi, R. Finite element modelling of RC beams retrofitted with CFRP fabrics. In Proceedings of the 7th International Symposium on Fiber-Reinforced Polymer Reinforcement for Concrete Structures, Kansas City, MO, USA, 6–9 November 2005; pp. 499–513. [Google Scholar]
- Reiner, J. A practical approach for the non-local simulation of progressive damage in quasi-isotropic fibre-reinforced composite laminates. Compos. Struct. 2021, 265, 113761. [Google Scholar] [CrossRef]
- Reiner, J.; Xu, X.; Zobeiry, N.; Vaziri, R.; Hallett, S.R.; Wisnom, M.R. Virtual characterization of nonlocal continuum damage model parameters using a high fidelity finite element model. Compos. Struct. 2021, 265, 113073. [Google Scholar] [CrossRef]
- Barbero, E.J. Finite Element Analysis of Composite Materials Using Ansys, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Hadjazi, K.; Sereir, Z.; Amziane, S. Cohesive zone model for the prediction of interfacial shear stresses in a composite-plate RC beam with an intermediate flexural crack. Compos. Struct. 2012, 94, 3574–3582. [Google Scholar] [CrossRef]
- Zidani, M.H.B.; Belakhdar, K.; Tounsi, A. Finite element analysis of initially damaged beams repaired with FRP plates. Compos. Struct. 2015, 134, 429–439. [Google Scholar] [CrossRef]
- Bennegadi, M.L.; Hadjazi, K.; Sereir, Z.; Amziane, S.; Mahi, B.E. General cohesive zone model for prediction of interfacial stresses induced by intermediate flexural crack of FRP-plated RC beams. Eng. Struct. 2016, 126, 147–157. [Google Scholar] [CrossRef]
- Shukri, A.A.; Shamsudin, M.F.; Ibrahim, Z.; Alengaram, U.J.; Hashim, H. Simulating intermediate crack debonding on RC beams strengthened with hybrid methods. Lat. Am. J. Solids. Struct. 2018, 15, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Razaqpur, A.G.; Lamberti, A.M.; Ascione, B.F. A nonlinear semi-analytical model for predicting debonding of FRP laminates from RC beams subjected to uniform or concentrated load. Constr. Build. Mater. 2020, 233, 117838. [Google Scholar] [CrossRef]
- Zhang, J.; Guo, R.; Li, S.; Zhao, S. Prediction of the IC debonding failure of FRP-strengthened RC beams based on the cohesive zone model. Lat. Am. J. Solids. Struct. 2020, 17, 1–29. [Google Scholar] [CrossRef]
- Supaviriyakit, T.; Pornpongsaroj, P.; Pimanmas, A. Finite element analysis of FRP-strengthened RC beams. Songklanakarin J. Sci. Technol. 2004, 26, 497–507. [Google Scholar]
- Zhang, S.; Teng, J.G. Finite element analysis of end cover separation in RC beams strengthened in flexure with FRP. Eng. Struct. 2014, 75, 550–560. [Google Scholar] [CrossRef]
- Sakr, M.A. Finite element modeling of debonding mechanisms in carbon fiber reinforced polymer-strengthened reinforced concrete continuous beams. Int. Fed. Struct. Conc. 2017, 19, 1002–1012. [Google Scholar] [CrossRef]
- Dassault Systemes Simulia Corp. ABAQUS Analysis User’s Manual; Dassault Systemes Simulia Corp.: Providence County, RI, USA, 2017. [Google Scholar]
- Carreira, D.J.; Chu, K. Stress-strain relationship for plain concrete in compression. ACI J. 1985, 82, 797–804. [Google Scholar]
- Hordijk, D.A. Local Approach to Fatigue of Concrete. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 1991. [Google Scholar]
- ACI (American Concrete Institute). Building Code Requirements for Structural Concrete; ACI318-19; ACI: Farmington Hills, MI, USA, 2019. [Google Scholar]
- CEB-FIP MC90, CEB-FIP Model Code; Thomas Telford: London, UK, 1990.
- Rots, J.G. Computational Modeling of Concrete Fracture. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 1998. [Google Scholar]
- Bažant, Z.P.; Oh, B.H. Crack band theory for fracture of concrete. Mater. Struct. 1983, 16, 155–177. [Google Scholar] [CrossRef] [Green Version]
- Obaidat, Y.T.; Heyden, S.; Dahlblom, O. The effect of CFRP and CFRP/concrete interface model when modeling retrofitted RC beams with FEM. Comput. Struct. 2010, 92, 1391–1398. [Google Scholar] [CrossRef]
- Obaidat, Y.T.; Heyden, S.; Dahlblom, O. Evaluation of Parameters of Bond Action between FRP and Concrete. J. Compos. Constr. 2013, 17, 626–635. [Google Scholar] [CrossRef]
- Al-Saawani, M. Mitigation of Plate-End Debonding in Flexural FRP-Strengthened RC Beams. Ph.D. Thesis, King Saud University, Riyadh, Saudi Arabia, 2021. [Google Scholar]
- Lubliner, J.; Oliver, J.; Oller, S.; Oñate, E. A plastic-damage model for concrete. Int. J. Solids Struct. 1989, 25, 299–329. [Google Scholar] [CrossRef]

| Parameter | Dilation Angle (Ψ) | Eccentricity (ϵ) | fb0/fc0 | K | Viscosity Parameter |
|---|---|---|---|---|---|
| Value | 30° | 0.1 | 1.16 | 0.667 | 0.0001 |
| Parameter | K0 (MPa/mm) | τmax (MPa) | Gcr (N/mm) | βw |
|---|---|---|---|---|
| Value |
| Beam | Clear Span, L (mm) | Shear Span, av (mm) | Shear Span-to-Depth Ratio, av/ds |
|---|---|---|---|
| S-1.5 | 2050 | 525 | 1.5 |
| S-2.0 | 2400 | 700 | 2.0 |
| S-2.5 | 2750 | 875 | 2.5 |
| S-3.0 | 3100 | 1050 | 3.0 |
| S-3.5 | 3500 | 1250 | 3.5 |
| S-5.0 | 4500 | 1750 | 5.0 |
| S-7.0 | 6000 | 2500 | 7.0 |
| Property | Elastic Modulus (GPa) | Poisson’s Ratio | Yield Stress (MPa) |
|---|---|---|---|
| Tension steel | 205 | 0.3 | 550 |
| Compression steel | 200 | 500 | |
| Stirrups | 200 | 350 |
| Parameter | E1 (GPa) | E2 (GPa) | ν12 | G12 (GPa) | G13 (GPa) | G23 (GPa) | fu (MPa) |
|---|---|---|---|---|---|---|---|
| Value | 95.8 | 6.143 | 0.29 | 1.55 | 1.22 | 1.22 | 984.6 |
| Beam | Experimental Results | FE Analysis Results | Pu,exp/Pu,FEM | 𝛿u,exp/𝛿u,FEM | ||||
|---|---|---|---|---|---|---|---|---|
| Pu,exp (kN) | 𝛿u,exp (mm) | Mode of Failure * | Pu,FEM (kN) | 𝛿u,FEM (mm) | Mode of Failure * | |||
| S-1.5 | 271.9 | 6.4 | CCS | 294.5 | 6.2 | CCS | 0.92 | 1.03 |
| S-2.0 | 271.7 | 11.4 | CCS | 290.5 | 10.9 | CCS | 0.94 | 1.05 |
| S-2.5 | 270.2 | 15.3 | CCS | 265.7 | 15.7 | CCS | 1.02 | 0.97 |
| S-3.0 | 269.8 | 22.8 | CCS | 260.0 | 22.5 | CCS | 1.04 | 1.01 |
| S-3.5 | 225.4 | 30.9 | ICD | 220.1 | 27.2 | ICD | 1.02 | 1.14 |
| S-5.0 | 165.1 | 45.4 | ICD | 167.0 | 44.5 | ICD | 0.99 | 1.02 |
| S-7.0 | 121.0 | 76.0 | ICD | 125.7 | 83.2 | ICD | 0.96 | 0.91 |
| Beam | Shear Span-to-Depth Ratio | Sv (mm) | Pu,FEM (kN) | ΔPu,FEM (kN) | Mode of Failure * |
|---|---|---|---|---|---|
| S-2.5/S-100 | 2.5 | 100 | 271.7 | - | CCS |
| S-2.5/S-200 | 200 | 236.7 | −12.9% | CCS | |
| S-2.5/S-300 | 300 | 228.5 | −15.9% | CCS | |
| S-5.0/S-100 | 5.0 | 100 | 173.9 | - | ICD |
| S-5.0/S-200 | 200 | 168.8 | −2.9% | ICD | |
| S-5.0/S-300 | 300 | 155.8 | −10.4% | ICD |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Saawani, M.A.; Al-Negheimish, A.I.; El-Sayed, A.K.; Alhozaimy, A.M. Finite Element Modeling of Debonding Failures in FRP-Strengthened Concrete Beams Using Cohesive Zone Model. Polymers 2022, 14, 1889. https://doi.org/10.3390/polym14091889
Al-Saawani MA, Al-Negheimish AI, El-Sayed AK, Alhozaimy AM. Finite Element Modeling of Debonding Failures in FRP-Strengthened Concrete Beams Using Cohesive Zone Model. Polymers. 2022; 14(9):1889. https://doi.org/10.3390/polym14091889
Chicago/Turabian StyleAl-Saawani, Mohammed A., Abdulaziz I. Al-Negheimish, Ahmed K. El-Sayed, and Abdulrahman M. Alhozaimy. 2022. "Finite Element Modeling of Debonding Failures in FRP-Strengthened Concrete Beams Using Cohesive Zone Model" Polymers 14, no. 9: 1889. https://doi.org/10.3390/polym14091889
APA StyleAl-Saawani, M. A., Al-Negheimish, A. I., El-Sayed, A. K., & Alhozaimy, A. M. (2022). Finite Element Modeling of Debonding Failures in FRP-Strengthened Concrete Beams Using Cohesive Zone Model. Polymers, 14(9), 1889. https://doi.org/10.3390/polym14091889






